Contributions to the theory of Ramanujan's function τ(n) and similar arithmetical functions
II. The order of the Fourier coefficients of integral modular forms
Published online by Cambridge University Press: 24 October 2008
Extract
Suppose that
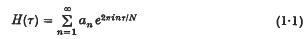
is an integral modular form of dimensions −κ, where κ > 0, and Stufe N, which vanishes at all the rational cusps of the fundamental region, and which is absolutely convergent for 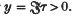 Then
Then
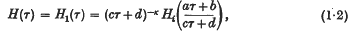
where a, b, c, d are integers such that ad − bc = 1.
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 35 , Issue 3 , July 1939 , pp. 357 - 372
- Copyright
- Copyright © Cambridge Philosophical Society 1939
References
* Cf. for example, Klein, F. and Fricke, R., Elliptische Modulfunktionen, 1 (Leipzig, 1890), 395–7.Google Scholar
* Salié, H., “Zur Abschätzung der Fourierkoeffizienten ganzer Modulformen”, Math. Z. 36 (1931), 263–78.CrossRefGoogle Scholar
† Davenport, H., “On certain exponential sums”, J. reine angew. Math. 169 (1932), 158–76.Google Scholar
‡ Hauptkongruenzgruppe.
* Cf. Landau, E., Primzahlen, 1 (Leipzig, 1909), 483–92.Google Scholar
† This may be proved in several ways; cf., for example Hecke, E., “Über Modulfunktionen und die Dirichletschen Reihen mit Eulerscher Produktentwicklung I”, Math. Ann. 114 (1937), 1–28 (Satz 5).CrossRefGoogle Scholar
* Cf. for example E. Hecke, loc. cit., Satz 7.
† By the Wiener-Ikehara theorem we can deduce at once from Theorem 3 that
See Bochner, S., “Ein Satz von Landau und Ikehara”, Math. Z. 37 (1933), 1–9.CrossRefGoogle Scholar
‡ Landau, E., “Über die Anzahl der Gitterpunkte in gewissen Bereichen. II”, Nachr. Ges. Wiss. Göttingen (1915), pp. 209–43.Google Scholar
* | αγ, δ (n)| is not dependent on α, β.
† When (m, n)>1, (m, n, N) = 1, we denote by f m n (s) the function f γ,δ(s), where γ ≡ m, δ ≡ n (mod N), (γ, δ) = 1.
* This is trivial when ![]() It is true also for
It is true also for ![]() since Landau's theorem can be extended to show that
since Landau's theorem can be extended to show that
for any real α > − β, where R(a, x) is the sum of the residues of ![]() in the strip
in the strip ![]()
I write k′ where Landau has k to avoid confusion with the dimension − k.
- 196
- Cited by

