Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Adell, J. A.
and
de la Cal, J.
1996.
Bernstein-type operators diminish the φ-variation.
Constructive Approximation,
Vol. 12,
Issue. 4,
p.
489.
Odell, Edward
and
Tylli, Hans-Olav
2004.
Weakly compact approximation in Banach spaces.
Transactions of the American Mathematical Society,
Vol. 357,
Issue. 3,
p.
1125.
Blanco, A.
and
Grønbæk, N.
2009.
Amenability of algebras of approximable operators.
Israel Journal of Mathematics,
Vol. 171,
Issue. 1,
p.
127.


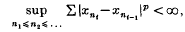
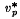 is of cotype 2 if
is of cotype 2 if 