Hostname: page-component-76fb5796d-22dnz Total loading time: 0 Render date: 2024-04-29T08:50:01.440Z Has data issue: false hasContentIssue false
  • English
  • Français

The equation A(t, u(t))′ + B(t, u(t)) = 0

Published online by Cambridge University Press:  24 October 2008

Bruce Calvert
Bruce Calvert
Affiliation:
Department of Mathematics, University of Auckland, Auckland, New Zealand
Get access Rights & Permissions [Opens in a new window]

Extract

The initial value problem for the equation

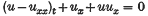
has been studied recently as a model for long waves in nonlinear dispersive systems. Benjamin, Bona and Mahony (2) introduced this equation as an alternative to the KdV equation of Korteweg-de Vries. Hence, it is referred to as the BBM equation. They studied solutions u(x, t) of the BBM equation for t ≥ 0 and x∈(− ∞, ∞), satisfying u(x, 0) = g(x). Bona and Bryant(1) carried through the study of the BBM equation for t ≥ 0 and x ∈ [0, ∞), satisfying u(x, 0) = g(x) and u(0, t) = h(t). The aim of this paper is to study the equation

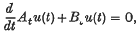
where At and Bt are mappings defined on subsets of Banach spaces, especially when At is a second order elliptic operator and B is a differential operator of lower order, defined on an unbounded subset Ω of .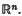

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 79 , Issue 3 , May 1976 , pp. 545 - 561
Copyright
Copyright © Cambridge Philosophical Society 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bona, J. L. and Bryant, P. J.A mathematical model for long waves generated by wave-makers in non-linear dispersive systems. Proc. Cambridge Philos. Soc. 73 (1973), 391–405.CrossRefGoogle Scholar
(2)Benjamin, T. B., Bona, J. L. and Mahony, J. J.Model equations for long waves in nonlinear dispersive systems. Philos. Trans. Roy. Soc. London, Ser. A 272 (1972), 47–78.Google Scholar
(3)BréZis, H.Opérateurs Maximaux Monotones et Semi-groupes de Contractions dans les Espaces de Hilbert. North Holland (Amsterdam, 1973).Google Scholar
(4)Brézis, H.On some degenerate nonlinear parabolic equations, Nonlinear Functional Analysis. Proc. Symp. Pure Math. 18 (1) A.M.S., 1970, 28–38.CrossRefGoogle Scholar
(5)Damlamian, A.Résolution d'une équation différentielle hyperbolique non linéaire par une méthode d'évolution avec normes variables. C.R. Acad. Sci. Paris 277 (1973), Série A 525–527.Google Scholar
(6)Day, M. M.Uniform convexity III. Bull. Amer. Math. Soc. 49 (1943), 745–750.CrossRefGoogle Scholar
(7)Krasnosel'skii, M. A.Topological Methods in the Theory of Nonlinear Integral Equations. MacMillan (New York, 1964) (Topologicheskiye metody v teariyi nelineinykh integral'-nykh uravnenii. Gostekhteoretizdat (Moscow, 1956)).Google Scholar
(8)Ladyzhenskaya, O. A. and Ural'tseva, N.Linear and Quasilinear Elliptic Equations, Academic Press (New York, London, 1968). (Lineynyyeskrazilineynyye uravneniya ellipticheskogo tipa. Nauka Press (Moscow, 1964)).Google Scholar
(9)Martin, R. H.Differential equations on closed subsets of a Bach space. Trans. Amer. Math. Soc. 179 (1973), 399–414.CrossRefGoogle Scholar
(10)Ricciardi, P. and Tubaro, L.Local existence for differential equations in Barach space. Boll. Un. Mat. Ital. 4 (8) (1973), 306–316.Google Scholar
(11)Brill, H. Cauchy Probleme für nichtlineare parabolische und pseudoparabolische Gleichungen. (Dissertation. Ruhr-Universität Bochum, Germany, 12 1974.)Google Scholar