Hostname: page-component-7dd5485656-bt4hw Total loading time: 0 Render date: 2025-10-31T02:09:17.579Z Has data issue: false hasContentIssue false
  • English
  • Français

Extension of normal functionals on W*-tensor products

Published online by Cambridge University Press:  24 October 2008

Simon Wassermann
Simon Wassermann
Affiliation:
University of Liverpool
Get access Rights & Permissions [Opens in a new window]

Extract

A deep result in the theory of W*-tensor products, the Commutation theorem, states that if M and N are W*-algebras faithfully represented as von Neumann algebras on the Hilbert spaces H and K, respectively, then the commutant 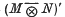in L(H ⊗ K) of the W*-tensor product of M and N coincides with the W*-tensor product 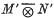of M′ and N′. Although special cases of this theorem were established successively by Misonou (2) and Sakai (3), the validity of the general result remained conjectural until the advent of the Tomita-Takesaki theory of Modular Hilbert algebras (6). As formulated, the Commutation theorem is a spatial result; that is, the W*-algebras in its statement are taken to act on specific Hilbert spaces. Not surprisingly, therefore, known proofs rely heavily on techniques of representation theory.

Information

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 78 , Issue 2 , September 1975 , pp. 301 - 307
Copyright
Copyright © Cambridge Philosophical Society 1975

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

(1)Grotblndieck, A. Produits tensoriels topologiques et espaces nucléaires, chap. I. Mem. Amer. Math. Soc. 16 (1955).CrossRefGoogle Scholar
(2)Misonou, Y.On the direct product of W*-algebras. Tôhoku Math. J. 6 (1954), 190–204.CrossRefGoogle Scholar
(3)Sakai, S.On the tensor product of W*-algebras. Amer. J. Math. 90 (1968), 335–341.CrossRefGoogle Scholar
(4)Sakai, S.C*-algebras and W*-algebras (Berlin, Springer-Verlag, 1971).Google Scholar
(5)Takesaki, M.On the cross-norm of the direct product of C*-algebras. Tôhoku Math. J. 16 (1964), 111–122.CrossRefGoogle Scholar
(6)Takesaki, M.Tomita's theory of Modular Hilbert algebras. Lecture notes no. 128 (Berlin, Springer-Verlag, 1970).Google Scholar
(7)Tomiyama, , Tensor products and projections of norm one in von Neumann algebras. Seminar notes of the Mathematical Institute, Copenhagen University, 1970.Google Scholar