No CrossRef data available.
A family of elliptic curves and cyclic cubic field extensions*
Published online by Cambridge University Press: 24 October 2008
Extract
Let K be a field with char K ≡ 2,3. We consider the problem of finding rational points over K on the family of elliptic curves Fλ, given in homogeneous coordinates (over 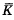 ) by
) by
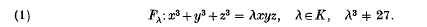
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 96 , Issue 1 , July 1984 , pp. 39 - 43
- Copyright
- Copyright © Cambridge Philosophical Society 1984
References
[3] Dofs, E.. On some classes of homogeneous ternary cubic diophantine equations. Ark. Mat. 13 (1975), 29–72.CrossRefGoogle Scholar
[4] Hubwitz, A.. Über ternare diophantische Gleichungen dritten Grades. Math. Werke, 2 (Birk-hauser, 1933), 446–468.Google Scholar
[5] Milnor, J. and Stasheff, J.. Characteristic classes. Annals of Math. Studies, vol. 76 (Princeton University Press, 1974).CrossRefGoogle Scholar
[7] Mordell, L.. On the rational solutions of the indeterminate equations of the 3rd and 4th degree. Proc. Cambridge Philos. Soc. 21 (1922), 179–192.Google Scholar
[8] Mordell, L.. The diophantine equation x3 + y3 + z3 + kxyz = 0. Colloque sur la thiorie des nombres (Bruxelles, 1955), 67–76.Google Scholar
[9] Thomas, E. and Vasqtjez, A.. Diophantine equations arising from cubic number fields. J. Number Theory 13 (1981), 398–414.CrossRefGoogle Scholar
[10] Weil, A.. L'arithmetique sur les courbes algébriqes. Acta Math. 52 (1929), 281–315.Google Scholar

