Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Drury, S. W.
and
Marshall, B. P.
1987.
Fourier restriction theorems for degenerate curves.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 101,
Issue. 3,
p.
541.
Marshall, B. P.
1988.
Decay rates of Fourier transforms of curves.
Transactions of the American Mathematical Society,
Vol. 310,
Issue. 1,
p.
115.
Wainger, Stephen
1989.
Harmonic Analysis and Partial Differential Equations.
Vol. 1384,
Issue. ,
p.
91.
Guo, Kanghui
1989.
On the p-approximate property for hypersurfaces of ℝn.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 105,
Issue. 3,
p.
503.
Drury, S. W.
1990.
Degenerate curves and harmonic analysis.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 108,
Issue. 1,
p.
89.
Oberlin, Daniel M.
2003.
Affine dimension: Measuring the vestiges of curvature.
Michigan Mathematical Journal,
Vol. 51,
Issue. 1,
Bak, Jong-Guk
Lee, Jungjin
and
Lee, Sanghyuk
2007.
Weighted restriction theorems for space curves.
Journal of Mathematical Analysis and Applications,
Vol. 334,
Issue. 2,
p.
1232.
BAK, JONG-GUK
OBERLIN, DANIEL M.
and
SEEGER, ANDREAS
2008.
RESTRICTION OF FOURIER TRANSFORMS TO CURVES II: SOME CLASSES WITH VANISHING TORSION.
Journal of the Australian Mathematical Society,
Vol. 85,
Issue. 1,
p.
1.
Dendrinos, Spyridon
and
Wright, James
2008.
Fourier restriction, polynomial curves and a geometric inequality.
Comptes Rendus. Mathématique,
Vol. 346,
Issue. 1-2,
p.
45.
Dendrinos, Spyridon
Laghi, Norberto
and
Wright, James
2009.
Universal Lp improving for averages along polynomial curves in low dimensions.
Journal of Functional Analysis,
Vol. 257,
Issue. 5,
p.
1355.
Oberlin, Daniel
2009.
A uniform estimate for Fourier restriction to simple curves.
Proceedings of the American Mathematical Society,
Vol. 137,
Issue. 12,
p.
4227.
Oberlin, Daniel M.
2010.
Convolution with measures on flat curves in low dimensions.
Journal of Functional Analysis,
Vol. 259,
Issue. 7,
p.
1799.
Stovall, Betsy
2010.
Endpoint Lp→Lq bounds for integration along certain polynomial curves.
Journal of Functional Analysis,
Vol. 259,
Issue. 12,
p.
3205.
Dendrinos, Spyridon
Folch-Gabayet, Magali
and
Wright, James
2010.
An affine-invariant inequality for rational functions and applications in harmonic analysis.
Proceedings of the Edinburgh Mathematical Society,
Vol. 53,
Issue. 3,
p.
639.
Dendrinos, Spyridon
and
Stovall, Betsy
2012.
Uniform estimates for the X-ray transform restricted to polynomial curves.
Journal of Functional Analysis,
Vol. 262,
Issue. 12,
p.
4986.
Gressman, Philip T.
2013.
Uniform Sublevel Radon-like Inequalities.
Journal of Geometric Analysis,
Vol. 23,
Issue. 2,
p.
611.
Stovall, Betsy
2014.
UniformLp-improving for weighted averages on curves.
Analysis & PDE,
Vol. 7,
Issue. 5,
p.
1109.
Grafakos, Loukas
2014.
Modern Fourier Analysis.
Vol. 250,
Issue. ,
p.
327.
Ham, Seheon
and
Lee, Sanghyuk
2014.
Restriction estimates for space curves with respect to general measures.
Advances in Mathematics,
Vol. 254,
Issue. ,
p.
251.
Bak, Jong-Guk
and
Ham, Seheon
2014.
Restriction of the Fourier transform to some complex curves.
Journal of Mathematical Analysis and Applications,
Vol. 409,
Issue. 2,
p.
1107.

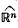 . One may ask whether
. One may ask whether 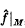 , the restriction of the Fourier transform of
, the restriction of the Fourier transform of 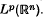 . Since, for
. Since, for 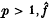 does not make sense pointwise, it is natural to introduce a measure σ on
does not make sense pointwise, it is natural to introduce a measure σ on