Hostname: page-component-848d4c4894-ndmmz Total loading time: 0 Render date: 2024-05-31T14:14:09.324Z Has data issue: false hasContentIssue false
  • English
  • Français

The generalization of modal subspaces in the complex domain

Published online by Cambridge University Press:  24 October 2008

H. Swann ,
C. P. Atkinson  and
B. L. Dhoopar
H. Swann
Affiliation:
University of California, Berkeley, and Indian Institute of Technology, Kanpur, India
C. P. Atkinson
Affiliation:
University of California, Berkeley, and Indian Institute of Technology, Kanpur, India
B. L. Dhoopar
Affiliation:
University of California, Berkeley, and Indian Institute of Technology, Kanpur, India
Get access Rights & Permissions [Opens in a new window]

Extract

The purpose of this paper is to present the concept of ‘modal subspaces’ for systems of coupled non-linear autonomous homogeneous second-order differential equations of the complex variables z1, z2. This development is an extension of the previous paper, entitled ‘Modal subspaces in the complex domain’, by Atkinson and Swann (6), which dealt with a pair of coupled non-linear autonomous homogeneous second-order differential equations of the form

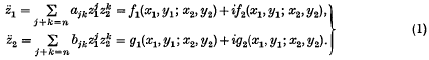
Differentiation is with respect to a real variable t and ajk and bjk are constants which may be complex: n is any positive integer: f1 and f2 are the real and imaginary parts respectively of 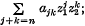g1 and g2 are real and imaginary parts respectively of 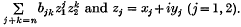and zj = xj + iyj (j = 1, 2).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 65 , Issue 3 , May 1969 , pp. 731 - 740
Copyright
Copyright © Cambridge Philosophical Society 1969

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Rosenberg, R. M. and Atkinson, C. P.On the natural modes and their stability in nonlinear two degree of freedom systems. Trans. ASME. Ser. E. J. Appl. Mech. 26 (1959), 377–385.CrossRefGoogle Scholar
(2)Atkinson, C. P., Bhatt, S. J. and Pacitti, T.The stability of the normal modes of nonlinear systems with polynomial restoring forces of high degree. Trans. ASME. Ser. E. J. Appl. Mech. 30 (1963), 193–198.CrossRefGoogle Scholar
(3)Rosenberg, R. M.The ATEB(H) functions and their properties. Quart. Appl. Math. 21, no. 1 (1963), 37–47.CrossRefGoogle Scholar
(4)Rosenberg, R. M.On normal vibrations of a general class of nonlinear dual mode systems. Trans. ASME. Ser. E. J. Appl. Mech. 28 (1961), 275–283.CrossRefGoogle Scholar
(5)Ince, E. L.Ordinary differential equations, ch. m (Dover 1963).Google Scholar
(6)Atkinson, C. P. and Swann, H.Modal subspaces in the complex domain, Report no. AM-65–11, Office of Research Services, University of California, Berkeley, California, 1965Google Scholar
(7)Atkinson, C. P., Swann, H. and Dhoopar, B. L. A.monograph on modal subspaces in the complex domain, Report no. AM-66–14. Office of Research Services, University of California, Berkeley, California, 10 1966.Google Scholar