Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Murasugi, Kunio
1989.
On invariants of graphs with applications to knot theory.
Transactions of the American Mathematical Society,
Vol. 314,
Issue. 1,
p.
1.
Murasugi, Kunio
1991.
Algebraic Topology Poznań 1989.
Vol. 1474,
Issue. ,
p.
83.
Murasugi, Kunio
1991.
On the braid index of alternating links.
Transactions of the American Mathematical Society,
Vol. 326,
Issue. 1,
p.
237.
Hara, Masao
and
Yamamoto, Makoto
1992.
Some links with non-adequate minimal-crossing diagrams.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 111,
Issue. 2,
p.
283.
Millett, Kenneth C.
1992.
Topological Aspects of the Dynamics of Fluids and Plasmas.
p.
29.
Jaeger, François
1993.
Plane graphs and link invariants.
Discrete Mathematics,
Vol. 114,
Issue. 1-3,
p.
253.
Liang, Chengzhi
Cerf, Corinne
and
Mislow, Kurt
1996.
Specification of chirality for links and knots.
Journal of Mathematical Chemistry,
Vol. 19,
Issue. 3,
p.
241.
Hoste, Jim
Thistlethwaite, Morwen
and
Weeks, Jeff
1998.
The first 1,701,936 knots.
The Mathematical Intelligencer,
Vol. 20,
Issue. 4,
p.
33.
Greene, Michael T
and
Wiest, Bert
1998.
A natural framing of knots.
Geometry & Topology,
Vol. 2,
Issue. 1,
p.
31.
HONGLER, CAM VAN QUACH
2001.
ON THE NULLIFICATION WRITHE, THE SIGNATURE AND THE CHIRALITY OF ALTERNATING LINKS.
Journal of Knot Theory and Its Ramifications,
Vol. 10,
Issue. 04,
p.
537.
Lee, Sang Youl
Park, Chan-Young
and
Seo, Myoungsoo
2001.
On adequate links and homogeneous links.
Bulletin of the Australian Mathematical Society,
Vol. 64,
Issue. 3,
p.
395.
STOIMENOW, ALEXANDER
2002.
SOME INEQUALITIES BETWEEN KNOT INVARIANTS.
International Journal of Mathematics,
Vol. 13,
Issue. 04,
p.
373.
Kauffman, Louis H.
2003.
Encyclopedia of Physical Science and Technology.
p.
199.
Manturov, Vassily
2004.
Knot Theory.
JABLAN, SLAVIK
and
SAZDANOVIĆ, RADMILA
2007.
UNLINKING NUMBER AND UNLINKING GAP.
Journal of Knot Theory and Its Ramifications,
Vol. 16,
Issue. 10,
p.
1331.
Stoimenow, A.
2008.
Tait’s conjectures and odd crossing number amphicheiral knots.
Bulletin of the American Mathematical Society,
Vol. 45,
Issue. 2,
p.
285.
Berglund, Michael
Cantarella, Jason
Casey, Meredith Perrie
Dannenberg, Eleanor
George, Whitney
Johnson, Aja
Kelley, Amelia
LaPointe, Al
Mastin, Matt
Parsley, Jason
Rooney, Jacob
and
Whitaker, Rachel
2012.
Intrinsic Symmetry Groups of Links with 8 and Fewer Crossings.
Symmetry,
Vol. 4,
Issue. 1,
p.
143.
HARA, MASAO
and
YAMAMOTO, MAKOTO
2012.
ON JONES POLYNOMIALS OF ALTERNATING PRETZEL KNOTS.
Journal of Knot Theory and Its Ramifications,
Vol. 21,
Issue. 14,
p.
1250127.
Jin, Xian’an
and
Cheng, Xiao-Sheng
2015.
Topological chirality of a type of DNA and protein polyhedral links.
Journal of Mathematical Chemistry,
Vol. 53,
Issue. 8,
p.
1791.
Vukovic, Ognjen
2015.
Predicting Financial Contagion and Crisis by Using Jones, Alexander Polynomial and Knot Theory.
Journal of Applied Mathematics and Physics,
Vol. 03,
Issue. 09,
p.
1073.

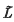 be its reduced (or proper) alternating diagram. Let
be its reduced (or proper) alternating diagram. Let 