Article contents
The L1-norm of exponential sums in 

Published online by Cambridge University Press: 16 January 2013
Abstract
Let A be a finite set of integers and FA(x) = ∑a∈A exp(2πiax) be its exponential sum. McGehee, Pigno and Smith and Konyagin have independently proved that ∥FA∥1 ≥ c log|A| for some absolute constant c. The lower bound has the correct order of magnitude and was first conjectured by Littlewood. In this paper we present lower bounds on the L1-norm of exponential sums of sets in the d-dimensional grid 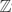 d. We show that ∥FA∥1 is considerably larger than log|A| when A ⊂
d. We show that ∥FA∥1 is considerably larger than log|A| when A ⊂ 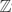 d has multidimensional structure. We furthermore prove similar lower bounds for sets in
d has multidimensional structure. We furthermore prove similar lower bounds for sets in 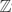 , which in a technical sense are multidimensional and discuss their connection to an inverse result on the theorem of McGehee, Pigno and Smith and Konyagin.
, which in a technical sense are multidimensional and discuss their connection to an inverse result on the theorem of McGehee, Pigno and Smith and Konyagin.
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 154 , Issue 3 , May 2013 , pp. 381 - 392
- Copyright
- Copyright © Cambridge Philosophical Society 2013
References
REFERENCES
- 1
- Cited by

