In 1966, Hewitt and Zuckerman(3,4) proved that if G is a non-discrete locally compact Abelian group with Haar measure λ, then there exists a non-negative, continuous regular measure μon G that is singular to λ(μ ┴ λ) such that μ(G)= 1, μ * μ is absolutely continuous with respect to λ(μ * μ ≪ λ), and the Lebesgue-Radon-Nikodym derivative of μ * μ with respect to λ is in 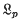(G, λ) for all real p > 1. They showed also that such a μ can be chosen so that the support of μ * μ contains any preassigned σ-compact subset of G. It is the purpose of the present paper to extend this result to obtain large independent sets of such measures. Among other things the present results show that, for such groups, the radical of the measure algebra modulo the 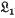-algebra has large dimension. This answers a question (6.4) left open in (3).