Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Millett, Kenneth C.
and
Rawdon, Eric J.
2003.
Energy, ropelength, and other physical aspects of equilateral knots.
Journal of Computational Physics,
Vol. 186,
Issue. 2,
p.
426.
Hernandes, M. E.
Hernandes, M. E. Rodrigues
and
Ruas, M. A. S.
2007.
$${\mathcal{A}}_e$$ -codimension of germs of analytic curves.
manuscripta mathematica,
Vol. 124,
Issue. 2,
p.
237.
Wall, C. T. C.
2008.
Projection genericity of space curves.
Journal of Topology,
Vol. 1,
Issue. 2,
p.
362.
Greuel, Gert-Martin
and
Le, Cong Trinh
2008.
On deformations of maps and curve singularities.
manuscripta mathematica,
Vol. 127,
Issue. 1,
p.
1.
Sharland, Ayşe Altıntaş
2014.
Examples of finitely determined map-germs of corank 2 from n-space to (n + 1)-space.
International Journal of Mathematics,
Vol. 25,
Issue. 05,
p.
1450044.
Henrique Ament, Daiane Alice
and
Nuño‐Ballesteros, Juan José
2017.
Mond's conjecture for maps between curves.
Mathematische Nachrichten,
Vol. 290,
Issue. 17-18,
p.
2845.
Sharland, Ayşe
2019.
Examples of Finitely Determined Map-Germs of Corank 3 Supporting Mond's μ ⩾ τ-Type Conjecture.
Experimental Mathematics,
Vol. 28,
Issue. 3,
p.
257.
Fernández de Bobadilla, J.
Nuño-Ballesteros, J. J.
and
Peñafort-Sanchis, G.
2019.
A Jacobian module for disentanglements and applications to Mond’s conjecture.
Revista Matemática Complutense,
Vol. 32,
Issue. 2,
p.
395.
Ament, D. A. H.
Nuño-Ballesteros, J. J.
and
Tomazella, J. N.
2020.
Image Milnor number and 𝒜
e
-codimension for maps between weighted homogeneous irreducible curves.
Advances in Geometry,
Vol. 20,
Issue. 3,
p.
319.
Peñafort Sanchis, Guillermo
2020.
Reflection maps.
Mathematische Annalen,
Vol. 378,
Issue. 1-2,
p.
559.
Pallarés, Irma
and
Peñafort Sanchis, Guillermo
2021.
Image Milnor Number Formulas for Weighted-Homogeneous Map-Germs.
Results in Mathematics,
Vol. 76,
Issue. 3,
Brasselet, Jean-Paul
2022.
Handbook of Geometry and Topology of Singularities III.
p.
303.
Mond, David
and
Nuño-Ballesteros, Juan José
2022.
Handbook of Geometry and Topology of Singularities III.
p.
81.
Giménez Conejero, R
and
Nuño-Ballesteros, J J
2022.
The Image Milnor Number And Excellent Unfoldings.
The Quarterly Journal of Mathematics,
Vol. 73,
Issue. 1,
p.
45.
Giménez Conejero, R.
and
Nuño-Ballesteros, J.J.
2022.
Singularities of mappings on ICIS and applications to Whitney equisingularity.
Advances in Mathematics,
Vol. 408,
Issue. ,
p.
108660.
Giménez Conejero, R.
and
Nuño-Ballesteros, J. J.
2024.
A weak version of the Mond conjecture.
Collectanea Mathematica,
Vol. 75,
Issue. 3,
p.
753.
Hepler, Brian
2024.
Deformation Formulas for Parameterized Hypersurfaces.
Annales de l'Institut Fourier,
Vol. 74,
Issue. 3,
p.
1153.
Breva Ribes, I.
and
Oset Sinha, R.
2025.
Augmentation of Singularities: $$\mu /\tau $$-type Conjectures and Simplicity.
Results in Mathematics,
Vol. 80,
Issue. 8,
Muñoz-Cabello, C.
Nuño-Ballesteros, J. J.
and
Oset Sinha, R.
2025.
A Proof of the Mond Conjecture for Wave Fronts.
Bulletin of the Brazilian Mathematical Society, New Series,
Vol. 56,
Issue. 2,
Conejero, R. Giménez
2025.
Isotypical components of the homology of ICIS and images of deformations of map germs.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
p.
1.
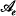 -codimension and the vanishing topology of parametrized curve singularities
-codimension and the vanishing topology of parametrized curve singularities
