Hostname: page-component-76fb5796d-2lccl Total loading time: 0 Render date: 2024-04-25T07:09:03.805Z Has data issue: false hasContentIssue false
  • English
  • Français

On growth of homology torsion in amenable groups

Published online by Cambridge University Press:  14 July 2016

ADITI KAR ,
PETER KROPHOLLER  and
NIKOLAY NIKOLOV
ADITI KAR
Affiliation:
University of Southampton e-mails: a.kar@soton.ac.uk; p.h.kropholler@soton.ac.uk
PETER KROPHOLLER
Affiliation:
University of Southampton e-mails: a.kar@soton.ac.uk; p.h.kropholler@soton.ac.uk
NIKOLAY NIKOLOV
Affiliation:
University of Oxford e-mail: nikolov@maths.ox.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Suppose an amenable group G is acting freely on a simply connected simplicial complex 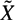$\~{X}$ with compact quotient X. Fix n ≥ 1, assume 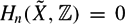$H_n(\~{X}, \mathbb{Z}) = 0$ and let (Hi) be a Farber chain in G. We prove that the torsion of the integral homology in dimension n of 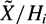$\~{X}/H_i$ grows subexponentially in [G : Hi]. This fails if X is not compact. We provide the first examples of amenable groups for which torsion in homology grows faster than any given function. These examples include some solvable groups of derived length 3 which is the minimal possible.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 162 , Issue 2 , March 2017 , pp. 337 - 351
Copyright
Copyright © Cambridge Philosophical Society 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Abért, M., Gelander, T. and Nikolov, N. Rank, combinatorial cost and homology torsion growth in higher rank lattices. arXiv/1509.01711.Google Scholar
[2] Abért, M., Jaikin–Zapirain, A. and Nikolov, N. The rank gradient from a combinatorial viewpoint. Groups Geom. Dyn. 5 (2) (2011), 213–230.Google Scholar
[3] Bergeron, N. and Venkatesh, A. The asymptotic growth of torsion homology for arithmetic groups. J. Inst. Math. Jussieu 12 (2) (2013), 391–447.Google Scholar
[4] Frigerio, R., Löh, C., Pagliantini, C. and Sauer, R.. Integral foliated simplicial volume of aspherical manifolds. arxiv/1506.05567.Google Scholar
[5] Hall, P. On the finiteness of certain soluble groups. Proc. London Math. Soc. (3) 9 (1959), 595–622.CrossRefGoogle Scholar
[6] Jacobson, N. Basic Algebra. I. (W. H. Freeman and Company, New York, second edition, 1985).Google Scholar
[7] Jeanes, S. C. and Wilson, J. S. On finitely generated groups with many profinite-closed subgroups. Arch. Math. (Basel) 31 (2) (1978/79), 120–122.Google Scholar
[8] Kropholler, P. H. and Wilson, J. S. Torsion in profinite completions. J. Pure Appl. Algebra 88 (1–3) (1993), 143–154.CrossRefGoogle Scholar
[9] Li, H. and Thom, A. Entropy, determinants, and L 2-torsion. J. Amer. Math. Soc. 27 (1) (2014), 239–292.Google Scholar
[10] Lück, W. Survey on analytic and topological torsion. In The Legacy of Bernhard Riemann After one Hundred and Fifty Years. Advanced Lectures in Mathematics vol. 35. (Higher Education Press, Beijing, 2016), pp. 379–416.Google Scholar
[11] Lück, W. Approximating L 2-invariants and homology growth. Geom. Funct. Anal. 23 (2) (2013), 622–663.Google Scholar
[12] Lück, W. and Osin, D. Approximating the first L 2-Betti number of residually finite groups. J. Topol. Anal. 3 (2) (2011), 153–160.Google Scholar
[13] Ornstein, D. S. and Weiss, B. Ergodic theory of amenable group actions. I. The Rohlin lemma. Bull. Amer. Math. Soc. (N.S.) 2 (1) (1980), 161–164.Google Scholar
[14] Robinson, D. J. S. Finiteness Conditions and Generalised Soluble Groups. Part 2. (Springer-Verlag, New York-Berlin, 1972). Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 63.Google Scholar
[15] Sauer, R. Volume and homology growth of aspherical manifolds. arXiv:1403.7319v3.Google Scholar
[16] Wehrfritz, B. A. F. Infinite Linear Groups. An Account of the Group-Theoretic Properties of Infinite Groups of Matrices (Springer-Verlag, New York-Heidelberg, 1973). Ergebnisse der Matematik und ihrer Grenzgebiete, Band 76.Google Scholar
[17] Weiss, B. Monotileable amenable groups. In Topology, Ergodic Theory, Real Algebraic Geometry Amer. Math. Soc. Transl. Ser. 2 vol. 202. (Amer. Math. Soc., Providence, RI, 2001), pp. 257–262.Google Scholar
[18] Wilson, J. S. Structure theory for branch groups. In Geometric and Cohomological Methods in Group Theory London Math. Soc. Lecture Note Ser. vol. 358. (Cambridge University Press, Cambridge, 2009), pp. 306–320.CrossRefGoogle Scholar