Hostname: page-component-848d4c4894-m9kch Total loading time: 0 Render date: 2024-05-21T13:45:24.927Z Has data issue: false hasContentIssue false
  • English
  • Français

On radial basis approximation on periodic grids

Published online by Cambridge University Press:  24 October 2008

Martin D. Buhmann  and
Charles A. Micchelli
Martin D. Buhmann
Affiliation:
Magdalene College, University of Cambridge, Cambridge CB3 OAG
Charles A. Micchelli
Affiliation:
IBM T.J. Watson Research Center, P.O. Box 218, Yorktown Heights NY 10598, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

A radial basis function approximation in n variables has the form

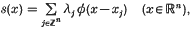
where ø:ℝn → ℝ denotes the n-variate, spherically symmetric function associated with a prescribed radial basis function ø+:ℝ+ → ℝ, i.e. ø = ø+(‖ · ‖), the norm being Euclidean. The 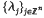are real coefficients (often, approximants s above are considered where only finitely many λjs are non-zero), and 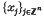is a fixed set of points in ℝn (of course, only the xj with non-zero coefficient λj affect s). Thus s is a linear combination of translates of a radially symmetric function which can be of global support, the simplest choice being 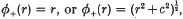, where c is a positive parameter. The latter is referred to as the multiquadric function and is usefull in applications.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 112 , Issue 2 , September 1992 , pp. 317 - 334
Copyright
Copyright © Cambridge Philosophical Society 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Beatson, R. K. and Powell, M. J. D.. Univariate multiquadric approximation: quasi- interpolation to scattered data. Report DAMTP 1990/NA7, University of Cambridge.Google Scholar
[2]Buhmann, M. B.. Multivariable interpolation using radial basis functions. Ph.D. thesis, University of Cambridge (1989).Google Scholar
[3]Buhmann, M. D. and Micchelli, C. A.. Multiply monotone functions for cardinal interpolation. Adv. in Appl. Math. 12 (1991), 358–386.CrossRefGoogle Scholar
[4]Buhmann, M. P. and Dyn, N.. Error estimates for multiquadric interpolation. In Curves and Surfaces (editors Laurent, P. J., LeMéhauté, A., Schumaker, L. L.). (Academic Press, 1991), pp. 51–58.CrossRefGoogle Scholar
[5]Jackson, I. R. H.. Radial basis function methods for multivariable approximation. Ph.D. thesis, University of Cambridge (1988).Google Scholar
[6]Jones, D. S.. The Theory of Generalised Functions (Cambridge University Press, 1982).CrossRefGoogle Scholar
[7]Karlin, S.. Total Positivity, vol. 1 (Stanford University Press, 1968).Google Scholar
[8]Light, W. A. and Cheney, E. W.. Quasi-interpolation with translates of a function having non-compact support. Constr. Approx. 8 (1992), 35–48.CrossRefGoogle Scholar
[9]Madych, W. R. and Nelson, S. A.. Multivariate interpolation and conditionally positive definite functions II. Math. Comp. 54 (1990), 211–230.CrossRefGoogle Scholar
[10]Powell, M. J. D.. The theory of radial basis function approximation in 1990. In Numerical Analysis II: Wavelets, Subdivision and Radial Basis Functions (editor Light, W. A.) (Oxford University Press, 1992), pp. 105–210.Google Scholar
[11]Stein, E. M. and Weiss, G.. Introduction to Fourier Analysis on Euclidean Spaces (Princeton University Press, 1971).Google Scholar
[12]Stoer, J.. Einführung in die Numerische Mathematik, vol. 1 (Springer-Verlag, 1983).CrossRefGoogle Scholar
[13]Wu, Z. and Schaback, R.. Local error estimates for radial basis function interpolation of scattered data. Report, University of Gottingen (1990).Google Scholar