Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hall, R. R.
1986.
On some theorems of Hurwitz and Sheil-Small.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 100,
Issue. 2,
p.
365.
FitzGerald, Carl H.
1987.
Complex Analysis I.
Vol. 1275,
Issue. ,
p.
131.
Abu-Muhanna, Y.
and
Lyzzaik, A.
1988.
A geometric criterion for decomposition and multivalence.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 103,
Issue. 3,
p.
487.
Lyzzaik, Abdallah
1991.
On the valence of some classes of harmonic maps.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 110,
Issue. 2,
p.
313.
Lyzzaik, Abdallah
1998.
A Note on the Valency of Harmonic Maps.
Journal of Mathematical Analysis and Applications,
Vol. 218,
Issue. 2,
p.
611.
Wilmshurst, A.
1998.
The valence of harmonic polynomials.
Proceedings of the American Mathematical Society,
Vol. 126,
Issue. 7,
p.
2077.
Bshouty, Daoud
Hengartner, Walter
Lyzzaik, Abdallah
and
Weitsman, Allen
2001.
Valency of Harmonic Mappings onto Bounded Convex Domains.
Computational Methods and Function Theory,
Vol. 1,
Issue. 2,
p.
479.
Lyzzaik, Abdallah
2001.
Quasihomeomorphisms and univalent harmonic mappings onto punctured bounded convex domains.
Pacific Journal of Mathematics,
Vol. 200,
Issue. 1,
p.
159.
Duren, Peter
2004.
Harmonic Mappings in the Plane.
Zwonek, W.
2022.
Complex Geodesics in Tube Domains and Their Role in the Study of Harmonic Mappings in the Disc.
Analysis Mathematica,
Vol. 48,
Issue. 2,
p.
601.

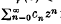 is either constant or an
is either constant or an 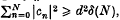 where
where 