Hostname: page-component-7dd5485656-7jgsp Total loading time: 0 Render date: 2025-10-31T13:11:47.974Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Hausdorff measure of Brownian paths in the plane

Published online by Cambridge University Press:  24 October 2008

P. Erdős  and
S. J. Taylor
P. Erdős
Affiliation:
University of Birmingham
S. J. Taylor
Affiliation:
University of Birmingham
Get access Rights & Permissions [Opens in a new window]

Extract

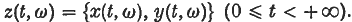Ω will denote the space of all plane paths ω, so that ω is a short way of denoting the curve . we assume that there is a probability measure μ defined on a Borel field 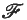of (measurable) subsets of Ω, so that the system (Ω, 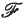, μ) forms a mathematical model for Brownian paths in the plane. [For details of the definition of μ, see for example (9).] let L(a, b; μ) be the plane set of points z(t, ω) for a≤t≤b. Then with probability 1, L(a, b; μ) is a continuous curve in the plane. The object of the present note is to consider the measure of this point set L(a, b; ω).

Information

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 57 , Issue 2 , April 1961 , pp. 209 - 222
Copyright
Copyright © Cambridge Philosophical Society 1961

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

(1)Besicovitch, A. S., On existence of subsets of finite measure of sets of infinite measure. Indag. Math. 14 (1952), 339–44.CrossRefGoogle Scholar
(2)Dvoretzky, A., and Erdős, P., Some problems on random walk in space. Proc. Second Berkeley Symposium (1951), 353–67.Google Scholar
(3)Erdős, P., and Taylor, S. J., Some problems concerning the structure of random walk paths. Acta Math. Acad. Sci. Hungar. 11 (1960), 137–62.CrossRefGoogle Scholar
(4)Hausdorff, F., Dimension und äusseres Mass. Math. Ann. 79 (1918), 157–79.CrossRefGoogle Scholar
(5)Kametani, S., On Hausdorff's measures and generalised capacities with some of their applications to the theory of functions. Jap. J. Math. 19 (1946), 217–57.CrossRefGoogle Scholar
(6)Lévy, P., Théorie de l'addition des variables alétoires (Paris, 1937).Google Scholar
(7)Lévy, P., Le mouvement Brownien plan. Amer. J. Math. 62 (1940), 487–550.CrossRefGoogle Scholar
(8)Lévy, P., La mesure de Hausdorff de la courbe du mouvement brownien. Giom. Ist. Ital. Attuari, 16 (1953), 1–37.Google Scholar
(9)Taylor, S. J., The Hausdorff α-dimensional measure of Brownian paths in n-space. Proc. Camb. Phil. Soc. 49 (1953), 31–9.CrossRefGoogle Scholar
(10)Taylor, S. J., On the connection between Hausdorff measures and generalised capacity (to appear shortly).Google Scholar