Article contents
On the lines passing through two conjugates of a Salem number
Published online by Cambridge University Press: 01 January 2008
Abstract
We show that the number of distinct non-parallel lines passing through two conjugates of an algebraic number α of degree d ≥ 3 is at most [d2/2]-d+2, its conjugates being in general position if this number is attained. If, for instance, d ≥ 4 is even, then the conjugates of α ∈ 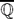 of degree d are in general position if and only if α has 2 real conjugates, d-2 complex conjugates, no three distinct conjugates of α lie on a line and any two lines that pass through two distinct conjugates of α are non-parallel, except for d/2-1 lines parallel to the imaginary axis. Our main result asserts that the conjugates of any Salem number are in general position. We also ask two natural questions about conjugates of Pisot numbers which lead to the equation α1+α2=α3+α4 in distinct conjugates of a Pisot number. The Pisot number
of degree d are in general position if and only if α has 2 real conjugates, d-2 complex conjugates, no three distinct conjugates of α lie on a line and any two lines that pass through two distinct conjugates of α are non-parallel, except for d/2-1 lines parallel to the imaginary axis. Our main result asserts that the conjugates of any Salem number are in general position. We also ask two natural questions about conjugates of Pisot numbers which lead to the equation α1+α2=α3+α4 in distinct conjugates of a Pisot number. The Pisot number 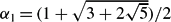 shows that this equation has such a solution.
shows that this equation has such a solution.
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 144 , Issue 1 , January 2008 , pp. 29 - 37
- Copyright
- Copyright © Cambridge Philosophical Society 2008
References
REFERENCES
- 5
- Cited by

