Article contents
On the stability of the set of hyperbolic closed orbits of a Hamiltonian
Published online by Cambridge University Press: 03 June 2010
Abstract
Let H be a Hamiltonian, e ∈ H(M) ⊂ ℝ and ƐH, e a connected component of H−1({e}) without singularities. A Hamiltonian system, say a triple (H, e, ƐH, e), is Anosov if ƐH, e is uniformly hyperbolic. The Hamiltonian system (H, e, ƐH, e) is a Hamiltonian star system if all the closed orbits of ƐH, e are hyperbolic and the same holds for a connected component of 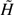 −1({ẽ}), close to ƐH, e, for any Hamiltonian
−1({ẽ}), close to ƐH, e, for any Hamiltonian 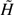 , in some C2-neighbourhood of H, and ẽ in some neighbourhood of e.
, in some C2-neighbourhood of H, and ẽ in some neighbourhood of e.
In this paper we show that a Hamiltonian star system, defined on a four-dimensional symplectic manifold, is Anosov. We also prove the stability conjecture for Hamiltonian systems on a four-dimensional symplectic manifold. Moreover, we prove the openness and the structural stability of Anosov Hamiltonian systems defined on a 2d-dimensional manifold, d ≥ 2.
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 149 , Issue 2 , September 2010 , pp. 373 - 383
- Copyright
- Copyright © Cambridge Philosophical Society 2010
References
REFERENCES
- 8
- Cited by

