Article contents
On the structure of simplicial categories associated to quasi-categories
Published online by Cambridge University Press: 11 March 2011
Abstract
The homotopy coherent nerve from simplicial categories to simplicial sets and its left adjoint 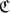 are important to the study of (∞, 1)-categories because they provide a means for comparing two models of their respective homotopy theories, giving a Quillen equivalence between the model structures for quasi-categories and simplicial categories. The functor
are important to the study of (∞, 1)-categories because they provide a means for comparing two models of their respective homotopy theories, giving a Quillen equivalence between the model structures for quasi-categories and simplicial categories. The functor 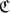 also gives a cofibrant replacement for ordinary categories, regarded as trivial simplicial categories. However, the hom-spaces of the simplicial category
also gives a cofibrant replacement for ordinary categories, regarded as trivial simplicial categories. However, the hom-spaces of the simplicial category 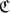 X arising from a quasi-category X are not well understood. We show that when X is a quasi-category, all Λ21 horns in the hom-spaces of its simplicial category can be filled. We prove, unexpectedly, that for any simplicial set X, the hom-spaces of
X arising from a quasi-category X are not well understood. We show that when X is a quasi-category, all Λ21 horns in the hom-spaces of its simplicial category can be filled. We prove, unexpectedly, that for any simplicial set X, the hom-spaces of 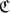 X are 3-coskeletal. We characterize the quasi-categories whose simplicial categories are locally quasi, finding explicit examples of 3-dimensional horns that cannot be filled in all other cases. Finally, we show that when X is the nerve of an ordinary category,
X are 3-coskeletal. We characterize the quasi-categories whose simplicial categories are locally quasi, finding explicit examples of 3-dimensional horns that cannot be filled in all other cases. Finally, we show that when X is the nerve of an ordinary category, 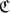 X is isomorphic to the simplicial category obtained from the standard free simplicial resolution, showing that the two known cofibrant “simplicial thickenings” of ordinary categories coincide, and furthermore its hom-spaces are 2-coskeletal.
X is isomorphic to the simplicial category obtained from the standard free simplicial resolution, showing that the two known cofibrant “simplicial thickenings” of ordinary categories coincide, and furthermore its hom-spaces are 2-coskeletal.
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 150 , Issue 3 , May 2011 , pp. 489 - 504
- Copyright
- Copyright © Cambridge Philosophical Society 2011
References
REFERENCES
- 5
- Cited by

