Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hunt, Brian
1998.
The Hausdorff dimension of graphs of Weierstrass functions.
Proceedings of the American Mathematical Society,
Vol. 126,
Issue. 3,
p.
791.
Yao, Kui
Su, Wei Yi
and
Zhou, Song Ping
2006.
The Fractional Derivatives of a Fractal Function.
Acta Mathematica Sinica, English Series,
Vol. 22,
Issue. 3,
p.
719.
Barański, Krzysztof
Bárány, Balázs
and
Romanowska, Julia
2014.
On the dimension of the graph of the classical Weierstrass function.
Advances in Mathematics,
Vol. 265,
Issue. ,
p.
32.
Barański, Krzysztof
2015.
Fractal Geometry and Stochastics V.
Vol. 70,
Issue. ,
p.
77.
Shen, Weixiao
2018.
Hausdorff dimension of the graphs of the classical Weierstrass functions.
Mathematische Zeitschrift,
Vol. 289,
Issue. 1-2,
p.
223.
LÜ, XIAOTAO
CHEN, JIN
WEN, ZHIXIONG
and
WU, WEN
2020.
LIMIT BEHAVIOR OF THE QUASI-LINEAR DISCRETE FUNCTIONS.
Fractals,
Vol. 28,
Issue. 03,
p.
2050041.
Ren, Haojie
and
Shen, Weixiao
2021.
A Dichotomy for the Weierstrass-type functions.
Inventiones mathematicae,
Vol. 226,
Issue. 3,
p.
1057.
Navish, A. A.
Priya, M.
and
Uthayakumar, R.
2023.
The relationship between the order of (k, s)-Riemann-Liouville fractional integral and the fractal dimensions of a fractal function.
The Journal of Analysis,
Vol. 31,
Issue. 1,
p.
261.
Katsevich, Alexander
2023.
Resolution of 2 Dimensional Reconstruction of Functions with Nonsmooth Edges from Discrete Radon Transform Data.
SIAM Journal on Applied Mathematics,
Vol. 83,
Issue. 2,
p.
695.
Yu, Binyan
and
Liang, Yongshun
2024.
On the Katugampola fractional integral and dimensional analysis of the fractal basin boundary for a random dynamical system.
Physica D: Nonlinear Phenomena,
Vol. 468,
Issue. ,
p.
134289.
Guo, Lixin
Yin, Zihan
Kang, Jing
Selmi, Bilel
and
Li, Zhiming
2025.
Fractal dimensions of the dispersive wave equation.
The European Physical Journal Special Topics,

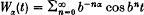 with
with 