No CrossRef data available.
Article contents
Pair correlations of the leVeque sequence on the polydisc
Published online by Cambridge University Press: 01 July 2008
Abstract
We consider a system of “forms” defined for ẕ = (zij) on a subset of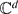 
by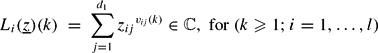
where d = d1 + ⋅ ⋅ ⋅ + dl and for each pair of integers (i,j) with 1 ≤ i ≤ l, 1 ≤ j ≤ di we denote by 
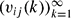a strictly increasing sequence of natural numbers. Let 
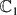= {z ∈ 
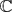: |z| < 1} and let 
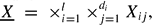where for each pair (i, j) we have Xij = 
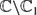. We study the distribution of the sequence on the l-polydisc 
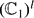defined by the coordinatewise polar fractional parts of the sequence Xk(ẕ) = (L1(ẕ)(k),. . ., Ll(ẕ)(k)) for typical ẕ in 
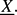More precisely for arcs I1, . . ., I2l in 
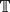, let B = I1 × ⋅ ⋅ ⋅ × I2l be a box in 
and for each N ≥ 1 define a pair correlation function by
and a discrepancy by ΔN =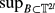 
{VN(B) − N(N−1)leb(B)}, where the supremum is over all boxes in . We show, subject to a non-resonance condition on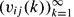 
, that given ε > 0 we have ΔN = o(N
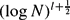(log log N)1+ε) for almost every 
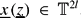. Similar results on extremal discrepancy are also proved. Our results complement those of I. Berkes, W. Philipp, M. Pollicott, Z. Rudnick, P. Sarnak, R Tichy and the author in the real setting.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 145 , Issue 1 , July 2008 , pp. 197 - 203
- Copyright
- Copyright © Cambridge Philosophical Society 2008
References
REFERENCES
[C]Cassels, J. W. S.. Some metrical theorems of Diophantine approximation. II. J. London Math. Soc. 25 (1950), 180–184.CrossRefGoogle Scholar
[F]Fefferman, C.. On the convergence of multiple Fourier series. Bull. Amer. Math. Soc. 77 (1971), 744–745.CrossRefGoogle Scholar
[BTP]Berkes, I., Philipp, W. and Tichy, R.. Pair correlations and U-statistics for independent and weakly dependent random variables. Illinois J. Math. 45 (2001), no. 2, 559–580.CrossRefGoogle Scholar
[BP]Berkes, I. and Philipp, W.. The size of trigonometric and Walsh series and uniform distribution 
od 1. J. London Math. Soc. (2) 50 (1994), no. 3, 454–464.Google Scholar
od 1. J. London Math. Soc. (2) 50 (1994), no. 3, 454–464.Google Scholar[H]Hunt, R. A.. On the convergence of Fourier series. 1968 Orthogonal Expansions and their continuous analogues (Proc. Conf., Edwardsville, Ill 1967) pp. 235–255 (Southern Illinois University Press).Google Scholar
[KN]Kuipers, L. and Niederreiter, H.. Uniform distribution of sequences. Pure and Applied Mathematics (Wiley-Interscience, John Wiley & Sons, 1974).Google Scholar
[L]Le Veque, W. J.. The distribution modulo 1 of trigonometric sequences. Duke Math. J. 20 (1953), 367–374.Google Scholar
[MV]Montgomery, H. L. and Vaaler, J. D.. Maximal variants of basic inequalities. Proceedings of the Congress on Number Theory (Spanish) (Zarauz, 1984), 181–197 (University Pas Vasco-Euskal Herriko Unib., Bilbao, 1989).Google Scholar
[Na]Nair, R.. Some theorems on metric uniform distribution using L2 methods. J. Number Theory 35, no. 1 (1990), 18–52.CrossRefGoogle Scholar
[NaP]Nair, R. and Pollicott, M.. Pair correlations of sequences in higher dimensions. Israel J. Math. 157 (2007), 219–238.CrossRefGoogle Scholar
[No]Nowak, W. G.. Zur asymptotischen Verteilung der Potenzen komplexer Zahlen. Arch. Math. (Basil) 40 (1983), no. 1, 69–72.CrossRefGoogle Scholar
[RS]Rudnick, Z. and Sarnak, P.. The pair correlation function of fractional parts of polynomials. Comm. Math. Phys. 194 (1998), no. 1, 61–70.CrossRefGoogle Scholar
[S]Sjölin, P.. Convergence almost everywhere of certain singular integrals and multiple Fourier series. Ark. Mat. 9 (1971) 65–90.CrossRefGoogle Scholar