Article contents
The primitive ideal space of the C*-algebra of the affine semigroup of algebraic integers
Published online by Cambridge University Press: 01 October 2012
Abstract
The purpose of this paper is to give a complete description of the primitive ideal space of the C*-algebra 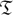 [R] associated to the ring of integers R in a number field K in the recent paper [5]. As explained in [5],
[R] associated to the ring of integers R in a number field K in the recent paper [5]. As explained in [5], 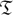 [R] can be realized as the Toeplitz C*-algebra of the affine semigroup R ⋊ R× over R and as a full corner of a crossed product C0(
[R] can be realized as the Toeplitz C*-algebra of the affine semigroup R ⋊ R× over R and as a full corner of a crossed product C0(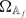 ) ⋊ K ⋊ K*, where
) ⋊ K ⋊ K*, where 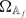 is a certain adelic space. Therefore Prim(
is a certain adelic space. Therefore Prim(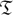 [R]) is homeomorphic to the primitive ideal space of this crossed product. Using a recent result of Sierakowski together with the fact that every quasi-orbit for the action of K ⋊ K* on
[R]) is homeomorphic to the primitive ideal space of this crossed product. Using a recent result of Sierakowski together with the fact that every quasi-orbit for the action of K ⋊ K* on 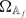 contains at least one point with trivial stabilizer we show that Prim(
contains at least one point with trivial stabilizer we show that Prim(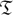 [R]) is homeomorphic to the quasi-orbit space for the action of K ⋊ K* on
[R]) is homeomorphic to the quasi-orbit space for the action of K ⋊ K* on 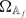 , which in turn may be identified with the power set
, which in turn may be identified with the power set 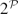 of the set of prime ideals
of the set of prime ideals 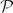 of R equipped with the power-cofinite topology.
of R equipped with the power-cofinite topology.
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 154 , Issue 1 , January 2013 , pp. 119 - 126
- Copyright
- Copyright © Cambridge Philosophical Society 2012
References
REFERENCES
- 10
- Cited by

