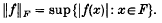Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mehta, H. S.
Mehta, R. D.
and
Vasavada, M. H.
1993.
Bishop decompositions for vector function spaces.
Proceedings of the Indian Academy of Sciences - Section A,
Vol. 103,
Issue. 2,
Hernández-Muñoz, Salvador
1994.
Approximation and extension of continuous functions.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 57,
Issue. 2,
p.
149.

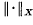 , where for each non-empty closed
, where for each non-empty closed