Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
James, G. D.
1978.
On a conjecture of Carter concerning irreducible Specht modules.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 83,
Issue. 1,
p.
11.
Morris, A. O.
and
Yaseen, A. K.
1986.
Some combinatorial results involving shifted Young diagrams.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 99,
Issue. 1,
p.
23.
Richards, Matthew J.
1996.
Some decomposition numbers for Hecke algebras of general linear groups.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 119,
Issue. 3,
p.
383.
Andrews, G. E.
Bessenrodt, C.
and
Olsson, J. B.
1996.
A refinement of a partition identity and blocks of some modular characters.
Archiv der Mathematik,
Vol. 66,
Issue. 2,
p.
101.
James, Gordon
and
Mathas, Andrew
2002.
Equating decomposition numbers for different primes.
Journal of Algebra,
Vol. 258,
Issue. 2,
p.
599.
Tsushima, Yukio
2003.
On some SR(H)-blocks for the symmetric groups.
Journal of Algebra,
Vol. 270,
Issue. 1,
p.
281.
Lyle, Sinéad
2003.
Some reducible Specht modules.
Journal of Algebra,
Vol. 269,
Issue. 2,
p.
536.
James, Gordon
and
Mathas, Andrew
2004.
Symmetric group blocks of small defect.
Journal of Algebra,
Vol. 279,
Issue. 2,
p.
566.
James, Gordon
Lyle, Sinéad
and
Mathas, Andrew
2006.
Rouquier blocks.
Mathematische Zeitschrift,
Vol. 252,
Issue. 3,
p.
511.
Ruff, Oliver
2006.
Completely splittable representations of symmetric groups and affine Hecke algebras.
Journal of Algebra,
Vol. 305,
Issue. 2,
p.
1197.
Lyle, Sinéad
and
Mathas, Andrew
2007.
Blocks of cyclotomic Hecke algebras.
Advances in Mathematics,
Vol. 216,
Issue. 2,
p.
854.
Chuang, Joseph
and
Turner, Will
2008.
Cubist algebras.
Advances in Mathematics,
Vol. 217,
Issue. 4,
p.
1614.
Fayers, Matthew
2011.
The t-core of an s-core.
Journal of Combinatorial Theory, Series A,
Vol. 118,
Issue. 5,
p.
1525.
Ellers, Harald
and
Murray, John
2014.
Centralizer Algebras and Degenerate Affine Hecke Algebras.
Communications in Algebra,
Vol. 42,
Issue. 3,
p.
1074.
Gerber, T.
Hiss, G.
and
Jacon, N.
2015.
Harish-Chandra Series in Finite Unitary Groups and Crystal Graphs.
International Mathematics Research Notices,
Mohommed, Eman F.
Ibrahim, Haslinda
Mahmood, Ammar Seddiq
and
Ahmad, Nazihah
2015.
Embedding chain movement in James diagram for partitioning beta number.
Vol. 1691,
Issue. ,
p.
040019.
Mohommed, Eman F.
Ibrahim, Haslinda
Ahmad, Nazihah
and
Mahmood, Ammar
2016.
Embedding the outer chain movement for main partition of β-number with length [1, 0, 0,…].
Vol. 1761,
Issue. ,
p.
020076.
Fayers, Matthew
2018.
Irreducible projective representations of the symmetric group which remain irreducible in characteristic 2.
Proceedings of the London Mathematical Society,
Vol. 116,
Issue. 4,
p.
878.
Irie, Yuki
2018.
p-Saturations of Welter’s game and the irreducible representations of symmetric groups.
Journal of Algebraic Combinatorics,
Vol. 48,
Issue. 2,
p.
247.
Mohommed, Eman F
2019.
Constructing a Nested Chain in James Abacus Diagram.
Journal of Physics: Conference Series,
Vol. 1294,
Issue. 3,
p.
032019.
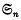 there are in a given q-block. None of the results of section 2 is original. In the next section we give a new definition, the p-power diagram, which is closely connected with the p-quotient. This concept is interesting because when p is prime a condition involving the p-power diagram appears to be a necessary and sufficient criterion for the diagram to be p-regular and the corresponding ordinary irreducible representation of
there are in a given q-block. None of the results of section 2 is original. In the next section we give a new definition, the p-power diagram, which is closely connected with the p-quotient. This concept is interesting because when p is prime a condition involving the p-power diagram appears to be a necessary and sufficient criterion for the diagram to be p-regular and the corresponding ordinary irreducible representation of 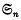 to remain irreducible modulo p. In this paper we derive combinatorial results involving the p-power diagram, and in a later article we investigate the relevant representation theory.
to remain irreducible modulo p. In this paper we derive combinatorial results involving the p-power diagram, and in a later article we investigate the relevant representation theory.
