Spectral asymmetry and Riemannian Geometry. I
Published online by Cambridge University Press: 24 October 2008
Extract
1. Introduction. The main purpose of this paper is to present a generalization of Hirzebruch's signature theorem for the case of manifolds with boundary. Our result is in the framework of Riemannian geometry and can be viewed as analogous to the Gauss–Bonnet theorem for manifolds with boundary, although there is a very significant difference between the two cases which is, in a sense, the central topic of the paper. To explain this difference let us begin by recalling that the classical Gauss–Bonnet theorem for a surface X with boundary Y asserts that the Euler characteristic E(X) is given by a formula:
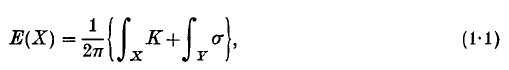
where K is the Gauss curvature of X and σ is the geodesic curvature of Y in X. In particular if, near the boundary, X is isometric to the product Y x R+, the boundary integral in (1.1) vanishes and the formula is the same as for closed surfaces. Similar remarks hold in higher dimensions. Now if X is a closed oriented Riemannian manifold of dimension 4, there is another formula relating cohomological invariants with curvature in addition to the Gauss–Bonnet formula. This expresses the signature of the quadratic form on H2(X, R) by an integral formula

where p1 is the differential 4-form representing the first Pontrjagin class and is given in terms of the curvature matrix R by p1 = (2π)−2Tr R2. It is natural to ask if (1.2) continues to hold for manifolds with boundary, provided the metric is a product near the boundary. Simple examples show that this is false, so that in general
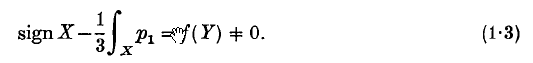
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 77 , Issue 1 , January 1975 , pp. 43 - 69
- Copyright
- Copyright © Cambridge Philosophical Society 1975
References
REFERENCES
- 1015
- Cited by

