Hostname: page-component-cb9f654ff-pvkqz Total loading time: 0 Render date: 2025-07-31T15:33:50.077Z Has data issue: false hasContentIssue false
  • English
  • Français

The structure of type I JBW-algebras

Published online by Cambridge University Press:  24 October 2008

P. J. Stagey
P. J. Stagey
Affiliation:
La Trobe University
Get access Rights & Permissions [Opens in a new window]

Extract

A complete normed real Jordan algebra A with 1 is said to be a JB-algebra if and only if, for all a, b ∈ A,

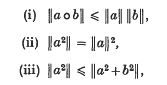
where o denotes the Jordan product on A. If A is a Banach dual space then A is known as a JBW-algebra. In this case, by Theorem 3·9 of (7),

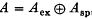
where Aex is an exceptional Jordan algebra and Asp is Jordan isomorphic to a JW-algebra (i.e. a weakly closed Jordan algebra of self-adjoint operators on a complex Hilbert space). Theorem 3–9 of (7) gives a description of Aex and so in this paper attention will be restricted to JW-algebras. Such an algebra A is said to be of type I if there exists an idempotent e in A with central cover equal to 1 such that e is abelian i.e. such that eAe is commutative as a set of operators. (See § 7 of (11) for further details.) A type I algebra A is said to be of type In, where n is some cardinal number, if there exists an orthogonal family {eα: α ∈ Λ} of n abelian projections in A such that Σαeα = 1 and such that, for each α ≠ β, there exists a symmetry sαβ in A with eβ = sαβeαsαβ. (A symmetry is an element sαβ of A such that 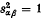). By theorems 15 and 16 of (11) any type I JW-algebra A can be uniquely decomposed into a direct sum of type In(α) JW-algebras for suitable cardinal numbers n(α). Thus in order to investigate the structure of type I JW-algebras it is sufficient to consider type In JW-algebras.

Information

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 90 , Issue 3 , November 1981 , pp. 477 - 482
Copyright
Copyright © Cambridge Philosophical Society 1981

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

(1)Alfsen, E. M., Hanche-Olsen, H. and Shultz, F. W.State spaces of C*-algebras. Acta Math. 144 (1980), 267–305.CrossRefGoogle Scholar
(2)Alfsen, E. M., Shuiltz, F. W. and Størmer, E.A Gelfand-Neumark theorem for Jordan algebras. Advances in Math. 23 (1973), 11–56.Google Scholar
(3)Dixmier, J.Les algèbres d'opérateurs dans l'espace Hubertien (Gauthier-Villars, Paris, 1969).Google Scholar
(4)Ionescu, Tulcea A. and Ionescu, Tulcea C.Topics in the theory of lifting (Ergebnisse der Mathematik und ihrer Grenzgebiete 43, Springer, Berlin-Heidelberg-New York, 1969).Google Scholar
(5)Kaplansky, I.Rings of operators (Benjamin, New York, 1963).Google Scholar
(6)Sakai, S.C*-algebras and W*-algebras (Ergebnisse der Mathematik und ihrer Grenzgebiete 60, Springer, Berlin-Heidelberg-New York, 1971).Google Scholar
(7)Shultz, F. W.On normed Jordan algebras which are Banach dual spaces. J. Funct. Anal. 31 (1979), 360–376.CrossRefGoogle Scholar
(8)Stacey, P. J.Type I2 JBW-algebras. Quart. J. Math. Oxford (2), (1981, to appear).Google Scholar
(9)Stacey, P. J.Local and global splittings in the state space of a JB-algebra. Math. Ann., (1981, to appear).CrossRefGoogle Scholar
(10)Størmer, E.Jordan algebras of type I. Acta Math. 115 (1966), 165–184.CrossRefGoogle Scholar
(11)Topping, D.Jordan algebras of self-adjoint operators (Mem. Amer. Math. Soc. 53, Amer. Math. Soc., Providence, R.I., 1965).CrossRefGoogle Scholar