Hostname: page-component-669899f699-7xsfk Total loading time: 0 Render date: 2025-05-03T08:40:15.779Z Has data issue: false hasContentIssue false
  • English
  • Français

FLAG AREA MEASURES

Part of: Polytopes and polyhedra General convexity

Published online by Cambridge University Press:  23 July 2019

Judit Abardia-Evéquoz ,
Andreas Bernig  and
Susanna Dann
Judit Abardia-Evéquoz
Affiliation:
Institut für Mathematik, Goethe-Universität Frankfurt am Main, Robert-Mayer-Str. 10, 60054 Frankfurt, Germany email abardia@math.uni-frankfurt.de
Andreas Bernig
Affiliation:
Institut für Mathematik, Goethe-Universität Frankfurt am Main, Robert-Mayer-Str. 10, 60054 Frankfurt, Germany email bernig@math.uni-frankfurt.de
Susanna Dann
Affiliation:
Departamento de Matemáticas, Universidad de los Andes, Carrera 1 No 18A-12, 111711 Bogotá, Colombia email s.dann@uniandes.edu.co
Get access

Abstract

A flag area measure on an $n$-dimensional euclidean vector space is a continuous translation-invariant valuation with values in the space of signed measures on the flag manifold consisting of a unit vector 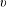$v$ and a 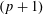$(p+1)$-dimensional linear subspace containing 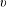$v$ with 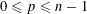$0\leqslant p\leqslant n-1$. Using local parallel sets, Hinderer constructed examples of 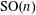$\text{SO}(n)$-covariant flag area measures. There is an explicit formula for his flag area measures evaluated on polytopes, which involves the squared cosine of the angle between two subspaces. We construct a more general sequence of smooth 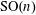$\text{SO}(n)$-covariant flag area measures via integration over the normal cycle of appropriate differential forms. We provide an explicit description of our measures on polytopes, which involves an arbitrary elementary symmetric polynomial in the squared cosines of the principal angles between two subspaces. Moreover, we show that these flag area measures span the space of all smooth 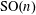$\text{SO}(n)$-covariant flag area measures, which gives a classification result in the spirit of Hadwiger’s theorem.

MSC classification

Primary: 52A39: Mixed volumes and related topics
Secondary: 52B45: Dissections and valuations (Hilbert's third problem, etc.)
Type
Research Article
Information
Mathematika , Volume 65 , Issue 4 , 2019 , pp. 958 - 989
Copyright
Copyright © University College London 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Álvarez Paiva, J. C. and Fernandes, E., Gelfand transforms and Crofton formulas. Selecta Math. (N.S.) 13(3) 2007, 369–390.10.1007/s00029-007-0045-5Google Scholar
Aomoto, K., Jacobi polynomials associated with Selberg integrals. SIAM J. Math. Anal. 18(2) 1987, 545–549.10.1137/0518042Google Scholar
Berline, N., Getzler, E. and Vergne, M., Heat Kernels and Dirac Operators (Grundlehren Text Editions), Springer (Berlin, 2004). Corrected reprint of the 1992 original.Google Scholar
Bernig, A. and Bröcker, L., Valuations on manifolds and Rumin cohomology. J. Differential Geom. 75(3) 2007, 433–457.10.4310/jdg/1175266280Google Scholar
Bernig, A. and Faifman, D., Valuation theory of indefinite orthogonal groups. J. Funct. Anal. 273(6) 2017, 2167–2247.10.1016/j.jfa.2017.06.005Google Scholar
Bernig, A. and Fu, J. H. G., Hermitian integral geometry. Ann. of Math. (2) 173 2011, 907–945.10.4007/annals.2011.173.2.7Google Scholar
Bernig, A., Fu, J. H. G. and Solanes, G., Integral geometry of complex space forms. Geom. Funct. Anal. 24(2) 2014, 403–492.10.1007/s00039-014-0251-1Google Scholar
Forrester, P. J. and Ole Warnaar, S., The importance of the Selberg integral. Bull. Amer. Math. Soc. (N.S.) 45(4) 2008, 489–534.10.1090/S0273-0979-08-01221-4Google Scholar
Fu, J. H. G., Kinematic formulas in integral geometry. Indiana Univ. Math. J. 39(4) 1990, 1115–1154.10.1512/iumj.1990.39.39052Google Scholar
Gallagher, P. X. and Proulx, R. J., Orthogonal and unitary invariants of families of subspaces. In Contributions to Algebra (Collection of Papers Dedicated to Ellis Kolchin), Academic Press (New York, 1977), 157–164.Google Scholar
Goodey, P., Hinderer, W., Hug, D., Rataj, J. and Weil, W., A flag representation of projection functions. Adv. Geom. 17(3) 2017, 303–322.10.1515/advgeom-2017-0022Google Scholar
Hinderer, W., Hug, D. and Weil, W., Extensions of translation invariant valuations on polytopes. Mathematika 61(1) 2015, 236–258.10.1112/S0025579314000187Google Scholar
Hug, D., Rataj, J. and Weil, W., Flag representations of mixed volumes and mixed functionals of convex bodies. J. Math. Anal. Appl. 460(2) 2018, 745–776.10.1016/j.jmaa.2017.12.039Google Scholar
Hug, D., Türk, I. and Weil, W., Flag measures for convex bodies. In Asymptotic Geometric Analysis (Fields Institute Communications 68 ), Springer (New York, 2013), 145–187.10.1007/978-1-4614-6406-8_7Google Scholar
Huybrechts, D., Complex Geometry (Universitext), Springer (Berlin, 2005).Google Scholar
James, A. T., Normal multivariate analysis and the orthogonal group. Ann. Math. Stat. 25 1954, 40–75.10.1214/aoms/1177728846Google Scholar
Jordan, C., Essai sur la géométrie à n dimensions. Bull. Soc. Math. France 3 1875, 103–174.10.24033/bsmf.90Google Scholar
Klain, D. A. and Rota, G.-C., Introduction to Geometric Probability (Lezioni Lincee. [Lincei Lectures]), Cambridge University Press (Cambridge, 1997).Google Scholar
Santaló, L. A., Integral Geometry and Geometric Probability (Encyclopedia of Mathematics and its Applications, 1 ), Addison-Wesley (Reading, MA–London–Amsterdam, 1976). With a foreword by Mark Kac.Google Scholar
Schneider, R., Kinematische Berührmaße für konvexe Körper. Abh. Math. Semin. Univ. Hambg. 44 1976, 12–23 1975.10.1007/BF02992942Google Scholar
Schneider, R., Curvature measures of convex bodies. Ann. Mat. Pura Appl. (4) 116 1978, 101–134.10.1007/BF02413869Google Scholar
Schneider, R., Convex Bodies: the Brunn-Minkowski Theory, 2nd expanded edn. (Encyclopedia of Mathematics and its Applications 151 ), Cambridge University Press (Cambridge, 2014).Google Scholar
Schneider, R. and Weil, W., Stochastic and Integral Geometry (Probability and its Applications), Springer (Berlin, 2008).10.1007/978-3-540-78859-1Google Scholar
Selberg, A., Remarks on a multiple integral. Norsk Mat. Tidsskr. 26 1944, 71–78.Google Scholar
Sepanski, M. R., Compact Lie Groups (Graduate Texts in Mathematics 235 ), Springer (New York, 2007).10.1007/978-0-387-49158-5Google Scholar
Spivak, M., A Comprehensive Introduction to Differential Geometry, Vol. II, 3rd edn., Publish or Perish (Wilmington, DE, 1999).Google Scholar
Spivak, M., A Comprehensive Introduction to Differential Geometry, Vol. III, 3rd edn., Publish or Perish (Wilmington, DE, 1999).Google Scholar
Steiner, J., Über parallele Flächen. Monatsber. Preu. Akad. Wiss. 1840, 114–118 [Gesammelte werke, Vol. 2, Reimer (Berlin, 1882), pp. 171–176].Google Scholar
Wannerer, T., Integral geometry of unitary area measures. Adv. Math. 263 2014, 1–44.10.1016/j.aim.2014.06.005Google Scholar
Zähle, M., Integral and current representation of Federer’s curvature measures. Arch. Math. (Basel) 46(6) 1986, 557–567.10.1007/BF01195026Google Scholar