Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ramharter, G.
1983.
Extremal values of continuants.
Proceedings of the American Mathematical Society,
Vol. 89,
Issue. 2,
p.
189.
Ramharter, G.
1983.
Some metrical properties of continued fractions.
Mathematika,
Vol. 30,
Issue. 1,
p.
117.
Moran, W.
Pearce, C. E. M.
and
Pollington, A. D.
1992.
T‐numbers form anM0set.
Mathematika,
Vol. 39,
Issue. 1,
p.
18.
Pollington, Andrew D.
and
Velani, Sanju L.
2000.
On a problem in simultaneous diophantine approximation: Littlewood's conjecture.
Acta Mathematica,
Vol. 185,
Issue. 2,
p.
287.
Bugeaud, Yann
2002.
Nombres de Liouville et nombres normaux.
Comptes Rendus. Mathématique,
Vol. 335,
Issue. 2,
p.
117.
Adamczewski, Boris
and
Allouche, Jean-Paul
2007.
Reversals and palindromes in continued fractions.
Theoretical Computer Science,
Vol. 380,
Issue. 3,
p.
220.
Hochman, Michael
and
Shmerkin, Pablo
2015.
Equidistribution from fractal measures.
Inventiones mathematicae,
Vol. 202,
Issue. 1,
p.
427.
Shi, Ronggang
and
Tseng, Jimmy
2015.
Simultaneous Dense and Nondense Orbits and the Space of Lattices.
International Mathematics Research Notices,
Vol. 2015,
Issue. 21,
p.
11276.
Jordan, Thomas
and
Sahlsten, Tuomas
2016.
Fourier transforms of Gibbs measures for the Gauss map.
Mathematische Annalen,
Vol. 364,
Issue. 3-4,
p.
983.
Kristensen, Simon
2016.
Diophantine Analysis.
p.
61.
Fraser, Jonathan M.
and
Sahlsten, Tuomas
2018.
On the Fourier analytic structure of the Brownian graph.
Analysis & PDE,
Vol. 11,
Issue. 1,
p.
115.
Li, Jialun
2018.
Decrease of Fourier coefficients of stationary measures.
Mathematische Annalen,
Vol. 372,
Issue. 3-4,
p.
1189.
Li, Jialun
and
Sahlsten, Tuomas
2020.
Fourier transform of self-affine measures.
Advances in Mathematics,
Vol. 374,
Issue. ,
p.
107349.
Technau, Niclas
and
Zafeiropoulos, Agamemnon
2020.
The Discrepancy of (nkx)k=1∞ With Respect to Certain Probability Measures.
The Quarterly Journal of Mathematics,
Vol. 71,
Issue. 2,
p.
573.
Gao, Xiang
Ma, Jihua
Song, Kunkun
and
Zhang, Yanfang
2020.
On the Fourier transform of coin-tossing type measures.
Journal of Mathematical Analysis and Applications,
Vol. 484,
Issue. 1,
p.
123706.
Algom, Amir
Rodriguez Hertz, Federico
and
Wang, Zhiren
2021.
Pointwise normality and Fourier decay for self-conformal measures.
Advances in Mathematics,
Vol. 393,
Issue. ,
p.
108096.
Chow, Sam
and
Zafeiropoulos, Agamemnon
2021.
FULLY INHOMOGENEOUS MULTIPLICATIVE DIOPHANTINE APPROXIMATION OF BADLY APPROXIMABLE NUMBERS.
Mathematika,
Vol. 67,
Issue. 3,
p.
639.
Pollington, Andrew D
Velani, Sanju
Zafeiropoulos, Agamemnon
and
Zorin, Evgeniy
2022.
Inhomogeneous Diophantine Approximation onM0-Sets with Restricted Denominators.
International Mathematics Research Notices,
Vol. 2022,
Issue. 11,
p.
8571.
Baker, Simon
2022.
Equidistribution Results for Self-Similar Measures.
International Mathematics Research Notices,
Vol. 2022,
Issue. 16,
p.
12378.
Hambrook, Kyle
and
Yu, Han
2023.
Non-Salem Sets in Metric Diophantine Approximation.
International Mathematics Research Notices,
Vol. 2023,
Issue. 15,
p.
13136.
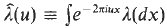 vanishes at infinity. Aside from the Riemann-Lebesgue Lemma, no purely metrical property of E can ensure that E is an M0-set. For the sets FN, however, metrical properties can be used to construct the measure λ.
vanishes at infinity. Aside from the Riemann-Lebesgue Lemma, no purely metrical property of E can ensure that E is an M0-set. For the sets FN, however, metrical properties can be used to construct the measure λ.
