Hostname: page-component-848d4c4894-4hhp2 Total loading time: 0 Render date: 2024-04-30T14:41:10.532Z Has data issue: false hasContentIssue false
  • English
  • Français

Density and covering properties of intervals of ℝn

Part of: Classical measure theory

Published online by Cambridge University Press:  26 February 2010

Tamás Keleti
Tamás Keleti
Affiliation:
Department of Analysis, Eötvös Loránd University, Pázmány Péter sétány 1/c, H-1117 Budapest, Hungary. E-mail: elek@cs.elte.hu
Get access

Abstract

The key result of this paper proves the existence of functions ρn(h) for which, whenever H is a (Lebesgue) measurable subset of the n-dimensional unit cube In with measure |H| > h and ℛ is a class of subintervals (n-dimensional axis-parallel rectangles) of In that covers H, then there exists an interval R∈ℛ in which the density of H is greater than ρn(h); that is, |H∩R|/|R|>ρn (h) (=(h/2n)2). It is shown how to use this result to find 4 points of a measurable subset of the unit square which are the vertices of an axis-parallel rectangle that has quite large intersection with the original set. Density and covering properties of classes of subsets of ℝn are introduced and investigated. As a consequence, a covering property of the class of intervals of ℝn is obtained: if ℛ is a family of n-dimensional intervals with 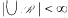, then there is a finite sequence R1, …, Rm∈ℛ such that 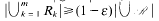and .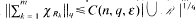

MSC classification

Secondary: 28A75: Length, area, volume, other geometric measure theory
Type
Research Article
Information
Mathematika , Volume 47 , Issue 1-2 , December 2000 , pp. 229 - 242
Copyright
Copyright © University College London 2000

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Carbery, A., Christ, M. and Wright, J.. Multidimensional van der Corput and sublevel set estimates J. Amer. Math. Soc. 12 (1999), 981–1015.CrossRefGoogle Scholar
2.Cordoba, A. and Fefferman, R.. A geometric proof for the strong maximal theorem. Ann. of Math., 102 (1975), 95–100.Google Scholar
3.Cruz-Uribe, D., SFO, and Neugebauer, C. J.. The structure of the reverse Holder classes. Trans. Amer. Math. Soc., 347 (1995), 2941–2960.Google Scholar
4.Erdős, P.On extremal problems of graphs and generalized graphs. Israel J. Math., 2 (1964), 183–190.CrossRefGoogle Scholar
5.Guzmán, M. de. An inequality for the Hardy-Littlewood maximal operator with respect to a product of differentiation bases. Studio Math., 49 (1974), 185–194.CrossRefGoogle Scholar
6.Guzman, M. de. Differentiation of Integrals in . Springer Lecture Notes in Mathematics 481 (Berlin, 1975).CrossRefGoogle Scholar
7.Guzmán, M. de. Real Variable Methods in Fourier Analysis. North-Holland, Mathematics Studies 46 (Amsterdam, 1981).Google Scholar
8.Keleti, T.. A covering property of some classes of sets in . Acta Univ. Carol. Math. Phys., 39 (1998), 111–118.Google Scholar
9.Reiman, I.. Über ein problem von K. Zarankiewicz. Acta Math. Acad. Sci. Hung., 9 (1958), 269–273.CrossRefGoogle Scholar