Article contents
A GENERALIZATION OF THE DISCRETE VERSION OF MINKOWSKI’S FUNDAMENTAL THEOREM
Published online by Cambridge University Press: 29 February 2016
Abstract
One of the most fruitful results from Minkowski’s geometric viewpoint on number theory is his so-called first fundamental theorem. It provides an optimal upper bound for the volume of a 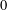 $0$ -symmetric convex body whose only interior lattice point is the origin. Minkowski also obtained a discrete analog by proving optimal upper bounds on the number of lattice points in the boundary of such convex bodies. Whereas the volume inequality has been generalized to any number of interior lattice points already by van der Corput in the 1930s, a corresponding result for the discrete case remained to be proven. Our main contribution is a corresponding optimal relation between the number of boundary and interior lattice points of a
$0$ -symmetric convex body whose only interior lattice point is the origin. Minkowski also obtained a discrete analog by proving optimal upper bounds on the number of lattice points in the boundary of such convex bodies. Whereas the volume inequality has been generalized to any number of interior lattice points already by van der Corput in the 1930s, a corresponding result for the discrete case remained to be proven. Our main contribution is a corresponding optimal relation between the number of boundary and interior lattice points of a 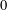 $0$ -symmetric convex body. The proof relies on a congruence argument and a difference set estimate from additive combinatorics.
$0$ -symmetric convex body. The proof relies on a congruence argument and a difference set estimate from additive combinatorics.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2016
References
- 7
- Cited by

