Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Randrianantoanina, Narcisse
1996.
Complemented Copies of ℓ1 and Pełczyński's Property (V*) in Bochner Function Spaces.
Canadian Journal of Mathematics,
Vol. 48,
Issue. 3,
p.
625.
2003.
Vol. 2,
Issue. ,
p.
1007.
Dodos, Pandelis
2006.
Codings of separable compact subsets of the first Baire class.
Annals of Pure and Applied Logic,
Vol. 142,
Issue. 1-3,
p.
425.
Dodos, Pandelis
and
Kanellopoulos, Vassilis
2008.
On pairs of definable orthogonal families.
Illinois Journal of Mathematics,
Vol. 52,
Issue. 1,
Debs, Gabriel
2009.
Borel extractions of converging sequences in compact sets of Borel functions.
Journal of Mathematical Analysis and Applications,
Vol. 350,
Issue. 2,
p.
731.
Moschovakis, Yiannis N.
2010.
Kleene's Amazing Second Recursion Theorem.
The Bulletin of Symbolic Logic,
Vol. 16,
Issue. 2,
p.
189.
Dodos, Pandelis
2011.
Operators whose dual has non-separable range.
Journal of Functional Analysis,
Vol. 260,
Issue. 5,
p.
1285.
Marciszewski, Witold
and
Pol, Roman
2012.
On Borel almost disjoint families.
Monatshefte für Mathematik,
Vol. 168,
Issue. 3-4,
p.
545.
Debs, Gabriel
2014.
Recent Progress in General Topology III.
p.
205.
Gregoriades, Vassilios
2015.
Choice free fixed point property in separable Banach spaces.
Proceedings of the American Mathematical Society,
Vol. 143,
Issue. 5,
p.
2143.
Corral, C.
Guzmán, O.
López-Callejas, C.
Memarpanahi, P.
Szeptycki, P.
and
Todorčević, S.
2024.
Infinite dimensional sequential compactness: Sequential compactness based on barriers.
Canadian Journal of Mathematics,
p.
1.

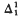 sequence of continuous functions on some recursively presentable Polish space, such that any pointwise cluster point of (
sequence of continuous functions on some recursively presentable Polish space, such that any pointwise cluster point of (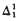 -subsequence of (
-subsequence of (