Hostname: page-component-76fb5796d-vvkck Total loading time: 0 Render date: 2024-04-26T06:49:09.342Z Has data issue: false hasContentIssue false
  • English
  • Français

A FLAG VECTOR OF A 3-SPHERE THAT IS NOT THE FLAG VECTOR OF A 4-POLYTOPE

Part of: Polytopes and polyhedra

Published online by Cambridge University Press:  08 December 2016

Philip Brinkmann  and
Günter M. Ziegler
Philip Brinkmann
Affiliation:
Institut für Mathematik, FU Berlin, Arnimallee 2, 14195 Berlin, Germany email philip.brinkmann@fu-berlin.de
Günter M. Ziegler
Affiliation:
Institut für Mathematik, FU Berlin, Arnimallee 2, 14195 Berlin, Germany email ziegler@math.fu-berlin.de
Get access

Abstract

We present a first example of a flag vector of a polyhedral sphere that is not the flag vector of any polytope. Namely, there is a unique 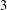$3$-sphere with the parameters 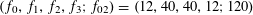$(f_{0},f_{1},f_{2},f_{3};f_{02})=(12,40,40,12;120)$, but this sphere is not realizable by a convex 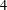$4$-polytope. The 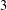$3$-sphere, which is 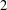$2$-simple and 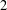$2$-simplicial, was found by Werner [Linear constraints on face numbers of polytopes. PhD Thesis, TU Berlin, Germany, 2009]; we present results of a computer enumeration which imply that the sphere with these parameters is unique. We prove that it is non-polytopal in two ways: first, we show that it has no oriented matroid, and thus it is not realizable; this proof was found by computer, but can be verified by hand. The second proof is again a computer-based oriented matroid proof and shows that for exactly one of the facets this sphere does not even have a diagram based on this facet. Using the non-polytopality, we finally prove that the sphere is not even embeddable as a polytopal complex.

MSC classification

Primary: 52B05: Combinatorial properties (number of faces, shortest paths, etc.)
Secondary: 52B11: $n$-dimensional polytopes 52B40: Matroids (realizations in the context of convex polytopes, convexity in combinatorial structures, etc.)
Type
Research Article
Information
Mathematika , Volume 63 , Issue 1 , 2017 , pp. 260 - 271
Copyright
Copyright © University College London 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Achterberg, T., SCIP: solving constraint integer programs. Math. Program. Comput. 1(1) 2009, 1–41.Google Scholar
Altshuler, A. and Steinberg, L., The complete enumeration of the 4-polytopes and 3-spheres with eight vertices. Pacific J. Math. 117 1985, 1–16.Google Scholar
Barnette, D. W., The minimum number of vertices of a simple polytope. Israel J. Math. 10 1971, 121–125.CrossRefGoogle Scholar
Bayer, M. M., The extended f-vectors of 4-polytopes. J. Combin. Theory Ser. A 44 1987, 141–151.Google Scholar
Bayer, M. M. and Billera, L. J., Generalized Dehn–Sommerville relations for polytopes, spheres and Eulerian partially ordered sets. Invent. Math. 79 1985, 143–157.CrossRefGoogle Scholar
Billera, L. J. and Lee, C. W., A proof of the sufficiency of McMullen’s conditions for f-vectors of simplicial polytopes. J. Combin. Theory Ser. A 31 1981, 237–255.Google Scholar
Björner, A., Las Vergnas, M., Sturmfels, B., White, N. and Ziegler, G. M., Oriented Matroids (Encyclopedia of Mathematics 46 ), 2nd edn., Cambridge University Press (Cambridge, 1998) , first edition: 1993.Google Scholar
Bokowski, J., Oriented matroids. In Handbook of Convex Geometry, Vol. A (eds Gruber, P. and Wills, J.), North-Holland (Amsterdam, 1993), 555–602.Google Scholar
Bokowski, J., Bremner, D. and Gévay, G., Symmetric matroid polytopes and their generation. European J. Combin. 30 2009, 1758–1777.Google Scholar
Bokowski, J. and Richter, J., On the finding of final polynomials. European J. Combin. 11 1990, 21–34.CrossRefGoogle Scholar
Bokowski, J. and Sturmfels, B., Computational Synthetic Geometry (Lecture Notes in Mathematics 1355 ), Springer (Berlin–Heidelberg, 1989).Google Scholar
Bremner, D., mpc, Software package for matroid polytopes, 2012,http://www.cs.unb.ca/profs/bremner/software/mpc/.Google Scholar
Brinkmann, P. and Ziegler, G. M., Small $f$ -vectors of $3$ -spheres and of $4$ -polytopes. Preprint, 2016,arXiv:1610.01028.Google Scholar
Ewald, G., Combinatorial Convexity and Algebraic Geometry (Graduate Texts in Mathematics 168 ), Springer (New York, 1996).Google Scholar
Firsching, M., Realizability and inscribability for simplicial polytopes via nonlinear optimization. Preprint, 2015, arXiv:1508.02531.Google Scholar
Goodman, J. E. and Pollack, R., Upper bounds for configurations and polytopes in ℝ d . Discrete Comput. Geom. 1 1986, 219–227.Google Scholar
Grünbaum, B., Convex Polytopes (Graduate Texts in Mathematics 221 ) 2nd edn. (eds Kaibel, V., Klee, V. and Ziegler, G. M.), Springer (New York, 2003) , original edition: Interscience, London, 1967.Google Scholar
Höppner, A. and Ziegler, G. M., A census of flag-vectors of 4-polytopes. In Polytopes—Combinatorics and Computation (DMV Seminars 29 ) (eds Kalai, G. and Ziegler, G. M.), Birkhäuser (Basel, 2000), 105–110.CrossRefGoogle Scholar
Kalai, G., A simple way to tell a simple polytope from its graph. J. Combin. Theory Ser. A 49 1988, 381–383.Google Scholar
Kalai, G., Many triangulated spheres. Discrete Comput. Geom. 3 1988, 1–14.CrossRefGoogle Scholar
McMullen, P., The numbers of faces of simplicial polytopes. Israel J. Math. 9 1971, 559–570.Google Scholar
Miyata, H., Studies on classifications and constructions of combinatorial structures related to oriented matroids. PhD Thesis, University of Tokyo, 2011.Google Scholar
Moise, E. E., Geometric Topology in Dimensions 2 and 3 (Graduate Texts in Mathematics 47 ), Springer (New York, 1977).Google Scholar
Paffenholz, A., The 2s2s pages. Web page with data, 2005–2011,http://polymake.org/polytopes/paffenholz/www/2s2s.html.Google Scholar
Paffenholz, A. and Werner, A., Constructions for 4-polytopes and the cone of flag vectors. In Algebraic and Geometric Combinatorics (Contemporary Mathematics 423 ) (ed. Athanasiadis, C. A. et al. ), American Mathematical Society (Providence, RI, 2006), 283–303.Google Scholar
Paffenholz, A. and Ziegler, G. M., The E t -construction for lattices, spheres and polytopes. Discrete Comput. Geom. 32 2004, 601–621.CrossRefGoogle Scholar
Pfeifle, J. and Ziegler, G. M., Many triangulated 3-spheres. Math. Ann. 330 2004, 829–837.Google Scholar
Polthier, K., Hildebrandt, K., Preuss, U. and Reitebuch, U. et al. , JavaView 4.0, 1999–2013,http://www.javaview.de.Google Scholar
Stanley, R. P., The number of faces of simplicial convex polytopes. Adv. Math. 35 1980, 236–238.Google Scholar
Steinitz, E., Über die Eulersche Polyederrelation. Arch. Math. Phys. (3) 11 1906, 86–88.Google Scholar
Steinitz, E., Polyeder und Raumeinteilungen (Encyklopädie der mathematischen Wissenschaften mit Einschluss ihrer Anwendungen, Band III.1.2 9 ) (eds Meyer, W. F. and Mohrmann, H.), Teubner (Leipzig, 1922), 1–139. Ch. AB12.Google Scholar
Steinitz, E. and Rademacher, H., Vorlesungen über die Theorie der Polyeder, Springer (Berlin, 1934) , reprint: Springer, 1976.Google Scholar
Werner, A., Linear constraints on face numbers of polytopes. PhD Thesis, TU Berlin, Germany, 2009. Published at https://opus4.kobv.de/.Google Scholar
Ziegler, G. M., Lectures on Polytopes (Graduate Texts in Mathematics 152 ), Springer (New York, 1995) , updated 7th printing: 2007.Google Scholar
Ziegler, G. M., Face numbers of 4-polytopes and 3-spheres. In Proc. Int. Congr. Mathematicians (ICM 2002, Beijing), Vol. III (ed. Tatsien, L.), Higher Education Press (Beijing, 2002), 625–634.Google Scholar
Ziegler, G. M., Convex polytopes: extremal constructions and f-vector shapes. In Geometric Combinatorics, Proc. Park City Mathematical Institute (PCMI) 2004 (eds Miller, E., Reiner, V. and Sturmfels, B.), American Mathematical Society (Providence, RI, 2007), 617–691.Google Scholar