Article contents
On a problem of hardy and ramanujan
Published online by Cambridge University Press: 26 February 2010
Extract
Some sixty years ago Hardy and Ramanujan [6]introduced the notion of normal order of an arithmetic function.
A real-valued arithmetic function f)n) is said to have a normal order if there is a function g(n), which is non-negative and non-decreasing for all sufficiently large integers n, so that, for each fixed ε > 0, the integers n, for which the inequality
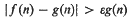
is satisfied, have asymptotic density zero. Thus, in this certain sense, f(n) behaves almost surely like g(n). We say that f(n) has the normal order g(n). In their original paper Hardy and Ramanujan asked that the function g(n) be “elementary”, but this is a requirement that subsequent researchers have dropped.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1976
References
1.Birch, B. J.. “Multiplicative functions with non-decreasing normal order”, Journ. London Math. Soc., 42 (1967), 149–151.CrossRefGoogle Scholar
3.Elliott, P. D. T. A.. “The law of large numbers for additive arithmetic functions”, Math. Proc. Camb. Phil. Soc., 77 (1975), 33–71.CrossRefGoogle Scholar
4.Elliott, P. D. T. A.. “Sur les fonctions arithmétiques additives”, C.R. Acad. Sci. Paris, 278 (1974), 1573–1575.Google Scholar
5.Elliott, P. D. T. A.. “On connections between the Turán-Kubilius inequality and the Large Sieve: Some applications”, Amer. Math. Soc. Symposia, Vol. 24 (1973), 77–82.Google Scholar
6.Hardy, G. H. and Ramanujan, S.. “The normal number of prime factors of a number n”, Quart. J. Math., 48 (1917), 76–92.Google Scholar
7.Hardy, G. H. and Wright, E. M.. An Introduction to the Theory of Numbers, fourth edition (Oxford University Press, Oxford, 1960).Google Scholar
8.Narkiewicz, W.. “On additive functions with a non-decreasing normal order”, Colloquium Math., 32 (1974), 137–142.CrossRefGoogle Scholar
10.Segal, S. L.. “A note on normal order and the Euler ø-function”, J. London Math. Soc., 39 (1964), 400–404.CrossRefGoogle Scholar
11.Segal, S. L.. “On non-decreasing normal orders”, J. London Math. Soc., 40 (1965), 459–466.CrossRefGoogle Scholar
12.Turan, P.. “On a theorem of Hardy and Ramanujan”, J. London Math. Soc., 9 (1934), 274–276.CrossRefGoogle Scholar
- 3
- Cited by

