Hostname: page-component-7dd5485656-npwhs Total loading time: 0 Render date: 2025-10-31T20:35:00.226Z Has data issue: false hasContentIssue false
  • English
  • Français

ON BILINEAR EXPONENTIAL AND CHARACTER SUMS WITH RECIPROCALS OF POLYNOMIALS

Part of: Exponential sums and character sums Diophantine equations

Published online by Cambridge University Press:  16 May 2016

Igor E. Shparlinski
Igor E. Shparlinski*
Affiliation:
Department of Pure Mathematics, University of New South Wales, Sydney, NSW 2052, Australia email igor.shparlinski@unsw.edu.au
Get access

Abstract

We give non-trivial bounds for the bilinear sums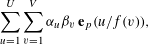

$$\begin{eqnarray}\mathop{\sum }_{u=1}^{U}\mathop{\sum }_{v=1}^{V}\unicode[STIX]{x1D6FC}_{u}\unicode[STIX]{x1D6FD}_{v}\,\mathbf{e}_{p}(u/f(v)),\end{eqnarray}$$
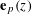where $\,\mathbf{e}_{p}(z)$ is a non-trivial additive character of the prime finite field 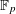$\mathbb{F}_{p}$ of 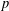$p$ elements, with integers 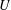$U$ , 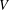$V$ , a polynomial 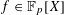$f\in \mathbb{F}_{p}[X]$ and some complex weights 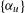$\{\unicode[STIX]{x1D6FC}_{u}\}$ , 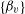$\{\unicode[STIX]{x1D6FD}_{v}\}$ . In particular, for 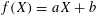$f(X)=aX+b$ , we obtain new bounds of bilinear sums with Kloosterman fractions. We also obtain new bounds for similar sums with multiplicative characters of 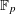$\mathbb{F}_{p}$ .

MSC classification

Primary: 11L07: Estimates on exponential sums
Secondary: 11D79: Congruences in many variables

Information

Type
Research Article
Information
Mathematika , Volume 62 , Issue 3 , 2016 , pp. 842 - 859
Copyright
Copyright © University College London 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bettin, S. and Chandee, V., Trilinear forms with Kloosterman fractions, Preprint, 2015, arXiv:1502.00769.Google Scholar
Bourgain, J., More on the sum-product phenomenon in prime fields and its applications. Int. J. Number Theory 1 2005, 1–32.CrossRefGoogle Scholar
Bourgain, J. and Garaev, M. Z., On a variant of sum-product estimates and explicit exponential sum bounds in prime fields. Math. Proc. Cambridge Philos. Soc. 146 2008, 1–21.Google Scholar
Bourgain, J. and Garaev, M. Z., Sumsets of reciprocals in prime fields and multilinear Kloosterman sums. Izv. Math. 78 2014, 656–707.CrossRefGoogle Scholar
Bourgain, J., Konyagin, S. V. and Shparlinski, I. E., Character sums and deterministic polynomial root finding in finite fields. Math. Comp. 43 2015, 4261–4269.Google Scholar
Chang, M.-C., Sparsity of the intersection of polynomial images of an interval. Acta Arith. 165 2014, 243–249.Google Scholar
Chang, M.-C., Cilleruelo, J., Garaev, M. Z., Hernández, J., Shparlinski, I. E. and Zumalacárregui, A., Points on curves in small boxes and applications. Michigan Math. J. 63 2014, 503–534.Google Scholar
Chang, M.-C. and Shparlinski, I. E., Double character sums over subgroups and intervals. Bull. Aust. Math. Soc. 90 2014, 376–390.CrossRefGoogle Scholar
Cilleruelo, J. and Garaev, M. Z., Concentration of points on two and three dimensional modular hyperbolas and applications. Geom. Funct. Anal. 21 2011, 892–904.CrossRefGoogle Scholar
Cilleruelo, J., Garaev, M. Z., Ostafe, A. and Shparlinski, I. E., On the concentration of points of polynomial maps and applications. Math. Z. 272 2012, 825–837.Google Scholar
Cilleruelo, J., Shparlinski, I. E. and Zumalacárregui, A., Isomorphism classes of elliptic curves over a finite field in some thin families. Math. Res. Lett. 19 2012, 335–343.CrossRefGoogle Scholar
Cobeli, C. and Zaharescu, A., Distribution of a sparse set of fractions modulo q . Bull. Lond. Math. Soc. 33 2001, 138–148.Google Scholar
Davenport, H. and Erdős, P., The distribution of quadratic and higher residues. Publ. Math. Debrecen 2 1952, 252–265.Google Scholar
Drmota, M. and Tichy, R., Sequences, Discrepancies and Applications, Springer (Berlin, 1997).Google Scholar
Gómez-Pérez, D. and Gutierrez, J., On the linear complexity and lattice test of nonlinear pseudorandom number generators. In Applied Algebra and Number Theory, Cambridge University Press (Cambridge, 2014), 91–101.Google Scholar
Hardy, G. H. and Wright, E. M., An Introduction to the Theory of Numbers, Oxford University Press (Oxford, 1979).Google Scholar
Iwaniec, H. and Kowalski, E., Analytic Number Theory, American Mathematical Society (Providence, RI, 2004).Google Scholar
Karatsuba, A. A., The distribution of values of Dirichlet characters on additive sequences. Dokl. Acad. Sci. USSR 319 1991, 543–545; (in Russian).Google Scholar
Kerr, B., Solutions to polynomial congruences in well shaped sets. Bull. Aust. Math. Soc. 88 2013, 435–447.Google Scholar
Moreno, C. J. and Moreno, O., Exponential sums and Goppa codes, 1. Proc. Amer. Math. Soc. 111 1991, 523–531.Google Scholar
Shao, X., Character sums over unions of intervals. Forum Math. 27 2015, 3017–3026.Google Scholar
Shparlinski, I. E., Exponential sums with Farey fractions. Bull. Pol. Acad. Sci. Math. 57 2009, 101–107.Google Scholar
Shparlinski, I. E., Close values of shifted modular inversions and the decisional modular inversion hidden number problem. Adv. Math. Commun. 9 2015, 169–176.Google Scholar
Shparlinski, I. E., Linear congruences with ratios. Proc. Amer. Math. Soc. 144 2016, 2837–2846.Google Scholar
Vinogradov, I. M., The Method of Trigonometrical Sums in the Theory of Numbers (Proceedings of the Steklov Institute of Mathematics 23 ), Acad. Sci. USSR (Moscow–Leningrad, 1947).Google Scholar
Wooley, T. D., Translation invariance, exponential sums, and Warings problem. In Proceedings of the International Congress of Mathematicians (Seoul 2014), Kyung Moon (Seoul, 2014), 505–529.Google Scholar
Zaharescu, A., Averages of short exponential sums. Acta Arith. 88 1999, 223–231.Google Scholar
Zaharescu, A., Averages of short exponential sums, II. Acta Arith. 100 2001, 339–348.Google Scholar