Article contents
Rational approximations to algebraic numbers
Published online by Cambridge University Press: 26 February 2010
Extract
It was remarked by Liouville in 1844 that there is an obvious limit to the accuracy with which algebraic numbers can be approximated by rational numbers; if α is an algebraic number of degree n (at least 2) then
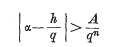
for all rational numbers h/q, where A is a positive number depending only on α.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1955
References
page 1 note † The result is an immediate deduction from the definition of an algebraic number; see, for example, Davenport, , The Higher Arithmetic (London 1952), 165–167Google Scholar.
page 1 note ‡ Acta Mathematica, 79 (1947), 225–240CrossRefGoogle Scholar. The algebraic part of Dyson's work was simplified by Mahler, , Proc. K. Akad. Wet. Amsterdam, 52 (1949), 1175–1184Google Scholar. Another proof of Dyson's result was given by Schneider, in Archiv der Math., 1 (1948–9), 288–295CrossRefGoogle Scholar. Dyson's result (with a generalization) was apparently obtained independently by Gelfond; see his Transcendental and algebraic numbers (Moscow 1952, in Russian), Chapter 1Google Scholar.
page 2 note † See Skolem, , Diophantische Gleichungen (Ergebnisse der Math. V4, Berlin, 1938), Chapter 6, §2Google Scholar.
page 2 note ‡ Math. Zeitschrift, 9 (1921), 173–213Google Scholar.
page 3 note † J. für die reine und angew. Math., 175 (1936), 182–192Google Scholar, Lemma 1, formula (7). This paper contains a proof that κ ≤ 2 provided that the solutions of (1) satisfy a certain very restrictive condition.
page 3 note ‡ Since writing this paper I find that generalized Wronskians were used by Siegel [Math. Annalen, 84 (1921), 80–99CrossRefGoogle Scholar] in a similar connection. See also Kellogg, , Comptes rendus des séances de la Soc. Math. de France, 41 (1912), 19–21Google Scholar, where the main result (Lemma 1 below) is stated without proof.
page 3 note § It should perhaps be remarked (though it is immaterial to our argument) that the generalized Wronskians and their derivatives may satisfy identities, by virtue of which the vanishing of some of the generalized Wronskians implies the vanishing of the others,
page 6 note † See, for example, Perron, , Algebra I (Berlin, 1927, 1931, 1951), Satz 88Google Scholar. The deduction does not depend on the separation of the variables between G and W.
page 9 note † The exponent θr 1 is of course a non-negative integer, and can be supposed to be a positive integer.
page 14 note † The case of even r would in fact suffice for the application later, since we could choose r 1, …, r m in §8 so as to be even.
- 339
- Cited by

