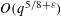Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Pierce, Lillian B.
and
Xu, Junyan
2020.
Burgess bounds for short character sums evaluated at forms.
Algebra & Number Theory,
Vol. 14,
Issue. 7,
p.
1911.
Pierce, Lillian B.
2021.
On Superorthogonality.
The Journal of Geometric Analysis,
Vol. 31,
Issue. 7,
p.
7096.
Baier, Stephan
and
Haldar, Anup
2022.
Asymptotic behavior of small solutions of quadratic congruences in three variables modulo prime powers.
Research in Number Theory,
Vol. 8,
Issue. 3,
Baier, Stephan
and
Chattopadhyay, Aishik
2025.
Small solutions of generic ternary quadratic congruences to general moduli.
Finite Fields and Their Applications,
Vol. 103,
Issue. ,
p.
102571.
Bag, Nilanjan
Baier, Stephan
and
Haldar, Anup
2025.
Multiple exponential sums and their applications to quadratic congruences.
Mathematische Nachrichten,
Vol. 298,
Issue. 11,
p.
3599.
Chu, Rena
2025.
Estimates for short character sums evaluated at homogeneous polynomials.
Journal of the London Mathematical Society,
Vol. 112,
Issue. 5,