Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Sjölin, Per
1993.
Estimates of spherial averages of Fourier transforms and dimensions of sets.
Mathematika,
Vol. 40,
Issue. 2,
p.
322.
Bourgain, Jean
1994.
Hausdorff dimension and distance sets.
Israel Journal of Mathematics,
Vol. 87,
Issue. 1-3,
p.
193.
Muravnik, A.B.
2001.
Recent Progress in Functional Analysis, Proceedings of the International Functional Analysis Meeting on the Occasion of the 70th Birthday of Professor Manuel Valdivia.
Vol. 189,
Issue. ,
p.
335.
Mitsis, Themis
2001.
A note on the distance set problem in the plane.
Proceedings of the American Mathematical Society,
Vol. 130,
Issue. 6,
p.
1669.
Hare, Kathryn E.
and
Roginskaya, Maria
2003.
Multipliers of spherical harmonics and energy of measures on the sphere.
Arkiv för Matematik,
Vol. 41,
Issue. 2,
p.
281.
Hare, Kathryn
and
Roginskaya, Maria
2003.
The energy of signed measures.
Proceedings of the American Mathematical Society,
Vol. 132,
Issue. 2,
p.
397.
Hofmann, S.
and
Iosevich, A.
2004.
Circular averages and Falconer/Erdös distance conjecture in the plane for random metrics.
Proceedings of the American Mathematical Society,
Vol. 133,
Issue. 1,
p.
133.
Iosevich, A.
and
Rudnev, M.
2007.
Erdös distance problem in vector spaces over finite fields.
Transactions of the American Mathematical Society,
Vol. 359,
Issue. 12,
p.
6127.
IOSEVICH, A.
and
RUDNEV, M.
2009.
FREIMAN THEOREM, FOURIER TRANSFORM AND ADDITIVE STRUCTURE OF MEASURES.
Journal of the Australian Mathematical Society,
Vol. 86,
Issue. 1,
p.
97.
Alexandrov, Alexey
and
Rozenblum, Grigori
2009.
Finite rank Toeplitz operators: Some extensions of D. Luecking's theorem.
Journal of Functional Analysis,
Vol. 256,
Issue. 7,
p.
2291.
Shayya, Bassam
2011.
Measures with Fourier Transforms in L2 of a Half-space.
Canadian Mathematical Bulletin,
Vol. 54,
Issue. 1,
p.
172.
Eswarathasan, Suresh
Iosevich, Alex
and
Taylor, Krystal
2011.
Fourier integral operators, fractal sets, and the regular value theorem.
Advances in Mathematics,
Vol. 228,
Issue. 4,
p.
2385.
Barceló, Juan Antonio
Bennett, Jonathan
Carbery, Anthony
and
Rogers, Keith M.
2011.
On the dimension of divergence sets of dispersive equations.
Mathematische Annalen,
Vol. 349,
Issue. 3,
p.
599.
Iosevich, Alex
Mourgoglou, Mihalis
and
Senger, Steven
2012.
On sets of directions determined by subsets of ℝ d.
Journal d'Analyse Mathématique,
Vol. 116,
Issue. 1,
p.
355.
Koh, Doowon
and
Shen, Chun-Yen
2012.
The generalized Erdős–Falconer distance problems in vector spaces over finite fields.
Journal of Number Theory,
Vol. 132,
Issue. 11,
p.
2455.
Greenleaf, Allan
and
Iosevich, Alex
2012.
On triangles determined by subsets of the Euclidean plane, the associated bilinear operators and applications to discrete geometry.
Analysis & PDE,
Vol. 5,
Issue. 2,
p.
397.
Koh, Doowon
and
Pi, Youngjin
2013.
SIZE OF DOT PRODUCT SETS DETERMINED BY PAIRS OF SUBSETS OF VECTOR SPACES OVER FINITE FIELDS.
Journal of the Chungcheong Mathematical Society,
Vol. 26,
Issue. 4,
p.
853.
Rela, Ezequiel
2014.
Concrete Operators, Spectral Theory, Operators in Harmonic Analysis and Approximation.
Vol. 236,
Issue. ,
p.
421.
Fässler, Katrin
and
Orponen, Tuomas
2014.
On restricted families of projections in ℝ3
.
Proceedings of the London Mathematical Society,
Vol. 109,
Issue. 2,
p.
353.
Iosevich, A.
Rudnev, M.
Uriarte-Tuero, I.
Damanik, David
Ruzhansky, Michael
Vougalter, Vitali
and
Wong, M.W.
2014.
Theory of Dimension for Large Discrete Sets and Applications.
Mathematical Modelling of Natural Phenomena,
Vol. 9,
Issue. 5,
p.
148.

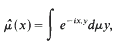
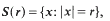
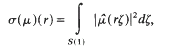
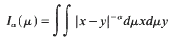
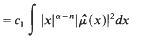
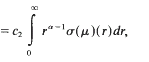
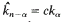 where
where 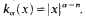 .
.