Hostname: page-component-77f85d65b8-g4pgd Total loading time: 0 Render date: 2026-04-17T20:59:17.040Z Has data issue: false hasContentIssue false
  • English
  • Français

Valuations and Tensor Weights on Polytopes

Part of: Polytopes and polyhedra

Published online by Cambridge University Press:  21 December 2009

Peter McMullen
Peter McMullen
Affiliation:
Department of Mathematics, University College London, Gower Street, London, WC1E 6BT.
Get access

Abstract

Let 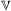be a finite-dimensional vector space over a square-root closed ordered field 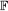(this restriction permits an inner product with corresponding norm to be imposed on 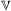). Many properties of the family 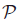:=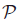(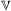) of convex polytopes in 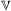can be expressed in terms of valuations (or finitely additive measures). Valuations such as volume, surface area and the Euler characteristic are translation invariant, but others, such as the moment vector and inertia tensor, display a polynomial behaviour under translation. The common framework for such valuations is the polytope (or Minkowski) ring Π:=Π(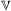), and its quotients under various powers of the ideal T of Π which is naturally associated with translations. A central result in the theory is that, in all but one trivial respect, the ring Π/T is actually a graded algebra over 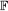. Unfortunately, while the quotients Π/Tk+1 are still graded rings for k > 1, they now only possess a rational algebra structure; to obtain an algebra over 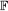, some (weak) continuity assumptions have to be made, although these can be achieved algebraically, by factoring out a further ideal A, the algebra ideal.

MSC classification

Secondary: 52B05: Combinatorial properties (number of faces, shortest paths, etc.) 52B45: Dissections and valuations (Hilbert's third problem, etc.)

Information

Type
Research Article
Information
Mathematika , Volume 53 , Issue 1 , June 2006 , pp. 1 - 47
Copyright
Copyright © University College London 2006

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

1Alesker, S., Algebraic structures on valuations, their properties and applications. Proc. I.C.M. 2002, vol. II, Higher Ed. Press (Beijing, 2002), 757–764.Google Scholar
2Alesker, S., The multiplicative structure on continuous polynomial valuations. Geom. Funct. Anal. 14 (2004), 1–26.CrossRefGoogle Scholar
3Betke, U., Mixed volumes of polytopes. Archiv Math. 58 (1992), 388–391.CrossRefGoogle Scholar
4Billera, L.J., The algebra of piecewise polynomial functions. Advances Math. 76 (1989), 170–183.CrossRefGoogle Scholar
5Billera, L.J. and Sturmfels, B., Fiber polytopes. Annals Math. 135 (1992), 527–549.CrossRefGoogle Scholar
6Bonnesen, T. and Fenchel, W., Theorie der Konvexen Körper. Springer (Berlin, 1934).Google Scholar
7Brion, M., Piecewise polynomial functions, convex polytopes and enumerative geometry. Parameter Spaces, Banach Center Publications 36 (1996), 25–44.Google Scholar
8Brion, M., The structure of the polytope algebra. Tôhoku Math. J. (2) 49 (1997), 1–32.CrossRefGoogle Scholar
9Fischer, K.G. and Shapiro, J., The prime ideal structure of the Minkowski ring of polytopes. J. Pure Appl. Alg. 78 (1992), 239–251.CrossRefGoogle Scholar
10Green, G., An Essay on the Application of Mathematical Analysis to the Theories of Electricity and Magnetism. Privately published (Nottingham, 1828). (Reprinted in J. reine angew. Math. 39 (1850), 73–89; 44 (1852), 356–374; 47 (1854), 161–221.)Google Scholar
11Groemer, H., Minkowski addition and mixed volumes. Geom. Ded. 6 (1977), 141–163.CrossRefGoogle Scholar
12Grünbaum, B., Convex Polytopes. Wiley-Interscience (New York, 1967). (2nd edition prepared by V. Kaibel, V.L. Klee and G.M. Ziegler, Springer (2003).)Google Scholar
13Huber, B. and Sturmfels, B., A polyhedral method for solving sparse polynomial systems. Math. Comp. 64 (1995), 1541–1555.CrossRefGoogle Scholar
14Jessen, B. and Thorup, A., The algebra of polytopes in affine spaces. Math. Scand. 43 (1978), 211–240.CrossRefGoogle Scholar
15Lawrence, J., Minkowski rings (unpublished manuscript).Google Scholar
16Lee, C.W., P.L. spheres, convex polytopes, and stress. Discrete Comput. Geom. 15 (1996), 389–421.CrossRefGoogle Scholar
17McMullen, P., Weakly continuous valuations on convex polytopes. Arch. Math. 41 (1983), 555–564.CrossRefGoogle Scholar
18McMullen, P., Angle-sum relations for polyhedral sets. Mathematika 33 (1986), 175–188.CrossRefGoogle Scholar
19McMullen, P., The polytope algebra. Advances Math. 78 (1989), 76–130.CrossRefGoogle Scholar
20McMullen, P., On simple polytopes. Inventiones Math. 113 (1993), 419–444.CrossRefGoogle Scholar
21McMullen, P., Valuations and dissections. Chapter 3.6 in Handbook of Convex Geometry (ed. Gruber, P.M. and Wills, J.M.), North-Holland (1993).Google Scholar
22McMullen, P., Separation in the polytope algebra. Beiträge Alg. Geom. 34 (1993), 15–30.Google Scholar
23McMullen, P., Weights on polytopes. Discrete Comput. Geom. 15 (1996), 363–388.CrossRefGoogle Scholar
24McMullen, P., Polytope algebras, tensor weights and piecewise polynomials. In Intuitive Geometry (ed. Szabo, L.), Bolyai Soc. Math. Stud. 6 (1997), 159–177.Google Scholar
25McMullen, P., Fibre tilings. Mathematika 50 (2003), 1–33.CrossRefGoogle Scholar
26McMullen, P., Mixed fibre polytopes. Discrete Comput. Geom. 32 (2004), 521–532.CrossRefGoogle Scholar
27McMullen, P. and Schneider, R., Valuations on convex bodies. In Convexity and Its Applications (ed. Gruber, P.M. and Wills, J.M.), Birkhäuser (Basel, 1983), 170–247.CrossRefGoogle Scholar
28McMullen, P., Schneider, R. and Shephard, G.C., Monotypic polytopes and their intersection properties. Geom. Ded. 3 (1974), 99–129.CrossRefGoogle Scholar
29Morelli, R., A theory of polyhedra. Advances Math. 97 (1993), 1–73.CrossRefGoogle Scholar
30Paterson, H.D., On the Combinatorics of Convex Polytopes. Ph.D. Thesis, University of London (2004).Google Scholar
31Pukhlikov, A.V. and Khovanskiĭ, A.G., Finitely additive measures of virtual polytopes. St. Petersburg Math. J. 4 (1993), 337–356 (translated from Russian).Google Scholar
32Rota, G.-C., On the foundations of combinatorial theory, I: Theory of Möbius functions. Z. Wahrscheinlichkeitstheorie verw. Geb. 2 (1964), 340–368.CrossRefGoogle Scholar
33Sah, C.-H., Hilbert's Third Problem: Scissors Congruence. Pitman (San Francisco, 1979).Google Scholar
34Schneider, R., Polytopes and Brunn-Minkowski theory. In Polytopes: Abstract, Convex and Computational (eds. Bisztriczky, T., McMullen, P., Schneider, R. and Weiss, A. Ivić), NATO ASI Series C 440, Kluwer (Dordrecht etc., 1994), 273–299.CrossRefGoogle Scholar
35Schneider, R., Mixed polytopes. Discrete Comput. Geom. 29 (2003), 575–593.CrossRefGoogle Scholar
36Tverberg, H., How to cut a convex polytope into simplices. Geom. Dedicata 3 (1974), 239–240.CrossRefGoogle Scholar
37Ziegler, G.M., Lectures on Polytopes. Graduate Texts in Mathematics 152, Springer (Berlin, 1995).CrossRefGoogle Scholar