1. Introduction
Let
![]() $X$
be a compact connected Riemann surface. Since the fundamental group
$X$
be a compact connected Riemann surface. Since the fundamental group
![]() $\pi _1(X)$
of
$\pi _1(X)$
of
![]() $X$
is finitely presented, and
$X$
is finitely presented, and
![]() ${\rm GL}(r,{\mathbb C})$
is an affine algebraic group defined over
${\rm GL}(r,{\mathbb C})$
is an affine algebraic group defined over
![]() $\mathbb C$
, the space of homomorphisms
$\mathbb C$
, the space of homomorphisms
![]() ${\rm Hom}(\pi _1(X),\, {\rm GL}(r,{\mathbb C}))$
is an affine complex algebraic variety. The adjoint action of
${\rm Hom}(\pi _1(X),\, {\rm GL}(r,{\mathbb C}))$
is an affine complex algebraic variety. The adjoint action of
![]() ${\rm GL}(r,{\mathbb C})$
on itself produces an action of
${\rm GL}(r,{\mathbb C})$
on itself produces an action of
![]() ${\rm GL}(r,{\mathbb C})$
on
${\rm GL}(r,{\mathbb C})$
on
![]() ${\rm Hom}(\pi _1(X),\, {\rm GL}(r,{\mathbb C}))$
. The moduli space
${\rm Hom}(\pi _1(X),\, {\rm GL}(r,{\mathbb C}))$
. The moduli space
of equivalence classes of representations has an algebraic symplectic structure which was constructed by Goldman [Reference GoldmanGol] and Atiyah and Bott [Reference Atiyah and BottAtBo]. Let
![]() ${\mathcal M}_C(r)$
be the moduli space of holomorphic connections on
${\mathcal M}_C(r)$
be the moduli space of holomorphic connections on
![]() $X$
of rank
$X$
of rank
![]() $r$
. This moduli space also has an algebraic symplectic structure. The Riemann–Hilbert correspondence identifies
$r$
. This moduli space also has an algebraic symplectic structure. The Riemann–Hilbert correspondence identifies
![]() ${\mathcal M}_R(r)$
with
${\mathcal M}_R(r)$
with
![]() ${\mathcal M}_C(r)$
. The Riemann–Hilbert correspondence is only complex analytic and not algebraic, and consequently the identification between
${\mathcal M}_C(r)$
. The Riemann–Hilbert correspondence is only complex analytic and not algebraic, and consequently the identification between
![]() ${\mathcal M}_R(r)$
and
${\mathcal M}_R(r)$
and
![]() ${\mathcal M}_C(r)$
is complex analytic but not algebraic. However, the transport of the symplectic form on
${\mathcal M}_C(r)$
is complex analytic but not algebraic. However, the transport of the symplectic form on
![]() ${\mathcal M}_R(r)$
to
${\mathcal M}_R(r)$
to
![]() ${\mathcal M}_C(r)$
by this complex analytic identification actually remains algebraic. This paper is divided into two parts. The first part is related to the fact that
${\mathcal M}_C(r)$
by this complex analytic identification actually remains algebraic. This paper is divided into two parts. The first part is related to the fact that
![]() ${\mathcal M}_C(r)$
has an algebraic symplectic structure. The second part is related to the fact that the Riemann–Hilbert correspondence is not algebraic.
${\mathcal M}_C(r)$
has an algebraic symplectic structure. The second part is related to the fact that the Riemann–Hilbert correspondence is not algebraic.
First, let us discuss on the first part. Fix finitely many distinct points
![]() $x_1,\, \ldots ,\, x_n$
of
$x_1,\, \ldots ,\, x_n$
of
![]() $X$
and denote the divisor
$X$
and denote the divisor
![]() $x_1 + \cdots +x_n$
on
$x_1 + \cdots +x_n$
on
![]() $X$
by
$X$
by
![]() $D$
. Consider logarithmic connections on
$D$
. Consider logarithmic connections on
![]() $X$
of rank
$X$
of rank
![]() $r$
whose polar part is supported on
$r$
whose polar part is supported on
![]() $D$
. The corresponding moduli space is known to have a Poisson structure. This Poisson structure is not symplectic if
$D$
. The corresponding moduli space is known to have a Poisson structure. This Poisson structure is not symplectic if
![]() $n\, \gt \, 0$
.
$n\, \gt \, 0$
.
It is shown in Corollary 4.24 that the Poisson structure on the moduli space of logarithmic connections can be elevated to a symplectic structure by introducing frames, over the points of
![]() $D$
, of the holomorphic vector bundle underlying the logarithmic connections. This entails construction of the moduli space of framed logarithmic connections that occupy a large fraction of the article. The key theorem in the first part of this paper is Theorem4.21, which establishes the
$D$
, of the holomorphic vector bundle underlying the logarithmic connections. This entails construction of the moduli space of framed logarithmic connections that occupy a large fraction of the article. The key theorem in the first part of this paper is Theorem4.21, which establishes the
![]() $d$
-closedness of the canonical nondegenerate
$d$
-closedness of the canonical nondegenerate
![]() $2$
-form on the moduli space of framed connections. This produces a Poisson structure on the moduli space of logarithmic connections; a geometric invariant theoretic construction of this moduli space was given by Nitsure [Reference NitsureNit].
$2$
-form on the moduli space of framed connections. This produces a Poisson structure on the moduli space of logarithmic connections; a geometric invariant theoretic construction of this moduli space was given by Nitsure [Reference NitsureNit].
In [Reference Biswas, Logares and Peón-NietoBLP1] and [Reference Biswas, Logares and Peón-NietoBLP2], generalized Higgs bundles on
![]() $X$
were considered where the Higgs fields are allowed to have poles along a fixed divisor
$X$
were considered where the Higgs fields are allowed to have poles along a fixed divisor
![]() $D$
on
$D$
on
![]() $X$
. The corresponding moduli spaces have a Poisson structure which was constructed independently by Bottacin [Reference BottacinBo] and Markman [Reference MarkmanMark]. It was shown in [Reference Biswas, Logares and Peón-NietoBLP1] and [Reference Biswas, Logares and Peón-NietoBLP2] that by imposing frames of the vector bundles underlying the Higgs bundles, over
$X$
. The corresponding moduli spaces have a Poisson structure which was constructed independently by Bottacin [Reference BottacinBo] and Markman [Reference MarkmanMark]. It was shown in [Reference Biswas, Logares and Peón-NietoBLP1] and [Reference Biswas, Logares and Peón-NietoBLP2] that by imposing frames of the vector bundles underlying the Higgs bundles, over
![]() $D$
, these Poisson structures can be enhanced to symplectic structure. The present work is an analogue of [Reference Biswas, Logares and Peón-NietoBLP2] for connections in place of Higgs fields.
$D$
, these Poisson structures can be enhanced to symplectic structure. The present work is an analogue of [Reference Biswas, Logares and Peón-NietoBLP2] for connections in place of Higgs fields.
The moduli space of logarithmic parabolic connections was constructed in [Reference Inaba, Iwasaki and SaitoIIS] and [Reference InabaIna]. If we fix eigenvalues of residues of logarithmic parabolic connections, then the moduli space of logarithmic parabolic connections with the fixed eigenvalues of residues has a canonical symplectic structure. In § 4.6, we discuss a relationship between the framed logarithmic connections and the logarithmic parabolic connections. As an outcome, it is proved that the moduli space of logarithmic parabolic connections has a canonical Poisson structure, whose restriction to the locus of fixed eigenvalues of residues induces the symplectic structure due to [Reference Inaba, Iwasaki and SaitoIIS] and [Reference InabaIna] (Corollary 4.25). Moreover, this Poisson structure satisfies the condition that the forgetful map to the moduli space of logarithmic connections, that forgets the parabolic structure, is a Poisson map. The restriction of this Poisson map to the loci of fixed eigenvalues of residues is an isomorphism if the eigenvalues are generic, and it produces a resolution of singularities if the eigenvalues are special.
Now let us discuss the second part. In this part, we focus on the algebraic moduli space of logarithmic parabolic connections such that eigenvalues of residues are fixed. We call this moduli space the de Rham moduli space. This moduli space is related to other moduli spaces having rich geometric structures. First, there is the moduli space of equivalence classes of representations of the fundamental group
![]() $\pi _1(X\setminus D)$
with fixed local monodromy data around the points of
$\pi _1(X\setminus D)$
with fixed local monodromy data around the points of
![]() $D$
, which is known as the character variety. The relationship between the moduli space of logarithmic parabolic connections and the character variety is given by the Riemann–Hilbert correspondence. In the framework of [Reference Inaba, Iwasaki and SaitoIIS] and [Reference InabaIna], the Riemann–Hilbert correspondence gives a simultaneous family of holomorphic maps from the de Rham moduli spaces to the character varieties over all the eigenvalues of residues. This Riemann–Hilbert morphism is biholomorphic when the eigenvalues of residues are generic, and it is an analytic resolution of singularities when the eigenvalues of residues are special. Note that the characteristic variety in [Reference Inaba, Iwasaki and SaitoIIS] and [Reference InabaIna] is not smooth for special eigenvalues of residues, but its singularities actually well explain the geometry of special solutions of the isomonodromy equation (see [Reference Saito and TerajimaSaTe]). Simpson introduced in [Reference SimpsonSim1] the notion of a filtered local system which bijectively corresponds to the parabolic connections under the assumption that the eigenvalues of residues are fixed. In [Reference YamakawaYa], Yamakawa constructed the algebraic moduli space of filtered local systems, which is actually nonsingular. We call it the Betti moduli space. Yamakawa proved in [Reference YamakawaYa] that the Riemann–Hilbert morphism is a biholomorphism between the de Rham moduli space and the Betti moduli space. Secondly, there is the moduli space of logarithmic parabolic Higgs bundles with fixed eigenvalues of residues together with stability data. We call this moduli space the Dolbeault moduli space. The relation between these moduli spaces is given by the logarithmic version of the non-abelian Hodge theory constructed by Simpson in [Reference SimpsonSim1].
$D$
, which is known as the character variety. The relationship between the moduli space of logarithmic parabolic connections and the character variety is given by the Riemann–Hilbert correspondence. In the framework of [Reference Inaba, Iwasaki and SaitoIIS] and [Reference InabaIna], the Riemann–Hilbert correspondence gives a simultaneous family of holomorphic maps from the de Rham moduli spaces to the character varieties over all the eigenvalues of residues. This Riemann–Hilbert morphism is biholomorphic when the eigenvalues of residues are generic, and it is an analytic resolution of singularities when the eigenvalues of residues are special. Note that the characteristic variety in [Reference Inaba, Iwasaki and SaitoIIS] and [Reference InabaIna] is not smooth for special eigenvalues of residues, but its singularities actually well explain the geometry of special solutions of the isomonodromy equation (see [Reference Saito and TerajimaSaTe]). Simpson introduced in [Reference SimpsonSim1] the notion of a filtered local system which bijectively corresponds to the parabolic connections under the assumption that the eigenvalues of residues are fixed. In [Reference YamakawaYa], Yamakawa constructed the algebraic moduli space of filtered local systems, which is actually nonsingular. We call it the Betti moduli space. Yamakawa proved in [Reference YamakawaYa] that the Riemann–Hilbert morphism is a biholomorphism between the de Rham moduli space and the Betti moduli space. Secondly, there is the moduli space of logarithmic parabolic Higgs bundles with fixed eigenvalues of residues together with stability data. We call this moduli space the Dolbeault moduli space. The relation between these moduli spaces is given by the logarithmic version of the non-abelian Hodge theory constructed by Simpson in [Reference SimpsonSim1].
In the case where the polar divisor
![]() $D$
is empty, Simpson introduced in [Reference SimpsonSim2] and [Reference SimpsonSim3], the three moduli spaces in his framework: the de Rham moduli space, the Dolbeault moduli space and the Betti moduli space. These are algebraic moduli spaces and are related to each other by the non-abelian Hodge theory and the Riemann–Hilbert correspondence. However, the algebraic structures of these moduli spaces are very different. In this paper, we consider the logarithmic version of these three moduli spaces. First, our Betti moduli space is affine when the eigenvalues of the residues are generic. So the transcendence degree of its affine coordinate ring is equal to the dimension of the moduli space. On the other hand, the transcendence degree of the ring of global algebraic functions on the Dolbeault moduli space is exactly the half of the dimension of the moduli space, a fact which is deduced from the properness of the Hitchin map. In some cases, the global algebraic functions on the de Rham moduli spaces are simply the constant scalars [Reference Biswas and RaghavendraBiRa]. For general logarithmic connections, the coefficients of the characteristic polynomial of residue at each singular point give algebraic functions on the moduli space. The main theorem of the second part of this paper is Theorem5.22, which states that the transcendence degree of the ring of global algebraic functions on our de Rham moduli space is less than or equal to that of our Dolbeault moduli space. In particular, our de Rham moduli space is not affine (this was announced in [Reference Biswas, Inaba, Komyo and SaitoBIKS]). To be precise, there was in fact an inadequate argument on finite generation of a graded ring in the outline of the proof of [Reference Biswas, Inaba, Komyo and SaitoBIKS, Theorem 10]. In this paper, we reconstruct a proof of it through a refinement of the statement (see Theorem5.22). As a consequence of Theorem5.22, the Riemann–Hilbert morphism, which appears in [Reference Inaba, Iwasaki and SaitoIIS], [Reference InabaIna], is not algebraic in the logarithmic case (see Corollary 5.25).
$D$
is empty, Simpson introduced in [Reference SimpsonSim2] and [Reference SimpsonSim3], the three moduli spaces in his framework: the de Rham moduli space, the Dolbeault moduli space and the Betti moduli space. These are algebraic moduli spaces and are related to each other by the non-abelian Hodge theory and the Riemann–Hilbert correspondence. However, the algebraic structures of these moduli spaces are very different. In this paper, we consider the logarithmic version of these three moduli spaces. First, our Betti moduli space is affine when the eigenvalues of the residues are generic. So the transcendence degree of its affine coordinate ring is equal to the dimension of the moduli space. On the other hand, the transcendence degree of the ring of global algebraic functions on the Dolbeault moduli space is exactly the half of the dimension of the moduli space, a fact which is deduced from the properness of the Hitchin map. In some cases, the global algebraic functions on the de Rham moduli spaces are simply the constant scalars [Reference Biswas and RaghavendraBiRa]. For general logarithmic connections, the coefficients of the characteristic polynomial of residue at each singular point give algebraic functions on the moduli space. The main theorem of the second part of this paper is Theorem5.22, which states that the transcendence degree of the ring of global algebraic functions on our de Rham moduli space is less than or equal to that of our Dolbeault moduli space. In particular, our de Rham moduli space is not affine (this was announced in [Reference Biswas, Inaba, Komyo and SaitoBIKS]). To be precise, there was in fact an inadequate argument on finite generation of a graded ring in the outline of the proof of [Reference Biswas, Inaba, Komyo and SaitoBIKS, Theorem 10]. In this paper, we reconstruct a proof of it through a refinement of the statement (see Theorem5.22). As a consequence of Theorem5.22, the Riemann–Hilbert morphism, which appears in [Reference Inaba, Iwasaki and SaitoIIS], [Reference InabaIna], is not algebraic in the logarithmic case (see Corollary 5.25).
Regarding the above three moduli spaces, we are mostly interested in the case where
![]() $X$
is defined over the field of complex numbers. However, it is also worth considering the case where the base field is of positive characteristic. When the base field is of positive characteristic, N. Katz introduced the notion of
$X$
is defined over the field of complex numbers. However, it is also worth considering the case where the base field is of positive characteristic. When the base field is of positive characteristic, N. Katz introduced the notion of
![]() $p$
-curvature in [Reference KatzKa], from which Laszlo and Pauly derived the proper Hitchin map on a de Rham moduli space (see [Reference Laszlo and PaulyLaPa]). By the investigation of the Hitchin map on a de Rham moduli space by Groechenig in [Reference GroechenigGroe], the ring of global algebraic functions on the de Rham moduli space of connections without pole has the same transcendence degree as that of the ring of global algebraic functions on the Dolbeault moduli space, when the characteristic of the base field is positive. So the similar inequality as in Theorem5.22 for connections without pole becomes the equality for curves when the base field is of positive characteristic, while the inequality is strict for curves of higher genus defined over the field of complex numbers (see [Reference Biswas and RaghavendraBiRa]).
$p$
-curvature in [Reference KatzKa], from which Laszlo and Pauly derived the proper Hitchin map on a de Rham moduli space (see [Reference Laszlo and PaulyLaPa]). By the investigation of the Hitchin map on a de Rham moduli space by Groechenig in [Reference GroechenigGroe], the ring of global algebraic functions on the de Rham moduli space of connections without pole has the same transcendence degree as that of the ring of global algebraic functions on the Dolbeault moduli space, when the characteristic of the base field is positive. So the similar inequality as in Theorem5.22 for connections without pole becomes the equality for curves when the base field is of positive characteristic, while the inequality is strict for curves of higher genus defined over the field of complex numbers (see [Reference Biswas and RaghavendraBiRa]).
Analogous to the regular case in [Reference BiswasBi], we can also show in the logarithmic case that the pullback, via the Riemann–Hilbert morphism, of the canonical algebraic symplectic form on the Betti moduli space coincides with that on the de Rham moduli space. Although not stated explicitly, it can also be found in the proof of [Reference InabaIna, Proposition 7.3]. This was also proved in the earlier work in the rank two case by Iwasaki [Reference IwasakiIw1]. In fact, the main point of [Reference IwasakiIw1] is the construction of the isomonodromic lift of the family of symplectic forms. A more conceptual construction of the isomonodromic lift of the family of symplectic forms was constructed by Komyo in [Reference KomyoKo], from the moduli theoretic point of view, by using the cohomological description of the isomonodromic deformation given in [Reference Biswas, Heu and HurtubiseBHH].
Boalch proved the following: The monodromy map between any moduli space of unramified irregular singular connections of any rank on a curve of genus zero and its corresponding wild character variety is symplectic structure preserving [Reference BoalchBo1, p. 182, Theorem 6.1] (see also [Reference BoalchBo2]). The algebraic moduli space of unramified irregular singular connections and its algebraic symplectic structure are constructed in [Reference Inaba and SaitoInSa].
Now we give a brief outline of the contents of this paper.
§ 2 provides general notions of framed principal
![]() $G$
-bundles on a compact Riemann surface
$G$
-bundles on a compact Riemann surface
![]() $X$
and also of framed
$X$
and also of framed
![]() $G$
-connections.
$G$
-connections.
From § 3, we restrict to the case of
![]() $G\,=\,{\rm GL}(r,\mathbb{C})$
. §§ 3.1 provides the formulation of moduli problem for framed connections. §§ 3.2 provides the construction of the moduli space of framed
$G\,=\,{\rm GL}(r,\mathbb{C})$
. §§ 3.1 provides the formulation of moduli problem for framed connections. §§ 3.2 provides the construction of the moduli space of framed
![]() ${\rm GL}(r,\mathbb{C})$
-connections as a Deligne–Mumford stack and also the irreducibility of its open substack where the underlying framed bundles are simple.
${\rm GL}(r,\mathbb{C})$
-connections as a Deligne–Mumford stack and also the irreducibility of its open substack where the underlying framed bundles are simple.
§ 4 is devoted to the construction of a canonical
![]() $2$
-form on the moduli space of framed connections and also to prove its
$2$
-form on the moduli space of framed connections and also to prove its
![]() $d$
-closedness. The main technical part is §§ 4.3. Over the open subset where the underlying framed bundles are simple, the canonical
$d$
-closedness. The main technical part is §§ 4.3. Over the open subset where the underlying framed bundles are simple, the canonical
![]() $2$
-form on the moduli space of framed connections becomes
$2$
-form on the moduli space of framed connections becomes
![]() $d$
-closed (Propositions Proposition 4.7 and 4.17). Its proof is essentially reduced to the
$d$
-closed (Propositions Proposition 4.7 and 4.17). Its proof is essentially reduced to the
![]() $d$
-closedness of the canonical
$d$
-closedness of the canonical
![]() $2$
-form on the character variety constructed by Goldman in [Reference GoldmanGol] when the genus of
$2$
-form on the character variety constructed by Goldman in [Reference GoldmanGol] when the genus of
![]() $X$
is greater than
$X$
is greater than
![]() $1$
. When the genus of
$1$
. When the genus of
![]() $X$
is zero or one, the proof of
$X$
is zero or one, the proof of
![]() $d$
-closedness is reduced to that for the form on the moduli space of parabolic connections given in [Reference InabaIna]. In §§ 4.4, we prove the
$d$
-closedness is reduced to that for the form on the moduli space of parabolic connections given in [Reference InabaIna]. In §§ 4.4, we prove the
![]() $d$
-closedness of the canonical
$d$
-closedness of the canonical
![]() $2$
-form on the entire moduli space of simple framed connections (see Theorem4.21), which is the main theorem of the first half. Its proof is reduced to Propositions 4.7 and 4.17 through an argument for extending the polar divisor. §§ 4.5 and 4.6 are immediate consequences of Theorem4.21. We can see that the Poisson structure on several known moduli spaces of connections can be reconstructed from the symplectic structure on the moduli space of framed connections.
$2$
-form on the entire moduli space of simple framed connections (see Theorem4.21), which is the main theorem of the first half. Its proof is reduced to Propositions 4.7 and 4.17 through an argument for extending the polar divisor. §§ 4.5 and 4.6 are immediate consequences of Theorem4.21. We can see that the Poisson structure on several known moduli spaces of connections can be reconstructed from the symplectic structure on the moduli space of framed connections.
§ 5 is devoted to establishing an upper bound for the transcendence degree of the ring of global algebraic functions on the moduli space of parabolic connections. In §§ 5.1, we recall the notions of parabolic connections and parabolic Higgs bundles, which work over the base field of arbitrary characteristic. In §§ 5.2, we prove in Proposition 5.14 that the locus of non-simple underlying quasi-parabolic bundles has codimension at least
![]() $2$
in the moduli space of parabolic connections. The proof is carried out by constructing a parameter space of non-simple quasi-parabolic bundles and a compatible connections on them. The essential part is to bound the dimension of the parameter space of non-simple quasi-parabolic bundles (see Propositions 5.10, 5.11, 5.12 and 5.13). Since we need to verify many cases, the proofs of these propositions contain a considerable amount of calculation, but each step is checked by relatively elementary arguments. By virtue of Proposition 5.14, the ring of global algebraic functions on the moduli space of parabolic connections can be replaced with that on the open loci where the underlying quasi-parabolic bundles are simple. §§ 5.3 provides the main estimate for the transcendence degree of the global algebraic functions on the moduli space of parabolic connections. Over the moduli space of simple quasi-parabolic bundles, we construct in Proposition 5.21 something like a relative compactification of a Deligne–Hitchin family, whose generic fiber is a relative compactification of the moduli space of compatible parabolic connections and whose special fiber is that of parabolic Higgs bundles. This family gives a family of sheaves of graded rings over the moduli space of simple quasi-parabolic bundles. A rough idea of the proof of Theorem5.22 is to estimate the transcendence degree of the ring of global sections of this sheaf of graded rings. In order to correct the flaw in the proof of [Reference Biswas, Inaba, Komyo and SaitoBIKS, Theorem 10], we actually consider the subring generated by a suitable transcendence basis of the graded ring over a generic fiber and compare it with that on the special fiber.
$2$
in the moduli space of parabolic connections. The proof is carried out by constructing a parameter space of non-simple quasi-parabolic bundles and a compatible connections on them. The essential part is to bound the dimension of the parameter space of non-simple quasi-parabolic bundles (see Propositions 5.10, 5.11, 5.12 and 5.13). Since we need to verify many cases, the proofs of these propositions contain a considerable amount of calculation, but each step is checked by relatively elementary arguments. By virtue of Proposition 5.14, the ring of global algebraic functions on the moduli space of parabolic connections can be replaced with that on the open loci where the underlying quasi-parabolic bundles are simple. §§ 5.3 provides the main estimate for the transcendence degree of the global algebraic functions on the moduli space of parabolic connections. Over the moduli space of simple quasi-parabolic bundles, we construct in Proposition 5.21 something like a relative compactification of a Deligne–Hitchin family, whose generic fiber is a relative compactification of the moduli space of compatible parabolic connections and whose special fiber is that of parabolic Higgs bundles. This family gives a family of sheaves of graded rings over the moduli space of simple quasi-parabolic bundles. A rough idea of the proof of Theorem5.22 is to estimate the transcendence degree of the ring of global sections of this sheaf of graded rings. In order to correct the flaw in the proof of [Reference Biswas, Inaba, Komyo and SaitoBIKS, Theorem 10], we actually consider the subring generated by a suitable transcendence basis of the graded ring over a generic fiber and compare it with that on the special fiber.
2. Framed
 $G$
-connections
$G$
-connections
Let
![]() $X$
be a compact connected Riemann surface, and let
$X$
be a compact connected Riemann surface, and let
![]() $x_1,\, \ldots ,\, x_n$
be finitely many distinct points on
$x_1,\, \ldots ,\, x_n$
be finitely many distinct points on
![]() $X$
. Let
$X$
. Let
be the reduced effective divisor on
![]() $X$
. For notational convenience, the subset
$X$
. For notational convenience, the subset
![]() $\{x_1,\,\ldots ,\, x_n\}\, \subset \, X$
will also be denoted by
$\{x_1,\,\ldots ,\, x_n\}\, \subset \, X$
will also be denoted by
![]() $D$
. Denote by
$D$
. Denote by
![]() $K_X$
the holomorphic cotangent bundle of
$K_X$
the holomorphic cotangent bundle of
![]() $X$
.
$X$
.
2.1 Framed principal
 $G$
-bundles
$G$
-bundles
Let
![]() $G$
be a connected complex reductive affine algebraic group. The Lie algebra of
$G$
be a connected complex reductive affine algebraic group. The Lie algebra of
![]() $G$
will be denoted by
$G$
will be denoted by
![]() $\mathfrak g$
. Let
$\mathfrak g$
. Let
be a holomorphic principal
![]() $G$
-bundle over
$G$
-bundle over
![]() $X$
. For any point
$X$
. For any point
![]() $x\,\in \, X$
, the fiber
$x\,\in \, X$
, the fiber
![]() $p^{-1} (x) \subset E_G$
will be denoted by
$p^{-1} (x) \subset E_G$
will be denoted by
![]() $(E_G)_x$
.
$(E_G)_x$
.
Definition 2.1 (See [Reference Biswas, Logares and Peón-NietoBLP2,p. 5]).For each point
![]() $x$
of the subset
$x$
of the subset
![]() $D$
in (2.1), fix a closed complex Lie proper subgroup
$D$
in (2.1), fix a closed complex Lie proper subgroup
A framing of
![]() $E_G$
over the divisor
$E_G$
over the divisor
![]() $D$
is a map
$D$
is a map
such that
![]() $\phi (x) \,\in \,(E_G)_x/ H_x$
for every
$\phi (x) \,\in \,(E_G)_x/ H_x$
for every
![]() $x \,\in \, D$
. A framed principal
$x \,\in \, D$
. A framed principal
![]() $G$
-bundle on X is a holomorphic principal
$G$
-bundle on X is a holomorphic principal
![]() $G$
-bundle
$G$
-bundle
![]() $E_G$
on X equipped with a framing over
$E_G$
on X equipped with a framing over
![]() $D$
.
$D$
.
A framing
![]() $\phi$
of
$\phi$
of
![]() $E_G$
produces a reduction of structure group
$E_G$
produces a reduction of structure group
to
![]() $H_x$
at each point
$H_x$
at each point
![]() $x\, \in \, D$
, where
$x\, \in \, D$
, where
![]() $q_x\, :\, (E_G)_x\, \longrightarrow \, (E_G)_x/ H_x$
is the quotient map.
$q_x\, :\, (E_G)_x\, \longrightarrow \, (E_G)_x/ H_x$
is the quotient map.
2.2 Adjoint bundle for framed principal
 $G$
-bundles
$G$
-bundles
Let
![]() $T_{E_G/X}\, \longrightarrow \, E_G$
be the relative tangent bundle for the projection
$T_{E_G/X}\, \longrightarrow \, E_G$
be the relative tangent bundle for the projection
![]() $p$
in (2.2). Using the action of the group
$p$
in (2.2). Using the action of the group
![]() $G$
on
$G$
on
![]() $E_G$
, this relative tangent bundle
$E_G$
, this relative tangent bundle
![]() $T_{E_G/X}$
is identified with the trivial vector bundle
$T_{E_G/X}$
is identified with the trivial vector bundle
![]() $E_G\times \mathfrak{g} \,\longrightarrow \, E_G$
with fiber
$E_G\times \mathfrak{g} \,\longrightarrow \, E_G$
with fiber
![]() $\mathfrak{g} \,=\, {\rm Lie}(G)$
. The quotient
$\mathfrak{g} \,=\, {\rm Lie}(G)$
. The quotient
![]() $(T_{E_G/X})/G$
is a vector bundle over
$(T_{E_G/X})/G$
is a vector bundle over
![]() $X$
. The above identification of
$X$
. The above identification of
![]() $T_{E_G/X}$
with
$T_{E_G/X}$
with
![]() $E_G\times \mathfrak{g}$
produces an identification of
$E_G\times \mathfrak{g}$
produces an identification of
![]() $(T_{E_G/X})/G$
with the vector bundle on
$(T_{E_G/X})/G$
with the vector bundle on
![]() $X$
associated to the principal
$X$
associated to the principal
![]() $G$
-bundle
$G$
-bundle
![]() $E_G$
for the adjoint action of
$E_G$
for the adjoint action of
![]() $G$
on
$G$
on
![]() $\mathfrak{g}$
. This associated vector bundle, which is denoted by
$\mathfrak{g}$
. This associated vector bundle, which is denoted by
![]() ${\rm ad}(E_G)$
, is called the adjoint bundle for
${\rm ad}(E_G)$
, is called the adjoint bundle for
![]() $E_G$
. The fiber over any
$E_G$
. The fiber over any
![]() $x \,\in \, X$
for the natural projection
$x \,\in \, X$
for the natural projection
![]() ${\rm ad}(E_G) \,\longrightarrow \,X$
will be denoted by
${\rm ad}(E_G) \,\longrightarrow \,X$
will be denoted by
![]() ${\rm ad}(E_G)_x$
; it is a Lie algebra isomorphic to
${\rm ad}(E_G)_x$
; it is a Lie algebra isomorphic to
![]() $\mathfrak g$
.
$\mathfrak g$
.
Since the group
![]() $G$
is reductive, its Lie algebra
$G$
is reductive, its Lie algebra
![]() $\mathfrak g$
admits
$\mathfrak g$
admits
![]() $G$
-invariant nondegenerate symmetric bilinear forms. Fix a
$G$
-invariant nondegenerate symmetric bilinear forms. Fix a
![]() $G$
-invariant nondegenerate symmetric bilinear form
$G$
-invariant nondegenerate symmetric bilinear form
on
![]() $\mathfrak{g}$
. From the above construction of
$\mathfrak{g}$
. From the above construction of
![]() ${\rm ad}(E_G)$
it follows that given any point
${\rm ad}(E_G)$
it follows that given any point
![]() $z\,\in \, (E_G)_y$
there is a corresponding isomorphism of Lie algebras
$z\,\in \, (E_G)_y$
there is a corresponding isomorphism of Lie algebras
![]() $I_z\, :\, \mathfrak{g} \longrightarrow {\rm ad}(E_G)_y$
. Using
$I_z\, :\, \mathfrak{g} \longrightarrow {\rm ad}(E_G)_y$
. Using
![]() $I_z$
, the form
$I_z$
, the form
![]() $\sigma$
in (2.4) produces a symmetric nondegenerate bilinear form on the fiber
$\sigma$
in (2.4) produces a symmetric nondegenerate bilinear form on the fiber
![]() ${\rm ad}(E_G)_y$
; this bilinear form on
${\rm ad}(E_G)_y$
; this bilinear form on
![]() ${\rm ad}(E_G)_y$
constructed using
${\rm ad}(E_G)_y$
constructed using
![]() $\sigma$
is actually independent of the choice of the point
$\sigma$
is actually independent of the choice of the point
![]() $z$
because
$z$
because
![]() $\sigma$
is
$\sigma$
is
![]() $G$
-invariant. Let
$G$
-invariant. Let
be the bilinear form constructed as above using
![]() $\sigma$
.
$\sigma$
.
Let
![]() $\phi$
be a framing of
$\phi$
be a framing of
![]() $E_G$
over
$E_G$
over
![]() $D$
. For every
$D$
. For every
![]() $x\, \in \, D$
, define the Lie subalgebra
$x\, \in \, D$
, define the Lie subalgebra
(see (2.3)).
2.3 Framing of
 $G$
-connections
$G$
-connections
Take a holomorphic principal
![]() $G$
-bundle
$G$
-bundle
![]() $E_G$
over
$E_G$
over
![]() $X$
. Let
$X$
. Let
![]() $TE_G$
be the holomorphic tangent bundle of
$TE_G$
be the holomorphic tangent bundle of
![]() $E_G$
. Consider the action of
$E_G$
. Consider the action of
![]() $G$
on
$G$
on
![]() $TE_G$
given by the tautological action of
$TE_G$
given by the tautological action of
![]() $G$
on
$G$
on
![]() $E_G$
. The quotient
$E_G$
. The quotient
is a holomorphic vector bundle over
![]() $X$
; it is called the Atiyah algebra for
$X$
; it is called the Atiyah algebra for
![]() $E_G$
. The Lie bracket operation of the vector fields on
$E_G$
. The Lie bracket operation of the vector fields on
![]() $E_G$
produces a Lie algebra structure on the coherent sheaf associated to
$E_G$
produces a Lie algebra structure on the coherent sheaf associated to
![]() ${\rm At} (E_G)$
. There is a short exact sequence of holomorphic vector bundles on
${\rm At} (E_G)$
. There is a short exact sequence of holomorphic vector bundles on
![]() $X$
,
$X$
,
where the projection
![]() $p_{{\rm At}}$
is given by the differential
$p_{{\rm At}}$
is given by the differential
![]() $dp$
of the map
$dp$
of the map
![]() $p$
in (2.2) [Reference AtiyahAt1]. All the homomorphisms in (2.7) are compatible with the Lie algebra structures. Define a holomorphic vector bundle
$p$
in (2.2) [Reference AtiyahAt1]. All the homomorphisms in (2.7) are compatible with the Lie algebra structures. Define a holomorphic vector bundle
![]() ${\rm At}_D (E_G)$
over
${\rm At}_D (E_G)$
over
![]() $X$
as
$X$
as
Then (2.7) gives the following short exact sequence of holomorphic vector bundles on
![]() $X$
:
$X$
:
where
![]() $p_{{\rm At}_D}$
is the restriction, to
$p_{{\rm At}_D}$
is the restriction, to
![]() ${\rm At}_D (E_G)\, \subset \, {\rm At} (E_G)$
, of the homomorphism
${\rm At}_D (E_G)\, \subset \, {\rm At} (E_G)$
, of the homomorphism
![]() $p_{{\rm At}}$
in (2.7).
$p_{{\rm At}}$
in (2.7).
Definition 2.2 [Reference AtiyahAt1].A holomorphic connection on
![]() $E_G$
is a holomorphic homomorphism of vector bundles
$E_G$
is a holomorphic homomorphism of vector bundles
such that
![]() $ p_{{\rm At}} \circ \nabla \,=\,{\rm Id}_{TX}$
, where
$ p_{{\rm At}} \circ \nabla \,=\,{\rm Id}_{TX}$
, where
![]() $p_{{\rm At}}$
is the projection in (2.7). A
$p_{{\rm At}}$
is the projection in (2.7). A
![]() $D$
-twisted holomorphic connection on
$D$
-twisted holomorphic connection on
![]() $E_G$
(also called a logarithmic connection on
$E_G$
(also called a logarithmic connection on
![]() $E_G$
with polar part on
$E_G$
with polar part on
![]() $D$
) is a holomorphic homomorphism of vector bundles
$D$
) is a holomorphic homomorphism of vector bundles
such that
![]() $ p_{{\rm At}_D} \circ \nabla \,=\,{\rm Id}_{TX(-D)}$
, where
$ p_{{\rm At}_D} \circ \nabla \,=\,{\rm Id}_{TX(-D)}$
, where
![]() $p_{{\rm At}_D}$
is the homomorphism in (2.8).
$p_{{\rm At}_D}$
is the homomorphism in (2.8).
For a
![]() $D$
-twisted holomorphic connection
$D$
-twisted holomorphic connection
![]() $\nabla$
on
$\nabla$
on
![]() $E_G$
, consider the commutative diagram
$E_G$
, consider the commutative diagram
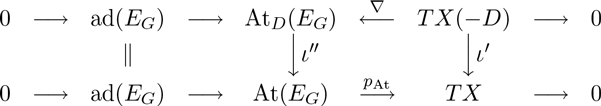
where
![]() $\iota '$
and
$\iota '$
and
![]() $\iota ''$
are the natural inclusion homomorphisms. For any point
$\iota ''$
are the natural inclusion homomorphisms. For any point
![]() $x\, \in \, D$
, the homomorphism of fibers
$x\, \in \, D$
, the homomorphism of fibers
vanishes, and hence
![]() $(p_{{\rm At}}\circ \iota ''\circ \nabla )(TX(-D)_x)\,=\, 0$
by the commutativity of the above diagram. Consequently, we have
$(p_{{\rm At}}\circ \iota ''\circ \nabla )(TX(-D)_x)\,=\, 0$
by the commutativity of the above diagram. Consequently, we have
Note that for any point
![]() $x\, \in \, D$
, using the Poincaré adjunction formula it follows that
$x\, \in \, D$
, using the Poincaré adjunction formula it follows that
The element
is called the residue of the logarithmic connection
![]() $\nabla$
at
$\nabla$
at
![]() $x$
. To describe this residue explicitly, first recall that a holomorphic connection on
$x$
. To describe this residue explicitly, first recall that a holomorphic connection on
![]() $E_G$
furnishes lift of holomorphic vector fields on any open subset
$E_G$
furnishes lift of holomorphic vector fields on any open subset
![]() $U$
of
$U$
of
![]() $X$
to
$X$
to
![]() $G$
–invariant holomorphic vector fields on
$G$
–invariant holomorphic vector fields on
![]() $E_G\big \vert _{p^{-1}(U)}$
. Similarly, a
$E_G\big \vert _{p^{-1}(U)}$
. Similarly, a
![]() $D$
-twisted holomorphic connection
$D$
-twisted holomorphic connection
![]() $\nabla$
furnishes lift of holomorphic vector fields on any open subset
$\nabla$
furnishes lift of holomorphic vector fields on any open subset
![]() $U\, \subset \, X$
, vanishing on
$U\, \subset \, X$
, vanishing on
![]() $D\cap U$
, to the
$D\cap U$
, to the
![]() $G$
–invariant holomorphic vector fields on
$G$
–invariant holomorphic vector fields on
![]() $E_G\big \vert _{p^{-1}(U)}$
. In other words, these lifts are locally defined
$E_G\big \vert _{p^{-1}(U)}$
. In other words, these lifts are locally defined
![]() $G$
–invariant holomorphic sections of
$G$
–invariant holomorphic sections of
![]() $TE_G(-\log p^{-1}(D))$
. Therefore, given a vector field
$TE_G(-\log p^{-1}(D))$
. Therefore, given a vector field
![]() $v$
defined on a neighborhood of
$v$
defined on a neighborhood of
![]() $x_i\, \in \, D$
of
$x_i\, \in \, D$
of
![]() $X$
, such that
$X$
, such that
![]() $v(x_i)\,=\,0$
and
$v(x_i)\,=\,0$
and
![]() $a_{x_i}(v(x_i))\, \not =\, 0$
(see (2.9)), its lift
$a_{x_i}(v(x_i))\, \not =\, 0$
(see (2.9)), its lift
![]() $\widetilde {v}$
to
$\widetilde {v}$
to
![]() $E_G$
for
$E_G$
for
![]() $\nabla$
may be nonzero on
$\nabla$
may be nonzero on
![]() $p^{-1}(x_i)$
because
$p^{-1}(x_i)$
because
![]() $\widetilde {v}$
may be a nonzero vertical vector field on
$\widetilde {v}$
may be a nonzero vertical vector field on
![]() $p^{-1}(x_i)$
. The residue of
$p^{-1}(x_i)$
. The residue of
![]() $\nabla$
at
$\nabla$
at
![]() $x_i$
is
$x_i$
is
![]() $\widetilde {v}(p^{-1}(x_i))/a_{x_i}(v(x_i))\, \in \, {\rm ad}(E_G)_{x_i}$
(see (2.9)).
$\widetilde {v}(p^{-1}(x_i))/a_{x_i}(v(x_i))\, \in \, {\rm ad}(E_G)_{x_i}$
(see (2.9)).
For any
![]() $x \in D$
, let
$x \in D$
, let
be the annihilator of
![]() $\mathcal{H}_x \,\subset \,{\rm ad}(E_G)_x$
, defined in (2.6), with respect to the bilinear form
$\mathcal{H}_x \,\subset \,{\rm ad}(E_G)_x$
, defined in (2.6), with respect to the bilinear form
![]() $\widehat {\sigma }(x)$
in (2.5).
$\widehat {\sigma }(x)$
in (2.5).
Definition 2.3. A framed
![]() $G$
-connection is a triple of the form
$G$
-connection is a triple of the form
![]() $(E_G,\,\nabla ,\,\phi )$
, where
$(E_G,\,\nabla ,\,\phi )$
, where
![]() $(E_G,\, \phi )$
is a framed principal
$(E_G,\, \phi )$
is a framed principal
![]() $G$
-bundle and
$G$
-bundle and
![]() $\nabla \,\colon \, TX(-D) \,\longrightarrow \,{\rm At}_D(E_G)$
is a
$\nabla \,\colon \, TX(-D) \,\longrightarrow \,{\rm At}_D(E_G)$
is a
![]() $D$
-twisted connection such that
$D$
-twisted connection such that
![]() ${\rm res}_{x} (\nabla )\, \in \, \mathcal{H}^{\perp }_{x} \,\subset \, {\rm ad}(E_G)_{x}$
for every
${\rm res}_{x} (\nabla )\, \in \, \mathcal{H}^{\perp }_{x} \,\subset \, {\rm ad}(E_G)_{x}$
for every
![]() $x\,\in \, D$
, where
$x\,\in \, D$
, where
![]() $\mathcal{H}^{\perp }_{x}$
is constructed in (2.10).
$\mathcal{H}^{\perp }_{x}$
is constructed in (2.10).
2.4 Infinitesimal deformations
Consider the following
![]() $2$
-term complex of sheaves on
$2$
-term complex of sheaves on
![]() $X$
:
$X$
:
Lemma 2.4 (See [Reference Biswas, Logares and Peón-NietoBLP2, Lemma 3.5] and [Reference ChenCh, Proposition 4.4]).Assume that
![]() $H_x\,=\, \{e \}$
for every
$H_x\,=\, \{e \}$
for every
![]() $x\,\in \, D$
. The infinitesimal deformations of the framed
$x\,\in \, D$
. The infinitesimal deformations of the framed
![]() $G$
-connection
$G$
-connection
![]() $(E_G,\, \nabla ,\, \phi )$
are parametrized by the elements of the first hypercohomology
$(E_G,\, \nabla ,\, \phi )$
are parametrized by the elements of the first hypercohomology
![]() $\mathbb{H}^1(\mathcal{C}_{\bullet })$
of the complex in (2.11).
$\mathbb{H}^1(\mathcal{C}_{\bullet })$
of the complex in (2.11).
Let
be a framed
![]() $G$
-connection (see Definition 2.3). Consider the subspace
$G$
-connection (see Definition 2.3). Consider the subspace
![]() $\mathcal{H}_x \,\subset \, {\rm ad}(E_G)_x$
in (2.6). Let
$\mathcal{H}_x \,\subset \, {\rm ad}(E_G)_x$
in (2.6). Let
![]() ${\rm ad}_{\phi }(E_G)$
and
${\rm ad}_{\phi }(E_G)$
and
![]() ${\rm ad}^n_{\phi }(E_G)$
be the holomorphic vector bundles on
${\rm ad}^n_{\phi }(E_G)$
be the holomorphic vector bundles on
![]() $X$
defined by the following short exact sequences of coherent analytic sheaves on
$X$
defined by the following short exact sequences of coherent analytic sheaves on
![]() $X$
:
$X$
:
and
respectively.
Lemma 2.5. The
![]() $D$
-twisted connection
$D$
-twisted connection
![]() $\widehat {\nabla }$
in (2.12) gives a holomorphic differential operator
$\widehat {\nabla }$
in (2.12) gives a holomorphic differential operator
If
![]() $\widehat {\nabla }$
is a framed
$\widehat {\nabla }$
is a framed
![]() $G$
-connection, then
$G$
-connection, then
![]() $\nabla$
sends the subsheaf
$\nabla$
sends the subsheaf
![]() ${\rm ad}_{\phi } (E_G)$
in (2.13) to
${\rm ad}_{\phi } (E_G)$
in (2.13) to
![]() ${\rm ad}^n_{\phi } (E_G) \otimes K_X (D)$
, where
${\rm ad}^n_{\phi } (E_G) \otimes K_X (D)$
, where
![]() ${\rm ad}^n_{\phi }(E_G)$
is constructed in (2.14).
${\rm ad}^n_{\phi }(E_G)$
is constructed in (2.14).
Proof. Let
![]() $s$
be a holomorphic section of
$s$
be a holomorphic section of
![]() ${\rm ad} (E_G)$
defined over an open subset
${\rm ad} (E_G)$
defined over an open subset
![]() $U\, \subset \, X$
. Then
$U\, \subset \, X$
. Then
![]() $s$
defines a
$s$
defines a
![]() $G$
–invariant holomorphic vector field on
$G$
–invariant holomorphic vector field on
![]() $p^{-1}(U)\, \subset \, E_G$
which is vertical for the projection
$p^{-1}(U)\, \subset \, E_G$
which is vertical for the projection
![]() $p$
in (2.2); this vertical vector field on
$p$
in (2.2); this vertical vector field on
![]() $p^{-1}(U)$
will be denoted by
$p^{-1}(U)$
will be denoted by
![]() $\widetilde s$
. Take any
$\widetilde s$
. Take any
![]() $t\, \in \, H^0(U,\, TX(-D))$
. Let
$t\, \in \, H^0(U,\, TX(-D))$
. Let
be the horizontal lift of
![]() $t$
for the
$t$
for the
![]() $D$
-twisted connection
$D$
-twisted connection
![]() $\widehat \nabla$
in (2.12). Now consider the Lie bracket of vector fields
$\widehat \nabla$
in (2.12). Now consider the Lie bracket of vector fields
Note that
![]() $[\widetilde {t},\, \widetilde {s}]$
is
$[\widetilde {t},\, \widetilde {s}]$
is
![]() $G$
–invariant because both
$G$
–invariant because both
![]() $\widetilde {s}$
and
$\widetilde {s}$
and
![]() $\widetilde {t}$
are. Furthermore,
$\widetilde {t}$
are. Furthermore,
![]() $[\widetilde {t}, \, \widetilde {s}]$
is vertical for the projection
$[\widetilde {t}, \, \widetilde {s}]$
is vertical for the projection
![]() $p$
, because
$p$
, because
![]() $\widetilde {s}$
is vertical and
$\widetilde {s}$
is vertical and
![]() $\widetilde {t}$
is
$\widetilde {t}$
is
![]() $G$
–invariant. Indeed, for any holomorphic function
$G$
–invariant. Indeed, for any holomorphic function
![]() $f$
on
$f$
on
![]() $U$
, evidently
$U$
, evidently
![]() $\widetilde {s}(f\circ p)\,=\, 0$
(recall that
$\widetilde {s}(f\circ p)\,=\, 0$
(recall that
![]() $\widetilde s$
is vertical), and we also have that
$\widetilde s$
is vertical), and we also have that
![]() $\widetilde {t}(f\circ p)$
is
$\widetilde {t}(f\circ p)$
is
![]() $G$
-invariant, so
$G$
-invariant, so
![]() $\widetilde {s}(\widetilde {t} (f\circ p))\, =\, 0$
. Consequently,
$\widetilde {s}(\widetilde {t} (f\circ p))\, =\, 0$
. Consequently,
![]() $[\widetilde {t},\, \widetilde {s}]$
produces a holomorphic section of
$[\widetilde {t},\, \widetilde {s}]$
produces a holomorphic section of
![]() ${\rm ad}(E_G)$
over
${\rm ad}(E_G)$
over
![]() $U$
; this section of
$U$
; this section of
![]() ${\rm ad} (E_G)$
over
${\rm ad} (E_G)$
over
![]() $U$
will be denoted by
$U$
will be denoted by
![]() $[t,\, s]'$
. Next, note that a holomorphic function
$[t,\, s]'$
. Next, note that a holomorphic function
![]() $f$
on
$f$
on
![]() $U$
satisfies
$U$
satisfies
because
![]() $\widetilde {s} (f\circ p)\,=\, 0$
(recall that
$\widetilde {s} (f\circ p)\,=\, 0$
(recall that
![]() $\widetilde s$
is a vertical vector field). Consequently, there is a homomorphism
$\widetilde s$
is a vertical vector field). Consequently, there is a homomorphism
uniquely defined by the equation
where
![]() $s$
and
$s$
and
![]() $t$
are locally defined holomorphic sections of
$t$
are locally defined holomorphic sections of
![]() ${\rm ad} (E_G)$
and
${\rm ad} (E_G)$
and
![]() $TX(-D)$
respectively, while
$TX(-D)$
respectively, while
![]() $\langle -,\, -\rangle$
is the natural pairing
$\langle -,\, -\rangle$
is the natural pairing
![]() $TX(-D)\otimes K_X(D)\, \longrightarrow \, {\mathcal O}_X$
.
$TX(-D)\otimes K_X(D)\, \longrightarrow \, {\mathcal O}_X$
.
Recall from Definition 2.3 that
![]() ${\rm res}_{x} ( \nabla )\, \in \, \mathcal{H}^{\perp }_{x}$
. Therefore, from the property of residues mentioned earlier, it follows immediately that
${\rm res}_{x} ( \nabla )\, \in \, \mathcal{H}^{\perp }_{x}$
. Therefore, from the property of residues mentioned earlier, it follows immediately that
![]() $\widetilde {t}(x)\, \in \, {\mathcal H}^\perp _x$
for every
$\widetilde {t}(x)\, \in \, {\mathcal H}^\perp _x$
for every
![]() $x\, \in \, D$
. Now if
$x\, \in \, D$
. Now if
![]() $s$
is a locally defined holomorphic section of
$s$
is a locally defined holomorphic section of
![]() ${\rm ad}_{\phi } (E_G)$
, then
${\rm ad}_{\phi } (E_G)$
, then
![]() $\widetilde {s}(x)\, \in \, {\mathcal H}_x$
. Next, note that
$\widetilde {s}(x)\, \in \, {\mathcal H}_x$
. Next, note that
because
for all
![]() $a,\, b,\, c\,\in \, {\rm ad}(E_G)_x$
(this is derived using the given condition on
$a,\, b,\, c\,\in \, {\rm ad}(E_G)_x$
(this is derived using the given condition on
![]() $\sigma$
that it is
$\sigma$
that it is
![]() $G$
-invariant). As a consequence of (2.15), the homomorphism
$G$
-invariant). As a consequence of (2.15), the homomorphism
![]() $\nabla$
maps the subsheaf
$\nabla$
maps the subsheaf
![]() ${\rm ad}_{\phi } (E_G)$
to
${\rm ad}_{\phi } (E_G)$
to
![]() ${\rm ad}^n_{\phi } (E_G) \otimes K_X (D)$
.
${\rm ad}^n_{\phi } (E_G) \otimes K_X (D)$
.
In view of Lemma 2.5, the following
![]() $2$
-term complex of sheaves on
$2$
-term complex of sheaves on
![]() $X$
is obtained:
$X$
is obtained:
The next lemma is straightforward to prove.
3. Construction of the moduli space
We now assume that
![]() $G\,=\,{\rm GL}(r,\mathbb{C})$
. Fix a closed complex algebraic proper subgroup
$G\,=\,{\rm GL}(r,\mathbb{C})$
. Fix a closed complex algebraic proper subgroup
![]() $H_x \,\subsetneq \, G$
for each
$H_x \,\subsetneq \, G$
for each
![]() $x\in D$
, and set
$x\in D$
, and set
![]() $H\,=\, \{ H_x \}_{x \in D}$
to be the collection of subgroups indexed by the points of
$H\,=\, \{ H_x \}_{x \in D}$
to be the collection of subgroups indexed by the points of
![]() $D$
. For a framed vector bundle
$D$
. For a framed vector bundle
![]() $(E,\, \phi )$
, if
$(E,\, \phi )$
, if
![]() $E_G$
is the principal
$E_G$
is the principal
![]() ${\rm GL}(r,\mathbb{C})$
-bundle associated to the vector bundle
${\rm GL}(r,\mathbb{C})$
-bundle associated to the vector bundle
![]() $E$
, then
$E$
, then
![]() ${\rm ad}(E_G)\,=\, {\rm End}(E)$
. Define
${\rm ad}(E_G)\,=\, {\rm End}(E)$
. Define
(see Lemma 2.5).
3.1 Definition of the moduli functors
A framed
![]() ${\rm GL}(r,\mathbb{C})$
-connection
${\rm GL}(r,\mathbb{C})$
-connection
![]() $(E,\,\phi , \, \nabla )$
on
$(E,\,\phi , \, \nabla )$
on
![]() $X$
will be called simple if
$X$
will be called simple if
Definition 3.1. Define a stack
![]() $\mathcal{M}^{H}_{\textrm {FC}}(d)$
of simple framed
$\mathcal{M}^{H}_{\textrm {FC}}(d)$
of simple framed
![]() ${\rm GL}(r,\mathbb{C})$
-connections, for
${\rm GL}(r,\mathbb{C})$
-connections, for
![]() $H$
, by breaking it into the following two cases, A and B.
$H$
, by breaking it into the following two cases, A and B.
-
(A) If
 $\mathbb{C}^* \cdot \textrm { Id}\, \not \subset \, H_x$
for some
$\mathbb{C}^* \cdot \textrm { Id}\, \not \subset \, H_x$
for some
 $x\,\in \, D$
, then define a stack
$x\,\in \, D$
, then define a stack
 $\mathcal{M}^{H}_{\textrm {FC}}(d)$
over the category of locally Noetherian schemes over
$\mathcal{M}^{H}_{\textrm {FC}}(d)$
over the category of locally Noetherian schemes over
 $\textrm { Spec}\mathbb{C}$
whose objects are quadruples
$\textrm { Spec}\mathbb{C}$
whose objects are quadruples
 $(S,\, E,\, \phi \,= \,\{ \phi _{x\times S} \}_{x \in D} ,\, \nabla )$
of the following type.
$(S,\, E,\, \phi \,= \,\{ \phi _{x\times S} \}_{x \in D} ,\, \nabla )$
of the following type.
-
(1)
 $S$
is a locally Noetherian scheme over
$S$
is a locally Noetherian scheme over
 $\textrm { Spec}\mathbb{C}$
, and
$\textrm { Spec}\mathbb{C}$
, and
 $E\, \longrightarrow \, X\times S$
is a vector bundle of rank
$E\, \longrightarrow \, X\times S$
is a vector bundle of rank
 $r$
with
$r$
with
 $\deg (E|_{X\times s})\,=\,d$
for any geometric point
$\deg (E|_{X\times s})\,=\,d$
for any geometric point
 $s$
of
$s$
of
 $S$
.
$S$
. -
(2)
 $\phi _{x\times S}$
is a section of the structure map
Here the action of the group scheme
$\phi _{x\times S}$
is a section of the structure map
Here the action of the group scheme \begin{align*} {\rm Isom}_{S} (\mathcal{O}_{x\times S}^{\oplus r} ,\, \, E|_{x\times S} )/ (H_x \times S) \longrightarrow x\times S. \end{align*}
\begin{align*} {\rm Isom}_{S} (\mathcal{O}_{x\times S}^{\oplus r} ,\, \, E|_{x\times S} )/ (H_x \times S) \longrightarrow x\times S. \end{align*}
 $H_x \times S$
over
$H_x \times S$
over
 $S$
on
$S$
on
 ${\rm Isom}_{S} (\mathcal{O}_{x\times S}^{\oplus r},\, \, E|_{x\times S})$
is the restriction of the natural transitive action of the group scheme
${\rm Isom}_{S} (\mathcal{O}_{x\times S}^{\oplus r},\, \, E|_{x\times S})$
is the restriction of the natural transitive action of the group scheme
 ${\rm GL}(r,\mathbb{C}) \times S$
over
${\rm GL}(r,\mathbb{C}) \times S$
over
 $S$
on
$S$
on
 ${\rm Isom}_{S} (\mathcal{O}_{x\times S}^{\oplus r},\, \, E|_{x\times S})$
given by the standard action of
${\rm Isom}_{S} (\mathcal{O}_{x\times S}^{\oplus r},\, \, E|_{x\times S})$
given by the standard action of
 ${\rm GL}(r,{\mathbb C})$
on
${\rm GL}(r,{\mathbb C})$
on
 $\mathcal{O}_{x\times S}^{\oplus r}$
. Define a
$\mathcal{O}_{x\times S}^{\oplus r}$
. Define a
 $S$
-scheme
$S$
-scheme
 $\widetilde {S}$
and a map
$\widetilde {S}$
and a map
 $\widetilde {S} \,\longrightarrow \,{\rm Isom}_{S} (\mathcal{O}_{x\times S}^{\oplus r},\,\, E|_{x\times S} )$
such that the diagram
$\widetilde {S} \,\longrightarrow \,{\rm Isom}_{S} (\mathcal{O}_{x\times S}^{\oplus r},\,\, E|_{x\times S} )$
such that the diagram

is Cartesian. Let
be the isomorphism given by the map \begin{align*}\widetilde {\phi }_{x \times \widetilde {S}}\,\colon \, \mathcal{O}_{x\times \widetilde {S}}^{\oplus r} \,\xrightarrow {\ \sim \ }\, E_{\widetilde {S}}|_{x\times \widetilde {S}} \end{align*}
\begin{align*}\widetilde {\phi }_{x \times \widetilde {S}}\,\colon \, \mathcal{O}_{x\times \widetilde {S}}^{\oplus r} \,\xrightarrow {\ \sim \ }\, E_{\widetilde {S}}|_{x\times \widetilde {S}} \end{align*}
 $\widetilde {S}\,\longrightarrow \, {\rm Isom}_{S}(\mathcal{O}_{x\times S}^{\oplus r},\, \,E|_{x\times S})$
.
$\widetilde {S}\,\longrightarrow \, {\rm Isom}_{S}(\mathcal{O}_{x\times S}^{\oplus r},\, \,E|_{x\times S})$
.
-
(3)
 $\nabla \,\colon \, E \,\longrightarrow \, E \otimes K_{X}(D)$
is a relative connection, relative to
$\nabla \,\colon \, E \,\longrightarrow \, E \otimes K_{X}(D)$
is a relative connection, relative to
 $S$
.
$S$
. -
(4) Let
 ${\rm res}_{x\times \widetilde {S}}(\nabla _{\widetilde {S}}) \,\in \, {\rm End}(E_{\widetilde {S}})|_{x\times \widetilde {S}}$
be the residue of the induced connection
${\rm res}_{x\times \widetilde {S}}(\nabla _{\widetilde {S}}) \,\in \, {\rm End}(E_{\widetilde {S}})|_{x\times \widetilde {S}}$
be the residue of the induced connection
 $\nabla _{\widetilde {S}}\,\colon \,E_{\widetilde {S}}\,\longrightarrow \, E_{\widetilde {S}} \otimes K_{X}(D)$
. Then
$\nabla _{\widetilde {S}}\,\colon \,E_{\widetilde {S}}\,\longrightarrow \, E_{\widetilde {S}} \otimes K_{X}(D)$
. Then
 $\widetilde {\phi }^{-1}_{x \times \widetilde {S}} \circ {\rm res}_{x\times \widetilde {S}}(\nabla _{\widetilde {S}}) \circ \widetilde {\phi }_{x \times \widetilde {S}} \,\,\in \,\, \mathfrak{h}^{\perp } \otimes \mathcal{O}_{\widetilde {S}}$
.
$\widetilde {\phi }^{-1}_{x \times \widetilde {S}} \circ {\rm res}_{x\times \widetilde {S}}(\nabla _{\widetilde {S}}) \circ \widetilde {\phi }_{x \times \widetilde {S}} \,\,\in \,\, \mathfrak{h}^{\perp } \otimes \mathcal{O}_{\widetilde {S}}$
. -
(5) For each point
 $s\,\in \, S$
, the framed
$s\,\in \, S$
, the framed
 ${\rm GL}(r,\mathbb{C})$
-connection
${\rm GL}(r,\mathbb{C})$
-connection
 $(E_s,\,\phi _s, \, \nabla _s)$
is simple. Recall that
$(E_s,\,\phi _s, \, \nabla _s)$
is simple. Recall that
 $(E_s,\,\phi _s, \, \nabla _s)$
is simple if
$(E_s,\,\phi _s, \, \nabla _s)$
is simple if
 \begin{align*} {\rm ker}\left (H^0(X,\,\mathcal{E}nd_{\phi _s}(E_s) )\, \xrightarrow {\nabla _s}\, H^0( X,\, \mathcal{E}nd_{\phi _s}^n(E_s)\otimes K_X(D))\right ) \,=\,0\, . \end{align*}
\begin{align*} {\rm ker}\left (H^0(X,\,\mathcal{E}nd_{\phi _s}(E_s) )\, \xrightarrow {\nabla _s}\, H^0( X,\, \mathcal{E}nd_{\phi _s}^n(E_s)\otimes K_X(D))\right ) \,=\,0\, . \end{align*}
A morphism
in \begin{align*} (S,\, E,\, \phi ,\,\nabla ) \longrightarrow (S',\, E',\, \phi ',\, \nabla ' ) \end{align*}
\begin{align*} (S,\, E,\, \phi ,\,\nabla ) \longrightarrow (S',\, E',\, \phi ',\, \nabla ' ) \end{align*}
 $\mathcal{M}^{H}_{\textrm {FC}}$
is a Cartesian square
$\mathcal{M}^{H}_{\textrm {FC}}$
is a Cartesian square

such that the diagram

is commutative and
 $(\widetilde {\phi }'_{x \times \widetilde {S}})^{-1}\circ \sigma _{\widetilde {S}} \circ \widetilde {\phi }_{x \times \widetilde {S}}\, \in \, H_{x} \times \widetilde {S}$
for each
$(\widetilde {\phi }'_{x \times \widetilde {S}})^{-1}\circ \sigma _{\widetilde {S}} \circ \widetilde {\phi }_{x \times \widetilde {S}}\, \in \, H_{x} \times \widetilde {S}$
for each
 $x \,\in \, D$
.
$x \,\in \, D$
. -
-
(B) If
 $\mathbb{C}^* e \,\subset \, H_x$
for all
$\mathbb{C}^* e \,\subset \, H_x$
for all
 $x\,\in \, D$
, then define
$x\,\in \, D$
, then define
 $\mathcal{M}^{H}_{\textrm {FC}}(d)$
to be the stackification of
$\mathcal{M}^{H}_{\textrm {FC}}(d)$
to be the stackification of
 ${\rm pre-}\mathcal{M}^{H}_{\textrm {FC}}(d)$
(see [
Reference OlssonOls
,Theorem 4.6.5]). Here,
${\rm pre-}\mathcal{M}^{H}_{\textrm {FC}}(d)$
(see [
Reference OlssonOls
,Theorem 4.6.5]). Here,
 ${\rm pre-}\mathcal{M}^{H}_{\textrm {FC}}(d)$
is the fibered category over the category of locally Noetherian schemes over
${\rm pre-}\mathcal{M}^{H}_{\textrm {FC}}(d)$
is the fibered category over the category of locally Noetherian schemes over
 $\textrm { Spec}\,\mathbb{C}$
whose objects are quadruples
$\textrm { Spec}\,\mathbb{C}$
whose objects are quadruples
 $(S,\, E,\, \phi \,=\, \{ \phi _{x\times S} \}_{x \in D} ,\,\nabla )$
that satisfy (1), (3) and (4) as above as well as the following (2’) and (5’).
$(S,\, E,\, \phi \,=\, \{ \phi _{x\times S} \}_{x \in D} ,\,\nabla )$
that satisfy (1), (3) and (4) as above as well as the following (2’) and (5’).
-
(2)′:
 $\phi _{x\times S}$
is a section of the structure map
Here the action of the group scheme
$\phi _{x\times S}$
is a section of the structure map
Here the action of the group scheme \begin{align*} {\rm Isom}_{S} (\mathcal{O}_{x\times S}^{\oplus r},\, \, E|_{x\times S} )/ (H_x \times S) \, \longrightarrow \, x\times S. \end{align*}
\begin{align*} {\rm Isom}_{S} (\mathcal{O}_{x\times S}^{\oplus r},\, \, E|_{x\times S} )/ (H_x \times S) \, \longrightarrow \, x\times S. \end{align*}
 $H_x \times S$
, over
$H_x \times S$
, over
 $S$
, on
$S$
, on
 ${\rm Isom}_{S} (\mathcal{O}_{x\times S}^{\oplus r} ,\, \, E|_{x\times S} )$
is the restriction of the natural transitive group action of the group scheme
${\rm Isom}_{S} (\mathcal{O}_{x\times S}^{\oplus r} ,\, \, E|_{x\times S} )$
is the restriction of the natural transitive group action of the group scheme
 ${\rm GL}(r,\mathbb{C}) \times S$
over
${\rm GL}(r,\mathbb{C}) \times S$
over
 $S$
on
$S$
on
 ${\rm Isom}_{S} (\mathcal{O}_{x\times S}^{\oplus r},\,\, E|_{x\times S})$
given by the standard action of
${\rm Isom}_{S} (\mathcal{O}_{x\times S}^{\oplus r},\,\, E|_{x\times S})$
given by the standard action of
 ${\rm GL}(r,{\mathbb C})$
on
${\rm GL}(r,{\mathbb C})$
on
 $\mathcal{O}_{x\times S}^{\oplus r}$
. Define a
$\mathcal{O}_{x\times S}^{\oplus r}$
. Define a
 $S$
-scheme
$S$
-scheme
 $\widehat {S}$
and a map
$\widehat {S}$
and a map
 $\widehat {S} \,\longrightarrow \, {\rm Isom}_{S} (\mathcal{O}_{x\times S}^{\oplus r},\, \, E|_{x\times S}) / (\mathbb{C}^* e \times S)$
such that the diagram
$\widehat {S} \,\longrightarrow \, {\rm Isom}_{S} (\mathcal{O}_{x\times S}^{\oplus r},\, \, E|_{x\times S}) / (\mathbb{C}^* e \times S)$
such that the diagram

is Cartesian. Denote by
 $\widehat {\phi }_{x \times \widehat {S}}\,\colon \, \mathbb{P}(\mathcal{O}_{x\times \widehat {S}}^{\oplus r}) \,\stackrel {\sim }{\longrightarrow }\, \mathbb{P}( E_{\widehat {S}}|_{x\times \widehat {S}})$
the isomorphism given by the map
$\widehat {\phi }_{x \times \widehat {S}}\,\colon \, \mathbb{P}(\mathcal{O}_{x\times \widehat {S}}^{\oplus r}) \,\stackrel {\sim }{\longrightarrow }\, \mathbb{P}( E_{\widehat {S}}|_{x\times \widehat {S}})$
the isomorphism given by the map
 $\widehat {S} \,\longrightarrow \,{\rm Isom}_{S} (\mathcal{O}_{x\times S}^{\oplus r}, \,\,E|_{x\times S}) / (\mathbb{C}^* e \times S)$
.
$\widehat {S} \,\longrightarrow \,{\rm Isom}_{S} (\mathcal{O}_{x\times S}^{\oplus r}, \,\,E|_{x\times S}) / (\mathbb{C}^* e \times S)$
. -
(5)′:
 $(E_s,\,\phi _s, \, \nabla _s)$
is simple for each point
$(E_s,\,\phi _s, \, \nabla _s)$
is simple for each point
 $s \,\in \, S$
, that is,
$s \,\in \, S$
, that is,
 \begin{align*} {\rm ker}(H^0(X,\,\mathcal{E}nd_{\phi _s}(E_s) )\, \xrightarrow {\nabla _s}\, H^0( X,\, \mathcal{E}nd_{\phi _s}^n(E_s)\otimes K_X(D))) \,=\, \mathbb{C}. \end{align*}
\begin{align*} {\rm ker}(H^0(X,\,\mathcal{E}nd_{\phi _s}(E_s) )\, \xrightarrow {\nabla _s}\, H^0( X,\, \mathcal{E}nd_{\phi _s}^n(E_s)\otimes K_X(D))) \,=\, \mathbb{C}. \end{align*}
A morphism
in \begin{align*} (S,\, E,\, \phi ,\, \nabla ) \longrightarrow (S',\, E',\, \phi ',\, \nabla ' ) \end{align*}
\begin{align*} (S,\, E,\, \phi ,\, \nabla ) \longrightarrow (S',\, E',\, \phi ',\, \nabla ' ) \end{align*}
 ${\rm pre-}\mathcal{M}^{H}_{\textrm {FC}}(d)$
is a triple
${\rm pre-}\mathcal{M}^{H}_{\textrm {FC}}(d)$
is a triple
 $(\mathcal{L},\, \sigma ,\, \widetilde {\sigma })$
, where
$(\mathcal{L},\, \sigma ,\, \widetilde {\sigma })$
, where
 $\mathcal{L}$
is a line bundle on
$\mathcal{L}$
is a line bundle on
 $S'$
and
$S'$
and
 $\sigma ,\, \widetilde {\sigma }$
are maps that fit in a Cartesian square
$\sigma ,\, \widetilde {\sigma }$
are maps that fit in a Cartesian square

such that the diagram

is commutative and
for each \begin{align*}(\widehat {\phi }'_{x \times \widehat {S}} )^{-1}\circ \overline {\sigma }_{x\times \widehat {S}} \circ \widehat {\phi }_{x \times \widehat {S}} \,\in \, (H_{x}/\mathbb{C}^*e ) \times \widehat {S}\end{align*}
\begin{align*}(\widehat {\phi }'_{x \times \widehat {S}} )^{-1}\circ \overline {\sigma }_{x\times \widehat {S}} \circ \widehat {\phi }_{x \times \widehat {S}} \,\in \, (H_{x}/\mathbb{C}^*e ) \times \widehat {S}\end{align*}
 $x \,\in \, D$
, where
$x \,\in \, D$
, where
 $\overline {\sigma }_{x\times \widehat {S}}\, \colon \,\mathbb{P}(E_{\widehat {S}}|_{x \times \widehat {S}})\,\longrightarrow \, \mathbb{P}(E_{\widehat {S}}'|_{x \times \widehat {S}})$
is induced by
$\overline {\sigma }_{x\times \widehat {S}}\, \colon \,\mathbb{P}(E_{\widehat {S}}|_{x \times \widehat {S}})\,\longrightarrow \, \mathbb{P}(E_{\widehat {S}}'|_{x \times \widehat {S}})$
is induced by
 $\sigma$
.
$\sigma$
.
-
We say that
![]() $\sigma$
is an automorphism of a framed
$\sigma$
is an automorphism of a framed
![]() $G$
-connection
$G$
-connection
![]() $(E,\,\phi ,\,\nabla )$
if
$(E,\,\phi ,\,\nabla )$
if
![]() $\sigma$
is a holomorphic automorphism of the vector bundle
$\sigma$
is a holomorphic automorphism of the vector bundle
![]() $E$
on
$E$
on
![]() $X$
such that the diagram
$X$
such that the diagram
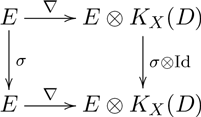
is commutative and
![]() $ \sigma |_{x}\circ \phi _{x}$
coincides with
$ \sigma |_{x}\circ \phi _{x}$
coincides with
![]() $\phi _{x}$
in the quotient
$\phi _{x}$
in the quotient
![]() ${\rm Isom}(\mathcal{O}_{x}^{\oplus r} , \,\, E|_x)/H_x$
for each
${\rm Isom}(\mathcal{O}_{x}^{\oplus r} , \,\, E|_x)/H_x$
for each
![]() $x\,\in \, D$
. Denote by
$x\,\in \, D$
. Denote by
![]() ${\rm Aut}(E,\,\phi ,\,\nabla )$
the space of all automorphisms of a framed
${\rm Aut}(E,\,\phi ,\,\nabla )$
the space of all automorphisms of a framed
![]() $G$
-connection
$G$
-connection
![]() $(E,\,\phi ,\,\nabla )$
.
$(E,\,\phi ,\,\nabla )$
.
Proposition 3.2. Assume that
![]() $\mathbb{C}^* \cdot \textrm { Id}\, \not \subset \, H_x$
for some
$\mathbb{C}^* \cdot \textrm { Id}\, \not \subset \, H_x$
for some
![]() $x\,\in \, D$
. Let
$x\,\in \, D$
. Let
![]() $(E,\,\phi ,\, \nabla )$
be a simple framed
$(E,\,\phi ,\, \nabla )$
be a simple framed
![]() $G$
-connection over
$G$
-connection over
![]() $X$
(see Definition 3.1(5)). Then
$X$
(see Definition 3.1(5)). Then
![]() ${\rm Aut}(E,\phi ,\nabla )$
is a finite group.
${\rm Aut}(E,\phi ,\nabla )$
is a finite group.
Proof. The space
![]() ${\rm Aut}(E,\,\phi ,\,\nabla )$
has the structure of a group scheme of finite type over
${\rm Aut}(E,\,\phi ,\,\nabla )$
has the structure of a group scheme of finite type over
![]() $\mathbb{C}$
. We can see that the tangent space of
$\mathbb{C}$
. We can see that the tangent space of
![]() ${\rm Aut}(E,\,\phi ,\,\nabla )$
at the identity element is isomorphic to
${\rm Aut}(E,\,\phi ,\,\nabla )$
at the identity element is isomorphic to
which is zero because
![]() $(E,\,\phi ,\,\nabla )$
is simple. Consequently,
$(E,\,\phi ,\,\nabla )$
is simple. Consequently,
![]() ${\rm Aut}(E,\,\phi ,\,\nabla )$
is a finite group.
${\rm Aut}(E,\,\phi ,\,\nabla )$
is a finite group.
Proposition 3.3. Assume that
![]() $H_x\,=\,\{ e\}$
for all
$H_x\,=\,\{ e\}$
for all
![]() $x\,\in \, D$
. Let
$x\,\in \, D$
. Let
![]() $(E,\,\phi ,\,\nabla )$
be a simple framed
$(E,\,\phi ,\,\nabla )$
be a simple framed
![]() $G$
-connection over
$G$
-connection over
![]() $X$
associated to
$X$
associated to
![]() $\{H_x\}_{x\in D}$
. Then
$\{H_x\}_{x\in D}$
. Then
![]() ${\rm Aut}(E,\,\phi ,\,\nabla ) \,=\, \{ {\rm Id}_{E}\}$
.
${\rm Aut}(E,\,\phi ,\,\nabla ) \,=\, \{ {\rm Id}_{E}\}$
.
Proof. An automorphism
![]() $\sigma \,\in \,{\rm Aut}(E,\,\phi ,\,\nabla )$
is an automorphism of the vector bundle
$\sigma \,\in \,{\rm Aut}(E,\,\phi ,\,\nabla )$
is an automorphism of the vector bundle
![]() $E$
such that
$E$
such that
![]() $\nabla \circ \sigma \,=\, \sigma \circ \nabla$
and
$\nabla \circ \sigma \,=\, \sigma \circ \nabla$
and
![]() $\phi _x\circ \sigma |_x\circ \phi _x^{-1}\,\in \, H_x$
for all
$\phi _x\circ \sigma |_x\circ \phi _x^{-1}\,\in \, H_x$
for all
![]() $x \,\in \, D$
. Since
$x \,\in \, D$
. Since
![]() $H_x\,=\,\{ e\}$
by the assumption, it follows that
$H_x\,=\,\{ e\}$
by the assumption, it follows that
![]() $\sigma |_x\,=\,{\rm Id}|_{E|_x}$
for all
$\sigma |_x\,=\,{\rm Id}|_{E|_x}$
for all
![]() $x\,\in \, D$
. Now set
$x\,\in \, D$
. Now set
Then
![]() $\widetilde {\sigma }|_x\,=\,0$
for all
$\widetilde {\sigma }|_x\,=\,0$
for all
![]() $x\,\in \, D$
, and it is straightforward to check that
$x\,\in \, D$
, and it is straightforward to check that
![]() $\nabla \circ \widetilde {\sigma } - \widetilde {\sigma } \circ \nabla \,=\,0$
, that is,
$\nabla \circ \widetilde {\sigma } - \widetilde {\sigma } \circ \nabla \,=\,0$
, that is,
Since
![]() $(E,\,\phi ,\,\nabla )$
is simple, it follows that
$(E,\,\phi ,\,\nabla )$
is simple, it follows that
![]() $\widetilde {\sigma }\,=\,0$
, and hence
$\widetilde {\sigma }\,=\,0$
, and hence
![]() $\sigma \,=\, {\rm Id}_{E}$
.
$\sigma \,=\, {\rm Id}_{E}$
.
Proposition 3.4. Assume that
![]() $\mathbb{C}^* \cdot \textrm { Id}\, \subset \, H_{x}$
for all
$\mathbb{C}^* \cdot \textrm { Id}\, \subset \, H_{x}$
for all
![]() $x\,\in \, D$
. If
$x\,\in \, D$
. If
![]() $(E,\,\phi ,\, \nabla )$
is a simple framed
$(E,\,\phi ,\, \nabla )$
is a simple framed
![]() $G$
-connection over
$G$
-connection over
![]() $X$
, then the quotient
$X$
, then the quotient
![]() ${\rm Aut}(E,\phi ,\nabla )/(\mathbb{C}^* \cdot \textrm { Id})$
is a finite group.
${\rm Aut}(E,\phi ,\nabla )/(\mathbb{C}^* \cdot \textrm { Id})$
is a finite group.
Proof. The tangent space of
![]() ${\rm Aut}(E,\,\phi ,\,\nabla )/(\mathbb{C}^* \cdot \textrm { Id})$
is zero, because we have that
${\rm Aut}(E,\,\phi ,\,\nabla )/(\mathbb{C}^* \cdot \textrm { Id})$
is zero, because we have that
![]() $(E,\,\phi ,\,\nabla )$
is simple. Consequently,
$(E,\,\phi ,\,\nabla )$
is simple. Consequently,
![]() ${\rm Aut}(E,\,\phi ,\,\nabla )/(\mathbb{C}^* \cdot \textrm { Id})$
is a finite group.
${\rm Aut}(E,\,\phi ,\,\nabla )/(\mathbb{C}^* \cdot \textrm { Id})$
is a finite group.
3.2 Representation of moduli functors as Deligne–Mumford stacks
Proposition 3.5. The stack
![]() $\mathcal{M}^{H}_{\textrm {FC}}(d)$
in Definition 3.1 is a Deligne–Mumford stack.
$\mathcal{M}^{H}_{\textrm {FC}}(d)$
in Definition 3.1 is a Deligne–Mumford stack.
Proof. Fix a very ample line bundle
![]() $\mathcal{O}_{X}(1)$
on the curve
$\mathcal{O}_{X}(1)$
on the curve
![]() $X$
. Define a polynomial
$X$
. Define a polynomial
![]() $\theta _d(m)$
in
$\theta _d(m)$
in
![]() $m$
to be
$m$
to be
where
![]() $d_X\,\,:=\,\, \deg \mathcal{O}_X(1)$
and
$d_X\,\,:=\,\, \deg \mathcal{O}_X(1)$
and
![]() $g$
is the genus of
$g$
is the genus of
![]() $X$
. Let
$X$
. Let
denote the fibered category whose objects are simple framed
![]() ${\rm GL}(r,\mathbb{C})$
-connections
${\rm GL}(r,\mathbb{C})$
-connections
![]() $(E,\,\phi ,\,\nabla )$
on
$(E,\,\phi ,\,\nabla )$
on
![]() $X\times S$
such that:
$X\times S$
such that:
-
(1)
 $H^1(X,\, E_s (m_0-1))\,=\,0$
for each
$H^1(X,\, E_s (m_0-1))\,=\,0$
for each
 $s\,\in \, S$
;
$s\,\in \, S$
; -
(2)
 $\chi (E_s(m))\,= \,\theta _d(m)$
for each
$\chi (E_s(m))\,= \,\theta _d(m)$
for each
 $s \,\in \, S$
and all
$s \,\in \, S$
and all
 $m \,\in \, \mathbb{Z}$
.
$m \,\in \, \mathbb{Z}$
.
The fibered categories
![]() $\Sigma _{m_0}^{d}$
in (3.1) form an open covering of
$\Sigma _{m_0}^{d}$
in (3.1) form an open covering of
![]() $\mathcal{M}^{H}_{\textrm {FC}} (d)$
. So we only have to prove that each
$\mathcal{M}^{H}_{\textrm {FC}} (d)$
. So we only have to prove that each
![]() $\Sigma _{m_0}^{d}$
is a Deligne–Mumford stack.
$\Sigma _{m_0}^{d}$
is a Deligne–Mumford stack.
Let
be the universal quotient sheaf of the Quot-scheme
![]() ${\rm Quot}^{\theta _d}_{(\mathcal{O}_X(-m_0)^{\oplus \theta _d(m_0)}/X)}$
. Define the open subset
${\rm Quot}^{\theta _d}_{(\mathcal{O}_X(-m_0)^{\oplus \theta _d(m_0)}/X)}$
. Define the open subset
![]() $Q^d_{m_0}$
of
$Q^d_{m_0}$
of
![]() ${\rm Quot}^{\theta _d}_{(\mathcal{O}_X(-m_0)^{\oplus \theta _d(m_0)}/X)}$
by
${\rm Quot}^{\theta _d}_{(\mathcal{O}_X(-m_0)^{\oplus \theta _d(m_0)}/X)}$
by
 \begin{align*} Q^d_{m_0} \, \,:=\, \,\left \{ s \,\in \, {\rm Quot}^{\theta _d}_{(\mathcal{O}_X(-m_0)^{\oplus \theta _d(m_0)}/X)} \ \middle | \ \begin{array}{l} \rm (i)\ h^0(X,\,\ \mathcal{E}_s(m_0)\ )\,=\,\theta\ _d(m_0);\\ \rm (ii)\ h^i(X,\,\ \mathcal{E}_s(m_0-i)\ )\,=\,0\,\,\ for\ all\ i\,\gt\ \,0;\ and\\ \rm (iii)\ \mathcal{E}_s\ is\ locally\ free. \end{array} \right \}. \end{align*}
\begin{align*} Q^d_{m_0} \, \,:=\, \,\left \{ s \,\in \, {\rm Quot}^{\theta _d}_{(\mathcal{O}_X(-m_0)^{\oplus \theta _d(m_0)}/X)} \ \middle | \ \begin{array}{l} \rm (i)\ h^0(X,\,\ \mathcal{E}_s(m_0)\ )\,=\,\theta\ _d(m_0);\\ \rm (ii)\ h^i(X,\,\ \mathcal{E}_s(m_0-i)\ )\,=\,0\,\,\ for\ all\ i\,\gt\ \,0;\ and\\ \rm (iii)\ \mathcal{E}_s\ is\ locally\ free. \end{array} \right \}. \end{align*}
There is a locally free
![]() $\mathcal{O}_{Q^d_{m_0}}$
–module
$\mathcal{O}_{Q^d_{m_0}}$
–module
![]() $\mathscr{H}\,\,_D$
such that
$\mathscr{H}\,\,_D$
such that
![]() $\boldsymbol{V}^*(\mathscr{H}\,\,_D)\,\,:=\,\,{\rm Spec}({\rm Sym}^*\mathscr{H}\,\,_D)$
represents the functor
$\boldsymbol{V}^*(\mathscr{H}\,\,_D)\,\,:=\,\,{\rm Spec}({\rm Sym}^*\mathscr{H}\,\,_D)$
represents the functor
for any Noetherian schemes
![]() $S$
over
$S$
over
![]() $Q^d_{m_0}$
. There is a universal family
$Q^d_{m_0}$
. There is a universal family
for every
![]() $x \,\in \,D$
. Define
$x \,\in \,D$
. Define
![]() $\widetilde {Q}^{d}_{m_0}$
as follows:
$\widetilde {Q}^{d}_{m_0}$
as follows:
Consider the map
![]() $\widetilde {Q}^{d}_{m_0} \, \longrightarrow \, Q^d_{m_0}$
. For each Noetherian scheme
$\widetilde {Q}^{d}_{m_0} \, \longrightarrow \, Q^d_{m_0}$
. For each Noetherian scheme
![]() $S$
over
$S$
over
![]() $Q^d_{m_0}$
, the natural transitive group action of
$Q^d_{m_0}$
, the natural transitive group action of
![]() $G \times S$
on
$G \times S$
on
induces an action on
![]() $\widetilde {Q}^{d}_{m_0}$
of the group scheme
$\widetilde {Q}^{d}_{m_0}$
of the group scheme
![]() $\left (\prod _{x \in D}G\right )\times Q^d_{m_0}$
over
$\left (\prod _{x \in D}G\right )\times Q^d_{m_0}$
over
![]() $Q^d_{m_0}$
. The group scheme
$Q^d_{m_0}$
. The group scheme
![]() $\left (\prod _{x \in D}H_x\right )\times Q^d_{m_0}$
acts on
$\left (\prod _{x \in D}H_x\right )\times Q^d_{m_0}$
acts on
![]() $\widetilde {Q}^{d}_{m_0}$
by restricting this action of
$\widetilde {Q}^{d}_{m_0}$
by restricting this action of
![]() $(\prod _{x \in D}G)\times Q^d_{m_0}$
on
$(\prod _{x \in D}G)\times Q^d_{m_0}$
on
![]() $\widetilde {Q}^{d}_{m_0}$
. Set
$\widetilde {Q}^{d}_{m_0}$
. Set
Let
![]() $\widetilde {\mathcal{E}}$
be the pull-back of the family
$\widetilde {\mathcal{E}}$
be the pull-back of the family
![]() $\mathcal{E}$
under the map
$\mathcal{E}$
under the map
![]() $X \times \widetilde {Q}^{d,H}_{m_0} \, \longrightarrow \, X \times Q^d_{m_0}$
. We have a family
$X \times \widetilde {Q}^{d,H}_{m_0} \, \longrightarrow \, X \times Q^d_{m_0}$
. We have a family
![]() $\widetilde {\phi }_x$
of sections of
$\widetilde {\phi }_x$
of sections of
induced by
![]() $\varphi ^x$
. Put
$\varphi ^x$
. Put
![]() $\widetilde {\phi }\,\,:=\,\,\{\widetilde {\phi }_x \}_{x \in D}$
.
$\widetilde {\phi }\,\,:=\,\,\{\widetilde {\phi }_x \}_{x \in D}$
.
Let
be the natural projection map. Let
![]() ${\rm At}(\widetilde {\mathcal{E}})$
be the Atiyah bundle for
${\rm At}(\widetilde {\mathcal{E}})$
be the Atiyah bundle for
![]() $\widetilde {\mathcal{E}}$
. Then there is a short exact sequence
$\widetilde {\mathcal{E}}$
. Then there is a short exact sequence
Set
![]() ${\rm At}_{D} (\widetilde {\mathcal{E}}) \,\,\,:=\,\,\, {\rm symb}_1^{-1}\left (T_{X\times \widetilde {Q}^{d,H}_{m_0} /\widetilde {Q}^{d,H}_{m_0}}(-D\times \widetilde {Q}^{d,H}_{m_0}) \right )$
. The natural short exact sequences of Atiyah bundles induces an exact sequence as follows.
${\rm At}_{D} (\widetilde {\mathcal{E}}) \,\,\,:=\,\,\, {\rm symb}_1^{-1}\left (T_{X\times \widetilde {Q}^{d,H}_{m_0} /\widetilde {Q}^{d,H}_{m_0}}(-D\times \widetilde {Q}^{d,H}_{m_0}) \right )$
. The natural short exact sequences of Atiyah bundles induces an exact sequence as follows.
In particular, there are two compositions of maps
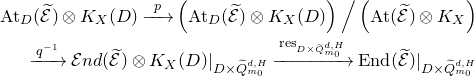 \begin{align} \begin{aligned} {\rm At}_{D} (\widetilde {\mathcal{E}}) \otimes K_X(D) \xrightarrow {\,\,\, p\,\,} \left ( {\rm At}_{D} (\widetilde {\mathcal{E}}) \otimes K_X(D) \right ) \Big /\left ( {\rm At}(\widetilde {\mathcal{E}}) \otimes K_{X} \right ) \\ \qquad \xrightarrow {\, q^{-1}\, } \mathcal{E}nd(\widetilde {\mathcal{E}}) \otimes K_{X}(D)|_{D\times \widetilde {Q}^{d,H}_{m_0}} \xrightarrow {\, {\rm res}_{D \times \widetilde {Q}^{d,H}_{m_0}} \,} {\rm End} (\widetilde {\mathcal{E}})|_{D\times \widetilde {Q}^{d,H}_{m_0}} \end{aligned} \end{align}
\begin{align} \begin{aligned} {\rm At}_{D} (\widetilde {\mathcal{E}}) \otimes K_X(D) \xrightarrow {\,\,\, p\,\,} \left ( {\rm At}_{D} (\widetilde {\mathcal{E}}) \otimes K_X(D) \right ) \Big /\left ( {\rm At}(\widetilde {\mathcal{E}}) \otimes K_{X} \right ) \\ \qquad \xrightarrow {\, q^{-1}\, } \mathcal{E}nd(\widetilde {\mathcal{E}}) \otimes K_{X}(D)|_{D\times \widetilde {Q}^{d,H}_{m_0}} \xrightarrow {\, {\rm res}_{D \times \widetilde {Q}^{d,H}_{m_0}} \,} {\rm End} (\widetilde {\mathcal{E}})|_{D\times \widetilde {Q}^{d,H}_{m_0}} \end{aligned} \end{align}
and
Here,
![]() ${\rm res}_{D \times \widetilde {Q}^{d,H}_{m_0}}$
is the residue map
${\rm res}_{D \times \widetilde {Q}^{d,H}_{m_0}}$
is the residue map
Using the family
![]() $\widetilde {\phi }$
of framings and the Lie subgroups
$\widetilde {\phi }$
of framings and the Lie subgroups
![]() $H_x$
for each
$H_x$
for each
![]() $x\,\in \,D$
, we may define a subsheaf
$x\,\in \,D$
, we may define a subsheaf
![]() $\mathcal{H}^{\perp }_{x \times \widetilde {Q}^{d,H}_{m_0}} \,\subset \, {\rm End} (\widetilde {\mathcal{E}})|_{D\times \widetilde {Q}^{d,H}_{m_0}}$
as in (2.10). Define subsheaves
$\mathcal{H}^{\perp }_{x \times \widetilde {Q}^{d,H}_{m_0}} \,\subset \, {\rm End} (\widetilde {\mathcal{E}})|_{D\times \widetilde {Q}^{d,H}_{m_0}}$
as in (2.10). Define subsheaves
![]() ${\rm At}^{\widetilde {\phi }}_{D} (\widetilde {\mathcal{E}}) \,\subset \, {\rm At}_{D} (\widetilde {\mathcal{E}})$
and
${\rm At}^{\widetilde {\phi }}_{D} (\widetilde {\mathcal{E}}) \,\subset \, {\rm At}_{D} (\widetilde {\mathcal{E}})$
and
![]() $\mathcal{E}nd_{\widetilde {\phi }}^n(\widetilde {\mathcal{E}}) \,\subset \, \mathcal{E}nd(\widetilde {\mathcal{E}})$
such that
$\mathcal{E}nd_{\widetilde {\phi }}^n(\widetilde {\mathcal{E}}) \,\subset \, \mathcal{E}nd(\widetilde {\mathcal{E}})$
such that
![]() ${\rm At}^{\widetilde {\phi }}_{D} (\widetilde {\mathcal{E}}) \otimes K_X(D)$
is the inverse image of
${\rm At}^{\widetilde {\phi }}_{D} (\widetilde {\mathcal{E}}) \otimes K_X(D)$
is the inverse image of
![]() $\mathcal{H}^{\perp }_{x \times \widetilde {Q}^{d,H}_{m_0}}$
under the composition of maps in (3.4) and
$\mathcal{H}^{\perp }_{x \times \widetilde {Q}^{d,H}_{m_0}}$
under the composition of maps in (3.4) and
![]() $\mathcal{E}nd_{\widetilde {\phi }}^n(\widetilde {\mathcal{E}})\otimes K_X(D)$
is the inverse image of
$\mathcal{E}nd_{\widetilde {\phi }}^n(\widetilde {\mathcal{E}})\otimes K_X(D)$
is the inverse image of
![]() $\mathcal{H}^{\perp }_{x \times \widetilde {Q}^{d,H}_{m_0}}$
under the composition of maps in (3.5).
$\mathcal{H}^{\perp }_{x \times \widetilde {Q}^{d,H}_{m_0}}$
under the composition of maps in (3.5).
By [Reference GrothendieckGrot1, Theorem 7.7.6], there is a unique coherent sheaf
![]() $\mathscr{H}\,\,$
on
$\mathscr{H}\,\,$
on
![]() $\widetilde {Q}^{d,H}_{m_0}$
(up to isomorphism) such that
$\widetilde {Q}^{d,H}_{m_0}$
(up to isomorphism) such that
for any
![]() $\widetilde {Q}^{d,H}_{m_0}$
-scheme
$\widetilde {Q}^{d,H}_{m_0}$
-scheme
![]() $Q'$
and any quasi-coherent sheaf
$Q'$
and any quasi-coherent sheaf
![]() $M$
on
$M$
on
![]() $Q'$
. Here,
$Q'$
. Here,
![]() $\pi _{Q'}$
is the natural projection
$\pi _{Q'}$
is the natural projection
![]() $X \times Q' \,\longrightarrow \, Q'$
. Set
$X \times Q' \,\longrightarrow \, Q'$
. Set
There is a natural morphism
![]() $\varphi \,\in \, \mathcal{H}\textrm {om}_{\mathcal{O}_{\boldsymbol{V} (\mathscr{H}\,\,)}} (\mathscr{H}\,\,_{\boldsymbol{V} (\mathscr{H}\,\,)} ,\, \mathcal{O}_{\boldsymbol{V} (\mathscr{H}\,\,)})$
by the definition of
$\varphi \,\in \, \mathcal{H}\textrm {om}_{\mathcal{O}_{\boldsymbol{V} (\mathscr{H}\,\,)}} (\mathscr{H}\,\,_{\boldsymbol{V} (\mathscr{H}\,\,)} ,\, \mathcal{O}_{\boldsymbol{V} (\mathscr{H}\,\,)})$
by the definition of
![]() $\boldsymbol{V} (\mathscr{H}\,\,)$
. In view of the isomorphism in (3.6), there is an element
$\boldsymbol{V} (\mathscr{H}\,\,)$
. In view of the isomorphism in (3.6), there is an element
![]() $\varphi ' \,\in \, \pi _*( ( {\rm At}^{\widetilde {\phi }}_{D} (\widetilde {\mathcal{E}}) \otimes K_X(D) )_{\boldsymbol{V} (\mathscr{H}\,\,)})$
corresponding to
$\varphi ' \,\in \, \pi _*( ( {\rm At}^{\widetilde {\phi }}_{D} (\widetilde {\mathcal{E}}) \otimes K_X(D) )_{\boldsymbol{V} (\mathscr{H}\,\,)})$
corresponding to
![]() $\varphi$
. The morphism
$\varphi$
. The morphism
![]() ${\rm symb}_1^{D}$
induces a morphism
${\rm symb}_1^{D}$
induces a morphism
Using this morphism, there is a function
![]() $f_{{\rm symb}_1^{D}}$
on
$f_{{\rm symb}_1^{D}}$
on
![]() $\boldsymbol{V} (\mathscr{H}\,\,)$
corresponding to
$\boldsymbol{V} (\mathscr{H}\,\,)$
corresponding to
![]() $\varphi '$
. Denote by
$\varphi '$
. Denote by
![]() $I_{{\rm symb}_1^{D}}$
the ideal sheaf of
$I_{{\rm symb}_1^{D}}$
the ideal sheaf of
![]() $\mathcal{O}_{\boldsymbol{V} (\mathscr{H}\,\,)}$
generated by
$\mathcal{O}_{\boldsymbol{V} (\mathscr{H}\,\,)}$
generated by
![]() $f_{{\rm symb}_1^{D}}-1$
. Put
$f_{{\rm symb}_1^{D}}-1$
. Put
Also, denote by
![]() $\widetilde {\mathcal{E}}$
the pull-back of
$\widetilde {\mathcal{E}}$
the pull-back of
![]() $\widetilde {\mathcal{E}}$
under the natural morphism
$\widetilde {\mathcal{E}}$
under the natural morphism
![]() $X \times Z^{d,H}_{m_0} \,\longrightarrow \, X\times \widetilde {Q}^{d,H}_{m_0,{\rm spl}}$
, and let
$X \times Z^{d,H}_{m_0} \,\longrightarrow \, X\times \widetilde {Q}^{d,H}_{m_0,{\rm spl}}$
, and let
be a universal relative connection on
![]() $\widetilde {\mathcal{E}}$
, which is determined by
$\widetilde {\mathcal{E}}$
, which is determined by
![]() $\varphi '$
. Define the open subset
$\varphi '$
. Define the open subset
![]() $(Z^{d,H}_{m_0})'$
of
$(Z^{d,H}_{m_0})'$
of
![]() $Z^{d,H}_{m_0}$
by
$Z^{d,H}_{m_0}$
by
and denote by
![]() $\big (\widetilde {\mathcal{E}},\, \widetilde {\phi }\,=\, \big \{[\widetilde {\phi }_{x\times (Z^{d,H}_{m_0})'}] \big \}_{x\in D},\, \widetilde {\nabla }\big )$
a universal family of
$\big (\widetilde {\mathcal{E}},\, \widetilde {\phi }\,=\, \big \{[\widetilde {\phi }_{x\times (Z^{d,H}_{m_0})'}] \big \}_{x\in D},\, \widetilde {\nabla }\big )$
a universal family of
![]() $m_0$
-regular simple framed
$m_0$
-regular simple framed
![]() $G$
-connections on
$G$
-connections on
![]() $X\times (Z^{d,H}_{m_0})'$
. Here,
$X\times (Z^{d,H}_{m_0})'$
. Here,
![]() $m_0$
-regular means
$m_0$
-regular means
![]() $H^1(X,\, \widetilde {\mathcal{E}}_s (m_0-1))\,=\,0$
for each
$H^1(X,\, \widetilde {\mathcal{E}}_s (m_0-1))\,=\,0$
for each
![]() $s\,\in \, (Z^{d,H}_{m_0})'$
.
$s\,\in \, (Z^{d,H}_{m_0})'$
.
Now, consider the case where
![]() $\mathbb{C}^* \cdot \textrm { Id}\, \not \subset \, H_x$
for some
$\mathbb{C}^* \cdot \textrm { Id}\, \not \subset \, H_x$
for some
![]() $x\,\in \, D$
. There exists an action of
$x\,\in \, D$
. There exists an action of
![]() ${\rm GL}(\theta _d(m_0),\mathbb{C})$
on
${\rm GL}(\theta _d(m_0),\mathbb{C})$
on
![]() $(Z^{d,H}_{m_0})'$
given by
$(Z^{d,H}_{m_0})'$
given by
on
![]() $S$
-points for
$S$
-points for
![]() $g \,\in \, {\rm GL}(\theta _d(m_0),\mathbb{C})_S$
. Consider the map
$g \,\in \, {\rm GL}(\theta _d(m_0),\mathbb{C})_S$
. Consider the map
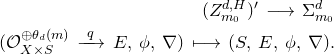 \begin{align*} \begin{aligned} (Z^{d,H}_{m_0})' \,\longrightarrow \, \Sigma _{m_0}^{d} \\ (\mathcal{O}_{X\times S}^{\oplus \theta _{d}(m)}\,\xrightarrow {\,\,q\,\,}\, E, \,\phi ,\, \nabla ) \,\longmapsto \, (S,\, E,\, \phi ,\, \nabla ). \end{aligned} \end{align*}
\begin{align*} \begin{aligned} (Z^{d,H}_{m_0})' \,\longrightarrow \, \Sigma _{m_0}^{d} \\ (\mathcal{O}_{X\times S}^{\oplus \theta _{d}(m)}\,\xrightarrow {\,\,q\,\,}\, E, \,\phi ,\, \nabla ) \,\longmapsto \, (S,\, E,\, \phi ,\, \nabla ). \end{aligned} \end{align*}
This map gives an isomorphism
Here,
![]() $\big [ \, (Z^{d,H}_{m_0})' \, \big / \, {\rm GL}(\theta _d(m_0),\mathbb{C}) \, \big ]$
is a quotient stack. Consequently,
$\big [ \, (Z^{d,H}_{m_0})' \, \big / \, {\rm GL}(\theta _d(m_0),\mathbb{C}) \, \big ]$
is a quotient stack. Consequently,
![]() $\Sigma _{m_0}^{d}$
is an algebraic stack. Using Proposition 3.2, it follows that
$\Sigma _{m_0}^{d}$
is an algebraic stack. Using Proposition 3.2, it follows that
![]() $\Sigma _{m_0}^{d}$
is in fact a Deligne–Mumford stack (see [Reference OlssonOls, Corollary 8.4.2]).
$\Sigma _{m_0}^{d}$
is in fact a Deligne–Mumford stack (see [Reference OlssonOls, Corollary 8.4.2]).
Next, we consider the case where
![]() $\mathbb{C}^* \cdot \textrm { Id}\, \subset \, H_x$
for every
$\mathbb{C}^* \cdot \textrm { Id}\, \subset \, H_x$
for every
![]() $x\,\in \, D$
. The
$x\,\in \, D$
. The
![]() $\mathbb{C}^*$
-action on
$\mathbb{C}^*$
-action on
![]() $(Z^{d,H}_{m_0})'$
is trivial, because
$(Z^{d,H}_{m_0})'$
is trivial, because
![]() $\mathbb{C}^* \cdot \textrm { Id}\, \subset \, H_x$
for all
$\mathbb{C}^* \cdot \textrm { Id}\, \subset \, H_x$
for all
![]() $x\,\in \, D$
. There exists a natural action of
$x\,\in \, D$
. There exists a natural action of
![]() ${\rm PGL}(\theta _d(m_0),\,\mathbb{C})$
on
${\rm PGL}(\theta _d(m_0),\,\mathbb{C})$
on
![]() $(Z^{d,H}_{m_0})'$
. Define a map
$(Z^{d,H}_{m_0})'$
. Define a map
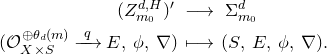 \begin{align*} \begin{aligned} (Z^{d,H}_{m_0})' \,\,&\longrightarrow \,\, \Sigma _{m_0}^{d}\\ (\mathcal{O}_{X\times S}^{\oplus \theta _{d}(m)}\xrightarrow {\,\,q\,\,} E,\, \phi ,\,\nabla ) \,&\longmapsto \, (S,\, E,\, \phi ,\, \nabla ). \end{aligned} \end{align*}
\begin{align*} \begin{aligned} (Z^{d,H}_{m_0})' \,\,&\longrightarrow \,\, \Sigma _{m_0}^{d}\\ (\mathcal{O}_{X\times S}^{\oplus \theta _{d}(m)}\xrightarrow {\,\,q\,\,} E,\, \phi ,\,\nabla ) \,&\longmapsto \, (S,\, E,\, \phi ,\, \nabla ). \end{aligned} \end{align*}
It is straightforward to check that this map gives an isomorphism
Then
![]() $\Sigma _{m_0}^{d}$
is an algebraic stack. By Proposition 3.4, it follows that
$\Sigma _{m_0}^{d}$
is an algebraic stack. By Proposition 3.4, it follows that
![]() $\Sigma _{m_0}^{d}$
is in fact a Deligne–Mumford stack (see [Reference OlssonOls, Corollary 8.4.2]).
$\Sigma _{m_0}^{d}$
is in fact a Deligne–Mumford stack (see [Reference OlssonOls, Corollary 8.4.2]).
Remark 3.6. If
![]() $H_x \,=\, {e}$
for all
$H_x \,=\, {e}$
for all
![]() $x\,in \, D$
, then
$x\,in \, D$
, then
![]() $\mathcal{M}^{H}_{\textrm {FC}}(d)$
is an algebraic space by Proposition 3.3.
$\mathcal{M}^{H}_{\textrm {FC}}(d)$
is an algebraic space by Proposition 3.3.
Remark 3.7. In the proof of Proposition 3.5, we introduced the coherent sheaf
![]() $\mathscr{H}\,\,$
which is characterized by the property (3.6). Since
$\mathscr{H}\,\,$
which is characterized by the property (3.6). Since
![]() $\mathscr{H}\,\,$
is not necessarily locally free, we cannot see the irreducibility of the moduli space
$\mathscr{H}\,\,$
is not necessarily locally free, we cannot see the irreducibility of the moduli space
![]() $\mathcal{M}^H_{{\rm FC}}(d)$
immediately from its construction.
$\mathcal{M}^H_{{\rm FC}}(d)$
immediately from its construction.
Define an open substack of
![]() $\mathcal{M}^{H}_{\textrm {FC}}(d)$
as follows:
$\mathcal{M}^{H}_{\textrm {FC}}(d)$
as follows:
Here we say that
![]() $(E_s,\,\phi _s)$
is simple if
$(E_s,\,\phi _s)$
is simple if
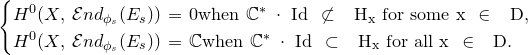 \begin{align*} \begin{cases} H^0(X,\, \mathcal{E}nd_{\phi _s}( E_s) )\, =\,0 \rm when\ \mathbb{C}^*\ \cdot\ \mathrm{Id}\ \,\not \subset\ \,\ H_x\ for\ some\ x\ \,\in\ \,\ D, \\ H^0(X,\, \mathcal{E}nd_{\phi _s}( E_s) ) \,=\,\mathbb{C} \rm when\ \mathbb{C}^*\ \cdot\ \mathrm{Id}\ \,\subset\ \,\ H_x\ for\ all\ x\ \,\in\ \,\ D. \end{cases} \end{align*}
\begin{align*} \begin{cases} H^0(X,\, \mathcal{E}nd_{\phi _s}( E_s) )\, =\,0 \rm when\ \mathbb{C}^*\ \cdot\ \mathrm{Id}\ \,\not \subset\ \,\ H_x\ for\ some\ x\ \,\in\ \,\ D, \\ H^0(X,\, \mathcal{E}nd_{\phi _s}( E_s) ) \,=\,\mathbb{C} \rm when\ \mathbb{C}^*\ \cdot\ \mathrm{Id}\ \,\subset\ \,\ H_x\ for\ all\ x\ \,\in\ \,\ D. \end{cases} \end{align*}
We adopt the above definition of simple framed bundle in order that the loci
![]() $\mathcal{M}^{H}_{\textrm {FC}}(d)^{\circ }$
becomes open in
$\mathcal{M}^{H}_{\textrm {FC}}(d)^{\circ }$
becomes open in
![]() $\mathcal{M}^{H}_{\textrm {FC}}(d)$
.
$\mathcal{M}^{H}_{\textrm {FC}}(d)$
.
Proposition 3.8. The open substack
![]() $\mathcal{M}^{H}_{\textrm {FC}}(d)^{\circ }$
in (3.7) is irreducible.
$\mathcal{M}^{H}_{\textrm {FC}}(d)^{\circ }$
in (3.7) is irreducible.
Proof. Fix a very ample line bundle
![]() $\mathcal{O}_{X}(1)$
on the curve
$\mathcal{O}_{X}(1)$
on the curve
![]() $X$
. Let
$X$
. Let
![]() $\theta _d(m)$
be a polynomial in
$\theta _d(m)$
be a polynomial in
![]() $m$
defined as in Proposition 3.5. Let
$m$
defined as in Proposition 3.5. Let
![]() $(\Sigma _{m_0}^{d})^{\circ }$
denote the substack of
$(\Sigma _{m_0}^{d})^{\circ }$
denote the substack of
![]() $\mathcal{M}^{H}_{\textrm {FC}}(d)^{\circ }$
whose objects are framed
$\mathcal{M}^{H}_{\textrm {FC}}(d)^{\circ }$
whose objects are framed
![]() ${\rm GL}(r,\mathbb{C})$
-connections
${\rm GL}(r,\mathbb{C})$
-connections
![]() $(E,\,\phi ,\,\nabla )$
on
$(E,\,\phi ,\,\nabla )$
on
![]() $X$
such that:
$X$
such that:
-
(1)
 $(E,\,\phi )$
is simple;
$(E,\,\phi )$
is simple; -
(2)
 $H^1(X,\, E (m_0-1))\,=\,0$
;
$H^1(X,\, E (m_0-1))\,=\,0$
; -
(3)
 $\chi (E(m))\,= \,\theta _d(m)$
for all
$\chi (E(m))\,= \,\theta _d(m)$
for all
 $m \,\in \, \mathbb{Z}$
.
$m \,\in \, \mathbb{Z}$
.
To prove the proposition it suffices to show that
![]() $(\Sigma _{m_0}^{d})^{\circ }$
is irreducible.
$(\Sigma _{m_0}^{d})^{\circ }$
is irreducible.
Let
![]() $V$
be a
$V$
be a
![]() $\theta _d(m_0)$
-dimensional vector space so that the underlying vector bundle
$\theta _d(m_0)$
-dimensional vector space so that the underlying vector bundle
![]() $E$
of any object of
$E$
of any object of
![]() $(\Sigma _{m_0}^{d})^{\circ }$
is described as the following quotient:
$(\Sigma _{m_0}^{d})^{\circ }$
is described as the following quotient:
Take a subspace
![]() $V_r \,\subset \, V$
such that
$V_r \,\subset \, V$
such that
![]() $\dim (V_r) \,=\,r$
. Taking the dual of the above quotient, and tensoring with
$\dim (V_r) \,=\,r$
. Taking the dual of the above quotient, and tensoring with
![]() $\mathcal{O}_X (-m_0)$
, we have the following short exact sequence
$\mathcal{O}_X (-m_0)$
, we have the following short exact sequence
where
![]() $F$
is the quotient for the injective map
$F$
is the quotient for the injective map
![]() $E^{\vee }(-m_0) \,\longrightarrow \, V_r^{\vee } \otimes \mathcal{O}_X$
. So for each object of
$E^{\vee }(-m_0) \,\longrightarrow \, V_r^{\vee } \otimes \mathcal{O}_X$
. So for each object of
![]() $(\Sigma _{m_0}^{d})^{\circ }$
, there is a point of
$(\Sigma _{m_0}^{d})^{\circ }$
, there is a point of
![]() ${\rm Quot}^N_{(V_r^{\vee }\otimes \mathcal{O}_X)/X}$
which determines the underlying vector bundle of the object. Here
${\rm Quot}^N_{(V_r^{\vee }\otimes \mathcal{O}_X)/X}$
which determines the underlying vector bundle of the object. Here
![]() $N$
is the length of
$N$
is the length of
![]() $F$
. Note that
$F$
. Note that
![]() $N$
remains constant for the underlying vector bundles. We will show that
$N$
remains constant for the underlying vector bundles. We will show that
![]() ${\rm Quot}^N_{(V_r^{\vee }\otimes \mathcal{O}_X)/X}$
is irreducible.
${\rm Quot}^N_{(V_r^{\vee }\otimes \mathcal{O}_X)/X}$
is irreducible.
The Quot-scheme
![]() ${\rm Quot}^N_{(V_r^{\vee }\otimes \mathcal{O}_X)/X}$
is smooth, because the obstructions to deformations of
${\rm Quot}^N_{(V_r^{\vee }\otimes \mathcal{O}_X)/X}$
is smooth, because the obstructions to deformations of
lie in
Define the map
 \begin{align*} \begin{aligned} f_N \,\,\colon \,\, {\rm Quot}^N_{(V_r^{\vee }\otimes \mathcal{O}_X)/X} \, \longrightarrow \, {\rm Hilb}^N_{X}\\ [\, q \colon V_r^{\vee } \otimes \mathcal{O}_X \longrightarrow F \,] \, \longmapsto \, {\rm Divisor} ( {\rm det} ({\rm Ker}\, q \,\longrightarrow \, V_r^{\vee } \otimes \mathcal{O}_X)). \end{aligned} \end{align*}
\begin{align*} \begin{aligned} f_N \,\,\colon \,\, {\rm Quot}^N_{(V_r^{\vee }\otimes \mathcal{O}_X)/X} \, \longrightarrow \, {\rm Hilb}^N_{X}\\ [\, q \colon V_r^{\vee } \otimes \mathcal{O}_X \longrightarrow F \,] \, \longmapsto \, {\rm Divisor} ( {\rm det} ({\rm Ker}\, q \,\longrightarrow \, V_r^{\vee } \otimes \mathcal{O}_X)). \end{aligned} \end{align*}
Let
![]() $H'$
be the Zariski open subset of
$H'$
be the Zariski open subset of
![]() ${\rm Hilb}^N_{X}$
which consists of distinct points on
${\rm Hilb}^N_{X}$
which consists of distinct points on
![]() $X$
, or in other words,
$X$
, or in other words,
![]() $H'$
parametrizes the reduced subschemes. This Zariski open subset
$H'$
parametrizes the reduced subschemes. This Zariski open subset
![]() $H'$
is in fact irreducible. The map
$H'$
is in fact irreducible. The map
is a
![]() $(\mathbb{P}^{r-1}\times \cdots \times \mathbb{P}^{r-1})$
-bundle; here
$(\mathbb{P}^{r-1}\times \cdots \times \mathbb{P}^{r-1})$
-bundle; here
![]() $\mathbb{P}^{r-1}\times \cdots \times \mathbb{P}^{r-1}$
is the product of
$\mathbb{P}^{r-1}\times \cdots \times \mathbb{P}^{r-1}$
is the product of
![]() $N$
-copies of
$N$
-copies of
![]() $\mathbb{P}^{r-1}$
. Hence
$\mathbb{P}^{r-1}$
. Hence
![]() $f_N^{-1}(H')$
is irreducible. Take a point
$f_N^{-1}(H')$
is irreducible. Take a point
![]() $x \,=\, N_1 z_1+ \cdots +N_l z_l$
on
$x \,=\, N_1 z_1+ \cdots +N_l z_l$
on
![]() ${\rm Hilb}^N_{X}$
, where
${\rm Hilb}^N_{X}$
, where
![]() $\sum _{i=1}^l N_i\, =\,N$
and
$\sum _{i=1}^l N_i\, =\,N$
and
![]() $z_1,\,\cdots ,\,z_l$
are distinct points on
$z_1,\,\cdots ,\,z_l$
are distinct points on
![]() $X$
. A point on
$X$
. A point on
![]() $f^{-1}_N(x)$
can be described as a collection
$f^{-1}_N(x)$
can be described as a collection
![]() $\left ( \, q_i \,\colon \, V_r^{\vee } \otimes \mathcal{O}_{z_i,X} \,\longrightarrow \, F_i\, \right )_{i=1}^l$
for which
$\left ( \, q_i \,\colon \, V_r^{\vee } \otimes \mathcal{O}_{z_i,X} \,\longrightarrow \, F_i\, \right )_{i=1}^l$
for which
![]() ${\rm length}(F_i)\,=\,N_i$
. Consider the map
${\rm length}(F_i)\,=\,N_i$
. Consider the map
![]() $({\rm Ker}\, q_i )_{z_i} \,\longrightarrow \, V_r^{\vee } \otimes \mathcal{O}_{z_i,X}$
corresponding to a point on
$({\rm Ker}\, q_i )_{z_i} \,\longrightarrow \, V_r^{\vee } \otimes \mathcal{O}_{z_i,X}$
corresponding to a point on
![]() $f^{-1}_N(x)$
. Note that
$f^{-1}_N(x)$
. Note that
![]() $({\rm Ker}\, q_i )_{z_i}\,\cong \, \mathcal{O}_{z_i,X}^{\oplus r}$
. We have a matrix representation of
$({\rm Ker}\, q_i )_{z_i}\,\cong \, \mathcal{O}_{z_i,X}^{\oplus r}$
. We have a matrix representation of
![]() $({\rm Ker}\, q_i )_{z_i} \,\longrightarrow \, V_r^{\vee } \otimes \mathcal{O}_{z_i,X}$
as follows:
$({\rm Ker}\, q_i )_{z_i} \,\longrightarrow \, V_r^{\vee } \otimes \mathcal{O}_{z_i,X}$
as follows:
 \begin{align*} \left(\ \begin{matrix}1 &&&&& \\ &\ddots &&&& \\ &&1 &&& \\ &&& z^{l_{i,1}} && \\ &&&& \ddots & \\ &&&&&z^{l_{i,s_i}} \end{matrix}\right), \end{align*}
\begin{align*} \left(\ \begin{matrix}1 &&&&& \\ &\ddots &&&& \\ &&1 &&& \\ &&& z^{l_{i,1}} && \\ &&&& \ddots & \\ &&&&&z^{l_{i,s_i}} \end{matrix}\right), \end{align*}
where the maximal ideal
![]() $\mathfrak{m}_{z_i}$
is
$\mathfrak{m}_{z_i}$
is
![]() $\{z=0 \}$
, and
$\{z=0 \}$
, and
![]() $1,\,z^{l_{i,1}},\,\ldots ,\,z^{l_{i,s_i}}$
are invariant factors of
$1,\,z^{l_{i,1}},\,\ldots ,\,z^{l_{i,s_i}}$
are invariant factors of
For any tuple of complex numbers
![]() $a_1^{(i)},\,\ldots ,\,a_{s_i}^{(i)}$
, there is a deformation of
$a_1^{(i)},\,\ldots ,\,a_{s_i}^{(i)}$
, there is a deformation of
![]() $({\rm Ker}\, q_i )_{z_i} \,\longrightarrow \, V_r^{\vee } \otimes \mathcal{O}_{z_i,X}$
$({\rm Ker}\, q_i )_{z_i} \,\longrightarrow \, V_r^{\vee } \otimes \mathcal{O}_{z_i,X}$
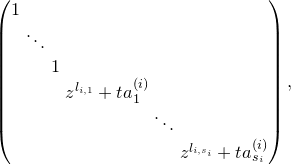 \begin{align*} \left( \begin{matrix} 1&&&& \\& \ddots &&&&\\&& 1&&& \\ &&&z^{l_{i,1}}+t a_{1}^{(i)}&& \\&&&& \ddots& \\ &&&&&z^{l_{i,s_i}}+ t a_{s_i}^{(i)} \end{matrix}\right), \end{align*}
\begin{align*} \left( \begin{matrix} 1&&&& \\& \ddots &&&&\\&& 1&&& \\ &&&z^{l_{i,1}}+t a_{1}^{(i)}&& \\&&&& \ddots& \\ &&&&&z^{l_{i,s_i}}+ t a_{s_i}^{(i)} \end{matrix}\right), \end{align*}
over
![]() $X \times {\rm Spec}\, \mathbb{C}[t]$
. When the complex numbers
$X \times {\rm Spec}\, \mathbb{C}[t]$
. When the complex numbers
![]() $a_1^{(i)},\,\cdots ,\,a_{s_i}^{(i)}$
are generic, we have a deformation moving from a point on
$a_1^{(i)},\,\cdots ,\,a_{s_i}^{(i)}$
are generic, we have a deformation moving from a point on
![]() $f^{-1}_N(x)$
, where
$f^{-1}_N(x)$
, where
![]() $x \,=\, N_1 z_1+ \cdots +N_l z_l$
, to a point on
$x \,=\, N_1 z_1+ \cdots +N_l z_l$
, to a point on
![]() $f_N^{-1}(H')$
. Therefore,
$f_N^{-1}(H')$
. Therefore,
![]() ${\rm Quot}^N_{(V_r^{\vee }\otimes \mathcal{O}_X)/X}$
is irreducible.
${\rm Quot}^N_{(V_r^{\vee }\otimes \mathcal{O}_X)/X}$
is irreducible.
Consider the open subset
Here, denote
![]() $E_q\,\,:=\,\,({\rm ker} q)^{\vee } (-m_0)$
for a quotient
$E_q\,\,:=\,\,({\rm ker} q)^{\vee } (-m_0)$
for a quotient
![]() $q$
. By definition,
$q$
. By definition,
![]() $E_q$
is locally free and satisfies the condition
$E_q$
is locally free and satisfies the condition
![]() $\chi (E_q (m)) = \theta _d(m)$
for all
$\chi (E_q (m)) = \theta _d(m)$
for all
![]() $m \, \in \, \mathbb{Z}$
. Let
$m \, \in \, \mathbb{Z}$
. Let
![]() $\widetilde {Q}'$
be the scheme over
$\widetilde {Q}'$
be the scheme over
![]() $Q'$
which parametrizes quotients
$Q'$
which parametrizes quotients
![]() $q$
in
$q$
in
![]() $Q'$
and framings of
$Q'$
and framings of
![]() $E_q$
, which is constructed as in the proof of Proposition 3.5. Now define
$E_q$
, which is constructed as in the proof of Proposition 3.5. Now define
![]() $(\widetilde {Q}')^{\circ }$
as follows:
$(\widetilde {Q}')^{\circ }$
as follows:
Here,
![]() $(\widetilde {\mathcal{E}} ,\, \widetilde {\phi } )$
is the family of vector bundles
$(\widetilde {\mathcal{E}} ,\, \widetilde {\phi } )$
is the family of vector bundles
![]() $E_q$
and framings of
$E_q$
and framings of
![]() $E_q$
in
$E_q$
in
![]() $\widetilde {Q}'$
induced by the universal family of
$\widetilde {Q}'$
induced by the universal family of
![]() $\widetilde {Q}'$
. Since
$\widetilde {Q}'$
. Since
![]() ${\rm Quot}^N_{(V_r^{\vee }\otimes \mathcal{O}_X)/X}$
is irreducible,
${\rm Quot}^N_{(V_r^{\vee }\otimes \mathcal{O}_X)/X}$
is irreducible,
![]() $(\widetilde {Q}')^{\circ }$
is also irreducible. Let
$(\widetilde {Q}')^{\circ }$
is also irreducible. Let
![]() $(Z')^{\circ }$
be the scheme over
$(Z')^{\circ }$
be the scheme over
![]() $(\widetilde {Q}')^{\circ }$
which parametrizes quotients
$(\widetilde {Q}')^{\circ }$
which parametrizes quotients
![]() $q$
with framings of
$q$
with framings of
![]() $E_q$
in
$E_q$
in
![]() $(\widetilde {Q}')^{\circ }$
and connections on
$(\widetilde {Q}')^{\circ }$
and connections on
![]() $E_q$
that are compatible with the framings. The scheme
$E_q$
that are compatible with the framings. The scheme
![]() $(Z')^{\circ }$
is also constructed as in the proof of Proposition 3.5. It is straightforward to check that
$(Z')^{\circ }$
is also constructed as in the proof of Proposition 3.5. It is straightforward to check that
![]() $(Z')^{\circ }$
is smooth and each fiber of
$(Z')^{\circ }$
is smooth and each fiber of
![]() $(Z')^{\circ } \,\longrightarrow \, (\widetilde {Q}')^{\circ }$
is an affine space which is isomorphic to
$(Z')^{\circ } \,\longrightarrow \, (\widetilde {Q}')^{\circ }$
is an affine space which is isomorphic to
![]() $H^0(X,\, {\rm End}_{\phi }^n (E) \otimes K_X(D))$
. So
$H^0(X,\, {\rm End}_{\phi }^n (E) \otimes K_X(D))$
. So
![]() $(Z')^{\circ }$
is irreducible. Since a natural map from
$(Z')^{\circ }$
is irreducible. Since a natural map from
![]() $(Z')^{\circ }$
to
$(Z')^{\circ }$
to
![]() $(\Sigma _{m_0}^{d})^{\circ }$
is induced and this map is surjective, we conclude that
$(\Sigma _{m_0}^{d})^{\circ }$
is induced and this map is surjective, we conclude that
![]() $(\Sigma _{m_0}^{d})^{\circ }$
is irreducible. This completes the proof of the proposition.
$(\Sigma _{m_0}^{d})^{\circ }$
is irreducible. This completes the proof of the proposition.
4. Symplectic structures of the moduli spaces
Throughout this section it is assumed that
![]() $G\,=\,{\rm GL}(r,\mathbb{C})$
.
$G\,=\,{\rm GL}(r,\mathbb{C})$
.
4.1 Cotangent bundle of the moduli space of simple framed bundles
In this subsection, we assume that
![]() $H_x\,=\,\{ e \}\, \subset \, {\rm GL}(r,\mathbb{C})$
for all
$H_x\,=\,\{ e \}\, \subset \, {\rm GL}(r,\mathbb{C})$
for all
![]() $x \,\in \, D$
. Let
$x \,\in \, D$
. Let
![]() $\mathcal{N}^e(d)$
be the following moduli space:
$\mathcal{N}^e(d)$
be the following moduli space:
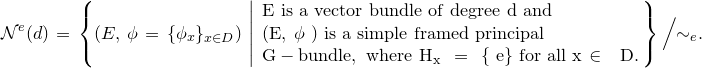 \begin{align} {\mathcal{N}^e(d)\,=\, \left \{\left (E,\,\phi \,=\, \{ \phi _x \}_{x \in D}\right )\ \middle | \ \begin{array}{l} \rm E\ is\ a\ vector\ bundle\ of\ degree\ d\ and\\ \rm (E,\,\phi\ )\ is\ a\ simple\ framed\ principal\\ \rm G-bundle,\ where\ H_x\ \,=\,\ \{\ e\}\ for\ all\ x\,\in\ \,\ D. \end{array} \right \}{\Big /}\Large {\sim }_{e}}. \end{align}
\begin{align} {\mathcal{N}^e(d)\,=\, \left \{\left (E,\,\phi \,=\, \{ \phi _x \}_{x \in D}\right )\ \middle | \ \begin{array}{l} \rm E\ is\ a\ vector\ bundle\ of\ degree\ d\ and\\ \rm (E,\,\phi\ )\ is\ a\ simple\ framed\ principal\\ \rm G-bundle,\ where\ H_x\ \,=\,\ \{\ e\}\ for\ all\ x\,\in\ \,\ D. \end{array} \right \}{\Big /}\Large {\sim }_{e}}. \end{align}
Here,
![]() $(E,\, \phi ) \,\sim _e\, (E',\, \phi ' )$
if there exists an isomorphism
$(E,\, \phi ) \,\sim _e\, (E',\, \phi ' )$
if there exists an isomorphism
![]() $\sigma \,\colon \, E\,\longrightarrow \, E'$
of vector bundles such that the composition of homomorphisms
$\sigma \,\colon \, E\,\longrightarrow \, E'$
of vector bundles such that the composition of homomorphisms
![]() $(\phi '_{x})^{-1} \circ \sigma |_{x}\circ \phi _{x}$
is the identity map of
$(\phi '_{x})^{-1} \circ \sigma |_{x}\circ \phi _{x}$
is the identity map of
![]() ${\mathbb C}^r$
for each
${\mathbb C}^r$
for each
![]() $x\,\in \, D$
. Since the tangent space of
$x\,\in \, D$
. Since the tangent space of
![]() $\mathcal{N}^e(d)$
at
$\mathcal{N}^e(d)$
at
![]() $(E,\,\phi )$
is
$(E,\,\phi )$
is
![]() $H^1(X,\,\mathcal{E}nd(E)(-D))$
[Reference Biswas, Logares and Peón-NietoBLP1, Lemma 2.5], using the Serre duality it follows that the cotangent space of
$H^1(X,\,\mathcal{E}nd(E)(-D))$
[Reference Biswas, Logares and Peón-NietoBLP1, Lemma 2.5], using the Serre duality it follows that the cotangent space of
![]() $\mathcal{N}^e(d)$
at
$\mathcal{N}^e(d)$
at
![]() $(E,\,\phi )$
is
$(E,\,\phi )$
is
![]() $H^0 (X,\, \mathcal{E}nd(E) \otimes K_X(D))$
. Let
$H^0 (X,\, \mathcal{E}nd(E) \otimes K_X(D))$
. Let
![]() $T^*\mathcal{N}^e(d)$
be the cotangent bundle of
$T^*\mathcal{N}^e(d)$
be the cotangent bundle of
![]() $\mathcal{N}^e(d)$
. For
$\mathcal{N}^e(d)$
. For
![]() $\theta \, \in \, H^0 (X,\, \mathcal{E}nd(E) \otimes K_X(D))$
, define the following
$\theta \, \in \, H^0 (X,\, \mathcal{E}nd(E) \otimes K_X(D))$
, define the following
![]() $2$
-term complex:
$2$
-term complex:
The tangent space
![]() $T_{(E,\phi ,\theta )}T^*\mathcal{N}^e(d)$
at
$T_{(E,\phi ,\theta )}T^*\mathcal{N}^e(d)$
at
![]() $(E,\,\phi ,\,\theta )$
is
$(E,\,\phi ,\,\theta )$
is
![]() $\mathbb{H}^1(\mathcal{C}_{\bullet }^{{\rm Higgs}})$
[Reference Biswas, Logares and Peón-NietoBLP1, Lemma 2.7]. Given an affine open covering
$\mathbb{H}^1(\mathcal{C}_{\bullet }^{{\rm Higgs}})$
[Reference Biswas, Logares and Peón-NietoBLP1, Lemma 2.7]. Given an affine open covering
![]() $\{ U_{\alpha } \}$
of
$\{ U_{\alpha } \}$
of
![]() $X$
, the hypercohomology
$X$
, the hypercohomology
![]() $\mathbb{H}^1(\mathcal{C}_{\bullet }^{{\rm Higgs}})$
admits a description in terms of Čech cohomology. In this description, the
$\mathbb{H}^1(\mathcal{C}_{\bullet }^{{\rm Higgs}})$
admits a description in terms of Čech cohomology. In this description, the
![]() $1$
-cocycles are pairs
$1$
-cocycles are pairs
![]() $(\{ u_{\alpha \beta } \} ,\, \{ v_{\alpha } \})$
, where
$(\{ u_{\alpha \beta } \} ,\, \{ v_{\alpha } \})$
, where
such that
![]() $u_{\beta \gamma }-u_{\alpha \gamma }+u_{\alpha \beta }\,=\,0$
and
$u_{\beta \gamma }-u_{\alpha \gamma }+u_{\alpha \beta }\,=\,0$
and
![]() $v_{\beta }-v_{\alpha }\,=\, [\theta ,\, u_{\alpha \beta }]$
. The
$v_{\beta }-v_{\alpha }\,=\, [\theta ,\, u_{\alpha \beta }]$
. The
![]() $1$
-coboundaries are of the form
$1$
-coboundaries are of the form
![]() $(\{w_{\alpha }-w_{\beta } \} ,\, \{[w_\alpha ,\, \theta ]\})$
, where
$(\{w_{\alpha }-w_{\beta } \} ,\, \{[w_\alpha ,\, \theta ]\})$
, where
![]() $w_{\alpha } \,\in \, \mathcal{E}nd(E)(-D)(U_{\alpha })$
.
$w_{\alpha } \,\in \, \mathcal{E}nd(E)(-D)(U_{\alpha })$
.
We define a canonical
![]() $1$
-form
$1$
-form
![]() $\phi _{\mathcal{N}^e(d) }$
on the cotangent bundle
$\phi _{\mathcal{N}^e(d) }$
on the cotangent bundle
![]() $T^*\mathcal{N}^e(d)$
by
$T^*\mathcal{N}^e(d)$
by
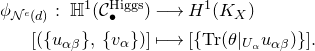 \begin{align} \begin{aligned} \begin{split} \phi _{\mathcal{N}^e(d) } \,\colon \, \mathbb{H}^1 (\mathcal{C}_{\bullet }^{{\rm Higgs}}) &\longrightarrow H^1(K_X) \\ [(\{ u_{\alpha \beta } \},\, \{ v_{\alpha } \} )] &\longmapsto [ \{ {\rm Tr}(\theta |_{U_{\alpha }} u_{\alpha \beta } ) \}]. \end{split} \end{aligned} \end{align}
\begin{align} \begin{aligned} \begin{split} \phi _{\mathcal{N}^e(d) } \,\colon \, \mathbb{H}^1 (\mathcal{C}_{\bullet }^{{\rm Higgs}}) &\longrightarrow H^1(K_X) \\ [(\{ u_{\alpha \beta } \},\, \{ v_{\alpha } \} )] &\longmapsto [ \{ {\rm Tr}(\theta |_{U_{\alpha }} u_{\alpha \beta } ) \}]. \end{split} \end{aligned} \end{align}
Lemma 4.1. Let
![]() $\Phi _{T^*\mathcal{N}^e(d)}$
be the Liouville
$\Phi _{T^*\mathcal{N}^e(d)}$
be the Liouville
![]() $2$
-form on the cotangent bundle
$2$
-form on the cotangent bundle
![]() $T^*\mathcal{N}^e(d)$
, that is,
$T^*\mathcal{N}^e(d)$
, that is,
![]() $\Phi _{T^*\mathcal{N}^e(d)}$
is the exterior derivative of the canonical
$\Phi _{T^*\mathcal{N}^e(d)}$
is the exterior derivative of the canonical
![]() $1$
-form
$1$
-form
![]() $\phi _{\mathcal{N}^e(d) }$
in (4.2). The Liouville
$\phi _{\mathcal{N}^e(d) }$
in (4.2). The Liouville
![]() $2$
-form
$2$
-form
![]() $\Phi _{T^*\mathcal{N}^e(d)}$
coincides with the bilinear form
$\Phi _{T^*\mathcal{N}^e(d)}$
coincides with the bilinear form
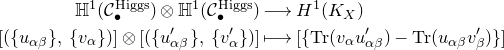 \begin{align*} \begin{aligned} \mathbb{H}^1 (\mathcal{C}_{\bullet }^{{\rm Higgs}}) \otimes \mathbb{H}^1 (\mathcal{C}_{\bullet }^{{\rm Higgs}}) &\longrightarrow H^1(K_X) \\ [(\{ u_{\alpha \beta } \},\, \{ v_{\alpha } \} )] \otimes [(\{ u'_{\alpha \beta } \},\, \{ v'_{\alpha } \} )] &\longmapsto [\{{\rm Tr} ( v_{\alpha } u'_{\alpha \beta } )- {\rm Tr} (u_{\alpha \beta } v'_{\beta } ) \}] \end{aligned} \end{align*}
\begin{align*} \begin{aligned} \mathbb{H}^1 (\mathcal{C}_{\bullet }^{{\rm Higgs}}) \otimes \mathbb{H}^1 (\mathcal{C}_{\bullet }^{{\rm Higgs}}) &\longrightarrow H^1(K_X) \\ [(\{ u_{\alpha \beta } \},\, \{ v_{\alpha } \} )] \otimes [(\{ u'_{\alpha \beta } \},\, \{ v'_{\alpha } \} )] &\longmapsto [\{{\rm Tr} ( v_{\alpha } u'_{\alpha \beta } )- {\rm Tr} (u_{\alpha \beta } v'_{\beta } ) \}] \end{aligned} \end{align*}
on the Čech cohomology.
Proof. Let
![]() $v$
and
$v$
and
![]() $v'$
be tangent vectors of
$v'$
be tangent vectors of
![]() $T^*\mathcal{N}^e(d)$
at
$T^*\mathcal{N}^e(d)$
at
![]() $(E,\,\phi ,\,\theta ) \,\in \, T^*\mathcal{N}^e(d)$
. Let
$(E,\,\phi ,\,\theta ) \,\in \, T^*\mathcal{N}^e(d)$
. Let
be the derivative corresponding to
![]() $v$
. Take an affine open subset
$v$
. Take an affine open subset
![]() $U\,\subset \, T^*\mathcal{N}^e(d)$
such that
$U\,\subset \, T^*\mathcal{N}^e(d)$
such that
![]() $(E,\,\phi ,\,\theta ) \,\in \, U$
, and also take an affine open covering
$(E,\,\phi ,\,\theta ) \,\in \, U$
, and also take an affine open covering
![]() $\{ U_{\alpha } \}$
of
$\{ U_{\alpha } \}$
of
![]() $X\times U$
such that there is a trivialization
$X\times U$
such that there is a trivialization
for each
![]() $U_{\alpha }$
. Set
$U_{\alpha }$
. Set
![]() $g_{\alpha \beta }\,\,:=\,\,g_{\alpha } \circ g^{-1}_{\beta }$
and
$g_{\alpha \beta }\,\,:=\,\,g_{\alpha } \circ g^{-1}_{\beta }$
and
![]() $\theta _{\alpha }\,\,:=\,\, g_{\alpha } \circ \theta |_{U_{\alpha }} \circ g_{\alpha }^{-1}$
. We may describe the tangent vector
$\theta _{\alpha }\,\,:=\,\, g_{\alpha } \circ \theta |_{U_{\alpha }} \circ g_{\alpha }^{-1}$
. We may describe the tangent vector
![]() $v$
as
$v$
as
where
![]() $u_{\alpha \beta }\,\,:=\,\, g_{\alpha }^{-1} \circ ( D_{v}(g_{\alpha \beta } )g_{\alpha \beta }^{-1} ) \circ g_{\alpha }$
and
$u_{\alpha \beta }\,\,:=\,\, g_{\alpha }^{-1} \circ ( D_{v}(g_{\alpha \beta } )g_{\alpha \beta }^{-1} ) \circ g_{\alpha }$
and
![]() $v_{\alpha }\,\,:=\,\, g_{\alpha }^{-1} \circ ( D_v \theta _{\alpha }) \circ g_{\alpha }$
. The exterior derivative of
$v_{\alpha }\,\,:=\,\, g_{\alpha }^{-1} \circ ( D_v \theta _{\alpha }) \circ g_{\alpha }$
. The exterior derivative of
![]() $\phi _{\mathcal{N}^e(d) }$
is computed as follows:
$\phi _{\mathcal{N}^e(d) }$
is computed as follows:
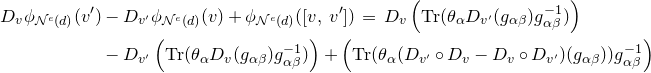 \begin{align*} \begin{aligned} D_{v}\phi _{\mathcal{N}^e(d)} ( v') & - D_{v'}\phi _{\mathcal{N}^e(d)} (v) + \phi _{\mathcal{N}^e(d) }([v,\, v']) \, =\, D_{v} \left ( {\rm Tr}( \theta _{\alpha } D_{v'}(g_{\alpha \beta } )g_{\alpha \beta }^{-1} ) \right )\\ & - D_{v'} \left ( {\rm Tr} ( \theta _{\alpha } D_{v}(g_{\alpha \beta } )g_{\alpha \beta }^{-1} ) \right ) + \left ( {\rm Tr} ( \theta _{\alpha } (D_{v'} \circ D_{v} - D_{v} \circ D_{v'} )(g_{\alpha \beta } ) )g_{\alpha \beta }^{-1} \right ) \end{aligned} \end{align*}
\begin{align*} \begin{aligned} D_{v}\phi _{\mathcal{N}^e(d)} ( v') & - D_{v'}\phi _{\mathcal{N}^e(d)} (v) + \phi _{\mathcal{N}^e(d) }([v,\, v']) \, =\, D_{v} \left ( {\rm Tr}( \theta _{\alpha } D_{v'}(g_{\alpha \beta } )g_{\alpha \beta }^{-1} ) \right )\\ & - D_{v'} \left ( {\rm Tr} ( \theta _{\alpha } D_{v}(g_{\alpha \beta } )g_{\alpha \beta }^{-1} ) \right ) + \left ( {\rm Tr} ( \theta _{\alpha } (D_{v'} \circ D_{v} - D_{v} \circ D_{v'} )(g_{\alpha \beta } ) )g_{\alpha \beta }^{-1} \right ) \end{aligned} \end{align*}
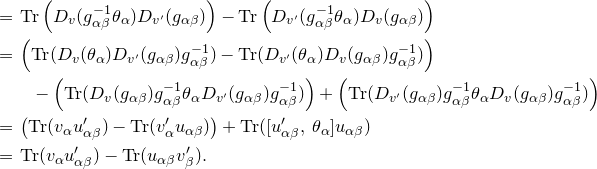 \begin{align*} \begin{aligned} & \quad=\,{\rm Tr} \left ( D_{v}(g_{\alpha \beta }^{-1} \theta _{\alpha } ) D_{v'}(g_{\alpha \beta } ) \right ) -{\rm Tr} \left ( D_{v'}( g_{\alpha \beta }^{-1}\theta _{\alpha })D_{v}(g_{\alpha \beta } ) \right ) \\ & \quad= \,\left ( {\rm Tr}( D_{v}(\theta _{\alpha } ) D_{v'}(g_{\alpha \beta } )g_{\alpha \beta }^{-1} ) - {\rm Tr} ( D_{v'}( \theta _{\alpha })D_{v}(g_{\alpha \beta } )g_{\alpha \beta }^{-1} ) \right ) \\ & \quad\qquad -\left ( {\rm Tr}(D_{v}(g_{\alpha \beta })g_{\alpha \beta }^{-1} \theta _{\alpha } D_{v'}(g_{\alpha \beta } )g_{\alpha \beta }^{-1} ) \right ) +\left ( {\rm Tr} ( D_{v'}( g_{\alpha \beta })g_{\alpha \beta }^{-1} \theta _{\alpha }D_{v}(g_{\alpha \beta } ) g_{\alpha \beta }^{-1} ) \right ) \\ & \quad= \,\left ( {\rm Tr} ( v_{\alpha } u'_{\alpha \beta } )- {\rm Tr} (v'_{\alpha }u_{\alpha \beta } ) \right ) + {\rm Tr} ( [u'_{\alpha \beta } ,\, \theta _{\alpha }]u_{\alpha \beta } ) \\ & \quad=\, {\rm Tr} ( v_{\alpha } u'_{\alpha \beta } )- {\rm Tr} (u_{\alpha \beta } v'_{\beta }). \end{aligned} \end{align*}
\begin{align*} \begin{aligned} & \quad=\,{\rm Tr} \left ( D_{v}(g_{\alpha \beta }^{-1} \theta _{\alpha } ) D_{v'}(g_{\alpha \beta } ) \right ) -{\rm Tr} \left ( D_{v'}( g_{\alpha \beta }^{-1}\theta _{\alpha })D_{v}(g_{\alpha \beta } ) \right ) \\ & \quad= \,\left ( {\rm Tr}( D_{v}(\theta _{\alpha } ) D_{v'}(g_{\alpha \beta } )g_{\alpha \beta }^{-1} ) - {\rm Tr} ( D_{v'}( \theta _{\alpha })D_{v}(g_{\alpha \beta } )g_{\alpha \beta }^{-1} ) \right ) \\ & \quad\qquad -\left ( {\rm Tr}(D_{v}(g_{\alpha \beta })g_{\alpha \beta }^{-1} \theta _{\alpha } D_{v'}(g_{\alpha \beta } )g_{\alpha \beta }^{-1} ) \right ) +\left ( {\rm Tr} ( D_{v'}( g_{\alpha \beta })g_{\alpha \beta }^{-1} \theta _{\alpha }D_{v}(g_{\alpha \beta } ) g_{\alpha \beta }^{-1} ) \right ) \\ & \quad= \,\left ( {\rm Tr} ( v_{\alpha } u'_{\alpha \beta } )- {\rm Tr} (v'_{\alpha }u_{\alpha \beta } ) \right ) + {\rm Tr} ( [u'_{\alpha \beta } ,\, \theta _{\alpha }]u_{\alpha \beta } ) \\ & \quad=\, {\rm Tr} ( v_{\alpha } u'_{\alpha \beta } )- {\rm Tr} (u_{\alpha \beta } v'_{\beta }). \end{aligned} \end{align*}
This completes the proof of the lemma.
4.2 2-form on
 $\mathcal{M}^{e}_{{\rm FC}} (d)$
$\mathcal{M}^{e}_{{\rm FC}} (d)$
As before, assume that
![]() $H_x\,=\,\{ e \}\, \subset \, {\rm GL}(r,\mathbb{C})$
for every
$H_x\,=\,\{ e \}\, \subset \, {\rm GL}(r,\mathbb{C})$
for every
![]() $x \,\in \, D$
. Let
$x \,\in \, D$
. Let
![]() $\mathbb{K}$
denote the following complex of coherent sheaves on
$\mathbb{K}$
denote the following complex of coherent sheaves on
![]() $X$
:
$X$
:
where
![]() $\mathcal{O}_{X }$
and
$\mathcal{O}_{X }$
and
![]() $K_X$
are at the
$K_X$
are at the
![]() $0$
-th position and
$0$
-th position and
![]() $1$
-position, respectively, and
$1$
-position, respectively, and
![]() $d$
is the de Rham differential.
$d$
is the de Rham differential.
Consider the complex
![]() $\mathcal{C}_{\bullet }$
in (2.11). Define a pairing
$\mathcal{C}_{\bullet }$
in (2.11). Define a pairing
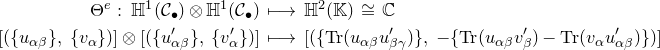 \begin{align} \Theta ^e \,\colon \, \mathbb{H}^1 (\mathcal{C}_{\bullet }) \otimes \mathbb{H}^1 (\mathcal{C}_{\bullet }) \,&\longmapsto \,\mathbb{H}^2(\mathbb{K}) \,\cong \,\mathbb{C}\nonumber \\ \,[(\{u_{\alpha \beta } \} ,\, \{ v_{\alpha } \})]\otimes [(\{u'_{\alpha \beta } \},\, \{ v'_{\alpha } \})] \,&\longmapsto \, [(\{ {\rm Tr} (u_{\alpha \beta }u'_{\beta \gamma }) \},\, - \{{\rm Tr}(u_{\alpha \beta }v'_{\beta })-{\rm Tr}(v_{\alpha }u'_{\alpha \beta }) \})] \end{align}
\begin{align} \Theta ^e \,\colon \, \mathbb{H}^1 (\mathcal{C}_{\bullet }) \otimes \mathbb{H}^1 (\mathcal{C}_{\bullet }) \,&\longmapsto \,\mathbb{H}^2(\mathbb{K}) \,\cong \,\mathbb{C}\nonumber \\ \,[(\{u_{\alpha \beta } \} ,\, \{ v_{\alpha } \})]\otimes [(\{u'_{\alpha \beta } \},\, \{ v'_{\alpha } \})] \,&\longmapsto \, [(\{ {\rm Tr} (u_{\alpha \beta }u'_{\beta \gamma }) \},\, - \{{\rm Tr}(u_{\alpha \beta }v'_{\beta })-{\rm Tr}(v_{\alpha }u'_{\alpha \beta }) \})] \end{align}
in terms of the Čech cohomology with respect to an affine open covering
![]() $\{ U_{\alpha }\}$
of
$\{ U_{\alpha }\}$
of
![]() $X$
.
$X$
.
Lemma 4.2. The pairing
![]() $\Theta ^e$
in (4.4) satisfies the identity
$\Theta ^e$
in (4.4) satisfies the identity
Thus,
![]() $\Theta ^e$
is skew-symmetric, and hence produces a
$\Theta ^e$
is skew-symmetric, and hence produces a
![]() $2$
-form on
$2$
-form on
![]() $\mathcal{M}^e_{{\rm FC}} (d)$
(see Lemma 2.4).
$\mathcal{M}^e_{{\rm FC}} (d)$
(see Lemma 2.4).
Proof. Let
![]() $v\,=\, [(\{u_{\alpha \beta } \} ,\, \{ v_{\alpha } \})]$
be an element of
$v\,=\, [(\{u_{\alpha \beta } \} ,\, \{ v_{\alpha } \})]$
be an element of
![]() $\mathbb{H}^1 (\mathcal{C}_{\bullet })$
. We compute
$\mathbb{H}^1 (\mathcal{C}_{\bullet })$
. We compute
![]() $\Theta ^e(v,\,v)$
as follows:
$\Theta ^e(v,\,v)$
as follows:
 \begin{align*} \begin{aligned}\Theta ^e(v,\,v) &=\, [(\{ {\rm Tr} (u_{\alpha \beta }u_{\beta \gamma }) \},\, - \{{\rm Tr}(u_{\alpha \beta }v_{\beta })-{\rm Tr}(v_{\alpha }u_{\alpha \beta }) \})] \\ &=\, [(\{ {\rm Tr} (u_{\alpha \beta }u_{\beta \gamma }) \},\, - \{{\rm Tr}(u_{\alpha \beta }(v_{\beta }-v_{\alpha })) \})] \\ &=\, [(\{ {\rm Tr} (u_{\alpha \beta }u_{\beta \gamma }) \},\, - \{{\rm Tr}(u_{\alpha \beta }(\nabla \circ u_{\alpha \beta } - u_{\alpha \beta } \circ \nabla ) ) \})] \\ &=\, \left [\left (\left \{ {\rm Tr} (u_{\alpha \beta }u_{\beta \gamma }) \right \},\, - \left \{ d \left ( \tfrac {1}{2}{\rm Tr}(u^2_{\alpha \beta } ) \right )\right \}\right )\right ]. \end{aligned} \end{align*}
\begin{align*} \begin{aligned}\Theta ^e(v,\,v) &=\, [(\{ {\rm Tr} (u_{\alpha \beta }u_{\beta \gamma }) \},\, - \{{\rm Tr}(u_{\alpha \beta }v_{\beta })-{\rm Tr}(v_{\alpha }u_{\alpha \beta }) \})] \\ &=\, [(\{ {\rm Tr} (u_{\alpha \beta }u_{\beta \gamma }) \},\, - \{{\rm Tr}(u_{\alpha \beta }(v_{\beta }-v_{\alpha })) \})] \\ &=\, [(\{ {\rm Tr} (u_{\alpha \beta }u_{\beta \gamma }) \},\, - \{{\rm Tr}(u_{\alpha \beta }(\nabla \circ u_{\alpha \beta } - u_{\alpha \beta } \circ \nabla ) ) \})] \\ &=\, \left [\left (\left \{ {\rm Tr} (u_{\alpha \beta }u_{\beta \gamma }) \right \},\, - \left \{ d \left ( \tfrac {1}{2}{\rm Tr}(u^2_{\alpha \beta } ) \right )\right \}\right )\right ]. \end{aligned} \end{align*}
On the other hand,
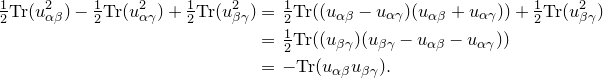 \begin{align*} \begin{aligned} \tfrac {1}{2}{\rm Tr}(u^2_{\alpha \beta } ) -\tfrac {1}{2}{\rm Tr}(u^2_{\alpha \gamma }) +\tfrac {1}{2}{\rm Tr}(u^2_{\beta \gamma }) &=\, \tfrac {1}{2}{\rm Tr}((u_{\alpha \beta } -u_{\alpha \gamma } )(u_{\alpha \beta } +u_{\alpha \gamma } )) +\tfrac {1}{2}{\rm Tr}(u^2_{\beta \gamma }) \\ &=\, \tfrac {1}{2}{\rm Tr}((u_{\beta \gamma } )(u_{\beta \gamma } -u_{\alpha \beta } -u_{\alpha \gamma } )) \\ &=\,- {\rm Tr}(u_{\alpha \beta }u_{\beta \gamma }). \end{aligned} \end{align*}
\begin{align*} \begin{aligned} \tfrac {1}{2}{\rm Tr}(u^2_{\alpha \beta } ) -\tfrac {1}{2}{\rm Tr}(u^2_{\alpha \gamma }) +\tfrac {1}{2}{\rm Tr}(u^2_{\beta \gamma }) &=\, \tfrac {1}{2}{\rm Tr}((u_{\alpha \beta } -u_{\alpha \gamma } )(u_{\alpha \beta } +u_{\alpha \gamma } )) +\tfrac {1}{2}{\rm Tr}(u^2_{\beta \gamma }) \\ &=\, \tfrac {1}{2}{\rm Tr}((u_{\beta \gamma } )(u_{\beta \gamma } -u_{\alpha \beta } -u_{\alpha \gamma } )) \\ &=\,- {\rm Tr}(u_{\alpha \beta }u_{\beta \gamma }). \end{aligned} \end{align*}
Combining these, it follows that
![]() $\Theta ^e(v,\,v)\,=\,0$
in
$\Theta ^e(v,\,v)\,=\,0$
in
![]() $\mathbb{H}^2(\mathbb{K})$
.
$\mathbb{H}^2(\mathbb{K})$
.
Remark 4.3. We have constructed a 2-form
![]() $\Theta ^e$
on
$\Theta ^e$
on
![]() $\mathcal{M}^e_{{\rm FC}} (d)$
by (4.4). On the other hand, there exists another definition of this 2-form from a differential geometric perspective; this will be explained below. First, recall a description of
$\mathcal{M}^e_{{\rm FC}} (d)$
by (4.4). On the other hand, there exists another definition of this 2-form from a differential geometric perspective; this will be explained below. First, recall a description of
![]() $\mathbb{H}^1 (\mathcal{C}_{\bullet })$
as a Dolbeault cohomology. (See the proof of Theorem 3.2 of [Reference BiswasBi].) Let
$\mathbb{H}^1 (\mathcal{C}_{\bullet })$
as a Dolbeault cohomology. (See the proof of Theorem 3.2 of [Reference BiswasBi].) Let
![]() $\overline {\partial }'$
and
$\overline {\partial }'$
and
![]() $\overline {\partial }'_1$
be the Dolbeault operators for the holomorphic vector bundles
$\overline {\partial }'_1$
be the Dolbeault operators for the holomorphic vector bundles
![]() $\mathcal{E}nd(E)(-D)$
and
$\mathcal{E}nd(E)(-D)$
and
![]() $\mathcal{E}nd(E)(D)$
, respectively. Consider the Dolbeault resolution of the complex
$\mathcal{E}nd(E)(D)$
, respectively. Consider the Dolbeault resolution of the complex
![]() $\mathcal{C}_{\bullet }$
:
$\mathcal{C}_{\bullet }$
:
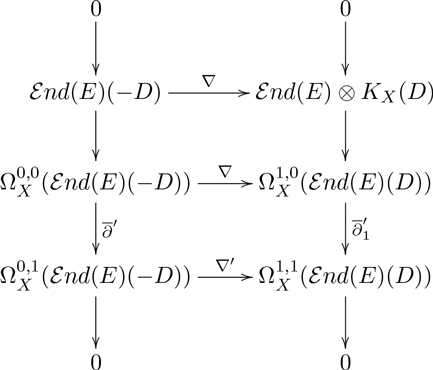
where
![]() $\nabla '$
is constructed using
$\nabla '$
is constructed using
![]() $\nabla$
and the usual differential operator
$\nabla$
and the usual differential operator
![]() $\partial$
on
$\partial$
on
![]() $(0,\,1)$
-forms on
$(0,\,1)$
-forms on
![]() $X$
. Note that
$X$
. Note that
This produces the following complex of vector spaces
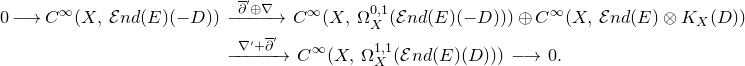 \begin{align*} \begin{aligned} 0 \longrightarrow C^{\infty }(X,\,\mathcal{E}nd(E)(-D)) \,&\xrightarrow {\ \overline {\partial }' \oplus \nabla \ }\, C^{\infty }(X,\,\Omega ^{0,1}_X (\mathcal{E}nd(E)(-D)))\oplus C^{\infty }(X,\, \mathcal{E}nd(E)\otimes K_X(D))\\ &\xrightarrow {\ \nabla '+\overline {\partial }'\ }\, C^{\infty }(X,\, \Omega ^{1,1}_X (\mathcal{E}nd(E)(D))) \,\longrightarrow \, 0. \end{aligned} \end{align*}
\begin{align*} \begin{aligned} 0 \longrightarrow C^{\infty }(X,\,\mathcal{E}nd(E)(-D)) \,&\xrightarrow {\ \overline {\partial }' \oplus \nabla \ }\, C^{\infty }(X,\,\Omega ^{0,1}_X (\mathcal{E}nd(E)(-D)))\oplus C^{\infty }(X,\, \mathcal{E}nd(E)\otimes K_X(D))\\ &\xrightarrow {\ \nabla '+\overline {\partial }'\ }\, C^{\infty }(X,\, \Omega ^{1,1}_X (\mathcal{E}nd(E)(D))) \,\longrightarrow \, 0. \end{aligned} \end{align*}
Since the Dolbeault complex is a fine resolution of
![]() $\mathcal{C}_{\bullet }$
, it follows immediately that
$\mathcal{C}_{\bullet }$
, it follows immediately that
Then the
![]() $2$
-form
$2$
-form
![]() $\Theta ^e$
in (4.4) can be described using the Dolbeault cohomology in the following way:
$\Theta ^e$
in (4.4) can be described using the Dolbeault cohomology in the following way:
4.3 Symplectic structure on
 $\mathcal{M}^{e}_{{\rm FC}} (d)^{\circ }$
$\mathcal{M}^{e}_{{\rm FC}} (d)^{\circ }$
Now take the restriction of
![]() $\Theta ^e$
to
$\Theta ^e$
to
![]() $\mathcal{M}^{e}_{{\rm FC}}(d)^{\circ }$
; here,
$\mathcal{M}^{e}_{{\rm FC}}(d)^{\circ }$
; here,
![]() $\mathcal{M}^{e}_{{\rm FC}}(d)^{\circ }$
is the open substack of
$\mathcal{M}^{e}_{{\rm FC}}(d)^{\circ }$
is the open substack of
![]() $\mathcal{M}^{e}_{{\rm FC}}(d)$
defined in (3.7), or in other words, the underlying framed bundle
$\mathcal{M}^{e}_{{\rm FC}}(d)$
defined in (3.7), or in other words, the underlying framed bundle
![]() $(E, \, \phi )$
of any
$(E, \, \phi )$
of any
![]() $(E,\, \phi ,\, \nabla )\, \in \, \mathcal{M}^{e}_{{\rm FC}}(d)^{\circ }$
satisfies the condition that it is simple. Denote this restriction of
$(E,\, \phi ,\, \nabla )\, \in \, \mathcal{M}^{e}_{{\rm FC}}(d)^{\circ }$
satisfies the condition that it is simple. Denote this restriction of
![]() $\Theta ^e$
to
$\Theta ^e$
to
![]() $\mathcal{M}^{e}_{{\rm FC}}(d)^{\circ }$
by
$\mathcal{M}^{e}_{{\rm FC}}(d)^{\circ }$
by
![]() $\Theta ^e|_{\mathcal{M}^{e}_{{\rm FC}}(d)^{\circ }}$
. It will be shown that this restriction of
$\Theta ^e|_{\mathcal{M}^{e}_{{\rm FC}}(d)^{\circ }}$
. It will be shown that this restriction of
![]() $\Theta ^e$
is a symplectic form.
$\Theta ^e$
is a symplectic form.
Let
be the forgetful map that simply forgets the connection. Take an analytic open subset
![]() $U\, \subset \, \mathcal{N}^e(d)$
, which is assumed to be small enough. Then there exist sections, over
$U\, \subset \, \mathcal{N}^e(d)$
, which is assumed to be small enough. Then there exist sections, over
![]() $U$
, of the map
$U$
, of the map
![]() $p_1$
in (4.5). Let
$p_1$
in (4.5). Let
be a holomorphic section. Using
![]() $s$
, an isomorphism
$s$
, an isomorphism
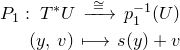 \begin{align} P_1\,\colon \, T^*U \,\xrightarrow {\ \cong \ }\, p_1^{-1}(U) \\ (y,\,v) \,\longmapsto \,s(y) + v\nonumber \end{align}
\begin{align} P_1\,\colon \, T^*U \,\xrightarrow {\ \cong \ }\, p_1^{-1}(U) \\ (y,\,v) \,\longmapsto \,s(y) + v\nonumber \end{align}
is obtained. The restriction, to
![]() $p_1^{-1}(U)$
, of the form
$p_1^{-1}(U)$
, of the form
![]() $\Theta ^e|_{\mathcal{M}^{e}_{{\rm FC}}(d)^{\circ }}$
is denoted by
$\Theta ^e|_{\mathcal{M}^{e}_{{\rm FC}}(d)^{\circ }}$
is denoted by
![]() $\Theta ^e|_{p_1^{-1}(U)}$
.
$\Theta ^e|_{p_1^{-1}(U)}$
.
Lemma 4.4. Let
![]() $\Phi _U$
be the Liouville
$\Phi _U$
be the Liouville
![]() $2$
-form on the cotangent bundle
$2$
-form on the cotangent bundle
![]() $T^*U$
. Then,
$T^*U$
. Then,
where
![]() $\Theta ^e|_{p_1^{-1}(U)}$
is the restriction of the form in (4.4) and
$\Theta ^e|_{p_1^{-1}(U)}$
is the restriction of the form in (4.4) and
![]() $p_1$
is the projection in (4.5), while
$p_1$
is the projection in (4.5), while
![]() $P_1$
is the isomorphism in (4.6).
$P_1$
is the isomorphism in (4.6).
Proof. Take a point
![]() $z\,=\,(E,\,\phi ,\,\nabla )$
of
$z\,=\,(E,\,\phi ,\,\nabla )$
of
![]() $p_1^{-1}(U)$
. Let
$p_1^{-1}(U)$
. Let
![]() $\nabla (E,\,\phi )$
be the connection associated to the point
$\nabla (E,\,\phi )$
be the connection associated to the point
![]() $s\circ p_1(z)$
. The image of
$s\circ p_1(z)$
. The image of
![]() $z$
under the map
$z$
under the map
![]() $P^{-1}_1$
in (4.6) is as follows:
$P^{-1}_1$
in (4.6) is as follows:
Let
![]() $[(\{u_{\alpha \beta } \} ,\,\{ v_{\beta } \})]$
be an element of
$[(\{u_{\alpha \beta } \} ,\,\{ v_{\beta } \})]$
be an element of
![]() $\mathbb{H}^1((\mathcal{C}_{\bullet })_z)$
, where
$\mathbb{H}^1((\mathcal{C}_{\bullet })_z)$
, where
![]() $(\mathcal{C}_{\bullet })_z$
is the complex in (2.11) associated to
$(\mathcal{C}_{\bullet })_z$
is the complex in (2.11) associated to
![]() $z\,=\,(E,\,\phi ,\, \nabla )$
. Recall from Lemma 2.4 that
$z\,=\,(E,\,\phi ,\, \nabla )$
. Recall from Lemma 2.4 that
![]() $\mathbb{H}^1((\mathcal{C}_{\bullet })_z)$
is the tangent space of
$\mathbb{H}^1((\mathcal{C}_{\bullet })_z)$
is the tangent space of
![]() $p_1^{-1}(U)$
at
$p_1^{-1}(U)$
at
![]() $z$
. Note that
$z$
. Note that
![]() $u_{\alpha \beta }$
and
$u_{\alpha \beta }$
and
![]() $v_{\alpha }$
satisfy the equality
$v_{\alpha }$
satisfy the equality
Let
![]() $[(\{u_{\alpha \beta }\},\, \{ v^s_{\alpha } \})]$
be the element of
$[(\{u_{\alpha \beta }\},\, \{ v^s_{\alpha } \})]$
be the element of
![]() $\mathbb{H}^1((\mathcal{C}_{\bullet })_{s\circ p_1(z)})$
such that
$\mathbb{H}^1((\mathcal{C}_{\bullet })_{s\circ p_1(z)})$
such that
Note that
![]() $u_{\alpha \beta }$
and
$u_{\alpha \beta }$
and
![]() $v^s_{\alpha }$
satisfy the equality
$v^s_{\alpha }$
satisfy the equality
Since
it follows that
![]() $[(\{ u_{\alpha \beta } \} ,\,\{v_{\alpha }-v_{\alpha }^s \})]$
is an element of
$[(\{ u_{\alpha \beta } \} ,\,\{v_{\alpha }-v_{\alpha }^s \})]$
is an element of
![]() $\mathbb{H}^1 (\mathcal{C}^{{\rm Higgs}}_{\bullet })$
; recall that
$\mathbb{H}^1 (\mathcal{C}^{{\rm Higgs}}_{\bullet })$
; recall that
![]() $\mathbb{H}^1 (\mathcal{C}^{{\rm Higgs}}_{\bullet })$
is the tangent space of
$\mathbb{H}^1 (\mathcal{C}^{{\rm Higgs}}_{\bullet })$
is the tangent space of
![]() $T^*U$
at
$T^*U$
at
![]() $P_1^{-1}(z)$
(see (4.6)). There is a map
$P_1^{-1}(z)$
(see (4.6)). There is a map
This map coincides with
![]() $(P_1^{-1})_* \,\colon \,\mathbb{H}^1 ((\mathcal{C}_{\bullet })_z) \, \longrightarrow \,\mathbb{H}^1 (\mathcal{C}^{{\rm Higgs}}_{\bullet })$
.
$(P_1^{-1})_* \,\colon \,\mathbb{H}^1 ((\mathcal{C}_{\bullet })_z) \, \longrightarrow \,\mathbb{H}^1 (\mathcal{C}^{{\rm Higgs}}_{\bullet })$
.
Now we compute the map
as follows:
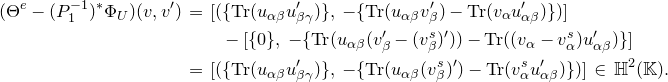 \begin{align*} \begin{aligned} (\Theta ^e - (P_1^{-1})^* \Phi _U)(v,v') \,&=\, [(\{ {\rm Tr} (u_{\alpha \beta }u'_{\beta \gamma }) \},\, - \{ {\rm Tr}(u_{\alpha \beta }v'_{\beta })-{\rm Tr}(v_{\alpha }u'_{\alpha \beta }) \})] \\ &\qquad - [ \{ 0 \},\,- \{ {\rm Tr}(u_{\alpha \beta }(v'_{\beta }-(v_{\beta }^s)')) -{\rm Tr}((v_{\alpha }-v_{\alpha }^s) u'_{\alpha \beta }) \} ]\\ &=\,[(\{ {\rm Tr} (u_{\alpha \beta }u'_{\beta \gamma }) \},\, - \{{\rm Tr}(u_{\alpha \beta }(v^s_{\beta })')-{\rm Tr}(v^s_{\alpha }u'_{\alpha \beta }) \})] \,\in \,\mathbb{H}^2(\mathbb{K}). \end{aligned} \end{align*}
\begin{align*} \begin{aligned} (\Theta ^e - (P_1^{-1})^* \Phi _U)(v,v') \,&=\, [(\{ {\rm Tr} (u_{\alpha \beta }u'_{\beta \gamma }) \},\, - \{ {\rm Tr}(u_{\alpha \beta }v'_{\beta })-{\rm Tr}(v_{\alpha }u'_{\alpha \beta }) \})] \\ &\qquad - [ \{ 0 \},\,- \{ {\rm Tr}(u_{\alpha \beta }(v'_{\beta }-(v_{\beta }^s)')) -{\rm Tr}((v_{\alpha }-v_{\alpha }^s) u'_{\alpha \beta }) \} ]\\ &=\,[(\{ {\rm Tr} (u_{\alpha \beta }u'_{\beta \gamma }) \},\, - \{{\rm Tr}(u_{\alpha \beta }(v^s_{\beta })')-{\rm Tr}(v^s_{\alpha }u'_{\alpha \beta }) \})] \,\in \,\mathbb{H}^2(\mathbb{K}). \end{aligned} \end{align*}
On the other hand, we compute
as follows:
 \begin{align*} \begin{aligned} p_1^* (s^* \Theta ^e)(v,\,v') = p_1^* (s^* \Theta ^e)([(\{u_{\alpha \beta }\},\, \{ v^s_{\alpha } \})] ,[(\{u'_{\alpha \beta }\}, \,\{ (v^s_{\alpha })' \})]) \\ =[(\{ {\rm Tr} (u_{\alpha \beta }u'_{\beta \gamma }) \},\, - \{{\rm Tr}(u_{\alpha \beta }(v^s_{\beta })')-{\rm Tr}(v^s_{\alpha }u'_{\alpha \beta }) \})] \,\in \, \mathbb{H}^1(\mathbb{K}). \end{aligned} \end{align*}
\begin{align*} \begin{aligned} p_1^* (s^* \Theta ^e)(v,\,v') = p_1^* (s^* \Theta ^e)([(\{u_{\alpha \beta }\},\, \{ v^s_{\alpha } \})] ,[(\{u'_{\alpha \beta }\}, \,\{ (v^s_{\alpha })' \})]) \\ =[(\{ {\rm Tr} (u_{\alpha \beta }u'_{\beta \gamma }) \},\, - \{{\rm Tr}(u_{\alpha \beta }(v^s_{\beta })')-{\rm Tr}(v^s_{\alpha }u'_{\alpha \beta }) \})] \,\in \, \mathbb{H}^1(\mathbb{K}). \end{aligned} \end{align*}
Therefore, we have the equality
![]() $\Theta ^e|_{p_1^{-1}(U)} - (P_1^{-1})^* \Phi _U \,=\, p_1^* (s^* \Theta ^e|_{p_1^{-1}(U)})$
.
$\Theta ^e|_{p_1^{-1}(U)} - (P_1^{-1})^* \Phi _U \,=\, p_1^* (s^* \Theta ^e|_{p_1^{-1}(U)})$
.
It will now be shown that the restriction of
![]() $\Theta ^e$
to
$\Theta ^e$
to
![]() $\mathcal{M}^{e}_{{\rm FC}}(d)^{\circ }$
is nondegenerate.
$\mathcal{M}^{e}_{{\rm FC}}(d)^{\circ }$
is nondegenerate.
Corollary 4.5. The
![]() $2$
-form
$2$
-form
![]() $\Theta ^e|_{\mathcal{M}^{e}_{{\rm FC}}(d)^{\circ }}$
is nondegenerate.
$\Theta ^e|_{\mathcal{M}^{e}_{{\rm FC}}(d)^{\circ }}$
is nondegenerate.
Proof. For any point
![]() $(E,\,\phi ,\,\nabla )\, \in \, \mathcal{M}^{e}_{\textrm {FC}}(d)^{\circ }$
and any tangent vectors
$(E,\,\phi ,\,\nabla )\, \in \, \mathcal{M}^{e}_{\textrm {FC}}(d)^{\circ }$
and any tangent vectors
![]() $v,\, w\, \in \, T_{(E,\phi ,\nabla )} \mathcal{M}^{e}_{\textrm {FC}}(d)^{\circ }$
, we have
$v,\, w\, \in \, T_{(E,\phi ,\nabla )} \mathcal{M}^{e}_{\textrm {FC}}(d)^{\circ }$
, we have
when one of
![]() $v$
and
$v$
and
![]() $w$
is vertical for the projection
$w$
is vertical for the projection
![]() $p_1$
in (4.5). So, if
$p_1$
in (4.5). So, if
![]() $w$
is vertical, from Lemma 4.4 it follows that
$w$
is vertical, from Lemma 4.4 it follows that
Since
![]() $\Phi _U$
is a symplectic form, there is a tangent vector
$\Phi _U$
is a symplectic form, there is a tangent vector
![]() $v\, \in \, T_{(E,\phi ,\nabla )} \mathcal{M}^{e}_{\textrm {FC}}(d)^{\circ }$
such that
$v\, \in \, T_{(E,\phi ,\nabla )} \mathcal{M}^{e}_{\textrm {FC}}(d)^{\circ }$
such that
Now from (4.7) it follows that
![]() $\Theta ^e(E,\,\phi ,\,\nabla )(v,\, w)\, \not =\, 0$
.
$\Theta ^e(E,\,\phi ,\,\nabla )(v,\, w)\, \not =\, 0$
.
Since the vertical tangent spaces for the projection
![]() $T^*U\, \longrightarrow \, U$
are Lagrangian for the Liouville
$T^*U\, \longrightarrow \, U$
are Lagrangian for the Liouville
![]() $2$
-form
$2$
-form
![]() $\Phi _U$
, given any non-vertical tangent vector
$\Phi _U$
, given any non-vertical tangent vector
for the projection
![]() $T^*U\, \longrightarrow \, U$
, there is a vertical tangent vector
$T^*U\, \longrightarrow \, U$
, there is a vertical tangent vector
for the projection
![]() $T^*U\, \longrightarrow \, U$
such that
$T^*U\, \longrightarrow \, U$
such that
![]() $(P_1^{-1})^* \Phi _U (E,\,\phi ,\,\nabla )(v,\, w)\,\not =\, 0$
. Now from (4.7) it follows that
$(P_1^{-1})^* \Phi _U (E,\,\phi ,\,\nabla )(v,\, w)\,\not =\, 0$
. Now from (4.7) it follows that
![]() $\Theta ^e(E,\,\phi ,\,\nabla )(v,\, w)\, \not =\, 0$
. Consequently, the form
$\Theta ^e(E,\,\phi ,\,\nabla )(v,\, w)\, \not =\, 0$
. Consequently, the form
![]() $\Theta ^e\vert _{p^{-1}(U)}$
is nondegenerate.
$\Theta ^e\vert _{p^{-1}(U)}$
is nondegenerate.
Remark 4.6. It was shown above that the restriction of
![]() $\Theta ^e$
to
$\Theta ^e$
to
![]() $\mathcal{M}^{e}_{{\rm FC}}(d)^{\circ }$
is nondegenerate by using Lemma 4.4. We will show that the 2-form
$\mathcal{M}^{e}_{{\rm FC}}(d)^{\circ }$
is nondegenerate by using Lemma 4.4. We will show that the 2-form
![]() $\Theta ^e$
on
$\Theta ^e$
on
![]() $\mathcal{M}^{e}_{{\rm FC}}(d)$
is nondegenerate by using the Serre duality (Proposition 4.18 below). So it can be shown that the restriction of
$\mathcal{M}^{e}_{{\rm FC}}(d)$
is nondegenerate by using the Serre duality (Proposition 4.18 below). So it can be shown that the restriction of
![]() $\Theta ^e$
to
$\Theta ^e$
to
![]() $\mathcal{M}^{e}_{{\rm FC}}(d)^{\circ }$
is nondegenerate without using Lemma 4.4. Nevertheless, we have discussed nondegeneracy of the restriction of
$\mathcal{M}^{e}_{{\rm FC}}(d)^{\circ }$
is nondegenerate without using Lemma 4.4. Nevertheless, we have discussed nondegeneracy of the restriction of
![]() $\Theta ^e$
by using this lemma because this argument highlights another important perspective. Lemma 4.4 will be used below in the proof of the
$\Theta ^e$
by using this lemma because this argument highlights another important perspective. Lemma 4.4 will be used below in the proof of the
![]() $d$
-closedness of the restriction of
$d$
-closedness of the restriction of
![]() $\Theta ^e$
. Moreover, the
$\Theta ^e$
. Moreover, the
![]() $d$
-closedness of the restriction of
$d$
-closedness of the restriction of
![]() $\Theta ^e$
will be used below in the proof of the
$\Theta ^e$
will be used below in the proof of the
![]() $d$
-closedness of
$d$
-closedness of
![]() $\Theta ^e$
on
$\Theta ^e$
on
![]() $\mathcal{M}^{e}_{\textrm {FC}}(d)$
.
$\mathcal{M}^{e}_{\textrm {FC}}(d)$
.
Proposition 4.7. Assume that
![]() $g\,\geqslant \, 2$
. Let
$g\,\geqslant \, 2$
. Let
![]() ${\mathcal M}^e_{{\rm FC}}(d)^{\circ }$
be the open subspace of
${\mathcal M}^e_{{\rm FC}}(d)^{\circ }$
be the open subspace of
![]() $\mathcal{M}^{e}_{{\rm FC}}(d)$
defined in (3.7) for
$\mathcal{M}^{e}_{{\rm FC}}(d)$
defined in (3.7) for
![]() $H=\{e\}$
. Then the restriction
$H=\{e\}$
. Then the restriction
![]() $\Theta ^e|_{\mathcal{M}^{e}_{{\rm FC}}(d)^{\circ }}$
of the nondegenerate
$\Theta ^e|_{\mathcal{M}^{e}_{{\rm FC}}(d)^{\circ }}$
of the nondegenerate
![]() $2$
-form
$2$
-form
![]() $\Theta ^e$
in (4.4) is
$\Theta ^e$
in (4.4) is
![]() $d$
-closed.
$d$
-closed.
Proof. The moduli space
![]() $\mathcal{N}^e(d)$
in (4.1) has the open subset
$\mathcal{N}^e(d)$
in (4.1) has the open subset
![]() $\mathcal{N}^e(d)^{\circ }$
defined by
$\mathcal{N}^e(d)^{\circ }$
defined by
Also, let
![]() $\mathcal{M}_{{\rm FC}}^{e}(d)^{\circ \circ }\, \subset \, \mathcal{M}_{{\rm FC}}^{e}(d)^{\circ }$
(see Definition 3.1) be the open subset
$\mathcal{M}_{{\rm FC}}^{e}(d)^{\circ \circ }\, \subset \, \mathcal{M}_{{\rm FC}}^{e}(d)^{\circ }$
(see Definition 3.1) be the open subset
The openness of both
![]() $\mathcal{N}^e(d)^{\circ }$
and
$\mathcal{N}^e(d)^{\circ }$
and
![]() $\mathcal{M}_{{\rm FC}}^{e} (d)^{\circ \circ }$
follows from [Reference MaruyamaMaru, p. 635, Theorem 2.8(B)]. The moduli spaces
$\mathcal{M}_{{\rm FC}}^{e} (d)^{\circ \circ }$
follows from [Reference MaruyamaMaru, p. 635, Theorem 2.8(B)]. The moduli spaces
![]() $\mathcal{N}^e(d)^{\circ }$
and
$\mathcal{N}^e(d)^{\circ }$
and
![]() $\mathcal{M}_{{\rm FC}}^{e}(d)^{\circ \circ }$
are non-empty because
$\mathcal{M}_{{\rm FC}}^{e}(d)^{\circ \circ }$
are non-empty because
![]() $g\,\geqslant \, 2$
.
$g\,\geqslant \, 2$
.
To prove that the form
![]() $\Theta ^e|_{\mathcal{M}^{e}_{{\rm FC}}(d)^{\circ }}$
on
$\Theta ^e|_{\mathcal{M}^{e}_{{\rm FC}}(d)^{\circ }}$
on
![]() $\mathcal{M}_{{\rm FC}}^{e}(d)^{\circ }$
is closed, it suffices to show that the restriction of
$\mathcal{M}_{{\rm FC}}^{e}(d)^{\circ }$
is closed, it suffices to show that the restriction of
![]() $\Theta ^e|_{\mathcal{M}^{e}_{{\rm FC}}(d)^{\circ }}$
to
$\Theta ^e|_{\mathcal{M}^{e}_{{\rm FC}}(d)^{\circ }}$
to
![]() $\mathcal{M}_{{\rm FC}}^{e}(d)^{\circ \circ }$
is closed.
$\mathcal{M}_{{\rm FC}}^{e}(d)^{\circ \circ }$
is closed.
Let
![]() $p_{1,0}\, :\, \mathcal{M}^{e}_{\textrm {FC}}(d)^{\circ \circ } \,\longrightarrow \,\mathcal{N}^e(d)^{\circ }$
be the restriction of the forgetful map
$p_{1,0}\, :\, \mathcal{M}^{e}_{\textrm {FC}}(d)^{\circ \circ } \,\longrightarrow \,\mathcal{N}^e(d)^{\circ }$
be the restriction of the forgetful map
![]() $p_1$
in (4.5). Take a sufficiently small analytic open subset
$p_1$
in (4.5). Take a sufficiently small analytic open subset
![]() $U \, \subset \, \mathcal{N}^e(d)^{\circ }$
such that there is a holomorphic section
$U \, \subset \, \mathcal{N}^e(d)^{\circ }$
such that there is a holomorphic section
over
![]() $U$
, of
$U$
, of
![]() $p_{1,0}$
. Now, Lemma 4.4 says that
$p_{1,0}$
. Now, Lemma 4.4 says that
on
![]() $p_{1,0}^{-1}(U)$
. This implies that
$p_{1,0}^{-1}(U)$
. This implies that
on
![]() $p_{1,0}^{-1}(U)$
, because the Liouville
$p_{1,0}^{-1}(U)$
, because the Liouville
![]() $2$
-form is
$2$
-form is
![]() $d$
-closed.
$d$
-closed.
In view of (4.9), to prove the theorem it suffices to show the existence of a local holomorphic section
![]() $s\,\colon \, U \,\longrightarrow \, p^{-1}_{1,0}(U)$
of the map
$s\,\colon \, U \,\longrightarrow \, p^{-1}_{1,0}(U)$
of the map
![]() $p^{-1}_{1,0}$
such that
$p^{-1}_{1,0}$
such that
![]() $d(s^*\Theta ^e)\,=\, 0$
.
$d(s^*\Theta ^e)\,=\, 0$
.
We shall construct a holomorphic section
![]() $s\,\colon \, U \,\longrightarrow \, p^{-1}_{1,0}(U)$
such that
$s\,\colon \, U \,\longrightarrow \, p^{-1}_{1,0}(U)$
such that
For that, first define a moduli space
 \begin{align*} \mathcal{M}^{e}_{\textrm {FC}}(d)^{\circ \circ }_{0}\,\,:=\, \,\left \{ (E,\phi ,\nabla ) \ \middle | \ \begin{array}{l} E\ is\ a\ stable\ vector\ bundle\ of\ degree\ d,\ and\\ (E,\ \phi\ ,\nabla\ )\ is\ a\ framed\ \mathrm{GL}(r,\mathbb{C})-connection\ such\ that \\ \rm \mathrm{res}_{x_i}(\nabla\ )\,=\,0\ for\ i=1,\ldots\ ,n-1\ and\ \mathrm{res}_{x_n}(\ \nabla\ )=-\frac{d}{r}e \end{array} \right \}{\Big /}\Large {\sim }, \end{align*}
\begin{align*} \mathcal{M}^{e}_{\textrm {FC}}(d)^{\circ \circ }_{0}\,\,:=\, \,\left \{ (E,\phi ,\nabla ) \ \middle | \ \begin{array}{l} E\ is\ a\ stable\ vector\ bundle\ of\ degree\ d,\ and\\ (E,\ \phi\ ,\nabla\ )\ is\ a\ framed\ \mathrm{GL}(r,\mathbb{C})-connection\ such\ that \\ \rm \mathrm{res}_{x_i}(\nabla\ )\,=\,0\ for\ i=1,\ldots\ ,n-1\ and\ \mathrm{res}_{x_n}(\ \nabla\ )=-\frac{d}{r}e \end{array} \right \}{\Big /}\Large {\sim }, \end{align*}
where
![]() $e$
is the identity matrix. There is the natural inclusion map
$e$
is the identity matrix. There is the natural inclusion map
where
![]() $\mathcal{M}^{e}_{\textrm {FC}}(d)^{\circ \circ }$
is defined in (4.8). Also, define two moduli spaces
$\mathcal{M}^{e}_{\textrm {FC}}(d)^{\circ \circ }$
is defined in (4.8). Also, define two moduli spaces
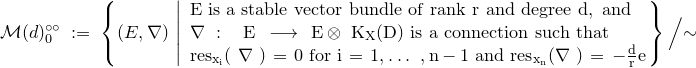 \begin{align*} \mathcal{M}(d)_{0}^{\circ \circ }\,\,:=\, \,\left \{ (E,\nabla ) \ \middle | \ \begin{array}{l} \rm E\ is\ a\ stable\ vector\ bundle\ of\ rank\ r\ and\ degree\ d,\ and\\ \rm \nabla\ \,\colon\ \,\ E\ \,\longrightarrow\ \,E\otimes\ K_X(D)\ is\ a\ connection\ such\ that\ \\ \rm \mathrm{res}_{x_i}(\ \nabla\ )\,=\,0\ for\ i\,=\,1,\ldots\ ,n-1\ and\ \mathrm{res}_{x_n}(\nabla\ )\,=\,-\frac{d}{r}e \end{array} \right \}{\Big /}\Large {\sim } \end{align*}
\begin{align*} \mathcal{M}(d)_{0}^{\circ \circ }\,\,:=\, \,\left \{ (E,\nabla ) \ \middle | \ \begin{array}{l} \rm E\ is\ a\ stable\ vector\ bundle\ of\ rank\ r\ and\ degree\ d,\ and\\ \rm \nabla\ \,\colon\ \,\ E\ \,\longrightarrow\ \,E\otimes\ K_X(D)\ is\ a\ connection\ such\ that\ \\ \rm \mathrm{res}_{x_i}(\ \nabla\ )\,=\,0\ for\ i\,=\,1,\ldots\ ,n-1\ and\ \mathrm{res}_{x_n}(\nabla\ )\,=\,-\frac{d}{r}e \end{array} \right \}{\Big /}\Large {\sim } \end{align*}
and
There are the forgetful maps
where
![]() $q_2$
and
$q_2$
and
![]() $p_2$
forget the framing while
$p_2$
forget the framing while
![]() $q_1$
forgets the connection.
$q_1$
forgets the connection.
Take an analytic open subset
![]() $U_0\,\subset \, \mathcal{N}(d)^{\circ }$
. Assume that
$U_0\,\subset \, \mathcal{N}(d)^{\circ }$
. Assume that
![]() $U_0$
is small enough and that the image of
$U_0$
is small enough and that the image of
![]() $U$
under the forgetful map
$U$
under the forgetful map
![]() $p_2 \,\colon \, \mathcal{N}^e (d)^{\circ }\,\longrightarrow \, \mathcal{N}(d)^{\circ }$
is contained in
$p_2 \,\colon \, \mathcal{N}^e (d)^{\circ }\,\longrightarrow \, \mathcal{N}(d)^{\circ }$
is contained in
![]() $U_0$
, by shrinking sufficiently the analytic open subset
$U_0$
, by shrinking sufficiently the analytic open subset
![]() $U$
. Take a holomorphic section
$U$
. Take a holomorphic section
of the forgetful map
![]() $q_1 \,\colon \, \mathcal{M}(d)^{\circ \circ }_{0}\,\longrightarrow \, \mathcal{N}(d)^{\circ }$
. Since
$q_1 \,\colon \, \mathcal{M}(d)^{\circ \circ }_{0}\,\longrightarrow \, \mathcal{N}(d)^{\circ }$
. Since
![]() $H_x\,=\,\{ e\}$
for all
$H_x\,=\,\{ e\}$
for all
![]() $x\in D$
, we may define a section
$x\in D$
, we may define a section
![]() $\widetilde {s}$
on
$\widetilde {s}$
on
![]() $U$
$U$
using the section
![]() $s_0$
. Define the section
$s_0$
. Define the section
![]() $s$
on
$s$
on
![]() $U$
of
$U$
of
![]() $p_{1,0} \,\colon \, p_1^{-1}(U)\,\longrightarrow \, U$
by
$p_{1,0} \,\colon \, p_1^{-1}(U)\,\longrightarrow \, U$
by
Now we shall prove that
for such a section.
To prove (4.12), first recall that the moduli space
![]() $\mathcal{M}(d)^{\circ \circ }_{0}$
is equipped with a natural symplectic structure. We briefly describe this symplectic structure on
$\mathcal{M}(d)^{\circ \circ }_{0}$
is equipped with a natural symplectic structure. We briefly describe this symplectic structure on
![]() $\mathcal{M}(d)^{\circ \circ }_{0}$
. The tangent space to
$\mathcal{M}(d)^{\circ \circ }_{0}$
. The tangent space to
![]() $\mathcal{M}(d)^{\circ \circ }_{0}$
at any point
$\mathcal{M}(d)^{\circ \circ }_{0}$
at any point
![]() $(E,\,\nabla )$
is isomorphic to the first hypercohomology
$(E,\,\nabla )$
is isomorphic to the first hypercohomology
![]() $\mathbb{H}^1(\mathcal{C}^0_{\bullet })$
, where
$\mathbb{H}^1(\mathcal{C}^0_{\bullet })$
, where
Define a nondegenerate
![]() $2$
-form
$2$
-form
![]() $\Theta _0$
on
$\Theta _0$
on
![]() $\mathcal{M}(d)^{\circ \circ }_{0}$
$\mathcal{M}(d)^{\circ \circ }_{0}$
exactly as done in (4.4). This
![]() $2$
-form
$2$
-form
![]() $\Theta _0$
is
$\Theta _0$
is
![]() $d$
-closed, which is proved in [Reference GoldmanGol].
$d$
-closed, which is proved in [Reference GoldmanGol].
Secondly, we show that
where
![]() $q_2$
and
$q_2$
and
![]() $\iota$
are the maps in (4.11) and (4.10) respectively. To prove (4.14), note that the tangent space of
$\iota$
are the maps in (4.11) and (4.10) respectively. To prove (4.14), note that the tangent space of
![]() $\mathcal{M}^{e}_{\textrm {FC}}(d)^{\circ \circ }_{0}$
at
$\mathcal{M}^{e}_{\textrm {FC}}(d)^{\circ \circ }_{0}$
at
![]() $(E,\,\phi ,\,\nabla )$
is isomorphic to the first hypercohomology
$(E,\,\phi ,\,\nabla )$
is isomorphic to the first hypercohomology
![]() $\mathbb{H}^1(\mathcal{C}'_{\bullet })$
of the complex
$\mathbb{H}^1(\mathcal{C}'_{\bullet })$
of the complex
For
![]() $[(\{u_{\alpha \beta }\} ,\{ v_{\alpha }\})]\,\in \, \mathbb{H}^1(\mathcal{C}'_{\bullet })$
, we have that
$[(\{u_{\alpha \beta }\} ,\{ v_{\alpha }\})]\,\in \, \mathbb{H}^1(\mathcal{C}'_{\bullet })$
, we have that
and
Therefore,
![]() $\iota ^* \Theta ^e$
and
$\iota ^* \Theta ^e$
and
![]() $q_2^* \Theta _0$
have the following identical description:
$q_2^* \Theta _0$
have the following identical description:
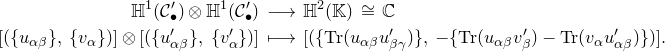 \begin{align*} \begin{aligned} \mathbb{H}^1(\mathcal{C}'_{\bullet }) \otimes \mathbb{H}^1(\mathcal{C}'_{\bullet }) \, &\longrightarrow \, \mathbb{H}^2(\mathbb{K}) \,\cong \, \mathbb{C} \\ [(\{ u_{\alpha \beta } \} ,\,\{ v_{\alpha }\}) ] \otimes [(\{ u_{\alpha \beta }' \} ,\,\{ v_{\alpha }'\}) ]\, &\longmapsto \, [(\{ {\rm Tr} (u_{\alpha \beta }u'_{\beta \gamma }) \},\, - \{{\rm Tr}(u_{\alpha \beta }v'_{\beta })-{\rm Tr}(v_{\alpha }u'_{\alpha \beta }) \})]. \end{aligned} \end{align*}
\begin{align*} \begin{aligned} \mathbb{H}^1(\mathcal{C}'_{\bullet }) \otimes \mathbb{H}^1(\mathcal{C}'_{\bullet }) \, &\longrightarrow \, \mathbb{H}^2(\mathbb{K}) \,\cong \, \mathbb{C} \\ [(\{ u_{\alpha \beta } \} ,\,\{ v_{\alpha }\}) ] \otimes [(\{ u_{\alpha \beta }' \} ,\,\{ v_{\alpha }'\}) ]\, &\longmapsto \, [(\{ {\rm Tr} (u_{\alpha \beta }u'_{\beta \gamma }) \},\, - \{{\rm Tr}(u_{\alpha \beta }v'_{\beta })-{\rm Tr}(v_{\alpha }u'_{\alpha \beta }) \})]. \end{aligned} \end{align*}
This proves (4.14).
Thirdly, by the equality
![]() $\iota ^* \Theta ^e \,=\, q_2^* \Theta _0$
in (4.14), we have
$\iota ^* \Theta ^e \,=\, q_2^* \Theta _0$
in (4.14), we have
Since
![]() $\Theta _0$
is
$\Theta _0$
is
![]() $d$
-closed, it follows that
$d$
-closed, it follows that
![]() $d(s^* \Theta ^e)\,=\,0$
, proving (4.12).
$d(s^* \Theta ^e)\,=\,0$
, proving (4.12).
Finally, from the combination of (4.12) and the equality
![]() $d \Theta ^e\,=\, p^*_{1,0} d (s^* \Theta ^e)$
(see (4.9)), it follows that
$d \Theta ^e\,=\, p^*_{1,0} d (s^* \Theta ^e)$
(see (4.9)), it follows that
![]() $d \Theta ^e\,=\,0$
on
$d \Theta ^e\,=\,0$
on
![]() $p^{-1}_{1,0}(U)$
. This implies that the
$p^{-1}_{1,0}(U)$
. This implies that the
![]() $2$
-form
$2$
-form
![]() $\Theta ^e$
is
$\Theta ^e$
is
![]() $d$
-closed on
$d$
-closed on
![]() $\mathcal{M}_{\textrm {FC}}^{e}(d)^{\circ }$
. As noted before, this proves the theorem.
$\mathcal{M}_{\textrm {FC}}^{e}(d)^{\circ }$
. As noted before, this proves the theorem.
Next, we show the
![]() $d$
-closedness of
$d$
-closedness of
![]() $\Theta ^e$
in (4.4) when
$\Theta ^e$
in (4.4) when
![]() $g\,=\,0$
and
$g\,=\,0$
and
![]() $g\,=\,1$
. For this purpose, we recall the definition of parabolic connections. Let
$g\,=\,1$
. For this purpose, we recall the definition of parabolic connections. Let
be an
![]() $n$
-pointed smooth projective curve of genus
$n$
-pointed smooth projective curve of genus
![]() $g$
over
$g$
over
![]() $\mathbb{C}$
, where
$\mathbb{C}$
, where
![]() $x_1, \,\cdots ,\,x_n$
are distinct points of
$x_1, \,\cdots ,\,x_n$
are distinct points of
![]() $X$
. Denote the reduced divisor
$X$
. Denote the reduced divisor
![]() $x_1+\cdots +x_n$
on
$x_1+\cdots +x_n$
on
![]() $X$
by
$X$
by
![]() $D(\boldsymbol{x})$
or simply by
$D(\boldsymbol{x})$
or simply by
![]() $D$
if there is no possibility of confusion. Take a positive integer
$D$
if there is no possibility of confusion. Take a positive integer
![]() $r$
.
$r$
.
Definition 4.8. A
![]() $\boldsymbol{x}$
-quasi-parabolic bundle of rank
$\boldsymbol{x}$
-quasi-parabolic bundle of rank
![]() $r$
and degree
$r$
and degree
![]() $d$
is a pair
$d$
is a pair
![]() $(E,\, \boldsymbol{l}\, =\, \{ l^{(i)}_* \}_{1\leqslant i \leqslant n})$
, where:
$(E,\, \boldsymbol{l}\, =\, \{ l^{(i)}_* \}_{1\leqslant i \leqslant n})$
, where:
-
(1)
 $E$
is an algebraic vector bundle on
$E$
is an algebraic vector bundle on
 $X$
of rank
$X$
of rank
 $r$
and degree
$r$
and degree
 $d$
;
$d$
; -
(2)
 $l^{(i)}_*$
is a filtration of subspaces
$l^{(i)}_*$
is a filtration of subspaces
 $E\big \vert _{x_i} \,=\, l_0^{(i)} \,\supset \, l_1^{(i)}\,\supset \,\cdots \,\supset \, l_r^{(i)}\,=\,0$
for every
$E\big \vert _{x_i} \,=\, l_0^{(i)} \,\supset \, l_1^{(i)}\,\supset \,\cdots \,\supset \, l_r^{(i)}\,=\,0$
for every
 $1\, \leqslant \, i\, \leqslant \, n$
such that
$1\, \leqslant \, i\, \leqslant \, n$
such that
 $\dim (l_j^{(i)}/l_{j+1}^{(i)})\,=\,1$
.
$\dim (l_j^{(i)}/l_{j+1}^{(i)})\,=\,1$
.
Let
![]() $\boldsymbol{\alpha }$
be a tuple
$\boldsymbol{\alpha }$
be a tuple
![]() $(\alpha ^{(i)}_j)^{1\leqslant i\leqslant n}_{1\leqslant j\leqslant r}$
of real numbers which satisfy the condition
$(\alpha ^{(i)}_j)^{1\leqslant i\leqslant n}_{1\leqslant j\leqslant r}$
of real numbers which satisfy the condition
for each
![]() $1\leqslant i\,\leqslant \, n$
and
$1\leqslant i\,\leqslant \, n$
and
![]() $\alpha ^{(i)}_j\,\neq \, \alpha ^{(i')}_{j'}$
for all
$\alpha ^{(i)}_j\,\neq \, \alpha ^{(i')}_{j'}$
for all
![]() $(i,\,j)\,\neq \,(i',\,j')$
. We call the tuple
$(i,\,j)\,\neq \,(i',\,j')$
. We call the tuple
![]() $\boldsymbol{\alpha }$
a parabolic weight. Take an element
$\boldsymbol{\alpha }$
a parabolic weight. Take an element
such that
![]() $\sum _{i,j} \nu ^{(i)}_j \,=\, -d \,\in \, \mathbb{Z}$
.
$\sum _{i,j} \nu ^{(i)}_j \,=\, -d \,\in \, \mathbb{Z}$
.
Definition 4.9. A quadruple
![]() $(E,\,\nabla ,\, \boldsymbol{l}\,=\,\{ l^{(i)}_* \}_{1\leqslant i \leqslant n},\boldsymbol{\alpha })$
is called an
$(E,\,\nabla ,\, \boldsymbol{l}\,=\,\{ l^{(i)}_* \}_{1\leqslant i \leqslant n},\boldsymbol{\alpha })$
is called an
![]() $(\boldsymbol{x},\, \boldsymbol{\nu })$
-parabolic connection of rank
$(\boldsymbol{x},\, \boldsymbol{\nu })$
-parabolic connection of rank
![]() $r$
and degree
$r$
and degree
![]() $d$
if:
$d$
if:
-
(1)
 $(E,\, \boldsymbol{l}\, =\, \{ l^{(i)}_* \}_{1\leqslant i \leqslant n})$
is an
$(E,\, \boldsymbol{l}\, =\, \{ l^{(i)}_* \}_{1\leqslant i \leqslant n})$
is an
 $\boldsymbol{x}$
-quasi-parabolic bundle of rank
$\boldsymbol{x}$
-quasi-parabolic bundle of rank
 $r$
and degree
$r$
and degree
 $d$
;
$d$
; -
(2)
 $\nabla \,\colon \, E \,\longrightarrow \,E\otimes K_{X}(D)$
is a logarithmic connection whose residue
$\nabla \,\colon \, E \,\longrightarrow \,E\otimes K_{X}(D)$
is a logarithmic connection whose residue
 ${\rm res}_{x_i}(\nabla )\,\colon \, E|_{x_i}\,\longrightarrow \, E|_{x_i}$
at each point
${\rm res}_{x_i}(\nabla )\,\colon \, E|_{x_i}\,\longrightarrow \, E|_{x_i}$
at each point
 $x_i$
for
$x_i$
for
 $1\,\leqslant \, i\,\leqslant \, n$
satisfies the condition
$1\,\leqslant \, i\,\leqslant \, n$
satisfies the condition
 $({\rm res}_{x_i}(\nabla )-\nu ^{(i)}_j {\rm Id}_{E|_{x_i}}) (l^{(i)}_j) \,\subset \, l_{j+1}^{(i)}$
for all
$({\rm res}_{x_i}(\nabla )-\nu ^{(i)}_j {\rm Id}_{E|_{x_i}}) (l^{(i)}_j) \,\subset \, l_{j+1}^{(i)}$
for all
 $j\,=\,0,\,\ldots ,\,r-1$
.
$j\,=\,0,\,\ldots ,\,r-1$
.
Definition 4.10. An
![]() $(\boldsymbol{x},\ \boldsymbol{\nu })$
-parabolic connection
$(\boldsymbol{x},\ \boldsymbol{\nu })$
-parabolic connection
![]() $(E,\ \nabla ,\ \boldsymbol{l},\,\boldsymbol{\alpha })$
is said to be
$(E,\ \nabla ,\ \boldsymbol{l},\,\boldsymbol{\alpha })$
is said to be
![]() $\boldsymbol{\alpha }$
-stable if the inequality
$\boldsymbol{\alpha }$
-stable if the inequality
 \begin{align*} \frac {\deg F+\sum _{i=1}^n\sum _{j=1}^r \alpha ^{(i)}_j \dim ( (F|_{x_i}\cap l^{(i)}_{j-1})/(F|_{x_i}\cap l^{(i)}_j)) } {\textrm { rank} F} \end{align*}
\begin{align*} \frac {\deg F+\sum _{i=1}^n\sum _{j=1}^r \alpha ^{(i)}_j \dim ( (F|_{x_i}\cap l^{(i)}_{j-1})/(F|_{x_i}\cap l^{(i)}_j)) } {\textrm { rank} F} \end{align*}
 \begin{align*} \lt \ \frac {\deg E+\sum _{i=1}^n\sum _{j=1}^r \alpha ^{(i)}_j \dim ( l^{(i)}_{j-1}/l^{(i)}_j ) } {\textrm { rank} E} \end{align*}
\begin{align*} \lt \ \frac {\deg E+\sum _{i=1}^n\sum _{j=1}^r \alpha ^{(i)}_j \dim ( l^{(i)}_{j-1}/l^{(i)}_j ) } {\textrm { rank} E} \end{align*}
holds for every subbundle
![]() $0\,\neq \, F\,\subsetneq \, E$
for which
$0\,\neq \, F\,\subsetneq \, E$
for which
![]() $\nabla (F)\,\subset \, F\otimes \Omega^1_X(D)$
. We say that
$\nabla (F)\,\subset \, F\otimes \Omega^1_X(D)$
. We say that
![]() $(E,\ \nabla ,\ \boldsymbol{l},\,\boldsymbol{\alpha })$
is
$(E,\ \nabla ,\ \boldsymbol{l},\,\boldsymbol{\alpha })$
is
![]() $\boldsymbol{\alpha }$
-semistable if the weaker inequality “
$\boldsymbol{\alpha }$
-semistable if the weaker inequality “
![]() $\leqslant$
’ holds (instead of “
$\leqslant$
’ holds (instead of “
![]() $\lt$
’).
$\lt$
’).
Remark 4.11. In the non-abelian Hodge correspondence (see [Reference SimpsonSim1]), the parabolic weight
![]() $\boldsymbol{\alpha }$
is an important datum needed to connect to the parabolic Higgs bundles. Since we focus on the algebraic moduli spaces, we omit the parabolic weight
$\boldsymbol{\alpha }$
is an important datum needed to connect to the parabolic Higgs bundles. Since we focus on the algebraic moduli spaces, we omit the parabolic weight
![]() $\boldsymbol{\alpha }$
to denote the parabolic connection. So we denote a parabolic connection by
$\boldsymbol{\alpha }$
to denote the parabolic connection. So we denote a parabolic connection by
![]() $(E,\,\nabla ,\, \boldsymbol{l})$
, even though there is the parabolic weight
$(E,\,\nabla ,\, \boldsymbol{l})$
, even though there is the parabolic weight
![]() $\boldsymbol{\alpha }$
in the background.
$\boldsymbol{\alpha }$
in the background.
In the inequality for the stability condition in Definition 4.10, we may replace the parabolic weight with a tuple of rational numbers which is very close to
![]() $\boldsymbol{\alpha }$
. We have the following.
$\boldsymbol{\alpha }$
. We have the following.
Theorem 4.12 ([Reference InabaIna, Theorem 2.2]).The moduli space
![]() ${\mathcal M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu })$
of
${\mathcal M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu })$
of
![]() $\boldsymbol{\alpha }$
-stable
$\boldsymbol{\alpha }$
-stable
![]() $(\boldsymbol{x},\boldsymbol{\nu })$
-parabolic connections exists as a quasi-projective scheme over
$(\boldsymbol{x},\boldsymbol{\nu })$
-parabolic connections exists as a quasi-projective scheme over
![]() $\textrm { Spec}\mathbb{C}$
.
$\textrm { Spec}\mathbb{C}$
.
Let
![]() $(E,\, \boldsymbol{l})$
be a
$(E,\, \boldsymbol{l})$
be a
![]() $\boldsymbol{x}$
-quasi-parabolic bundle. Set
$\boldsymbol{x}$
-quasi-parabolic bundle. Set
We denote the invertible elements of
![]() $\textrm { End}(E,\,\boldsymbol{l})$
by
$\textrm { End}(E,\,\boldsymbol{l})$
by
![]() ${\textrm { Aut}}(E,\,\boldsymbol{l})$
.
${\textrm { Aut}}(E,\,\boldsymbol{l})$
.
Definition 4.13. A
![]() $\boldsymbol{x}$
-quasi-parabolic bundle
$\boldsymbol{x}$
-quasi-parabolic bundle
![]() $(E,\, \boldsymbol{l})$
is said to be simple if
$(E,\, \boldsymbol{l})$
is said to be simple if
![]() $\textrm { End}(E,\, \boldsymbol{l}) \,=\,\mathbb{C}$
, which is equivalent to the condition
$\textrm { End}(E,\, \boldsymbol{l}) \,=\,\mathbb{C}$
, which is equivalent to the condition
![]() ${\textrm { Aut}}(E,\, \boldsymbol{l}) \,=\,\mathbb{C}^{*}$
.
${\textrm { Aut}}(E,\, \boldsymbol{l}) \,=\,\mathbb{C}^{*}$
.
Remark 4.14. For each
![]() $x_i$
, let
$x_i$
, let
![]() ${\bf H}_{x_i}\subset {\rm GL}_r(\mathbb{C})$
be the Borel subgroup consisting of the upper triangular matrices. Then a framed
${\bf H}_{x_i}\subset {\rm GL}_r(\mathbb{C})$
be the Borel subgroup consisting of the upper triangular matrices. Then a framed
![]() ${\rm GL}_r(\mathbb{C})$
–bundle with respect to the structure subgroups
${\rm GL}_r(\mathbb{C})$
–bundle with respect to the structure subgroups
![]() $({\bf H}_{x_i}\subset {\rm GL}_r(\mathbb{C}))_{1\leqslant i\leqslant n}$
is equivalent to an
$({\bf H}_{x_i}\subset {\rm GL}_r(\mathbb{C}))_{1\leqslant i\leqslant n}$
is equivalent to an
![]() $\boldsymbol{x}$
-quasi-parabolic bundle. The above definition of simple quasi-parabolic bundle is equivalent to that of a simple framed bundle with this structure subgroup in the sense of Definition 3.1. A framed
$\boldsymbol{x}$
-quasi-parabolic bundle. The above definition of simple quasi-parabolic bundle is equivalent to that of a simple framed bundle with this structure subgroup in the sense of Definition 3.1. A framed
![]() ${\rm GL}_r(\mathbb{C})$
–connection with respect to the structure subgroups
${\rm GL}_r(\mathbb{C})$
–connection with respect to the structure subgroups
![]() $({\bf H}_{x_i}\subset {\rm GL}_r(\mathbb{C}))_{1\leqslant i\leqslant n}$
is equivalent to an
$({\bf H}_{x_i}\subset {\rm GL}_r(\mathbb{C}))_{1\leqslant i\leqslant n}$
is equivalent to an
![]() $(\boldsymbol{x},\ \boldsymbol{0})$
-parabolic connection, where
$(\boldsymbol{x},\ \boldsymbol{0})$
-parabolic connection, where
![]() ${\bf 0}\,\in \,\mathbb{C}^{nr}$
is defined by
${\bf 0}\,\in \,\mathbb{C}^{nr}$
is defined by
![]() $\nu ^{(i)}_j\,=\,0$
for any
$\nu ^{(i)}_j\,=\,0$
for any
![]() $i,\,j$
.
$i,\,j$
.
For an
![]() $(\boldsymbol{x},\, \boldsymbol{\nu })$
-parabolic connection
$(\boldsymbol{x},\, \boldsymbol{\nu })$
-parabolic connection
![]() $(E,\,\nabla ,\, \boldsymbol{l})$
, set
$(E,\,\nabla ,\, \boldsymbol{l})$
, set
and denote by
![]() ${\textrm { Aut}}(E,\,\nabla ,\,\boldsymbol{l})$
the invertible elements in
${\textrm { Aut}}(E,\,\nabla ,\,\boldsymbol{l})$
the invertible elements in
![]() $\textrm { End}(E,\,\nabla ,\,\boldsymbol{l})$
.
$\textrm { End}(E,\,\nabla ,\,\boldsymbol{l})$
.
Definition 4.15. An
![]() $(\boldsymbol{x},\, \boldsymbol{\nu })$
-parabolic connection
$(\boldsymbol{x},\, \boldsymbol{\nu })$
-parabolic connection
![]() $(E,\,\nabla ,\, \boldsymbol{l})$
is said to be simple if
$(E,\,\nabla ,\, \boldsymbol{l})$
is said to be simple if
![]() $\textrm { End} (E,\,\nabla ,\, \boldsymbol{l}) \,=\,\mathbb{C}$
, which is equivalent to the condition
$\textrm { End} (E,\,\nabla ,\, \boldsymbol{l}) \,=\,\mathbb{C}$
, which is equivalent to the condition
![]() ${\textrm { Aut}} (E,\,\nabla ,\, \boldsymbol{l}) \,=\,\mathbb{C}^*$
.
${\textrm { Aut}} (E,\,\nabla ,\, \boldsymbol{l}) \,=\,\mathbb{C}^*$
.
An argument similar to the one in Proposition 3.5 proves the following proposition.
Proposition 4.16. The moduli space
![]() ${\mathcal M}_{{\rm PC}}(\boldsymbol{\nu })$
of simple
${\mathcal M}_{{\rm PC}}(\boldsymbol{\nu })$
of simple
![]() $(\boldsymbol{x},\boldsymbol{\nu })$
-parabolic connections exists as an algebraic space. The moduli space
$(\boldsymbol{x},\boldsymbol{\nu })$
-parabolic connections exists as an algebraic space. The moduli space
![]() ${\mathcal M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu })$
of
${\mathcal M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu })$
of
![]() $\boldsymbol{\alpha }$
-stable
$\boldsymbol{\alpha }$
-stable
![]() $(\boldsymbol{x},\boldsymbol{\nu })$
-parabolic connections is a Zariski open subspace of
$(\boldsymbol{x},\boldsymbol{\nu })$
-parabolic connections is a Zariski open subspace of
![]() ${\mathcal M}_{{\rm PC}}(\boldsymbol{\nu })$
.
${\mathcal M}_{{\rm PC}}(\boldsymbol{\nu })$
.
Proposition 4.17. Assume that either
![]() $g\,=\,0$
or
$g\,=\,0$
or
![]() $g\,=\,1$
and:
$g\,=\,1$
and:
-
(1)
 $nr-2r-2\,\gt \,0$
if
$nr-2r-2\,\gt \,0$
if
 $g\,=\,0$
;
$g\,=\,0$
; -
(2)
 $n\,\geqslant \, 2$
if
$n\,\geqslant \, 2$
if
 $g\,=\,1$
.
$g\,=\,1$
.
Let
![]() ${\mathcal M}^e_{{\rm FC}}(d)^{\circ }$
be the open subspace of
${\mathcal M}^e_{{\rm FC}}(d)^{\circ }$
be the open subspace of
![]() $\mathcal{M}^{e}_{{\rm FC}}(d)$
defined in (3.7) for
$\mathcal{M}^{e}_{{\rm FC}}(d)$
defined in (3.7) for
![]() $H\,=\,\{e\}$
. Then the restriction
$H\,=\,\{e\}$
. Then the restriction
![]() $\Theta ^e|_{\mathcal{M}^{e}_{{\rm FC}}(d)^{\circ }}$
of the nondegenerate
$\Theta ^e|_{\mathcal{M}^{e}_{{\rm FC}}(d)^{\circ }}$
of the nondegenerate
![]() $2$
-form
$2$
-form
![]() $\Theta ^e$
in (4.4) is
$\Theta ^e$
in (4.4) is
![]() $d$
-closed.
$d$
-closed.
Proof. Consider the forgetful map
![]() $p_1\,\colon \, \mathcal{M}^{e}_{\textrm {FC}}(d)^{\circ } \,\longrightarrow \, \mathcal{N}^e(d)$
in (4.5), and take a sufficiently small analytic open subset
$p_1\,\colon \, \mathcal{M}^{e}_{\textrm {FC}}(d)^{\circ } \,\longrightarrow \, \mathcal{N}^e(d)$
in (4.5), and take a sufficiently small analytic open subset
![]() $U\, \subset \, \mathcal{N}^e(d)$
. For a holomorphic section
$U\, \subset \, \mathcal{N}^e(d)$
. For a holomorphic section
![]() $s\,\colon \, U \,\longrightarrow \, p_1^{-1}(U)$
of
$s\,\colon \, U \,\longrightarrow \, p_1^{-1}(U)$
of
![]() $p_1$
such that
$p_1$
such that
we have
![]() $d \:\! \Theta ^e|_{\mathcal{M}^{e}_{{\rm FC}}(d)^{\circ }}\,=\,0$
by the same argument as in the proof of Theorem 4.7. We will now construct such a section
$d \:\! \Theta ^e|_{\mathcal{M}^{e}_{{\rm FC}}(d)^{\circ }}\,=\,0$
by the same argument as in the proof of Theorem 4.7. We will now construct such a section
![]() $s$
.
$s$
.
Let
![]() $\mathcal{N}_{{\rm par}} (d)$
be the moduli space of simple
$\mathcal{N}_{{\rm par}} (d)$
be the moduli space of simple
![]() $\boldsymbol{x}$
-quasi-parabolic bundles of rank
$\boldsymbol{x}$
-quasi-parabolic bundles of rank
![]() $r$
and degree
$r$
and degree
![]() $d$
. For each
$d$
. For each
![]() $x \,\in \, D$
, set the complex Lie proper subgroup
$x \,\in \, D$
, set the complex Lie proper subgroup
![]() $H_x$
to be the subgroup of
$H_x$
to be the subgroup of
![]() ${\rm GL}(r,\mathbb{C})$
consisting of the upper triangular matrices. It may be mentioned that an
${\rm GL}(r,\mathbb{C})$
consisting of the upper triangular matrices. It may be mentioned that an
![]() $\boldsymbol{x}$
-quasi-parabolic bundle is the same as a framed bundle with respect to
$\boldsymbol{x}$
-quasi-parabolic bundle is the same as a framed bundle with respect to
![]() $\{ H_x\}_{x \in D}$
. For a framed bundle
$\{ H_x\}_{x \in D}$
. For a framed bundle
![]() $(E,\,\phi )$
, we can associate a quasi-parabolic bundle
$(E,\,\phi )$
, we can associate a quasi-parabolic bundle
![]() $(E,\,\boldsymbol{l})$
whose filtration
$(E,\,\boldsymbol{l})$
whose filtration
![]() $l^{(i)}_*$
on
$l^{(i)}_*$
on
![]() $E|_{x_i}$
is induced by the framing
$E|_{x_i}$
is induced by the framing
![]() $\phi _{x_i}$
of
$\phi _{x_i}$
of
![]() $E|_{x_i}$
for each
$E|_{x_i}$
for each
![]() $1\,\leqslant \, i\,\leqslant \, n$
. Setting
$1\,\leqslant \, i\,\leqslant \, n$
. Setting
there is a natural morphism
Take an element
such that
![]() $\sum _{i,j} \nu _{j}^{(i)} \,=\, -d$
. Let
$\sum _{i,j} \nu _{j}^{(i)} \,=\, -d$
. Let
![]() $\mathcal{M}_{{\rm PC}} (\boldsymbol{\nu })^{\circ }$
be the moduli space defined by
$\mathcal{M}_{{\rm PC}} (\boldsymbol{\nu })^{\circ }$
be the moduli space defined by
Define the locally closed subspace
![]() $\mathcal{M}_{{\rm FC}}^{e} (\boldsymbol{\nu })^{\circ }$
of
$\mathcal{M}_{{\rm FC}}^{e} (\boldsymbol{\nu })^{\circ }$
of
![]() $\mathcal{M}_{{\rm FC}}^{e} (d)^{\circ }$
by
$\mathcal{M}_{{\rm FC}}^{e} (d)^{\circ }$
by
 \begin{align*} &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \mathcal{M}_{{\rm FC}}^{e} (\boldsymbol{\nu})^{\circ } \, \,:=\, \\ &\left \{ (E,\, \phi ,\,\nabla ) \,\in \, \mathcal{M}_{{\rm FC}}^{e} (d)^{\circ } \ \middle | \ \begin{array}{l} \rm the\ framed\ bundle\ (E,\phi\ )\ belongs\ to\ {\mathcal N}^e(d)^{\circ\ } \\ \rm and\ (E,\,\boldsymbol{l})\,:=\,q_B(E,\,\phi)\ satisfies \\ \rm (\mathrm{res}_{x}(\nabla)-\nu^{(i)}_{j}\ \mathrm{Id}_{E|_{x_i}})\ (l^{(i)}_{j})\,\subset\,l_{j+1}^{(i)}\ for\ 0\leqslant\ j\leqslant\ r-1 \end{array} \right \}{\Big /}\Large {\sim }. \end{align*}
\begin{align*} &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \mathcal{M}_{{\rm FC}}^{e} (\boldsymbol{\nu})^{\circ } \, \,:=\, \\ &\left \{ (E,\, \phi ,\,\nabla ) \,\in \, \mathcal{M}_{{\rm FC}}^{e} (d)^{\circ } \ \middle | \ \begin{array}{l} \rm the\ framed\ bundle\ (E,\phi\ )\ belongs\ to\ {\mathcal N}^e(d)^{\circ\ } \\ \rm and\ (E,\,\boldsymbol{l})\,:=\,q_B(E,\,\phi)\ satisfies \\ \rm (\mathrm{res}_{x}(\nabla)-\nu^{(i)}_{j}\ \mathrm{Id}_{E|_{x_i}})\ (l^{(i)}_{j})\,\subset\,l_{j+1}^{(i)}\ for\ 0\leqslant\ j\leqslant\ r-1 \end{array} \right \}{\Big /}\Large {\sim }. \end{align*}
In the above definition we have
![]() $\phi \,=\,\{\phi _x\}_{x\in D}$
, where
$\phi \,=\,\{\phi _x\}_{x\in D}$
, where
![]() $\phi _x\,\colon \, \mathcal{O}_X^{\oplus r}|_x \,\longrightarrow \, E\vert _x$
are isomorphisms defining a framing of
$\phi _x\,\colon \, \mathcal{O}_X^{\oplus r}|_x \,\longrightarrow \, E\vert _x$
are isomorphisms defining a framing of
![]() $E$
over
$E$
over
![]() $D$
. Since a framing defines a parabolic structure, there is a natural map
$D$
. Since a framing defines a parabolic structure, there is a natural map
Notice that
![]() $\mathcal{M}_{{\rm PC}} (\boldsymbol{\nu })^{\circ }$
is non-empty by virtue of the assumption in the proposition, and so is
$\mathcal{M}_{{\rm PC}} (\boldsymbol{\nu })^{\circ }$
is non-empty by virtue of the assumption in the proposition, and so is
![]() $\mathcal{M}_{{\rm FC}}^{e} (\boldsymbol{\nu })^{\circ }$
. Consider the complex
$\mathcal{M}_{{\rm FC}}^{e} (\boldsymbol{\nu })^{\circ }$
. Consider the complex
for
![]() $\{ H_x\}_{x \in D}$
. Here,
$\{ H_x\}_{x \in D}$
. Here,
![]() ${\rm ad}_{\phi } (E_G)$
and
${\rm ad}_{\phi } (E_G)$
and
![]() ${\rm ad}^n_{\phi } (E_G) \otimes K_X (D)$
are defined as in (2.16). The tangent space of
${\rm ad}^n_{\phi } (E_G) \otimes K_X (D)$
are defined as in (2.16). The tangent space of
![]() $\mathcal{M}_{{\rm PC}} (\boldsymbol{\nu })^{\circ }$
at
$\mathcal{M}_{{\rm PC}} (\boldsymbol{\nu })^{\circ }$
at
![]() $(E,\,\nabla , \,\boldsymbol{l})$
is
$(E,\,\nabla , \,\boldsymbol{l})$
is
![]() $\mathbb{H}^1(\mathcal{D}^{{\rm par}}_{\bullet })$
. There is also a natural morphism
$\mathbb{H}^1(\mathcal{D}^{{\rm par}}_{\bullet })$
. There is also a natural morphism
which is étale locally an affine space bundle whose fiber is isomorphic to
![]() $H^0(X,\,{\rm ad}^n_{\phi }(E_G)\otimes K_X(D))$
. So there is a non-empty analytic open subset
$H^0(X,\,{\rm ad}^n_{\phi }(E_G)\otimes K_X(D))$
. So there is a non-empty analytic open subset
![]() $U\,\subset \, {\mathcal N}^{{\rm par}}(d)^{\circ }$
with a local section
$U\,\subset \, {\mathcal N}^{{\rm par}}(d)^{\circ }$
with a local section
![]() $s^{{\rm par}}\,\colon \, U \,\longrightarrow \, (p_0^{{\rm par}})^{-1}(U)$
of
$s^{{\rm par}}\,\colon \, U \,\longrightarrow \, (p_0^{{\rm par}})^{-1}(U)$
of
![]() $p_0^{{\rm par}}$
. Consider the commutative diagram
$p_0^{{\rm par}}$
. Consider the commutative diagram
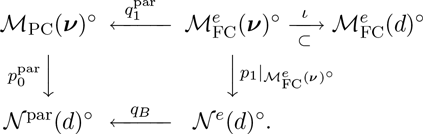
whose left square is Cartesian. The local section
![]() $s^{{\rm par}}$
of
$s^{{\rm par}}$
of
![]() $p_0^{{\rm par}}$
produces a local section
$p_0^{{\rm par}}$
produces a local section
of
![]() $p_1|_{\mathcal{M}_{{\rm FC}}^{e} (\boldsymbol{\nu })^{\circ }}$
. Let
$p_1|_{\mathcal{M}_{{\rm FC}}^{e} (\boldsymbol{\nu })^{\circ }}$
. Let
![]() $\Theta _{{\rm par}}$
be the symplectic structure on
$\Theta _{{\rm par}}$
be the symplectic structure on
![]() $\mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }} (\boldsymbol{\nu })$
constructed in [Reference InabaIna]. This symplectic form
$\mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }} (\boldsymbol{\nu })$
constructed in [Reference InabaIna]. This symplectic form
![]() $\Theta _{{\rm par}}$
is described as follows:
$\Theta _{{\rm par}}$
is described as follows:
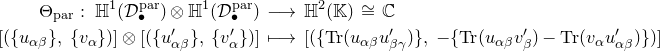 \begin{align} \begin{aligned} \Theta _{{\rm par}} \,\colon \, \mathbb{H}^1 (\mathcal{D}^{{\rm par}}_{\bullet }) \otimes \mathbb{H}^1 (\mathcal{D}^{{\rm par}}_{\bullet }) \,&\longrightarrow \, \mathbb{H}^2(\mathbb{K}) \,\cong \, \mathbb{C} \\ [(\{u_{\alpha \beta } \} ,\, \{ v_{\alpha } \})]\otimes [(\{u'_{\alpha \beta } \} ,\, \{ v'_{\alpha } \})] \,&\longmapsto \, [(\{ {\rm Tr} (u_{\alpha \beta }u'_{\beta \gamma }) \},\, - \{{\rm Tr}(u_{\alpha \beta }v'_{\beta })-{\rm Tr}(v_{\alpha }u'_{\alpha \beta }) \})] \end{aligned} \end{align}
\begin{align} \begin{aligned} \Theta _{{\rm par}} \,\colon \, \mathbb{H}^1 (\mathcal{D}^{{\rm par}}_{\bullet }) \otimes \mathbb{H}^1 (\mathcal{D}^{{\rm par}}_{\bullet }) \,&\longrightarrow \, \mathbb{H}^2(\mathbb{K}) \,\cong \, \mathbb{C} \\ [(\{u_{\alpha \beta } \} ,\, \{ v_{\alpha } \})]\otimes [(\{u'_{\alpha \beta } \} ,\, \{ v'_{\alpha } \})] \,&\longmapsto \, [(\{ {\rm Tr} (u_{\alpha \beta }u'_{\beta \gamma }) \},\, - \{{\rm Tr}(u_{\alpha \beta }v'_{\beta })-{\rm Tr}(v_{\alpha }u'_{\alpha \beta }) \})] \end{aligned} \end{align}
in terms of the Čech cohomology constructed using an affine open covering
![]() $\{ U_{\alpha }\}$
(see [Reference InabaIna, Proposition 7.2]). The symplectic form
$\{ U_{\alpha }\}$
(see [Reference InabaIna, Proposition 7.2]). The symplectic form
![]() $\Theta _{{\rm par}}$
is
$\Theta _{{\rm par}}$
is
![]() $d$
-closed [Reference InabaIna, Proposition 7.3]. Since the images of
$d$
-closed [Reference InabaIna, Proposition 7.3]. Since the images of
![]() $\Theta ^e$
and
$\Theta ^e$
and
![]() $\Theta _{{\rm par}}$
in
$\Theta _{{\rm par}}$
in
![]() $\mathbb{H}^2(\mathbb{K})$
have the same description in terms of Čech cohomology (see (4.4) and (4.18)), it follows that
$\mathbb{H}^2(\mathbb{K})$
have the same description in terms of Čech cohomology (see (4.4) and (4.18)), it follows that
Since
![]() $\Theta ^{{\rm par}}$
is
$\Theta ^{{\rm par}}$
is
![]() $d$
-closed, so is
$d$
-closed, so is
![]() $\iota ^* \Theta ^e|_{\mathcal{M}_{{\rm FC}}^{e} (d)^{\circ } }$
. Set
$\iota ^* \Theta ^e|_{\mathcal{M}_{{\rm FC}}^{e} (d)^{\circ } }$
. Set
![]() $s\,\,:=\,\,\iota \circ s_1\,\colon \, U\,\longrightarrow \, p_1^{-1}(U)$
, which is a local section of
$s\,\,:=\,\,\iota \circ s_1\,\colon \, U\,\longrightarrow \, p_1^{-1}(U)$
, which is a local section of
![]() $U_1$
. Then the pullback
$U_1$
. Then the pullback
![]() $s^*(\Theta ^e)\,=\, s_1^*\iota ^*\Theta ^e|_{\mathcal{M}_{{\rm FC}}^{e} (d)^{\circ } }$
is
$s^*(\Theta ^e)\,=\, s_1^*\iota ^*\Theta ^e|_{\mathcal{M}_{{\rm FC}}^{e} (d)^{\circ } }$
is
![]() $d$
-closed and so is
$d$
-closed and so is
![]() $\Theta ^e|_{\mathcal{M}_{{\rm FC}}^{e} (d)^{\circ } }$
by the first remark in this proof.
$\Theta ^e|_{\mathcal{M}_{{\rm FC}}^{e} (d)^{\circ } }$
by the first remark in this proof.
4.4 Symplectic structure on
 $\mathcal{M}^{e}_{{\rm FC}} (d)$
$\mathcal{M}^{e}_{{\rm FC}} (d)$
In § 4.2,a 2-form
![]() $\Theta ^e$
on
$\Theta ^e$
on
![]() $\mathcal{M}^{e}_{{\rm FC}} (d)$
was constructed. In the previous section, we considered the restriction of
$\mathcal{M}^{e}_{{\rm FC}} (d)$
was constructed. In the previous section, we considered the restriction of
![]() $\Theta ^e$
on
$\Theta ^e$
on
![]() $\mathcal{M}^{e}_{{\rm FC}} (d)^{\circ } \,\subset \, \mathcal{M}^{e}_{{\rm FC}} (d)$
. It was shown that this restriction is a symplectic form. Note that in the proof of the
$\mathcal{M}^{e}_{{\rm FC}} (d)^{\circ } \,\subset \, \mathcal{M}^{e}_{{\rm FC}} (d)$
. It was shown that this restriction is a symplectic form. Note that in the proof of the
![]() $d$
-closedness of this restriction, we used irreducibility of
$d$
-closedness of this restriction, we used irreducibility of
![]() $\mathcal{M}^{e}_{{\rm FC}} (d)^{\circ }$
(Proposition 3.8) implicitly. In this section, we shall show that the 2-form
$\mathcal{M}^{e}_{{\rm FC}} (d)^{\circ }$
(Proposition 3.8) implicitly. In this section, we shall show that the 2-form
![]() $\Theta ^e$
on
$\Theta ^e$
on
![]() $\mathcal{M}^{e}_{{\rm FC}} (d)$
is a symplectic form. In the proof of the
$\mathcal{M}^{e}_{{\rm FC}} (d)$
is a symplectic form. In the proof of the
![]() $d$
-closedness of
$d$
-closedness of
![]() $\Theta ^e$
, we will use the
$\Theta ^e$
, we will use the
![]() $d$
-closedness of
$d$
-closedness of
![]() $\Theta ^e|_{\mathcal{M}^{e}_{{\rm FC}} (d)^{\circ }}$
on
$\Theta ^e|_{\mathcal{M}^{e}_{{\rm FC}} (d)^{\circ }}$
on
![]() $\mathcal{M}^{e}_{{\rm FC}} (d)^{\circ }$
for another effective divisor
$\mathcal{M}^{e}_{{\rm FC}} (d)^{\circ }$
for another effective divisor
![]() $\widetilde {D}$
, instead of any argument on the irreducibility of
$\widetilde {D}$
, instead of any argument on the irreducibility of
![]() $\mathcal{M}^{e}_{{\rm FC}} (d)$
.
$\mathcal{M}^{e}_{{\rm FC}} (d)$
.
Proposition 4.18. The
![]() $2$
-form
$2$
-form
![]() $\Theta ^e$
on
$\Theta ^e$
on
![]() $\mathcal{M}^{e}_{{\rm FC}} (d)$
is nondegenerate.
$\mathcal{M}^{e}_{{\rm FC}} (d)$
is nondegenerate.
Proof. Recall that the 2-form
![]() $\Theta ^e$
is defined in (4.4). Let
$\Theta ^e$
is defined in (4.4). Let
![]() $\xi _{\Theta ^H} \,\colon \, \mathbb{H}^1({\mathcal C}_{\bullet })\,\longrightarrow \, \mathbb{H}^1({\mathcal C}_{\bullet })^*$
be the homomorphism induced by
$\xi _{\Theta ^H} \,\colon \, \mathbb{H}^1({\mathcal C}_{\bullet })\,\longrightarrow \, \mathbb{H}^1({\mathcal C}_{\bullet })^*$
be the homomorphism induced by
![]() $\Theta ^H$
. Set
$\Theta ^H$
. Set
![]() $\mathcal{C}_0 \,\,:=\, \,{\mathcal E}nd(E)(-D)$
and
$\mathcal{C}_0 \,\,:=\, \,{\mathcal E}nd(E)(-D)$
and
![]() $\mathcal{C}_1 \,\,:=\, \,{\mathcal E}nd(E)\otimes K_X(D)$
. For the above defined map
$\mathcal{C}_1 \,\,:=\, \,{\mathcal E}nd(E)\otimes K_X(D)$
. For the above defined map
![]() $\xi _{\Theta ^H}$
, we have the following commutative diagram whose rows are exact:
$\xi _{\Theta ^H}$
, we have the following commutative diagram whose rows are exact:

where
![]() $b_1,\,b_2,\,b_3,\,b_4$
are Serre duality isomorphisms. So, from the five lemma, it follows that
$b_1,\,b_2,\,b_3,\,b_4$
are Serre duality isomorphisms. So, from the five lemma, it follows that
![]() $\xi _{\Theta ^H}$
is an isomorphism. In other words, the
$\xi _{\Theta ^H}$
is an isomorphism. In other words, the
![]() $2$
-form
$2$
-form
![]() $\Theta ^H$
is nondegenerate.
$\Theta ^H$
is nondegenerate.
Next, we shall investigate the
![]() $d$
-closedness of the
$d$
-closedness of the
![]() $2$
-form
$2$
-form
![]() $\Theta ^e$
on
$\Theta ^e$
on
![]() $\mathcal{M}^{e}_{{\rm FC}} (d)$
.
$\mathcal{M}^{e}_{{\rm FC}} (d)$
.
Lemma 4.19. Let
![]() $(E_0,\, \phi _0 , \, \nabla _0)$
be a point on
$(E_0,\, \phi _0 , \, \nabla _0)$
be a point on
![]() $\mathcal{M}^{e}_{{\rm FC}} (d)$
. For this point on
$\mathcal{M}^{e}_{{\rm FC}} (d)$
. For this point on
![]() $\mathcal{M}^{e}_{{\rm FC}} (d)$
, there exist a reduced effective divisor
$\mathcal{M}^{e}_{{\rm FC}} (d)$
, there exist a reduced effective divisor
![]() $\widetilde {D}$
and an isomorphism
$\widetilde {D}$
and an isomorphism
![]() $\widetilde {\phi }_0 \,\colon \, \mathcal{O}_{\widetilde {D}}^{\oplus r} \,\longrightarrow \, E_0|_{\widetilde {D}}$
such that
$\widetilde {\phi }_0 \,\colon \, \mathcal{O}_{\widetilde {D}}^{\oplus r} \,\longrightarrow \, E_0|_{\widetilde {D}}$
such that
![]() $\widetilde {D} \,\supset \, D$
,
$\widetilde {D} \,\supset \, D$
,
![]() $\widetilde {\phi }_0 |_D \,=\, \phi _0$
and
$\widetilde {\phi }_0 |_D \,=\, \phi _0$
and
![]() $(E_0,\,\widetilde {\phi }_0)$
is simple.
$(E_0,\,\widetilde {\phi }_0)$
is simple.
Proof. Take a reduced effective divisor
![]() $\widetilde {D}$
such that
$\widetilde {D}$
such that
![]() $\widetilde {D} \,\supset \, D$
and
$\widetilde {D} \,\supset \, D$
and
![]() $H^0(X, \,\mathcal{E}nd (E_0) (-\widetilde {D}) ) \,=\,0$
. Moreover, take an isomorphism
$H^0(X, \,\mathcal{E}nd (E_0) (-\widetilde {D}) ) \,=\,0$
. Moreover, take an isomorphism
![]() $\widetilde {\phi }_0 \,\colon \, \mathcal{O}_{\widetilde {D}}^{\oplus r} \,\longrightarrow \, E_0|_{\widetilde {D}}$
such that
$\widetilde {\phi }_0 \,\colon \, \mathcal{O}_{\widetilde {D}}^{\oplus r} \,\longrightarrow \, E_0|_{\widetilde {D}}$
such that
![]() $\widetilde {\phi }_0 |_D \,=\, \phi _0$
. We will show that
$\widetilde {\phi }_0 |_D \,=\, \phi _0$
. We will show that
![]() $(E_0,\,\widetilde {\phi }_0)$
is simple. For that, let
$(E_0,\,\widetilde {\phi }_0)$
is simple. For that, let
![]() $\textbf {g}$
be an automorphism of
$\textbf {g}$
be an automorphism of
![]() $(E_0,\,\widetilde {\phi }_0)$
, that is,
$(E_0,\,\widetilde {\phi }_0)$
, that is,
![]() $\textbf {g}$
is an automorphism of
$\textbf {g}$
is an automorphism of
![]() $E_0$
such that the diagram
$E_0$
such that the diagram
is commutative. So the restriction
![]() $\textbf {g}|_{\widetilde {D}}$
is the identity map. Therefore, we have
$\textbf {g}|_{\widetilde {D}}$
is the identity map. Therefore, we have
Since
![]() $H^0(X, \,\mathcal{E}nd (E_0) (-\widetilde {D})) =\,0$
, it follows that
$H^0(X, \,\mathcal{E}nd (E_0) (-\widetilde {D})) =\,0$
, it follows that
![]() $\textbf {g}\,=\, {\rm Id}_{E_0}$
. In other words,
$\textbf {g}\,=\, {\rm Id}_{E_0}$
. In other words,
![]() $(E_0,\,\widetilde {\phi }_0)$
is simple.
$(E_0,\,\widetilde {\phi }_0)$
is simple.
Take an open covering
where each
![]() $\Sigma _{m_0}^{d}$
is the open substack of
$\Sigma _{m_0}^{d}$
is the open substack of
![]() $\mathcal{M}^{e}_{{\rm FC}} (d)$
defined in (3.1). Recall that a very ample line bundle
$\mathcal{M}^{e}_{{\rm FC}} (d)$
defined in (3.1). Recall that a very ample line bundle
![]() $\mathcal{O}_{X}(1)$
on the curve
$\mathcal{O}_{X}(1)$
on the curve
![]() $X$
is fixed; set
$X$
is fixed; set
![]() $\theta _d(m)\,\,:=\,\,r d_X m+d+r(1-g)$
, where
$\theta _d(m)\,\,:=\,\,r d_X m+d+r(1-g)$
, where
![]() $d_X\,\,:=\,\, \deg \mathcal{O}_X(1)$
and
$d_X\,\,:=\,\, \deg \mathcal{O}_X(1)$
and
![]() $g$
is the genus of
$g$
is the genus of
![]() $X$
. The above open substack
$X$
. The above open substack
![]() $\Sigma _{m_0}^{d}$
is the fibered category whose objects are simple framed
$\Sigma _{m_0}^{d}$
is the fibered category whose objects are simple framed
![]() ${\rm GL}(r,\mathbb{C})$
–connections
${\rm GL}(r,\mathbb{C})$
–connections
![]() $(E,\,\phi ,\,\nabla )$
on
$(E,\,\phi ,\,\nabla )$
on
![]() $X\times S$
such that:
$X\times S$
such that:
-
(a)
 $H^1(X,\, E_s (m_0-1))\,=\,0$
for each
$H^1(X,\, E_s (m_0-1))\,=\,0$
for each
 $s\,\in \, S$
;
$s\,\in \, S$
; -
(b)
 $\chi (E_s(m))\,= \,\theta _d(m)$
for each
$\chi (E_s(m))\,= \,\theta _d(m)$
for each
 $s \,\in \, S$
and all
$s \,\in \, S$
and all
 $m \,\in \, \mathbb{Z}$
.
$m \,\in \, \mathbb{Z}$
.
By the argument in the proof of Proposition 3.5, the substack
![]() $\Sigma _{m_0}^{d}$
is of finite type.
$\Sigma _{m_0}^{d}$
is of finite type.
Lemma 4.20. There exists a reduced effective divisor
![]() $\widetilde {D} \,\supset \, D$
such that for any points
$\widetilde {D} \,\supset \, D$
such that for any points
there is an isomorphism
![]() $\widetilde {\phi }\, \colon \, \mathcal{O}_{\widetilde {D}}^{\oplus r} \,\longrightarrow \,E|_{\widetilde {D}}$
satisfying the conditions that
$\widetilde {\phi }\, \colon \, \mathcal{O}_{\widetilde {D}}^{\oplus r} \,\longrightarrow \,E|_{\widetilde {D}}$
satisfying the conditions that
![]() $\widetilde {\phi }|_D \,=\, \phi$
and
$\widetilde {\phi }|_D \,=\, \phi$
and
![]() $(E,\,\widetilde {\phi })$
is simple.
$(E,\,\widetilde {\phi })$
is simple.
Proof. Take a point
![]() $s_0 \,=\, (E,\,\phi , \, \nabla ) \, \in \, \Sigma _{m_0}^{d}$
. By Lemma 4.19, there exists a reduced effective divisor
$s_0 \,=\, (E,\,\phi , \, \nabla ) \, \in \, \Sigma _{m_0}^{d}$
. By Lemma 4.19, there exists a reduced effective divisor
![]() $\widetilde {D}_{s_0}$
together with an isomorphism
$\widetilde {D}_{s_0}$
together with an isomorphism
![]() $\widetilde \phi \,\colon \, \mathcal{O}_{\widetilde {D}_{s_0}}^{\oplus r} \,\longrightarrow \, E|_{\widetilde {D}_{s_0}}$
satisfying the following three conditions:
$\widetilde \phi \,\colon \, \mathcal{O}_{\widetilde {D}_{s_0}}^{\oplus r} \,\longrightarrow \, E|_{\widetilde {D}_{s_0}}$
satisfying the following three conditions:
![]() $\widetilde {D}_{s_0} \,\supset \, D$
,
$\widetilde {D}_{s_0} \,\supset \, D$
,
![]() $\widetilde \phi |_D\, =\, \phi$
and
$\widetilde \phi |_D\, =\, \phi$
and
![]() $(E,\,\widetilde \phi )$
is simple.
$(E,\,\widetilde \phi )$
is simple.
Take an open substack
![]() $U_s \,\subset \, \Sigma _{m_0}^{d}$
, where
$U_s \,\subset \, \Sigma _{m_0}^{d}$
, where
![]() ${s_0} \,\in \, U_{s_0}$
and
${s_0} \,\in \, U_{s_0}$
and
![]() $U_{s_0}$
is small enough, and take a universal family
$U_{s_0}$
is small enough, and take a universal family
![]() $(\widetilde {E}, \, \psi ,\, \widetilde \nabla )$
over
$(\widetilde {E}, \, \psi ,\, \widetilde \nabla )$
over
![]() $X \times U_{s_0}$
. Since
$X \times U_{s_0}$
. Since
![]() $\widetilde E$
is locally trivial, we may take a lift
$\widetilde E$
is locally trivial, we may take a lift
![]() $\widetilde {\psi } \,\colon \, \mathcal{O}_{\widetilde {D}_{s_0} \times U_{s_0}}^{\oplus r} \,\longrightarrow \,\widetilde {E}|_{\widetilde {D}_{s_0}\times U_{s_0}}$
such that
$\widetilde {\psi } \,\colon \, \mathcal{O}_{\widetilde {D}_{s_0} \times U_{s_0}}^{\oplus r} \,\longrightarrow \,\widetilde {E}|_{\widetilde {D}_{s_0}\times U_{s_0}}$
such that
![]() $\widetilde \psi |_{D\times U_{s_0}} = \psi$
. Note that
$\widetilde \psi |_{D\times U_{s_0}} = \psi$
. Note that
![]() $(\widetilde {E}, \, \widetilde \psi )|_{X \times {s_0} } \cong (E, \, \widetilde \phi )$
, which is simple. Since we have the requirement that
$(\widetilde {E}, \, \widetilde \psi )|_{X \times {s_0} } \cong (E, \, \widetilde \phi )$
, which is simple. Since we have the requirement that
![]() $H^0(X \times s ,\, \mathcal{E}nd (\widetilde E|_{X \times s}) (-\widetilde D_{s_0}) )\,=\,0$
is an open condition, we may assume that
$H^0(X \times s ,\, \mathcal{E}nd (\widetilde E|_{X \times s}) (-\widetilde D_{s_0}) )\,=\,0$
is an open condition, we may assume that
![]() $(\widetilde {E}, \, \widetilde \psi )$
is a family of simple framed bundles. Consider an open covering
$(\widetilde {E}, \, \widetilde \psi )$
is a family of simple framed bundles. Consider an open covering
![]() $ \Sigma _{m_0}^{d} \,=\, \bigcup _{s_0} U_{s_0}$
. Since
$ \Sigma _{m_0}^{d} \,=\, \bigcup _{s_0} U_{s_0}$
. Since
![]() $\Sigma _{m_0}^{d}$
is of finite type, we may cover
$\Sigma _{m_0}^{d}$
is of finite type, we may cover
![]() $ \Sigma _{m_0}^{d}$
by a finite number of the open substacks
$ \Sigma _{m_0}^{d}$
by a finite number of the open substacks
![]() $\{U_{s_0}\}_{s_0}$
:
$\{U_{s_0}\}_{s_0}$
:
 \begin{align*}\Sigma _{m_0}^{d} \,=\, \bigcup _{i=1}^{m} U_{s_{i}},\end{align*}
\begin{align*}\Sigma _{m_0}^{d} \,=\, \bigcup _{i=1}^{m} U_{s_{i}},\end{align*}
where
![]() $s_1,\,\ldots ,\,s_m$
are points on
$s_1,\,\ldots ,\,s_m$
are points on
![]() $ \Sigma _{m_0}^{d}$
. Now take
$ \Sigma _{m_0}^{d}$
. Now take
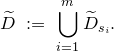 \begin{align*} \widetilde {D} \,\,:=\,\, \bigcup _{i=1}^{m} \widetilde D_{s_i}. \end{align*}
\begin{align*} \widetilde {D} \,\,:=\,\, \bigcup _{i=1}^{m} \widetilde D_{s_i}. \end{align*}
Then, by the construction of
![]() $\widetilde {D}$
, for any points
$\widetilde {D}$
, for any points
![]() $(E,\,\phi , \, \nabla )\,\in \, \Sigma _{m_0}^{d}$
, there exists an isomorphism
$(E,\,\phi , \, \nabla )\,\in \, \Sigma _{m_0}^{d}$
, there exists an isomorphism
![]() $\widetilde {\phi } \,\colon \, \mathcal{O}_{\widetilde {D}}^{\oplus r} \,\longrightarrow \, E|_{\widetilde {D}}$
such that
$\widetilde {\phi } \,\colon \, \mathcal{O}_{\widetilde {D}}^{\oplus r} \,\longrightarrow \, E|_{\widetilde {D}}$
such that
![]() $\widetilde \phi |_D \,=\, \phi$
and
$\widetilde \phi |_D \,=\, \phi$
and
![]() $(E,\,\widetilde {\phi })$
is simple.
$(E,\,\widetilde {\phi })$
is simple.
Theorem 4.21. The nondegenerate
![]() $2$
-form
$2$
-form
![]() $\Theta ^e$
on
$\Theta ^e$
on
![]() $\mathcal{M}^{e}_{{\rm FC}} (d)$
defined by (4.4) is
$\mathcal{M}^{e}_{{\rm FC}} (d)$
defined by (4.4) is
![]() $d$
-closed.
$d$
-closed.
Proof. Consider the open covering
![]() $\mathcal{M}^{e}_{{\rm FC}} (d)\,=\, \bigcup _{m_0} \Sigma ^d_{m_0}$
in (4.19). It is enough to prove that the restriction
$\mathcal{M}^{e}_{{\rm FC}} (d)\,=\, \bigcup _{m_0} \Sigma ^d_{m_0}$
in (4.19). It is enough to prove that the restriction
![]() $\Theta ^e|_{\Sigma ^d_{m_0}}$
is
$\Theta ^e|_{\Sigma ^d_{m_0}}$
is
![]() $d$
-closed for each
$d$
-closed for each
![]() $m_0$
. Take a reduced effective divisor
$m_0$
. Take a reduced effective divisor
![]() $\widetilde D$
as in Lemma 4.20. Let
$\widetilde D$
as in Lemma 4.20. Let
![]() $\mathcal{M}^{e}_{{\rm FC}} (d,\,\widetilde {D})$
be the Deligne–Mumford stack constructed in Proposition 3.5 for
$\mathcal{M}^{e}_{{\rm FC}} (d,\,\widetilde {D})$
be the Deligne–Mumford stack constructed in Proposition 3.5 for
![]() $\widetilde D$
. Let
$\widetilde D$
. Let
![]() $\mathcal{M}^{e}_{{\rm FC}} (d,\widetilde {D})^{\circ }$
be the Deligne–Mumford stack whose objects are objects of
$\mathcal{M}^{e}_{{\rm FC}} (d,\widetilde {D})^{\circ }$
be the Deligne–Mumford stack whose objects are objects of
![]() $\mathcal{M}^{e}_{{\rm FC}} (d,\widetilde {D})$
such that the underlying framed bundles are simple. In other words, we have
$\mathcal{M}^{e}_{{\rm FC}} (d,\widetilde {D})$
such that the underlying framed bundles are simple. In other words, we have
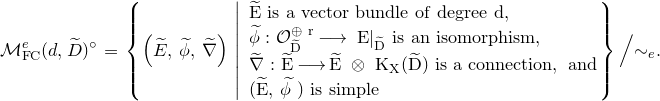 \begin{align*} \mathcal{M}^{e}_{{\rm FC}} (d,\widetilde {D})^{\circ }\,=\, \left \{\left ( \widetilde E,\, \widetilde {\phi } ,\, \widetilde {\nabla }\right )\ \middle | \ \begin{array}{l} \rm \widetilde E\ is\ a\ vector\ bundle\ of\ degree\ d,\\ \rm \widetilde \phi \,\colon \mathcal{O}_{\widetilde {D}}^{\oplus\ r} \longrightarrow \ E|_{\widetilde {D}}\ is\ an\ isomorphism,\\ \rm \widetilde \nabla \,\colon \widetilde {E} \longrightarrow \widetilde {E}\ \otimes\ K_{X}(\widetilde {D})\ is\ a\ connection,\ and \\ \rm (\widetilde E,\, \widetilde {\phi\ })\ is\ simple \end{array} \right \} {\Big /}\Large {\sim }_{e}. \end{align*}
\begin{align*} \mathcal{M}^{e}_{{\rm FC}} (d,\widetilde {D})^{\circ }\,=\, \left \{\left ( \widetilde E,\, \widetilde {\phi } ,\, \widetilde {\nabla }\right )\ \middle | \ \begin{array}{l} \rm \widetilde E\ is\ a\ vector\ bundle\ of\ degree\ d,\\ \rm \widetilde \phi \,\colon \mathcal{O}_{\widetilde {D}}^{\oplus\ r} \longrightarrow \ E|_{\widetilde {D}}\ is\ an\ isomorphism,\\ \rm \widetilde \nabla \,\colon \widetilde {E} \longrightarrow \widetilde {E}\ \otimes\ K_{X}(\widetilde {D})\ is\ a\ connection,\ and \\ \rm (\widetilde E,\, \widetilde {\phi\ })\ is\ simple \end{array} \right \} {\Big /}\Large {\sim }_{e}. \end{align*}
Taking the degree of
![]() $\widetilde {D}$
to be sufficiently large, the canonical
$\widetilde {D}$
to be sufficiently large, the canonical
![]() $2$
-form
$2$
-form
![]() $\Theta ^e|_{\mathcal{M}^{e}_{{\rm FC}} (d,\widetilde {D})^{\circ }}$
on
$\Theta ^e|_{\mathcal{M}^{e}_{{\rm FC}} (d,\widetilde {D})^{\circ }}$
on
![]() $\mathcal{M}^{e}_{{\rm FC}} (d,\widetilde {D})^{\circ }$
is
$\mathcal{M}^{e}_{{\rm FC}} (d,\widetilde {D})^{\circ }$
is
![]() $d$
-closed by Propositions 4.7 and 4.17. Define a moduli space
$d$
-closed by Propositions 4.7 and 4.17. Define a moduli space
![]() $\mathcal{M}^{e}_{{\rm FC}} (d,\widetilde {D},D)$
as follows:
$\mathcal{M}^{e}_{{\rm FC}} (d,\widetilde {D},D)$
as follows:
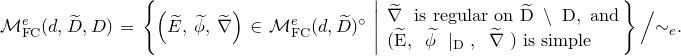 \begin{align*} {\mathcal{M}^{e}_{{\rm FC}} (d,\widetilde {D},D)\,=\, \left \{\left ( \widetilde E,\, \widetilde {\phi } ,\, \widetilde {\nabla }\right ) \,\in \,\mathcal{M}^{e}_{{\rm FC}} (d,\widetilde {D})^{\circ } \ \middle | \ \begin{array}{l} \rm \widetilde \nabla\ \ is\ regular\ on\ \widetilde {D}\ \setminus\ D,\ and \\ \rm (\widetilde E,\,\ \widetilde {\phi\ }\ |_D\ ,\,\ \widetilde \nabla\ )\ is\ simple \end{array} \right \}{\Big /}\Large {\sim }_{e}}. \end{align*}
\begin{align*} {\mathcal{M}^{e}_{{\rm FC}} (d,\widetilde {D},D)\,=\, \left \{\left ( \widetilde E,\, \widetilde {\phi } ,\, \widetilde {\nabla }\right ) \,\in \,\mathcal{M}^{e}_{{\rm FC}} (d,\widetilde {D})^{\circ } \ \middle | \ \begin{array}{l} \rm \widetilde \nabla\ \ is\ regular\ on\ \widetilde {D}\ \setminus\ D,\ and \\ \rm (\widetilde E,\,\ \widetilde {\phi\ }\ |_D\ ,\,\ \widetilde \nabla\ )\ is\ simple \end{array} \right \}{\Big /}\Large {\sim }_{e}}. \end{align*}
Let
![]() $\iota \,:\, \mathcal{M}^{e}_{{\rm FC}} (d,\widetilde {D},D)\, \longrightarrow \, \mathcal{M}^{e}_{{\rm FC}} (d,\widetilde {D})^{\circ }$
be the natural inclusion map and
$\iota \,:\, \mathcal{M}^{e}_{{\rm FC}} (d,\widetilde {D},D)\, \longrightarrow \, \mathcal{M}^{e}_{{\rm FC}} (d,\widetilde {D})^{\circ }$
be the natural inclusion map and
![]() $\pi$
the natural map from
$\pi$
the natural map from
![]() $\mathcal{M}^{e}_{{\rm FC}} (d,\widetilde {D},D)$
to
$\mathcal{M}^{e}_{{\rm FC}} (d,\widetilde {D},D)$
to
![]() $\mathcal{M}^{e}_{{\rm FC}} (d)$
induced by the restriction of framings to
$\mathcal{M}^{e}_{{\rm FC}} (d)$
induced by the restriction of framings to
![]() $D$
:
$D$
:
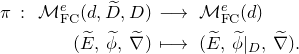 \begin{align*} \begin{aligned} \pi \,\, \colon \,\, \mathcal{M}^{e}_{{\rm FC}} (d,\widetilde {D},D) \,&\longrightarrow \,\, \mathcal{M}^{e}_{{\rm FC}} (d) \\ (\widetilde E,\, \widetilde {\phi },\, \widetilde {\nabla }) \,&\longmapsto \,\, (\widetilde E,\, \widetilde {\phi }|_D,\, \widetilde {\nabla }). \end{aligned} \end{align*}
\begin{align*} \begin{aligned} \pi \,\, \colon \,\, \mathcal{M}^{e}_{{\rm FC}} (d,\widetilde {D},D) \,&\longrightarrow \,\, \mathcal{M}^{e}_{{\rm FC}} (d) \\ (\widetilde E,\, \widetilde {\phi },\, \widetilde {\nabla }) \,&\longmapsto \,\, (\widetilde E,\, \widetilde {\phi }|_D,\, \widetilde {\nabla }). \end{aligned} \end{align*}
This map
![]() $\pi$
is smooth. By Lemma 4.20, the open substack
$\pi$
is smooth. By Lemma 4.20, the open substack
![]() $\Sigma _{m_0}^{d}$
is contained in the image of
$\Sigma _{m_0}^{d}$
is contained in the image of
![]() $\pi$
. We consider the following maps.
$\pi$
. We consider the following maps.
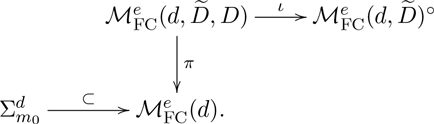
Let
![]() $\Theta ^e_{\widetilde {D}}$
be the 2-form on
$\Theta ^e_{\widetilde {D}}$
be the 2-form on
![]() $\mathcal{M}^{e}_{{\rm FC}} (d,\widetilde {D})^{\circ }$
defined in (4.4). By the definition of
$\mathcal{M}^{e}_{{\rm FC}} (d,\widetilde {D})^{\circ }$
defined in (4.4). By the definition of
![]() $\Theta ^e$
and
$\Theta ^e$
and
![]() $\Theta ^e_{\widetilde {D}}$
, which are described by the same formula via the Čech cohomology, we have
$\Theta ^e_{\widetilde {D}}$
, which are described by the same formula via the Čech cohomology, we have
As
![]() $\Theta ^e_{\widetilde {D}}$
is
$\Theta ^e_{\widetilde {D}}$
is
![]() $d$
-closed by Propositions 4.7 and 4.17, we conclude that
$d$
-closed by Propositions 4.7 and 4.17, we conclude that
![]() $\pi ^* \Theta ^e$
is
$\pi ^* \Theta ^e$
is
![]() $d$
-closed. Since
$d$
-closed. Since
![]() $\pi$
is smooth, and the image of
$\pi$
is smooth, and the image of
![]() $\pi$
contains the open substack
$\pi$
contains the open substack
![]() $\Sigma _{m_0}^{d}$
, it follows that
$\Sigma _{m_0}^{d}$
, it follows that
![]() $\Theta ^e|_{\Sigma ^d_{m_0}}$
is
$\Theta ^e|_{\Sigma ^d_{m_0}}$
is
![]() $d$
-closed.
$d$
-closed.
4.5 Symplectic structure on
 $\mathcal{M}^{H}_{{\rm FC}} (d)$
$\mathcal{M}^{H}_{{\rm FC}} (d)$
Fix a complex Lie proper subgroup
![]() $H_x\,\subsetneq \, {\rm GL}(r,\mathbb{C})$
for each
$H_x\,\subsetneq \, {\rm GL}(r,\mathbb{C})$
for each
![]() $x\,\in \, D$
.
$x\,\in \, D$
.
Consider the complexes
![]() $\mathcal{D}_{\bullet }$
and
$\mathcal{D}_{\bullet }$
and
![]() $\mathbb{K}$
constructed in (2.16) and (4.3) respectively. Note that the pairing
$\mathbb{K}$
constructed in (2.16) and (4.3) respectively. Note that the pairing
![]() ${\rm ad}(E_G)\otimes {\rm ad} (E_G)\, \longrightarrow \, {\mathcal O}_X$
in (2.5) produces a pairing
${\rm ad}(E_G)\otimes {\rm ad} (E_G)\, \longrightarrow \, {\mathcal O}_X$
in (2.5) produces a pairing
The restriction of the pairing
![]() $\widehat {\sigma }$
(see (2.5))
$\widehat {\sigma }$
(see (2.5))
and the homomorphism
constructed using
![]() $\widehat \sigma$
, together produce a homomorphism
$\widehat \sigma$
, together produce a homomorphism
of complexes. Let
be the homomorphism of hypercohomologies induced by this homomorphism of complexes. Now, the composition of the natural homomorphism
with the above homomorphism of hypercohomologies produces a pairing
In terms of the Čech cohomology with respect to an affine open covering
![]() $\{ U_{\alpha }\}$
, the pairing
$\{ U_{\alpha }\}$
, the pairing
![]() $\Theta ^H$
in (4.20) is of the form
$\Theta ^H$
in (4.20) is of the form
This pairing in (4.20) gives a 2-form on
![]() $\mathcal{M}^{H}_{{\rm FC}} (d)$
. We also denote by
$\mathcal{M}^{H}_{{\rm FC}} (d)$
. We also denote by
![]() $\Theta ^H$
this 2-form on
$\Theta ^H$
this 2-form on
![]() $\mathcal{M}^{H}_{{\rm FC}} (d)$
. Then
$\mathcal{M}^{H}_{{\rm FC}} (d)$
. Then
![]() $\Theta ^H$
is nondegenerate by the argument as after [Reference Biswas, Inaba, Komyo and SaitoBIKS, Theorem 5] by applying [Reference Biswas, Logares and Peón-NietoBLP2, Proposition 4.1]. Now it will be shown that
$\Theta ^H$
is nondegenerate by the argument as after [Reference Biswas, Inaba, Komyo and SaitoBIKS, Theorem 5] by applying [Reference Biswas, Logares and Peón-NietoBLP2, Proposition 4.1]. Now it will be shown that
![]() $\Theta ^H$
is
$\Theta ^H$
is
![]() $d$
-closed.
$d$
-closed.
Definition 4.22. Let
![]() $\mathcal{M}^{e}_{\textrm {FC}}(d)_{\mathfrak{h}^{\perp }}$
be the stack over the category of locally Noetherian schemes whose objects are quadruples
$\mathcal{M}^{e}_{\textrm {FC}}(d)_{\mathfrak{h}^{\perp }}$
be the stack over the category of locally Noetherian schemes whose objects are quadruples
![]() $(S,\, E, \,\phi =\{\phi _{x\times S} \}_{x\in D} ,\,\nabla )$
that satisfy (1), (3) and (5) in Definition 3.1 and the following
$(S,\, E, \,\phi =\{\phi _{x\times S} \}_{x\in D} ,\,\nabla )$
that satisfy (1), (3) and (5) in Definition 3.1 and the following
![]() $(2)''$
and
$(2)''$
and
![]() $(4)''$
.
$(4)''$
.
-
(2)′′
 $\phi _{x\times S}$
be a section of the structure map Denote by
$\phi _{x\times S}$
be a section of the structure map Denote by \begin{align*} {\rm Isom}_{S} (\mathcal{O}_{x\times S}^{\oplus r}, \, E\big \vert _{x\times S}) \,\longrightarrow \, x\times S\, . \end{align*}
the isomorphism given by the map
\begin{align*} {\rm Isom}_{S} (\mathcal{O}_{x\times S}^{\oplus r}, \, E\big \vert _{x\times S}) \,\longrightarrow \, x\times S\, . \end{align*}
the isomorphism given by the map \begin{align*}\varphi _{x \times S}\,\,\colon \,\, \mathcal{O}_{x\times S}^{\oplus r}\,\xrightarrow {\ \sim \ }\, E\big \vert _{x\times S}\end{align*}
\begin{align*}\varphi _{x \times S}\,\,\colon \,\, \mathcal{O}_{x\times S}^{\oplus r}\,\xrightarrow {\ \sim \ }\, E\big \vert _{x\times S}\end{align*}
 $x\times S\,\longrightarrow \, {\rm Isom}_{S} (\mathcal{O}_{x\times S}^{\oplus r}, \, E\big \vert _{x\times S})$
.
$x\times S\,\longrightarrow \, {\rm Isom}_{S} (\mathcal{O}_{x\times S}^{\oplus r}, \, E\big \vert _{x\times S})$
.
-
(4)′′ Let
 ${\rm res}_{x\times S}(\nabla ) \,\in \, {\rm End}(E)\big \vert _{x\times S}$
be the residue matrix of the connection
${\rm res}_{x\times S}(\nabla ) \,\in \, {\rm End}(E)\big \vert _{x\times S}$
be the residue matrix of the connection
 $\nabla$
along
$\nabla$
along
 $x\times S$
. Then
$x\times S$
. Then
 $\phi ^{-1}_{x \times S} \circ {\rm res}_{x\times S}(\nabla ) \circ \phi _{x \times S} \,\in \, \mathfrak{h}^{\perp } \otimes \mathcal{O}_{S}$
.
$\phi ^{-1}_{x \times S} \circ {\rm res}_{x\times S}(\nabla ) \circ \phi _{x \times S} \,\in \, \mathfrak{h}^{\perp } \otimes \mathcal{O}_{S}$
.
A morphism
in
![]() $\mathcal{M}^{e}_{\textrm {FC}}(d)_{\mathfrak{h}^{\perp }}$
is a Cartesian square
$\mathcal{M}^{e}_{\textrm {FC}}(d)_{\mathfrak{h}^{\perp }}$
is a Cartesian square
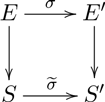
such that the diagram
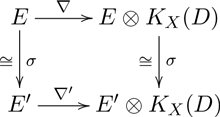
commutes and the composition
![]() $(\phi '_{x\times S})^{-1} \circ \sigma |_{x\times S}\circ \phi _{x\times S}$
coincides with the identity map of
$(\phi '_{x\times S})^{-1} \circ \sigma |_{x\times S}\circ \phi _{x\times S}$
coincides with the identity map of
![]() $\mathcal{O}_{x\times S}^{\oplus r}$
for each
$\mathcal{O}_{x\times S}^{\oplus r}$
for each
![]() $x\,\in \, D$
.
$x\,\in \, D$
.
Theorem 4.23. The nondegenerate
![]() $2$
-form
$2$
-form
![]() $\Theta ^H$
on
$\Theta ^H$
on
![]() $\mathcal{M}^{H}_{{\rm FC}} (d)$
defined by (4.20) is
$\mathcal{M}^{H}_{{\rm FC}} (d)$
defined by (4.20) is
![]() $d$
-closed.
$d$
-closed.
Proof. Consider the diagram

where
![]() $\pi _1$
and
$\pi _1$
and
![]() $\pi _2$
are the natural maps. It is straightforward to check that
$\pi _2$
are the natural maps. It is straightforward to check that
Since
![]() $\Theta ^e$
is
$\Theta ^e$
is
![]() $d$
-closed, the form
$d$
-closed, the form
![]() $\pi _2^*\Theta ^H$
is also
$\pi _2^*\Theta ^H$
is also
![]() $d$
-closed. This implies that
$d$
-closed. This implies that
![]() $\Theta ^H$
is
$\Theta ^H$
is
![]() $d$
-closed, because the map
$d$
-closed, because the map
![]() $\pi _2$
is dominant.
$\pi _2$
is dominant.
4.6 Poisson structure
In this subsection, we will see the details of the Poisson structure mentioned in the introduction. This is influenced by a construction done in [Reference Biswas, Bottacin and GómezBBG].
Let
![]() $\mathcal{M}_{\textrm {{C}}}(d)$
be the moduli space of pairs
$\mathcal{M}_{\textrm {{C}}}(d)$
be the moduli space of pairs
![]() $(E,\, \nabla )$
, where
$(E,\, \nabla )$
, where
![]() $E$
is a holomorphic vector bundle on
$E$
is a holomorphic vector bundle on
![]() $X$
of rank
$X$
of rank
![]() $r$
and degree
$r$
and degree
![]() $d$
, and
$d$
, and
![]() $\nabla$
is a logarithmic connection on
$\nabla$
is a logarithmic connection on
![]() $E$
whose singular part is contained in
$E$
whose singular part is contained in
![]() $D$
, such that
$D$
, such that
![]() $(E,\,\nabla )$
is simple in the sense that the endomorphisms of
$(E,\,\nabla )$
is simple in the sense that the endomorphisms of
![]() $E$
preserving
$E$
preserving
![]() $\nabla$
are just the constant scalar multiplications. In [Reference NitsureNit], Nitsure constructed the moduli space
$\nabla$
are just the constant scalar multiplications. In [Reference NitsureNit], Nitsure constructed the moduli space
![]() ${\mathcal M}^{{\rm ss}}_{{\rm C}}(d)$
of semistable logarithmic connections, which contains the moduli space of stable logarithmic connections
${\mathcal M}^{{\rm ss}}_{{\rm C}}(d)$
of semistable logarithmic connections, which contains the moduli space of stable logarithmic connections
![]() ${\mathcal M}^{{\rm s}}_{{\rm C}}(d)$
as a Zariski open subset. By its definition, our moduli space
${\mathcal M}^{{\rm s}}_{{\rm C}}(d)$
as a Zariski open subset. By its definition, our moduli space
![]() $\mathcal{M}_{\textrm {{C}}}(d)$
contains
$\mathcal{M}_{\textrm {{C}}}(d)$
contains
![]() ${\mathcal M}^{{\rm s}}_{{\rm C}}(d)$
as a Zariski open subspace. Recall that a description of the tangent space of this moduli space is given in [Reference NitsureNit]. For
${\mathcal M}^{{\rm s}}_{{\rm C}}(d)$
as a Zariski open subspace. Recall that a description of the tangent space of this moduli space is given in [Reference NitsureNit]. For
![]() $(E,\, \nabla )\, \in \,\mathcal{M}_{\textrm {{C}}}(d)$
, the tangent space of
$(E,\, \nabla )\, \in \,\mathcal{M}_{\textrm {{C}}}(d)$
, the tangent space of
![]() $\mathcal{M}_{\textrm {{C}}}(d)$
at
$\mathcal{M}_{\textrm {{C}}}(d)$
at
![]() $(E,\nabla )$
is
$(E,\nabla )$
is
where
![]() ${\mathcal C}_0\,=\,{\mathcal End}(E)(-D)$
,
${\mathcal C}_0\,=\,{\mathcal End}(E)(-D)$
,
![]() ${\mathcal C}_1\,=\,{\mathcal End}(E)\otimes K_X(D)$
and the map
${\mathcal C}_1\,=\,{\mathcal End}(E)\otimes K_X(D)$
and the map
![]() ${\mathcal End}(E) \,\longrightarrow \, {\mathcal C}_1$
is defined by
${\mathcal End}(E) \,\longrightarrow \, {\mathcal C}_1$
is defined by
![]() $u \,\longmapsto \,\nabla \circ u- u \circ \nabla$
. The cotangent space is
$u \,\longmapsto \,\nabla \circ u- u \circ \nabla$
. The cotangent space is
over which there is a canonical pairing
Consider the open subspace
of the moduli space
![]() ${\mathcal M}^e_{\textrm { FC}}(d)$
of simple framed connections. Then, there is a natural forgetful map
${\mathcal M}^e_{\textrm { FC}}(d)$
of simple framed connections. Then, there is a natural forgetful map
and the induced map
![]() $\pi ^*$
on the cotangent spaces makes the diagram
$\pi ^*$
on the cotangent spaces makes the diagram
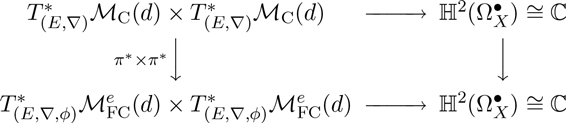
commutative. The bottom horizontal arrow satisfies the Jacobi identity, because it corresponds to the symplectic form on the moduli space
![]() ${\mathcal M}^e_{\textrm { FC}}(d)$
given in Theorem4.21. So the pairing in (4.21) is also skew-symmetric and satisfies the Jacobi identity. Thus, the following corollary is obtained.
${\mathcal M}^e_{\textrm { FC}}(d)$
given in Theorem4.21. So the pairing in (4.21) is also skew-symmetric and satisfies the Jacobi identity. Thus, the following corollary is obtained.
Corollary 4.24. The moduli space
![]() $\mathcal{M}_{\textrm {{C}}}(d)$
has a Poisson structure defined by the Poisson bracket in (4.21). Furthermore, the morphism
$\mathcal{M}_{\textrm {{C}}}(d)$
has a Poisson structure defined by the Poisson bracket in (4.21). Furthermore, the morphism
![]() $\pi$
in (4.22) becomes a Poisson map.
$\pi$
in (4.22) becomes a Poisson map.
We will see a slightly different view of the Poisson structure on the moduli space
![]() $\mathcal{M}_{\textrm {{C}}}(d)$
. Set
$\mathcal{M}_{\textrm {{C}}}(d)$
. Set
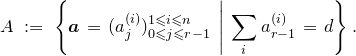 \begin{align*} A\,\,:=\,\, \left \{ \boldsymbol{a}\,=\,(a^{(i)}_j)^{1\leqslant i\leqslant n}_{0\leqslant j\leqslant r-1}\,\, \middle |\,\, \sum _i a^{(i)}_{r-1}\,=\,d \right \}. \end{align*}
\begin{align*} A\,\,:=\,\, \left \{ \boldsymbol{a}\,=\,(a^{(i)}_j)^{1\leqslant i\leqslant n}_{0\leqslant j\leqslant r-1}\,\, \middle |\,\, \sum _i a^{(i)}_{r-1}\,=\,d \right \}. \end{align*}
By associating the coefficients of the characteristic polynomial of
![]() ${\sf res}_{x_i}(\nabla )$
at each point
${\sf res}_{x_i}(\nabla )$
at each point
![]() $x_i\in D$
, we can define a morphism
$x_i\in D$
, we can define a morphism
whose fiber
![]() ${\mathcal M}_{\textrm { C}}(\boldsymbol{a})$
over
${\mathcal M}_{\textrm { C}}(\boldsymbol{a})$
over
![]() $\boldsymbol{a}\,\in \, A$
is smooth for generic
$\boldsymbol{a}\,\in \, A$
is smooth for generic
![]() $\boldsymbol{a}$
but has singularities for special
$\boldsymbol{a}$
but has singularities for special
![]() $\boldsymbol{a}$
. Consider the moduli space of simple parabolic connections
$\boldsymbol{a}$
. Consider the moduli space of simple parabolic connections
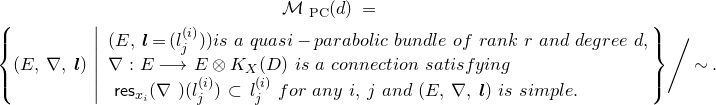 \begin{align*}&\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad{\mathcal M}_{\textrm { PC}}(d)\ =\nonumber \\ &\left . \left \{ (E,\,\nabla ,\,\boldsymbol{l}) \ \middle | \ \begin{array}{l} (E,\,\boldsymbol{l}=(l^{(i)}_j)) is\ a\ quasi-parabolic\ bundle\ of\ rank\ r\ and\ degree\ d, \\ \nabla \,\colon E\longrightarrow \,E\otimes K_X(D)\ is\ a\ connection\ satisfying \\ {\sf\ res}_{x_i}(\nabla\ )(l^{(i)}_j)\,\subset \, l^{(i)}_j\ for\ any\ i,\,j\ and\ (E,\,\nabla,\,\boldsymbol{l})\ is\ simple. \end{array} \right \} \right / \sim . \end{align*}
\begin{align*}&\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad{\mathcal M}_{\textrm { PC}}(d)\ =\nonumber \\ &\left . \left \{ (E,\,\nabla ,\,\boldsymbol{l}) \ \middle | \ \begin{array}{l} (E,\,\boldsymbol{l}=(l^{(i)}_j)) is\ a\ quasi-parabolic\ bundle\ of\ rank\ r\ and\ degree\ d, \\ \nabla \,\colon E\longrightarrow \,E\otimes K_X(D)\ is\ a\ connection\ satisfying \\ {\sf\ res}_{x_i}(\nabla\ )(l^{(i)}_j)\,\subset \, l^{(i)}_j\ for\ any\ i,\,j\ and\ (E,\,\nabla,\,\boldsymbol{l})\ is\ simple. \end{array} \right \} \right / \sim . \end{align*}
For the open subspace
of
![]() ${\mathcal M}_{\textrm { PC}}(d)$
, there is a canonical morphism
${\mathcal M}_{\textrm { PC}}(d)$
, there is a canonical morphism
which is generically finite. Set
![]() $\Lambda \,\,:=\,\,\left \{ (\nu ^{(i)}_j)^{1\leqslant i\leqslant n}_{0\leqslant j\leqslant r-1} \, \in \, \mathbb{C}^{nr} \ \middle | \ d+\sum _{i,j}\nu ^{(i)}_j\,=\,0 \right \}$
. Then we have a smooth morphism
$\Lambda \,\,:=\,\,\left \{ (\nu ^{(i)}_j)^{1\leqslant i\leqslant n}_{0\leqslant j\leqslant r-1} \, \in \, \mathbb{C}^{nr} \ \middle | \ d+\sum _{i,j}\nu ^{(i)}_j\,=\,0 \right \}$
. Then we have a smooth morphism
whose fiber over any
![]() $\boldsymbol{\nu }\,\in \,\Lambda$
is the moduli space
$\boldsymbol{\nu }\,\in \,\Lambda$
is the moduli space
![]() ${\mathcal M}_{\textrm { PC}}(\boldsymbol{\nu })$
of
${\mathcal M}_{\textrm { PC}}(\boldsymbol{\nu })$
of
![]() $\boldsymbol{\nu }$
-parabolic connections. The morphism in (4.24) induces a map between the fibers of (4.23) and (4.25)
$\boldsymbol{\nu }$
-parabolic connections. The morphism in (4.24) induces a map between the fibers of (4.23) and (4.25)
which is an isomorphism for generic
![]() $\boldsymbol{a}$
and a resolution of singularities of
$\boldsymbol{a}$
and a resolution of singularities of
![]() ${\mathcal M}_{\textrm { C}}(\boldsymbol{a})$
for special
${\mathcal M}_{\textrm { C}}(\boldsymbol{a})$
for special
![]() $\boldsymbol{a}$
, where
$\boldsymbol{a}$
, where
![]() $\boldsymbol{a}\,=\,(a^{(i)}_j)$
is determined by
$\boldsymbol{a}\,=\,(a^{(i)}_j)$
is determined by
![]() $\boldsymbol{\nu }\,=\,(\nu ^{(i)}_j)$
as follows:
$\boldsymbol{\nu }\,=\,(\nu ^{(i)}_j)$
as follows:
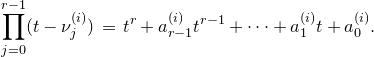 \begin{align*}\prod _{j=0}^{r-1}(t-\nu ^{(i)}_j)\,=\,t^r+a^{(i)}_{r-1}t^{r-1}+\cdots +a^{(i)}_1t+a^{(i)}_0.\end{align*}
\begin{align*}\prod _{j=0}^{r-1}(t-\nu ^{(i)}_j)\,=\,t^r+a^{(i)}_{r-1}t^{r-1}+\cdots +a^{(i)}_1t+a^{(i)}_0.\end{align*}
Roughly speaking, the moduli space
![]() ${\mathcal M}_{\textrm { C}}(\boldsymbol{a})$
for special
${\mathcal M}_{\textrm { C}}(\boldsymbol{a})$
for special
![]() $\boldsymbol{a}$
gives a partial resolution of singularities of the corresponding character variety, which we will define precisely later in (5.24). The meaning of the singularities of character varieties and their exceptional loci in the moduli space
$\boldsymbol{a}$
gives a partial resolution of singularities of the corresponding character variety, which we will define precisely later in (5.24). The meaning of the singularities of character varieties and their exceptional loci in the moduli space
![]() ${\mathcal M}_{\textrm { PC}}(\boldsymbol{\nu })$
(or precisely,
${\mathcal M}_{\textrm { PC}}(\boldsymbol{\nu })$
(or precisely,
![]() ${\mathcal M}_{\textrm { PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu })$
) is explained in [Reference IwasakiIw2] and [Reference Inaba, Iwasaki and SaitoIIS] from the viewpoint of the isomonodromic deformation, and their classification in the case of Painlevé equations is given in [Reference Saito and TerajimaSaTe].
${\mathcal M}_{\textrm { PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu })$
) is explained in [Reference IwasakiIw2] and [Reference Inaba, Iwasaki and SaitoIIS] from the viewpoint of the isomonodromic deformation, and their classification in the case of Painlevé equations is given in [Reference Saito and TerajimaSaTe].
Setting
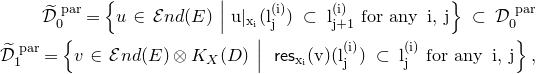 \begin{align*} \widetilde {\mathcal D}^{\textrm { par}}_0 = \left \{ u \, \in \, {\mathcal End}(E) \ \middle | \ \rm u|_{x_i}(l^{(i)}_j)\ \subset\ l^{(i)}_{j+1}\ for\ any\,\ i,\,j \right \} \ \subset \ {\mathcal D}^{\textrm { par}}_0 \\ \widetilde {\mathcal D}^{\textrm { par}}_1 = \left \{ v \, \in \, {\mathcal End}(E)\otimes K_X(D) \ \middle | \ \rm {\sf\ res}_{x_i}(v)(l^{(i)}_j)\ \subset\ l^{(i)}_j\ for\ any\,\ i,\,j \right \}, \\ \end{align*}
\begin{align*} \widetilde {\mathcal D}^{\textrm { par}}_0 = \left \{ u \, \in \, {\mathcal End}(E) \ \middle | \ \rm u|_{x_i}(l^{(i)}_j)\ \subset\ l^{(i)}_{j+1}\ for\ any\,\ i,\,j \right \} \ \subset \ {\mathcal D}^{\textrm { par}}_0 \\ \widetilde {\mathcal D}^{\textrm { par}}_1 = \left \{ v \, \in \, {\mathcal End}(E)\otimes K_X(D) \ \middle | \ \rm {\sf\ res}_{x_i}(v)(l^{(i)}_j)\ \subset\ l^{(i)}_j\ for\ any\,\ i,\,j \right \}, \\ \end{align*}
we can define a complex
![]() ${\mathcal D}^{\textrm { par}}_0\, \longrightarrow \, \widetilde {\mathcal D}^{\textrm { par}}_1$
,
${\mathcal D}^{\textrm { par}}_0\, \longrightarrow \, \widetilde {\mathcal D}^{\textrm { par}}_1$
,
![]() $u \,\longmapsto \, \nabla \circ u-u \circ \nabla$
, which induces complexes
$u \,\longmapsto \, \nabla \circ u-u \circ \nabla$
, which induces complexes
![]() $\widetilde {\mathcal D}^{\textrm { par}}_0 \,\longrightarrow \, {\mathcal D}^{\textrm { par}}_1$
and
$\widetilde {\mathcal D}^{\textrm { par}}_0 \,\longrightarrow \, {\mathcal D}^{\textrm { par}}_1$
and
![]() $\widetilde {\mathcal D}^{\textrm { par}}_0\,\longrightarrow \, \widetilde {\mathcal D}^{\textrm { par}}_1$
. The tangent space of the moduli space
$\widetilde {\mathcal D}^{\textrm { par}}_0\,\longrightarrow \, \widetilde {\mathcal D}^{\textrm { par}}_1$
. The tangent space of the moduli space
![]() ${\mathcal M}_{\textrm { PC}}(d)$
is
${\mathcal M}_{\textrm { PC}}(d)$
is
![]() $T{{\mathcal M}_{\textrm { PC}}(d)}\,=\, \mathbb{H}^1({\mathcal D}^{\textrm { par}}_0 \to \widetilde {\mathcal D}^{\textrm { par}}_1)$
and the cotangent space is its dual
$T{{\mathcal M}_{\textrm { PC}}(d)}\,=\, \mathbb{H}^1({\mathcal D}^{\textrm { par}}_0 \to \widetilde {\mathcal D}^{\textrm { par}}_1)$
and the cotangent space is its dual
So we can define a canonical pairing
Let
![]() $B$
be the Borel subgroup of
$B$
be the Borel subgroup of
![]() ${\rm GL}(r,\mathbb{C})$
consisting of upper triangular matrices, and let
${\rm GL}(r,\mathbb{C})$
consisting of upper triangular matrices, and let
![]() $U$
be the subgroup of
$U$
be the subgroup of
![]() $B$
consisting of matrices whose diagonal entries are
$B$
consisting of matrices whose diagonal entries are
![]() $1$
. Consider the open subspace
$1$
. Consider the open subspace
of
![]() ${\mathcal M}^U_{\textrm { FC}}(d)$
, which is the moduli space of framed connections in Definition 3.1 with
${\mathcal M}^U_{\textrm { FC}}(d)$
, which is the moduli space of framed connections in Definition 3.1 with
![]() $H\,=\,U$
. Associating the corresponding parabolic connection, we can define a morphism
$H\,=\,U$
. Associating the corresponding parabolic connection, we can define a morphism
which becomes a
![]() $\big (\prod _{D}B/U\big )\big /\mathbb{C}^*$
-bundle. By construction, the diagram
$\big (\prod _{D}B/U\big )\big /\mathbb{C}^*$
-bundle. By construction, the diagram
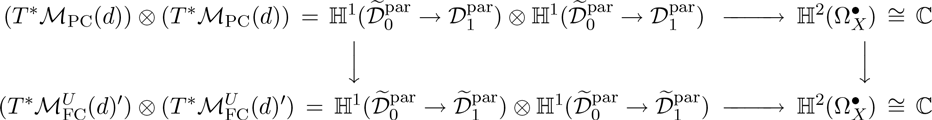
is commutative. The lower horizontal arrow is the Poisson bracket corresponding to the symplectic form on the moduli space
![]() ${\mathcal M}^U_{\textrm { FC}}(d)$
given by Theorem4.23. So the pairing in (4.26) defines a Poisson structure on the moduli space
${\mathcal M}^U_{\textrm { FC}}(d)$
given by Theorem4.23. So the pairing in (4.26) defines a Poisson structure on the moduli space
![]() ${\mathcal M}_{\textrm { PC}}(d)$
, and the morphism in (4.27) is a Poisson map.
${\mathcal M}_{\textrm { PC}}(d)$
, and the morphism in (4.27) is a Poisson map.
We can also see that the pairing in (4.26) commutes with the Poisson bracket on
![]() ${\mathcal M}_{\textrm { PC}}(\boldsymbol{\nu })$
corresponding to the symplectic form. So the canonical inclusion
${\mathcal M}_{\textrm { PC}}(\boldsymbol{\nu })$
corresponding to the symplectic form. So the canonical inclusion
![]() ${\mathcal M}_{\textrm { PC}}(\boldsymbol{\nu }) \, \hookrightarrow \,{\mathcal M}_{\textrm { PC}}(d)$
is also a Poisson map.
${\mathcal M}_{\textrm { PC}}(\boldsymbol{\nu }) \, \hookrightarrow \,{\mathcal M}_{\textrm { PC}}(d)$
is also a Poisson map.
The canonical map
![]() $\mathbb{H}^1({\mathcal C}_0\to {\mathcal End}(E)\otimes K_X) \,\longrightarrow \, \mathbb{H}^1(\widetilde {\mathcal D}^{\textrm { par}}_0 \,\rightarrow \, {\mathcal D}^{\textrm { par}}_1)$
coincides with the map
$\mathbb{H}^1({\mathcal C}_0\to {\mathcal End}(E)\otimes K_X) \,\longrightarrow \, \mathbb{H}^1(\widetilde {\mathcal D}^{\textrm { par}}_0 \,\rightarrow \, {\mathcal D}^{\textrm { par}}_1)$
coincides with the map
on the cotangent spaces induced by the morphism in (4.24), which means that the Poisson bracket in (4.21) commutes with that in (4.26). Combining the above, the following corollary is obtained.
Corollary 4.25. The moduli space
![]() ${\mathcal M}_{\textrm { PC}}(d)$
of parabolic connections has a Poisson structure defined by the Poisson bracket given in (
4.26
). Furthermore, the morphism
${\mathcal M}_{\textrm { PC}}(d)$
of parabolic connections has a Poisson structure defined by the Poisson bracket given in (
4.26
). Furthermore, the morphism
![]() ${\mathcal M}_{\textrm { PC}}(d)' \, \longrightarrow \, \mathcal{M}_{\textrm {{C}}}(d)$
in (
4.24
) becomes a Poisson map for this Poisson structure.
${\mathcal M}_{\textrm { PC}}(d)' \, \longrightarrow \, \mathcal{M}_{\textrm {{C}}}(d)$
in (
4.24
) becomes a Poisson map for this Poisson structure.
5. The moduli space of parabolic connections is not affine
5.1 Moduli space of parabolic connections and parabolic Higgs bundles
Throughout this section, we assume that
![]() $k$
is an algebraically closed field of arbitrary characteristic.
$k$
is an algebraically closed field of arbitrary characteristic.
Let
be an
![]() $n$
-pointed smooth projective curve of genus
$n$
-pointed smooth projective curve of genus
![]() $g$
over
$g$
over
![]() $k$
, where
$k$
, where
![]() $x_1, \,\ldots ,\,x_n$
are distinct
$x_1, \,\ldots ,\,x_n$
are distinct
![]() $k$
-valued points of
$k$
-valued points of
![]() $X$
. Denote the reduced divisor
$X$
. Denote the reduced divisor
![]() $x_1+\cdots +x_n$
on
$x_1+\cdots +x_n$
on
![]() $X$
by
$X$
by
![]() $D$
. Take a positive integer
$D$
. Take a positive integer
![]() $r$
which is not divisible by the characteristic of
$r$
which is not divisible by the characteristic of
![]() $k$
, and take an integer
$k$
, and take an integer
![]() $d$
and an element
$d$
and an element
such that the equality
![]() $\sum _{i,j} \nu ^{(i)}_j \,=\, -d$
holds in
$\sum _{i,j} \nu ^{(i)}_j \,=\, -d$
holds in
![]() $k$
. Take a collection of rational numbers
$k$
. Take a collection of rational numbers
satisfying the conditions:
-
(i)
 $0\,\lt \,\alpha ^{(i)}_1\,\lt \,\cdots \,\lt \,\alpha ^{(i)}_r\,\lt \,1$
;
$0\,\lt \,\alpha ^{(i)}_1\,\lt \,\cdots \,\lt \,\alpha ^{(i)}_r\,\lt \,1$
; -
(ii)
 $\alpha ^{(i)}_j\,\neq \,\alpha ^{(i')}_{j'}$
for
$\alpha ^{(i)}_j\,\neq \,\alpha ^{(i')}_{j'}$
for
 $(i,\,j)\,\neq \, (i',\,j')$
.
$(i,\,j)\,\neq \, (i',\,j')$
.
An
![]() $(\boldsymbol{x},\ \boldsymbol{\nu })$
-parabolic connection on
$(\boldsymbol{x},\ \boldsymbol{\nu })$
-parabolic connection on
![]() $X$
is defined exactly in the same way as Definition 4.9. Although a parabolic connection includes the data of a parabolic weight, we omit it and simply write
$X$
is defined exactly in the same way as Definition 4.9. Although a parabolic connection includes the data of a parabolic weight, we omit it and simply write
![]() $(E,\,\nabla ,\, \boldsymbol{l})$
. The definition of
$(E,\,\nabla ,\, \boldsymbol{l})$
. The definition of
![]() $\boldsymbol{\alpha }$
-stability of a parabolic connection is also defined in the same way as Definition 4.10.
$\boldsymbol{\alpha }$
-stability of a parabolic connection is also defined in the same way as Definition 4.10.
In the proof of the existence of the moduli space of stable parabolic connections in [Reference InabaIna, Theorem 2.2] , we used the embedding to the moduli space of parabolic
![]() $\Lambda^1_D$
-triples ([Reference Inaba, Iwasaki and SaitoIIS, Theorem 5.1]; this argument also works over a field of arbitrary characteristic. So we have the following theorem.
$\Lambda^1_D$
-triples ([Reference Inaba, Iwasaki and SaitoIIS, Theorem 5.1]; this argument also works over a field of arbitrary characteristic. So we have the following theorem.
Theorem 5.1. There exists a coarse moduli scheme
![]() $\mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu })$
of
$\mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu })$
of
![]() $\boldsymbol{\alpha }$
-stable
$\boldsymbol{\alpha }$
-stable
![]() $(\boldsymbol{x},\, \boldsymbol{\nu })$
-parabolic connections on a smooth projective curve
$(\boldsymbol{x},\, \boldsymbol{\nu })$
-parabolic connections on a smooth projective curve
![]() $X$
over
$X$
over
![]() $k$
. Furthermore,
$k$
. Furthermore,
![]() $\mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu })$
is quasi-projective over
$\mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu })$
is quasi-projective over
![]() $k$
.
$k$
.
Definition 5.2 [Reference MumfordMu, Lecture 14, page 99]. Let
![]() $Y$
be a projective variety over
$Y$
be a projective variety over
![]() $k$
, and let
$k$
, and let
![]() ${\mathcal O}_Y(1)$
be a very ample line bundle on
${\mathcal O}_Y(1)$
be a very ample line bundle on
![]() $Y$
. Take an integer
$Y$
. Take an integer
![]() $n_0$
. A coherent sheaf
$n_0$
. A coherent sheaf
![]() $E$
on
$E$
on
![]() $Y$
is called
$Y$
is called
![]() $n_0$
-regular if
$n_0$
-regular if
holds for all
![]() $i\,\gt \,0$
.
$i\,\gt \,0$
.
We will denote
![]() $E\otimes {\mathcal O}_Y(m)$
by
$E\otimes {\mathcal O}_Y(m)$
by
![]() $E(m)$
for an integer
$E(m)$
for an integer
![]() $m$
.
$m$
.
Definition 5.3. Let
![]() $Y$
be a projective variety over
$Y$
be a projective variety over
![]() $k$
. A set
$k$
. A set
![]() $\mathcal T$
of coherent sheaves on
$\mathcal T$
of coherent sheaves on
![]() $Y$
is called bounded if there is a scheme
$Y$
is called bounded if there is a scheme
![]() $S$
of finite type over
$S$
of finite type over
![]() $k$
, and a coherent sheaf
$k$
, and a coherent sheaf
![]() $\mathcal E$
on
$\mathcal E$
on
![]() $Y\times S$
such that for any member
$Y\times S$
such that for any member
![]() $E\,\in \, {\mathcal T}$
, there is a
$E\,\in \, {\mathcal T}$
, there is a
![]() $k$
-valued point
$k$
-valued point
![]() $s\,\in \, S$
such that
$s\,\in \, S$
such that
![]() ${\mathcal E}|_{Y\times \{s\}}\,\cong \, E$
.
${\mathcal E}|_{Y\times \{s\}}\,\cong \, E$
.
The following lemma is a useful tool to show the boundedness of a family of coherent sheaves.
Lemma 5.4 [Reference KleimanKl, Theorem 1.13].Let
![]() $Y$
be a projective variety over
$Y$
be a projective variety over
![]() $k$
, and let
$k$
, and let
![]() ${\mathcal O}_Y(1)$
be a very ample line bundle on
${\mathcal O}_Y(1)$
be a very ample line bundle on
![]() $Y$
. Then a set
$Y$
. Then a set
![]() $\mathcal T$
of coherent sheaves on
$\mathcal T$
of coherent sheaves on
![]() $Y$
is bounded if and only if there is an integer
$Y$
is bounded if and only if there is an integer
![]() $n_0$
such that all the members of
$n_0$
such that all the members of
![]() $\mathcal T$
are
$\mathcal T$
are
![]() $n_0$
-regular and the set
$n_0$
-regular and the set
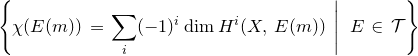 \begin{align*}\left \{ \chi (E(m))\,=\, \sum _i (-1)^i \dim H^i(X,\, E(m)) \,\, \middle |\,\,\, E\,\in \,{\mathcal T}\right \}\end{align*}
\begin{align*}\left \{ \chi (E(m))\,=\, \sum _i (-1)^i \dim H^i(X,\, E(m)) \,\, \middle |\,\,\, E\,\in \,{\mathcal T}\right \}\end{align*}
of Hilbert polynomials
![]() $\chi (E(m))$
in
$\chi (E(m))$
in
![]() $m$
of the members
$m$
of the members
![]() $E$
of
$E$
of
![]() $\mathcal T$
is finite.
$\mathcal T$
is finite.
In the same way as Proposition 4.16, the moduli space of simple
![]() $(\boldsymbol{x}, \,\boldsymbol{\nu })$
-parabolic connections
$(\boldsymbol{x}, \,\boldsymbol{\nu })$
-parabolic connections
![]() $\mathcal{M}_{{\rm PC}}(\boldsymbol{\nu })$
is an algebraic space over
$\mathcal{M}_{{\rm PC}}(\boldsymbol{\nu })$
is an algebraic space over
![]() $k$
, and the moduli space
$k$
, and the moduli space
![]() $\mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu })$
of
$\mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu })$
of
![]() $\boldsymbol{\alpha }$
-stable
$\boldsymbol{\alpha }$
-stable
![]() $(\boldsymbol{x},\, \boldsymbol{\nu })$
-parabolic connections is a Zariski open subspace of
$(\boldsymbol{x},\, \boldsymbol{\nu })$
-parabolic connections is a Zariski open subspace of
![]() $\mathcal{M}_{{\rm PC}}(\boldsymbol{\nu })$
. Since
$\mathcal{M}_{{\rm PC}}(\boldsymbol{\nu })$
. Since
![]() $\mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu })$
is quasi-projective over
$\mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu })$
is quasi-projective over
![]() $k$
, we can take an integer
$k$
, we can take an integer
![]() $n_0$
such that for all
$n_0$
such that for all
![]() $(E,\,\nabla ,\,\boldsymbol{l})\,\in \, \mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu })$
, the underlying vector bundle
$(E,\,\nabla ,\,\boldsymbol{l})\,\in \, \mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu })$
, the underlying vector bundle
![]() $E$
is
$E$
is
![]() $n_0$
-regular.
$n_0$
-regular.
Fix a line bundle
![]() $L$
on
$L$
on
![]() $X$
and a logarithmic connection
$X$
and a logarithmic connection
such that
![]() ${\rm res}_{x_i}(\nabla _L)\,=\,\sum _{j=0}^{r-1}\nu ^{(i)}_j$
for all
${\rm res}_{x_i}(\nabla _L)\,=\,\sum _{j=0}^{r-1}\nu ^{(i)}_j$
for all
![]() $1\,\leqslant \, i\,\leqslant \, n$
. Set
$1\,\leqslant \, i\,\leqslant \, n$
. Set
These are closed subspaces of
![]() $\mathcal{M}_{{\rm PC}}(\boldsymbol{\nu })$
and
$\mathcal{M}_{{\rm PC}}(\boldsymbol{\nu })$
and
![]() $ \mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu })$
, respectively. Setting
$ \mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu })$
, respectively. Setting
there is a canonical open immersion
Set
Then
![]() $\mathcal{M}_{{\rm PC}}^{n_0\textrm { -reg}}(\boldsymbol{\nu },\nabla _L)$
is a closed subspace of
$\mathcal{M}_{{\rm PC}}^{n_0\textrm { -reg}}(\boldsymbol{\nu },\nabla _L)$
is a closed subspace of
![]() $\mathcal{M}^{n_0\textrm { -reg}}_{{\rm PC}}(\boldsymbol{\nu })$
and it contains
$\mathcal{M}^{n_0\textrm { -reg}}_{{\rm PC}}(\boldsymbol{\nu })$
and it contains
![]() $\mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu },\nabla _L)$
as a Zariski open subspace.
$\mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu },\nabla _L)$
as a Zariski open subspace.
Under the assumption that the rank
![]() $r$
is not divisible by the characteristic of
$r$
is not divisible by the characteristic of
![]() $k$
, the proof of the smoothness of the moduli space given in [Reference InabaIna, Theorem 2.1] works because the assumption ensures that the Killing form on
$k$
, the proof of the smoothness of the moduli space given in [Reference InabaIna, Theorem 2.1] works because the assumption ensures that the Killing form on
![]() ${\rm sl}(r,k)$
remains nondegenerate. This is elaborated in the following proposition.
${\rm sl}(r,k)$
remains nondegenerate. This is elaborated in the following proposition.
Proposition 5.5. Assume that the rank
![]() $r$
is not divisible by the characteristic of
$r$
is not divisible by the characteristic of
![]() $k$
. Then the moduli space
$k$
. Then the moduli space
![]() $\mathcal{M}_{{\rm PC}}(\boldsymbol{\nu },\nabla _L)$
is smooth over
$\mathcal{M}_{{\rm PC}}(\boldsymbol{\nu },\nabla _L)$
is smooth over
![]() $k$
, and so is its open subspace
$k$
, and so is its open subspace
![]() $\mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu },\nabla _L)$
.
$\mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu },\nabla _L)$
.
Proof. We use the criterion of smoothness in [Reference GrothendieckGrot2, Proposition 17.14.2]. Let
![]() $A$
be an Artinian local ring over
$A$
be an Artinian local ring over
![]() $k$
with the maximal ideal
$k$
with the maximal ideal
![]() $\mathfrak{m}$
, and let
$\mathfrak{m}$
, and let
![]() $I$
be an ideal of
$I$
be an ideal of
![]() $A$
such that
$A$
such that
![]() $\mathfrak{m}I\,=\,0$
. Suppose that we are given a morphism
$\mathfrak{m}I\,=\,0$
. Suppose that we are given a morphism
![]() $\textrm { Spec} A/I\,\longrightarrow \,\mathcal{M}_{{\rm PC}}(\boldsymbol{\nu },\nabla _L)$
that corresponds to a flat family
$\textrm { Spec} A/I\,\longrightarrow \,\mathcal{M}_{{\rm PC}}(\boldsymbol{\nu },\nabla _L)$
that corresponds to a flat family
![]() $(E,\,\nabla ,\,\boldsymbol{l})$
of parabolic connections on
$(E,\,\nabla ,\,\boldsymbol{l})$
of parabolic connections on
![]() $X\times \textrm { Spec} A/I$
over
$X\times \textrm { Spec} A/I$
over
![]() $A/I$
. It suffices to construct a flat family
$A/I$
. It suffices to construct a flat family
![]() $(\widetilde {E},\,\widetilde {\nabla },\,\widetilde {\boldsymbol{l}})$
of
$(\widetilde {E},\,\widetilde {\nabla },\,\widetilde {\boldsymbol{l}})$
of
![]() $\boldsymbol{\nu }$
-parabolic connections on
$\boldsymbol{\nu }$
-parabolic connections on
![]() $X\times \textrm { Spec} A$
over
$X\times \textrm { Spec} A$
over
![]() $\textrm { Spec} A$
that is a lift of
$\textrm { Spec} A$
that is a lift of
![]() $(E,\,\nabla ,\,\boldsymbol{l})$
.
$(E,\,\nabla ,\,\boldsymbol{l})$
.
There is an isomorphism
![]() $\varphi \,\colon \, \det E\,\xrightarrow {\,\,\sim \,\,\,}\, L\otimes A/I$
such that
$\varphi \,\colon \, \det E\,\xrightarrow {\,\,\sim \,\,\,}\, L\otimes A/I$
such that
![]() $(\nabla _L\otimes A/I)\circ \varphi \,=\,(\varphi \otimes {\rm id})\circ {\textrm { Tr}}(\nabla )$
. Take an affine open covering
$(\nabla _L\otimes A/I)\circ \varphi \,=\,(\varphi \otimes {\rm id})\circ {\textrm { Tr}}(\nabla )$
. Take an affine open covering
![]() $\{U_{\alpha }\}$
of
$\{U_{\alpha }\}$
of
![]() $X$
satisfying the condition that there is an isomorphism
$X$
satisfying the condition that there is an isomorphism
Set
![]() $\overline {\phi _{\alpha }}\,\,:=\,\,\phi _{\alpha }\otimes A/\mathfrak{m}$
and
$\overline {\phi _{\alpha }}\,\,:=\,\,\phi _{\alpha }\otimes A/\mathfrak{m}$
and
![]() $\overline {\varphi }\,\,:=\,\,\varphi \otimes A/\mathfrak{m}$
. After replacing
$\overline {\varphi }\,\,:=\,\,\varphi \otimes A/\mathfrak{m}$
. After replacing
![]() $\phi _{\alpha }$
with
$\phi _{\alpha }$
with
![]() $(1+r^{-1}a)\phi _{\alpha }$
for some
$(1+r^{-1}a)\phi _{\alpha }$
for some
![]() $a\,\in \, I{\mathcal O}_{U_{\alpha }}$
, we may assume that
$a\,\in \, I{\mathcal O}_{U_{\alpha }}$
, we may assume that
as maps from
![]() $L\otimes A/I$
to
$L\otimes A/I$
to
![]() ${\mathcal O}_{U_{\alpha }\times \textrm { Spec} A/I}$
. Set
${\mathcal O}_{U_{\alpha }\times \textrm { Spec} A/I}$
. Set
![]() $E_{\alpha }\,\,:=\,\,{\mathcal O}_{U_{\alpha }\times \textrm { Spec} A}^{\oplus r}$
and put
$E_{\alpha }\,\,:=\,\,{\mathcal O}_{U_{\alpha }\times \textrm { Spec} A}^{\oplus r}$
and put
Choose a lift
of
![]() $\phi _{\beta }\circ \phi _{\alpha }^{-1}$
. Replacing
$\phi _{\beta }\circ \phi _{\alpha }^{-1}$
. Replacing
![]() $\theta _{\beta \alpha }$
with
$\theta _{\beta \alpha }$
with
![]() $(1+r^{-1}b)\theta _{\beta \alpha }$
for some
$(1+r^{-1}b)\theta _{\beta \alpha }$
for some
![]() $b\,\in \, I{\mathcal O}_{U_{\alpha \beta }\times \textrm { Spec} A}$
, we may assume that the following equality holds
$b\,\in \, I{\mathcal O}_{U_{\alpha \beta }\times \textrm { Spec} A}$
, we may assume that the following equality holds
as maps from
![]() $\det (E_{\alpha })|_{U_{\alpha \beta }\times \textrm { Spec} A}$
to
$\det (E_{\alpha })|_{U_{\alpha \beta }\times \textrm { Spec} A}$
to
![]() $\det (E_{\beta })|_{U_{\alpha \beta }\times \textrm { Spec} A}$
. If
$\det (E_{\beta })|_{U_{\alpha \beta }\times \textrm { Spec} A}$
. If
![]() $x_i\,\in \, U_{\alpha }$
, then we take a quasi-parabolic structure
$x_i\,\in \, U_{\alpha }$
, then we take a quasi-parabolic structure
![]() $l^{\alpha }_*$
on
$l^{\alpha }_*$
on
![]() $E_{\alpha }$
at
$E_{\alpha }$
at
![]() $x_i\times \textrm { Spec} A$
that is a lift of
$x_i\times \textrm { Spec} A$
that is a lift of
![]() $l^{(i)}_*$
. Take a relative connection
$l^{(i)}_*$
. Take a relative connection
such that
![]() $\nabla _{\alpha }\otimes A/I\,=\, \phi _{\alpha }\circ \nabla |_{U_{\alpha }\times \textrm { Spec} A/I}\circ \phi _{\alpha }^{-1}$
and
$\nabla _{\alpha }\otimes A/I\,=\, \phi _{\alpha }\circ \nabla |_{U_{\alpha }\times \textrm { Spec} A/I}\circ \phi _{\alpha }^{-1}$
and
![]() $\big ({\rm res}_{x_i\times \textrm { Spec} A}(\nabla _{\alpha })-\nu ^{(i)}_j\big ) (l^{\alpha }_j)\,\subset \, l^{\alpha }_{j+1}$
for all
$\big ({\rm res}_{x_i\times \textrm { Spec} A}(\nabla _{\alpha })-\nu ^{(i)}_j\big ) (l^{\alpha }_j)\,\subset \, l^{\alpha }_{j+1}$
for all
![]() $0\,\leqslant \, j\,\leqslant \, r-1$
. After replacing
$0\,\leqslant \, j\,\leqslant \, r-1$
. After replacing
![]() $\nabla _{\alpha }$
with
$\nabla _{\alpha }$
with
![]() $\nabla _{\alpha }+r^{-1}\eta \otimes {\rm id}_{E_{\alpha }}$
for some
$\nabla _{\alpha }+r^{-1}\eta \otimes {\rm id}_{E_{\alpha }}$
for some
![]() $\eta \,\in \, I \, \Omega^1_{U_{\alpha }\times \textrm { Spec} A/\textrm { Spec} A}$
, we may assume that
$\eta \,\in \, I \, \Omega^1_{U_{\alpha }\times \textrm { Spec} A/\textrm { Spec} A}$
, we may assume that
![]() $\varphi _{\alpha }{\textrm { Tr}}(\nabla _{\alpha })\varphi _{\alpha }^{-1}\,=\,\nabla _L\otimes {\rm id}_A$
. Put
$\varphi _{\alpha }{\textrm { Tr}}(\nabla _{\alpha })\varphi _{\alpha }^{-1}\,=\,\nabla _L\otimes {\rm id}_A$
. Put
![]() $(\overline {E},\,\overline {\nabla },\,\overline {\boldsymbol{l}})\,\,:=\,\, (E,\,\nabla ,\,\boldsymbol{l})\otimes A/\mathfrak{m}$
and set
$(\overline {E},\,\overline {\nabla },\,\overline {\boldsymbol{l}})\,\,:=\,\, (E,\,\nabla ,\,\boldsymbol{l})\otimes A/\mathfrak{m}$
and set
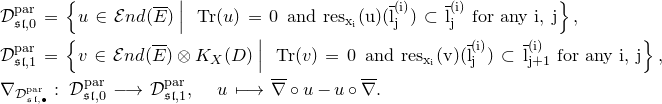 \begin{align*} &{\mathcal D}^{{\rm par}}_{\mathfrak{sl},0} \,=\, \left \{ u\,\in \,{\mathcal End}(\overline {E}) \, \middle | \,\, \textrm { Tr}(u)\,=\,0\, \rm \ and\ {\rm res}_{x_i}(u)(\overline {l}^{(i)}_j)\,\subset \, \overline {l}^{(i)}_j \rm \ for\ any\ i,\,j \right \}, \\ &{\mathcal D}^{{\rm par}}_{\mathfrak{sl},1} \,=\, \left \{ v\,\in \,{\mathcal End}(\overline {E})\otimes K_X(D) \, \middle | \,\, \textrm { Tr}(v)\,=\,0\, \rm \ and\ {\rm res}_{x_i}(v)(\overline {l}^{(i)}_j)\,\subset \, \overline {l}^{(i)}_{j+1} \rm \ for\ any\ i,\,j \right \}, \\ &\nabla _{{\mathcal D}^{{\rm par}}_{\mathfrak{sl},\bullet }} \,\colon \, {\mathcal D}^{{\rm par}}_{\mathfrak{sl},0} \, \longrightarrow \, {\mathcal D}^{{\rm par}}_{\mathfrak{sl},1}, \quad \,u \, \longmapsto \, \overline {\nabla }\circ u-u\circ \overline {\nabla }. \end{align*}
\begin{align*} &{\mathcal D}^{{\rm par}}_{\mathfrak{sl},0} \,=\, \left \{ u\,\in \,{\mathcal End}(\overline {E}) \, \middle | \,\, \textrm { Tr}(u)\,=\,0\, \rm \ and\ {\rm res}_{x_i}(u)(\overline {l}^{(i)}_j)\,\subset \, \overline {l}^{(i)}_j \rm \ for\ any\ i,\,j \right \}, \\ &{\mathcal D}^{{\rm par}}_{\mathfrak{sl},1} \,=\, \left \{ v\,\in \,{\mathcal End}(\overline {E})\otimes K_X(D) \, \middle | \,\, \textrm { Tr}(v)\,=\,0\, \rm \ and\ {\rm res}_{x_i}(v)(\overline {l}^{(i)}_j)\,\subset \, \overline {l}^{(i)}_{j+1} \rm \ for\ any\ i,\,j \right \}, \\ &\nabla _{{\mathcal D}^{{\rm par}}_{\mathfrak{sl},\bullet }} \,\colon \, {\mathcal D}^{{\rm par}}_{\mathfrak{sl},0} \, \longrightarrow \, {\mathcal D}^{{\rm par}}_{\mathfrak{sl},1}, \quad \,u \, \longmapsto \, \overline {\nabla }\circ u-u\circ \overline {\nabla }. \end{align*}
Then we get a cohomology class
![]() $[\{\theta _{\gamma \alpha }^{-1}\theta _{\gamma \beta }\theta _{\beta \alpha }-{\rm id}\},\, \{ \theta _{\beta \alpha }^{-1}\circ \nabla _{\beta }\circ \theta _{\beta \alpha }-\nabla _{\alpha }\}] \,\in \, \mathbb{H}^2({\mathcal D}^{{\rm par}}_{\mathfrak{sl},\bullet }) \otimes I$
whose vanishing is equivalent to the existence of a lift
$[\{\theta _{\gamma \alpha }^{-1}\theta _{\gamma \beta }\theta _{\beta \alpha }-{\rm id}\},\, \{ \theta _{\beta \alpha }^{-1}\circ \nabla _{\beta }\circ \theta _{\beta \alpha }-\nabla _{\alpha }\}] \,\in \, \mathbb{H}^2({\mathcal D}^{{\rm par}}_{\mathfrak{sl},\bullet }) \otimes I$
whose vanishing is equivalent to the existence of a lift
![]() $(\widetilde {E},\,\widetilde {\nabla },\,\widetilde {\boldsymbol{l}}) \,\in \,{\mathcal M}_{{\rm PC}}(\boldsymbol{\nu },\nabla _L)(A)$
of
$(\widetilde {E},\,\widetilde {\nabla },\,\widetilde {\boldsymbol{l}}) \,\in \,{\mathcal M}_{{\rm PC}}(\boldsymbol{\nu },\nabla _L)(A)$
of
![]() $(E,\,\nabla ,\,\boldsymbol{l})$
. There is a commutative diagram with exact rows
$(E,\,\nabla ,\,\boldsymbol{l})$
. There is a commutative diagram with exact rows

induced by the Serre duality. Take any member
Since
![]() $(\overline {E},\,\overline {\nabla },\,\overline {\boldsymbol{l}})$
is simple, we can write
$(\overline {E},\,\overline {\nabla },\,\overline {\boldsymbol{l}})$
is simple, we can write
![]() $u\,=\,c\cdot {\rm id}_{\overline {E}}$
for some
$u\,=\,c\cdot {\rm id}_{\overline {E}}$
for some
![]() $c\,\in \, k$
. By the definition of
$c\,\in \, k$
. By the definition of
![]() ${\mathcal D}^{{\rm par}}_{\mathfrak{sl},0}$
, we have
${\mathcal D}^{{\rm par}}_{\mathfrak{sl},0}$
, we have
![]() $0\,=\,{\textrm { Tr}}(u)\,=\,{\textrm { Tr}}(c\,{\rm id}_{\overline {E}})\,=\,rc$
. Since
$0\,=\,{\textrm { Tr}}(u)\,=\,{\textrm { Tr}}(c\,{\rm id}_{\overline {E}})\,=\,rc$
. Since
![]() $r^{-1}\,\in \,k^{\times }$
by the assumption, we have
$r^{-1}\,\in \,k^{\times }$
by the assumption, we have
![]() $c\,=\,0$
. Thus,
$c\,=\,0$
. Thus,
![]() $u\,=\,0$
, and we have
$u\,=\,0$
, and we have
![]() $\mathbb{H}^0({\mathcal D}^{{\rm par}}_{\mathfrak{sl},\bullet })\,=\,0$
. So the obstruction space
$\mathbb{H}^0({\mathcal D}^{{\rm par}}_{\mathfrak{sl},\bullet })\,=\,0$
. So the obstruction space
![]() $\mathbb{H}^2({\mathcal D}^{{\rm par}}_{\mathfrak{sl},\bullet }) \,\cong \, \mathbb{H}^0({\mathcal D}^{{\rm par}}_{\mathfrak{sl},\bullet })^{\vee }$
vanishes, and there is a lift
$\mathbb{H}^2({\mathcal D}^{{\rm par}}_{\mathfrak{sl},\bullet }) \,\cong \, \mathbb{H}^0({\mathcal D}^{{\rm par}}_{\mathfrak{sl},\bullet })^{\vee }$
vanishes, and there is a lift
![]() $(\widetilde {E},\,\widetilde {\nabla },\,\widetilde {l})\,\in \, {\mathcal M}_{{\rm PC}}(\boldsymbol{\nu },\nabla _L)(A)$
of
$(\widetilde {E},\,\widetilde {\nabla },\,\widetilde {l})\,\in \, {\mathcal M}_{{\rm PC}}(\boldsymbol{\nu },\nabla _L)(A)$
of
![]() $(E,\nabla ,l)$
. This means that
$(E,\nabla ,l)$
. This means that
![]() ${\mathcal M}_{{\rm PC}}(\boldsymbol{\nu },\nabla _L)$
is smooth.
${\mathcal M}_{{\rm PC}}(\boldsymbol{\nu },\nabla _L)$
is smooth.
Using Proposition 5.5 and a similar calculation as in Lemma 2.6, we have the following proposition.
Proposition 5.6 [Reference InabaIna, Theorem 2.1, Propositions 5.1, 5.2 and 5.3]. The dimension of the moduli space
![]() $\mathcal{M}_{{\rm PC}}(\boldsymbol{\nu },\nabla _L)$
is
$\mathcal{M}_{{\rm PC}}(\boldsymbol{\nu },\nabla _L)$
is
![]() $2(r^2-1)(g-1)+nr(r-1)$
, which is same as the dimension of its open subspace
$2(r^2-1)(g-1)+nr(r-1)$
, which is same as the dimension of its open subspace
![]() $\mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu },\nabla _L)$
.
$\mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu },\nabla _L)$
.
We can similarly define the Higgs bundles. As before,
![]() $\boldsymbol{\alpha }$
is a parabolic weight. Take a tuple
$\boldsymbol{\alpha }$
is a parabolic weight. Take a tuple
![]() $\boldsymbol{\mu }\,=\,(\mu ^{(i)}_j)^{1\leqslant i\leqslant n}_{0\leqslant j\leqslant r-1}\,\in \,k^{nr}$
satisfying the following condition:
$\boldsymbol{\mu }\,=\,(\mu ^{(i)}_j)^{1\leqslant i\leqslant n}_{0\leqslant j\leqslant r-1}\,\in \,k^{nr}$
satisfying the following condition:
 \begin{align*} \sum _{i=1}^n\sum _{j=0}^{r-1} \mu ^{(i)}_j\ =\ 0. \end{align*}
\begin{align*} \sum _{i=1}^n\sum _{j=0}^{r-1} \mu ^{(i)}_j\ =\ 0. \end{align*}
We say that a tuple
![]() $(E,\,\Phi , \,\boldsymbol{l}\,=\,\{l^{(i)}_*\}_{1\leqslant i\leqslant n})$
(equipped with a parabolic weight
$(E,\,\Phi , \,\boldsymbol{l}\,=\,\{l^{(i)}_*\}_{1\leqslant i\leqslant n})$
(equipped with a parabolic weight
![]() $\boldsymbol{\alpha }$
) is an
$\boldsymbol{\alpha }$
) is an
![]() $(\boldsymbol{x},\,\boldsymbol{\mu })$
-parabolic Higgs bundle if:
$(\boldsymbol{x},\,\boldsymbol{\mu })$
-parabolic Higgs bundle if:
-
(1)
 $E$
is an algebraic vector bundle on
$E$
is an algebraic vector bundle on
 $X$
of rank
$X$
of rank
 $r$
and degree
$r$
and degree
 $d$
;
$d$
; -
(2)
 $\Phi \,\colon \, E\,\longrightarrow \, E\otimes K_{X}(D)$
is an
$\Phi \,\colon \, E\,\longrightarrow \, E\otimes K_{X}(D)$
is an
 ${\mathcal O}_X$
-linear homomorphism;
${\mathcal O}_X$
-linear homomorphism; -
(3)
 $l^{(i)}_*$
is a filtrationfor every
$l^{(i)}_*$
is a filtrationfor every \begin{align*}E\big \vert _{x_i} \,=\, l_0^{(i)} \,\supset \, l_1^{(i)} \,\supset \,\cdots \,\supset \, l_r^{(i)}\,=\,0\end{align*}
\begin{align*}E\big \vert _{x_i} \,=\, l_0^{(i)} \,\supset \, l_1^{(i)} \,\supset \,\cdots \,\supset \, l_r^{(i)}\,=\,0\end{align*}
 $x_i$
such that
$x_i$
such that
 $\dim (l_j^{(i)}/l_{j+1}^{(i)})\,=\,1$
and
$\dim (l_j^{(i)}/l_{j+1}^{(i)})\,=\,1$
and
 $({\rm res}_{x_i}(\Phi )-\mu ^{(i)}_j)(l^{(i)}_j) \,\subset \, l_{j+1}^{(i)}$
for all
$({\rm res}_{x_i}(\Phi )-\mu ^{(i)}_j)(l^{(i)}_j) \,\subset \, l_{j+1}^{(i)}$
for all
 $j\,=\,0,\,\cdots ,\,r-1$
.
$j\,=\,0,\,\cdots ,\,r-1$
.
An
![]() $(\boldsymbol{x},\,\boldsymbol{\mu })$
-parabolic Higgs bundle
$(\boldsymbol{x},\,\boldsymbol{\mu })$
-parabolic Higgs bundle
![]() $(E,\,\Phi ,\,\boldsymbol{l})$
is said to be simple if every endomorphism
$(E,\,\Phi ,\,\boldsymbol{l})$
is said to be simple if every endomorphism
that commutes with
![]() $\Phi$
and preserves
$\Phi$
and preserves
![]() $\boldsymbol{l}$
is a constant scalar multiplication
$\boldsymbol{l}$
is a constant scalar multiplication
![]() $f\,=\,c\,{\rm Id}_E$
for some
$f\,=\,c\,{\rm Id}_E$
for some
![]() $c\,\in \,k$
. Denote by
$c\,\in \,k$
. Denote by
![]() $\mathcal{M}_{{\rm Higgs}}(\boldsymbol{\mu })$
the moduli space of simple
$\mathcal{M}_{{\rm Higgs}}(\boldsymbol{\mu })$
the moduli space of simple
![]() $\boldsymbol{\mu }$
-parabolic Higgs bundles. Define
$\boldsymbol{\mu }$
-parabolic Higgs bundles. Define
![]() $\boldsymbol{\alpha }$
-stability for parabolic Higgs bundles analogous to Definition 4.10. If we replace
$\boldsymbol{\alpha }$
-stability for parabolic Higgs bundles analogous to Definition 4.10. If we replace
![]() $n_0$
by a sufficiently large integer, we may assume that for every
$n_0$
by a sufficiently large integer, we may assume that for every
![]() $\boldsymbol{\alpha }$
-stable
$\boldsymbol{\alpha }$
-stable
![]() $(\boldsymbol{x},\,\boldsymbol{\mu })$
-parabolic Higgs bundle
$(\boldsymbol{x},\,\boldsymbol{\mu })$
-parabolic Higgs bundle
![]() $(E,\,\Phi ,\,\boldsymbol{l})$
, the underlying vector bundle
$(E,\,\Phi ,\,\boldsymbol{l})$
, the underlying vector bundle
![]() $E$
is
$E$
is
![]() $n_0$
-regular.
$n_0$
-regular.
Fix a line bundle
![]() $L$
on
$L$
on
![]() $X$
together with a homomorphism
$X$
together with a homomorphism
![]() $\Phi _L\, \colon \, L\, \longrightarrow \, L\otimes K_X$
of
$\Phi _L\, \colon \, L\, \longrightarrow \, L\otimes K_X$
of
![]() ${\mathcal O}_X$
–modules such that
${\mathcal O}_X$
–modules such that
![]() ${\sf res}_{x_i}(\Phi _L)\,=\,\sum _{j=0}^{r-1}\mu ^{(i)}_j$
for any
${\sf res}_{x_i}(\Phi _L)\,=\,\sum _{j=0}^{r-1}\mu ^{(i)}_j$
for any
![]() $i$
. Set
$i$
. Set
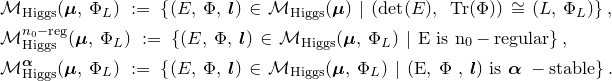 \begin{align*} &\mathcal{M}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L) \, \,:=\,\, \left \{ (E,\,\Phi ,\,\boldsymbol{l})\,\in \, \mathcal{M}_{{\rm Higgs}}(\boldsymbol{\mu }) \,\,\big \vert \,\, (\det (E),\,{\textrm { Tr}}(\Phi ))\,\cong \,(L,\,\Phi _L) \right \}, \\ &\mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L) \, \,:=\,\, \left \{ (E,\,\Phi ,\,\boldsymbol{l})\,\in \, \mathcal{M}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L) \,\,\big \vert \,\, \rm E\ is\ n_0-regular \right \}, \\ &\mathcal{M}^{\boldsymbol{\alpha }}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L) \, \,:=\,\, \left \{ (E,\,\Phi ,\,\boldsymbol{l})\,\in \, \mathcal{M}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L) \,\,\big \vert \,\, \rm (E,\,\Phi\ ,\,\boldsymbol{l})\ is\ \boldsymbol{\alpha\ }-stable \right \}. \end{align*}
\begin{align*} &\mathcal{M}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L) \, \,:=\,\, \left \{ (E,\,\Phi ,\,\boldsymbol{l})\,\in \, \mathcal{M}_{{\rm Higgs}}(\boldsymbol{\mu }) \,\,\big \vert \,\, (\det (E),\,{\textrm { Tr}}(\Phi ))\,\cong \,(L,\,\Phi _L) \right \}, \\ &\mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L) \, \,:=\,\, \left \{ (E,\,\Phi ,\,\boldsymbol{l})\,\in \, \mathcal{M}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L) \,\,\big \vert \,\, \rm E\ is\ n_0-regular \right \}, \\ &\mathcal{M}^{\boldsymbol{\alpha }}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L) \, \,:=\,\, \left \{ (E,\,\Phi ,\,\boldsymbol{l})\,\in \, \mathcal{M}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L) \,\,\big \vert \,\, \rm (E,\,\Phi\ ,\,\boldsymbol{l})\ is\ \boldsymbol{\alpha\ }-stable \right \}. \end{align*}
The same calculations as in the proof of Propositions 5.5 and Proposition 5.6 yield the following proposition.
Proposition 5.7 (See [Reference Boden and YokogawaBoYo, § 2.1], [Reference YokogawaYo, Theorem 2.8]). Assume that
![]() $r$
is not divisible by the characteristic of
$r$
is not divisible by the characteristic of
![]() $k$
. Then the moduli space
$k$
. Then the moduli space
![]() $ \mathcal{M}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L)$
is smooth and
$ \mathcal{M}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L)$
is smooth and
![]() $\dim \mathcal{M}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L) \,=\,2(r^2-1)(g-1)+nr(r-1)$
. Furthermore, the open subspace
$\dim \mathcal{M}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L) \,=\,2(r^2-1)(g-1)+nr(r-1)$
. Furthermore, the open subspace
![]() $\mathcal{M}^{\boldsymbol{\alpha }}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L)$
of
$\mathcal{M}^{\boldsymbol{\alpha }}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L)$
of
![]() $\mathcal{M}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L)$
consisting of
$\mathcal{M}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L)$
consisting of
![]() $\boldsymbol{\alpha }$
-stable parabolic Higgs bundles is quasi-projective.
$\boldsymbol{\alpha }$
-stable parabolic Higgs bundles is quasi-projective.
It is known that there is no non-constant global algebraic function on the moduli space of logarithmic connections with central residues on a compact Riemann surface of genus at least
![]() $3$
[Reference Biswas and RaghavendraBiRa]. In the logarithmic case, the same statement was proved in [Reference ArinkinAr] in a very special case when
$3$
[Reference Biswas and RaghavendraBiRa]. In the logarithmic case, the same statement was proved in [Reference ArinkinAr] in a very special case when
![]() $g\,=\,0$
,
$g\,=\,0$
,
![]() $r\,=\,2$
and
$r\,=\,2$
and
![]() $n\,=\,4$
. In [Reference Biswas and RaghavendraBiRa], the Betti number of the moduli space of stable vector bundles assumed one of the key roles. A similar result is proved in [Reference SinghSin]. We will prove, in this section, a weaker result that the moduli space
$n\,=\,4$
. In [Reference Biswas and RaghavendraBiRa], the Betti number of the moduli space of stable vector bundles assumed one of the key roles. A similar result is proved in [Reference SinghSin]. We will prove, in this section, a weaker result that the moduli space
![]() $\mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu },\,\nabla _L)$
of
$\mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu },\,\nabla _L)$
of
![]() $(\boldsymbol{x},\,\boldsymbol{\nu })$
-parabolic connections is not affine for any genus, except for several special cases. We use a part of the ideas in [Reference Biswas and RaghavendraBiRa] and compare the transcendence degree of the ring of global algebraic functions on the moduli space
$(\boldsymbol{x},\,\boldsymbol{\nu })$
-parabolic connections is not affine for any genus, except for several special cases. We use a part of the ideas in [Reference Biswas and RaghavendraBiRa] and compare the transcendence degree of the ring of global algebraic functions on the moduli space
![]() $\mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu },\,\nabla _L)$
of parabolic connections with that on the moduli space
$\mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu },\,\nabla _L)$
of parabolic connections with that on the moduli space
![]() $\mathcal{M}_{{\rm Higgs}}^{\boldsymbol{\alpha }}(\boldsymbol{0},\,0)$
of parabolic Higgs bundles. Our argument also works over the base field of positive characteristic, which is consistent with the existence of the Hitchin map on the moduli space of connections ([Reference Laszlo and PaulyLaPa], [Reference GroechenigGroe]).
$\mathcal{M}_{{\rm Higgs}}^{\boldsymbol{\alpha }}(\boldsymbol{0},\,0)$
of parabolic Higgs bundles. Our argument also works over the base field of positive characteristic, which is consistent with the existence of the Hitchin map on the moduli space of connections ([Reference Laszlo and PaulyLaPa], [Reference GroechenigGroe]).
5.2 Codimension estimation for non-simple underlying bundle
This subsection provides an improvement of the result of [Reference InabaIna, § 5]. Throughout this subsection,
![]() $k$
is assumed to be an algebraically closed field of arbitrary characteristic.
$k$
is assumed to be an algebraically closed field of arbitrary characteristic.
Now, let
![]() $X$
be a smooth projective irreducible curve over
$X$
be a smooth projective irreducible curve over
![]() $\textrm { Spec}\, k$
of genus is
$\textrm { Spec}\, k$
of genus is
![]() $g$
, and let
$g$
, and let
![]() $D\,=\,x_1+ \cdots +x_n$
be a reduced divisor on
$D\,=\,x_1+ \cdots +x_n$
be a reduced divisor on
![]() $X$
. Fix a line bundle
$X$
. Fix a line bundle
![]() $L$
of degree
$L$
of degree
![]() $d$
on
$d$
on
![]() $X$
. Consider the set
$X$
. Consider the set
of isomorphism classes of quasi-parabolic bundles
![]() $(E,\,\boldsymbol{l})$
on
$(E,\,\boldsymbol{l})$
on
![]() $(X,\,D)$
such that:
$(X,\,D)$
such that:
-
(i)
 $E$
is an algebraic vector bundle on
$E$
is an algebraic vector bundle on
 $X$
of rank
$X$
of rank
 $r$
with
$r$
with
 $\det E\,\cong \,L$
;
$\det E\,\cong \,L$
; -
(ii)
 $\boldsymbol{l}$
is a quasi-parabolic structure consisting of filtrationsfor every
$\boldsymbol{l}$
is a quasi-parabolic structure consisting of filtrationsfor every \begin{align*}E|_{x_i}\,=\,l^{(i)}_0\,\supsetneq \, l^{(i)}_1\,\supsetneq \,\cdots \,\supsetneq \, l^{(i)}_{r-1}\,\supsetneq \, l^{(i)}_r\,=\,0\end{align*}
\begin{align*}E|_{x_i}\,=\,l^{(i)}_0\,\supsetneq \, l^{(i)}_1\,\supsetneq \,\cdots \,\supsetneq \, l^{(i)}_{r-1}\,\supsetneq \, l^{(i)}_r\,=\,0\end{align*}
 $x_i\,\in \, D$
;
$x_i\,\in \, D$
;
-
(iii)
 $E_0$
is
$E_0$
is
 $n_0$
-regular.
$n_0$
-regular.
By virtue of Lemma 5.4, there is a scheme
![]() $Z$
of finite type over
$Z$
of finite type over
![]() $\textrm {Spec}\, k$
and a flat family
$\textrm {Spec}\, k$
and a flat family
![]() $(\widetilde {E},\,\widetilde {\boldsymbol{l}})$
of quasi-parabolic bundles on
$(\widetilde {E},\,\widetilde {\boldsymbol{l}})$
of quasi-parabolic bundles on
![]() $X\times Z$
over
$X\times Z$
over
![]() $Z$
such that every member
$Z$
such that every member
![]() $(E,\,\boldsymbol{l})\,\in \, {\mathcal N}^{n_0\textrm { -reg}}_{{\rm par}}(L)$
is isomorphic to
$(E,\,\boldsymbol{l})\,\in \, {\mathcal N}^{n_0\textrm { -reg}}_{{\rm par}}(L)$
is isomorphic to
![]() $(\widetilde {E},\,\widetilde {\boldsymbol{l}})|_{X\times \{p\}}$
for some point
$(\widetilde {E},\,\widetilde {\boldsymbol{l}})|_{X\times \{p\}}$
for some point
![]() $p\,\in \, S$
. Consider the subset
$p\,\in \, S$
. Consider the subset
of
![]() $|{\mathcal N}^{n_0\textrm { -reg}}_{{\rm par}}(L)|$
consisting of simple quasi-parabolic bundles, where
$|{\mathcal N}^{n_0\textrm { -reg}}_{{\rm par}}(L)|$
consisting of simple quasi-parabolic bundles, where
![]() $\textrm { End}(E,\,\boldsymbol{l})$
is defined by
$\textrm { End}(E,\,\boldsymbol{l})$
is defined by
Definition 5.8. Let,
![]() $X$
be a smooth projective curve over
$X$
be a smooth projective curve over
![]() $k$
. For a vector bundle
$k$
. For a vector bundle
![]() $E$
on
$E$
on
![]() $X$
, we set
$X$
, we set
![]() $\mu (E)\,\,:=\,\,\deg (E)/\textrm { rank}(E)$
, and call it the slope of
$\mu (E)\,\,:=\,\,\deg (E)/\textrm { rank}(E)$
, and call it the slope of
![]() $E$
.
$E$
.
We will construct a parameter space of
![]() $\left | {\mathcal N}^{n_0\textrm { -reg}}_{{\rm par}}(L) \right | \setminus \left | {\mathcal N}^{n_0\textrm { -reg}}_{{\rm par}}(L)^{\circ } \right |$
whose dimension is at most
$\left | {\mathcal N}^{n_0\textrm { -reg}}_{{\rm par}}(L) \right | \setminus \left | {\mathcal N}^{n_0\textrm { -reg}}_{{\rm par}}(L)^{\circ } \right |$
whose dimension is at most
![]() $(r^2-1)(g-1)+nr(r-1)/2-2$
. For its proof, we need the following lemma.
$(r^2-1)(g-1)+nr(r-1)/2-2$
. For its proof, we need the following lemma.
Lemma 5.9. Let
![]() $X$
be a smooth projective curve over
$X$
be a smooth projective curve over
![]() $k$
of genus
$k$
of genus
![]() $g\,\geqslant \, 2$
, and let
$g\,\geqslant \, 2$
, and let
![]() $E$
and
$E$
and
![]() $F$
be semistable vector bundles on
$F$
be semistable vector bundles on
![]() $X$
satisfying the condition
$X$
satisfying the condition
![]() $\mu (E)\,\gt \,\mu (F)$
. Then the following inequality holds:
$\mu (E)\,\gt \,\mu (F)$
. Then the following inequality holds:
Proof. By the Serre duality, we have
![]() $\dim \textrm { Ext}^1_X(F,\,E)\,=\, \dim \textrm { Hom}(E,\,F\otimes K_X)$
. Choose a general point
$\dim \textrm { Ext}^1_X(F,\,E)\,=\, \dim \textrm { Hom}(E,\,F\otimes K_X)$
. Choose a general point
![]() $x\,\in \, X$
.
$x\,\in \, X$
.
First, consider the case where
![]() $\deg (E^{\vee }\otimes F\otimes {\mathcal O}_X(x))\,\gt \,0$
. In this case, we have
$\deg (E^{\vee }\otimes F\otimes {\mathcal O}_X(x))\,\gt \,0$
. In this case, we have
![]() $\textrm { Hom}(F,\, E\otimes {\mathcal O}_X(-x))\,=\,0$
. Note that we have
$\textrm { Hom}(F,\, E\otimes {\mathcal O}_X(-x))\,=\,0$
. Note that we have
![]() $\deg (F^{\vee }\otimes E\otimes {\mathcal O}_X(-x))\,\gt \,-\textrm { rank}(E)\textrm { rank}(F)$
, because
$\deg (F^{\vee }\otimes E\otimes {\mathcal O}_X(-x))\,\gt \,-\textrm { rank}(E)\textrm { rank}(F)$
, because
![]() $\mu (E)\,\gt \,\mu (F)$
. By the Riemann–Roch theorem, we have
$\mu (E)\,\gt \,\mu (F)$
. By the Riemann–Roch theorem, we have
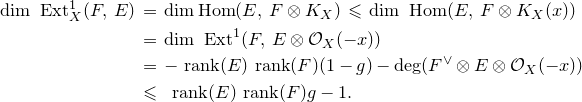 \begin{align*} \dim \textrm { Ext}^1_X(F,\,E)\, &=\, \dim \textrm {Hom}(E,\,F\otimes K_X) \,\leqslant \, \dim \textrm { Hom}(E,\,F\otimes K_X(x))\nonumber\\ &=\, \dim \textrm { Ext}^1(F,\,E\otimes {\mathcal O}_X(-x))\,\\ &=\, -\textrm { rank}(E)\textrm { rank}(F)(1-g)-\deg (F^{\vee }\otimes E\otimes {\mathcal O}_X(-x)) \nonumber\\ & \leqslant \ \textrm { rank}(E)\textrm { rank}(F)g-1. \end{align*}
\begin{align*} \dim \textrm { Ext}^1_X(F,\,E)\, &=\, \dim \textrm {Hom}(E,\,F\otimes K_X) \,\leqslant \, \dim \textrm { Hom}(E,\,F\otimes K_X(x))\nonumber\\ &=\, \dim \textrm { Ext}^1(F,\,E\otimes {\mathcal O}_X(-x))\,\\ &=\, -\textrm { rank}(E)\textrm { rank}(F)(1-g)-\deg (F^{\vee }\otimes E\otimes {\mathcal O}_X(-x)) \nonumber\\ & \leqslant \ \textrm { rank}(E)\textrm { rank}(F)g-1. \end{align*}
Second, consider the case where
![]() $\deg (E^{\vee }\otimes F\otimes {\mathcal O}_X(x))\,\lt \,0$
. Take general points
$\deg (E^{\vee }\otimes F\otimes {\mathcal O}_X(x))\,\lt \,0$
. Take general points
![]() $x_1,\,\cdots ,\,x_{2g-3}$
of
$x_1,\,\cdots ,\,x_{2g-3}$
of
![]() $X$
. Then we get exact sequences
$X$
. Then we get exact sequences
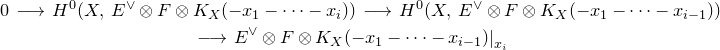 \begin{align*} 0 \,&\longrightarrow \, H^0(X,\,E^{\vee }\otimes F\otimes K_X(-x_1-\cdots -x_i)) \,\longrightarrow \, H^0(X,\,E^{\vee }\otimes F\otimes K_X(-x_1-\cdots -x_{i-1})) \\ &\qquad\qquad\qquad\qquad\qquad\longrightarrow \, E^{\vee }\otimes F\otimes K_X(-x_1-\cdots -x_{i-1})\big |_{x_i} \end{align*}
\begin{align*} 0 \,&\longrightarrow \, H^0(X,\,E^{\vee }\otimes F\otimes K_X(-x_1-\cdots -x_i)) \,\longrightarrow \, H^0(X,\,E^{\vee }\otimes F\otimes K_X(-x_1-\cdots -x_{i-1})) \\ &\qquad\qquad\qquad\qquad\qquad\longrightarrow \, E^{\vee }\otimes F\otimes K_X(-x_1-\cdots -x_{i-1})\big |_{x_i} \end{align*}
for
![]() $i\,=\,1,\,\cdots ,\,2g-3$
. Note that the condition
$i\,=\,1,\,\cdots ,\,2g-3$
. Note that the condition
![]() $\deg (E^{\vee }\otimes F(x))\,\lt \,0$
implies that
$\deg (E^{\vee }\otimes F(x))\,\lt \,0$
implies that
![]() $\mu (E)\,\gt \,\mu (F\otimes K_X(-x_1-\cdots -x_{2g-3}))$
, which yields
$\mu (E)\,\gt \,\mu (F\otimes K_X(-x_1-\cdots -x_{2g-3}))$
, which yields
because
![]() $E$
and
$E$
and
![]() $F$
are semistable. So we have
$F$
are semistable. So we have
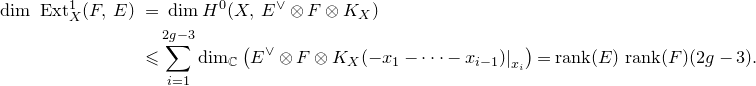 \begin{align*} \dim \textrm { Ext}^1_X(F,\,E) \ &=\ \dim H^0(X,\,E^{\vee }\otimes F\otimes K_X) \\& \leqslant \sum _{i=1}^{2g-3} \dim _{\mathbb{C}} \left (E^{\vee }\otimes F\otimes K_X(-x_1-\cdots -x_{i-1})\big |_{x_i}\right ) = \textrm {rank}(E)\textrm { rank}(F)(2g-3). \end{align*}
\begin{align*} \dim \textrm { Ext}^1_X(F,\,E) \ &=\ \dim H^0(X,\,E^{\vee }\otimes F\otimes K_X) \\& \leqslant \sum _{i=1}^{2g-3} \dim _{\mathbb{C}} \left (E^{\vee }\otimes F\otimes K_X(-x_1-\cdots -x_{i-1})\big |_{x_i}\right ) = \textrm {rank}(E)\textrm { rank}(F)(2g-3). \end{align*}
Consider the remaining case where
![]() $\deg ( E^{\vee }\otimes F(t))\,=\,0$
. Take general points
$\deg ( E^{\vee }\otimes F(t))\,=\,0$
. Take general points
![]() $x_1,\,\cdots ,\,x_{2g-3}\,\in \, X$
. Then we have
$x_1,\,\cdots ,\,x_{2g-3}\,\in \, X$
. Then we have
![]() $\mu (E)\,=\,\mu (F\otimes K_X(-x_1-\cdots -x_{2g-3}))$
. We can write
$\mu (E)\,=\,\mu (F\otimes K_X(-x_1-\cdots -x_{2g-3}))$
. We can write
![]() ${\rm gr}(E)\,=\,\bigoplus _i E_i$
and
${\rm gr}(E)\,=\,\bigoplus _i E_i$
and
![]() ${\rm gr}(F)\,=\,\bigoplus _jF_j$
for stable vector bundles
${\rm gr}(F)\,=\,\bigoplus _jF_j$
for stable vector bundles
![]() $E_i$
and
$E_i$
and
![]() $F_j$
such that
$F_j$
such that
![]() $\mu (E_i)\,=\,\mu (E)\,=\,\mu (F)\,=\,\mu (F_j)$
for any
$\mu (E_i)\,=\,\mu (E)\,=\,\mu (F)\,=\,\mu (F_j)$
for any
![]() $i,\,j$
. If we take
$i,\,j$
. If we take
![]() $x_1,\,\cdots ,\,x_{2g-3}$
sufficiently generic, then we may assume
$x_1,\,\cdots ,\,x_{2g-3}$
sufficiently generic, then we may assume
![]() $E_i\,\not \cong \, F_j\otimes K_X(-x_1-\cdots -x_{2g-3})$
for any
$E_i\,\not \cong \, F_j\otimes K_X(-x_1-\cdots -x_{2g-3})$
for any
![]() $i,\,j$
. Then we have
$i,\,j$
. Then we have
![]() $\textrm { Hom}(E,\,F\otimes K_X(-x_1-\cdots -x_{2g-3}))\,=\,0$
. By the same argument as before, we have the inequality
$\textrm { Hom}(E,\,F\otimes K_X(-x_1-\cdots -x_{2g-3}))\,=\,0$
. By the same argument as before, we have the inequality
![]() $\dim \textrm { Ext}^1_X(E,F)\,\leqslant \, \textrm { rank}(E)\textrm { rank}(F)(2g-3)$
.
$\dim \textrm { Ext}^1_X(E,F)\,\leqslant \, \textrm { rank}(E)\textrm { rank}(F)(2g-3)$
.
Proposition 5.10. Let
![]() $X$
be a smooth projective curve over
$X$
be a smooth projective curve over
![]() $k$
of genus
$k$
of genus
![]() $g\,\geqslant \, 2$
, and let
$g\,\geqslant \, 2$
, and let
![]() $L$
be a line bundle of degree
$L$
be a line bundle of degree
![]() $d$
on
$d$
on
![]() $X$
. Assume that the integers
$X$
. Assume that the integers
![]() $r$
and
$r$
and
![]() $n$
satisfy the conditions
$n$
satisfy the conditions
![]() $r\,\geqslant \, 2$
and
$r\,\geqslant \, 2$
and
![]() $n\,\geqslant \, 1$
. Then there exists a scheme
$n\,\geqslant \, 1$
. Then there exists a scheme
![]() $Z$
of finite type over
$Z$
of finite type over
![]() $\textrm { Spec}\, k$
and a flat family
$\textrm { Spec}\, k$
and a flat family
![]() $(\mathcal{E},\,\ell )$
of quasi-parabolic bundles on
$(\mathcal{E},\,\ell )$
of quasi-parabolic bundles on
![]() $X\times Z$
over
$X\times Z$
over
![]() $Z$
such that:
$Z$
such that:
-
(a)
 $\dim Z \,\,\leqslant \,\, (r^2-1)(g-1)+r(r-1)n/2-2$
;
$\dim Z \,\,\leqslant \,\, (r^2-1)(g-1)+r(r-1)n/2-2$
; -
(b)
 $\dim \textrm {End}\left ((\mathcal{E},\ell )\big \vert _{X\times \{z\}}\right )\,\,\geqslant \,\, 2$
for any
$\dim \textrm {End}\left ((\mathcal{E},\ell )\big \vert _{X\times \{z\}}\right )\,\,\geqslant \,\, 2$
for any
 $z\,\in \, Z$
;
$z\,\in \, Z$
;
and each member of the complement
![]() $\left | {\mathcal N}^{n_0\textrm { -reg}}_{{\rm par}}(L) \right | \setminus \left | {\mathcal N}^{n_0\textrm { -reg}}_{{\rm par}}(L)^{\circ } \right |$
is isomorphic to
$\left | {\mathcal N}^{n_0\textrm { -reg}}_{{\rm par}}(L) \right | \setminus \left | {\mathcal N}^{n_0\textrm { -reg}}_{{\rm par}}(L)^{\circ } \right |$
is isomorphic to
![]() $(\mathcal{E},\,\ell )|_{X\times \{z\}}$
for some point
$(\mathcal{E},\,\ell )|_{X\times \{z\}}$
for some point
![]() $z\,\in \, Z$
.
$z\,\in \, Z$
.
Proof. Take a quasi-parabolic bundle
![]() $(E,\,\boldsymbol{l})$
on
$(E,\,\boldsymbol{l})$
on
![]() $(X,\,D)$
with
$(X,\,D)$
with
![]() $\det E\, \cong \, L$
. Choose a point
$\det E\, \cong \, L$
. Choose a point
![]() $x_i\,\in \, D$
and
$x_i\,\in \, D$
and
![]() $l^{(i)}_j\,\subset \, E|_{x_i}$
. Then
$l^{(i)}_j\,\subset \, E|_{x_i}$
. Then
![]() $E'\,\,:=\,\,\ker (E\,\rightarrow \, E|_{x_i}/l^{(i)}_j)$
has a canonical quasi-parabolic structure
$E'\,\,:=\,\,\ker (E\,\rightarrow \, E|_{x_i}/l^{(i)}_j)$
has a canonical quasi-parabolic structure
![]() $\boldsymbol{l'}$
induced by
$\boldsymbol{l'}$
induced by
![]() $\boldsymbol{l}$
. The correspondence
$\boldsymbol{l}$
. The correspondence
![]() $(E,\,\boldsymbol{l})\,\longmapsto \, (E',\,\boldsymbol{l'})$
gives a bijection between the set of isomorphism classes of quasi-parabolic bundles; it is called an elementary transformation or a Hecke modification. After applying a finite number of elementary transformations, it may be assumed that
$(E,\,\boldsymbol{l})\,\longmapsto \, (E',\,\boldsymbol{l'})$
gives a bijection between the set of isomorphism classes of quasi-parabolic bundles; it is called an elementary transformation or a Hecke modification. After applying a finite number of elementary transformations, it may be assumed that
![]() $r$
and
$r$
and
![]() $d$
are coprime.
$d$
are coprime.
Take a member
![]() $(E,\,\boldsymbol{l})\,\in \, |{\mathcal N}^{n_0\textrm { -reg}}_{{\rm par}}(L)| \setminus |{\mathcal N}^{n_0\textrm { -reg}}_{{\rm par}}(L)^{\circ }|$
. Since
$(E,\,\boldsymbol{l})\,\in \, |{\mathcal N}^{n_0\textrm { -reg}}_{{\rm par}}(L)| \setminus |{\mathcal N}^{n_0\textrm { -reg}}_{{\rm par}}(L)^{\circ }|$
. Since
![]() $\dim \textrm { End}(E,\,\boldsymbol{l})\,\gt \,1$
by the definition, we have
$\dim \textrm { End}(E,\,\boldsymbol{l})\,\gt \,1$
by the definition, we have
![]() $\dim \textrm { End}(E)\,\gt \,1$
and
$\dim \textrm { End}(E)\,\gt \,1$
and
![]() $E$
is not a semistable vector bundle. Let
$E$
is not a semistable vector bundle. Let
be the Harder–Narasimhan filtration of
![]() $E$
; note that
$E$
; note that
![]() $m\,\geqslant \, 2$
because
$m\,\geqslant \, 2$
because
![]() $E$
is not semistable. Set
$E$
is not semistable. Set
![]() $\overline {E}_1\,\,:=\,\,E_1$
,
$\overline {E}_1\,\,:=\,\,E_1$
,
![]() $\overline {E}_s\,\,:=\,\,E_s/E_{s-1}$
for
$\overline {E}_s\,\,:=\,\,E_s/E_{s-1}$
for
![]() $s\,\geqslant \, 2$
and
$s\,\geqslant \, 2$
and
![]() $r_s\,\,:=\,\,\textrm { rank}\,\overline {E}_s$
. By the definition of a Harder–Narasimhan filtration, each
$r_s\,\,:=\,\,\textrm { rank}\,\overline {E}_s$
. By the definition of a Harder–Narasimhan filtration, each
![]() $\overline {E}_s$
is semistable for
$\overline {E}_s$
is semistable for
![]() $1\,\leqslant \, s\,\leqslant \, m$
and the inequalities
$1\,\leqslant \, s\,\leqslant \, m$
and the inequalities
![]() $\mu (\overline {E}_1)\,\gt \,\mu (\overline {E}_2)\,\gt \,\cdots \,\gt \,\mu (\overline {E}_m)$
hold. Each semistable vector bundle
$\mu (\overline {E}_1)\,\gt \,\mu (\overline {E}_2)\,\gt \,\cdots \,\gt \,\mu (\overline {E}_m)$
hold. Each semistable vector bundle
![]() $\overline {E}_s$
has a Jordan–Hölder filtration
$\overline {E}_s$
has a Jordan–Hölder filtration
with
![]() $\gamma _s\,\geqslant \,1$
. Set
$\gamma _s\,\geqslant \,1$
. Set
![]() $\overline {E}^{(1)}_s\,\,:=\,\,E^{(1)}_s$
,
$\overline {E}^{(1)}_s\,\,:=\,\,E^{(1)}_s$
,
![]() $\overline {E}^{(i)}_s\,\,:=\, \,E^{(i)}_s/E^{(i-1)}_s$
for
$\overline {E}^{(i)}_s\,\,:=\, \,E^{(i)}_s/E^{(i-1)}_s$
for
![]() $2\,\leqslant \, i\,\leqslant \,\gamma _s$
,
$2\,\leqslant \, i\,\leqslant \,\gamma _s$
,
![]() $r^{(i)}_s\,\,:=\,\,\textrm { rank}\overline {E}^{(i)}_s$
and
$r^{(i)}_s\,\,:=\,\,\textrm { rank}\overline {E}^{(i)}_s$
and
![]() $d^{(i)}_s\,\,:=\,\,\deg \overline {E}^{(i)}_s$
. Then, each
$d^{(i)}_s\,\,:=\,\,\deg \overline {E}^{(i)}_s$
. Then, each
![]() $\overline {E}^{(i)}_s$
is a stable bundle on
$\overline {E}^{(i)}_s$
is a stable bundle on
![]() $X$
and
$X$
and
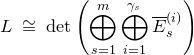 \begin{align*} L \ \cong \ \det \left (\bigoplus _{s=1}^m \bigoplus _{i=1}^{\gamma _s} \overline {E}^{(i)}_s\right ) \end{align*}
\begin{align*} L \ \cong \ \det \left (\bigoplus _{s=1}^m \bigoplus _{i=1}^{\gamma _s} \overline {E}^{(i)}_s\right ) \end{align*}
holds.
Let us consider the converse. If stable bundles
![]() $\{\overline {E}^{(i)}_s\}$
are given,
$\{\overline {E}^{(i)}_s\}$
are given,
![]() $\{\overline {E}_s\}$
are given by successive extensions
$\{\overline {E}_s\}$
are given by successive extensions
with
![]() $E^{(\gamma _s)}_s\,=\,\overline {E}_s$
. If
$E^{(\gamma _s)}_s\,=\,\overline {E}_s$
. If
![]() $\{\overline {E}_s\}$
are given, then
$\{\overline {E}_s\}$
are given, then
![]() $E$
is given by successive extensions
$E$
is given by successive extensions
with
![]() $E_m\,=\,E$
. By its definition,
$E_m\,=\,E$
. By its definition,
![]() $\boldsymbol{l}$
is given by a filtration
$\boldsymbol{l}$
is given by a filtration
![]() $E\big \vert _{x_i}\,=\,l^{(i)}_0\,\supset \, l^{(i)}_1\,\supset \,\cdots \,\supset \, l^{(i)}_{r-1}\,\supset \, l^{(i)}_r\,=\,0$
for each
$E\big \vert _{x_i}\,=\,l^{(i)}_0\,\supset \, l^{(i)}_1\,\supset \,\cdots \,\supset \, l^{(i)}_{r-1}\,\supset \, l^{(i)}_r\,=\,0$
for each
![]() $1\,\leqslant \, i\,\leqslant \, n$
.
$1\,\leqslant \, i\,\leqslant \, n$
.
We will construct a parameter space of the above data, but we avoid the case of
![]() $m\,=\,2$
and
$m\,=\,2$
and
![]() $\gamma _1\,=\,\gamma _2\,=\,1$
and postpone its proof until later. This is because this case needs an extra argument.
$\gamma _1\,=\,\gamma _2\,=\,1$
and postpone its proof until later. This is because this case needs an extra argument.
Excluding the case where
![]() $m\,=\,2$
and
$m\,=\,2$
and
![]() $\gamma _1\,=\,\gamma _2\,=\,1$
, we first construct the parameter space of the above data with the further restricted conditions:
$\gamma _1\,=\,\gamma _2\,=\,1$
, we first construct the parameter space of the above data with the further restricted conditions:
-
(a)
 $\overline {E}^{(i)}_s\,\not \cong \, \overline {E}^{(j)}_s$
for
$\overline {E}^{(i)}_s\,\not \cong \, \overline {E}^{(j)}_s$
for
 $i\,\neq \, j$
;
$i\,\neq \, j$
;
Set
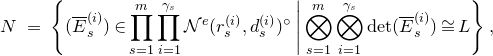 \begin{align*} N\ =\ \left \{ (\overline {E}^{(i)}_s) \in \prod _{s=1}^m \prod _{i=1}^{\gamma _s} {\mathcal N}^e (r^{(i)}_s,d^{(i)}_s)^{\circ } \,\middle |\, \bigotimes _{s=1}^m\bigotimes _{i=1}^{\gamma _s} \det (\overline {E}^{(i)}_s) \cong L \right \}, \end{align*}
\begin{align*} N\ =\ \left \{ (\overline {E}^{(i)}_s) \in \prod _{s=1}^m \prod _{i=1}^{\gamma _s} {\mathcal N}^e (r^{(i)}_s,d^{(i)}_s)^{\circ } \,\middle |\, \bigotimes _{s=1}^m\bigotimes _{i=1}^{\gamma _s} \det (\overline {E}^{(i)}_s) \cong L \right \}, \end{align*}
where
![]() ${\mathcal N}^e (r^{(i)}_s, d^{(i)}_s)^{\circ }$
is the moduli space of stable vector bundles on
${\mathcal N}^e (r^{(i)}_s, d^{(i)}_s)^{\circ }$
is the moduli space of stable vector bundles on
![]() $X$
of rank
$X$
of rank
![]() $r^{(i)}_s$
and of degree
$r^{(i)}_s$
and of degree
![]() $d^{(i)}_s$
. Since
$d^{(i)}_s$
. Since
![]() $\dim {\mathcal N}^e (r^{(i)}_s, d^{(i)}_s)^{\circ } \,=\,(r^{(i)}_s)^2(g-1)+1$
, we have
$\dim {\mathcal N}^e (r^{(i)}_s, d^{(i)}_s)^{\circ } \,=\,(r^{(i)}_s)^2(g-1)+1$
, we have
![]() $\dim N\,=\,\sum _{s=1}^m \sum _{i=1}^{\gamma _s} \big ( (r^{(i)}_s)^2(g-1)+1\big ) -g$
. Take a quasi-finite covering
$\dim N\,=\,\sum _{s=1}^m \sum _{i=1}^{\gamma _s} \big ( (r^{(i)}_s)^2(g-1)+1\big ) -g$
. Take a quasi-finite covering
![]() $N'\,\longrightarrow \, N$
whose image consists of those points such that
$N'\,\longrightarrow \, N$
whose image consists of those points such that
![]() $\overline {E}^{(i)}_s\,\not \cong \,\overline {E}^{(i')}_{s'}$
for
$\overline {E}^{(i)}_s\,\not \cong \,\overline {E}^{(i')}_{s'}$
for
![]() $(i,\,s)\,\neq \,(i',\,s')$
. We may take a universal family of vector bundles
$(i,\,s)\,\neq \,(i',\,s')$
. We may take a universal family of vector bundles
![]() $\{\overline {\mathcal E}^{(i)}_s\}^{1\leqslant i\leqslant \gamma _s}_{1\leqslant s\leqslant m}$
on
$\{\overline {\mathcal E}^{(i)}_s\}^{1\leqslant i\leqslant \gamma _s}_{1\leqslant s\leqslant m}$
on
![]() $X\times N'$
over
$X\times N'$
over
![]() $N'$
such that
$N'$
such that
![]() $\bigotimes _{s=1}^m\bigotimes _{i=1}^{\gamma _s} \det \big ( \overline {\mathcal E}^{(i)}_s \big ) \,\cong \, L\otimes {\mathcal L'}$
for some line bundle
$\bigotimes _{s=1}^m\bigotimes _{i=1}^{\gamma _s} \det \big ( \overline {\mathcal E}^{(i)}_s \big ) \,\cong \, L\otimes {\mathcal L'}$
for some line bundle
![]() $\mathcal L'$
on
$\mathcal L'$
on
![]() $N'$
. After replacing
$N'$
. After replacing
![]() $N'$
with a disjoint union of locally closed subsets, we may further assume that:
$N'$
with a disjoint union of locally closed subsets, we may further assume that:
-
(1) the relative
 $\textrm { Ext}$
-sheaves
$\textrm { Ext}$
-sheaves
 $\textrm { Ext}^p_{X\times N'/N'} \big ( \overline {\mathcal E}^{(i)}_s ,\, \overline {\mathcal E}^{(j)}_s \big )$
are locally free sheaves on
$\textrm { Ext}^p_{X\times N'/N'} \big ( \overline {\mathcal E}^{(i)}_s ,\, \overline {\mathcal E}^{(j)}_s \big )$
are locally free sheaves on
 $N'$
for
$N'$
for
 $1\,\leqslant \, s\,\leqslant \, m$
,
$1\,\leqslant \, s\,\leqslant \, m$
,
 $p\,=\,0,\,1$
and any
$p\,=\,0,\,1$
and any
 $j\,\lt \,i$
;
$j\,\lt \,i$
; -
(2) the canonical maps
 $\textrm { Ext}^p_{X\times N'/N'} \big ( \overline {\mathcal E}^{(i)}_s ,\, \overline {\mathcal E}^{(j)}_s \big )\big |_z \,\longrightarrow \, \textrm { Ext}^p_{X\times \{z\}}\big ( \overline {\mathcal E}^{(i)}_s|_{X\times \{z\}} , \, \overline {\mathcal E}^{(j)}_s|_{X\times \{z\}} \big )$
are isomorphisms for all points
$\textrm { Ext}^p_{X\times N'/N'} \big ( \overline {\mathcal E}^{(i)}_s ,\, \overline {\mathcal E}^{(j)}_s \big )\big |_z \,\longrightarrow \, \textrm { Ext}^p_{X\times \{z\}}\big ( \overline {\mathcal E}^{(i)}_s|_{X\times \{z\}} , \, \overline {\mathcal E}^{(j)}_s|_{X\times \{z\}} \big )$
are isomorphisms for all points
 $z\in N'$
.
$z\in N'$
.
Set
for every
![]() $1\,\leqslant \, s\,\leqslant \, m$
, where
$1\,\leqslant \, s\,\leqslant \, m$
, where
![]() ${\rm Sym}\left (\textrm { Ext}^1_{X\times N'/N'} \big ( \overline {\mathcal E}^{(2)}_s ,\, \overline {\mathcal E}^{(1)}_s \big )^{\vee }\right )$
is the symmetric algebra of
${\rm Sym}\left (\textrm { Ext}^1_{X\times N'/N'} \big ( \overline {\mathcal E}^{(2)}_s ,\, \overline {\mathcal E}^{(1)}_s \big )^{\vee }\right )$
is the symmetric algebra of
![]() $\textrm { Ext}^1_{X\times N'/N'} \big ( \overline {\mathcal E}^{(2)}_s ,\, \overline {\mathcal E}^{(1)}_s \big )^{\vee }$
over
$\textrm { Ext}^1_{X\times N'/N'} \big ( \overline {\mathcal E}^{(2)}_s ,\, \overline {\mathcal E}^{(1)}_s \big )^{\vee }$
over
![]() ${\mathcal O}_{N'}$
. Then there is a universal extension
${\mathcal O}_{N'}$
. Then there is a universal extension
on
![]() $X\times P^{(2)}_s$
. Once
$X\times P^{(2)}_s$
. Once
![]() $P^{(2)}_s,\ldots ,P^{(i)}_s$
and
$P^{(2)}_s,\ldots ,P^{(i)}_s$
and
![]() ${\mathcal E}^{(2)}_s,\,\ldots ,\,{\mathcal E}^{(i)}_s$
are defined, we set
${\mathcal E}^{(2)}_s,\,\ldots ,\,{\mathcal E}^{(i)}_s$
are defined, we set
There is a universal extension
on
![]() $X\times P^{(i+1)}_s$
. Set
$X\times P^{(i+1)}_s$
. Set
![]() $P_s\,\,:=\,\,P^{(\gamma _s)}_s$
for
$P_s\,\,:=\,\,P^{(\gamma _s)}_s$
for
![]() $1\,\leqslant \, s\,\leqslant \, m$
,
$1\,\leqslant \, s\,\leqslant \, m$
,
![]() $P\,\,:=\,\, P_1\times _{N'}\times \cdots \times _{N'} P_m$
and
$P\,\,:=\,\, P_1\times _{N'}\times \cdots \times _{N'} P_m$
and
![]() $\overline {\mathcal E}_s\,\,:=\,\,{\mathcal E}^{(\gamma _s)}_s\otimes _{O_{P_s}}{\mathcal O}_P$
. After replacing
$\overline {\mathcal E}_s\,\,:=\,\,{\mathcal E}^{(\gamma _s)}_s\otimes _{O_{P_s}}{\mathcal O}_P$
. After replacing
![]() $P$
with a disjoint union of locally closed subsets, we may assume that:
$P$
with a disjoint union of locally closed subsets, we may assume that:
the relative
 $\textrm { Ext}$
-sheaves
$\textrm { Ext}$
-sheaves
 $\textrm { Ext}^p_{X\times P/P} \big ( \overline {\mathcal E}_s,\,\overline {\mathcal E}_{s'}\big )$
are all locally free sheaves on
$\textrm { Ext}^p_{X\times P/P} \big ( \overline {\mathcal E}_s,\,\overline {\mathcal E}_{s'}\big )$
are all locally free sheaves on
 $P$
for
$P$
for
 $p\,=\,0,\,1$
and
$p\,=\,0,\,1$
and
 $s'\,\lt \,s$
;
$s'\,\lt \,s$
;the canonical homomorphisms
 $\textrm { Ext}^p_{X\times P/P} \big ( \overline {\mathcal E}_s,\,\overline {\mathcal E}_{s'}\big )\big |_z \,\longrightarrow \,\textrm { Ext}^p_{X\times P/P} \big ( \overline {\mathcal E}_s\big |_{X\times \{z\}},\, \overline {\mathcal E}_{s'}\big |_{X\times \{z\}}\big )$
are isomorphisms for all points
$\textrm { Ext}^p_{X\times P/P} \big ( \overline {\mathcal E}_s,\,\overline {\mathcal E}_{s'}\big )\big |_z \,\longrightarrow \,\textrm { Ext}^p_{X\times P/P} \big ( \overline {\mathcal E}_s\big |_{X\times \{z\}},\, \overline {\mathcal E}_{s'}\big |_{X\times \{z\}}\big )$
are isomorphisms for all points
 $z\,\in \, P$
.
$z\,\in \, P$
.
Set
Then there is a universal extension
![]() $0\,\longrightarrow \, \overline {\mathcal E}_1 \,\longrightarrow \, {\mathcal E}_2 \,\longrightarrow \, \overline {\mathcal E}_2 \otimes {\mathcal O}_{Q_2}(1) \, \longrightarrow \, 0$
on
$0\,\longrightarrow \, \overline {\mathcal E}_1 \,\longrightarrow \, {\mathcal E}_2 \,\longrightarrow \, \overline {\mathcal E}_2 \otimes {\mathcal O}_{Q_2}(1) \, \longrightarrow \, 0$
on
![]() $X\times Q_2$
. Once
$X\times Q_2$
. Once
![]() $Q_2,\,\cdots ,\, Q_s$
and
$Q_2,\,\cdots ,\, Q_s$
and
![]() ${\mathcal E}_2,\,\cdots ,\, {\mathcal E}_s$
are defined, set
${\mathcal E}_2,\,\cdots ,\, {\mathcal E}_s$
are defined, set
Then there are universal extensions
![]() $0\,\longrightarrow \, {\mathcal E}_s \,\longrightarrow \,{\mathcal E}_{s+1} \, \longrightarrow \, \overline {\mathcal E}_{s+1} \otimes {\mathcal O}_{Q_{s+1}}(1) \, \longrightarrow \, 0$
for
$0\,\longrightarrow \, {\mathcal E}_s \,\longrightarrow \,{\mathcal E}_{s+1} \, \longrightarrow \, \overline {\mathcal E}_{s+1} \otimes {\mathcal O}_{Q_{s+1}}(1) \, \longrightarrow \, 0$
for
![]() $1\,\leqslant \, s\,\leqslant \, m-1$
. Set
$1\,\leqslant \, s\,\leqslant \, m-1$
. Set
Let
![]() $Y_Q$
be the flag bundle over
$Y_Q$
be the flag bundle over
![]() $Q$
whose fiber over any
$Q$
whose fiber over any
![]() $q\,\in \, Q$
is the parameter space of the filtrations
$q\,\in \, Q$
is the parameter space of the filtrations
Then there is a universal family of filtrations
![]() $\ell$
so that
$\ell$
so that
![]() $({\mathcal E},\,\ell )$
becomes a flat family of quasi-parabolic bundles on
$({\mathcal E},\,\ell )$
becomes a flat family of quasi-parabolic bundles on
![]() $X\times Y_Q$
over
$X\times Y_Q$
over
![]() $Y_Q$
. Let
$Y_Q$
. Let
![]() $Z_Q$
be the reduced closed subscheme of
$Z_Q$
be the reduced closed subscheme of
![]() $Y_Q$
consisting of the points
$Y_Q$
consisting of the points
![]() $y$
such that
$y$
such that
![]() $\dim \textrm { End}\left ( ({\mathcal E} ,\,\ell ) |_{X\times y}\right )\,\geqslant \, 2$
.
$\dim \textrm { End}\left ( ({\mathcal E} ,\,\ell ) |_{X\times y}\right )\,\geqslant \, 2$
.
We want to prove that the dimension of
![]() $Z_Q$
is at most
$Z_Q$
is at most
![]() $(r^2-1)(g-1)+nr(r-1)/2-2$
. Recall that
$(r^2-1)(g-1)+nr(r-1)/2-2$
. Recall that
![]() $\dim N'\,=\,-g+\sum _{s=1}^m \sum _{i=1}^{\gamma _s} \big ( (r^{(i)}_s)^2(g-1)+1\big )$
. Since there are exact sequences
$\dim N'\,=\,-g+\sum _{s=1}^m \sum _{i=1}^{\gamma _s} \big ( (r^{(i)}_s)^2(g-1)+1\big )$
. Since there are exact sequences
for
![]() $1\,\leqslant \, j\,\lt \,i$
, the dimension of
$1\,\leqslant \, j\,\lt \,i$
, the dimension of
![]() $\mathbb{P}_* (\textrm {Ext}^1(\overline {E}^{(i)}_s ,\, E^{(i-1)}_s))$
is at most
$\mathbb{P}_* (\textrm {Ext}^1(\overline {E}^{(i)}_s ,\, E^{(i-1)}_s))$
is at most
![]() $ -1+\sum _{j\lt i} \dim \textrm { Ext}^1(\overline {E}^{(i)}_s,\,\overline {E}^{(j)}_s)$
. Furthermore, the Riemann–Roch theorem implies that
$ -1+\sum _{j\lt i} \dim \textrm { Ext}^1(\overline {E}^{(i)}_s,\,\overline {E}^{(j)}_s)$
. Furthermore, the Riemann–Roch theorem implies that
![]() $\dim \textrm { Ext}^1(\overline {E}^{(i)}_s,\,\overline {E}^{(j)}_s)\,=\, r^{(i)}_s r^{(j)}_s(g-1)$
, because
$\dim \textrm { Ext}^1(\overline {E}^{(i)}_s,\,\overline {E}^{(j)}_s)\,=\, r^{(i)}_s r^{(j)}_s(g-1)$
, because
![]() $\overline {E}^{(i)}_s$
and
$\overline {E}^{(i)}_s$
and
![]() $\overline {E}^{(j)}_s$
are stable vector bundles of the same slope and
$\overline {E}^{(j)}_s$
are stable vector bundles of the same slope and
![]() $E^{(i)}_s\,\not \cong \, E^{(j)}_s$
. Therefore, the dimension of the fibers of
$E^{(i)}_s\,\not \cong \, E^{(j)}_s$
. Therefore, the dimension of the fibers of
![]() $P^{(i+1)}_s\,=\, \mathbb{P}_*\textrm { Ext}^1_{X\times _{N'} P^{(i)}_s/P^{(i)}_s} \big ( \overline {\mathcal E}^{(i+1)}_s ,\, {\mathcal E}^{(i)}_s \big )$
over
$P^{(i+1)}_s\,=\, \mathbb{P}_*\textrm { Ext}^1_{X\times _{N'} P^{(i)}_s/P^{(i)}_s} \big ( \overline {\mathcal E}^{(i+1)}_s ,\, {\mathcal E}^{(i)}_s \big )$
over
![]() $P^{(i)}_s$
is at most
$P^{(i)}_s$
is at most
![]() $-1+\sum _{j=1}^{i-1} r^{(i)}_s r^{(j)}_s (g-1)$
, which implies that the dimension of the fibers of
$-1+\sum _{j=1}^{i-1} r^{(i)}_s r^{(j)}_s (g-1)$
, which implies that the dimension of the fibers of
![]() $P_s\,=\,P^{(\gamma _s)}_s$
over
$P_s\,=\,P^{(\gamma _s)}_s$
over
![]() $N'$
is at most
$N'$
is at most
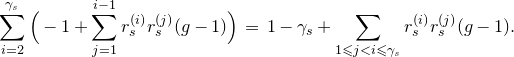 \begin{align} \sum _{i=2}^{\gamma _s} \Big ( -1 +\sum _{j=1}^{i-1} r^{(i)}_s r^{(j)}_s (g-1) \Big ) \, =\, 1-\gamma _s+ \sum _{1\leqslant j\lt i\leqslant \gamma _s} r^{(i)}_s r^{(j)}_s(g-1). \end{align}
\begin{align} \sum _{i=2}^{\gamma _s} \Big ( -1 +\sum _{j=1}^{i-1} r^{(i)}_s r^{(j)}_s (g-1) \Big ) \, =\, 1-\gamma _s+ \sum _{1\leqslant j\lt i\leqslant \gamma _s} r^{(i)}_s r^{(j)}_s(g-1). \end{align}
Since the extensions in (5.4) do not split, we can see, by an argument similar to the above, that the dimension of the fibers of
![]() $Q$
over
$Q$
over
![]() $P_1\times _{N'}\times \cdots \times _{N'} P_m$
is at most
$P_1\times _{N'}\times \cdots \times _{N'} P_m$
is at most
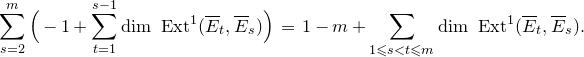 \begin{align} \sum _{s=2}^m \Big ( -1+\sum _{t=1}^{s-1} \dim \textrm { Ext}^1(\overline {E}_t, \overline {E}_s) \Big ) \,=\, 1-m+\sum _{1\leqslant s\lt t\leqslant m} \dim \textrm { Ext}^1(\overline {E}_t, \overline {E}_s). \end{align}
\begin{align} \sum _{s=2}^m \Big ( -1+\sum _{t=1}^{s-1} \dim \textrm { Ext}^1(\overline {E}_t, \overline {E}_s) \Big ) \,=\, 1-m+\sum _{1\leqslant s\lt t\leqslant m} \dim \textrm { Ext}^1(\overline {E}_t, \overline {E}_s). \end{align}
By Lemma 5.9, we have the inequality
Using the equality
![]() $r_s\,=\,r^{(1)}_s+\cdots +r^{(\gamma _s)}_s$
we get the following:
$r_s\,=\,r^{(1)}_s+\cdots +r^{(\gamma _s)}_s$
we get the following:
 \begin{align} \begin{split} &\dim Q \: \:\leqslant \: -g+\sum _{s=1}^m \sum _{i=1}^{\gamma _s} \big ( (r^{(i)}_s)^2(g-1)+1\big ) +\sum _{s=1}^m \Big (1-\gamma _s +\sum _{1\leqslant j\lt i \leqslant \gamma _s} r^{(i)}_sr^{(j)}_s(g-1) \Big ) \\ &\qquad+1-m+\sum _{1\leqslant s\lt t\leqslant m} (2r_s r_t (g-1)-1) \\ &\quad\leqslant \,\, -g+m+\sum _{s=1}^m (r^{(1)}_s+\cdots +r^{(\gamma _s)}_s)^2(g-1) -\sum _{s=1}^m (\gamma _s-1) \\ &\qquad+1-m+\sum _{1\leqslant s\lt t\leqslant m} 2r_s r_t (g-1) -\frac {m(m-1)}{2} \\ &\quad =\, (r^2-1)(g-1)-\frac {m(m-1)}{2} -\sum _{s=1}^m (\gamma _s-1). \end{split} \end{align}
\begin{align} \begin{split} &\dim Q \: \:\leqslant \: -g+\sum _{s=1}^m \sum _{i=1}^{\gamma _s} \big ( (r^{(i)}_s)^2(g-1)+1\big ) +\sum _{s=1}^m \Big (1-\gamma _s +\sum _{1\leqslant j\lt i \leqslant \gamma _s} r^{(i)}_sr^{(j)}_s(g-1) \Big ) \\ &\qquad+1-m+\sum _{1\leqslant s\lt t\leqslant m} (2r_s r_t (g-1)-1) \\ &\quad\leqslant \,\, -g+m+\sum _{s=1}^m (r^{(1)}_s+\cdots +r^{(\gamma _s)}_s)^2(g-1) -\sum _{s=1}^m (\gamma _s-1) \\ &\qquad+1-m+\sum _{1\leqslant s\lt t\leqslant m} 2r_s r_t (g-1) -\frac {m(m-1)}{2} \\ &\quad =\, (r^2-1)(g-1)-\frac {m(m-1)}{2} -\sum _{s=1}^m (\gamma _s-1). \end{split} \end{align}
Taking into account the condition
![]() $m\,\geqslant \, 2$
, we have
$m\,\geqslant \, 2$
, we have
![]() $\dim Q\,\leqslant \, (r^2-1)(g-1)-2$
, because we avoid the case where
$\dim Q\,\leqslant \, (r^2-1)(g-1)-2$
, because we avoid the case where
![]() $m\,=\,2$
and
$m\,=\,2$
and
![]() $\gamma _1\,=\,\gamma _2\,=\,1$
. Since the dimension of the fibers of
$\gamma _1\,=\,\gamma _2\,=\,1$
. Since the dimension of the fibers of
![]() $Y_Q$
over
$Y_Q$
over
![]() $Q$
is
$Q$
is
![]() $nr(r-1)/2$
, and
$nr(r-1)/2$
, and
![]() $Z_Q$
is contained in
$Z_Q$
is contained in
![]() $Y_Q$
, we have
$Y_Q$
, we have
![]() $\dim Z_Q\,\leqslant \, \dim Q+nr(r-1)/2\,\leqslant \, (r^2-1)(g-1)+nr(r-1)/2-2$
.
$\dim Z_Q\,\leqslant \, \dim Q+nr(r-1)/2\,\leqslant \, (r^2-1)(g-1)+nr(r-1)/2-2$
.
Consider the case where one of the extensions (5.3) and (5.4) splits, while again excluding the case of
![]() $m\,=\,2$
and
$m\,=\,2$
and
![]() $\gamma _1\,=\,\gamma _2\,=\,1$
. In this case, we replace
$\gamma _1\,=\,\gamma _2\,=\,1$
. In this case, we replace
![]() $P^{(i+1)}_s\,=\,\mathbb{P}_*\textrm { Ext}^1_{X\times P^{(i)}_s/P^{(i)}_s} (\overline {\mathcal E}^{(i+1)}_s,\, {\mathcal E}^{(i)}_s )$
with
$P^{(i+1)}_s\,=\,\mathbb{P}_*\textrm { Ext}^1_{X\times P^{(i)}_s/P^{(i)}_s} (\overline {\mathcal E}^{(i+1)}_s,\, {\mathcal E}^{(i)}_s )$
with
![]() $P^{(i+1)}_s\,=\,P^{(i)}_s$
or replace
$P^{(i+1)}_s\,=\,P^{(i)}_s$
or replace
![]() $Q_{s+1}\,=\,\mathbb{P}_*\textrm { Ext}^1_{X\times Q_s/Q_s}(\overline {\mathcal E}_{s+1},\,{\mathcal E}_s)$
with
$Q_{s+1}\,=\,\mathbb{P}_*\textrm { Ext}^1_{X\times Q_s/Q_s}(\overline {\mathcal E}_{s+1},\,{\mathcal E}_s)$
with
![]() $Q_{s+1}\,=\,Q_s$
(depending on which extension splits). So, the replacement of the estimation of (5.6) does not affect the calculation in (5.7). Thus, the inequality
$Q_{s+1}\,=\,Q_s$
(depending on which extension splits). So, the replacement of the estimation of (5.6) does not affect the calculation in (5.7). Thus, the inequality
![]() $\dim Q\,\leqslant \, (r^2-1)(g-1)-2$
still holds, and we get that
$\dim Q\,\leqslant \, (r^2-1)(g-1)-2$
still holds, and we get that
![]() $\dim Z_Q\,\leqslant \, (r^2-1)(g-1)+nr(r-1)/2-2$
.
$\dim Z_Q\,\leqslant \, (r^2-1)(g-1)+nr(r-1)/2-2$
.
Next, consider the case where
![]() $\overline {E}^{(i)}_s\,\cong \, \overline {E}^{(j)}_s$
for some
$\overline {E}^{(i)}_s\,\cong \, \overline {E}^{(j)}_s$
for some
![]() $i\,\neq \, j$
. In the calculation of (5.5), we should replace
$i\,\neq \, j$
. In the calculation of (5.5), we should replace
![]() $\dim \textrm { Ext}^1_X(\overline {E}^{(i)}_s ,\, \overline {E}^{(j)}_s)\,=\,r^{(i)}_s r^{(j)}_s(g-1)$
with
$\dim \textrm { Ext}^1_X(\overline {E}^{(i)}_s ,\, \overline {E}^{(j)}_s)\,=\,r^{(i)}_s r^{(j)}_s(g-1)$
with
![]() $\dim \textrm { Ext}^1_X(\overline {E}^{(i)}_s , \,\overline {E}^{(j)}_s) \,=\,r^{(i)}_s r^{(j)}_s(g-1)+1$
in the term related to the above pair
$\dim \textrm { Ext}^1_X(\overline {E}^{(i)}_s , \,\overline {E}^{(j)}_s) \,=\,r^{(i)}_s r^{(j)}_s(g-1)+1$
in the term related to the above pair
![]() $(i,\, j)$
. However, we replace the condition
$(i,\, j)$
. However, we replace the condition
![]() $\overline {E}^{(i)}_s\,\not \cong \, \overline {E}^{(j)}_s$
with the condition
$\overline {E}^{(i)}_s\,\not \cong \, \overline {E}^{(j)}_s$
with the condition
![]() $\overline {E}^{(i)}_s\,\cong \, \overline {E}^{(j)}_s$
in the definition of
$\overline {E}^{(i)}_s\,\cong \, \overline {E}^{(j)}_s$
in the definition of
![]() $N'$
. So, the calculation of (5.7) is still valid and we get the inequality
$N'$
. So, the calculation of (5.7) is still valid and we get the inequality
![]() $\dim Z_Q\,\leqslant \, (r^2-1)(g-1)+nr(r-1)-2$
.
$\dim Z_Q\,\leqslant \, (r^2-1)(g-1)+nr(r-1)-2$
.
Consider now the remaining case where
![]() $m\,=\,2$
and
$m\,=\,2$
and
![]() $\gamma _1\,=\,\gamma _2\,=\,1$
. In this case,
$\gamma _1\,=\,\gamma _2\,=\,1$
. In this case,
![]() $Q$
is a parameter space of the extensions
$Q$
is a parameter space of the extensions
where
![]() $E_1,\, E_2$
are stable vector bundles such that
$E_1,\, E_2$
are stable vector bundles such that
![]() $\mu (E_1)\,=\,\mu _1\,\gt \,\mu _2\,=\,\mu (E_2)$
. In the calculation of (5.7), we have
$\mu (E_1)\,=\,\mu _1\,\gt \,\mu _2\,=\,\mu (E_2)$
. In the calculation of (5.7), we have
![]() $\dim Q\,\leqslant \, (r^2-1)(g-1)-1$
in this case. So, we have
$\dim Q\,\leqslant \, (r^2-1)(g-1)-1$
in this case. So, we have
![]() $\dim Z_Q\,\leqslant \, (r^2-1)(g-1)+nr(r-1)/2-1$
. Note that an automorphism
$\dim Z_Q\,\leqslant \, (r^2-1)(g-1)+nr(r-1)/2-1$
. Note that an automorphism
![]() $\textbf {g}$
of
$\textbf {g}$
of
![]() $E$
makes the diagram
$E$
makes the diagram

commutative and we have
![]() $\textbf {g}_1\,=\, c_1{\rm id}_{E_1}$
and
$\textbf {g}_1\,=\, c_1{\rm id}_{E_1}$
and
![]() $\textbf {g}_2\,=\,c_2{\rm id}_{E_2}$
for some
$\textbf {g}_2\,=\,c_2{\rm id}_{E_2}$
for some
![]() $c_1,\, c_2\,\in \, k^{\times }$
.
$c_1,\, c_2\,\in \, k^{\times }$
.
Consider the case where
![]() $\textrm { Hom}(E_2,\,E_1)\,=\,0$
for generic members
$\textrm { Hom}(E_2,\,E_1)\,=\,0$
for generic members
![]() $(E_1,\, E_2)$
of
$(E_1,\, E_2)$
of
![]() $N'$
. In that case, the dimension of the locus
$N'$
. In that case, the dimension of the locus
![]() $\textrm { Hom}(E_2,\,E_1)\,\neq \, 0$
in
$\textrm { Hom}(E_2,\,E_1)\,\neq \, 0$
in
![]() $Z_Q$
is at most
$Z_Q$
is at most
![]() $(r^2-1)(g-1)+nr(r-1)-2$
. For a general member
$(r^2-1)(g-1)+nr(r-1)-2$
. For a general member
![]() $(E_1,\, E_2)$
of
$(E_1,\, E_2)$
of
![]() $N'$
, the automorphisms
$N'$
, the automorphisms
![]() $\textbf {g}$
of
$\textbf {g}$
of
![]() $E$
are given by
$E$
are given by
![]() $(c_1,\, c_2)\,\in \, k^{\times }\times k^{\times }$
satisfying the conditions
$(c_1,\, c_2)\,\in \, k^{\times }\times k^{\times }$
satisfying the conditions
![]() $\textbf {g}_1\,=\,c_1{\rm id}_{E_1}$
and
$\textbf {g}_1\,=\,c_1{\rm id}_{E_1}$
and
![]() $\textbf {g}_2\,=\, c_2{\rm id}_{E_2}$
. Let
$\textbf {g}_2\,=\, c_2{\rm id}_{E_2}$
. Let
![]() $v\,=\, v_1e_1+\cdots +v_re_r$
be a generator of
$v\,=\, v_1e_1+\cdots +v_re_r$
be a generator of
![]() $l^{(1)}_{r-1}$
with respect to a chosen basis
$l^{(1)}_{r-1}$
with respect to a chosen basis
![]() $e_1,\,\ldots ,\, e_r$
of
$e_1,\,\ldots ,\, e_r$
of
![]() $E|_{x_1}$
such that
$E|_{x_1}$
such that
![]() $e_1,\,\ldots ,\, e_{r_1}$
generates
$e_1,\,\ldots ,\, e_{r_1}$
generates
![]() $E_1|_{x_1}$
. Applying the automorphisms of
$E_1|_{x_1}$
. Applying the automorphisms of
![]() $E$
of the above form, we can normalize
$E$
of the above form, we can normalize
![]() $l^{(1)}_{r-1}$
so that a generator
$l^{(1)}_{r-1}$
so that a generator
![]() $v\,=\,v_1e_1+\cdots +v_re_r$
of
$v\,=\,v_1e_1+\cdots +v_re_r$
of
![]() $l^{(1)}_{r-1}$
satisfies
$l^{(1)}_{r-1}$
satisfies
![]() $v_i\,=\,v_{r_1+j}$
or
$v_i\,=\,v_{r_1+j}$
or
![]() $v_iv_{r_1+j}\,=\,0$
for some
$v_iv_{r_1+j}\,=\,0$
for some
![]() $i,\,j$
with
$i,\,j$
with
![]() $1\,\leqslant \, i\,\leqslant \, r_1$
and
$1\,\leqslant \, i\,\leqslant \, r_1$
and
![]() $1\,\leqslant \,j\,\leqslant \, r_2$
. The reduced subscheme of
$1\,\leqslant \,j\,\leqslant \, r_2$
. The reduced subscheme of
![]() $Z_Q$
defined by this condition is of dimension at most
$Z_Q$
defined by this condition is of dimension at most
![]() $(r^2-1)(g-1)+nr(r-1)-2$
.
$(r^2-1)(g-1)+nr(r-1)-2$
.
Consider the case where
![]() $\textrm { Hom}(E_2,\,E_1)\,\neq \, 0$
for generic members
$\textrm { Hom}(E_2,\,E_1)\,\neq \, 0$
for generic members
![]() $(E_1,\, E_2)$
of
$(E_1,\, E_2)$
of
![]() $N'$
. Then there are automorphisms of
$N'$
. Then there are automorphisms of
![]() $E$
of the form
$E$
of the form
![]() $c\cdot {\rm id}_E+h$
with
$c\cdot {\rm id}_E+h$
with
![]() $0\,\neq \, h\,\in \,\textrm { Hom}(E_2,\, E_1)$
. After replacing
$0\,\neq \, h\,\in \,\textrm { Hom}(E_2,\, E_1)$
. After replacing
![]() $(E_1,\,E_2)$
with
$(E_1,\,E_2)$
with
![]() $(E_1\otimes {\mathcal L}^{\otimes r_2},\, E_2\otimes {\mathcal L}^{\otimes -r_1})$
, for a generic member
$(E_1\otimes {\mathcal L}^{\otimes r_2},\, E_2\otimes {\mathcal L}^{\otimes -r_1})$
, for a generic member
![]() ${\mathcal L}\,\in \, \textrm { Pic}^0_X$
, we may assume that
${\mathcal L}\,\in \, \textrm { Pic}^0_X$
, we may assume that
![]() $h|_{x_1}\,\neq \, 0$
, because the locus of
$h|_{x_1}\,\neq \, 0$
, because the locus of
![]() $N'$
satisfying
$N'$
satisfying
![]() $\textrm { Hom}(E_2,\, E_1(-x_1))\,=\,\textrm { Hom}(E_2,\,E_1)$
is of dimension less than
$\textrm { Hom}(E_2,\, E_1(-x_1))\,=\,\textrm { Hom}(E_2,\,E_1)$
is of dimension less than
![]() $\dim N'$
. After applying the automorphisms of
$\dim N'$
. After applying the automorphisms of
![]() $E$
, we may normalize a generator
$E$
, we may normalize a generator
![]() $v\,=\,v_1e_1+\cdots +v_re_r$
of
$v\,=\,v_1e_1+\cdots +v_re_r$
of
![]() $l^{(1)}_{r-1}$
such that
$l^{(1)}_{r-1}$
such that
![]() $v_i\,=\,0$
for some
$v_i\,=\,0$
for some
![]() $1\,\leqslant \, i\,\leqslant \, r_1$
or
$1\,\leqslant \, i\,\leqslant \, r_1$
or
![]() $l^{(1)}_{r-1}\,\subset \,E_1|_{x_1}$
. The locus of
$l^{(1)}_{r-1}\,\subset \,E_1|_{x_1}$
. The locus of
![]() $Z_Q$
defined by this condition is of dimension at most
$Z_Q$
defined by this condition is of dimension at most
![]() $(r^2-1)(g-1)+nr(r-1)-2$
.
$(r^2-1)(g-1)+nr(r-1)-2$
.
The disjoint union of all of the
![]() $Z_Q$
in the above arguments and the flat family of quasi-parabolic bundles given by
$Z_Q$
in the above arguments and the flat family of quasi-parabolic bundles given by
![]() $({\mathcal E},\,\ell )$
satisfy the assertion of the proposition.
$({\mathcal E},\,\ell )$
satisfy the assertion of the proposition.
Proposition 5.11. Let
![]() $X$
be an elliptic curve over
$X$
be an elliptic curve over
![]() $k$
, and let
$k$
, and let
![]() $L$
be a line bundle of degree
$L$
be a line bundle of degree
![]() $d$
on
$d$
on
![]() $X$
. Assume that one of the following holds:
$X$
. Assume that one of the following holds:
 $n\,\geqslant \, 3$
and
$n\,\geqslant \, 3$
and
 $r\,\geqslant \, 2$
;
$r\,\geqslant \, 2$
; $n\,=\,2$
and
$n\,=\,2$
and
 $r\,\geqslant \, 3$
.
$r\,\geqslant \, 3$
.
Then there exists a scheme
![]() $Z$
of finite type over
$Z$
of finite type over
![]() $k$
and a flat family
$k$
and a flat family
![]() $(\widetilde {E},\,\widetilde {\boldsymbol{l}})$
of quasi-parabolic bundles on
$(\widetilde {E},\,\widetilde {\boldsymbol{l}})$
of quasi-parabolic bundles on
![]() $X\times Z$
over
$X\times Z$
over
![]() $Z$
such that:
$Z$
such that:
-
(a)
 $\dim Z \, \leqslant \, r(r-1)n/2-2$
;
$\dim Z \, \leqslant \, r(r-1)n/2-2$
; -
(b)
 $\dim \textrm { End}((\widetilde {E},\,\widetilde {\boldsymbol{l}})|_{X\times \{z\}})\,\geqslant \, 2$
for any
$\dim \textrm { End}((\widetilde {E},\,\widetilde {\boldsymbol{l}})|_{X\times \{z\}})\,\geqslant \, 2$
for any
 $z\,\in \, Z$
;
$z\,\in \, Z$
;
and each member of the complement
![]() $\left | {\mathcal N}^{n_0\textrm { -reg}}_{{\rm par}}(L) \right | \setminus \left | {\mathcal N}^{n_0\textrm { -reg}}_{{\rm par}}(L)^{\circ } \right |$
is isomorphic to
$\left | {\mathcal N}^{n_0\textrm { -reg}}_{{\rm par}}(L) \right | \setminus \left | {\mathcal N}^{n_0\textrm { -reg}}_{{\rm par}}(L)^{\circ } \right |$
is isomorphic to
![]() $(\widetilde {E},\,\widetilde {\boldsymbol{l}})|_{X\times \{z\}}$
for some point
$(\widetilde {E},\,\widetilde {\boldsymbol{l}})|_{X\times \{z\}}$
for some point
![]() $z\,\in \, Z$
.
$z\,\in \, Z$
.
Proof. As in the proof of Proposition 5.10, we may assume that
![]() $r$
and
$r$
and
![]() $d$
are coprime. Take a member
$d$
are coprime. Take a member
![]() $(E,\,\boldsymbol{l})\,\in \, \left | {\mathcal N}^{n_0\textrm { -reg}}_{{\rm par}}(L) \right | \setminus \left | {\mathcal N}^{n_0\textrm { -reg}}_{{\rm par}}(L)^{\circ } \right |$
. Since
$(E,\,\boldsymbol{l})\,\in \, \left | {\mathcal N}^{n_0\textrm { -reg}}_{{\rm par}}(L) \right | \setminus \left | {\mathcal N}^{n_0\textrm { -reg}}_{{\rm par}}(L)^{\circ } \right |$
. Since
![]() $\dim \textrm { End}(E,\,\boldsymbol{l})\,\geqslant \, 2$
, it follows that
$\dim \textrm { End}(E,\,\boldsymbol{l})\,\geqslant \, 2$
, it follows that
![]() $\dim \textrm { End}(E)\,\geqslant \, 2$
. As
$\dim \textrm { End}(E)\,\geqslant \, 2$
. As
![]() $r$
and
$r$
and
![]() $d$
are coprime, the vector bundle
$d$
are coprime, the vector bundle
![]() $E$
is not semistable. Let
$E$
is not semistable. Let
be the Harder–Narasimhan filtration of
![]() $E$
; note that
$E$
; note that
![]() $m\,\geqslant \, 2$
because
$m\,\geqslant \, 2$
because
![]() $E$
is not semistable. Setting
$E$
is not semistable. Setting
![]() $\overline {E}_1\,=\, E_1$
and
$\overline {E}_1\,=\, E_1$
and
![]() $\overline {E}_s\,\,:=\,\, E_s/E_{s-1}$
for
$\overline {E}_s\,\,:=\,\, E_s/E_{s-1}$
for
![]() $2\,\leqslant \, s \,\leqslant \, m$
, the slopes
$2\,\leqslant \, s \,\leqslant \, m$
, the slopes
![]() $\mu _t\,\,:=\,\,\mu (\overline {E}_t)$
satisfy the inequalities
$\mu _t\,\,:=\,\,\mu (\overline {E}_t)$
satisfy the inequalities
and we get extensions
Note that we have
![]() $\textrm { Ext}^1(\overline {E}_t,\, \overline {E}_s)\,\cong \, \textrm { Hom}(\overline {E}_s ,\, \overline {E}_t)^{\vee }\,=\,0$
for
$\textrm { Ext}^1(\overline {E}_t,\, \overline {E}_s)\,\cong \, \textrm { Hom}(\overline {E}_s ,\, \overline {E}_t)^{\vee }\,=\,0$
for
![]() $s\,\lt \,t$
, because
$s\,\lt \,t$
, because
![]() $\mu (\overline {E}_t)\,\lt \,\mu (\overline {E}_s)$
and
$\mu (\overline {E}_t)\,\lt \,\mu (\overline {E}_s)$
and
![]() $\overline {E}_s,\, \overline {E}_t$
are semistable. It follows that
$\overline {E}_s,\, \overline {E}_t$
are semistable. It follows that
![]() $\textrm { Ext}^1(\overline {E}_{s+1},\,E_s)\,=\, 0$
. So the extension (5.9) must split, and we have a decomposition
$\textrm { Ext}^1(\overline {E}_{s+1},\,E_s)\,=\, 0$
. So the extension (5.9) must split, and we have a decomposition
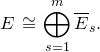 \begin{align*} E\,\cong \, \bigoplus _{s=1}^m \overline {E}_s. \end{align*}
\begin{align*} E\,\cong \, \bigoplus _{s=1}^m \overline {E}_s. \end{align*}
Let
![]() $\{\overline {F}^{(i)}_s\}_{i=1,\ldots ,\gamma _s}$
be the set of stable bundles arising in the direct summands of
$\{\overline {F}^{(i)}_s\}_{i=1,\ldots ,\gamma _s}$
be the set of stable bundles arising in the direct summands of
![]() ${\rm gr}(\overline {E}_s)$
. Fix an index
${\rm gr}(\overline {E}_s)$
. Fix an index
![]() $i\, \in \, \{1,\ldots ,\, \gamma _s\}$
. Let
$i\, \in \, \{1,\ldots ,\, \gamma _s\}$
. Let
![]() $G_i\,\subset \,\overline {E}_s$
be a maximal subbundle satisfying the condition
$G_i\,\subset \,\overline {E}_s$
be a maximal subbundle satisfying the condition
![]() $\textrm {Hom}(G_i,\, \overline {F}^{(i)}_s)\,=\,0$
. Then we have
$\textrm {Hom}(G_i,\, \overline {F}^{(i)}_s)\,=\,0$
. Then we have
![]() $\textrm { Hom}(\overline {F}^{(j)}_s,\,\overline {E}_s/G_i)\,=\,0$
for any
$\textrm { Hom}(\overline {F}^{(j)}_s,\,\overline {E}_s/G_i)\,=\,0$
for any
![]() $j\,\neq \, i$
, because otherwise the pullback of
$j\,\neq \, i$
, because otherwise the pullback of
![]() $\overline {F}^{(j)}_s\,\subset \, \overline {E}_s/G_i$
by the surjection
$\overline {F}^{(j)}_s\,\subset \, \overline {E}_s/G_i$
by the surjection
![]() $\overline {E}_s\,\longrightarrow \, \overline {E}_s/G_i$
contradicts the maximality of
$\overline {E}_s\,\longrightarrow \, \overline {E}_s/G_i$
contradicts the maximality of
![]() $G_i$
.
$G_i$
.
Taking account that
![]() $\overline {E}_s$
is semistable, we can see that
$\overline {E}_s$
is semistable, we can see that
![]() $\overline {E}_s/G_i$
is semistable of slope
$\overline {E}_s/G_i$
is semistable of slope
![]() $\mu (\overline {E}_s)$
and
$\mu (\overline {E}_s)$
and
![]() ${\rm gr}\big (\overline {E}_s/G_i\big )\,\cong \, \big (\overline {F}^{(i)}_s\big )^{\oplus u}$
for some positive integer
${\rm gr}\big (\overline {E}_s/G_i\big )\,\cong \, \big (\overline {F}^{(i)}_s\big )^{\oplus u}$
for some positive integer
![]() $u$
. So, we have
$u$
. So, we have
and the extension
![]() $0\,\longrightarrow \, G_i \,\longrightarrow \, \overline {E}_s \,\longrightarrow \,\overline {E}_s/G_i \,\longrightarrow \, 0$
must split. Applying the same argument to
$0\,\longrightarrow \, G_i \,\longrightarrow \, \overline {E}_s \,\longrightarrow \,\overline {E}_s/G_i \,\longrightarrow \, 0$
must split. Applying the same argument to
![]() $G_i$
, we finally get a decomposition
$G_i$
, we finally get a decomposition
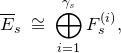 \begin{align*} \overline {E}_s\ \cong \ \bigoplus _{i=1}^{\gamma _s} F^{(i)}_s, \end{align*}
\begin{align*} \overline {E}_s\ \cong \ \bigoplus _{i=1}^{\gamma _s} F^{(i)}_s, \end{align*}
where
![]() $F^{(i)}_s$
is a semistable bundle satisfying the condition
$F^{(i)}_s$
is a semistable bundle satisfying the condition
![]() ${\rm gr}\big (F^{(i)}_s\big ) \,\cong \, \big (\overline {F}^{(i)}_s\big )^{\oplus u}$
for a positive integer
${\rm gr}\big (F^{(i)}_s\big ) \,\cong \, \big (\overline {F}^{(i)}_s\big )^{\oplus u}$
for a positive integer
![]() $u$
. Note that
$u$
. Note that
![]() $\mu (F^{(i)}_s)\,=\,\mu _s$
for any
$\mu (F^{(i)}_s)\,=\,\mu _s$
for any
![]() $i$
and these satisfy the inequalities in (5.8). We may further assume that
$i$
and these satisfy the inequalities in (5.8). We may further assume that
![]() $\overline {F}^{(i)}_s\,\not \cong \, \overline {F}^{(j)}_s$
for
$\overline {F}^{(i)}_s\,\not \cong \, \overline {F}^{(j)}_s$
for
![]() $i\,\neq \, j$
. Note that we have
$i\,\neq \, j$
. Note that we have
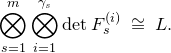 \begin{align} \bigotimes _{s=1}^m \bigotimes _{i=1}^{\gamma _s} \det F^{(i)}_s\ \cong \ L. \end{align}
\begin{align} \bigotimes _{s=1}^m \bigotimes _{i=1}^{\gamma _s} \det F^{(i)}_s\ \cong \ L. \end{align}
The moduli space of stable bundles parameterizing
![]() $\overline {F}^{(i)}_s$
is isomorphic to
$\overline {F}^{(i)}_s$
is isomorphic to
![]() $\textrm { Pic}^0_X\,\cong \, X$
for all
$\textrm { Pic}^0_X\,\cong \, X$
for all
![]() $i,\,s$
. Since we have
$i,\,s$
. Since we have
![]() $\dim \textrm { Ext}^1(\overline {F}^{(i)}_s,\,\overline {F}^{(i)}_s)\,=\,1$
for a stable vector bundle
$\dim \textrm { Ext}^1(\overline {F}^{(i)}_s,\,\overline {F}^{(i)}_s)\,=\,1$
for a stable vector bundle
![]() $\overline {F}^{(i)}_s$
, a successive non-split extension of
$\overline {F}^{(i)}_s$
, a successive non-split extension of
![]() $\overline {F}^{(i)}_s$
is unique up to an isomorphism. So, once
$\overline {F}^{(i)}_s$
is unique up to an isomorphism. So, once
![]() $\overline {F}^{(i)}_s$
is given, the extensions
$\overline {F}^{(i)}_s$
is given, the extensions
![]() $F^{(i)}_s$
of
$F^{(i)}_s$
of
![]() $\overline {F}^{(i)}_s$
are parameterized by a finite set. Taking into account the relation (5.10), the underlying vector bundles
$\overline {F}^{(i)}_s$
are parameterized by a finite set. Taking into account the relation (5.10), the underlying vector bundles
![]() $E$
of
$E$
of
![]() $(E,\,\boldsymbol{l})$
can be parameterized by a scheme
$(E,\,\boldsymbol{l})$
can be parameterized by a scheme
![]() $W$
of finite type over
$W$
of finite type over
![]() $\textrm { Spec}\, k$
whose dimension is
$\textrm { Spec}\, k$
whose dimension is
![]() $-1+\sum _{s=1}^m \gamma _s$
.
$-1+\sum _{s=1}^m \gamma _s$
.
Let
be the flag bundle parameterizing the quasi-parabolic structures on the vector bundles
![]() $E$
corresponding to the points of
$E$
corresponding to the points of
![]() $W$
. There is a universal family of quasi-parabolic bundles
$W$
. There is a universal family of quasi-parabolic bundles
![]() $(\widetilde {E},\,\widetilde {\boldsymbol{l}})$
on
$(\widetilde {E},\,\widetilde {\boldsymbol{l}})$
on
![]() $X\times Y$
over
$X\times Y$
over
![]() $Y$
. Since each fiber of
$Y$
. Since each fiber of
![]() $Y$
over
$Y$
over
![]() $W$
is of dimension
$W$
is of dimension
![]() $nr(r-1)/2$
, we have
$nr(r-1)/2$
, we have
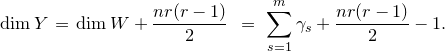 \begin{align*} \dim Y \,=\,\dim W+ \frac {nr(r-1)} {2} \ \,=\,\:\sum _{s=1}^m\gamma _s + \frac {nr(r-1)} {2} -1. \end{align*}
\begin{align*} \dim Y \,=\,\dim W+ \frac {nr(r-1)} {2} \ \,=\,\:\sum _{s=1}^m\gamma _s + \frac {nr(r-1)} {2} -1. \end{align*}
Write
![]() $(E,\,\boldsymbol{l})\,\,:=\,\,(\widetilde {E},\,\widetilde {\boldsymbol{l}})|_{X\times y}$
for each point
$(E,\,\boldsymbol{l})\,\,:=\,\,(\widetilde {E},\,\widetilde {\boldsymbol{l}})|_{X\times y}$
for each point
![]() $y\,\in \, Y$
.
$y\,\in \, Y$
.
Case A. Consider the case where the number of components in the decomposition
![]() $E\, =\, \bigoplus _{s,i}F^{(i)}_s$
is at least three. Choose a basis
$E\, =\, \bigoplus _{s,i}F^{(i)}_s$
is at least three. Choose a basis
![]() $e^{(i)}_{x,s,1},\,\cdots ,\, e^{(i)}_{x,s,r_{i,s}}$
of
$e^{(i)}_{x,s,1},\,\cdots ,\, e^{(i)}_{x,s,r_{i,s}}$
of
![]() $F^{(i)}_s|_x$
at each point
$F^{(i)}_s|_x$
at each point
![]() $x\,\in \,D$
for
$x\,\in \,D$
for
![]() $1\,\leqslant \, s\,\leqslant \, m$
and
$1\,\leqslant \, s\,\leqslant \, m$
and
![]() $1\,\leqslant \, i\,\leqslant \,\gamma _s$
. Let
$1\,\leqslant \, i\,\leqslant \,\gamma _s$
. Let
 \begin{align*} \sum _{s=1}^m\sum _{i=1}^{\gamma _s}\sum _{p=1}^{r_{i,s}} v^{(i)}_{x_2,s,p} e^{(i)}_{x_2,s,p} \end{align*}
\begin{align*} \sum _{s=1}^m\sum _{i=1}^{\gamma _s}\sum _{p=1}^{r_{i,s}} v^{(i)}_{x_2,s,p} e^{(i)}_{x_2,s,p} \end{align*}
be a generator of
![]() $l^{(2)}_{r-1}$
, and let
$l^{(2)}_{r-1}$
, and let
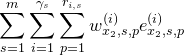 \begin{align*} \sum _{s=1}^m \sum _{i=1}^{\gamma _s}\sum _{p=1}^{r_{i,s}} w^{(i)}_{x_2,s,p} e^{(i)}_{x_2,s,p} \end{align*}
\begin{align*} \sum _{s=1}^m \sum _{i=1}^{\gamma _s}\sum _{p=1}^{r_{i,s}} w^{(i)}_{x_2,s,p} e^{(i)}_{x_2,s,p} \end{align*}
be a representative of a generator of
![]() $l^{(2)}_{r-2}/l^{(2)}_{r-1}$
. The group
$l^{(2)}_{r-2}/l^{(2)}_{r-1}$
. The group
![]() ${\textrm { Aut}} E$
of automorphisms of
${\textrm { Aut}} E$
of automorphisms of
![]() $E$
consists of the invertible elements of the ring of endomorphisms of
$E$
consists of the invertible elements of the ring of endomorphisms of
![]() $E$
:
$E$
:
 \begin{align*} \textrm { End} E\, =\, \bigg (\bigoplus _{s,i} \textrm { End} (F^{(i)}_s)\bigg ) \bigoplus \bigg (\bigoplus _{(s,i)\neq (t,j)} \textrm { Hom}(F^{(i)}_s,\,F^{(j)}_t)\bigg ). \end{align*}
\begin{align*} \textrm { End} E\, =\, \bigg (\bigoplus _{s,i} \textrm { End} (F^{(i)}_s)\bigg ) \bigoplus \bigg (\bigoplus _{(s,i)\neq (t,j)} \textrm { Hom}(F^{(i)}_s,\,F^{(j)}_t)\bigg ). \end{align*}
By the assumption, we can choose
![]() $F^{(i)}_s,\,F^{(i')}_{s'},\,F^{(j)}_t$
and
$F^{(i)}_s,\,F^{(i')}_{s'},\,F^{(j)}_t$
and
![]() $F^{(j')}_{t'}$
whose indices satisfy
$F^{(j')}_{t'}$
whose indices satisfy
![]() $s'\,\lt \,s$
,
$s'\,\lt \,s$
,
![]() $t'\,\lt \,t$
and
$t'\,\lt \,t$
and
![]() $((s,\,i),\,(s',\,i'))\,\neq \,((t,\,j),\,(t',\,j'))$
. So
$((s,\,i),\,(s',\,i'))\,\neq \,((t,\,j),\,(t',\,j'))$
. So
![]() ${\textrm { Aut}} E$
contains the three types of automorphisms:
${\textrm { Aut}} E$
contains the three types of automorphisms:
Note that the restriction maps
are not zero for generic choices of
![]() $F^{(i)}_s,\,F^{(i')}_{s'},\,F^{(j)}_t$
and
$F^{(i)}_s,\,F^{(i')}_{s'},\,F^{(j)}_t$
and
![]() $F^{(j')}_{t'}$
.
$F^{(j')}_{t'}$
.
If
![]() $F^{(i)}_s\,\neq \, F^{(j)}_t$
and
$F^{(i)}_s\,\neq \, F^{(j)}_t$
and
![]() $v^{(i)}_{x_2,s,p}\,\neq \, 0$
for some
$v^{(i)}_{x_2,s,p}\,\neq \, 0$
for some
![]() $p$
, then we may normalize a representative of a generator of
$p$
, then we may normalize a representative of a generator of
![]() $l^{(2)}_{r-2}/l^{(2)}_{r-1}$
such that
$l^{(2)}_{r-2}/l^{(2)}_{r-1}$
such that
![]() $w^{(i)}_{x_2,s,p}\,=\,0$
. Applying the actions of
$w^{(i)}_{x_2,s,p}\,=\,0$
. Applying the actions of
![]() ${\rm id}_E+\textrm { Hom}(F^{(i)}_s,\,F^{(i')}_{s'})$
and
${\rm id}_E+\textrm { Hom}(F^{(i)}_s,\,F^{(i')}_{s'})$
and
![]() ${\rm id}_E+\textrm { Hom}(F^{(j)}_t,\,F^{(j')}_{t'})$
, we may ensure that
${\rm id}_E+\textrm { Hom}(F^{(j)}_t,\,F^{(j')}_{t'})$
, we may ensure that
![]() $v^{(i')}_{x_2,s',p}\,=\,0$
for some
$v^{(i')}_{x_2,s',p}\,=\,0$
for some
![]() $p$
and
$p$
and
![]() $w^{(j')}_{x_2,t',q} w^{(j)}_{x_2,t,q'}\,=\,0$
for some
$w^{(j')}_{x_2,t',q} w^{(j)}_{x_2,t,q'}\,=\,0$
for some
![]() $q,\, q'$
. The Zariski closed subset
$q,\, q'$
. The Zariski closed subset
![]() $Y'$
defined by this condition is of dimension
$Y'$
defined by this condition is of dimension
![]() $\dim Y-2\,=\,\sum _{s=1}^m\gamma _s+nr(r-1)/2-3$
.
$\dim Y-2\,=\,\sum _{s=1}^m\gamma _s+nr(r-1)/2-3$
.
Assume that
![]() $F^{(i)}_s\,\neq \, F^{(j)}_t$
and
$F^{(i)}_s\,\neq \, F^{(j)}_t$
and
![]() $v^{(i)}_{x_2,s,p}\,=\,0$
for all
$v^{(i)}_{x_2,s,p}\,=\,0$
for all
![]() $p$
. If, in addition, the condition
$p$
. If, in addition, the condition
![]() $v^{(i)}_{x_2,s',p'}\,=\,0$
holds for all
$v^{(i)}_{x_2,s',p'}\,=\,0$
holds for all
![]() $p'$
, then such a locus is of dimension at most
$p'$
, then such a locus is of dimension at most
![]() $\dim Y-2\,=\,\sum _{s=1}^m\gamma _s+nr(r-1)/2-3$
. So, assume that
$\dim Y-2\,=\,\sum _{s=1}^m\gamma _s+nr(r-1)/2-3$
. So, assume that
![]() $v^{(i)}_{x_2,s',p'}\,\neq \, 0$
for some
$v^{(i)}_{x_2,s',p'}\,\neq \, 0$
for some
![]() $p'$
. Then we can normalize a representative of a generator of
$p'$
. Then we can normalize a representative of a generator of
![]() $l^{(2)}_{r-2}/l^{(2)}_{r-1}$
such that
$l^{(2)}_{r-2}/l^{(2)}_{r-1}$
such that
![]() $w^{(i)}_{x_2,s',p'}\,=\,0$
. Applying the action of
$w^{(i)}_{x_2,s',p'}\,=\,0$
. Applying the action of
![]() ${\rm id}_E+\textrm { Hom}(F^{(j)}_t,\,F^{(j')}_{t'})$
, we may have
${\rm id}_E+\textrm { Hom}(F^{(j)}_t,\,F^{(j')}_{t'})$
, we may have
![]() $w^{(j')}_{x_2,t',q} w^{(j)}_{x_2,t,q'}\,=\,0$
for some
$w^{(j')}_{x_2,t',q} w^{(j)}_{x_2,t,q'}\,=\,0$
for some
![]() $q,\,q'$
. The Zariski closed subset of
$q,\,q'$
. The Zariski closed subset of
![]() $Y'$
defined by the condition
$Y'$
defined by the condition
![]() $v^{(i)}_{x_2,s,p}\,=\,0$
for all
$v^{(i)}_{x_2,s,p}\,=\,0$
for all
![]() $p$
and
$p$
and
![]() $w^{(j')}_{x_2,t',q} w^{(j)}_{x_2,t,q'}\,=\,0$
for some
$w^{(j')}_{x_2,t',q} w^{(j)}_{x_2,t,q'}\,=\,0$
for some
![]() $q,\, q'$
is of dimension at most
$q,\, q'$
is of dimension at most
![]() $\dim Y-2\,=\,\sum _{s=1}^m\gamma _s+nr(r-1)/2-3$
.
$\dim Y-2\,=\,\sum _{s=1}^m\gamma _s+nr(r-1)/2-3$
.
Assume that
![]() $F^{(i)}_s\,=\,F^{(j)}_t$
. Then we have
$F^{(i)}_s\,=\,F^{(j)}_t$
. Then we have
![]() $F^{(i')}_{s'}\,\neq \, F^{(j')}_{t'}$
by the choices of
$F^{(i')}_{s'}\,\neq \, F^{(j')}_{t'}$
by the choices of
If
![]() $v^{(i)}_{x_2,s,p}\,\neq \, 0$
for some
$v^{(i)}_{x_2,s,p}\,\neq \, 0$
for some
![]() $p$
, then applying automorphisms in
$p$
, then applying automorphisms in
![]() ${\rm id}_E+\textrm { Hom}(F^{(i)}_s,\,F^{(i')}_{s'})$
and
${\rm id}_E+\textrm { Hom}(F^{(i)}_s,\,F^{(i')}_{s'})$
and
![]() ${\rm id}_E+\textrm { Hom}(F^{(j)}_t,\,F^{(j')}_{t'})$
, we may ensure that
${\rm id}_E+\textrm { Hom}(F^{(j)}_t,\,F^{(j')}_{t'})$
, we may ensure that
![]() $v^{(i')}_{x_2,s',p'}\,=\,v^{(i)}_{x_2,t',q'}\,=\,0$
for some
$v^{(i')}_{x_2,s',p'}\,=\,v^{(i)}_{x_2,t',q'}\,=\,0$
for some
![]() $p',\,q'$
. The Zariski closed subset of
$p',\,q'$
. The Zariski closed subset of
![]() $Y$
defined by this condition is of dimension at most
$Y$
defined by this condition is of dimension at most
![]() $\dim Y-2\,=\,\sum _{s=1}^m\gamma _s+nr(r-1)/2-3$
. Assume that
$\dim Y-2\,=\,\sum _{s=1}^m\gamma _s+nr(r-1)/2-3$
. Assume that
![]() $v^{(i)}_{x_2,s,p}\,=\,0$
for all
$v^{(i)}_{x_2,s,p}\,=\,0$
for all
![]() $p$
, while still assuming
$p$
, while still assuming
![]() $F^{(i)}_s\,=\,F^{(j)}_t$
. If, in addition, we have
$F^{(i)}_s\,=\,F^{(j)}_t$
. If, in addition, we have
![]() $v^{(i')}_{x_2,s',p'}\,=\,0$
for all
$v^{(i')}_{x_2,s',p'}\,=\,0$
for all
![]() $p'$
, then such a locus in
$p'$
, then such a locus in
![]() $Y$
is of dimension at most
$Y$
is of dimension at most
![]() $\dim Y-2\,=\,\sum _{s=1}^m\gamma _s+nr(r-1)/2-3$
. So, assume that
$\dim Y-2\,=\,\sum _{s=1}^m\gamma _s+nr(r-1)/2-3$
. So, assume that
![]() $v^{(i')}_{x_2,s',p'}\,\neq \, 0$
for some
$v^{(i')}_{x_2,s',p'}\,\neq \, 0$
for some
![]() $p'$
. Then we may normalize a representative of a generator of
$p'$
. Then we may normalize a representative of a generator of
![]() $l^{(2)}_{r-2}/l^{(2)}_{r-1}$
so that the condition
$l^{(2)}_{r-2}/l^{(2)}_{r-1}$
so that the condition
![]() $w^{(i')}_{x_2,s',p'}\,=\,0$
holds. Applying an automorphism in
$w^{(i')}_{x_2,s',p'}\,=\,0$
holds. Applying an automorphism in
![]() ${\rm id}_E+\textrm { Hom}(F^{(j)}_t,\,F^{(j')}_{t'})$
, we may have
${\rm id}_E+\textrm { Hom}(F^{(j)}_t,\,F^{(j')}_{t'})$
, we may have
![]() $w^{(j')}_{x_2,t',q'} w^{(j)}_{x_2,t,q} \,=\,0$
for some
$w^{(j')}_{x_2,t',q'} w^{(j)}_{x_2,t,q} \,=\,0$
for some
![]() $q,\,q'$
. The locus of
$q,\,q'$
. The locus of
![]() $Y$
defined by
$Y$
defined by
![]() $v^{(i')}_{x_2,s',p'}\,=\, 0$
for all
$v^{(i')}_{x_2,s',p'}\,=\, 0$
for all
![]() $p'$
and
$p'$
and
![]() $w^{(j')}_{x_2,t',q'} w^{(j)}_{x_2,t,q} \,=\, 0$
for some
$w^{(j')}_{x_2,t',q'} w^{(j)}_{x_2,t,q} \,=\, 0$
for some
![]() $q,\, q'$
is of dimension at most
$q,\, q'$
is of dimension at most
![]() $\dim Y-2\,=\,\sum _{s=1}^m\gamma _s+nr(r-1)/2-3$
.
$\dim Y-2\,=\,\sum _{s=1}^m\gamma _s+nr(r-1)/2-3$
.
Therefore, in all cases we can get a disjoint union
![]() $Y'$
of locally closed subsets of
$Y'$
of locally closed subsets of
![]() $Y$
and a flat family of quasi-parabolic bundles
$Y$
and a flat family of quasi-parabolic bundles
![]() $(\widetilde {E},\,\widetilde {\boldsymbol{l}})$
on
$(\widetilde {E},\,\widetilde {\boldsymbol{l}})$
on
![]() $X\times Y'$
over
$X\times Y'$
over
![]() $Y'$
, such that
$Y'$
, such that
![]() $\dim Y'\,\leqslant \,\sum _{s=1}^m\gamma _s+nr(r-1)/2-3$
and every member of
$\dim Y'\,\leqslant \,\sum _{s=1}^m\gamma _s+nr(r-1)/2-3$
and every member of
![]() $\left | {\mathcal N}^{n_0{\rm -reg}}_{{\rm par}}(L) \right | \setminus \left | {\mathcal N}^{n_0{\rm -reg}}_{{\rm par}}(L)^{\circ } \right |$
can be transformed by the actions of
$\left | {\mathcal N}^{n_0{\rm -reg}}_{{\rm par}}(L) \right | \setminus \left | {\mathcal N}^{n_0{\rm -reg}}_{{\rm par}}(L)^{\circ } \right |$
can be transformed by the actions of
![]() ${\rm id}_E+\textrm { Hom}(F^{(i)}_s,\,F^{(i')}_{s'})$
and
${\rm id}_E+\textrm { Hom}(F^{(i)}_s,\,F^{(i')}_{s'})$
and
![]() ${\rm id}_E+\textrm { Hom}(F^{(j)}_t,\,F^{(j')}_{t'})$
to a quasi-parabolic bundle
${\rm id}_E+\textrm { Hom}(F^{(j)}_t,\,F^{(j')}_{t'})$
to a quasi-parabolic bundle
![]() $(\widetilde {E},\,\widetilde {\boldsymbol{l}})|_{X\times y}$
for some
$(\widetilde {E},\,\widetilde {\boldsymbol{l}})|_{X\times y}$
for some
![]() $y\,\in \, Y'$
.
$y\,\in \, Y'$
.
Using the action of the group
![]() $\prod _{s,i} k^{\times } {\rm id}_{F^{(i)}_s}$
on a generator
$\prod _{s,i} k^{\times } {\rm id}_{F^{(i)}_s}$
on a generator
of
![]() $l^{(1)}_{r-1}$
we may have
$l^{(1)}_{r-1}$
we may have
![]() $(v^{(s)}_{x_1,i,p}-1)v^{(s)}_{x_1,i,p}\,=\,0$
for
$(v^{(s)}_{x_1,i,p}-1)v^{(s)}_{x_1,i,p}\,=\,0$
for
![]() $1\,\leqslant \, s\,\leqslant \, m$
,
$1\,\leqslant \, s\,\leqslant \, m$
,
![]() $1\,\leqslant \, i \,\leqslant \, \gamma _s$
and any
$1\,\leqslant \, i \,\leqslant \, \gamma _s$
and any
![]() $p$
. The Zariski closed subset
$p$
. The Zariski closed subset
![]() $Z$
of
$Z$
of
![]() $Y'$
defined by this condition satisfies
$Y'$
defined by this condition satisfies
![]() $\dim Z\, =\, \dim Y'-(-1+\sum _{s=1}^m\gamma _s) \leqslant nr(r-1)/2-2$
.
$\dim Z\, =\, \dim Y'-(-1+\sum _{s=1}^m\gamma _s) \leqslant nr(r-1)/2-2$
.
Case B. Consider the case where
![]() $E\,=\,F_1\oplus F_2$
with
$E\,=\,F_1\oplus F_2$
with
![]() $\mu (F_1)\,\gt \,\mu (F_2)$
,
$\mu (F_1)\,\gt \,\mu (F_2)$
,
![]() $r_i\,=\,\textrm {rank}\, F_i$
and each
$r_i\,=\,\textrm {rank}\, F_i$
and each
![]() $F_i$
is a successive extension of one stable vector bundle. In this case, we have
$F_i$
is a successive extension of one stable vector bundle. In this case, we have
![]() $m\,=\,2$
and
$m\,=\,2$
and
![]() $\gamma _1\,=\,\gamma _2\,=\,1$
. So, we have
$\gamma _1\,=\,\gamma _2\,=\,1$
. So, we have
![]() $\dim W\,=\, 1$
and
$\dim W\,=\, 1$
and
![]() $\dim Y \,=\, 1+nr(r-1)/2$
. Since
$\dim Y \,=\, 1+nr(r-1)/2$
. Since
![]() $\mu (F_1)\,\gt \,\mu (F_2)$
and
$\mu (F_1)\,\gt \,\mu (F_2)$
and
![]() $F_1,\, F_2$
are semistable, it follows that
$F_1,\, F_2$
are semistable, it follows that
![]() $\textrm { Hom}(F_2,\,F_1)\,=\,0$
. So, we have
$\textrm { Hom}(F_2,\,F_1)\,=\,0$
. So, we have
![]() $\dim \textrm { Hom}(F_2,\,F_1)\,=\,\deg (F_2^{\vee }\otimes F_1)\,\gt \,0$
by the Riemann–Roch theorem, and
$\dim \textrm { Hom}(F_2,\,F_1)\,=\,\deg (F_2^{\vee }\otimes F_1)\,\gt \,0$
by the Riemann–Roch theorem, and
 \begin{align} \dim \textrm { Hom}(F_2,\,F_1(-x)) \,=\, \begin{cases} \begin{array} {l@{\quad}l}\deg (F_2^{\vee }\otimes F_1(-x)) &\rm if\ \mu\ (F_2)\,\lt\ \,\ \mu\ (F_1(-x)), \\ \deg (F_2^{\vee }\otimes F_1(-x))\\\quad+\dim \textrm { Hom}(F_1(-x),F_2) &\rm if\ \mu\ (F_2)\,=\,\mu\ (F_1(-x)), \\ 0 &\rm if\ \mu\ (F_2)\,\gt\ \,\mu\ (F_1(-x)), \end{array} \end{cases}\end{align}
\begin{align} \dim \textrm { Hom}(F_2,\,F_1(-x)) \,=\, \begin{cases} \begin{array} {l@{\quad}l}\deg (F_2^{\vee }\otimes F_1(-x)) &\rm if\ \mu\ (F_2)\,\lt\ \,\ \mu\ (F_1(-x)), \\ \deg (F_2^{\vee }\otimes F_1(-x))\\\quad+\dim \textrm { Hom}(F_1(-x),F_2) &\rm if\ \mu\ (F_2)\,=\,\mu\ (F_1(-x)), \\ 0 &\rm if\ \mu\ (F_2)\,\gt\ \,\mu\ (F_1(-x)), \end{array} \end{cases}\end{align}
for a point
![]() $x$
of
$x$
of
![]() $X$
. In the case where
$X$
. In the case where
![]() $\mu (F_2)\,=\,\mu (F_1(-x))$
, we have either
$\mu (F_2)\,=\,\mu (F_1(-x))$
, we have either
or
![]() $\dim \textrm { Hom}(F_2,\,F_1(-x_2))\,=\,0$
, because
$\dim \textrm { Hom}(F_2,\,F_1(-x_2))\,=\,0$
, because
![]() $x_1\,\neq \, x_2$
. So, in all cases of (5.13), at least one of the maps
$x_1\,\neq \, x_2$
. So, in all cases of (5.13), at least one of the maps
is not zero. Choose a basis
![]() $e_{x_i,1},\,\ldots ,\,e_{x_i,r_1}$
of
$e_{x_i,1},\,\ldots ,\,e_{x_i,r_1}$
of
![]() $F_1|_{x_i}$
and a basis
$F_1|_{x_i}$
and a basis
![]() $e'_{x_i,1},\,\cdots ,\, e'_{x_i,r_2}$
of
$e'_{x_i,1},\,\cdots ,\, e'_{x_i,r_2}$
of
![]() $F_2|_{x_i}$
. Take a generator
$F_2|_{x_i}$
. Take a generator
![]() $v_{x_i,1}e_{x_i,1}+\cdots +v_{x_i,r_1}e_{x_i,r_1}+v'_{x_i,1}e'_{x_i,1}+\cdots +v'_{x_i,r_2}e'_{x_i,r_2}$
of
$v_{x_i,1}e_{x_i,1}+\cdots +v_{x_i,r_1}e_{x_i,r_1}+v'_{x_i,1}e'_{x_i,1}+\cdots +v'_{x_i,r_2}e'_{x_i,r_2}$
of
![]() $l^{(i)}_{r-1}$
. Applying the action of
$l^{(i)}_{r-1}$
. Applying the action of
![]() $1_E+\textrm { Hom}(F_2,\, F_1)$
, we may have
$1_E+\textrm { Hom}(F_2,\, F_1)$
, we may have
![]() $v_{x_2,q}\,=\,0$
for some
$v_{x_2,q}\,=\,0$
for some
![]() $q$
, or
$q$
, or
![]() $v'_{x_2,q'}\,=\,0$
for all
$v'_{x_2,q'}\,=\,0$
for all
![]() $q'$
. Moreover, applying the action of
$q'$
. Moreover, applying the action of
![]() $k^{\times }{\rm id}_{F_1}\times k^{\times }{\rm id}_{F_2}$
, we may have
$k^{\times }{\rm id}_{F_1}\times k^{\times }{\rm id}_{F_2}$
, we may have
![]() $v_{x_1,p}\,=\,v'_{x_1,p'}$
for some
$v_{x_1,p}\,=\,v'_{x_1,p'}$
for some
![]() $p,\,p'$
, or
$p,\,p'$
, or
![]() $v_{x_1,p}v'_{x_1,p'}\,=\,0$
for some
$v_{x_1,p}v'_{x_1,p'}\,=\,0$
for some
![]() $p,\, p'$
. Let
$p,\, p'$
. Let
![]() $Y'$
be a disjoint union of subvarieties of
$Y'$
be a disjoint union of subvarieties of
![]() $Y$
where the following two conditions hold:
$Y$
where the following two conditions hold:
![]() $v'_{x_2,q'}v_{x_2,q}\,=\,0$
for some
$v'_{x_2,q'}v_{x_2,q}\,=\,0$
for some
![]() $q,\, q'$
and
$q,\, q'$
and
![]() $(v_{x_1,p}-v'_{x_1,p'})v_{x_1,p}v'_{x_1,p'}\,=\,0$
for some
$(v_{x_1,p}-v'_{x_1,p'})v_{x_1,p}v'_{x_1,p'}\,=\,0$
for some
![]() $p,\, p'$
. Then we have
$p,\, p'$
. Then we have
and every member of the complement
![]() $\left | {\mathcal N}^{n_0\textrm { -reg}}_{{\rm par}}(L) \right | \setminus \left | {\mathcal N}^{n_0\textrm { -reg}}_{{\rm par}}(L)^{\circ } \right |$
can be transformed by the actions of
$\left | {\mathcal N}^{n_0\textrm { -reg}}_{{\rm par}}(L) \right | \setminus \left | {\mathcal N}^{n_0\textrm { -reg}}_{{\rm par}}(L)^{\circ } \right |$
can be transformed by the actions of
![]() $k^{\times }\cdot 1_{F_1}\times k^{\times }\cdot 1_{F_2}$
and
$k^{\times }\cdot 1_{F_1}\times k^{\times }\cdot 1_{F_2}$
and
![]() $1_E+\textrm { Hom}(F_2,\, F_1)$
to a quasi-parabolic bundle
$1_E+\textrm { Hom}(F_2,\, F_1)$
to a quasi-parabolic bundle
![]() $(\widetilde {E},\,\widetilde {\boldsymbol{l}})|_{X\times y}$
for some
$(\widetilde {E},\,\widetilde {\boldsymbol{l}})|_{X\times y}$
for some
![]() $y\,\in \, Y'$
. Let
$y\,\in \, Y'$
. Let
![]() $Y''$
be the Zariski closed subset of
$Y''$
be the Zariski closed subset of
![]() $Y'$
defined by
$Y'$
defined by
For each point
![]() $y\,\in \, Y''$
, write
$y\,\in \, Y''$
, write
![]() $(E,\,\boldsymbol{l})\,\,:=\,\, (\widetilde {E},\,\widetilde {\boldsymbol{l}})|_{X\times y}$
. Set
$(E,\,\boldsymbol{l})\,\,:=\,\, (\widetilde {E},\,\widetilde {\boldsymbol{l}})|_{X\times y}$
. Set
Then
![]() $H$
contains non-scalar automorphisms.
$H$
contains non-scalar automorphisms.
-
(I) Consider the case where
 $H\ \not \subset \ k^{\times }{\rm id}_E+\textrm { Hom}(F_2,F_1)$
. Take
$H\ \not \subset \ k^{\times }{\rm id}_E+\textrm { Hom}(F_2,F_1)$
. Take
 $\textbf {g}\,\in \, H\setminus \big ( k^{\times }{\rm id}_E+\textrm { Hom}(F_2,F_1)\big )$
. Then we can writewhere
$\textbf {g}\,\in \, H\setminus \big ( k^{\times }{\rm id}_E+\textrm { Hom}(F_2,F_1)\big )$
. Then we can writewhere \begin{align*} \textbf {g}\ =\ \left(\begin{array}{c@{\quad}c} c_1{\rm Id}_{F_1} & b \\ 0 & c_2{\rm Id}_{F_2} \end{array}\right), \end{align*}
\begin{align*} \textbf {g}\ =\ \left(\begin{array}{c@{\quad}c} c_1{\rm Id}_{F_1} & b \\ 0 & c_2{\rm Id}_{F_2} \end{array}\right), \end{align*}
 $c_1,\, c_2\,\in \, k^{\times }$
,
$c_1,\, c_2\,\in \, k^{\times }$
,
 $b\,\in \, \textrm { Hom}(F_2,\,F_1)$
and
$b\,\in \, \textrm { Hom}(F_2,\,F_1)$
and
 $c_1\,\neq \, c_2$
.
$c_1\,\neq \, c_2$
.-
(a) Consider the case where
 $n\,\geqslant \, 3$
. Since
$n\,\geqslant \, 3$
. Since
 $\textbf {g}|_{x_3}$
has distinct eigenvalues
$\textbf {g}|_{x_3}$
has distinct eigenvalues
 $c_1,\, c_2$
, the condition that
$c_1,\, c_2$
, the condition that
 $\textbf {g}|_{x_3}$
preserves
$\textbf {g}|_{x_3}$
preserves
 $l^{(3)}_{r-1}$
implies that
$l^{(3)}_{r-1}$
implies that
 $\dim Y''\,\leqslant \, \dim Y-1\leqslant nr(r-1)/2-2$
.
$\dim Y''\,\leqslant \, \dim Y-1\leqslant nr(r-1)/2-2$
. -
(b) Consider the case where
 $r\,\geqslant \, 3$
. In this case, we have either
$r\,\geqslant \, 3$
. In this case, we have either
 $r_1\,=\,\textrm { rank} F_1\,\geqslant \, 2$
or
$r_1\,=\,\textrm { rank} F_1\,\geqslant \, 2$
or
 $r_2\,=\,\textrm { rank} F_2\,\geqslant \, 2$
.
$r_2\,=\,\textrm { rank} F_2\,\geqslant \, 2$
. -
(i) Consider the case where
 $r_2\,\geqslant \, 2$
. If
$r_2\,\geqslant \, 2$
. If
 $l^{(i)}_{r-1}\,\subset \, F_1|_{x_i}$
for
$l^{(i)}_{r-1}\,\subset \, F_1|_{x_i}$
for
 $i\,=\,1$
or
$i\,=\,1$
or
 $i\,=\,2$
, then
$i\,=\,2$
, then
 $Y'$
can be replaced by the locus satisfying this condition and we get that
$Y'$
can be replaced by the locus satisfying this condition and we get that
 $\dim Y'\,\leqslant \, nr(r-1)/2-2$
. So, we may assume that
$\dim Y'\,\leqslant \, nr(r-1)/2-2$
. So, we may assume that
 $l^{(i)}_{r-1}\,\not \subset \, F_1|_{x_i}$
for
$l^{(i)}_{r-1}\,\not \subset \, F_1|_{x_i}$
for
 $i\,=\,1$
or
$i\,=\,1$
or
 $i\,=\,2$
. Then we have
$i\,=\,2$
. Then we have
 $\textbf {g}|_{l^{(i)}_{r-1}}\,=\,c_2{\rm id}_{l^{(i)}_{r-1}}$
, and
$\textbf {g}|_{l^{(i)}_{r-1}}\,=\,c_2{\rm id}_{l^{(i)}_{r-1}}$
, and
 $\textbf {g}$
induces a linear map
$\textbf {g}$
induces a linear map
 $\overline {\textbf {g}}\,\colon \, E|_{x_i}/l^{(i)}_{r-1} \,\longrightarrow \, E|_{x_i}/l^{(i)}_{r-1}$
. Since the eigenvalues of
$\overline {\textbf {g}}\,\colon \, E|_{x_i}/l^{(i)}_{r-1} \,\longrightarrow \, E|_{x_i}/l^{(i)}_{r-1}$
. Since the eigenvalues of
 $\overline {\textbf {g}}$
are
$\overline {\textbf {g}}$
are
 $c_1,\, c_2$
and
$c_1,\, c_2$
and
 $l^{(i)}_{r-2}/l^{(i)}_{r-1}$
is preserved by
$l^{(i)}_{r-2}/l^{(i)}_{r-1}$
is preserved by
 $\overline {\textbf {g}}$
, it follows that
$\overline {\textbf {g}}$
, it follows that
 $\dim Y''\,\leqslant \, \dim Y'-1\,\leqslant \, nr(r-1)/2-2$
.
$\dim Y''\,\leqslant \, \dim Y'-1\,\leqslant \, nr(r-1)/2-2$
. -
(ii) Consider the case where
 $r_1\,\geqslant \, 2$
. If
$r_1\,\geqslant \, 2$
. If
 $l^{(i)}_{r-1}\,\subset \, F_2|_{x_i}$
, then such a locus in
$l^{(i)}_{r-1}\,\subset \, F_2|_{x_i}$
, then such a locus in
 $Y'$
is of dimension at most
$Y'$
is of dimension at most
 $nr(r-1)/2-2$
. So we may assume that
$nr(r-1)/2-2$
. So we may assume that
 $l^{(i)}_{r-1}\,\not \subset \, F_2|_{x_i}$
. Since the induced map
$l^{(i)}_{r-1}\,\not \subset \, F_2|_{x_i}$
. Since the induced map
 $\overline {\textbf {g}}\,\colon \, E|_{x_i}/l^{(i)}_{r-1}\, \longrightarrow \, E|_{x_i}/l^{(i)}_{r-1}$
has distinct eigenvalues
$\overline {\textbf {g}}\,\colon \, E|_{x_i}/l^{(i)}_{r-1}\, \longrightarrow \, E|_{x_i}/l^{(i)}_{r-1}$
has distinct eigenvalues
 $c_1,\, c_2$
and
$c_1,\, c_2$
and
 $l^{(i)}_{r-2}/l^{(i)}_{r-1}$
is preserved by
$l^{(i)}_{r-2}/l^{(i)}_{r-1}$
is preserved by
 $\overline {\textbf {g}}$
, it follows that
$\overline {\textbf {g}}$
, it follows that
 $\dim Y''\,\leqslant \, \dim Y'-1\,\leqslant \, nr(r-1)/2-2$
.
$\dim Y''\,\leqslant \, \dim Y'-1\,\leqslant \, nr(r-1)/2-2$
.
-
-
(II) Consider the case where
 $H$
is contained in
$H$
is contained in
 $k^{\times }{\rm id}_E+\textrm { Hom}(F_2,\,F_1)$
.
$k^{\times }{\rm id}_E+\textrm { Hom}(F_2,\,F_1)$
.-
(a) Assume that
 $n\,\geqslant \, 3$
, in addition to
$n\,\geqslant \, 3$
, in addition to
 $H\,\subset \, k^{\times } {\rm id}_E+\textrm { Hom}(F_2,\,F_1)$
. We may assume that the composition of mapsis injective, because the non-injective locus in
$H\,\subset \, k^{\times } {\rm id}_E+\textrm { Hom}(F_2,\,F_1)$
. We may assume that the composition of mapsis injective, because the non-injective locus in \begin{align*} \left \{ a\,\in \,\textrm { Hom}(F_2,\,F_1) \,\big \vert \,\, {\rm id}_E+a\,\in \, H \right \} \,\hookrightarrow \, \textrm { Hom}(F_2,\,F_1)\,\longrightarrow \, \textrm { Hom}(F_2|_{x_3},\,F_1|_{x_3}) \end{align*}
\begin{align*} \left \{ a\,\in \,\textrm { Hom}(F_2,\,F_1) \,\big \vert \,\, {\rm id}_E+a\,\in \, H \right \} \,\hookrightarrow \, \textrm { Hom}(F_2,\,F_1)\,\longrightarrow \, \textrm { Hom}(F_2|_{x_3},\,F_1|_{x_3}) \end{align*}
 $Y'$
is of dimension at most
$Y'$
is of dimension at most
 $\dim Y'-1\leqslant nr(r-1)/2-2$
. Choose a basis
$\dim Y'-1\leqslant nr(r-1)/2-2$
. Choose a basis
 $e_{x_i,1},\, \ldots ,\, e_{x_i,r_1}$
of
$e_{x_i,1},\, \ldots ,\, e_{x_i,r_1}$
of
 $F_1|_{x_i}$
and a basis
$F_1|_{x_i}$
and a basis
 $e'_{x_i,1},\, \ldots ,\, e'_{x_i,r_2}$
of
$e'_{x_i,1},\, \ldots ,\, e'_{x_i,r_2}$
of
 $F_2|_{x_i}$
for
$F_2|_{x_i}$
for
 $i\,=\,1,\,2$
. Take a generator
$i\,=\,1,\,2$
. Take a generator
 $v_{x_i,1}e_{x_i,1}+\cdots +v_{x_i,r_1}e_{x_i,r_1} +v'_{x_i,1}e'_{x_i,1}+\cdots +v'_{x_i,r_2}e'_{x_i,r_2}$
of
$v_{x_i,1}e_{x_i,1}+\cdots +v_{x_i,r_1}e_{x_i,r_1} +v'_{x_i,1}e'_{x_i,1}+\cdots +v'_{x_i,r_2}e'_{x_i,r_2}$
of
 $l^{(i)}_{r-1}$
. Applying an automorphism
$l^{(i)}_{r-1}$
. Applying an automorphism
 ${\rm id}_E+a\,\in \, H$
with
${\rm id}_E+a\,\in \, H$
with
 $a\,\in \,\textrm { Hom}(F_2,\, F_1)$
satisfying the condition
$a\,\in \,\textrm { Hom}(F_2,\, F_1)$
satisfying the condition
 $a|_{x_3}\,\neq \, 0$
, we can normalize
$a|_{x_3}\,\neq \, 0$
, we can normalize
 $l^{(3)}_{r-1}$
so that the condition
$l^{(3)}_{r-1}$
so that the condition
 $v_{x_3,p}\,=\, 0$
holds for some
$v_{x_3,p}\,=\, 0$
holds for some
 $p$
or the condition
$p$
or the condition
 $v'_{x_3,p'}\,=\, 0$
holds for all
$v'_{x_3,p'}\,=\, 0$
holds for all
 $p'$
. The Zariski closed subset of
$p'$
. The Zariski closed subset of
 $Y''$
defined by this condition is of dimension at most
$Y''$
defined by this condition is of dimension at most
 $\dim Y'-1 \leqslant nr(r-1)/2-2$
.
$\dim Y'-1 \leqslant nr(r-1)/2-2$
.
-
(b) Consider the case where
 $r\,\geqslant \, 3$
while
$r\,\geqslant \, 3$
while
 $H\,\subset \, k^{\times }{\rm id}_E+\textrm { Hom}(F_2,F_1)$
is again assumed. We may assume the injectivity of the homomorphismbecause it holds for a generic point of
$H\,\subset \, k^{\times }{\rm id}_E+\textrm { Hom}(F_2,F_1)$
is again assumed. We may assume the injectivity of the homomorphismbecause it holds for a generic point of \begin{align*} \textrm { Hom}(F_2,\,F_1)\,\longrightarrow \, \textrm { Hom}(F_2|_{x_2},\,F_1|_{x_2}), \end{align*}
\begin{align*} \textrm { Hom}(F_2,\,F_1)\,\longrightarrow \, \textrm { Hom}(F_2|_{x_2},\,F_1|_{x_2}), \end{align*}
 $Y'$
. Take a basis
$Y'$
. Take a basis
 $f_1,\,f_2,\, \ldots ,\, f_r$
of
$f_1,\,f_2,\, \ldots ,\, f_r$
of
 $E|_{x_2}$
such that
$E|_{x_2}$
such that
 $f_1$
is a generator of
$f_1$
is a generator of
 $l^{(2)}_{r-1}$
. If there is an element
$l^{(2)}_{r-1}$
. If there is an element
 $1_E+a\,\in \, H$
such that
$1_E+a\,\in \, H$
such that
 $a\,\in \,\textrm { Hom}(F_2,\,F_1)\setminus \{0\}$
and
$a\,\in \,\textrm { Hom}(F_2,\,F_1)\setminus \{0\}$
and
 ${\rm Im}(a|_{x_2})\,\not \subset \, l^{(2)}_{r-1}$
, then, after applying such an automorphism, we can normalize a representative
${\rm Im}(a|_{x_2})\,\not \subset \, l^{(2)}_{r-1}$
, then, after applying such an automorphism, we can normalize a representative
 $a_2f_2+\cdots +a_rf_r$
of a generator of
$a_2f_2+\cdots +a_rf_r$
of a generator of
 $l^{(2)}_{r-2}/l^{(2)}_{r-1}$
so that the condition
$l^{(2)}_{r-2}/l^{(2)}_{r-1}$
so that the condition
 $a_p\,=\, 0$
holds for some
$a_p\,=\, 0$
holds for some
 $p\,\geqslant \, 2$
. Such a locus in
$p\,\geqslant \, 2$
. Such a locus in
 $Y$
is of dimension at most
$Y$
is of dimension at most
 $r(r-1)n/2-2$
. If the condition
$r(r-1)n/2-2$
. If the condition
 ${\rm Im}(a|_{x_2})\,\subset \, l^{(2)}_{r-1}$
holds for all
${\rm Im}(a|_{x_2})\,\subset \, l^{(2)}_{r-1}$
holds for all
 $a\,\in \,\textrm { Hom}(F_2,F_1)$
satisfying
$a\,\in \,\textrm { Hom}(F_2,F_1)$
satisfying
 ${\rm id}_E+a\,\in \, H$
, then we have
${\rm id}_E+a\,\in \, H$
, then we have
 $l^{(2)}_{r-1}\,=\, {\rm Im}(a|_{x_2})$
for such an
$l^{(2)}_{r-1}\,=\, {\rm Im}(a|_{x_2})$
for such an
 $a$
with
$a$
with
 $a\,\neq \, 0$
. So we may replace
$a\,\neq \, 0$
. So we may replace
 $Y'$
with a Zariski closed subset whose dimension is at most
$Y'$
with a Zariski closed subset whose dimension is at most
 $r(r-1)n/2-(r-1)\,\leqslant \, r(r-1)n/2-2$
, because
$r(r-1)n/2-(r-1)\,\leqslant \, r(r-1)n/2-2$
, because
 $r\,\geqslant \, 3$
.
$r\,\geqslant \, 3$
.
-
Therefore, in all cases, the disjoint union
![]() $Z$
of all the locally closed subsets of
$Z$
of all the locally closed subsets of
![]() $Y''$
in the above argument and the pullback of flat families
$Y''$
in the above argument and the pullback of flat families
![]() $(\widetilde {E},\,\widetilde {\boldsymbol{l}})|_{X\times Z}$
satisfy the assertion of the proposition.
$(\widetilde {E},\,\widetilde {\boldsymbol{l}})|_{X\times Z}$
satisfy the assertion of the proposition.
Proposition 5.12. Assume that
![]() $X\,=\,\mathbb{P}^1_k$
,
$X\,=\,\mathbb{P}^1_k$
,
![]() $L$
is a line bundle on
$L$
is a line bundle on
![]() $\mathbb{P}^1_k$
and one of the following two holds:
$\mathbb{P}^1_k$
and one of the following two holds:
-
(I)
 $n\,\geqslant \, 5$
and
$n\,\geqslant \, 5$
and
 $r\,\geqslant \, 2$
; or
$r\,\geqslant \, 2$
; or -
(II)
 $n\,=\,4$
and
$n\,=\,4$
and
 $r\,\geqslant \, 3$
.
$r\,\geqslant \, 3$
.
Then there exists a scheme
![]() $Z$
of finite type over
$Z$
of finite type over
![]() $\textrm { Spec}\, k$
and a flat family
$\textrm { Spec}\, k$
and a flat family
![]() $(\widetilde {E},\,\widetilde {\boldsymbol{l}})$
of quasi-parabolic bundles on
$(\widetilde {E},\,\widetilde {\boldsymbol{l}})$
of quasi-parabolic bundles on
![]() $\mathbb{P}^1\times Z$
over
$\mathbb{P}^1\times Z$
over
![]() $Z$
such that:
$Z$
such that:
 $\dim Z \,\leqslant \, -r^2+r(r-1)n/2-1$
;
$\dim Z \,\leqslant \, -r^2+r(r-1)n/2-1$
; $\dim \textrm { End}\left ( (\widetilde {E},\,\widetilde {\boldsymbol{l}})|_{\mathbb{P}^1\times \{z\}}\right ) \,\geqslant \, 2$
for any
$\dim \textrm { End}\left ( (\widetilde {E},\,\widetilde {\boldsymbol{l}})|_{\mathbb{P}^1\times \{z\}}\right ) \,\geqslant \, 2$
for any
 $z\,\in \,Z$
;
$z\,\in \,Z$
;
and each member of the complement
![]() $\left | {\mathcal N}^{n_0\textrm { -reg}}_{{\rm par}}(L) \right | \setminus \left | {\mathcal N}^{n_0\textrm { -reg}}_{{\rm par}}(L)^{\circ } \right |$
is isomorphic to
$\left | {\mathcal N}^{n_0\textrm { -reg}}_{{\rm par}}(L) \right | \setminus \left | {\mathcal N}^{n_0\textrm { -reg}}_{{\rm par}}(L)^{\circ } \right |$
is isomorphic to
![]() $(\widetilde {E},\,\widetilde {\boldsymbol{l}})|_{\mathbb{P}^1\times \{z\}}$
for some point
$(\widetilde {E},\,\widetilde {\boldsymbol{l}})|_{\mathbb{P}^1\times \{z\}}$
for some point
![]() $z\,\in \, Z$
.
$z\,\in \, Z$
.
Proof. Take a quasi-parabolic bundle
![]() $(E,\,\boldsymbol{l})$
. Write
$(E,\,\boldsymbol{l})$
. Write
with
![]() $a_1\,\lt \,\cdots \,\lt \,a_m$
. If
$a_1\,\lt \,\cdots \,\lt \,a_m$
. If
![]() $l^{(i)}_{r-1}\,\not \subset \, {\mathcal O}_{\mathbb{P}^1}(a_2)^{\oplus r_2}\big |_{x_i}\oplus \cdots \oplus {\mathcal O}_{\mathbb{P}^1}(a_m)^{\oplus r_m}\big |_{x_i}$
for some
$l^{(i)}_{r-1}\,\not \subset \, {\mathcal O}_{\mathbb{P}^1}(a_2)^{\oplus r_2}\big |_{x_i}\oplus \cdots \oplus {\mathcal O}_{\mathbb{P}^1}(a_m)^{\oplus r_m}\big |_{x_i}$
for some
![]() $i$
, set
$i$
, set
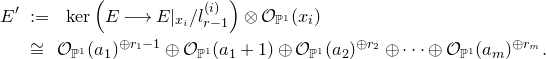 \begin{align*} \begin{aligned} E'\,\,&:=\,\, \ \ker \left ( E\longrightarrow E|_{x_i}/l^{(i)}_{r-1} \right ) \otimes {\mathcal O}_{\mathbb{P}^1}(x_i) \\ &\cong \, \ {\mathcal O}_{\mathbb{P}^1}(a_1)^{\oplus r_1-1}\oplus {\mathcal O}_{\mathbb{P}^1}(a_1+1) \oplus {\mathcal O}_{\mathbb{P}^1}(a_2)^{\oplus r_2}\oplus \cdots \oplus {\mathcal O}_{\mathbb{P}^1}(a_m)^{\oplus r_m}. \end{aligned} \end{align*}
\begin{align*} \begin{aligned} E'\,\,&:=\,\, \ \ker \left ( E\longrightarrow E|_{x_i}/l^{(i)}_{r-1} \right ) \otimes {\mathcal O}_{\mathbb{P}^1}(x_i) \\ &\cong \, \ {\mathcal O}_{\mathbb{P}^1}(a_1)^{\oplus r_1-1}\oplus {\mathcal O}_{\mathbb{P}^1}(a_1+1) \oplus {\mathcal O}_{\mathbb{P}^1}(a_2)^{\oplus r_2}\oplus \cdots \oplus {\mathcal O}_{\mathbb{P}^1}(a_m)^{\oplus r_m}. \end{aligned} \end{align*}
Repeating such process of elementary transformations and a twist by a line bundle, we may replace
![]() $(E,\,\boldsymbol{l})$
with a quasi-parabolic bundle which satisfies one of the following two conditions:
$(E,\,\boldsymbol{l})$
with a quasi-parabolic bundle which satisfies one of the following two conditions:
-
(A)
 $E\,\cong \,{\mathcal O}_{\mathbb{P}^1}^{\oplus r}$
;
$E\,\cong \,{\mathcal O}_{\mathbb{P}^1}^{\oplus r}$
; -
(B)
 $E\,=\,{\mathcal O}_{\mathbb{P}^1}(a_1)^{\oplus r_1}\oplus \cdots \oplus {\mathcal O}_{\mathbb{P}^1}(a_m)^{\oplus r_m}$
and
$E\,=\,{\mathcal O}_{\mathbb{P}^1}(a_1)^{\oplus r_1}\oplus \cdots \oplus {\mathcal O}_{\mathbb{P}^1}(a_m)^{\oplus r_m}$
and
 $l^{(i)}_{r-1}\subset {\mathcal O}_{\mathbb{P}^1}(a_2)^{\oplus r_2}\big |_{x_i}\oplus \cdots \oplus {\mathcal O}_{\mathbb{P}^1}(a_m)^{\oplus r_m}\big |_{x_i}$
for any
$l^{(i)}_{r-1}\subset {\mathcal O}_{\mathbb{P}^1}(a_2)^{\oplus r_2}\big |_{x_i}\oplus \cdots \oplus {\mathcal O}_{\mathbb{P}^1}(a_m)^{\oplus r_m}\big |_{x_i}$
for any
 $i$
, where
$i$
, where
 $a_1\,\lt \,a_2\,\lt \,\cdots \,\lt \,a_m$
.
$a_1\,\lt \,a_2\,\lt \,\cdots \,\lt \,a_m$
.
Case A. Consider the case where
![]() $E\,\cong \,{\mathcal O}_{\mathbb{P}^1}^{\oplus r}$
.
$E\,\cong \,{\mathcal O}_{\mathbb{P}^1}^{\oplus r}$
.
We will construct a parameter space for non-simple quasi-parabolic bundles
![]() $(E,\,\boldsymbol{l})$
satisfying
$(E,\,\boldsymbol{l})$
satisfying
![]() $E\,\cong \,{\mathcal O}_{\mathbb{P}^1}^{\oplus r}$
. Let
$E\,\cong \,{\mathcal O}_{\mathbb{P}^1}^{\oplus r}$
. Let
![]() $e_1,\,\cdots ,\,e_r$
be the basis of
$e_1,\,\cdots ,\,e_r$
be the basis of
![]() $E$
obtained by pulling back the canonical basis of
$E$
obtained by pulling back the canonical basis of
![]() ${\mathcal O}_{\mathbb{P}^1}^{\oplus r}$
via the isomorphism
${\mathcal O}_{\mathbb{P}^1}^{\oplus r}$
via the isomorphism
![]() $E\,\xrightarrow {\,\sim \,}\, {\mathcal O}_{\mathbb{P}^1}^{\oplus r}$
. We may assume that
$E\,\xrightarrow {\,\sim \,}\, {\mathcal O}_{\mathbb{P}^1}^{\oplus r}$
. We may assume that
![]() $l^{(1)}_*$
is given by
$l^{(1)}_*$
is given by
![]() $l^{(1)}_j\,=\,\langle e_1,\,\cdots ,\,e_{r-j} \rangle$
for
$l^{(1)}_j\,=\,\langle e_1,\,\cdots ,\,e_{r-j} \rangle$
for
![]() $j\,=\,0,\,\cdots ,\,r-1$
, after applying an automorphism of
$j\,=\,0,\,\cdots ,\,r-1$
, after applying an automorphism of
![]() $E$
. Applying automorphisms of
$E$
. Applying automorphisms of
![]() $E$
fixing
$E$
fixing
![]() $l^{(1)}_*$
, we may further assume that
$l^{(1)}_*$
, we may further assume that
![]() $l^{(2)}_*$
is given by
$l^{(2)}_*$
is given by
![]() $l^{(2)}_j\,=\,\langle e_{\sigma (1)},\,\cdots ,\, e_{\sigma (r-j)} \rangle$
for
$l^{(2)}_j\,=\,\langle e_{\sigma (1)},\,\cdots ,\, e_{\sigma (r-j)} \rangle$
for
![]() $j\,=\,0,1,\,\cdots ,\,r-1$
, where
$j\,=\,0,1,\,\cdots ,\,r-1$
, where
![]() $\sigma$
is a permutation of
$\sigma$
is a permutation of
![]() $\{1,\,\cdots ,\,r\}$
. Let
$\{1,\,\cdots ,\,r\}$
. Let
![]() $w_1e_1+\cdots +w_re_r$
be a generator of
$w_1e_1+\cdots +w_re_r$
be a generator of
![]() $l^{(3)}_{r-1}$
. Applying a diagonal automorphism of
$l^{(3)}_{r-1}$
. Applying a diagonal automorphism of
![]() $E$
, which automatically fixes
$E$
, which automatically fixes
![]() $l^{(1)}_*$
and
$l^{(1)}_*$
and
![]() $l^{(2)}_*$
, we may assume that either
$l^{(2)}_*$
, we may assume that either
![]() $w_i\,=\,1$
holds or
$w_i\,=\,1$
holds or
![]() $w_i\,=\, 0$
holds for any
$w_i\,=\, 0$
holds for any
![]() $i$
. Then the group of automorphisms of
$i$
. Then the group of automorphisms of
![]() $E$
fixing
$E$
fixing
![]() $l^{(1)}_*$
,
$l^{(1)}_*$
,
![]() $l^{(2)}_*$
and
$l^{(2)}_*$
and
![]() $l^{(3)}_{r-1}$
becomes
$l^{(3)}_{r-1}$
becomes
Since
![]() $\dim \textrm { End}(E,\,\boldsymbol{l})\,\geqslant \, 2$
by the assumption, it follows that either there is some
$\dim \textrm { End}(E,\,\boldsymbol{l})\,\geqslant \, 2$
by the assumption, it follows that either there is some
![]() $(i,\,j)$
with
$(i,\,j)$
with
![]() $i\,\lt \,j$
and
$i\,\lt \,j$
and
![]() $\sigma (i)\,\lt \,\sigma (j)$
or there is some
$\sigma (i)\,\lt \,\sigma (j)$
or there is some
![]() $i$
satisfying the condition
$i$
satisfying the condition
![]() $w_i\,=\,0$
.
$w_i\,=\,0$
.
-
(I) First assume that
 $n\,\geqslant \, 5$
and
$n\,\geqslant \, 5$
and
 $r\,\geqslant \, 2$
.
$r\,\geqslant \, 2$
.
-
(i) Consider the case where
 $w_{i_1}\,=\,0$
for some
$w_{i_1}\,=\,0$
for some
 $i_1$
. Then there are automorphisms
$i_1$
. Then there are automorphisms
 $(a_{ij})$
in
$(a_{ij})$
in
 $B''$
such that
$B''$
such that
 $a_{i_1i_1}\,=\,c\,\in \,k^{\times }$
,
$a_{i_1i_1}\,=\,c\,\in \,k^{\times }$
,
 $a_{ii}\,=\,1$
for
$a_{ii}\,=\,1$
for
 $i\neq i_1$
and
$i\neq i_1$
and
 $a_{ij}\,=\,0$
for all
$a_{ij}\,=\,0$
for all
 $i\,\neq \, j$
. Applying these automorphisms to a generator
$i\,\neq \, j$
. Applying these automorphisms to a generator
 $v\,=\,v_1e_1+\cdots +v_re_r$
of
$v\,=\,v_1e_1+\cdots +v_re_r$
of
 $l^{(4)}_{r-1}$
, normalize
$l^{(4)}_{r-1}$
, normalize
 $v$
so that one of the following holds:
$v$
so that one of the following holds: $v_{i_1}\,=\,0$
; or
$v_{i_1}\,=\,0$
; or $v_{i_1}\,\neq \, 0$
and
$v_{i_1}\,\neq \, 0$
and
 $v_{i'}\,=\,0$
for any
$v_{i'}\,=\,0$
for any
 $i'\,\neq \, i_1$
; or
$i'\,\neq \, i_1$
; or $v_{i_1}\,=\,v_{i'}\,\neq \, 0$
for some
$v_{i_1}\,=\,v_{i'}\,\neq \, 0$
for some
 $i'\,\neq \, i_1$
.
$i'\,\neq \, i_1$
.
So there is a parameter space of
 $l^{(4)}_{r-1}$
whose dimension is at most
$l^{(4)}_{r-1}$
whose dimension is at most
 $r-1-1\,=\,r-2$
.
$r-1-1\,=\,r-2$
.
-
(ii) Consider the case where
 $w_i\,=\,1$
for every
$w_i\,=\,1$
for every
 $i$
. Then there are some
$i$
. Then there are some
 $i_1\,\lt \,i_2$
with
$i_1\,\lt \,i_2$
with
 $\sigma (i_1)\,\lt \,\sigma (i_2)$
, because
$\sigma (i_1)\,\lt \,\sigma (i_2)$
, because
 $\dim B''\,\geqslant \,2$
. So there are automorphisms
$\dim B''\,\geqslant \,2$
. So there are automorphisms
 $(a_{ij})$
in
$(a_{ij})$
in
 $B''$
of the form
$B''$
of the form
 $a_{\sigma (i_1)\sigma (i_1)}\,=\,c\in k^{\times }\setminus \{1\}$
,
$a_{\sigma (i_1)\sigma (i_1)}\,=\,c\in k^{\times }\setminus \{1\}$
,
 $a_{\sigma (i_1)\sigma (i_2)}\,=\,1-c$
,
$a_{\sigma (i_1)\sigma (i_2)}\,=\,1-c$
,
 $a_{ii}\,=\,1$
for
$a_{ii}\,=\,1$
for
 $i\,\neq \, \sigma (i_1)$
and
$i\,\neq \, \sigma (i_1)$
and
 $a_{ij}\,=\,0$
if
$a_{ij}\,=\,0$
if
 $i\,\neq \, j$
and
$i\,\neq \, j$
and
 $(i,\,j)\,\neq \,(\sigma (i_1),\,\sigma (i_2))$
. Applying these automorphisms to a generator
$(i,\,j)\,\neq \,(\sigma (i_1),\,\sigma (i_2))$
. Applying these automorphisms to a generator
 $v\,=\,v_1e_1+\cdots +v_re_r$
of
$v\,=\,v_1e_1+\cdots +v_re_r$
of
 $l^{(4)}_{r-1}$
, normalize
$l^{(4)}_{r-1}$
, normalize
 $v$
so that one of the following holds:
$v$
so that one of the following holds: $v_{\sigma (i_2)}\,=\,0$
; or
$v_{\sigma (i_2)}\,=\,0$
; or $v_{\sigma (i_1)}\,=\,v_{\sigma (i_2)}\,\neq \, 0$
; or
$v_{\sigma (i_1)}\,=\,v_{\sigma (i_2)}\,\neq \, 0$
; or $v_{\sigma (i_1)}\,=\,0$
,
$v_{\sigma (i_1)}\,=\,0$
,
 $v_{\sigma (i_2)}\,\neq \, 0$
.
$v_{\sigma (i_2)}\,\neq \, 0$
.
So there is a parameter space of
 $l^{(4)}_{r-1}$
whose dimension is at most
$l^{(4)}_{r-1}$
whose dimension is at most
 $r-1-1\,=\,r-2$
.
$r-1-1\,=\,r-2$
.In both cases A(I)(i) and A(I)(ii), consider the group of automorphisms
Since \begin{align*} B'''\,\,:=\,\, \left \{ g\in B'' \,\, \middle |\,\,\, {\textbf{g}}\ \rm fixes\ l^{(1)}_*,\,l^{(2)}_*,\,l^{(3)}_{r-1}\ and\ l^{(4)}_{r-1} \right \}. \end{align*}
\begin{align*} B'''\,\,:=\,\, \left \{ g\in B'' \,\, \middle |\,\,\, {\textbf{g}}\ \rm fixes\ l^{(1)}_*,\,l^{(2)}_*,\,l^{(3)}_{r-1}\ and\ l^{(4)}_{r-1} \right \}. \end{align*}
 $(E,\,l)$
is not simple, there is an automorphism
$(E,\,l)$
is not simple, there is an automorphism
 $\textbf {g}$
in
$\textbf {g}$
in
 $B'''$
other than a scalar endomorphism. Then the parameter space of
$B'''$
other than a scalar endomorphism. Then the parameter space of
 $l^{(5)}_{r-1}$
preserved by
$l^{(5)}_{r-1}$
preserved by
 $\textbf {g}$
is of dimension at most
$\textbf {g}$
is of dimension at most
 $r-1-1$
. Thus, there is a parameter space of
$r-1-1$
. Thus, there is a parameter space of
 $l^{(1)}_*,\,\ldots ,\,l^{(n)}_*$
whose dimension is at most
$l^{(1)}_*,\,\ldots ,\,l^{(n)}_*$
whose dimension is at most \begin{align*} \sum _{j=1}^{r-2} j+2\bigg ( r-2+\sum _{j=1}^{r-2}j \,\bigg ) +(n-5)\sum _{j=1}^{r-1} j \,=\,-r^2+1+\frac {1}{2}r(r-1)n-2. \end{align*}
\begin{align*} \sum _{j=1}^{r-2} j+2\bigg ( r-2+\sum _{j=1}^{r-2}j \,\bigg ) +(n-5)\sum _{j=1}^{r-1} j \,=\,-r^2+1+\frac {1}{2}r(r-1)n-2. \end{align*}
-
(II) Assume that
 $n\,=\,4$
and
$n\,=\,4$
and
 $r\,\geqslant \, 3$
.
$r\,\geqslant \, 3$
.
-
(i) Assume that
 $w_{i_1}\,=\,0$
for some
$w_{i_1}\,=\,0$
for some
 $i_1$
. Then there are automorphisms
$i_1$
. Then there are automorphisms
 $(a_{ij})$
in
$(a_{ij})$
in
 $B''$
of the form
$B''$
of the form
 $a_{ii}\,=\,1\,\in \,k^{\times }$
for
$a_{ii}\,=\,1\,\in \,k^{\times }$
for
 $i\,\neq \, i_1$
,
$i\,\neq \, i_1$
,
 $a_{i_1i_1}\,=\,c\in \,k^{\times }$
and
$a_{i_1i_1}\,=\,c\in \,k^{\times }$
and
 $a_{ij}\,=\,0$
for all
$a_{ij}\,=\,0$
for all
 $i\,\neq \, j$
. For a representative
$i\,\neq \, j$
. For a representative
 $v\,=\,v_1e_1+\cdots +v_re_r\,\in \, l^{(3)}_{r-2}$
of a generator of
$v\,=\,v_1e_1+\cdots +v_re_r\,\in \, l^{(3)}_{r-2}$
of a generator of
 $l^{(3)}_{r-2}/l^{(3)}_{r-1}$
, we may assume, after adding an element of
$l^{(3)}_{r-2}/l^{(3)}_{r-1}$
, we may assume, after adding an element of
 $l^{(3)}_{r-1}$
, that
$l^{(3)}_{r-1}$
, that
 $v_{i_2}\,=\,0$
for some
$v_{i_2}\,=\,0$
for some
 $i_2\,\neq \, i_1$
. Applying an automorphism in
$i_2\,\neq \, i_1$
. Applying an automorphism in
 $B''$
of the above form, normalize
$B''$
of the above form, normalize
 $v$
so that one of the following holds:
$v$
so that one of the following holds:-
(1)
 $v_{i_1}\,=\,0$
; or
$v_{i_1}\,=\,0$
; or -
(2)
 $v_{i_1}\,\neq \, 0$
and
$v_{i_1}\,\neq \, 0$
and
 $v_{i'}\,=\,0$
for any
$v_{i'}\,=\,0$
for any
 $i'\,\neq \, i_1$
; or
$i'\,\neq \, i_1$
; or -
(3)
 $v_{i_1}\,=\,v_{i_3}\,\neq \, 0$
for some
$v_{i_1}\,=\,v_{i_3}\,\neq \, 0$
for some
 $i_3\,\neq \, i_1,\,i_2$
.
$i_3\,\neq \, i_1,\,i_2$
.
So there is a parameter space of
 $l^{(3)}_{r-2}$
whose dimension is at most
$l^{(3)}_{r-2}$
whose dimension is at most
 $r-2-1\,=\,r-3$
.
$r-2-1\,=\,r-3$
. -
-
(ii) Assume that
 $w_i\,=\,1$
for any
$w_i\,=\,1$
for any
 $i$
. Then there are some
$i$
. Then there are some
 $i_1\,\lt \,i_2$
with
$i_1\,\lt \,i_2$
with
 $\sigma (i_1)\,\lt \,\sigma (i_2)$
because
$\sigma (i_1)\,\lt \,\sigma (i_2)$
because
 $B''\,\neq \,k^{\times }{\rm id}$
. Then there are automorphisms
$B''\,\neq \,k^{\times }{\rm id}$
. Then there are automorphisms
 $(a_{ij})$
in
$(a_{ij})$
in
 $B''$
of the form
$B''$
of the form
 $a_{\sigma (i_1) \sigma (i_1)}\,=\,c\,\in \,k^{\times }\setminus \{1\}$
,
$a_{\sigma (i_1) \sigma (i_1)}\,=\,c\,\in \,k^{\times }\setminus \{1\}$
,
 $a_{\sigma (i_1) \sigma (i_2)}\,=\,1-c$
,
$a_{\sigma (i_1) \sigma (i_2)}\,=\,1-c$
,
 $a_{ii}\,=\,1$
for
$a_{ii}\,=\,1$
for
 $i\,\neq \, \sigma (i_1)$
and
$i\,\neq \, \sigma (i_1)$
and
 $a_{ij}\,=\,0$
if
$a_{ij}\,=\,0$
if
 $i\,\neq \, j$
and
$i\,\neq \, j$
and
 $(i,\,j)\,\neq \,(\sigma (i_1),\,\sigma (i_2))$
. For a representative
$(i,\,j)\,\neq \,(\sigma (i_1),\,\sigma (i_2))$
. For a representative
 $v\,=\,v_1e_1+\cdots +v_re_r\in l^{(3)}_{r-2}$
of a generator of
$v\,=\,v_1e_1+\cdots +v_re_r\in l^{(3)}_{r-2}$
of a generator of
 $l^{(3)}_{r-2}/l^{(3)}_{r-1}$
, we may assume, after adding an element of
$l^{(3)}_{r-2}/l^{(3)}_{r-1}$
, we may assume, after adding an element of
 $l^{(3)}_{r-1}$
, that
$l^{(3)}_{r-1}$
, that
 $v_{i'}\,=\,0$
for some
$v_{i'}\,=\,0$
for some
 $i' \,\neq \, \sigma (i_1),\,\sigma (i_2)$
. Applying an automorphism in
$i' \,\neq \, \sigma (i_1),\,\sigma (i_2)$
. Applying an automorphism in
 $B''$
, normalize
$B''$
, normalize
 $v$
so that one of the following holds:
$v$
so that one of the following holds: $v_{\sigma (i_1)}\,=\,v_{\sigma (i_2)}$
; or
$v_{\sigma (i_1)}\,=\,v_{\sigma (i_2)}$
; or $v_{\sigma (i_1)}v_{\sigma (i_2)}\,=\,0$
.
$v_{\sigma (i_1)}v_{\sigma (i_2)}\,=\,0$
.
So there is a parameter space of
 $l^{(3)}_{r-2}$
whose dimension is at most
$l^{(3)}_{r-2}$
whose dimension is at most
 $r-2-1\,=\,r-3$
.
$r-2-1\,=\,r-3$
.In both cases A(II)(i) and A(II)(ii), consider the group of automorphisms
Since \begin{align*} B'''\,\,:=\,\, \left \{ \textbf {g}\,\in \, B'' \,\, \middle | \,\: \rm \textbf {g}\ fixes\ l^{(1)}_*,\,l^{(2)}_*,\,l^{(3)}_{r-1}\ and\ l^{(3)}_{r-2} \right \}. \end{align*}
\begin{align*} B'''\,\,:=\,\, \left \{ \textbf {g}\,\in \, B'' \,\, \middle | \,\: \rm \textbf {g}\ fixes\ l^{(1)}_*,\,l^{(2)}_*,\,l^{(3)}_{r-1}\ and\ l^{(3)}_{r-2} \right \}. \end{align*}
 $(E,\,l)$
is not simple, there is an automorphism
$(E,\,l)$
is not simple, there is an automorphism
 $\textbf {g}$
in
$\textbf {g}$
in
 $B'''$
other than a scalar automorphism. The parameter space of
$B'''$
other than a scalar automorphism. The parameter space of
 $l^{(4)}_{r-1}$
preserved by
$l^{(4)}_{r-1}$
preserved by
 $\textbf {g}$
is of dimension at most
$\textbf {g}$
is of dimension at most
 $r-1-1\,=\,r-2$
. Thus, there is a parameter space of
$r-1-1\,=\,r-2$
. Thus, there is a parameter space of
 $l^{(1)}_*,\,\ldots ,\,l^{(n)}_*$
whose dimension is at most
$l^{(1)}_*,\,\ldots ,\,l^{(n)}_*$
whose dimension is at most \begin{align*} (r-3)+\sum _{j=1}^{r-3} j \:+(r-2)+\sum _{j=1}^{r-2} j \: + \,\frac {1}{2}r(r-1) (n-4) =\, -r^2-1+\frac {1}{2}r(r-1)n. \end{align*}
\begin{align*} (r-3)+\sum _{j=1}^{r-3} j \:+(r-2)+\sum _{j=1}^{r-2} j \: + \,\frac {1}{2}r(r-1) (n-4) =\, -r^2-1+\frac {1}{2}r(r-1)n. \end{align*}
Case B. Consider the case where
![]() $E\,\cong \, {\mathcal O}_{\mathbb{P}^1}(a_1)^{\oplus r_1}\oplus \cdots \oplus {\mathcal O}_{\mathbb{P}^1}(a_m)^{\oplus r_m}$
with
$E\,\cong \, {\mathcal O}_{\mathbb{P}^1}(a_1)^{\oplus r_1}\oplus \cdots \oplus {\mathcal O}_{\mathbb{P}^1}(a_m)^{\oplus r_m}$
with
![]() $a_1\,\lt \,a_2\,\lt \,\cdots \,\lt \,a_m$
and
$a_1\,\lt \,a_2\,\lt \,\cdots \,\lt \,a_m$
and
![]() $l^{(i)}_{r-1}\,\subset \, \big ( {\mathcal O}_{\mathbb{P}^1}(a_2)^{\oplus r_2}\oplus \cdots \oplus {\mathcal O}_{\mathbb{P}^1}(a_m)^{\oplus r_m}\big )\big |_{x_i}$
for any
$l^{(i)}_{r-1}\,\subset \, \big ( {\mathcal O}_{\mathbb{P}^1}(a_2)^{\oplus r_2}\oplus \cdots \oplus {\mathcal O}_{\mathbb{P}^1}(a_m)^{\oplus r_m}\big )\big |_{x_i}$
for any
![]() $i$
.
$i$
.
We choose a basis
![]() $e^{(i)}_{1,1},\,\cdots ,\,e^{(i)}_{1,r_1},\,e^{(i)}_{2,1},\,\cdots ,\,e^{(i)}_{2,r_2},\,\cdots , \,e^{(i)}_{m,1},\,\cdots ,\,e^{(i)}_{m,r_m}$
of
$e^{(i)}_{1,1},\,\cdots ,\,e^{(i)}_{1,r_1},\,e^{(i)}_{2,1},\,\cdots ,\,e^{(i)}_{2,r_2},\,\cdots , \,e^{(i)}_{m,1},\,\cdots ,\,e^{(i)}_{m,r_m}$
of
![]() $E\big \vert _{x_i}$
corresponding to the given decomposition
$E\big \vert _{x_i}$
corresponding to the given decomposition
![]() $E\big \vert _{x_i}\,=\, {\mathcal O}_{\mathbb{P}^1}(a_1)\big |_{x_i}^{\oplus r_1}\oplus \cdots \oplus {\mathcal O}_{\mathbb{P}^1}(a_m)\big |_{x_i}^{\oplus r_m}$
. For
$E\big \vert _{x_i}\,=\, {\mathcal O}_{\mathbb{P}^1}(a_1)\big |_{x_i}^{\oplus r_1}\oplus \cdots \oplus {\mathcal O}_{\mathbb{P}^1}(a_m)\big |_{x_i}^{\oplus r_m}$
. For
![]() $1\, \leqslant \, p\, \leqslant \, m$
, let
$1\, \leqslant \, p\, \leqslant \, m$
, let
be the projection to the
![]() $p$
-th direct summand. So any element
$p$
-th direct summand. So any element
![]() $v\,\in \, E\big \vert _{x_i}$
can be uniquely written as follows:
$v\,\in \, E\big \vert _{x_i}$
can be uniquely written as follows:
We want to choose suitable generators
![]() $v^{(i)}_{p^{(i)}(1),\,j^{(i)}(1)},\,\cdots ,\,v^{(i)}_{p^{(i)}(s),\,j^{(i)}(s)}$
of
$v^{(i)}_{p^{(i)}(1),\,j^{(i)}(1)},\,\cdots ,\,v^{(i)}_{p^{(i)}(s),\,j^{(i)}(s)}$
of
![]() $l^{(i)}_{r-s}$
. First, define a number
$l^{(i)}_{r-s}$
. First, define a number
![]() $p^{(i)}(1)$
with
$p^{(i)}(1)$
with
![]() $1\,\leqslant \, p^{(i)}(1)\,\leqslant \, m$
by setting
$1\,\leqslant \, p^{(i)}(1)\,\leqslant \, m$
by setting
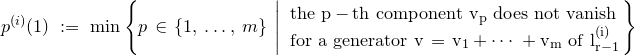 \begin{align*} p^{(i)}(1)\,\,:=\,\,\min \left \{ p\,\in \,\{1,\,\ldots ,\,m\}\, \, \middle |\, \: \begin{array}{l} \rm the\ p-th\ component\ v_p\ does\ not\ vanish \\ \rm for\ a\ generator\ v\,=\,v_1+\cdots\ +v_m\ of\ l^{(i)}_{r-1} \end{array} \right \} \end{align*}
\begin{align*} p^{(i)}(1)\,\,:=\,\,\min \left \{ p\,\in \,\{1,\,\ldots ,\,m\}\, \, \middle |\, \: \begin{array}{l} \rm the\ p-th\ component\ v_p\ does\ not\ vanish \\ \rm for\ a\ generator\ v\,=\,v_1+\cdots\ +v_m\ of\ l^{(i)}_{r-1} \end{array} \right \} \end{align*}
for each
![]() $1\,\leqslant \, i\,\leqslant \, n$
. So, we can choose an element
$1\,\leqslant \, i\,\leqslant \, n$
. So, we can choose an element
![]() $v\,=\,v_{p^{(i)}(1)}+v_{p^{(i)}(1)+1}+\cdots +v_m\in l^{(i)}_{r-1}$
with
$v\,=\,v_{p^{(i)}(1)}+v_{p^{(i)}(1)+1}+\cdots +v_m\in l^{(i)}_{r-1}$
with
![]() $v_{p^{(i)}(1)}\,\neq \, 0$
. Put
$v_{p^{(i)}(1)}\,\neq \, 0$
. Put
![]() $j^{(i)}(1)\,=\,1$
and set
$j^{(i)}(1)\,=\,1$
and set
![]() $v^{(i)}_{p^{(i)}(1),j^{(i)}(1)}\,\,:=\,\,v$
. Consider the projection
$v^{(i)}_{p^{(i)}(1),j^{(i)}(1)}\,\,:=\,\,v$
. Consider the projection
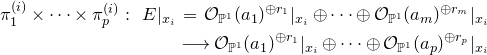 \begin{align*} \pi ^{(i)}_1\times \cdots \times \pi ^{(i)}_p \, \colon \ E|_{x_i} \, = \, {\mathcal O}_{\mathbb{P}^1}(a_1)^{\oplus r_1}|_{x_i}\oplus \cdots \oplus {\mathcal O}_{\mathbb{P}^1}(a_m)^{\oplus r_m}|_{x_i}\\ \longrightarrow {\mathcal O}_{\mathbb{P}^1}(a_1)^{\oplus r_1}|_{x_i}\oplus \cdots \oplus {\mathcal O}_{\mathbb{P}^1}(a_p)^{\oplus r_p}|_{x_i} \end{align*}
\begin{align*} \pi ^{(i)}_1\times \cdots \times \pi ^{(i)}_p \, \colon \ E|_{x_i} \, = \, {\mathcal O}_{\mathbb{P}^1}(a_1)^{\oplus r_1}|_{x_i}\oplus \cdots \oplus {\mathcal O}_{\mathbb{P}^1}(a_m)^{\oplus r_m}|_{x_i}\\ \longrightarrow {\mathcal O}_{\mathbb{P}^1}(a_1)^{\oplus r_1}|_{x_i}\oplus \cdots \oplus {\mathcal O}_{\mathbb{P}^1}(a_p)^{\oplus r_p}|_{x_i} \end{align*}
for
![]() $1\,\leqslant \, p\,\leqslant \, m$
. For
$1\,\leqslant \, p\,\leqslant \, m$
. For
![]() $2\,\leqslant \, s\,\leqslant \, r-1$
, define
$2\,\leqslant \, s\,\leqslant \, r-1$
, define
![]() $p^{(i)}(s)$
,
$p^{(i)}(s)$
,
![]() $j^{(i)}(s)$
and
$j^{(i)}(s)$
and
![]() $v^{(i)}_{p^{(i)}(s),j^{(i)}(s)}$
inductively on
$v^{(i)}_{p^{(i)}(s),j^{(i)}(s)}$
inductively on
![]() $s$
. For each integer
$s$
. For each integer
![]() $s$
with
$s$
with
![]() $2\,\leqslant \, s\,\leqslant \, r-1$
, define
$2\,\leqslant \, s\,\leqslant \, r-1$
, define
![]() $p^{(i)}(s)$
by the condition
$p^{(i)}(s)$
by the condition
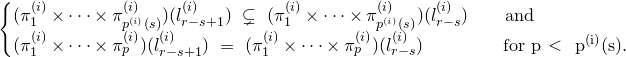 \begin{align*} \begin{cases} (\pi ^{(i)}_1\times \cdots \times \pi ^{(i)}_{p^{(i)}(s)}) (l^{(i)}_{r-s+1}) \,\,\subsetneq \,\, (\pi ^{(i)}_1\times \cdots \times \pi ^{(i)}_{p^{(i)}(s)}) (l^{(i)}_{r-s})\qquad{\rm and} \\ (\pi ^{(i)}_1\times \cdots \times \pi ^{(i)}_p) (l^{(i)}_{r-s+1}) \,\, =\,\, (\pi ^{(i)}_1\times \cdots \times \pi ^{(i)}_p) (l^{(i)}_{r-s}) \qquad\qquad \,\,\rm for\ p\,\lt\ \,p^{(i)}(s). \end{cases}\end{align*}
\begin{align*} \begin{cases} (\pi ^{(i)}_1\times \cdots \times \pi ^{(i)}_{p^{(i)}(s)}) (l^{(i)}_{r-s+1}) \,\,\subsetneq \,\, (\pi ^{(i)}_1\times \cdots \times \pi ^{(i)}_{p^{(i)}(s)}) (l^{(i)}_{r-s})\qquad{\rm and} \\ (\pi ^{(i)}_1\times \cdots \times \pi ^{(i)}_p) (l^{(i)}_{r-s+1}) \,\, =\,\, (\pi ^{(i)}_1\times \cdots \times \pi ^{(i)}_p) (l^{(i)}_{r-s}) \qquad\qquad \,\,\rm for\ p\,\lt\ \,p^{(i)}(s). \end{cases}\end{align*}
Set
Then we can take an element
![]() $v^{(i)}_{p^{(i)}(s), j^{(i)}(s)}$
of
$v^{(i)}_{p^{(i)}(s), j^{(i)}(s)}$
of
![]() $l^{(i)}_{r-s}$
such that
$l^{(i)}_{r-s}$
such that
By the construction, it follows that
![]() $l^{(i)}_{r-s}$
is generated by
$l^{(i)}_{r-s}$
is generated by
![]() $v^{(i)}_{p^{(i)}(1),j^{(i)}(1)},\,\cdots ,\,v^{(i)}_{p^{(i)}(s),j^{(i)}(s)}$
.
$v^{(i)}_{p^{(i)}(1),j^{(i)}(1)},\,\cdots ,\,v^{(i)}_{p^{(i)}(s),j^{(i)}(s)}$
.
Applying an automorphism of
![]() $E$
given by an element of
$E$
given by an element of
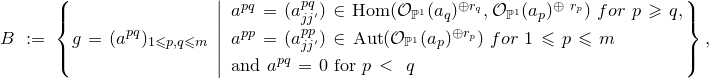 \begin{align*} B\,\,:=\,\, \left \{ g\,=\,(a^{pq})_{1\leqslant p,q\leqslant m}\, \, \middle |\, \: \begin{array}{l} a^{pq}\,=\,(a^{pq}_{jj'})\,\in \,\textrm {Hom}({\mathcal O}_{\mathbb{P}^1}(a_q)^{\oplus r_q}, {\mathcal O}_{\mathbb{P}^1}(a_p)^{\oplus\ r_p})\ for\ p\,\geqslant \, q, \\ [3pt] a^{pp}\,=\,(a^{pp}_{jj'})\,\in \,{\textrm {Aut}}({\mathcal O}_{\mathbb{P}^1}(a_p)^{\oplus r_p})\ for\ 1\,\leqslant \,p\,\leqslant \, m \\ [3pt]{\rm and} \ a^{pq}\,=\,0\ {\rm for}\ p\,\lt\ \,q \end{array} \right \}, \end{align*}
\begin{align*} B\,\,:=\,\, \left \{ g\,=\,(a^{pq})_{1\leqslant p,q\leqslant m}\, \, \middle |\, \: \begin{array}{l} a^{pq}\,=\,(a^{pq}_{jj'})\,\in \,\textrm {Hom}({\mathcal O}_{\mathbb{P}^1}(a_q)^{\oplus r_q}, {\mathcal O}_{\mathbb{P}^1}(a_p)^{\oplus\ r_p})\ for\ p\,\geqslant \, q, \\ [3pt] a^{pp}\,=\,(a^{pp}_{jj'})\,\in \,{\textrm {Aut}}({\mathcal O}_{\mathbb{P}^1}(a_p)^{\oplus r_p})\ for\ 1\,\leqslant \,p\,\leqslant \, m \\ [3pt]{\rm and} \ a^{pq}\,=\,0\ {\rm for}\ p\,\lt\ \,q \end{array} \right \}, \end{align*}
we may assume that
![]() $v^{(1)}_{p,j}\,=\,e^{(1)}_{p,j}$
for
$v^{(1)}_{p,j}\,=\,e^{(1)}_{p,j}$
for
![]() $1\,\leqslant \, p\,\leqslant \, m$
and
$1\,\leqslant \, p\,\leqslant \, m$
and
![]() $1\,\leqslant \, j\,\leqslant \, r_p$
. Note that the group of automorphisms of
$1\,\leqslant \, j\,\leqslant \, r_p$
. Note that the group of automorphisms of
![]() $E$
fixing
$E$
fixing
![]() $l^{(1)}_*$
is
$l^{(1)}_*$
is
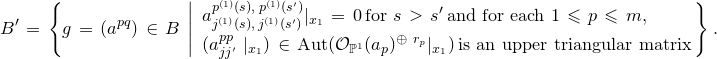 \begin{align*} B'\,=\,\left \{ g\,=\, (a^{pq})\,\in \, B \,\, \middle | \,\: \begin{array}{l} a^{p^{(1)}(s),\,p^{(1)}(s')}_{j^{(1)}(s), \, j^{(1)}(s')} |_{x_1}\,=\,0\, {\rm for}\ s\,\gt \,s'\, {\rm and\ for\ each}\ 1\,\leqslant\, p\,\leqslant\, m, \\ [4pt] (a^{pp}_{jj'}\ |_{x_1} )\,\in \,{\textrm {Aut}}({\mathcal O}_{\mathbb{P}^1}(a_p)^{\oplus\ r_p} |_{x_1})\,{\rm is\ an\ upper\ triangular\ matrix} \end{array} \right \}. \end{align*}
\begin{align*} B'\,=\,\left \{ g\,=\, (a^{pq})\,\in \, B \,\, \middle | \,\: \begin{array}{l} a^{p^{(1)}(s),\,p^{(1)}(s')}_{j^{(1)}(s), \, j^{(1)}(s')} |_{x_1}\,=\,0\, {\rm for}\ s\,\gt \,s'\, {\rm and\ for\ each}\ 1\,\leqslant\, p\,\leqslant\, m, \\ [4pt] (a^{pp}_{jj'}\ |_{x_1} )\,\in \,{\textrm {Aut}}({\mathcal O}_{\mathbb{P}^1}(a_p)^{\oplus\ r_p} |_{x_1})\,{\rm is\ an\ upper\ triangular\ matrix} \end{array} \right \}. \end{align*}
If
![]() $p\,\gt \,q$
, we can always take an element
$p\,\gt \,q$
, we can always take an element
![]() $g\,=\,(a^{pq}_{jj'})$
of
$g\,=\,(a^{pq}_{jj'})$
of
![]() $B'$
such that
$B'$
such that
![]() $a^{pq}_{jj'}\big |_{x_2}\,\neq \, 0$
. So, after applying an automorphism in
$a^{pq}_{jj'}\big |_{x_2}\,\neq \, 0$
. So, after applying an automorphism in
![]() $B'$
to
$B'$
to
![]() $l^{(2)}_*$
, it may be assumed that the condition
$l^{(2)}_*$
, it may be assumed that the condition
![]() $v^{(2)}_{p,j}\,=\,e^{(2)}_{p,\sigma _p(j)}$
holds for
$v^{(2)}_{p,j}\,=\,e^{(2)}_{p,\sigma _p(j)}$
holds for
![]() $1\,\leqslant \, j\,\leqslant \, r_p$
, where
$1\,\leqslant \, j\,\leqslant \, r_p$
, where
![]() $\sigma _p$
is a permutation of
$\sigma _p$
is a permutation of
![]() $\{1,\,\cdots ,\,r_p\}$
. The generator
$\{1,\,\cdots ,\,r_p\}$
. The generator
![]() $v^{(3)}_{p^{(3)}(1),p^{(3)}(1)}$
of
$v^{(3)}_{p^{(3)}(1),p^{(3)}(1)}$
of
![]() $l^{(3)}_{r-1}$
can be written as
$l^{(3)}_{r-1}$
can be written as
Consider the diagonal automorphisms
![]() $\textbf {g}\,=\,(a^{pq}_{jj'})$
of
$\textbf {g}\,=\,(a^{pq}_{jj'})$
of
![]() $E$
given by
$E$
given by
![]() $a^{pq}_{jj'}\,=\,0$
for
$a^{pq}_{jj'}\,=\,0$
for
![]() $(p,\,j)\,\neq \,(q,\,j')$
and
$(p,\,j)\,\neq \,(q,\,j')$
and
![]() $a^{pp}_{jj}\,\in \,k^{\times }$
for any
$a^{pp}_{jj}\,\in \,k^{\times }$
for any
![]() $(p,\,j)$
. After applying such automorphisms, normalize
$(p,\,j)$
. After applying such automorphisms, normalize
![]() $v^{(3)}_{1,1}$
such that either
$v^{(3)}_{1,1}$
such that either
![]() $w_{p,j}\,=\,1$
holds or
$w_{p,j}\,=\,1$
holds or
![]() $w_{p,j}\,=\,0$
holds for any
$w_{p,j}\,=\,0$
holds for any
![]() $p,\,j$
. Note that the conditions
$p,\,j$
. Note that the conditions
![]() $p^{(1)}(1)\,\geqslant \,2$
,
$p^{(1)}(1)\,\geqslant \,2$
,
![]() $p^{(2)}(1)\,\geqslant \, 2$
and
$p^{(2)}(1)\,\geqslant \, 2$
and
![]() $w_{1,1}\,=\,0$
hold, because of the assumption that
$w_{1,1}\,=\,0$
hold, because of the assumption that
![]() $l^{(i)}_{r-1}\,\subset \, \big ( {\mathcal O}_{\mathbb{P}^1}(a_2)^{\oplus r_2}\oplus \cdots \oplus {\mathcal O}_{\mathbb{P}^1}(a_m)^{\oplus r_m}\big )\big |_{x_i}$
for
$l^{(i)}_{r-1}\,\subset \, \big ( {\mathcal O}_{\mathbb{P}^1}(a_2)^{\oplus r_2}\oplus \cdots \oplus {\mathcal O}_{\mathbb{P}^1}(a_m)^{\oplus r_m}\big )\big |_{x_i}$
for
![]() $i\,=\,1,\,2,\,3$
.
$i\,=\,1,\,2,\,3$
.
(I) If
![]() $n\,\geqslant \,5$
, then we can give a parameter space of
$n\,\geqslant \,5$
, then we can give a parameter space of
![]() $l^{(i)}_{r-1}$
whose dimension is at most
$l^{(i)}_{r-1}$
whose dimension is at most
![]() $r-2$
for each
$r-2$
for each
![]() $4\,\leqslant \, i \,\leqslant \, n$
, because
$4\,\leqslant \, i \,\leqslant \, n$
, because
![]() $l^{(i)}_{r-1}\,\subset \, \big ( {\mathcal O}_{\mathbb{P}^1}(a_2)^{\oplus r_2}\oplus \cdots \oplus {\mathcal O}_{\mathbb{P}^1}(a_m)^{\oplus r_m}\big )\big |_{x_i}$
. So there is a parameter space of
$l^{(i)}_{r-1}\,\subset \, \big ( {\mathcal O}_{\mathbb{P}^1}(a_2)^{\oplus r_2}\oplus \cdots \oplus {\mathcal O}_{\mathbb{P}^1}(a_m)^{\oplus r_m}\big )\big |_{x_i}$
. So there is a parameter space of
![]() $(E,\,l)$
whose dimension is at most
$(E,\,l)$
whose dimension is at most
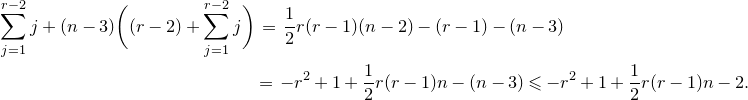 \begin{align*} \sum _{j=1}^{r-2} j + (n-3)\bigg ((r-2)+\sum _{j=1}^{r-2}j \bigg ) & \,=\, \frac {1}{2}r(r-1)(n-2)-(r-1)-(n-3) \\ &=\, -r^2+1+\frac {1}{2}r(r-1)n-(n-3) \leqslant -r^2+1+\frac {1}{2}r(r-1)n-2. \end{align*}
\begin{align*} \sum _{j=1}^{r-2} j + (n-3)\bigg ((r-2)+\sum _{j=1}^{r-2}j \bigg ) & \,=\, \frac {1}{2}r(r-1)(n-2)-(r-1)-(n-3) \\ &=\, -r^2+1+\frac {1}{2}r(r-1)n-(n-3) \leqslant -r^2+1+\frac {1}{2}r(r-1)n-2. \end{align*}
(II) Assume that
![]() $n\,=\,4$
and
$n\,=\,4$
and
![]() $r\,\geqslant \, 3$
. Recall that
$r\,\geqslant \, 3$
. Recall that
![]() $v^{(3)}_{p^{(3)}(1),p^{(3)}(1)}$
is a generator of
$v^{(3)}_{p^{(3)}(1),p^{(3)}(1)}$
is a generator of
![]() $l^{(3)}_{r-1}$
and we can write
$l^{(3)}_{r-1}$
and we can write
![]() $v^{(3)}_{p^{(3)}(1),p^{(3)}(1)}\,=\,\sum _{p,j} w_{p,j}e^{(3)}_{p,j}$
with
$v^{(3)}_{p^{(3)}(1),p^{(3)}(1)}\,=\,\sum _{p,j} w_{p,j}e^{(3)}_{p,j}$
with
![]() $w_{1,1}\,=\, 0$
. Take a representative
$w_{1,1}\,=\, 0$
. Take a representative
![]() $u\,=\,\sum _{p,j} u_{p,j} e^{(3)}_{p,j}\,\in \, l^{(3)}_{r-2}$
of a generator of
$u\,=\,\sum _{p,j} u_{p,j} e^{(3)}_{p,j}\,\in \, l^{(3)}_{r-2}$
of a generator of
![]() $l^{(3)}_{r-2}/l^{(3)}_{r-1}$
with the normalized condition
$l^{(3)}_{r-2}/l^{(3)}_{r-1}$
with the normalized condition
![]() $u_{p^{(3)}(1),j^{(3)}(1)}\,=\,0$
. Consider the diagonal automorphisms
$u_{p^{(3)}(1),j^{(3)}(1)}\,=\,0$
. Consider the diagonal automorphisms
![]() $\textbf {g}\,=\,(a^{pq}_{jj'})$
of
$\textbf {g}\,=\,(a^{pq}_{jj'})$
of
![]() $E$
determined by
$E$
determined by
![]() $a^{pq}_{jj'}\,=\,0$
for
$a^{pq}_{jj'}\,=\,0$
for
![]() $(p,\,j)\,\neq \, (q,\,j')$
,
$(p,\,j)\,\neq \, (q,\,j')$
,
![]() $a^{11}_{1,1}\,=\,c\,\in \,k^{\times }$
and
$a^{11}_{1,1}\,=\,c\,\in \,k^{\times }$
and
![]() $a^{p,p}_{j,j}\,=\,1\,\in \,k^{\times }$
for
$a^{p,p}_{j,j}\,=\,1\,\in \,k^{\times }$
for
![]() $(p,\,j)\,\neq \, (1,\,1)$
. Then such automorphisms preserve
$(p,\,j)\,\neq \, (1,\,1)$
. Then such automorphisms preserve
![]() $l^{(1)}_*$
,
$l^{(1)}_*$
,
![]() $l^{(2)}_*$
and
$l^{(2)}_*$
and
![]() $l^{(3)}_{r-1}$
. Choose an index
$l^{(3)}_{r-1}$
. Choose an index
![]() $(q,\,j')\,\neq \, (p^{(3)}(1),\,j^{(3)}(1)),\,(1,\,1)$
. Applying automorphisms of the above form to
$(q,\,j')\,\neq \, (p^{(3)}(1),\,j^{(3)}(1)),\,(1,\,1)$
. Applying automorphisms of the above form to
![]() $u$
, we may assume that one of the following holds:
$u$
, we may assume that one of the following holds:
-
(a)
 $u_{1,1}\,=\,0$
; or
$u_{1,1}\,=\,0$
; or -
(b)
 $u_{q,j'}\,=\,0$
; or
$u_{q,j'}\,=\,0$
; or -
(c)
 $u_{1,1}\,=\,u_{q,j'}\,\neq \, 0$
.
$u_{1,1}\,=\,u_{q,j'}\,\neq \, 0$
.
So we can give a parameter space of such
![]() $l^{(3)}_{r-2}$
whose dimension is at most
$l^{(3)}_{r-2}$
whose dimension is at most
![]() $r-3$
. Furthermore, the parameter space of
$r-3$
. Furthermore, the parameter space of
![]() $l^{(4)}_{r-1}$
is at most
$l^{(4)}_{r-1}$
is at most
![]() $r-2$
, because of the condition
$r-2$
, because of the condition
![]() $l^{(4)}_{r-1}\,\subset \, \big ( {\mathcal O}_{\mathbb{P}^1}(a_2)^{\oplus r_2}\oplus \cdots \oplus {\mathcal O}_{\mathbb{P}^1}(a_m)^{\oplus r_m}\big )\big |_{x_4}$
. So we can give a parameter space of
$l^{(4)}_{r-1}\,\subset \, \big ( {\mathcal O}_{\mathbb{P}^1}(a_2)^{\oplus r_2}\oplus \cdots \oplus {\mathcal O}_{\mathbb{P}^1}(a_m)^{\oplus r_m}\big )\big |_{x_4}$
. So we can give a parameter space of
![]() $(E,\,l)$
whose dimension is at most
$(E,\,l)$
whose dimension is at most
 \begin{align*} r-3+\sum _{j=1}^{r-3} j +(r-2)+\sum _{j=1}^{r-2} j \,=\,r^2-2r-1, \end{align*}
\begin{align*} r-3+\sum _{j=1}^{r-3} j +(r-2)+\sum _{j=1}^{r-2} j \,=\,r^2-2r-1, \end{align*}
which is equal to
![]() $-r^2+1+r(r-1)n/2-2$
as
$-r^2+1+r(r-1)n/2-2$
as
![]() $n\,=\,4$
.
$n\,=\,4$
.
Proposition 5.13. Assume that
![]() $X\,=\,\mathbb{P}^1_k$
,
$X\,=\,\mathbb{P}^1_k$
,
![]() $n\,=\,3$
,
$n\,=\,3$
,
![]() $r\,\geqslant \, 4$
and
$r\,\geqslant \, 4$
and
![]() $L$
is a line bundle on
$L$
is a line bundle on
![]() $\mathbb{P}^1_k$
. Then there exists a scheme
$\mathbb{P}^1_k$
. Then there exists a scheme
![]() $Z$
of finite type over
$Z$
of finite type over
![]() $\textrm {Spec}\, k$
, and a flat family
$\textrm {Spec}\, k$
, and a flat family
![]() $(\widetilde {E},\,\widetilde {\boldsymbol{l}})$
of quasi-parabolic bundles on
$(\widetilde {E},\,\widetilde {\boldsymbol{l}})$
of quasi-parabolic bundles on
![]() $\mathbb{P}^1\times Z$
over
$\mathbb{P}^1\times Z$
over
![]() $Z$
, such that:
$Z$
, such that:
-
(a)
 $\dim Z \,\leqslant \, (r^2-3r+2)/2-2$
;
$\dim Z \,\leqslant \, (r^2-3r+2)/2-2$
; -
(b)
 $\dim \textrm { End}\big ( (\widetilde {E},\,\widetilde {\boldsymbol{l}}) |_{\mathbb{P}^1\times \{z\}} \big ) \,\geqslant \, 2$
for any
$\dim \textrm { End}\big ( (\widetilde {E},\,\widetilde {\boldsymbol{l}}) |_{\mathbb{P}^1\times \{z\}} \big ) \,\geqslant \, 2$
for any
 $z\,\in \, Z$
;
$z\,\in \, Z$
;
and each member of
![]() $\left | {\mathcal N}^{n_0\textrm { -reg}}_{{\rm par}}(L) \right | \setminus \left | {\mathcal N}^{n_0\textrm { -reg}}_{{\rm par}}(L)^{\circ } \right |$
is isomorphic to
$\left | {\mathcal N}^{n_0\textrm { -reg}}_{{\rm par}}(L) \right | \setminus \left | {\mathcal N}^{n_0\textrm { -reg}}_{{\rm par}}(L)^{\circ } \right |$
is isomorphic to
![]() $(\widetilde {E},\,\widetilde {\boldsymbol{l}})|_{\mathbb{P}^1\times \{z\}}$
for some point
$(\widetilde {E},\,\widetilde {\boldsymbol{l}})|_{\mathbb{P}^1\times \{z\}}$
for some point
![]() $z\,\in \, Z$
.
$z\,\in \, Z$
.
Proof. First we fix a universal constant
As in the proof of Proposition 5.12, we may assume that the quasi-parabolic bundles
![]() $(E,\,\boldsymbol{l})$
satisfy one of the following conditions:
$(E,\,\boldsymbol{l})$
satisfy one of the following conditions:
-
(A)
 $E\,\cong \,{\mathcal O}_{\mathbb{P}^1}^{\oplus r}$
; or
$E\,\cong \,{\mathcal O}_{\mathbb{P}^1}^{\oplus r}$
; or -
(B)
 $E\,=\,{\mathcal O}_{\mathbb{P}^1}(a_1)^{\oplus r_1}\oplus \cdots \oplus {\mathcal O}_{\mathbb{P}^1}(a_m)^{\oplus r_m}$
and
$E\,=\,{\mathcal O}_{\mathbb{P}^1}(a_1)^{\oplus r_1}\oplus \cdots \oplus {\mathcal O}_{\mathbb{P}^1}(a_m)^{\oplus r_m}$
and
 $l^{(i)}_{r-1}\subset {\mathcal O}_{\mathbb{P}^1}(a_2)^{\oplus r_2}\big |_{x_i}\oplus \cdots \oplus {\mathcal O}_{\mathbb{P}^1}(a_m)^{\oplus r_m}\big |_{x_i}$
for any
$l^{(i)}_{r-1}\subset {\mathcal O}_{\mathbb{P}^1}(a_2)^{\oplus r_2}\big |_{x_i}\oplus \cdots \oplus {\mathcal O}_{\mathbb{P}^1}(a_m)^{\oplus r_m}\big |_{x_i}$
for any
 $i$
, where
$i$
, where
 $a_1\,\lt \,a_2\,\lt \,\cdots \,\lt \,a_m$
.
$a_1\,\lt \,a_2\,\lt \,\cdots \,\lt \,a_m$
.
Case A. First, consider the case where
![]() $E\,\cong \,{\mathcal O}_{\mathbb{P}^1}^{\oplus r}$
.
$E\,\cong \,{\mathcal O}_{\mathbb{P}^1}^{\oplus r}$
.
As in the proof of Proposition 5.12, we may assume that
![]() $l^{(1)}_*$
is determined by the standard basis
$l^{(1)}_*$
is determined by the standard basis
![]() $e_1,\,\cdots ,\,e_r$
and
$e_1,\,\cdots ,\,e_r$
and
![]() $l^{(2)}_*$
is determined by the basis
$l^{(2)}_*$
is determined by the basis
![]() $e_{\sigma (1)},\,\cdots ,\,e_{\sigma (r)}$
for a permutation
$e_{\sigma (1)},\,\cdots ,\,e_{\sigma (r)}$
for a permutation
![]() $\sigma$
of
$\sigma$
of
![]() $\{1,\,\cdots ,\,r\}$
while
$\{1,\,\cdots ,\,r\}$
while
![]() $l^{(3)}_{r-1}$
is generated by
$l^{(3)}_{r-1}$
is generated by
![]() $w\,=\,w_1e_1+\ldots +w_re_r$
with
$w\,=\,w_1e_1+\ldots +w_re_r$
with
![]() $w_i\,=\,1$
or
$w_i\,=\,1$
or
![]() $w_i\,=\,0$
for each
$w_i\,=\,0$
for each
![]() $i$
. Consider the following three cases:
$i$
. Consider the following three cases:
-
(a)
 $w_{i_1}\,=\,w_{i_2}\,=\,0$
for some
$w_{i_1}\,=\,w_{i_2}\,=\,0$
for some
 $i_1\,\neq \, i_2$
;
$i_1\,\neq \, i_2$
; -
(b)
 $w_{i_1}\,=\,0$
for some
$w_{i_1}\,=\,0$
for some
 $i_1$
and
$i_1$
and
 $w_i\,=\,1$
for any
$w_i\,=\,1$
for any
 $i\neq i_1$
;
$i\neq i_1$
; -
(c)
 $w_i\,=\,1$
for any
$w_i\,=\,1$
for any
 $i$
.
$i$
.
-
(a) Assume that
 $w_{i_1}\,=\,w_{i_2}\,=\,0$
for
$w_{i_1}\,=\,w_{i_2}\,=\,0$
for
 $i_1\,\neq \, i_2$
. Fix indices
$i_1\,\neq \, i_2$
. Fix indices
 $i_3,\,i_4$
such that
$i_3,\,i_4$
such that
 $w_{i_3}\,=\,1$
and
$w_{i_3}\,=\,1$
and
 $i_4\,\neq \, i_1,\,i_2,\,i_3$
. Consider the automorphisms
$i_4\,\neq \, i_1,\,i_2,\,i_3$
. Consider the automorphisms
 $(a_{ij})$
of
$(a_{ij})$
of
 $E$
satisfying
$E$
satisfying
 $a_{i_1i_1}\,=\,c_{i_1}\,\in \,k^{\times }$
,
$a_{i_1i_1}\,=\,c_{i_1}\,\in \,k^{\times }$
,
 $a_{i_2i_2}\,=\,c_{i_2}\,\in \,k^{\times }$
,
$a_{i_2i_2}\,=\,c_{i_2}\,\in \,k^{\times }$
,
 $a_{ii}\,=\,1$
for
$a_{ii}\,=\,1$
for
 $i\,\neq \, i_1,\,i_2$
and
$i\,\neq \, i_1,\,i_2$
and
 $a_{ij}\,=\,0$
for
$a_{ij}\,=\,0$
for
 $i\,\neq \, j$
. Then such automorphisms preserve
$i\,\neq \, j$
. Then such automorphisms preserve
 $l^{(1)}_*$
,
$l^{(1)}_*$
,
 $l^{(2)}_*$
and
$l^{(2)}_*$
and
 $l^{(3)}_{r-1}$
. Normalize a representative
$l^{(3)}_{r-1}$
. Normalize a representative
 $v\,=\,v_1e_1+\ldots +v_re_r\in l^{(3)}_{r-2}$
of a generator of
$v\,=\,v_1e_1+\ldots +v_re_r\in l^{(3)}_{r-2}$
of a generator of
 $l^{(3)}_{r-2}/l^{(3)}_{r-1}$
such that
$l^{(3)}_{r-2}/l^{(3)}_{r-1}$
such that
 $v_{i_3}\,=\,0$
after adding an element of
$v_{i_3}\,=\,0$
after adding an element of
 $l^{(3)}_{r-1}$
. Applying the above type of automorphisms to
$l^{(3)}_{r-1}$
. Applying the above type of automorphisms to
 $v$
, we can assume that one of the following statements holds:
$v$
, we can assume that one of the following statements holds:-
(i)
 $v_{i_1}\,=\,v_{i_2}\,=\,0$
;
$v_{i_1}\,=\,v_{i_2}\,=\,0$
; -
(ii)
 $v_{i_1}\,=\,v_{i_4}\,=\,0$
;
$v_{i_1}\,=\,v_{i_4}\,=\,0$
; -
(iii)
 $v_{i_2}\,=\,v_{i_4}\,=\,0$
;
$v_{i_2}\,=\,v_{i_4}\,=\,0$
; -
(iv)
 $v_{i_1}\,=\,0$
and
$v_{i_1}\,=\,0$
and
 $v_{i_2}\,=\,v_{i_4}\,\neq \, 0$
;
$v_{i_2}\,=\,v_{i_4}\,\neq \, 0$
; -
(v)
 $v_{i_2}\,=\,0$
and
$v_{i_2}\,=\,0$
and
 $v_{i_1}\,=\,v_{i_4}\,\neq \, 0$
;
$v_{i_1}\,=\,v_{i_4}\,\neq \, 0$
; -
(vi)
 $v_{i_1}\,=\,v_{i_2}\,\neq \, 0$
and
$v_{i_1}\,=\,v_{i_2}\,\neq \, 0$
and
 $v_{i_4}\,=\,0$
;
$v_{i_4}\,=\,0$
; -
(vii)
 $v_{i_1}\,=\,v_{i_2}\,=\,v_{i_4}\,\neq \, 0$
.
$v_{i_1}\,=\,v_{i_2}\,=\,v_{i_4}\,\neq \, 0$
.
So there is a parameter space of
 $l^{(3)}_{r-2}$
whose dimension is at most
$l^{(3)}_{r-2}$
whose dimension is at most
 $r-2-2\,=\,r-4$
. Adding the data of
$r-2-2\,=\,r-4$
. Adding the data of
 $l^{(3)}_{r-3},\,\cdots ,\,l^{(3)}_1$
, we can get a parameter space of
$l^{(3)}_{r-3},\,\cdots ,\,l^{(3)}_1$
, we can get a parameter space of
 $(E,\,\boldsymbol{l})$
whose dimension is at most
$(E,\,\boldsymbol{l})$
whose dimension is at most \begin{align*} (r-4) + \sum _{j=1}^{r-3} j \ = \ \frac {r^2-3r+2} {2} - 2. \end{align*}
\begin{align*} (r-4) + \sum _{j=1}^{r-3} j \ = \ \frac {r^2-3r+2} {2} - 2. \end{align*}
-
-
(b) Assume that
 $w_{i_1}\,=\,0$
for some
$w_{i_1}\,=\,0$
for some
 $i_1$
and
$i_1$
and
 $w_i\,=\,1$
for any
$w_i\,=\,1$
for any
 $i\,\neq \, i_1$
. Fix an index
$i\,\neq \, i_1$
. Fix an index
 $i_2$
other than
$i_2$
other than
 $i_1$
. For a representative
$i_1$
. For a representative
 $v\,=\,v_1e_1+\cdots +v_re_r\,\in \, l^{(3)}_{r-2}$
of a generator of
$v\,=\,v_1e_1+\cdots +v_re_r\,\in \, l^{(3)}_{r-2}$
of a generator of
 $l^{(3)}_{r-2}/l^{(3)}_{r-1}$
, we may assume, after adding an element of
$l^{(3)}_{r-2}/l^{(3)}_{r-1}$
, we may assume, after adding an element of
 $l^{(3)}_{r-1}$
, that
$l^{(3)}_{r-1}$
, that
 $v_{i_2}\,=\,0$
. Then we have one of the following three cases:
$v_{i_2}\,=\,0$
. Then we have one of the following three cases:-
(i)
 $v_{i_1}\,=\,0$
;
$v_{i_1}\,=\,0$
; -
(ii)
 $v_{i_1}\,\neq \, 0$
and
$v_{i_1}\,\neq \, 0$
and
 $v_i\,=\,0$
for any
$v_i\,=\,0$
for any
 $i\,\neq \, i_1,\,i_2$
;
$i\,\neq \, i_1,\,i_2$
; -
(iii)
 $v_{i_1}\,\neq \, 0$
and
$v_{i_1}\,\neq \, 0$
and
 $v_{i_3}\,\neq \, 0$
for some
$v_{i_3}\,\neq \, 0$
for some
 $i_3$
with
$i_3$
with
 $i_3\,\neq \, i_1$
and
$i_3\,\neq \, i_1$
and
 $i_3\,\neq \, i_2$
.
$i_3\,\neq \, i_2$
.
-
(i) Consider the case where
![]() $v_{i_1}\,=\,0$
. Then we can give a parameter space of
$v_{i_1}\,=\,0$
. Then we can give a parameter space of
![]() $l^{(3)}_{r-2}$
whose dimension is at most
$l^{(3)}_{r-2}$
whose dimension is at most
![]() $r-2-1\,=\,r-3$
. Consider the automorphisms
$r-2-1\,=\,r-3$
. Consider the automorphisms
![]() $\textbf {g}\,=\, (a_{ij})$
of
$\textbf {g}\,=\, (a_{ij})$
of
![]() $E$
given by
$E$
given by
![]() $a_{i_1i_1}\,=\,c\,\in \,k^{\times }$
,
$a_{i_1i_1}\,=\,c\,\in \,k^{\times }$
,
![]() $a_{ii}\,=\,1$
for
$a_{ii}\,=\,1$
for
![]() $i\,\neq \, i_1$
and
$i\,\neq \, i_1$
and
![]() $a_{ij}\,=\,0$
for
$a_{ij}\,=\,0$
for
![]() $i\,\neq \, j$
. Then such automorphisms preserve
$i\,\neq \, j$
. Then such automorphisms preserve
![]() $l^{(1)}_*$
,
$l^{(1)}_*$
,
![]() $l^{(2)}_*$
,
$l^{(2)}_*$
,
![]() $l^{(3)}_{r-1}$
and also
$l^{(3)}_{r-1}$
and also
![]() $l^{(3)}_{r-2}$
. Since
$l^{(3)}_{r-2}$
. Since
![]() $v\,\neq \, 0$
, we may choose an index
$v\,\neq \, 0$
, we may choose an index
![]() $i_3$
such that
$i_3$
such that
![]() $v_{i_3}\,\neq \, 0$
and
$v_{i_3}\,\neq \, 0$
and
![]() $i_3\,\neq \, i_1,\,i_2$
. For a representative
$i_3\,\neq \, i_1,\,i_2$
. For a representative
![]() $u\,=\,u_1e_1+\cdots +u_re_r\in l^{(3)}_{r-3}$
of a generator of
$u\,=\,u_1e_1+\cdots +u_re_r\in l^{(3)}_{r-3}$
of a generator of
![]() $l^{(3)}_{r-3}/l^{(3)}_{r-2}$
, we may assume, after adding an element in
$l^{(3)}_{r-3}/l^{(3)}_{r-2}$
, we may assume, after adding an element in
![]() $l^{(3)}_{r-2}$
, that
$l^{(3)}_{r-2}$
, that
![]() $u_{i_2}\,=\,u_{i_3}\,=\,0$
. After applying the above type of automorphisms to
$u_{i_2}\,=\,u_{i_3}\,=\,0$
. After applying the above type of automorphisms to
![]() $u$
, we may assume that one of the following statements holds:
$u$
, we may assume that one of the following statements holds:
 $u_{i_1}\,=\,0$
;
$u_{i_1}\,=\,0$
; $u_{i_1}\,\neq \, 0$
and
$u_{i_1}\,\neq \, 0$
and
 $u_i\,=\,0$
for
$u_i\,=\,0$
for
 $i\,\neq \, i_1,\,i_2,\,i_3$
;
$i\,\neq \, i_1,\,i_2,\,i_3$
; $u_{i_1}\,=\,u_{i_4}\,\neq \, 0$
for some
$u_{i_1}\,=\,u_{i_4}\,\neq \, 0$
for some
 $i_4\,\neq \, i_1,\,i_2,\,i_3$
.
$i_4\,\neq \, i_1,\,i_2,\,i_3$
.
In all these cases, there is a parameter space of
![]() $l^{(3)}_{r-3}$
whose dimension is at most
$l^{(3)}_{r-3}$
whose dimension is at most
![]() $r-3-1\,=\,r-4$
. Adding the data of
$r-3-1\,=\,r-4$
. Adding the data of
![]() $l^{(3)}_{r-4},\,\cdots ,\,l^{(3)}_1$
, we can get a parameter space of
$l^{(3)}_{r-4},\,\cdots ,\,l^{(3)}_1$
, we can get a parameter space of
![]() $(E,\,\boldsymbol{l})$
whose dimension is at most
$(E,\,\boldsymbol{l})$
whose dimension is at most
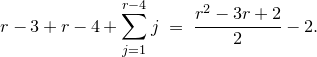 \begin{align*} r-3+r-4 + \sum _{j=1}^{r-4} j \ =\ \frac {r^2-3r+2} {2} - 2. \end{align*}
\begin{align*} r-3+r-4 + \sum _{j=1}^{r-4} j \ =\ \frac {r^2-3r+2} {2} - 2. \end{align*}
(ii) Consider the case where
![]() $v_{i_1}\,\neq \, 0$
and
$v_{i_1}\,\neq \, 0$
and
![]() $v_i\,=\,0$
for any
$v_i\,=\,0$
for any
![]() $i\,\neq \, i_1,\,i_2$
. Then
$i\,\neq \, i_1,\,i_2$
. Then
![]() $l^{(3)}_{r-2}$
is uniquely determined. So the dimension of the parameter space of such
$l^{(3)}_{r-2}$
is uniquely determined. So the dimension of the parameter space of such
![]() $(E,\,\boldsymbol{l})$
is at most
$(E,\,\boldsymbol{l})$
is at most
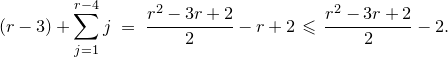 \begin{align*} (r-3)+\sum _{j=1}^{r-4} j \ =\ \frac {r^2-3r+2} {2} - r+2 \, \leqslant \, \frac {r^2-3r+2} {2}-2 . \end{align*}
\begin{align*} (r-3)+\sum _{j=1}^{r-4} j \ =\ \frac {r^2-3r+2} {2} - r+2 \, \leqslant \, \frac {r^2-3r+2} {2}-2 . \end{align*}
(iii) Consider the case where
![]() $v_{i_1}\,\neq \, 0$
and
$v_{i_1}\,\neq \, 0$
and
![]() $v_{i_3}\,\neq \, 0$
for some
$v_{i_3}\,\neq \, 0$
for some
![]() $i_3$
with
$i_3$
with
![]() $i_3\,\neq \, i_1$
and
$i_3\,\neq \, i_1$
and
![]() $i_3\,\neq \, i_2$
. Recall again that we normalize a representative
$i_3\,\neq \, i_2$
. Recall again that we normalize a representative
![]() $v\,\in \, l^{(3)}_{r-2}$
of a generator of
$v\,\in \, l^{(3)}_{r-2}$
of a generator of
![]() $l^{(3)}_{r-2}/l^{(3)}_{r-1}$
such that
$l^{(3)}_{r-2}/l^{(3)}_{r-1}$
such that
![]() $v_{i_2}\,=\,0$
. Suppose that the condition
$v_{i_2}\,=\,0$
. Suppose that the condition
![]() $\sigma (i)\,\gt \,\sigma (j)$
holds for any
$\sigma (i)\,\gt \,\sigma (j)$
holds for any
![]() $i\,\lt \,j$
. Then the automorphisms of
$i\,\lt \,j$
. Then the automorphisms of
![]() $E$
preserving
$E$
preserving
![]() $l^{(1)}_*$
and
$l^{(1)}_*$
and
![]() $l^{(2)}_*$
are only diagonal automorphisms
$l^{(2)}_*$
are only diagonal automorphisms
![]() $\textbf {g}\,=\,(a_{ij})$
, which satisfy the condition
$\textbf {g}\,=\,(a_{ij})$
, which satisfy the condition
![]() $a_{ij}\,=\,0$
for
$a_{ij}\,=\,0$
for
![]() $i\,\neq \, j$
. If
$i\,\neq \, j$
. If
![]() $\textbf {g}\,=\,(a_{ij})$
preserves
$\textbf {g}\,=\,(a_{ij})$
preserves
![]() $l^{(3)}_{r-1}\,=\,\langle w \rangle$
and
$l^{(3)}_{r-1}\,=\,\langle w \rangle$
and
![]() $l^{(3)}_{r-2}\,=\,\langle w,\,v\rangle$
in addition, then we have
$l^{(3)}_{r-2}\,=\,\langle w,\,v\rangle$
in addition, then we have
![]() $a_{ii}\,=\,a_{jj}$
for
$a_{ii}\,=\,a_{jj}$
for
![]() $i,\,j\,\neq \, i_1$
and
$i,\,j\,\neq \, i_1$
and
![]() $a_{i_1i_1}\,=\,a_{i_3i_3}$
. So
$a_{i_1i_1}\,=\,a_{i_3i_3}$
. So
![]() $\textbf {g}$
must be a constant scalar multiplication, which contradicts the assumption that
$\textbf {g}$
must be a constant scalar multiplication, which contradicts the assumption that
![]() $\dim {\textrm { Aut}}(E,\boldsymbol{l})\,\geqslant \,2$
. Thus, we have the following:
$\dim {\textrm { Aut}}(E,\boldsymbol{l})\,\geqslant \,2$
. Thus, we have the following:
There are
 $i_0\,\,\lt \,\,j_0$
satisfying
$i_0\,\,\lt \,\,j_0$
satisfying
 $\sigma (i_0)\,\,\lt \,\,\sigma (j_0)$
.
$\sigma (i_0)\,\,\lt \,\,\sigma (j_0)$
.
So, consider the following cases:
-
(
 $\alpha$
)
$\alpha$
)
 $\sigma (j_0)\,=\,i_1$
and
$\sigma (j_0)\,=\,i_1$
and
 $\sigma (i_0)\,=\,i_2$
;
$\sigma (i_0)\,=\,i_2$
; -
(
 $\beta$
)
$\beta$
)
 $\sigma (j_0)\,=\,i_1$
and
$\sigma (j_0)\,=\,i_1$
and
 $\sigma (i_0)\,\neq \, i_2$
;
$\sigma (i_0)\,\neq \, i_2$
; -
(
 $\gamma$
)
$\gamma$
)
 $\sigma (j_0)\,\neq \, i_1$
and
$\sigma (j_0)\,\neq \, i_1$
and
 $\sigma (i_0)\,=\,i_2$
;
$\sigma (i_0)\,=\,i_2$
; -
(
 $\delta$
)
$\delta$
)
 $\sigma (j_0)\,\neq \, i_1$
and
$\sigma (j_0)\,\neq \, i_1$
and
 $\sigma (i_0)\,\neq \, i_1,\,i_2$
;
$\sigma (i_0)\,\neq \, i_1,\,i_2$
; -
(
 $\epsilon$
)
$\epsilon$
)
 $\sigma (i_0)\,=\,i_1$
and
$\sigma (i_0)\,=\,i_1$
and
 $\{ j\,\in \,\{1,\,\cdots ,\,r\} \, \, \big \vert \, \: j\,\gt \,i,\; \sigma (j)\,\gt \,\sigma (i) \}\,=\,\emptyset$
for any
$\{ j\,\in \,\{1,\,\cdots ,\,r\} \, \, \big \vert \, \: j\,\gt \,i,\; \sigma (j)\,\gt \,\sigma (i) \}\,=\,\emptyset$
for any
 $i\,\neq \, i_0$
.
$i\,\neq \, i_0$
.
More precisely, in the remaining case other than (
![]() $\alpha$
), (
$\alpha$
), (
![]() $\beta$
), (
$\beta$
), (
![]() $\gamma$
) and (
$\gamma$
) and (
![]() $\delta$
), we have
$\delta$
), we have
![]() $\sigma (i_0)\,=\,i_1$
. If there are
$\sigma (i_0)\,=\,i_1$
. If there are
![]() $i'\,\neq \, i_0$
and
$i'\,\neq \, i_0$
and
![]() $j'\,\gt \,i'$
satisfying
$j'\,\gt \,i'$
satisfying
![]() $\sigma (j')\,\gt \,\sigma (i')$
, then we replace
$\sigma (j')\,\gt \,\sigma (i')$
, then we replace
![]() $(i_0,\,j_0)$
with
$(i_0,\,j_0)$
with
![]() $(i',\,j')$
and reduce to the case (
$(i',\,j')$
and reduce to the case (
![]() $\alpha$
), (
$\alpha$
), (
![]() $\beta$
), (
$\beta$
), (
![]() $\gamma$
) or (
$\gamma$
) or (
![]() $\delta$
). Otherwise, we may assume (
$\delta$
). Otherwise, we may assume (
![]() $\epsilon$
).
$\epsilon$
).
(
![]() $\alpha$
) Assume that
$\alpha$
) Assume that
![]() $\sigma (i_0)\,=\,i_2$
and
$\sigma (i_0)\,=\,i_2$
and
![]() $\sigma (j_0)\,=\,i_1$
. Consider the automorphisms
$\sigma (j_0)\,=\,i_1$
. Consider the automorphisms
![]() $\textbf {g}\,=\,(a_{ij})$
of
$\textbf {g}\,=\,(a_{ij})$
of
![]() $E$
given by
$E$
given by
![]() $a_{i_1i_1}\,=\,c\,\in \,k^{\times }$
,
$a_{i_1i_1}\,=\,c\,\in \,k^{\times }$
,
![]() $a_{\sigma (i_0)\sigma (j_0)}\,=\,a_{i_2i_1}\,=\,a\,\in \,k$
,
$a_{\sigma (i_0)\sigma (j_0)}\,=\,a_{i_2i_1}\,=\,a\,\in \,k$
,
![]() $a_{ii}\,=\,1$
for
$a_{ii}\,=\,1$
for
![]() $i\,\neq \, i_1\,=\,\sigma (j_0)$
and
$i\,\neq \, i_1\,=\,\sigma (j_0)$
and
![]() $a_{ij}\,=\,0$
for
$a_{ij}\,=\,0$
for
![]() $i\,\neq \, j$
satisfying
$i\,\neq \, j$
satisfying
![]() $(i,\,j)\,\neq \,(i_2,\,i_1)$
. Then such automorphisms preserve
$(i,\,j)\,\neq \,(i_2,\,i_1)$
. Then such automorphisms preserve
![]() $l^{(1)}_*$
,
$l^{(1)}_*$
,
![]() $l^{(2)}_*$
and
$l^{(2)}_*$
and
![]() $l^{(3)}_{r-1}$
. The coefficient of
$l^{(3)}_{r-1}$
. The coefficient of
![]() $e_{i_2}$
in
$e_{i_2}$
in
is
![]() $v_{\sigma (i_0)}+av_{\sigma (j_0)}\,=\,av_{\sigma (j_0)}$
because of
$v_{\sigma (i_0)}+av_{\sigma (j_0)}\,=\,av_{\sigma (j_0)}$
because of
![]() $v_{\sigma (i_0)}\,=\,v_{i_2}\,=\,0$
, and hence the normalized representative of a generator of
$v_{\sigma (i_0)}\,=\,v_{i_2}\,=\,0$
, and hence the normalized representative of a generator of
![]() $l^{(3)}_{r-2}/l^{(3)}_{r-1}$
becomes
$l^{(3)}_{r-2}/l^{(3)}_{r-1}$
becomes
If we choose an index
![]() $i_4$
other than
$i_4$
other than
![]() $i_1,\,i_2,\,i_3$
, we may assume that one of the following two holds:
$i_1,\,i_2,\,i_3$
, we may assume that one of the following two holds:
-
(a)
 $v_{i_1}\,=\,v_{i_3}\,=\,v_{i_4}\,\neq \, 0$
;
$v_{i_1}\,=\,v_{i_3}\,=\,v_{i_4}\,\neq \, 0$
; -
(b)
 $v_{i_1}\,=\,v_{i_3}\,\neq \, 0$
and
$v_{i_1}\,=\,v_{i_3}\,\neq \, 0$
and
 $v_{i_4}\,=\,0$
.
$v_{i_4}\,=\,0$
.
So we can give a parameter space for such
![]() $l^{(3)}_{r-2}$
whose dimension is at most
$l^{(3)}_{r-2}$
whose dimension is at most
![]() $r-4$
.
$r-4$
.
(
![]() $\beta$
) Assume that
$\beta$
) Assume that
![]() $\sigma (j_0)\,=\,i_1$
and
$\sigma (j_0)\,=\,i_1$
and
![]() $\sigma (i_0)\,\neq \,i_2$
. Consider the automorphisms
$\sigma (i_0)\,\neq \,i_2$
. Consider the automorphisms
![]() $\textbf {g}\,=\,(a_{ij})$
of
$\textbf {g}\,=\,(a_{ij})$
of
![]() $E$
given by
$E$
given by
![]() $a_{i_1i_1}\,=\,c\,\in \,k^{\times }$
,
$a_{i_1i_1}\,=\,c\,\in \,k^{\times }$
,
![]() $a_{\sigma (i_0)\sigma (j_0)}\,=\,a\,\in \,k$
,
$a_{\sigma (i_0)\sigma (j_0)}\,=\,a\,\in \,k$
,
![]() $a_{ii}\,=\,1$
for
$a_{ii}\,=\,1$
for
![]() $i\,\neq \, i_1\,=\,\sigma (j_0)$
and
$i\,\neq \, i_1\,=\,\sigma (j_0)$
and
![]() $a_{ij}\,=\,0$
for
$a_{ij}\,=\,0$
for
![]() $i\,\neq \, j$
satisfying
$i\,\neq \, j$
satisfying
![]() $(i,\,j)\,\neq \,(\sigma (i_0),\,\sigma (j_0))$
. Then such automorphisms preserve
$(i,\,j)\,\neq \,(\sigma (i_0),\,\sigma (j_0))$
. Then such automorphisms preserve
![]() $l^{(1)}_*$
,
$l^{(1)}_*$
,
![]() $l^{(2)}_*$
and
$l^{(2)}_*$
and
![]() $l^{(3)}_{r-1}\,=\,\langle w\rangle$
. Since
$l^{(3)}_{r-1}\,=\,\langle w\rangle$
. Since
we may assume that one of the following holds:
-
(a)
 $\sigma (i_0)\,\neq \, i_3$
and
$\sigma (i_0)\,\neq \, i_3$
and
 $v_{\sigma (i_0)}\,=\,v_{\sigma (j_0)}\,=\,v_{i_3}\,\neq \, 0$
;
$v_{\sigma (i_0)}\,=\,v_{\sigma (j_0)}\,=\,v_{i_3}\,\neq \, 0$
; -
(b)
 $\sigma (i_0)\,=\,i_3$
and
$\sigma (i_0)\,=\,i_3$
and
 $v_{\sigma (i_0)}\,=\,v_{\sigma (j_0)}\,=\,v_{i_4}\,\neq \, 0$
for some
$v_{\sigma (i_0)}\,=\,v_{\sigma (j_0)}\,=\,v_{i_4}\,\neq \, 0$
for some
 $i_4$
other than
$i_4$
other than
 $i_1,\,i_3,\,i_2$
;
$i_1,\,i_3,\,i_2$
; -
(c)
 $\sigma (i_0)\,=\,i_3$
,
$\sigma (i_0)\,=\,i_3$
,
 $v_{\sigma (i_0)}\,=\,v_{\sigma (j_0)}$
and
$v_{\sigma (i_0)}\,=\,v_{\sigma (j_0)}$
and
 $v_i\,=\,0$
for any
$v_i\,=\,0$
for any
 $i$
other than
$i$
other than
 $i_1(=\,\sigma (j_0)),\, i_3$
.
$i_1(=\,\sigma (j_0)),\, i_3$
.
So we can give a parameter space of such
![]() $l^{(3)}_{r-2}$
whose dimension is at most
$l^{(3)}_{r-2}$
whose dimension is at most
![]() $r-4$
.
$r-4$
.
(
![]() $\gamma$
) Assume that
$\gamma$
) Assume that
![]() $\sigma (j_0)\,\neq \, i_1$
and
$\sigma (j_0)\,\neq \, i_1$
and
![]() $\sigma (i_0)\,=\,i_2$
. In this case, consider the automorphisms
$\sigma (i_0)\,=\,i_2$
. In this case, consider the automorphisms
![]() $\textbf {g}\,=\,(a_{ij})$
of the form
$\textbf {g}\,=\,(a_{ij})$
of the form
![]() $a_{i_1i_1}\,=\,c\,\in \,k^{\times }$
,
$a_{i_1i_1}\,=\,c\,\in \,k^{\times }$
,
![]() $a_{i_2i_2}\,=\,a\,\in \,k^{\times }\setminus \{1\}$
,
$a_{i_2i_2}\,=\,a\,\in \,k^{\times }\setminus \{1\}$
,
![]() $a_{i_2\sigma (j_0)}\,=\,1-a$
,
$a_{i_2\sigma (j_0)}\,=\,1-a$
,
![]() $a_{ii}\,=\,1$
for
$a_{ii}\,=\,1$
for
![]() $i\,\neq \, i_1,\,i_2$
and
$i\,\neq \, i_1,\,i_2$
and
![]() $a_{ij}\,=\,0$
for any
$a_{ij}\,=\,0$
for any
![]() $i\,\neq \,j$
satisfying
$i\,\neq \,j$
satisfying
![]() $(i,\,j)\,\neq \, (i_2,\,\sigma (j_0))$
. Then such a
$(i,\,j)\,\neq \, (i_2,\,\sigma (j_0))$
. Then such a
![]() $\textbf {g}$
preserves
$\textbf {g}$
preserves
![]() $l^{(1)}_*$
,
$l^{(1)}_*$
,
![]() $l^{(2)}_*$
and
$l^{(2)}_*$
and
![]() $l^{(3)}_{r-1}$
. Since the
$l^{(3)}_{r-1}$
. Since the
![]() $e_{i_2}$
-coefficient of
$e_{i_2}$
-coefficient of
is
![]() $av_{i_2}+(1-a)v_{\sigma (j_0)}\,=\,(1-a)v_{\sigma (j_0)}$
, we should replace
$av_{i_2}+(1-a)v_{\sigma (j_0)}\,=\,(1-a)v_{\sigma (j_0)}$
, we should replace
![]() $\textbf {g}v$
with its normalization
$\textbf {g}v$
with its normalization
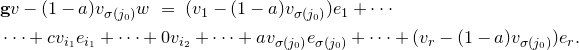 \begin{align*}&\textbf {g}v-(1-a)v_{\sigma (j_0)}w \,\, =\,\, (v_1-(1-a)v_{\sigma (j_0)})e_1+\cdots \\ &\cdots +cv_{i_1} e_{i_1} +\cdots+0v_{i_2}+\cdots +av_{\sigma (j_0)} e_{\sigma (j_0)} +\cdots +(v_r-(1-a)v_{\sigma (j_0)})e_r. \end{align*}
\begin{align*}&\textbf {g}v-(1-a)v_{\sigma (j_0)}w \,\, =\,\, (v_1-(1-a)v_{\sigma (j_0)})e_1+\cdots \\ &\cdots +cv_{i_1} e_{i_1} +\cdots+0v_{i_2}+\cdots +av_{\sigma (j_0)} e_{\sigma (j_0)} +\cdots +(v_r-(1-a)v_{\sigma (j_0)})e_r. \end{align*}
Fix an index
![]() $i_4$
other than
$i_4$
other than
![]() $\sigma (j_0)$
,
$\sigma (j_0)$
,
![]() $i_1$
and
$i_1$
and
![]() $i_2$
. After applying an automorphism of the above form, we may assume that one of the following holds:
$i_2$
. After applying an automorphism of the above form, we may assume that one of the following holds:
 $\sigma (j_0)\,\neq \, i_3$
and
$\sigma (j_0)\,\neq \, i_3$
and
 $v_{i_1}\,=\,v_{i_3}\,=\,v_{\sigma (j_0)}\,\neq \, 0$
;
$v_{i_1}\,=\,v_{i_3}\,=\,v_{\sigma (j_0)}\,\neq \, 0$
; $\sigma (j_0)\,\neq \, i_3$
and
$\sigma (j_0)\,\neq \, i_3$
and
 $v_{i_1}\,=\,v_{i_3}\,=\,\lambda _0 v_{\sigma (j_0)}\,\neq \, 0$
(see (5.14) for
$v_{i_1}\,=\,v_{i_3}\,=\,\lambda _0 v_{\sigma (j_0)}\,\neq \, 0$
(see (5.14) for
 $\lambda _0$
);
$\lambda _0$
); $\sigma (j_0)\,\neq \, i_3$
,
$\sigma (j_0)\,\neq \, i_3$
,
 $v_{i_1}\,=\,v_{i_3}\,\neq \, 0$
and
$v_{i_1}\,=\,v_{i_3}\,\neq \, 0$
and
 $v_{\sigma (j_0)}\,=\,0$
;
$v_{\sigma (j_0)}\,=\,0$
; $\sigma (j_0)\,=\,i_3$
and
$\sigma (j_0)\,=\,i_3$
and
 $v_{i_1}\,=\,v_{\sigma (j_0)}\,=\,v_{i_4}\,\neq \, 0$
;
$v_{i_1}\,=\,v_{\sigma (j_0)}\,=\,v_{i_4}\,\neq \, 0$
; $\sigma (j_0)\,=\,i_3$
,
$\sigma (j_0)\,=\,i_3$
,
 $v_{i_1}\,=\,v_{\sigma (j_0)}$
and
$v_{i_1}\,=\,v_{\sigma (j_0)}$
and
 $v_{i_4}\,=\,0$
.
$v_{i_4}\,=\,0$
.
So we can give a parameter space of such
![]() $l^{(3)}_{r-2}$
whose dimension is at most
$l^{(3)}_{r-2}$
whose dimension is at most
![]() $r-4$
.
$r-4$
.
(
![]() $\delta$
) Assume that
$\delta$
) Assume that
![]() $\sigma (j_0)\,\neq \, i_1$
and
$\sigma (j_0)\,\neq \, i_1$
and
![]() $\sigma (i_0)\,\neq \, i_1,\,i_2$
. Consider the automorphisms
$\sigma (i_0)\,\neq \, i_1,\,i_2$
. Consider the automorphisms
![]() $\textbf {g}\,=\,(a_{ij})$
of
$\textbf {g}\,=\,(a_{ij})$
of
![]() $E$
given by
$E$
given by
![]() $a_{i_1i_1}\,=\,c\,\in \,k^{\times }$
,
$a_{i_1i_1}\,=\,c\,\in \,k^{\times }$
,
![]() $a_{\sigma (i_0)\sigma (i_0)}\,=\,a\,\in \,k^{\times }$
,
$a_{\sigma (i_0)\sigma (i_0)}\,=\,a\,\in \,k^{\times }$
,
![]() $a_{\sigma (i_0),\, \sigma (j_0)}\,=\,1-a$
,
$a_{\sigma (i_0),\, \sigma (j_0)}\,=\,1-a$
,
![]() $a_{ii}\,=\,1$
for
$a_{ii}\,=\,1$
for
![]() $i\,\neq \, i_1,\, \sigma (i_0)$
and
$i\,\neq \, i_1,\, \sigma (i_0)$
and
![]() $a_{ij}\,=\,0$
for
$a_{ij}\,=\,0$
for
![]() $i\,\neq \, j$
satisfying
$i\,\neq \, j$
satisfying
![]() $(i,\,j)\,\neq \,(\sigma (i_0),\,\sigma (j_0))$
. Then such automorphisms preserve
$(i,\,j)\,\neq \,(\sigma (i_0),\,\sigma (j_0))$
. Then such automorphisms preserve
![]() $l^{(1)}_*$
,
$l^{(1)}_*$
,
![]() $l^{(2)}_*$
and
$l^{(2)}_*$
and
![]() $l^{(3)}_{r-1}$
, and we have
$l^{(3)}_{r-1}$
, and we have
In the case where
![]() $v_{\sigma (i_0)}\,=\,v_{\sigma (j_0)}$
, we can normalize
$v_{\sigma (i_0)}\,=\,v_{\sigma (j_0)}$
, we can normalize
![]() $v$
so that the condition
$v$
so that the condition
![]() $v_{i_1}\,=\,v_{i_3}$
holds. In the case where
$v_{i_1}\,=\,v_{i_3}$
holds. In the case where
![]() $v_{\sigma (i_0)}\,\neq \, v_{\sigma (j_0)}$
, we can normalize
$v_{\sigma (i_0)}\,\neq \, v_{\sigma (j_0)}$
, we can normalize
![]() $v$
so that one of the following holds:
$v$
so that one of the following holds:
-
(1)
 $\sigma (i_0)\,\neq \,i_3$
and
$\sigma (i_0)\,\neq \,i_3$
and
 $v_{i_1}\,=\,v_{\sigma (i_0)}\,=\,v_{i_3}\,\neq \, 0$
;
$v_{i_1}\,=\,v_{\sigma (i_0)}\,=\,v_{i_3}\,\neq \, 0$
; -
(2)
 $\sigma (i_0)\,=\,i_3$
and
$\sigma (i_0)\,=\,i_3$
and
 $v_{i_1}\,=\,v_{\sigma (i_0)}\,=\,v_{i_4}\neq 0$
for some
$v_{i_1}\,=\,v_{\sigma (i_0)}\,=\,v_{i_4}\neq 0$
for some
 $i_4$
other than
$i_4$
other than
 $i_1,\,i_2,\,i_3$
;
$i_1,\,i_2,\,i_3$
; -
(3)
 $\sigma (i_0)\,=\,i_3$
and
$\sigma (i_0)\,=\,i_3$
and
 $v_{i_1}\,=\,v_{\sigma (i_0)}\,=\,\lambda _0 v_{i_4}\,\neq \, 0$
for some
$v_{i_1}\,=\,v_{\sigma (i_0)}\,=\,\lambda _0 v_{i_4}\,\neq \, 0$
for some
 $i_4$
other than
$i_4$
other than
 $i_1,\,i_2,\,i_3$
(see (5.14) for
$i_1,\,i_2,\,i_3$
(see (5.14) for
 $\lambda _0$
);
$\lambda _0$
); -
(4)
 $\sigma (i_0)\,=\,i_3$
,
$\sigma (i_0)\,=\,i_3$
,
 $v_{i_1}\,=\,v_{\sigma (i_0)}\,\neq \, 0$
and
$v_{i_1}\,=\,v_{\sigma (i_0)}\,\neq \, 0$
and
 $v_{i_4}\,=\,0$
for some
$v_{i_4}\,=\,0$
for some
 $i_4$
other than
$i_4$
other than
 $i_1,\,i_2,\,i_3$
.
$i_1,\,i_2,\,i_3$
.
So we can give a parameter space of such
![]() $l^{(3)}_{r-2}$
whose dimension is at most
$l^{(3)}_{r-2}$
whose dimension is at most
![]() $r-4$
.
$r-4$
.
(
![]() $\epsilon$
) Assume that
$\epsilon$
) Assume that
![]() $\sigma (i_0)\,=\,i_1$
and that
$\sigma (i_0)\,=\,i_1$
and that
![]() $\{ j\,\gt \,i \, \,| \: \sigma (j)\,\gt \,\sigma (i)\}\,=\,\emptyset$
for all
$\{ j\,\gt \,i \, \,| \: \sigma (j)\,\gt \,\sigma (i)\}\,=\,\emptyset$
for all
![]() $i\,\neq \, i_0$
. Then the group of automorphisms of
$i\,\neq \, i_0$
. Then the group of automorphisms of
![]() $E$
preserving
$E$
preserving
![]() $l^{(1)}_*$
,
$l^{(1)}_*$
,
![]() $l^{(2)}_*$
and
$l^{(2)}_*$
and
![]() $l^{(3)}_{r-1}\,=\,\langle w \rangle$
becomes
$l^{(3)}_{r-1}\,=\,\langle w \rangle$
becomes
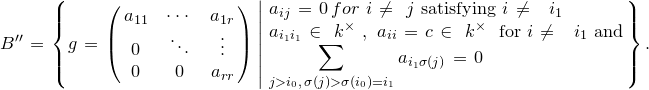 \begin{align*} B''\,=\, \left \{ g\,=\, \left(\begin{array}{c@{\quad}c@{\quad}c}a_{11}& \cdots &a_{1r} \\ 0& \ddots& \vdots \\ 0 &0& a_{rr} \end{array}\right) \, \middle | \: \begin{array}{l} a_{ij}\,=\,0\,for\ i\,\neq\ \,j\ {\rm satisfying}\ i\,\neq\ \,\ i_1\\ a_{i_1i_1}\,\in\ \,k^{\times\ },\ a_{ii}\,=\,c\,\in\ \,k^{\times\ }\ {\rm for}\ i\,\neq\ \,\ i_1\ {\rm and}\\ \displaystyle \sum _{j\gt i_0,\, \sigma (j)\gt \sigma (i_0)=i_1} a_{i_1\sigma (j)} \,=\,0 \end{array} \right \}. \end{align*}
\begin{align*} B''\,=\, \left \{ g\,=\, \left(\begin{array}{c@{\quad}c@{\quad}c}a_{11}& \cdots &a_{1r} \\ 0& \ddots& \vdots \\ 0 &0& a_{rr} \end{array}\right) \, \middle | \: \begin{array}{l} a_{ij}\,=\,0\,for\ i\,\neq\ \,j\ {\rm satisfying}\ i\,\neq\ \,\ i_1\\ a_{i_1i_1}\,\in\ \,k^{\times\ },\ a_{ii}\,=\,c\,\in\ \,k^{\times\ }\ {\rm for}\ i\,\neq\ \,\ i_1\ {\rm and}\\ \displaystyle \sum _{j\gt i_0,\, \sigma (j)\gt \sigma (i_0)=i_1} a_{i_1\sigma (j)} \,=\,0 \end{array} \right \}. \end{align*}
Suppose that for any index
![]() $j_1$
satisfying
$j_1$
satisfying
![]() $j_1\,\neq \, j_0$
and
$j_1\,\neq \, j_0$
and
![]() $i_0\,\lt \,j_1$
, we have
$i_0\,\lt \,j_1$
, we have
![]() $\sigma (i_0)\,\gt \,\sigma (j_1)$
. Then any automorphism
$\sigma (i_0)\,\gt \,\sigma (j_1)$
. Then any automorphism
![]() $\textbf {g}$
in
$\textbf {g}$
in
![]() $B''$
becomes diagonal. In other words,
$B''$
becomes diagonal. In other words,
![]() $\textbf {g}\,=\,(a_{ij})$
satisfies the following conditions:
$\textbf {g}\,=\,(a_{ij})$
satisfies the following conditions:
![]() $a_{ij}\,=\,0$
for
$a_{ij}\,=\,0$
for
![]() $i\,\neq \,j$
and there is a
$i\,\neq \,j$
and there is a
![]() $c\,\in \,k^{\times }$
such that
$c\,\in \,k^{\times }$
such that
![]() $a_{ii}\,=\,c$
for
$a_{ii}\,=\,c$
for
![]() $i\,\neq \, i_1$
. If
$i\,\neq \, i_1$
. If
![]() $\textbf {g}$
further preserves
$\textbf {g}$
further preserves
![]() $l^{(3)}_{r-2}$
, then we have
$l^{(3)}_{r-2}$
, then we have
![]() $a_{i_1i_1}\,=\,a_{i_3i_3}\,=\,c$
, because
$a_{i_1i_1}\,=\,a_{i_3i_3}\,=\,c$
, because
![]() $v_{i_1}\,\neq \, 0$
,
$v_{i_1}\,\neq \, 0$
,
![]() $v_{i_3}\,\neq \, 0$
and
$v_{i_3}\,\neq \, 0$
and
![]() $v_{i_2}\,=\,0$
. Thus
$v_{i_2}\,=\,0$
. Thus
![]() $\textbf {g}$
must be a constant scalar multiplication, which is a contradiction because
$\textbf {g}$
must be a constant scalar multiplication, which is a contradiction because
![]() $(E,\,l)$
is not simple.
$(E,\,l)$
is not simple.
So there is an index
![]() $j_1$
with
$j_1$
with
![]() $j_1\,\neq \, j_0$
satisfying the conditions
$j_1\,\neq \, j_0$
satisfying the conditions
![]() $i_0\,\lt \,j_1$
and
$i_0\,\lt \,j_1$
and
![]() $\sigma (i_0)\,\lt \,\sigma (j_1)$
. Consider the automorphisms
$\sigma (i_0)\,\lt \,\sigma (j_1)$
. Consider the automorphisms
![]() $\textbf {g}\,=\,(a_{ij})$
of the form
$\textbf {g}\,=\,(a_{ij})$
of the form
![]() $a_{i_1i_1}\,=\,c'\,\in \,k^{\times }$
,
$a_{i_1i_1}\,=\,c'\,\in \,k^{\times }$
,
![]() $a_{i_1\sigma (j_0)}\,=\,a\,=\,-a_{i_1\sigma (j_1)}\,\in \,k$
,
$a_{i_1\sigma (j_0)}\,=\,a\,=\,-a_{i_1\sigma (j_1)}\,\in \,k$
,
![]() $a_{ii}\,=\,1$
for
$a_{ii}\,=\,1$
for
![]() $i\,\neq \, i_1$
and
$i\,\neq \, i_1$
and
![]() $a_{ij}\,=\,0$
for any
$a_{ij}\,=\,0$
for any
![]() $i\,\neq \, j$
satisfying
$i\,\neq \, j$
satisfying
![]() $(i,\,j)\,\neq \,(i_1,\, \sigma (j_0)),\, (i_1,\,\sigma (j_1))$
. Recall that the representative
$(i,\,j)\,\neq \,(i_1,\, \sigma (j_0)),\, (i_1,\,\sigma (j_1))$
. Recall that the representative
![]() $v\,=\,\sum _{i=1}^r v_ie_i$
of a generator of
$v\,=\,\sum _{i=1}^r v_ie_i$
of a generator of
![]() $l^{(3)}_{r-2}/l^{(3)}_{r-1}$
is normalized so that
$l^{(3)}_{r-2}/l^{(3)}_{r-1}$
is normalized so that
![]() $v_{i_2}\,=\,0$
. We further normalize a representative
$v_{i_2}\,=\,0$
. We further normalize a representative
![]() $u\,=\,\sum _{i=1}^r u_i e_i\in l^{(3)}_{r-3}$
of a generator of
$u\,=\,\sum _{i=1}^r u_i e_i\in l^{(3)}_{r-3}$
of a generator of
![]() $l^{(3)}_{r-3}/l^{(3)}_{r-2}$
so that
$l^{(3)}_{r-3}/l^{(3)}_{r-2}$
so that
![]() $u_{i_2}\,=\,u_{i_3}\,=\,0$
. We may assume that
$u_{i_2}\,=\,u_{i_3}\,=\,0$
. We may assume that
![]() $\{ \sigma (j_0),\,\sigma (j_1)\}\,\neq \,\{i_2,\,i_3\}$
, because otherwise we can replace
$\{ \sigma (j_0),\,\sigma (j_1)\}\,\neq \,\{i_2,\,i_3\}$
, because otherwise we can replace
![]() $i_2$
or
$i_2$
or
![]() $i_3$
by another index
$i_3$
by another index
![]() $i_4$
other than
$i_4$
other than
![]() $i_1,\,i_2,\,i_3$
according to whether
$i_1,\,i_2,\,i_3$
according to whether
![]() $v_{i_4}\,=\,0$
or
$v_{i_4}\,=\,0$
or
![]() $v_{i_4}\,\neq \, 0$
. So assume that
$v_{i_4}\,\neq \, 0$
. So assume that
![]() $\sigma (j_0)\,\neq \, i_2,\,i_3$
. Applying an automorphism
$\sigma (j_0)\,\neq \, i_2,\,i_3$
. Applying an automorphism
![]() $\textbf {g}$
of the above form to
$\textbf {g}$
of the above form to
![]() $v$
and
$v$
and
![]() $u$
, we have
$u$
, we have
 \begin{align*} \textbf {g}v &\,=\, v_1e_1+\cdots +(c'v_{i_1}+av_{\sigma (j_0)}-av_{\sigma (j_1)})e_{i_1}+\cdots \\ &\quad+0e_{i_2}+\cdots +v_{\sigma (j_0)}e_{\sigma (j_0)} +\cdots +v_{\sigma (j_1)}e_{\sigma (j_1)}+\cdots +v_re_r, \\ \textbf {g}u &\,=\, u_1e_1+\cdots +(c'u_{i_1}+au_{\sigma (j_0)}-au_{\sigma (j_1)})e_{i_1}+\cdots \\ & \quad+0e_{i_2}+\cdots+0e_{i_3}+\cdots +u_{\sigma (j_0)}e_{\sigma (j_0)}+\cdots +u_{\sigma (j_1)}e_{\sigma (j_1)}+\cdots +u_re_r. \end{align*}
\begin{align*} \textbf {g}v &\,=\, v_1e_1+\cdots +(c'v_{i_1}+av_{\sigma (j_0)}-av_{\sigma (j_1)})e_{i_1}+\cdots \\ &\quad+0e_{i_2}+\cdots +v_{\sigma (j_0)}e_{\sigma (j_0)} +\cdots +v_{\sigma (j_1)}e_{\sigma (j_1)}+\cdots +v_re_r, \\ \textbf {g}u &\,=\, u_1e_1+\cdots +(c'u_{i_1}+au_{\sigma (j_0)}-au_{\sigma (j_1)})e_{i_1}+\cdots \\ & \quad+0e_{i_2}+\cdots+0e_{i_3}+\cdots +u_{\sigma (j_0)}e_{\sigma (j_0)}+\cdots +u_{\sigma (j_1)}e_{\sigma (j_1)}+\cdots +u_re_r. \end{align*}
So we may assume that one of the following holds:
-
(1)
 $v_{\sigma (j_0)}\,=\,v_{\sigma (j_1)}$
and
$v_{\sigma (j_0)}\,=\,v_{\sigma (j_1)}$
and
 $u_{\sigma (j_0)}\,=\,u_{\sigma (j_1)}$
;
$u_{\sigma (j_0)}\,=\,u_{\sigma (j_1)}$
; -
(2)
 $v_{\sigma (j_0)}\,=\,v_{\sigma (j_1)}$
,
$v_{\sigma (j_0)}\,=\,v_{\sigma (j_1)}$
,
 $u_{\sigma (j_0)}\,\neq \, u_{\sigma (j_1)}$
and
$u_{\sigma (j_0)}\,\neq \, u_{\sigma (j_1)}$
and
 $u_{i_1}\,=\,u_{\sigma (j_0)}-u_{\sigma (j_1)}$
;
$u_{i_1}\,=\,u_{\sigma (j_0)}-u_{\sigma (j_1)}$
; -
(3)
 $u_{\sigma (j_0)}\,=\,u_{\sigma (j_1)}$
,
$u_{\sigma (j_0)}\,=\,u_{\sigma (j_1)}$
,
 $v_{\sigma (j_0)}\,\neq \, v_{\sigma (j_1)}$
and
$v_{\sigma (j_0)}\,\neq \, v_{\sigma (j_1)}$
and
 $v_{i_1}\,=\,v_{\sigma (j_0)}-v_{\sigma (j_1)}$
;
$v_{i_1}\,=\,v_{\sigma (j_0)}-v_{\sigma (j_1)}$
; -
(4)
 $v_{\sigma (j_0)}-v_{\sigma (j_1)}\,\neq \, 0$
,
$v_{\sigma (j_0)}-v_{\sigma (j_1)}\,\neq \, 0$
,
 $u_{\sigma (j_0)}-u_{\sigma (j_1)}\,\neq \, 0$
,
$u_{\sigma (j_0)}-u_{\sigma (j_1)}\,\neq \, 0$
,
 $v_{i_1}(u_{\sigma (j_0)}-u_{\sigma (j_1)})-u_{i_1}(v_{\sigma (j_0)}-v_{\sigma (j_1)})\,=\,0$
and
$v_{i_1}(u_{\sigma (j_0)}-u_{\sigma (j_1)})-u_{i_1}(v_{\sigma (j_0)}-v_{\sigma (j_1)})\,=\,0$
and
 $v_{i_1}\,=\,v_{\sigma (j_0)}-v_{\sigma (j_1)}$
;
$v_{i_1}\,=\,v_{\sigma (j_0)}-v_{\sigma (j_1)}$
; -
(5)
 $v_{\sigma (j_0)}-v_{\sigma (j_1)}\,\neq \, 0$
,
$v_{\sigma (j_0)}-v_{\sigma (j_1)}\,\neq \, 0$
,
 $u_{\sigma (j_0)}-u_{\sigma (j_1)}\,\neq \, 0$
,
$u_{\sigma (j_0)}-u_{\sigma (j_1)}\,\neq \, 0$
,
 $v_{i_1}(u_{\sigma (j_0)}-u_{\sigma (j_1)})-u_{i_1}(v_{\sigma (j_0)}-v_{\sigma (j_1)})\,\neq \, 0$
,
$v_{i_1}(u_{\sigma (j_0)}-u_{\sigma (j_1)})-u_{i_1}(v_{\sigma (j_0)}-v_{\sigma (j_1)})\,\neq \, 0$
,
 $v_{i_1}\,=\,v_{\sigma (j_0)}-v_{\sigma (j_1)}$
and
$v_{i_1}\,=\,v_{\sigma (j_0)}-v_{\sigma (j_1)}$
and
 $u_{i_1}\,=\,\lambda _0(u_{\sigma (j_0)}-u_{\sigma (j_1)})$
.
$u_{i_1}\,=\,\lambda _0(u_{\sigma (j_0)}-u_{\sigma (j_1)})$
.
In each of the above cases, we can give a parameter space of
![]() $l^{(3)}_{r-2}$
and
$l^{(3)}_{r-2}$
and
![]() $l^{(3)}_{r-3}$
whose dimension is at most
$l^{(3)}_{r-3}$
whose dimension is at most
![]() $r-3+r-4\,=\,2r-7$
.
$r-3+r-4\,=\,2r-7$
.
In all cases of A(b)(iii), we can give a parameter space of
![]() $(E,\,\boldsymbol{l})$
whose dimension is at most
$(E,\,\boldsymbol{l})$
whose dimension is at most
(c) Consider the case where
![]() $w_\ell \,=\,1$
for any
$w_\ell \,=\,1$
for any
![]() $\ell$
.
$\ell$
.
(i) Assume further that there are
![]() $i_1\,\lt \,j_1$
and
$i_1\,\lt \,j_1$
and
![]() $i_2\,\lt \,j_2$
satisfying the conditions
$i_2\,\lt \,j_2$
satisfying the conditions
![]() $\sigma (i_1)\,\neq \, \sigma (i_2)$
,
$\sigma (i_1)\,\neq \, \sigma (i_2)$
,
![]() $\sigma (i_1)\,\lt \,\sigma (j_1)$
and
$\sigma (i_1)\,\lt \,\sigma (j_1)$
and
![]() $\sigma (i_2)\,\lt \,\sigma (j_2)$
. Let
$\sigma (i_2)\,\lt \,\sigma (j_2)$
. Let
![]() $B''$
be the group of automorphisms of
$B''$
be the group of automorphisms of
![]() $E$
preserving
$E$
preserving
![]() $l^{(1)}_*,\,l^{(2)}_*$
and
$l^{(1)}_*,\,l^{(2)}_*$
and
![]() $l^{(3)}_{r-1}$
. Then
$l^{(3)}_{r-1}$
. Then
![]() $B''$
contains two types of automorphisms
$B''$
contains two types of automorphisms
![]() $(a_{ij})$
,
$(a_{ij})$
,
![]() $(b_{ij})$
such that:
$(b_{ij})$
such that:
 $a_{\sigma (i_1)\,\sigma (i_1)}\,=\,c\,\in \,k^{\times }$
,
$a_{\sigma (i_1)\,\sigma (i_1)}\,=\,c\,\in \,k^{\times }$
,
 $a_{\sigma (i_1)\,\sigma (j_1)}\,=\,1-c$
,
$a_{\sigma (i_1)\,\sigma (j_1)}\,=\,1-c$
,
 $a_{ii}\,=\,1$
for
$a_{ii}\,=\,1$
for
 $i\,\neq \,\sigma (i_1)$
and
$i\,\neq \,\sigma (i_1)$
and
 $a_{ij}\,=\,0$
for
$a_{ij}\,=\,0$
for
 $i\,\neq \, j$
satisfying the condition
$i\,\neq \, j$
satisfying the condition
 $(i,\,j)\,\neq \, (\sigma (i_1),\,\sigma (j_1))$
;
$(i,\,j)\,\neq \, (\sigma (i_1),\,\sigma (j_1))$
; $b_{\sigma (i_2)\,\sigma (i_2)}\,=\,c'\,\in \,k^{\times }$
,
$b_{\sigma (i_2)\,\sigma (i_2)}\,=\,c'\,\in \,k^{\times }$
,
 $b_{\sigma (i_2)\,\sigma (j_2)}\,=\,1-c'$
,
$b_{\sigma (i_2)\,\sigma (j_2)}\,=\,1-c'$
,
 $b_{ii}\,=\,1$
for
$b_{ii}\,=\,1$
for
 $i\,\neq \, \sigma (i_2)$
and
$i\,\neq \, \sigma (i_2)$
and
 $b_{ij}\,=\,0$
for
$b_{ij}\,=\,0$
for
 $i\,\neq \, j$
satisfying the condition
$i\,\neq \, j$
satisfying the condition
 $(i,\,j)\,\neq \,(\sigma (i_2),\,\sigma (j_2))$
.
$(i,\,j)\,\neq \,(\sigma (i_2),\,\sigma (j_2))$
.
For a representative
![]() $v\,=\,v_1e_1+\cdots +v_re_r$
of a generator of
$v\,=\,v_1e_1+\cdots +v_re_r$
of a generator of
![]() $l^{(3)}_{r-2}/l^{(3)}_{r-1}$
, we may assume, after adding an element of
$l^{(3)}_{r-2}/l^{(3)}_{r-1}$
, we may assume, after adding an element of
![]() $l^{(3)}_{r-1}$
, that
$l^{(3)}_{r-1}$
, that
![]() $v_{i'_2}\,=\,0$
for some
$v_{i'_2}\,=\,0$
for some
![]() $i'_2$
such that
$i'_2$
such that
![]() $i'_2\,\neq \,\sigma (i_1),\,\sigma (j_1),\,\sigma (i_2)$
. We may further assume that
$i'_2\,\neq \,\sigma (i_1),\,\sigma (j_1),\,\sigma (i_2)$
. We may further assume that
![]() $i'_2\,\neq \, \sigma (j_2)$
if
$i'_2\,\neq \, \sigma (j_2)$
if
![]() $\sigma (i_1),\,\sigma (j_1),\,\sigma (i_2),\,\sigma (j_2)$
are not distinct. Applying automorphisms of the above type, we may assume that one of the following holds:
$\sigma (i_1),\,\sigma (j_1),\,\sigma (i_2),\,\sigma (j_2)$
are not distinct. Applying automorphisms of the above type, we may assume that one of the following holds:
-
(1)
 $j_1\,=\,j_2$
,
$j_1\,=\,j_2$
,
 $v_{\sigma (j_1)}\,=\,0$
and
$v_{\sigma (j_1)}\,=\,0$
and
 $(v_{\sigma (i_1)}-v_{\sigma (i_2)})v_{\sigma (i_1)}v_{\sigma (i_2)}\,=\,0$
;
$(v_{\sigma (i_1)}-v_{\sigma (i_2)})v_{\sigma (i_1)}v_{\sigma (i_2)}\,=\,0$
; -
(2)
 $j_1\,=\,j_2$
,
$j_1\,=\,j_2$
,
 $v_{\sigma (j_1)}\,\neq \, 0$
and
$v_{\sigma (j_1)}\,\neq \, 0$
and
 $(v_{\sigma (j_1)}-v_{\sigma (i_1)})(v_{\sigma (j_1)}-\lambda _0v_{\sigma (i_1)}) \,=\, (v_{\sigma (j_1)}-v_{\sigma (i_2)})(v_{\sigma (j_1)}-\lambda _0v_{\sigma (i_2)})\,=\,0$
;
$(v_{\sigma (j_1)}-v_{\sigma (i_1)})(v_{\sigma (j_1)}-\lambda _0v_{\sigma (i_1)}) \,=\, (v_{\sigma (j_1)}-v_{\sigma (i_2)})(v_{\sigma (j_1)}-\lambda _0v_{\sigma (i_2)})\,=\,0$
; -
(3)
 $j_1\,\neq \,j_2$
and
$j_1\,\neq \,j_2$
and
 $v_{\sigma (j_1)}(v_{\sigma (i_1)}-v_{\sigma (j_1)})\,=\,v_{\sigma (j_2)}(v_{\sigma (i_2)}-v_{\sigma (j_2)})\,=\,0$
;
$v_{\sigma (j_1)}(v_{\sigma (i_1)}-v_{\sigma (j_1)})\,=\,v_{\sigma (j_2)}(v_{\sigma (i_2)}-v_{\sigma (j_2)})\,=\,0$
; -
(4)
 $j_1\,\neq \, j_2$
,
$j_1\,\neq \, j_2$
,
 $0\,\neq \, v_{\sigma (j_1)}\,=\,\lambda _0v_{\sigma (i_1)}$
and
$0\,\neq \, v_{\sigma (j_1)}\,=\,\lambda _0v_{\sigma (i_1)}$
and
 $(v_{\sigma (i_2)}-v_{\sigma (j_2)})v_{\sigma (j_2)}\,=\, 0$
;
$(v_{\sigma (i_2)}-v_{\sigma (j_2)})v_{\sigma (j_2)}\,=\, 0$
; -
(5)
 $j_1\,\neq \, j_2$
,
$j_1\,\neq \, j_2$
,
 $(v_{\sigma (i_1)}-v_{\sigma (j_1)})v_{\sigma (j_1)}\,=\,0$
and
$(v_{\sigma (i_1)}-v_{\sigma (j_1)})v_{\sigma (j_1)}\,=\,0$
and
 $0\,\neq \, v_{\sigma (j_2)}\,=\,\lambda _0v_{\sigma (i_2)}$
;
$0\,\neq \, v_{\sigma (j_2)}\,=\,\lambda _0v_{\sigma (i_2)}$
; -
(6)
 $j_1\,\neq \, j_2$
,
$j_1\,\neq \, j_2$
,
 $v_{\sigma (i_1)}\,=\,\lambda _0v_{\sigma (j_1)}\,\neq \, 0$
and
$v_{\sigma (i_1)}\,=\,\lambda _0v_{\sigma (j_1)}\,\neq \, 0$
and
 $v_{\sigma (i_2)}\,=\,\lambda _0v_{\sigma (j_2)}\,\neq \, 0$
.
$v_{\sigma (i_2)}\,=\,\lambda _0v_{\sigma (j_2)}\,\neq \, 0$
.
So we can give a parameter space for
![]() $l^{(3)}_{r-2}$
whose dimension is at most
$l^{(3)}_{r-2}$
whose dimension is at most
![]() $r-2-2\,=\,r-4$
. Adding the data of
$r-2-2\,=\,r-4$
. Adding the data of
![]() $l^{(3)}_{r-3},\,\cdots ,\,l^{(3)}_1$
, we can get a parameter space for
$l^{(3)}_{r-3},\,\cdots ,\,l^{(3)}_1$
, we can get a parameter space for
![]() $(E,\,\boldsymbol{l})$
whose dimension is at most
$(E,\,\boldsymbol{l})$
whose dimension is at most
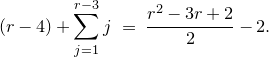 \begin{align*} (r-4)+\sum _{j=1}^{r-3} j \ =\ \frac {r^2-3r+2} {2} - 2. \end{align*}
\begin{align*} (r-4)+\sum _{j=1}^{r-3} j \ =\ \frac {r^2-3r+2} {2} - 2. \end{align*}
(ii) Consider the rest case of A-(c). So, there is at most one
![]() $i_0$
such that there is
$i_0$
such that there is
![]() $j\,\gt \,i_0$
for which
$j\,\gt \,i_0$
for which
![]() $\sigma (i_0)\,\lt \,\sigma (j)$
. Recall that we assumed that
$\sigma (i_0)\,\lt \,\sigma (j)$
. Recall that we assumed that
![]() $w_i\,=\,1$
for any
$w_i\,=\,1$
for any
![]() $i$
. Then the automorphism group
$i$
. Then the automorphism group
![]() $B''$
of
$B''$
of
![]() $E$
preserving
$E$
preserving
![]() $l^{(1)}_*$
,
$l^{(1)}_*$
,
![]() $l^{(2)}_*$
and
$l^{(2)}_*$
and
![]() $l^{(3)}_{r-1}$
becomes
$l^{(3)}_{r-1}$
becomes
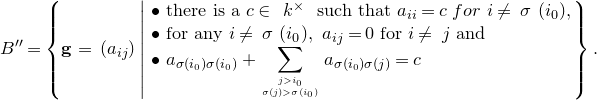 \begin{align*} B''= \left \{\textbf {g}\,=\, (a_{ij}) \, \middle | \: \begin{array}{l} \bullet {\rm \ there\ is\ a}\ c\in\ \,k^{\times\ }\ {\rm such\ that}\ a_{ii}=c\ for\ i\neq\ \sigma\ (i_0), \\ \bullet {\rm \ for\ any}\ i\neq\ \sigma\ (i_0),\ a_{ij}=0\ {\rm for}\ i\neq\ j\ {\rm and} \\ \bullet \ \displaystyle a_{\sigma (i_0)\sigma (i_0)}+\sum _{\genfrac {}{}{0pt}{}{j\gt i_0}{\sigma (j)\gt \sigma (i_0)}} a_{\sigma (i_0)\sigma (j)}=c \end{array} \right \}. \end{align*}
\begin{align*} B''= \left \{\textbf {g}\,=\, (a_{ij}) \, \middle | \: \begin{array}{l} \bullet {\rm \ there\ is\ a}\ c\in\ \,k^{\times\ }\ {\rm such\ that}\ a_{ii}=c\ for\ i\neq\ \sigma\ (i_0), \\ \bullet {\rm \ for\ any}\ i\neq\ \sigma\ (i_0),\ a_{ij}=0\ {\rm for}\ i\neq\ j\ {\rm and} \\ \bullet \ \displaystyle a_{\sigma (i_0)\sigma (i_0)}+\sum _{\genfrac {}{}{0pt}{}{j\gt i_0}{\sigma (j)\gt \sigma (i_0)}} a_{\sigma (i_0)\sigma (j)}=c \end{array} \right \}. \end{align*}
Since there are non-scalar automorphisms in
![]() $B''$
, there is some
$B''$
, there is some
![]() $j_0\,\gt \,i_0$
for which
$j_0\,\gt \,i_0$
for which
![]() $\sigma (j_0)\,\gt \,\sigma (i_0)$
. Choosing
$\sigma (j_0)\,\gt \,\sigma (i_0)$
. Choosing
![]() $i'_2$
other than
$i'_2$
other than
![]() $\sigma (i_0)$
and
$\sigma (i_0)$
and
![]() $\sigma (j_0)$
, we can normalize a representative
$\sigma (j_0)$
, we can normalize a representative
![]() $v\,=\,v_1e_1+\cdots +v_re_r$
of a generator of
$v\,=\,v_1e_1+\cdots +v_re_r$
of a generator of
![]() $l^{(3)}_{r-2}/l^{(3)}_{r-1}$
so that
$l^{(3)}_{r-2}/l^{(3)}_{r-1}$
so that
![]() $v_{i'_2}\,=\,0$
. Consider the automorphisms
$v_{i'_2}\,=\,0$
. Consider the automorphisms
![]() $\textbf {g}\,=\,(a_{ij})$
of
$\textbf {g}\,=\,(a_{ij})$
of
![]() $E$
given by
$E$
given by
![]() $a_{ii}\,=\,1$
for
$a_{ii}\,=\,1$
for
![]() $i\,\neq \,\sigma (i_0)$
,
$i\,\neq \,\sigma (i_0)$
,
![]() $a_{\sigma (i_0)\sigma (i_0)}\,=\,c\,\in \,k^{\times }$
,
$a_{\sigma (i_0)\sigma (i_0)}\,=\,c\,\in \,k^{\times }$
,
![]() $a_{\sigma (i_0)\sigma (j_0)}\,=\,1-c$
and
$a_{\sigma (i_0)\sigma (j_0)}\,=\,1-c$
and
![]() $a_{ij}\,=\,0$
for any
$a_{ij}\,=\,0$
for any
![]() $i\neq j$
such that
$i\neq j$
such that
![]() $(i,\,j)\,\neq \,(\sigma (i_0),\,\sigma (j_0))$
. Then such automorphisms preserve
$(i,\,j)\,\neq \,(\sigma (i_0),\,\sigma (j_0))$
. Then such automorphisms preserve
![]() $l^{(1)}_*$
,
$l^{(1)}_*$
,
![]() $l^{(2)}_*$
and
$l^{(2)}_*$
and
![]() $l^{(3)}_{r-1}$
. Choose
$l^{(3)}_{r-1}$
. Choose
![]() $i'_3$
other than
$i'_3$
other than
![]() $\sigma (i_0),\,\sigma (j_0),\, i'_2$
. Since
$\sigma (i_0),\,\sigma (j_0),\, i'_2$
. Since
![]() $v$
is sent to
$v$
is sent to
by the automorphism
![]() $\textbf {g}$
, we can assume that one of the following holds:
$\textbf {g}$
, we can assume that one of the following holds:
-
(
 $\alpha$
)
$\alpha$
)
 $v_{\sigma (i_0)}\,=\,v_{\sigma (j_0)}$
;
$v_{\sigma (i_0)}\,=\,v_{\sigma (j_0)}$
; -
(
 $\beta$
)
$\beta$
)
 $v_{\sigma (i_0)}\,\neq \, v_{\sigma (j_0)}$
and
$v_{\sigma (i_0)}\,\neq \, v_{\sigma (j_0)}$
and
 $v_{\sigma (j_0)}\,=\,v_{i'_3}$
;
$v_{\sigma (j_0)}\,=\,v_{i'_3}$
; -
(
 $\gamma$
)
$\gamma$
)
 $v_{\sigma (i_0)}\,\neq \, v_{\sigma (j_0)}$
,
$v_{\sigma (i_0)}\,\neq \, v_{\sigma (j_0)}$
,
 $v_{\sigma (j_0)}\,\neq \, v_{i'_3}$
and
$v_{\sigma (j_0)}\,\neq \, v_{i'_3}$
and
 $v_{\sigma (i_0)}\,=\,v_{i'_3}$
.
$v_{\sigma (i_0)}\,=\,v_{i'_3}$
.
If, in addition, we have
![]() $v_{i'_3}\,=\,0$
, then we can give a parameter space for such
$v_{i'_3}\,=\,0$
, then we can give a parameter space for such
![]() $l^{(3)}_{r-2}$
whose dimension is at most
$l^{(3)}_{r-2}$
whose dimension is at most
![]() $r-4$
. So we assume that
$r-4$
. So we assume that
![]() $v_{i'_3}\,\neq \, 0$
.
$v_{i'_3}\,\neq \, 0$
.
(
![]() $\alpha$
) Assume that the condition
$\alpha$
) Assume that the condition
![]() $v_{\sigma (i_0)}\,=\,v_{\sigma (j_0)}$
holds. Recall that we are assuming that
$v_{\sigma (i_0)}\,=\,v_{\sigma (j_0)}$
holds. Recall that we are assuming that
![]() $i'_2\,\neq \,\sigma (i_0),\,\sigma (j_0)$
and
$i'_2\,\neq \,\sigma (i_0),\,\sigma (j_0)$
and
![]() $i'_3\,\neq \, \sigma (i_0),\,\sigma (j_0),\,i'_2$
. Furthermore, we are normalizing
$i'_3\,\neq \, \sigma (i_0),\,\sigma (j_0),\,i'_2$
. Furthermore, we are normalizing
![]() $v$
so that
$v$
so that
![]() $v_{i'_2}\,=\,0$
. Consider the automorphisms
$v_{i'_2}\,=\,0$
. Consider the automorphisms
![]() $\textbf {g}\,=\,(a_{ij})$
given by
$\textbf {g}\,=\,(a_{ij})$
given by
![]() $a_{ii}\,=\,1$
for
$a_{ii}\,=\,1$
for
![]() $i\,\neq \,\sigma (i_0)$
,
$i\,\neq \,\sigma (i_0)$
,
![]() $a_{\sigma (i_0)\sigma (i_0)}\,=\,c\,\in \, k^{\times }$
,
$a_{\sigma (i_0)\sigma (i_0)}\,=\,c\,\in \, k^{\times }$
,
![]() $a_{\sigma (i_0)\sigma (j_0)}\,=\,1-c$
and
$a_{\sigma (i_0)\sigma (j_0)}\,=\,1-c$
and
![]() $a_{ij}\,=\,0$
for any
$a_{ij}\,=\,0$
for any
![]() $i\,\neq \,j$
such that
$i\,\neq \,j$
such that
![]() $(i,\,j)\,\neq \,(\sigma (i_0),\,\sigma (j_0))$
. Then such automorphisms
$(i,\,j)\,\neq \,(\sigma (i_0),\,\sigma (j_0))$
. Then such automorphisms
![]() $g$
preserve not only
$g$
preserve not only
![]() $l^{(1)}_*$
,
$l^{(1)}_*$
,
![]() $l^{(2)}_*$
and
$l^{(2)}_*$
and
![]() $l^{(3)}_{r-1}$
but also
$l^{(3)}_{r-1}$
but also
![]() $v$
. Consider a normalized representative
$v$
. Consider a normalized representative
![]() $u\,=\,u_1e_1+\cdots +u_re_r$
of a generator of
$u\,=\,u_1e_1+\cdots +u_re_r$
of a generator of
![]() $l^{(3)}_{r-3}/l^{(3)}_{r-2}$
such that
$l^{(3)}_{r-3}/l^{(3)}_{r-2}$
such that
![]() $u_{i'_2}\,=\,u_{i'_3}\,=\,0$
. Then
$u_{i'_2}\,=\,u_{i'_3}\,=\,0$
. Then
![]() $u$
is sent to
$u$
is sent to
by the above automorphism
![]() $\textbf {g}$
. Replacing
$\textbf {g}$
. Replacing
![]() $u$
by some
$u$
by some
![]() $\textbf {g}u$
, we may assume that one of the following holds:
$\textbf {g}u$
, we may assume that one of the following holds:
 $u_{\sigma (i_0)}\,=\,u_{\sigma (j_0)}$
;
$u_{\sigma (i_0)}\,=\,u_{\sigma (j_0)}$
; $u_{\sigma (i_0)}\,\neq \, u_{\sigma (j_0)}$
and
$u_{\sigma (i_0)}\,\neq \, u_{\sigma (j_0)}$
and
 $u_{\sigma (j_0)}\,=\,0$
;
$u_{\sigma (j_0)}\,=\,0$
; $u_{\sigma (i_0)}\,\neq \, u_{\sigma (j_0)}$
,
$u_{\sigma (i_0)}\,\neq \, u_{\sigma (j_0)}$
,
 $u_{\sigma (j_0)}\,\neq \, 0$
and
$u_{\sigma (j_0)}\,\neq \, 0$
and
 $u_{\sigma (i_0)}\,=\,0$
.
$u_{\sigma (i_0)}\,=\,0$
.
So we can give a parameter space for
![]() $(E,\,\boldsymbol{l})$
whose dimension is at most
$(E,\,\boldsymbol{l})$
whose dimension is at most
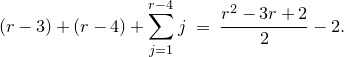 \begin{align*} (r-3)+(r-4)+\sum _{j=1}^{r-4} j\ =\ \frac {r^2-3r+2} {2} - 2. \end{align*}
\begin{align*} (r-3)+(r-4)+\sum _{j=1}^{r-4} j\ =\ \frac {r^2-3r+2} {2} - 2. \end{align*}
(
![]() $\beta$
) Assume that
$\beta$
) Assume that
![]() $v_{\sigma (i_0)}\,\neq \, v_{\sigma (j_0)}$
and
$v_{\sigma (i_0)}\,\neq \, v_{\sigma (j_0)}$
and
![]() $v_{\sigma (j_0)}\,=\,v_{i'_3}$
. Recall that we are assuming that
$v_{\sigma (j_0)}\,=\,v_{i'_3}$
. Recall that we are assuming that
![]() $v_{i'_3}\,\neq \, 0$
. After applying an automorphism in
$v_{i'_3}\,\neq \, 0$
. After applying an automorphism in
![]() $B''$
, we may assume that
$B''$
, we may assume that
![]() $v_{\sigma (i_0)}\,=\,\lambda _0 v_{i'_3}$
. So we can give a parameter space for such
$v_{\sigma (i_0)}\,=\,\lambda _0 v_{i'_3}$
. So we can give a parameter space for such
![]() $l^{(3)}_{r-2}$
of dimension at most
$l^{(3)}_{r-2}$
of dimension at most
![]() $r-4$
. Then we can give a parameter space for
$r-4$
. Then we can give a parameter space for
![]() $(E,\,\boldsymbol{l})$
whose dimension is at most
$(E,\,\boldsymbol{l})$
whose dimension is at most
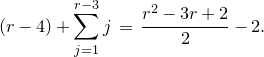 \begin{align*} (r-4)+\sum _{j=1}^{r-3} j \, =\,\frac {r^2-3r+2} {2} - 2. \end{align*}
\begin{align*} (r-4)+\sum _{j=1}^{r-3} j \, =\,\frac {r^2-3r+2} {2} - 2. \end{align*}
(
![]() $\gamma$
) Assume that
$\gamma$
) Assume that
![]() $v_{\sigma (i_0)}\,\neq \, v_{\sigma (j_0)}$
,
$v_{\sigma (i_0)}\,\neq \, v_{\sigma (j_0)}$
,
![]() $v_{\sigma (j_0)}\,\neq \, v_{i'_3}$
and
$v_{\sigma (j_0)}\,\neq \, v_{i'_3}$
and
![]() $v_{\sigma (i_0)}\,=\,v_{i'_3}$
. Note that there are non-scalar automorphisms
$v_{\sigma (i_0)}\,=\,v_{i'_3}$
. Note that there are non-scalar automorphisms
![]() $\textbf {g}\,=\,(a_{ij})\,\in \, B''$
preserving
$\textbf {g}\,=\,(a_{ij})\,\in \, B''$
preserving
![]() $l^{(3)}_{r-2}$
. Recall that there is a
$l^{(3)}_{r-2}$
. Recall that there is a
![]() $c\,\in \,k^{\times }$
such that
$c\,\in \,k^{\times }$
such that
![]() $a_{ii}\,=\,c$
for
$a_{ii}\,=\,c$
for
![]() $i\,\neq \, \sigma (i_0)$
. Since
$i\,\neq \, \sigma (i_0)$
. Since
![]() $\textbf {g}v\,\in \,\langle v,\,w\rangle$
, and the coefficient of
$\textbf {g}v\,\in \,\langle v,\,w\rangle$
, and the coefficient of
![]() $e_{i'_2}$
in
$e_{i'_2}$
in
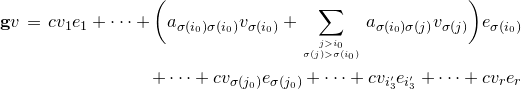 \begin{align*} \textbf {g}v \,=\, cv_1e_1+\cdots + \bigg ( a_{\sigma (i_0)\sigma (i_0)}v_{\sigma (i_0)}+ \sum _{\genfrac {}{}{0pt}{}{j\gt i_0}{\sigma (j)\gt \sigma (i_0)}} a_{\sigma (i_0)\sigma (j)}v_{\sigma (j)} \bigg ) e_{\sigma (i_0)} \\ \quad \quad +\cdots +cv_{\sigma (j_0)}e_{\sigma (j_0)}+\cdots +cv_{i'_3}e_{i'_3}+\cdots +cv_re_r \end{align*}
\begin{align*} \textbf {g}v \,=\, cv_1e_1+\cdots + \bigg ( a_{\sigma (i_0)\sigma (i_0)}v_{\sigma (i_0)}+ \sum _{\genfrac {}{}{0pt}{}{j\gt i_0}{\sigma (j)\gt \sigma (i_0)}} a_{\sigma (i_0)\sigma (j)}v_{\sigma (j)} \bigg ) e_{\sigma (i_0)} \\ \quad \quad +\cdots +cv_{\sigma (j_0)}e_{\sigma (j_0)}+\cdots +cv_{i'_3}e_{i'_3}+\cdots +cv_re_r \end{align*}
is zero, we must have
![]() $\textbf {g}v\,=\,cv$
. Comparing the coefficients of
$\textbf {g}v\,=\,cv$
. Comparing the coefficients of
![]() $e_{\sigma (i_0)}$
, we have
$e_{\sigma (i_0)}$
, we have
 \begin{align*} a_{\sigma (i_0)\sigma (i_0)}v_{\sigma (i_0)}+ \sum _{\genfrac {}{}{0pt}{}{j\gt i_0}{\sigma (j)\gt \sigma (i_0)}} a_{\sigma (i_0)\sigma (j)}v_{\sigma (j)} \,=\,c \, v_{\sigma (i_0)}. \end{align*}
\begin{align*} a_{\sigma (i_0)\sigma (i_0)}v_{\sigma (i_0)}+ \sum _{\genfrac {}{}{0pt}{}{j\gt i_0}{\sigma (j)\gt \sigma (i_0)}} a_{\sigma (i_0)\sigma (j)}v_{\sigma (j)} \,=\,c \, v_{\sigma (i_0)}. \end{align*}
Combining with the equality
 $\displaystyle a_{\sigma (i_0)\sigma (i_0)}+\sum _{\genfrac {}{}{0pt}{}{j\gt i_0}{\sigma (j)\gt \sigma (i_0)}} a_{\sigma (i_0)\sigma (j)}\,=\,c$
, it follows that
$\displaystyle a_{\sigma (i_0)\sigma (i_0)}+\sum _{\genfrac {}{}{0pt}{}{j\gt i_0}{\sigma (j)\gt \sigma (i_0)}} a_{\sigma (i_0)\sigma (j)}\,=\,c$
, it follows that
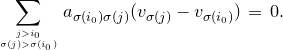 \begin{align*} \sum _{\genfrac {}{}{0pt}{}{j\gt i_0}{\sigma (j)\gt \sigma (i_0)}} a_{\sigma (i_0)\sigma (j)}(v_{\sigma (j)}-v_{\sigma (i_0)})\,=\,0. \end{align*}
\begin{align*} \sum _{\genfrac {}{}{0pt}{}{j\gt i_0}{\sigma (j)\gt \sigma (i_0)}} a_{\sigma (i_0)\sigma (j)}(v_{\sigma (j)}-v_{\sigma (i_0)})\,=\,0. \end{align*}
So there is
![]() $j_1\,\neq \, j_0$
for which
$j_1\,\neq \, j_0$
for which
![]() $j_1\,\gt \,i_0$
and
$j_1\,\gt \,i_0$
and
![]() $\sigma (j_1)\,\gt \,\sigma (i_0)$
.
$\sigma (j_1)\,\gt \,\sigma (i_0)$
.
If
![]() $v$
satisfies the condition
$v$
satisfies the condition
![]() $v_{\sigma (j_0)}\,=\,v_{\sigma (j_1)}$
, then, taking into account the condition (
$v_{\sigma (j_0)}\,=\,v_{\sigma (j_1)}$
, then, taking into account the condition (
![]() $\gamma$
), we can give a parameter space for such
$\gamma$
), we can give a parameter space for such
![]() $l^{(3)}_{r-2}$
of dimension at most
$l^{(3)}_{r-2}$
of dimension at most
![]() $r-2-2\,=\,r-4$
.
$r-2-2\,=\,r-4$
.
So we assume that
![]() $v_{\sigma (j_0)}\,\neq \, v_{\sigma (j_1)}$
. For
$v_{\sigma (j_0)}\,\neq \, v_{\sigma (j_1)}$
. For
![]() $a\,\in \,k^{\times }$
, we can construct an automorphism
$a\,\in \,k^{\times }$
, we can construct an automorphism
![]() $\textbf {g}\,=\,(a'_{ij})\,\in \, B''$
satisfying the following conditions:
$\textbf {g}\,=\,(a'_{ij})\,\in \, B''$
satisfying the following conditions:
-
(1)
 $a'_{ii}\,=\,1$
for
$a'_{ii}\,=\,1$
for
 $i\,\neq \,\sigma (i_0)$
;
$i\,\neq \,\sigma (i_0)$
; -
(2)
 $a'_{ij}\,=\,0$
for any
$a'_{ij}\,=\,0$
for any
 $i\,\neq \, j$
for which
$i\,\neq \, j$
for which
 $(i,\,j)\,\neq \,(\sigma (i_0),\,\sigma (j_0)),\,\, (\sigma (i_0),\,\sigma (j_1))$
;
$(i,\,j)\,\neq \,(\sigma (i_0),\,\sigma (j_0)),\,\, (\sigma (i_0),\,\sigma (j_1))$
; -
(3)
 $a'_{\sigma (i_0)\sigma (i_0)}\,=\,a$
,
$a'_{\sigma (i_0)\sigma (i_0)}\,=\,a$
,
 $a'_{\sigma (i_0)\sigma (j_0)}\,=\,b\,\in \,k$
,
$a'_{\sigma (i_0)\sigma (j_0)}\,=\,b\,\in \,k$
,
 $a'_{\sigma (i_0)\sigma (j_1)}\,=\,b'\,\in \,k$
;
$a'_{\sigma (i_0)\sigma (j_1)}\,=\,b'\,\in \,k$
; -
(4)
 $a+b+b'\,=\,1$
and
$a+b+b'\,=\,1$
and
 $av_{\sigma (i_0)}+bv_{\sigma (j_0)}+b'v_{\sigma (j_1)}\,=\,v_{\sigma (i_0)}$
.
$av_{\sigma (i_0)}+bv_{\sigma (j_0)}+b'v_{\sigma (j_1)}\,=\,v_{\sigma (i_0)}$
.
Indeed, if
![]() $a\,\in \,k^{\times }$
is given, then
$a\,\in \,k^{\times }$
is given, then
![]() $b'$
is determined by the equality
$b'$
is determined by the equality
and
![]() $b$
is determined by the condition
$b$
is determined by the condition
![]() $b\,=\,1-a-b'$
. Recall that we normalized
$b\,=\,1-a-b'$
. Recall that we normalized
![]() $v_{i'_2}\,=\,0$
and we are assuming that
$v_{i'_2}\,=\,0$
and we are assuming that
![]() $i'_3\,\neq \, i'_2,\,\sigma (i_0),\,\sigma (j_0)$
. Consider a representative
$i'_3\,\neq \, i'_2,\,\sigma (i_0),\,\sigma (j_0)$
. Consider a representative
![]() $u\,=\,u_1e_1+\cdots +u_re_r\in l^{(3)}_{r-3}$
of a generator of
$u\,=\,u_1e_1+\cdots +u_re_r\in l^{(3)}_{r-3}$
of a generator of
![]() $l^{(3)}_{r-3}/l^{(3)}_{r-2}$
satisfying the normalized condition
$l^{(3)}_{r-3}/l^{(3)}_{r-2}$
satisfying the normalized condition
![]() $u_{i'_2}\,=\,u_{i'_3}\,=\,0$
. Then the
$u_{i'_2}\,=\,u_{i'_3}\,=\,0$
. Then the
![]() $e_{i'_2}$
-coefficient and the
$e_{i'_2}$
-coefficient and the
![]() $e_{i'_3}$
-coefficient of
$e_{i'_3}$
-coefficient of
vanish, and the
![]() $e_{\sigma (i_0)}$
-coefficient of
$e_{\sigma (i_0)}$
-coefficient of
![]() $\textbf {g}u$
is
$\textbf {g}u$
is
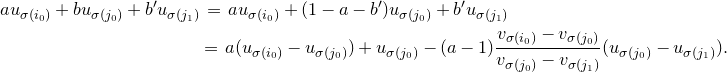 \begin{align*} au_{\sigma (i_0)}+bu_{\sigma (j_0)}+b'u_{\sigma (j_1)} & \,=\, au_{\sigma (i_0)}+(1-a-b')u_{\sigma (j_0)}+b'u_{\sigma (j_1)} \\ &=\, a(u_{\sigma (i_0)}-u_{\sigma (j_0)}) +u_{\sigma (j_0)} -(a-1)\frac {v_{\sigma (i_0)}-v_{\sigma (j_0)}} {v_{\sigma (j_0)}-v_{\sigma (j_1)}} (u_{\sigma (j_0)}-u_{\sigma (j_1)}). \end{align*}
\begin{align*} au_{\sigma (i_0)}+bu_{\sigma (j_0)}+b'u_{\sigma (j_1)} & \,=\, au_{\sigma (i_0)}+(1-a-b')u_{\sigma (j_0)}+b'u_{\sigma (j_1)} \\ &=\, a(u_{\sigma (i_0)}-u_{\sigma (j_0)}) +u_{\sigma (j_0)} -(a-1)\frac {v_{\sigma (i_0)}-v_{\sigma (j_0)}} {v_{\sigma (j_0)}-v_{\sigma (j_1)}} (u_{\sigma (j_0)}-u_{\sigma (j_1)}). \end{align*}
If
![]() $\displaystyle u_{\sigma (i_0)}-u_{\sigma (j_0)}\,\neq \, \frac {v_{\sigma (i_0)}-v_{\sigma (j_0)}} {v_{\sigma (j_0)}-v_{\sigma (j_1)}} (u_{\sigma (j_0)}-u_{\sigma (j_1)})$
, then we can normalize
$\displaystyle u_{\sigma (i_0)}-u_{\sigma (j_0)}\,\neq \, \frac {v_{\sigma (i_0)}-v_{\sigma (j_0)}} {v_{\sigma (j_0)}-v_{\sigma (j_1)}} (u_{\sigma (j_0)}-u_{\sigma (j_1)})$
, then we can normalize
![]() $u$
so that
$u$
so that
![]() $u_{\sigma (i_0)}\,=\,u_{\sigma (j_0)}$
. So we can give a parameter space for such
$u_{\sigma (i_0)}\,=\,u_{\sigma (j_0)}$
. So we can give a parameter space for such
![]() $l^{(3)}_{r-3}$
whose dimension is at most
$l^{(3)}_{r-3}$
whose dimension is at most
![]() $r-4$
. If the equality
$r-4$
. If the equality
![]() $\displaystyle u_{\sigma (i_0)}-u_{\sigma (j_0)}\,=\, \frac {v_{\sigma (i_0)}-v_{\sigma (j_0)}} {v_{\sigma (j_0)}-v_{\sigma (j_1)}} (u_{\sigma (j_0)}-u_{\sigma (j_1)})$
holds, then we can give a parameter space for such
$\displaystyle u_{\sigma (i_0)}-u_{\sigma (j_0)}\,=\, \frac {v_{\sigma (i_0)}-v_{\sigma (j_0)}} {v_{\sigma (j_0)}-v_{\sigma (j_1)}} (u_{\sigma (j_0)}-u_{\sigma (j_1)})$
holds, then we can give a parameter space for such
![]() $l^{(3)}_{r-3}$
whose dimension is at most
$l^{(3)}_{r-3}$
whose dimension is at most
![]() $r-4$
. Therefore, in all cases we can give a parameter space of
$r-4$
. Therefore, in all cases we can give a parameter space of
![]() $(E,\,\boldsymbol{l})$
whose dimension is at most
$(E,\,\boldsymbol{l})$
whose dimension is at most
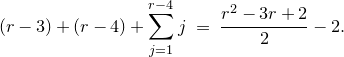 \begin{align*} (r-3)+(r-4)+\sum _{j=1}^{r-4} j \ =\ \frac {r^2-3r+2} {2} - 2. \end{align*}
\begin{align*} (r-3)+(r-4)+\sum _{j=1}^{r-4} j \ =\ \frac {r^2-3r+2} {2} - 2. \end{align*}
Case B. Consider the case where
![]() $E\,=\,{\mathcal O}_{\mathbb{P}^1}(a_1)^{\oplus r_1}\oplus \cdots \oplus {\mathcal O}_{\mathbb{P}^1}(a_m)^{\oplus r_m}$
with
$E\,=\,{\mathcal O}_{\mathbb{P}^1}(a_1)^{\oplus r_1}\oplus \cdots \oplus {\mathcal O}_{\mathbb{P}^1}(a_m)^{\oplus r_m}$
with
![]() $a_1\,\lt \,a_2\,\lt \,\cdots \,\lt \,a_m$
and
$a_1\,\lt \,a_2\,\lt \,\cdots \,\lt \,a_m$
and
![]() $l^{(i)}_{r-1}\,\subset \, {\mathcal O}_{\mathbb{P}^1}(a_2)^{\oplus r_2}\big |_{x_i}\oplus \cdots \oplus {\mathcal O}_{\mathbb{P}^1}(a_m)^{\oplus r_m}\big |_{x_i}$
for
$l^{(i)}_{r-1}\,\subset \, {\mathcal O}_{\mathbb{P}^1}(a_2)^{\oplus r_2}\big |_{x_i}\oplus \cdots \oplus {\mathcal O}_{\mathbb{P}^1}(a_m)^{\oplus r_m}\big |_{x_i}$
for
![]() $1\,\leqslant \, i\,\leqslant \,n$
.
$1\,\leqslant \, i\,\leqslant \,n$
.
As in the proof of Proposition 5.12, we choose a basis
![]() $e^{(i)}_{j,1},\,\cdots ,\,e^{(i)}_{j,r_j}$
of
$e^{(i)}_{j,1},\,\cdots ,\,e^{(i)}_{j,r_j}$
of
![]() ${\mathcal O}_{\mathbb{P}^1}(a_j)^{\oplus r_j}\big |_{t_i}$
for each
${\mathcal O}_{\mathbb{P}^1}(a_j)^{\oplus r_j}\big |_{t_i}$
for each
![]() $i,\,j$
and we choose suitable generators
$i,\,j$
and we choose suitable generators
![]() $v^{(i)}_{p^{(i)}(1),j^{(i)}(1)},\,\cdots ,\, v^{(i)}_{p^{(i)}(s),j^{(i)}(s)}$
of
$v^{(i)}_{p^{(i)}(1),j^{(i)}(1)},\,\cdots ,\, v^{(i)}_{p^{(i)}(s),j^{(i)}(s)}$
of
![]() $l^{(i)}_{r-s}$
. We may further assume that
$l^{(i)}_{r-s}$
. We may further assume that
![]() $l^{(i)}_{r-s}$
is generated by
$l^{(i)}_{r-s}$
is generated by
![]() $e^{(i)}_{p^{(i)}(1),j^{(i)}(1)},\,\cdots ,\,e^{(i)}_{p^{(i)}(s),j^{(i)}(s)}$
for
$e^{(i)}_{p^{(i)}(1),j^{(i)}(1)},\,\cdots ,\,e^{(i)}_{p^{(i)}(s),j^{(i)}(s)}$
for
![]() $i\,=\,1,\, 2$
. Since diagonal automorphisms
$i\,=\,1,\, 2$
. Since diagonal automorphisms
![]() $\textbf {g}\,=\,(a^{p,q}_{j,j'})$
of
$\textbf {g}\,=\,(a^{p,q}_{j,j'})$
of
![]() $E$
given by
$E$
given by
![]() $a^{pp}_{jj}\,\in \,k^{\times }$
and
$a^{pp}_{jj}\,\in \,k^{\times }$
and
![]() $a^{pq}_{jj'}\,=\,0$
for
$a^{pq}_{jj'}\,=\,0$
for
![]() $(p,\,j)\,\neq \,(q,\,j')$
preserve
$(p,\,j)\,\neq \,(q,\,j')$
preserve
![]() $l^{(1)}_*$
and
$l^{(1)}_*$
and
![]() $l^{(2)}_*$
, we can normalize the generator
$l^{(2)}_*$
, we can normalize the generator
of
![]() $l^{(3)}_{r-1}$
so that either
$l^{(3)}_{r-1}$
so that either
![]() $w_{p,j}\,=\,1$
or
$w_{p,j}\,=\,1$
or
![]() $w_{p,j}\,=\,0$
for any
$w_{p,j}\,=\,0$
for any
![]() $p,\,j$
. Note that
$p,\,j$
. Note that
![]() $w_{1,j}\,=\,0$
for
$w_{1,j}\,=\,0$
for
![]() $1\,\leqslant \, j\,\leqslant \,r_1$
by the assumption of Case (B). There are the following two possible cases:
$1\,\leqslant \, j\,\leqslant \,r_1$
by the assumption of Case (B). There are the following two possible cases:
-
(i)
 $r_1\,\geqslant \, 2$
;
$r_1\,\geqslant \, 2$
; -
(ii)
 $r_1\,=\,1$
.
$r_1\,=\,1$
.
(i) Assume that the condition
![]() $r_1\,\geqslant \, 2$
holds. After adding an element of
$r_1\,\geqslant \, 2$
holds. After adding an element of
![]() $l^{(3)}_{r-1}$
, we can assume that a representative
$l^{(3)}_{r-1}$
, we can assume that a representative
![]() $v\,=\,v_{1,1}e^{(3)}_{1,1}+\cdots +v_{m,r_m}e^{(3)}_{m,r_m}$
of a generator of
$v\,=\,v_{1,1}e^{(3)}_{1,1}+\cdots +v_{m,r_m}e^{(3)}_{m,r_m}$
of a generator of
![]() $l^{(3)}_{r-2}/l^{(3)}_{r-1}$
satisfies the condition
$l^{(3)}_{r-2}/l^{(3)}_{r-1}$
satisfies the condition
![]() $v_{p^{(3)}(1),j^{(3)}(1)}\,=\,0$
. Consider the automorphisms
$v_{p^{(3)}(1),j^{(3)}(1)}\,=\,0$
. Consider the automorphisms
![]() $\textbf {g}\,=\,(a^{p,q}_{j,j'})$
of
$\textbf {g}\,=\,(a^{p,q}_{j,j'})$
of
![]() $E$
given by
$E$
given by
![]() $a^{1,1}_{j,j}\,=\,c_j\,\in \,k^{\times }$
for
$a^{1,1}_{j,j}\,=\,c_j\,\in \,k^{\times }$
for
![]() $1\,\leqslant \, j\,\leqslant \, r_1$
,
$1\,\leqslant \, j\,\leqslant \, r_1$
,
![]() $a^{p,p}_{j,j}\,=\,c'\,\in \,k^{\times }$
for
$a^{p,p}_{j,j}\,=\,c'\,\in \,k^{\times }$
for
![]() $p\,\geqslant \, 2$
and
$p\,\geqslant \, 2$
and
![]() $1\,\leqslant \, j\,\leqslant \, r_p$
,
$1\,\leqslant \, j\,\leqslant \, r_p$
,
![]() $a^{p,q}_{j,j'}\,=\,0$
for
$a^{p,q}_{j,j'}\,=\,0$
for
![]() $(p,\,j)\,\neq \,(q,\,j')$
. Then such automorphisms preserve
$(p,\,j)\,\neq \,(q,\,j')$
. Then such automorphisms preserve
![]() $l^{(1)}_*$
,
$l^{(1)}_*$
,
![]() $l^{(2)}_*$
and
$l^{(2)}_*$
and
![]() $l^{(3)}_{r-1}$
. Since
$l^{(3)}_{r-1}$
. Since
we can assume that either
![]() $v_{1,j}\,=\,1$
or
$v_{1,j}\,=\,1$
or
![]() $v_{1,j}\,=\,0$
holds for any
$v_{1,j}\,=\,0$
holds for any
![]() $p,\,j$
. If
$p,\,j$
. If
![]() $r_1\,\gt \,2$
, then the parameter space for such generators of
$r_1\,\gt \,2$
, then the parameter space for such generators of
![]() $l^{(3)}_{r-2}/l^{(3)}_{r-1}$
is of dimension at most
$l^{(3)}_{r-2}/l^{(3)}_{r-1}$
is of dimension at most
![]() $r-4$
. If
$r-4$
. If
![]() $r_1\,=\,2$
, we may further assume that for some
$r_1\,=\,2$
, we may further assume that for some
![]() $(p',\,j')\,\neq \,(p^{(3)}(1),\,j^{(3)}(1))$
with
$(p',\,j')\,\neq \,(p^{(3)}(1),\,j^{(3)}(1))$
with
![]() $p'\,\geqslant \, 2$
the following holds: either
$p'\,\geqslant \, 2$
the following holds: either
![]() $v_{p',j'}\,=\,1$
or
$v_{p',j'}\,=\,1$
or
![]() $v_{p',j'}\,=\,0$
. So we can give a parameter space for
$v_{p',j'}\,=\,0$
. So we can give a parameter space for
![]() $l^{(3)}_{r-2}$
whose dimension is at most
$l^{(3)}_{r-2}$
whose dimension is at most
![]() $r-4$
. Adding the data
$r-4$
. Adding the data
![]() $l^{(3)}_{r-3},\,\cdots ,\,l^{(3)}_1$
, we can give a parameter space for
$l^{(3)}_{r-3},\,\cdots ,\,l^{(3)}_1$
, we can give a parameter space for
![]() $(E,\,\boldsymbol{l})$
whose dimension is at most
$(E,\,\boldsymbol{l})$
whose dimension is at most
(ii) Assume that
![]() $r_1\,=\,1$
. We again take a representative
$r_1\,=\,1$
. We again take a representative
![]() $v\,=\,v_{1,1}e^{(3)}_{1,1}+\cdots +v_{m,r_m}e^{(3)}_{m,r_m}$
of a generator of
$v\,=\,v_{1,1}e^{(3)}_{1,1}+\cdots +v_{m,r_m}e^{(3)}_{m,r_m}$
of a generator of
![]() $l^{(3)}_{r-2}/l^{(3)}_{r-1}$
so that
$l^{(3)}_{r-2}/l^{(3)}_{r-1}$
so that
![]() $v_{p^{(3)}(1),j^{(3)}(1)}\,=\,0$
. We may assume that one of the following holds:
$v_{p^{(3)}(1),j^{(3)}(1)}\,=\,0$
. We may assume that one of the following holds:
-
(
 $\alpha$
)
$\alpha$
)
 $v_{1,1}\,=\,0$
;
$v_{1,1}\,=\,0$
; -
(
 $\beta$
)
$\beta$
)
 $v_{1,1}\,\neq \, 0$
and
$v_{1,1}\,\neq \, 0$
and
 $(p^{(1)}(1),\,j^{(1)}(1))\,\neq \,(p^{(2)}(1),j^{(2)}(1))$
;
$(p^{(1)}(1),\,j^{(1)}(1))\,\neq \,(p^{(2)}(1),j^{(2)}(1))$
; -
(
 $\gamma$
)
$\gamma$
)
 $v_{1,1}\,\neq \, 0$
and
$v_{1,1}\,\neq \, 0$
and
 $(p^{(1)}(1),\,j^{(1)}(1))\,=\,(p^{(2)}(1),\,j^{(2)}(1))$
.
$(p^{(1)}(1),\,j^{(1)}(1))\,=\,(p^{(2)}(1),\,j^{(2)}(1))$
.
(
![]() $\alpha$
) Assume that
$\alpha$
) Assume that
![]() $v_{1,1}\,=\,0$
holds. After adding an element of
$v_{1,1}\,=\,0$
holds. After adding an element of
![]() $l^{(3)}_{r-1}$
, we can normalize
$l^{(3)}_{r-1}$
, we can normalize
![]() $v\,=\,v_{1,1}e^{(3)}_{1,1}+\cdots +v_{m,r_m}e^{(3)}_{m,r_m}$
so that
$v\,=\,v_{1,1}e^{(3)}_{1,1}+\cdots +v_{m,r_m}e^{(3)}_{m,r_m}$
so that
![]() $v_{p^{(3)}(1),j^{(3)}(1)}\,=\,0$
. Consider the automorphisms
$v_{p^{(3)}(1),j^{(3)}(1)}\,=\,0$
. Consider the automorphisms
![]() $\textbf {g}\,=\,(a^{p,q}_{j,j'})$
of
$\textbf {g}\,=\,(a^{p,q}_{j,j'})$
of
![]() $E$
given by
$E$
given by
![]() $a^{1,1}_{11}\,=\,c_1\,\in \,k^{\times }$
,
$a^{1,1}_{11}\,=\,c_1\,\in \,k^{\times }$
,
![]() $a^{p,p}_{j,j}\,=\,c_2\,\in \,k^{\times }$
for
$a^{p,p}_{j,j}\,=\,c_2\,\in \,k^{\times }$
for
![]() $p\,\geqslant \, 2$
and
$p\,\geqslant \, 2$
and
![]() $a^{p,q}_{j,j'}\,=\,0$
for
$a^{p,q}_{j,j'}\,=\,0$
for
![]() $(p,\,j)\,\neq \,(q,\,j')$
. Then such automorphisms preserve not only
$(p,\,j)\,\neq \,(q,\,j')$
. Then such automorphisms preserve not only
![]() $l^{(1)}_*$
,
$l^{(1)}_*$
,
![]() $l^{(2)}_*$
and
$l^{(2)}_*$
and
![]() $l^{(3)}_{r-1}$
but also
$l^{(3)}_{r-1}$
but also
![]() $l^{(3)}_{r-2}$
. Choose
$l^{(3)}_{r-2}$
. Choose
![]() $(q_1,\,j_1)$
such that
$(q_1,\,j_1)$
such that
![]() $q_1\,\geqslant \, 2$
,
$q_1\,\geqslant \, 2$
,
![]() $v_{q_1,j_1}\,\neq \, 0$
and
$v_{q_1,j_1}\,\neq \, 0$
and
![]() $(q_1,\,j_1)\,\neq \,(p^{(3)}(1),\,j^{(3)}(1))$
. We can normalize a representative
$(q_1,\,j_1)\,\neq \,(p^{(3)}(1),\,j^{(3)}(1))$
. We can normalize a representative
![]() $u\,=\,u_{1,1}e^{(3)}_{1,1}+\ldots +u_{m,r_m}e^{(3)}_{m,r_m}$
of a generator of
$u\,=\,u_{1,1}e^{(3)}_{1,1}+\ldots +u_{m,r_m}e^{(3)}_{m,r_m}$
of a generator of
![]() $l^{(3)}_{r-3}/l^{(3)}_{r-2}$
by adding an element of
$l^{(3)}_{r-3}/l^{(3)}_{r-2}$
by adding an element of
![]() $l^{(3)}_{r-2}$
such that
$l^{(3)}_{r-2}$
such that
![]() $u_{p^{(3)}(1),j^{(3)}(1)}\,=\,u_{q_1,j_1}\,=\,0$
. Take an index
$u_{p^{(3)}(1),j^{(3)}(1)}\,=\,u_{q_1,j_1}\,=\,0$
. Take an index
![]() $(q_2,\,j_2)$
other than
$(q_2,\,j_2)$
other than
![]() $(1,\,1)$
,
$(1,\,1)$
,
![]() $(p^{(3)}(1),\,j^{(3)}(1))$
and
$(p^{(3)}(1),\,j^{(3)}(1))$
and
![]() $(q_1,\,j_1)$
. Since
$(q_1,\,j_1)$
. Since
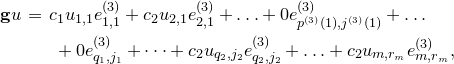 \begin{align*} &\textbf {g}u \,=\, c_1u_{1,1}e^{(3)}_{1,1}+c_2u_{2,1}e^{(3)}_{2,1}+\ldots+0e^{(3)}_{p^{(3)}(1),j^{(3)}(1)} + \ldots \\ &\quad \qquad+0e^{(3)}_{q_1,j_1}+\cdots +c_2u_{q_2,j_2}e^{(3)}_{q_2,j_2}+\ldots +c_2u_{m,r_m}e^{(3)}_{m,r_m}, \end{align*}
\begin{align*} &\textbf {g}u \,=\, c_1u_{1,1}e^{(3)}_{1,1}+c_2u_{2,1}e^{(3)}_{2,1}+\ldots+0e^{(3)}_{p^{(3)}(1),j^{(3)}(1)} + \ldots \\ &\quad \qquad+0e^{(3)}_{q_1,j_1}+\cdots +c_2u_{q_2,j_2}e^{(3)}_{q_2,j_2}+\ldots +c_2u_{m,r_m}e^{(3)}_{m,r_m}, \end{align*}
we may assume that one of the following holds:
 $u_{1,1}\,=\,u_{q_2,j_2}\,\neq \, 0$
;
$u_{1,1}\,=\,u_{q_2,j_2}\,\neq \, 0$
; $u_{1,1}\,=\,0$
;
$u_{1,1}\,=\,0$
; $u_{q_2,j_2}\,=\,0$
.
$u_{q_2,j_2}\,=\,0$
.
So we can give a parameter space for
![]() $l^{(3)}_{r-2},\,l^{(3)}_{r-3}$
whose dimension is at most
$l^{(3)}_{r-2},\,l^{(3)}_{r-3}$
whose dimension is at most
![]() $(r-3)+(r-4)$
. Adding the data
$(r-3)+(r-4)$
. Adding the data
![]() $l^{(3)}_{r-4},\,\cdots ,\,l^{(3)}_1$
, we can give a parameter space for
$l^{(3)}_{r-4},\,\cdots ,\,l^{(3)}_1$
, we can give a parameter space for
![]() $(E,\,\boldsymbol{l})$
whose dimension is at most
$(E,\,\boldsymbol{l})$
whose dimension is at most
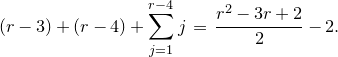 \begin{align*} (r-3)+(r-4) +\sum _{j=1}^{r-4} j \, =\,\frac {r^2-3r+2} {2} - 2. \end{align*}
\begin{align*} (r-3)+(r-4) +\sum _{j=1}^{r-4} j \, =\,\frac {r^2-3r+2} {2} - 2. \end{align*}
(
![]() $\beta$
) Assume that the conditions
$\beta$
) Assume that the conditions
![]() $v_{1,1}\,\neq \, 0$
and
$v_{1,1}\,\neq \, 0$
and
![]() $(p^{(1)}(1),\,j^{(1)}(1))\,\neq \,(p^{(2)}(1),\,j^{(2)}(1))$
hold. After replacing the indices
$(p^{(1)}(1),\,j^{(1)}(1))\,\neq \,(p^{(2)}(1),\,j^{(2)}(1))$
hold. After replacing the indices
![]() $i\,=\,1$
and
$i\,=\,1$
and
![]() $2$
if necessary, we may assume that
$2$
if necessary, we may assume that
![]() $(p^{(3)}(1),\,j^{(3)}(1))\,\neq \, (p^{(1)}(1),\,j^{(1)}(1))$
. Consider the automorphisms
$(p^{(3)}(1),\,j^{(3)}(1))\,\neq \, (p^{(1)}(1),\,j^{(1)}(1))$
. Consider the automorphisms
![]() $\textbf {g}\,=\,(a^{p,q}_{j,j'})$
of
$\textbf {g}\,=\,(a^{p,q}_{j,j'})$
of
![]() $E$
given by:
$E$
given by:
 $a^{1,1}_{1,1}\,=\,c_1\,\in \,k^{\times }$
and
$a^{1,1}_{1,1}\,=\,c_1\,\in \,k^{\times }$
and
 $a^{p,p}_{j,j}\,=\,c_2\,\in \,k^{\times }$
for
$a^{p,p}_{j,j}\,=\,c_2\,\in \,k^{\times }$
for
 $p\,\geqslant \,2$
and
$p\,\geqslant \,2$
and
 $1\,\leqslant \, j\,\leqslant \, r_p$
;
$1\,\leqslant \, j\,\leqslant \, r_p$
; $a^{p^{(1)}(1),1}_{j^{(1)}(1),1}\,\in \, \textrm { Hom}({\mathcal O}_{\mathbb{P}^1}(a_1),\,{\mathcal O}_{\mathbb{P}^1}(a_{p^{(1)}(1)}))$
satisfying
$a^{p^{(1)}(1),1}_{j^{(1)}(1),1}\,\in \, \textrm { Hom}({\mathcal O}_{\mathbb{P}^1}(a_1),\,{\mathcal O}_{\mathbb{P}^1}(a_{p^{(1)}(1)}))$
satisfying
 $a^{p^{(1)}(1),1}_{j^{(1)}(1),1}\big |_{x_2}\,=\,0$
; and
$a^{p^{(1)}(1),1}_{j^{(1)}(1),1}\big |_{x_2}\,=\,0$
; and $a^{p,q}_{j,j'}\,=\,0$
for any
$a^{p,q}_{j,j'}\,=\,0$
for any
 $(p,\,j)\,\neq \,(q,\,j')$
satisfying
$(p,\,j)\,\neq \,(q,\,j')$
satisfying
 $((p,\,j), \, (q, \, j') )\,\neq \,((p^{(1)}(1),\,j^{(1)}(1)), \, (1,\, 1))$
.
$((p,\,j), \, (q, \, j') )\,\neq \,((p^{(1)}(1),\,j^{(1)}(1)), \, (1,\, 1))$
.
Such automorphisms preserve
![]() $l^{(1)}_*$
,
$l^{(1)}_*$
,
![]() $l^{(2)}_*$
and
$l^{(2)}_*$
and
![]() $l^{(3)}_{r-1}\,=\,\big \langle v^{(3)}_{p^{(3)}(1),j^{(3)}(1)} \big \rangle$
. We can normalize the representative
$l^{(3)}_{r-1}\,=\,\big \langle v^{(3)}_{p^{(3)}(1),j^{(3)}(1)} \big \rangle$
. We can normalize the representative
![]() $v\,=\,v_{1,1}e^{(3)}_{1,1}+\ldots +v_{m,r_m}e^{(3)}_{m,r_m}$
of a generator of
$v\,=\,v_{1,1}e^{(3)}_{1,1}+\ldots +v_{m,r_m}e^{(3)}_{m,r_m}$
of a generator of
![]() $l^{(3)}_{r-2}/l^{(3)}_{r-1}$
after adding an element of
$l^{(3)}_{r-2}/l^{(3)}_{r-1}$
after adding an element of
![]() $l^{(3)}_{r-1}$
such that
$l^{(3)}_{r-1}$
such that
![]() $v_{p^{(3)}(1),j^{(3)}(1)}\,=\,0$
. Choose
$v_{p^{(3)}(1),j^{(3)}(1)}\,=\,0$
. Choose
![]() $(q_1,\,j_1)$
such that
$(q_1,\,j_1)$
such that
![]() $q_1\,\geqslant \, 2$
and
$q_1\,\geqslant \, 2$
and
![]() $(q_1,\,j_1)\,\neq \, (p^{(1)}(1),\,j^{(1)}(1)),\, (p^{(3)}(1),\,j^{(3)}(1))$
. For
$(q_1,\,j_1)\,\neq \, (p^{(1)}(1),\,j^{(1)}(1)),\, (p^{(3)}(1),\,j^{(3)}(1))$
. For
![]() $\textbf {g}\,=\,(a^{p,q}_{j,j'})\,\in \, B'$
, we have
$\textbf {g}\,=\,(a^{p,q}_{j,j'})\,\in \, B'$
, we have
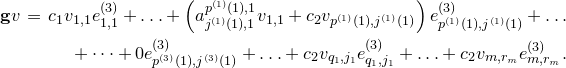 \begin{align*} \textbf {g}v \,=\, c_1v_{1,1}e^{(3)}_{1,1}+\ldots + \left ( a^{p^{(1)}(1),1}_{j^{(1)}(1),1}v_{1,1} +c_2v_{p^{(1)}(1),j^{(1)}(1)} \right ) e^{(3)}_{p^{(1)}(1),j^{(1)}(1)} +\ldots \\ \quad \quad +\cdots+0e^{(3)}_{p^{(3)}(1),j^{(3)}(1)} +\ldots +c_2v_{q_1,j_1}e^{(3)}_{q_1,j_1}+\ldots +c_2v_{m,r_m}e^{(3)}_{m,r_m}. \end{align*}
\begin{align*} \textbf {g}v \,=\, c_1v_{1,1}e^{(3)}_{1,1}+\ldots + \left ( a^{p^{(1)}(1),1}_{j^{(1)}(1),1}v_{1,1} +c_2v_{p^{(1)}(1),j^{(1)}(1)} \right ) e^{(3)}_{p^{(1)}(1),j^{(1)}(1)} +\ldots \\ \quad \quad +\cdots+0e^{(3)}_{p^{(3)}(1),j^{(3)}(1)} +\ldots +c_2v_{q_1,j_1}e^{(3)}_{q_1,j_1}+\ldots +c_2v_{m,r_m}e^{(3)}_{m,r_m}. \end{align*}
So we can normalize
![]() $v$
so that one of the following statements holds:
$v$
so that one of the following statements holds:
 $v_{1,1}\,=\,v_{p^{(1)}(1),j^{(1)}(1)}\,=\,v_{q_1,j_1}\,\neq \, 0$
;
$v_{1,1}\,=\,v_{p^{(1)}(1),j^{(1)}(1)}\,=\,v_{q_1,j_1}\,\neq \, 0$
; $v_{1,1}\,=\,v_{p^{(1)}(1),j^{(1)}(1)}\,\neq \, 0$
and
$v_{1,1}\,=\,v_{p^{(1)}(1),j^{(1)}(1)}\,\neq \, 0$
and
 $v_{q_1,j_1}\,=\,0$
.
$v_{q_1,j_1}\,=\,0$
.
Thus, we can give a parameter space for
![]() $l^{(3)}_{r-2}$
whose dimension is at most
$l^{(3)}_{r-2}$
whose dimension is at most
![]() $r-4$
. Adding the data
$r-4$
. Adding the data
![]() $l^{(3)}_{r-2},\,\cdots ,\,l^{(3)}_1$
, we can give a parameter space for
$l^{(3)}_{r-2},\,\cdots ,\,l^{(3)}_1$
, we can give a parameter space for
![]() $(E,\,\boldsymbol{l})$
whose dimension is at most
$(E,\,\boldsymbol{l})$
whose dimension is at most
(
![]() $\gamma$
) Assume that the following conditions hold:
$\gamma$
) Assume that the following conditions hold:
![]() $v_{1,1}\,\neq \, 0$
and
$v_{1,1}\,\neq \, 0$
and
![]() $(p^{(1)}(1),\,j^{(1)}(1))\,=\,(p^{(2)}(1),j^{(2)}(1))$
. By the definition,
$(p^{(1)}(1),\,j^{(1)}(1))\,=\,(p^{(2)}(1),j^{(2)}(1))$
. By the definition,
![]() $v^{(3)}_{p^{(3)}(1),j^{(3)}(1)} \,=\,w_{2,1}e^{(3)}_{2,1}+\ldots +w_{m,r_m}e^{(3)}_{m,r_m}$
is a fixed generator of
$v^{(3)}_{p^{(3)}(1),j^{(3)}(1)} \,=\,w_{2,1}e^{(3)}_{2,1}+\ldots +w_{m,r_m}e^{(3)}_{m,r_m}$
is a fixed generator of
![]() $l^{(3)}_{r-1}$
, and for any
$l^{(3)}_{r-1}$
, and for any
![]() $p,\,j$
, we have either
$p,\,j$
, we have either
![]() $w_{p,j}\,=\,1$
or
$w_{p,j}\,=\,1$
or
![]() $w_{p,j}\,=\,0$
. We can choose
$w_{p,j}\,=\,0$
. We can choose
![]() $(q_1,\,j_1)$
such that
$(q_1,\,j_1)$
such that
![]() $w_{q_1,\,j_1}\,=\,1$
. Take
$w_{q_1,\,j_1}\,=\,1$
. Take
![]() $(q_2,\,j_2)$
such that
$(q_2,\,j_2)$
such that
![]() $q_2\,\geqslant \, 2$
and
$q_2\,\geqslant \, 2$
and
![]() $(q_2,\,j_2)\,\neq \,(q_1,\,j_1),\, (p^{(1)}(1),\,j^{(1)}(1))$
. After replacing
$(q_2,\,j_2)\,\neq \,(q_1,\,j_1),\, (p^{(1)}(1),\,j^{(1)}(1))$
. After replacing
![]() $(q_1,\,j_1)$
and
$(q_1,\,j_1)$
and
![]() $(q_2,\,j_2)$
if necessary, we can assume that one of the following statements holds:
$(q_2,\,j_2)$
if necessary, we can assume that one of the following statements holds:
-
(
 $\gamma$
-1)
$\gamma$
-1)
 $w_{q_2,j_2}\,=\,0$
;
$w_{q_2,j_2}\,=\,0$
; -
(
 $\gamma$
-2)
$\gamma$
-2)
 $w_{p^{(1)}(1),j^{(1)}(1)}\,=\,0$
;
$w_{p^{(1)}(1),j^{(1)}(1)}\,=\,0$
; -
(
 $\gamma$
-3)
$\gamma$
-3)
 $w_{q_2,j_2}\,=\,w_{p^{(1)}(1),j^{(1)}(1)}\,=\,1$
and
$w_{q_2,j_2}\,=\,w_{p^{(1)}(1),j^{(1)}(1)}\,=\,1$
and
 $w_{p,j}\,=\,0$
for any
$w_{p,j}\,=\,0$
for any
 $(p,\,j)\,\neq \,(q_2,\, j_2),\, (p^{(1)}(1),\,j^{(1)}(1))$
;
$(p,\,j)\,\neq \,(q_2,\, j_2),\, (p^{(1)}(1),\,j^{(1)}(1))$
; -
(
 $\gamma$
-4)
$\gamma$
-4)
 $w_{q_2,\,j_2}\,=\,w_{p^{(1)}(1),j^{(1)}(1)}\,=\,1$
,
$w_{q_2,\,j_2}\,=\,w_{p^{(1)}(1),j^{(1)}(1)}\,=\,1$
,
 $(q_1,\,j_1)\,\neq \,(q_2,\,j_2),\, (p^{(1)}(1),\,j^{(1)}(1))$
and
$(q_1,\,j_1)\,\neq \,(q_2,\,j_2),\, (p^{(1)}(1),\,j^{(1)}(1))$
and
 $q_2\,\gt \,p^{(1)}(1)$
;
$q_2\,\gt \,p^{(1)}(1)$
; -
(
 $\gamma$
-5)
$\gamma$
-5)
 $w_{q_2,j_2}\,=\,w_{p^{(1)}(1),j^{(1)}(1)}\,=\,1$
,
$w_{q_2,j_2}\,=\,w_{p^{(1)}(1),j^{(1)}(1)}\,=\,1$
,
 $(q_1,\,j_1)\,\neq \,(q_2,\, j_2),\, (p^{(1)}(1),\,j^{(1)}(1))$
and
$(q_1,\,j_1)\,\neq \,(q_2,\, j_2),\, (p^{(1)}(1),\,j^{(1)}(1))$
and
 $q_2\,\leqslant \,p^{(1)}(1)$
.
$q_2\,\leqslant \,p^{(1)}(1)$
.
(
![]() $\gamma$
-1) Assume that the condition
$\gamma$
-1) Assume that the condition
![]() $w_{q_2,j_2}\,=\,0$
holds. Consider the diagonal automorphisms
$w_{q_2,j_2}\,=\,0$
holds. Consider the diagonal automorphisms
![]() $\textbf {g}\,=\,(a^{p,q}_{j,j'})$
of
$\textbf {g}\,=\,(a^{p,q}_{j,j'})$
of
![]() $E$
given by
$E$
given by
![]() $a^{1,1}_{1,1}\,=\,c_1\,\in \,k^{\times }$
,
$a^{1,1}_{1,1}\,=\,c_1\,\in \,k^{\times }$
,
![]() $a^{q_2,q_2}_{j_2,j_2}\,=\,c_2\,\in \,k^{\times }$
,
$a^{q_2,q_2}_{j_2,j_2}\,=\,c_2\,\in \,k^{\times }$
,
![]() $a^{p,p}_{j,j}\,=\,c_3\,\in \,k^{\times }$
for
$a^{p,p}_{j,j}\,=\,c_3\,\in \,k^{\times }$
for
![]() $(p,\,j)\,\neq \, (1,\, 1),\, (q_2,\, j_2)$
and
$(p,\,j)\,\neq \, (1,\, 1),\, (q_2,\, j_2)$
and
![]() $a^{p,q}_{j,j'}\,=\,0$
for
$a^{p,q}_{j,j'}\,=\,0$
for
![]() $(p,\,j)\,\neq \,(q,\,j')$
. Then such automorphisms preserve
$(p,\,j)\,\neq \,(q,\,j')$
. Then such automorphisms preserve
![]() $l^{(1)}_*$
,
$l^{(1)}_*$
,
![]() $l^{(2)}_*$
and
$l^{(2)}_*$
and
![]() $l^{(3)}_{r-1}$
. Consider a representative
$l^{(3)}_{r-1}$
. Consider a representative
![]() $v\,=\,v_{1,1}e^{(3)}_{1,1}+\ldots +v_{m,r_m}e^{(3)}_{m,r_m}$
of a generator of
$v\,=\,v_{1,1}e^{(3)}_{1,1}+\ldots +v_{m,r_m}e^{(3)}_{m,r_m}$
of a generator of
![]() $l^{(3)}_{r-2}/l^{(3)}_{r-1}$
with the normalizing condition
$l^{(3)}_{r-2}/l^{(3)}_{r-1}$
with the normalizing condition
![]() $v_{q_1,j_1}\,=\,0$
. Applying the above type of automorphisms to
$v_{q_1,j_1}\,=\,0$
. Applying the above type of automorphisms to
![]() $v$
, we have
$v$
, we have
So we can normalize
![]() $v$
so that one of the following holds:
$v$
so that one of the following holds:
-
(a)
 $v_{1,1}\,=\,v_{q_2,j_2}\,=\,v_{p^{(1)}(1),j^{(1)}(1)}\,\neq \, 0$
;
$v_{1,1}\,=\,v_{q_2,j_2}\,=\,v_{p^{(1)}(1),j^{(1)}(1)}\,\neq \, 0$
; -
(b)
 $v_{1,1}\,=\,v_{q_2,j_2}\,\neq \, 0$
and
$v_{1,1}\,=\,v_{q_2,j_2}\,\neq \, 0$
and
 $v_{p^{(1)}(1),j^{(1)}(1)}\,=\,0$
;
$v_{p^{(1)}(1),j^{(1)}(1)}\,=\,0$
; -
(c)
 $v_{1,1}\,=\,v_{p^{(1)}(1),j^{(1)}(1)}\,\neq \, 0$
and
$v_{1,1}\,=\,v_{p^{(1)}(1),j^{(1)}(1)}\,\neq \, 0$
and
 $v_{q_2,j_2}\,=\,0$
;
$v_{q_2,j_2}\,=\,0$
; -
(d)
 $v_{q_2,j_2}\,=\,v_{p^{(1)}(1),j^{(1)}(1)}\,=\,0$
.
$v_{q_2,j_2}\,=\,v_{p^{(1)}(1),j^{(1)}(1)}\,=\,0$
.
So we can give a parameter space for
![]() $l^{(3)}_{r-2}$
whose dimension is at most
$l^{(3)}_{r-2}$
whose dimension is at most
![]() $r-4$
.
$r-4$
.
(
![]() $\gamma$
-2) Assume that the condition
$\gamma$
-2) Assume that the condition
![]() $w_{p^{(1)}(1),j^{(1)}(1)}\,=\,0$
holds. In this case, we have
$w_{p^{(1)}(1),j^{(1)}(1)}\,=\,0$
holds. In this case, we have
![]() $(q_1,\,j_1)\,\neq \,(p^{(1)}(1),\,j^{(1)}(1))$
, because
$(q_1,\,j_1)\,\neq \,(p^{(1)}(1),\,j^{(1)}(1))$
, because
![]() $w_{q_1,j_1}\,=\,1\,\neq \, 0$
. Consider the automorphisms
$w_{q_1,j_1}\,=\,1\,\neq \, 0$
. Consider the automorphisms
![]() $\textbf {g}\,=\,(a^{p,q}_{j,j'})$
of
$\textbf {g}\,=\,(a^{p,q}_{j,j'})$
of
![]() $E$
given by
$E$
given by
![]() $a^{1,1}_{1,1}\,=\,c_1\,\in \,k^{\times }$
,
$a^{1,1}_{1,1}\,=\,c_1\,\in \,k^{\times }$
,
![]() $a^{p^{(1)}(1),p^{(1)}(1)}_{j^{(1)}(1),j^{(1)}(1)}\,=\,c_2\,\in \,k^{\times }$
,
$a^{p^{(1)}(1),p^{(1)}(1)}_{j^{(1)}(1),j^{(1)}(1)}\,=\,c_2\,\in \,k^{\times }$
,
![]() $a^{p,p}_{j,j}\,=\,c_3\,\in \,k^{\times }$
for
$a^{p,p}_{j,j}\,=\,c_3\,\in \,k^{\times }$
for
![]() $(p,\,j)\,\neq \, (1,\, 1),\, (p^{(1)}(1),\,j^{(1)}(1))$
and
$(p,\,j)\,\neq \, (1,\, 1),\, (p^{(1)}(1),\,j^{(1)}(1))$
and
![]() $a^{p,q}_{j,j'}\,=\,0$
for
$a^{p,q}_{j,j'}\,=\,0$
for
![]() $(p,\,j)\,\neq \,(q,\,j')$
. Then such automorphisms
$(p,\,j)\,\neq \,(q,\,j')$
. Then such automorphisms
![]() $\textbf {g}$
preserve
$\textbf {g}$
preserve
![]() $l^{(1)}_*$
,
$l^{(1)}_*$
,
![]() $l^{(2)}_*$
and
$l^{(2)}_*$
and
![]() $l^{(3)}_{r-1}$
. Normalize the representative
$l^{(3)}_{r-1}$
. Normalize the representative
![]() $v\,=\,v_{1,1}e^{(3)}_{1,1}+\ldots +v_{m,r_m}e^{(3)}_{m,r_m}$
of a generator of
$v\,=\,v_{1,1}e^{(3)}_{1,1}+\ldots +v_{m,r_m}e^{(3)}_{m,r_m}$
of a generator of
![]() $l^{(3)}_{r-2}/l^{(3)}_{r-1}$
so that
$l^{(3)}_{r-2}/l^{(3)}_{r-1}$
so that
![]() $v_{q_1,j_1}\,=\,0$
. Applying the above type of automorphism
$v_{q_1,j_1}\,=\,0$
. Applying the above type of automorphism
![]() $\textbf {g}$
to
$\textbf {g}$
to
![]() $v$
, we have
$v$
, we have
So we can assume that one of the following holds:
-
(a)
 $v_{1,1}\,=\,v_{p^{(1)}(1),j^{(1)}(1)}\,=\,v_{q_2,j_2}\,\neq \, 0$
;
$v_{1,1}\,=\,v_{p^{(1)}(1),j^{(1)}(1)}\,=\,v_{q_2,j_2}\,\neq \, 0$
; -
(b)
 $v_{1,1}\,=\,v_{p^{(1)}(1),j^{(1)}(1)}\,\neq \, 0$
and
$v_{1,1}\,=\,v_{p^{(1)}(1),j^{(1)}(1)}\,\neq \, 0$
and
 $v_{q_2,j_2}\,=\,0$
;
$v_{q_2,j_2}\,=\,0$
; -
(c)
 $v_{1,1}\,=\,v_{q_2,j_2}\,\neq \, 0$
and
$v_{1,1}\,=\,v_{q_2,j_2}\,\neq \, 0$
and
 $v_{p^{(1)}(1),j^{(1)}(1)}\,=\,0$
;
$v_{p^{(1)}(1),j^{(1)}(1)}\,=\,0$
; -
(d)
 $v_{p^{(1)}(1),j^{(1)}(1)}\,=\,v_{q_2,j_2}\,=\,0$
.
$v_{p^{(1)}(1),j^{(1)}(1)}\,=\,v_{q_2,j_2}\,=\,0$
.
So we can give a parameter space for
![]() $l^{(3)}_{r-2}$
whose dimension is at most
$l^{(3)}_{r-2}$
whose dimension is at most
![]() $r-4$
.
$r-4$
.
(
![]() $\gamma$
-3) Assume that
$\gamma$
-3) Assume that
![]() $w_{q_2,j_2}\,=\,w_{p^{(1)}(1),j^{(1)}(1)}\,=\,1$
and
$w_{q_2,j_2}\,=\,w_{p^{(1)}(1),j^{(1)}(1)}\,=\,1$
and
![]() $w_{p,j}\,=\,0$
for any
$w_{p,j}\,=\,0$
for any
![]() $(p,\,j)$
other than
$(p,\,j)$
other than
![]() $(q_2,\,j_2),\,(p^{(1)}(1),\,j^{(1)}(1))$
. In this case, we have
$(q_2,\,j_2),\,(p^{(1)}(1),\,j^{(1)}(1))$
. In this case, we have
![]() $(q_1,\,j_1)\,=\,(p^{(1)}(1),\,j^{(1)}(1))$
because
$(q_1,\,j_1)\,=\,(p^{(1)}(1),\,j^{(1)}(1))$
because
![]() $w_{q_1,j_1}\,=\,1\,\neq \, 0$
. Consider the diagonal automorphisms
$w_{q_1,j_1}\,=\,1\,\neq \, 0$
. Consider the diagonal automorphisms
![]() $\textbf {g}\,=\,(a^{p,q}_{j,j'})$
of
$\textbf {g}\,=\,(a^{p,q}_{j,j'})$
of
![]() $E$
given by
$E$
given by
![]() $a^{1,1}_{1,1}\,=\,c_1\,\in \,k^{\times }$
,
$a^{1,1}_{1,1}\,=\,c_1\,\in \,k^{\times }$
,
![]() $a^{q_2,q_2}_{k_2,j_2}\,=\,a^{p^{(1)}(1),p^{(1)}(1)}_{j^{(1)}(1),j^{(1)}(1)}\,=\,c_2\,\in \,k^{\times }$
,
$a^{q_2,q_2}_{k_2,j_2}\,=\,a^{p^{(1)}(1),p^{(1)}(1)}_{j^{(1)}(1),j^{(1)}(1)}\,=\,c_2\,\in \,k^{\times }$
,
![]() $a^{p,p}_{j,j}\,=\,c_3\,\in \,k^{\times }$
for
$a^{p,p}_{j,j}\,=\,c_3\,\in \,k^{\times }$
for
![]() $(p,\,j)\,\neq \,(1,\, 1),\, (q_2,\, j_2),\, (p^{(1)}(1),\, j^{(1)}(1))$
and
$(p,\,j)\,\neq \,(1,\, 1),\, (q_2,\, j_2),\, (p^{(1)}(1),\, j^{(1)}(1))$
and
![]() $a^{p,q}_{j,j'}\,=\,0$
for
$a^{p,q}_{j,j'}\,=\,0$
for
![]() $(p,\,j)\,\neq \, (q,\,j')$
. Such an automorphism
$(p,\,j)\,\neq \, (q,\,j')$
. Such an automorphism
![]() $\textbf {g}$
preserves
$\textbf {g}$
preserves
![]() $l^{(1)}_*$
,
$l^{(1)}_*$
,
![]() $l^{(2)}_*$
and
$l^{(2)}_*$
and
![]() $l^{(3)}_{r-1}$
. We again normalize the representative
$l^{(3)}_{r-1}$
. We again normalize the representative
![]() $v\,=\,v_{1,1}e^{(3)}_{1,1}+\ldots +v_{m,r_m}e^{(3)}_{m,r_m}$
of a generator of
$v\,=\,v_{1,1}e^{(3)}_{1,1}+\ldots +v_{m,r_m}e^{(3)}_{m,r_m}$
of a generator of
![]() $l^{(3)}_{r-2}/l^{(3)}_{r-1}$
such that
$l^{(3)}_{r-2}/l^{(3)}_{r-1}$
such that
![]() $v_{q_1,j_1}\,=\,0$
. Further, fix an index
$v_{q_1,j_1}\,=\,0$
. Further, fix an index
![]() $(q_3,\,j_3)$
other than
$(q_3,\,j_3)$
other than
![]() $(1,\,1),\, (q_1,\, j_1),\, (q_2,\, j_2)$
. Applying the above type of automorphisms to
$(1,\,1),\, (q_1,\, j_1),\, (q_2,\, j_2)$
. Applying the above type of automorphisms to
![]() $v$
, we have
$v$
, we have
So we may assume that one of the following holds:
 $v_{1,1}\,=\,v_{q_2,j_2}\,=\,v_{q_3,j_3}\,\neq \,0$
;
$v_{1,1}\,=\,v_{q_2,j_2}\,=\,v_{q_3,j_3}\,\neq \,0$
; $v_{1,1}\,=\,v_{q_2,j_2}\,\neq \, 0$
and
$v_{1,1}\,=\,v_{q_2,j_2}\,\neq \, 0$
and
 $v_{q_3,j_3}\,=\,0$
;
$v_{q_3,j_3}\,=\,0$
; $v_{1,1}\,=\,v_{q_3,j_3}\,\neq \, 0$
and
$v_{1,1}\,=\,v_{q_3,j_3}\,\neq \, 0$
and
 $v_{q_2,j_2}\,=\,0$
;
$v_{q_2,j_2}\,=\,0$
; $v_{q_2,j_2}\,=\,v_{q_3,j_3}\,=\,0$
.
$v_{q_2,j_2}\,=\,v_{q_3,j_3}\,=\,0$
.
Then we can give a parameter space for
![]() $l^{(3)}_{r-2}$
whose dimension is at most
$l^{(3)}_{r-2}$
whose dimension is at most
![]() $r-4$
.
$r-4$
.
(
![]() $\gamma$
-4) Assume that the following three conditions hold:
$\gamma$
-4) Assume that the following three conditions hold:
![]() $w_{q_2,j_2}\,=\, w_{p^{(1)}(1),j^{(1)}(1)}\,=\,1$
,
$w_{q_2,j_2}\,=\, w_{p^{(1)}(1),j^{(1)}(1)}\,=\,1$
,
![]() $(q_1,\,j_1)\,\neq \,(q_2,\,k_2),\, (p^{(1)}(1),\,j^{(1)}(1))$
and
$(q_1,\,j_1)\,\neq \,(q_2,\,k_2),\, (p^{(1)}(1),\,j^{(1)}(1))$
and
![]() $q_2\,\gt \,p^{(1)}(1)$
. In this case, we have
$q_2\,\gt \,p^{(1)}(1)$
. In this case, we have
![]() $a_1\,\leqslant \, a_{q_2}-2$
and we can take sections
$a_1\,\leqslant \, a_{q_2}-2$
and we can take sections
![]() $\alpha$
of
$\alpha$
of
![]() $\textrm { Hom}({\mathcal O}_{\mathbb{P}^1}(a_1),\,{\mathcal O}_{\mathbb{P}^1}(a_{q_2}))$
such that
$\textrm { Hom}({\mathcal O}_{\mathbb{P}^1}(a_1),\,{\mathcal O}_{\mathbb{P}^1}(a_{q_2}))$
such that
![]() $\alpha |_{x_1}\,=\,\alpha |_{x_2}\,=\,0$
but
$\alpha |_{x_1}\,=\,\alpha |_{x_2}\,=\,0$
but
![]() $\alpha |_{x_3}$
is arbitrary. Recall that
$\alpha |_{x_3}$
is arbitrary. Recall that
![]() $v\,=\,v_{1,1}e^{(3)}_{1,1}+\cdots +v_{m,r_m}e^{(3)}_{m,r_m}$
gives a representative of a generator of
$v\,=\,v_{1,1}e^{(3)}_{1,1}+\cdots +v_{m,r_m}e^{(3)}_{m,r_m}$
gives a representative of a generator of
![]() $l^{(3)}_{r-2}/l^{(3)}_{r-1}$
with
$l^{(3)}_{r-2}/l^{(3)}_{r-1}$
with
![]() $v_{1,1}\,\neq \, 0$
. We impose the normalizing condition
$v_{1,1}\,\neq \, 0$
. We impose the normalizing condition
![]() $v_{q_1,j_1}\,=\,0$
after adding an element of
$v_{q_1,j_1}\,=\,0$
after adding an element of
![]() $l^{(3)}_{r-1}$
to
$l^{(3)}_{r-1}$
to
![]() $v$
. Consider the automorphisms
$v$
. Consider the automorphisms
![]() $\textbf {g}\,=\,(a^{p,q}_{j,j'})$
of
$\textbf {g}\,=\,(a^{p,q}_{j,j'})$
of
![]() $E$
given by:
$E$
given by:
 $a^{1,1}_{1,1}\,=\,c_1\,\in \,k^{\times }$
,
$a^{1,1}_{1,1}\,=\,c_1\,\in \,k^{\times }$
,
 $a^{p,p}_{j,j}\,=\,c_2\,\in \,k^{\times }$
for
$a^{p,p}_{j,j}\,=\,c_2\,\in \,k^{\times }$
for
 $(p,\,j)\,\neq \,(1,\,1)$
;
$(p,\,j)\,\neq \,(1,\,1)$
; $a^{q_2,1}_{k_2,1}\,=\,\alpha \,\in \, \textrm { Hom}({\mathcal O}_{\mathbb{P}^1}(a_1),\, {\mathcal O}_{\mathbb{P}^1}(a_{q_2}))$
satisfying
$a^{q_2,1}_{k_2,1}\,=\,\alpha \,\in \, \textrm { Hom}({\mathcal O}_{\mathbb{P}^1}(a_1),\, {\mathcal O}_{\mathbb{P}^1}(a_{q_2}))$
satisfying
 $\alpha |_{x_1}\,=\,0$
,
$\alpha |_{x_1}\,=\,0$
,
 $\alpha |_{x_2}\,=\,0$
; and
$\alpha |_{x_2}\,=\,0$
; and $a^{p,q}_{j,j'}\,=\,0$
for any
$a^{p,q}_{j,j'}\,=\,0$
for any
 $(p,j,\,q,k)$
such that
$(p,j,\,q,k)$
such that
 $(p,\,j)\,\neq \,(q,\,j')$
and
$(p,\,j)\,\neq \,(q,\,j')$
and
 $(p,\,j,\,q,\, j)\,\neq \, (q_2,\,k_2,\,1,\,1)$
.
$(p,\,j,\,q,\, j)\,\neq \, (q_2,\,k_2,\,1,\,1)$
.
Then such automorphisms preserve
![]() $l^{(1)}_*$
,
$l^{(1)}_*$
,
![]() $l^{(2)}_*$
and
$l^{(2)}_*$
and
![]() $l^{(3)}_{r-1}$
. Applying such an automorphism, the representative
$l^{(3)}_{r-1}$
. Applying such an automorphism, the representative
![]() $v$
of a generator of
$v$
of a generator of
![]() $l^{(3)}_{r-2}/l^{(3)}_{r-1}$
is sent to
$l^{(3)}_{r-2}/l^{(3)}_{r-1}$
is sent to
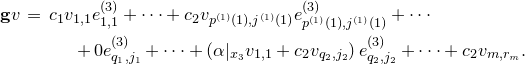 \begin{align*} &\textbf {g}v \,=\, c_1v_{1,1}e^{(3)}_{1,1}+\cdots + c_2v_{p^{(1)}(1),j^{(1)}(1)}e^{(3)}_{p^{(1)}(1),j^{(1)}(1)} +\cdots \\ &\qquad\quad \quad+0e^{(3)}_{q_1,j_1}+\cdots + \left ( \alpha |_{x_3} v_{1,1} +c_2 v_{q_2,j_2} \right ) e^{(3)}_{q_2,j_2} +\cdots +c_2v_{m,r_m}. \end{align*}
\begin{align*} &\textbf {g}v \,=\, c_1v_{1,1}e^{(3)}_{1,1}+\cdots + c_2v_{p^{(1)}(1),j^{(1)}(1)}e^{(3)}_{p^{(1)}(1),j^{(1)}(1)} +\cdots \\ &\qquad\quad \quad+0e^{(3)}_{q_1,j_1}+\cdots + \left ( \alpha |_{x_3} v_{1,1} +c_2 v_{q_2,j_2} \right ) e^{(3)}_{q_2,j_2} +\cdots +c_2v_{m,r_m}. \end{align*}
So we may assume that one of the following two hold:
-
(1)
 $v_{1,1}\,=\,v_{p^{(1)}(1),j^{(1)}(1)}\,=\,v_{q_2,j_2}\,\neq \, 0$
;
$v_{1,1}\,=\,v_{p^{(1)}(1),j^{(1)}(1)}\,=\,v_{q_2,j_2}\,\neq \, 0$
; -
(2)
 $v_{1,1}\,=\,v_{q_2,j_2}\,\neq \, 0$
and
$v_{1,1}\,=\,v_{q_2,j_2}\,\neq \, 0$
and
 $v_{p^{(1)}(1),j^{(1)}(1)}\,=\,0$
.
$v_{p^{(1)}(1),j^{(1)}(1)}\,=\,0$
.
So we can give a parameter space for
![]() $l^{(3)}_{r-2}$
whose dimension is at most
$l^{(3)}_{r-2}$
whose dimension is at most
![]() $r-4$
.
$r-4$
.
(
![]() $\gamma$
-5) Assume that the following three conditions hold:
$\gamma$
-5) Assume that the following three conditions hold:
![]() $w_{q_2,j_2}\,=\,w_{p^{(1)}(1),j^{(1)}(1)}\,=\,1$
,
$w_{q_2,j_2}\,=\,w_{p^{(1)}(1),j^{(1)}(1)}\,=\,1$
,
![]() $(q_1,\,j_1)\,\neq \,(q_2,\,j_2),\,(p^{(1)}(1),\,j^{(1)}(1))$
and
$(q_1,\,j_1)\,\neq \,(q_2,\,j_2),\,(p^{(1)}(1),\,j^{(1)}(1))$
and
![]() $q_2\,\leqslant \, p^{(1)}(1)$
. Consider the automorphisms
$q_2\,\leqslant \, p^{(1)}(1)$
. Consider the automorphisms
![]() $\textbf {g}\,=\, (a^{p,q}_{j,j'})$
of
$\textbf {g}\,=\, (a^{p,q}_{j,j'})$
of
![]() $E$
given by:
$E$
given by:
 $a^{1,1}_{1,1}\,=\,c_1\,\in \,k^{\times }$
,
$a^{1,1}_{1,1}\,=\,c_1\,\in \,k^{\times }$
,
 $a^{p^{(1)}(1),p^{(1)}(1)}_{j^{(1)}(1),j^{(1)}(1)}\,=\,c_2\,\in \,k^{\times }$
,for
$a^{p^{(1)}(1),p^{(1)}(1)}_{j^{(1)}(1),j^{(1)}(1)}\,=\,c_2\,\in \,k^{\times }$
,for \begin{align*}a^{p,p}_{j,j}\,=\,c_3\,\in \,k^{\times }\end{align*}
\begin{align*}a^{p,p}_{j,j}\,=\,c_3\,\in \,k^{\times }\end{align*}
 $(p,\,j)\,\neq \,(1,\,1),\,(p^{(1)}(1),\,j^{(1)}(1))$
;
$(p,\,j)\,\neq \,(1,\,1),\,(p^{(1)}(1),\,j^{(1)}(1))$
;
 $a^{p^{(1)}(1),q_2}_{j^{(1)}(1),j_2}\,=\,b\,\in \, \textrm { Hom}({\mathcal O}_{\mathbb{P}^1}(a_{q_2}),\, {\mathcal O}_{\mathbb{P}^1}(a_{p^{(1)}(1)}))$
such that
$a^{p^{(1)}(1),q_2}_{j^{(1)}(1),j_2}\,=\,b\,\in \, \textrm { Hom}({\mathcal O}_{\mathbb{P}^1}(a_{q_2}),\, {\mathcal O}_{\mathbb{P}^1}(a_{p^{(1)}(1)}))$
such that
 $c_2w_{p^{(1)}(1),j^{(1)}(1)}+b|_{x_3} w_{q_2,j_2}\,=\,c_3w_{p^{(1)}(1),j^{(1)}(1)}$
; and
$c_2w_{p^{(1)}(1),j^{(1)}(1)}+b|_{x_3} w_{q_2,j_2}\,=\,c_3w_{p^{(1)}(1),j^{(1)}(1)}$
; and $a^{p,q}_{j,j'}\,=\,0$
for any
$a^{p,q}_{j,j'}\,=\,0$
for any
 $(p,\,j,\,q,\,j)$
such that
$(p,\,j,\,q,\,j)$
such that
 $(p,\,j)\,\neq \, (q,\,j')$
and
$(p,\,j)\,\neq \, (q,\,j')$
and \begin{align*}(p,\,j,\,q,\,j')\,\neq \, (p^{(1)}(1),\,j^{(1)}(1),\,q_2,\,j_2).\end{align*}
\begin{align*}(p,\,j,\,q,\,j')\,\neq \, (p^{(1)}(1),\,j^{(1)}(1),\,q_2,\,j_2).\end{align*}
Note that we can always choose
![]() $b\,\in \, H^0({\mathcal O}_{\mathbb{P}^1}(a_{p^{(1)}(1)}-a_{q_2}))$
satisfying the condition that
$b\,\in \, H^0({\mathcal O}_{\mathbb{P}^1}(a_{p^{(1)}(1)}-a_{q_2}))$
satisfying the condition that
![]() $b|_{x_3} w_{q_2,j_2}\,=\,(c_3-c_2)w_{p^{(1)}(1),j^{(1)}(1)}$
for any given
$b|_{x_3} w_{q_2,j_2}\,=\,(c_3-c_2)w_{p^{(1)}(1),j^{(1)}(1)}$
for any given
![]() $c_2,\,c_3\,\in \,k^{\times }$
. Such automorphisms preserve
$c_2,\,c_3\,\in \,k^{\times }$
. Such automorphisms preserve
![]() $l^{(1)}_*$
,
$l^{(1)}_*$
,
![]() $l^{(2)}_*$
and
$l^{(2)}_*$
and
![]() $l^{(3)}_{r-1}$
. Applying such an automorphism, the representative
$l^{(3)}_{r-1}$
. Applying such an automorphism, the representative
![]() $v\,\in \, l^{(3)}_{r-2}$
of a generator of
$v\,\in \, l^{(3)}_{r-2}$
of a generator of
![]() $l^{(3)}_{r-2}/l^{(3)}_{r-1}$
is sent to
$l^{(3)}_{r-2}/l^{(3)}_{r-1}$
is sent to
 \begin{align*} \textbf {g}v \,=\, c_1v_{1,1}e^{(3)}_{1,1}+c_3v_{2,1}e^{(3)}_{2,1}+\cdots +\left ( c_2v_{p^{(1)}(1),j^{(1)}(1)}+b|_{x_3} v_{q_2,j_2} \right ) e^{(3)}_{p^{(1)}(1),j^{(1)}(1)} +\cdots \\ \quad \quad+\,0e^{(3)}_{q_1,j_1}+\cdots +c_3 v_{q_2,j_2} e^{(3)}_{q_2,j_2} +\cdots +c_3v_{m,r_m}. \end{align*}
\begin{align*} \textbf {g}v \,=\, c_1v_{1,1}e^{(3)}_{1,1}+c_3v_{2,1}e^{(3)}_{2,1}+\cdots +\left ( c_2v_{p^{(1)}(1),j^{(1)}(1)}+b|_{x_3} v_{q_2,j_2} \right ) e^{(3)}_{p^{(1)}(1),j^{(1)}(1)} +\cdots \\ \quad \quad+\,0e^{(3)}_{q_1,j_1}+\cdots +c_3 v_{q_2,j_2} e^{(3)}_{q_2,j_2} +\cdots +c_3v_{m,r_m}. \end{align*}
So we can assume that one of the following holds:
-
(a)
 $v_{1,1}\,=\,v_{p^{(1)}(1),j^{(1)}(1)}\,=\,v_{q_2,j_2}\,\neq \, 0$
;
$v_{1,1}\,=\,v_{p^{(1)}(1),j^{(1)}(1)}\,=\,v_{q_2,j_2}\,\neq \, 0$
; -
(b)
 $v_{1,1}\,=\,v_{p^{(1)}(1),j^{(1)}(1)}\,\neq \, 0$
and
$v_{1,1}\,=\,v_{p^{(1)}(1),j^{(1)}(1)}\,\neq \, 0$
and
 $v_{q_2,j_2}\,=\,0$
;
$v_{q_2,j_2}\,=\,0$
; -
(c)
 $v_{1,1}\,=\,v_{q_2,j_2}\,\neq \, 0$
and
$v_{1,1}\,=\,v_{q_2,j_2}\,\neq \, 0$
and
 $v_{p^{(1)}(1),j^{(1)}(1)}\,=\,0$
;
$v_{p^{(1)}(1),j^{(1)}(1)}\,=\,0$
; -
(d)
 $v_{p^{(1)}(1),j^{(1)}(1)}\,=\,v_{q_2,j_2}\,=\,0$
.
$v_{p^{(1)}(1),j^{(1)}(1)}\,=\,v_{q_2,j_2}\,=\,0$
.
Then we can give a parameter space for
![]() $l^{(3)}_{r-2}$
whose dimension is at most
$l^{(3)}_{r-2}$
whose dimension is at most
![]() $r-4$
.
$r-4$
.
In all cases of B(ii)(
![]() $\gamma$
), by adding the data
$\gamma$
), by adding the data
![]() $l^{(3)}_{r-3},\,\cdots ,\,l^{(3)}_1$
to the parameter space of
$l^{(3)}_{r-3},\,\cdots ,\,l^{(3)}_1$
to the parameter space of
![]() $l^{(3)}_{r-2}$
, we can give a parameter space for
$l^{(3)}_{r-2}$
, we can give a parameter space for
![]() $(E,\,\boldsymbol{l})$
whose dimension is at most
$(E,\,\boldsymbol{l})$
whose dimension is at most
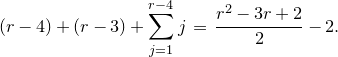 \begin{align*} (r-4)+(r-3)+\sum _{j=1}^{r-4} j \,=\,\frac {r^2-3r+2} {2} - 2. \end{align*}
\begin{align*} (r-4)+(r-3)+\sum _{j=1}^{r-4} j \,=\,\frac {r^2-3r+2} {2} - 2. \end{align*}
This completes the proof.
Define the open subset
![]() ${\mathcal M}^{n_0\textrm { -reg}}_{{\rm PC}}(\boldsymbol{\nu },\nabla _L)^{\circ }$
of
${\mathcal M}^{n_0\textrm { -reg}}_{{\rm PC}}(\boldsymbol{\nu },\nabla _L)^{\circ }$
of
![]() $\mathcal{M}_{{\rm PC}}^{n_0{\rm -reg}}(\boldsymbol{\nu },\nabla _L)$
,
$\mathcal{M}_{{\rm PC}}^{n_0{\rm -reg}}(\boldsymbol{\nu },\nabla _L)$
,
which consists of
![]() $\boldsymbol{\nu }$
-parabolic connections
$\boldsymbol{\nu }$
-parabolic connections
![]() $(E,\,\nabla ,\,\boldsymbol{l})$
with the determinant isomorphic to
$(E,\,\nabla ,\,\boldsymbol{l})$
with the determinant isomorphic to
![]() $(L,\nabla _L)$
such that the underlying quasi-parabolic bundle
$(L,\nabla _L)$
such that the underlying quasi-parabolic bundle
![]() $(E,\,\boldsymbol{l})$
is simple.
$(E,\,\boldsymbol{l})$
is simple.
Proposition 5.14. Let
![]() $X$
be a smooth projective curve of genus
$X$
be a smooth projective curve of genus
![]() $g$
over an algebraically closed field
$g$
over an algebraically closed field
![]() $k$
, and let
$k$
, and let
![]() $L$
be a line bundle on
$L$
be a line bundle on
![]() $X$
. Let
$X$
. Let
![]() $r$
and
$r$
and
![]() $n$
be positive integers such that
$n$
be positive integers such that
![]() $r$
is not divisible by the characteristic of
$r$
is not divisible by the characteristic of
![]() $k$
and one of the following holds:
$k$
and one of the following holds:
-
(1)
 $n\,\geqslant \, 1$
and
$n\,\geqslant \, 1$
and
 $r\,\geqslant \, 2$
are arbitrary if
$r\,\geqslant \, 2$
are arbitrary if
 $g\,\geqslant \, 2$
;
$g\,\geqslant \, 2$
; -
(2)
 $n\,\geqslant \, 2$
,
$n\,\geqslant \, 2$
,
 $r\geqslant 2$
and
$r\geqslant 2$
and
 $n+r\,\geqslant \, 5$
if
$n+r\,\geqslant \, 5$
if
 $g\,=\,1$
;
$g\,=\,1$
; -
(3)
 $n\,\geqslant \,3$
,
$n\,\geqslant \,3$
,
 $r\geqslant 2$
and
$r\geqslant 2$
and
 $n+r\,\geqslant \,7$
if
$n+r\,\geqslant \,7$
if
 $g\,=\,0$
.
$g\,=\,0$
.
Then the following holds:
Proof. By Propositions 5.10, 5.11, 5.12 and Proposition 5.13 there is a scheme
![]() $Z$
of finite type over
$Z$
of finite type over
![]() $k$
and a flat family
$k$
and a flat family
![]() $(\widetilde {E},\,\widetilde {\boldsymbol{l}})$
of quasi-parabolic bundles on
$(\widetilde {E},\,\widetilde {\boldsymbol{l}})$
of quasi-parabolic bundles on
![]() $X\times Z$
over
$X\times Z$
over
![]() $Z$
such that:
$Z$
such that:
-
(i)
 $\dim \textrm { End}((\widetilde {E},\,\widetilde {\boldsymbol{l}})|_{X\times z})\,\geqslant \, 2$
for any point
$\dim \textrm { End}((\widetilde {E},\,\widetilde {\boldsymbol{l}})|_{X\times z})\,\geqslant \, 2$
for any point
 $z\,\in \, Z$
;
$z\,\in \, Z$
; -
(ii)
 $\dim Z\leqslant (r^2-1)(g-1)+nr(r-1)/2-2$
; and
$\dim Z\leqslant (r^2-1)(g-1)+nr(r-1)/2-2$
; and -
(iii) each quasi-parabolic bundle in
 $\left | {\mathcal N}^{n_0{\rm -reg}}_{{\rm PC}}(L) \right | \setminus \left | {\mathcal N}^{n_0{\rm -reg}}_{{\rm PC}}(L)^{\circ } \right |$
is isomorphic to
$\left | {\mathcal N}^{n_0{\rm -reg}}_{{\rm PC}}(L) \right | \setminus \left | {\mathcal N}^{n_0{\rm -reg}}_{{\rm PC}}(L)^{\circ } \right |$
is isomorphic to
 $(\widetilde {E},\,\widetilde {\boldsymbol{l}})|_{X\times \{z\}}$
for some point
$(\widetilde {E},\,\widetilde {\boldsymbol{l}})|_{X\times \{z\}}$
for some point
 $z\,\in \, Z$
.
$z\,\in \, Z$
.
We may assume that there is an isomorphism
![]() $\varphi \,\colon \, \det (\widetilde {E})\,\xrightarrow {\,\,\sim \,\,\,}\, L\otimes {\mathcal L}$
for some line bundle
$\varphi \,\colon \, \det (\widetilde {E})\,\xrightarrow {\,\,\sim \,\,\,}\, L\otimes {\mathcal L}$
for some line bundle
![]() $\mathcal L$
on
$\mathcal L$
on
![]() $Z$
.
$Z$
.
Let
be the relative Atiyah exact sequence, where
![]() ${\rm At}(\widetilde {E})$
is the Atiyah bundle for
${\rm At}(\widetilde {E})$
is the Atiyah bundle for
![]() $\widetilde E$
. Setting
$\widetilde E$
. Setting
![]() ${\rm At}_D(\widetilde {E})$
to be the pullback of
${\rm At}_D(\widetilde {E})$
to be the pullback of
![]() $T_{X\times Z/Z}(-D\times Z)$
by the surjection
$T_{X\times Z/Z}(-D\times Z)$
by the surjection
![]() ${\rm At}(\widetilde {E})\,\longrightarrow \, T_{X\times Z/Z}$
in (5.16), we get a short exact sequence
${\rm At}(\widetilde {E})\,\longrightarrow \, T_{X\times Z/Z}$
in (5.16), we get a short exact sequence
By [Reference GrothendieckGrot1, Theorem 7.7.6], there exists a coherent sheaf
![]() $\mathcal H$
on
$\mathcal H$
on
![]() $Z$
and a functorial isomorphism
$Z$
and a functorial isomorphism
for any morphism
![]() $S\,\longrightarrow \, Z$
and any coherent sheaf
$S\,\longrightarrow \, Z$
and any coherent sheaf
![]() $\mathcal Q$
on
$\mathcal Q$
on
![]() $S$
. Set
$S$
. Set
![]() ${\mathcal V}\,\,:=\,\,\textrm { Spec} \left ( {\rm Sym}^*( {\mathcal H} )\right )$
. Then there is a universal section
${\mathcal V}\,\,:=\,\,\textrm { Spec} \left ( {\rm Sym}^*( {\mathcal H} )\right )$
. Then there is a universal section
![]() $\widetilde {\Psi }\,\colon \, T_{X\times {\mathcal V}/{\mathcal V}}(-D\times {\mathcal V}) \,\longrightarrow \,{\rm At}_D(\widetilde {E})$
. Note that the composition of maps
$\widetilde {\Psi }\,\colon \, T_{X\times {\mathcal V}/{\mathcal V}}(-D\times {\mathcal V}) \,\longrightarrow \,{\rm At}_D(\widetilde {E})$
. Note that the composition of maps
![]() ${\rm symb}\circ \widetilde {\Psi }$
defines a global section of
${\rm symb}\circ \widetilde {\Psi }$
defines a global section of
![]() ${\mathcal O}_{X\times {\mathcal V}}$
, which is a section of
${\mathcal O}_{X\times {\mathcal V}}$
, which is a section of
![]() ${\mathcal O}_{\mathcal V}$
. Let
${\mathcal O}_{\mathcal V}$
. Let
![]() ${\mathcal V}'$
be the closed subscheme of
${\mathcal V}'$
be the closed subscheme of
![]() $\mathcal V$
defined by the condition
$\mathcal V$
defined by the condition
![]() ${\rm symb}_1\circ \widetilde {\Psi }\,=\,1$
. Then the restriction
${\rm symb}_1\circ \widetilde {\Psi }\,=\,1$
. Then the restriction
![]() $\widetilde {\Psi }|_{{\mathcal V}'}$
defines a universal relative connection
$\widetilde {\Psi }|_{{\mathcal V}'}$
defines a universal relative connection
Let
![]() $B$
be the maximal closed subscheme of
$B$
be the maximal closed subscheme of
![]() $\mathcal V'$
such that
$\mathcal V'$
such that
![]() $\big ( {\sf res}_{x_i\times {\mathcal V'}}(\widetilde {\nabla }) -\nu ^{(i)}_j{\rm id}\big ) (\widetilde {l}^{(i)}_j)_{\mathcal V'} \,\subset \, (\widetilde {l}^{(i)}_{j+1})_{\mathcal V'}$
for any
$\big ( {\sf res}_{x_i\times {\mathcal V'}}(\widetilde {\nabla }) -\nu ^{(i)}_j{\rm id}\big ) (\widetilde {l}^{(i)}_j)_{\mathcal V'} \,\subset \, (\widetilde {l}^{(i)}_{j+1})_{\mathcal V'}$
for any
![]() $i,\,j$
and
$i,\,j$
and
![]() $(\varphi \otimes {\rm id})\circ \widetilde {\nabla }\circ \varphi ^{-1} \,=\,\nabla _L\otimes {\rm id}_{\mathcal L}$
. Set
$(\varphi \otimes {\rm id})\circ \widetilde {\nabla }\circ \varphi ^{-1} \,=\,\nabla _L\otimes {\rm id}_{\mathcal L}$
. Set
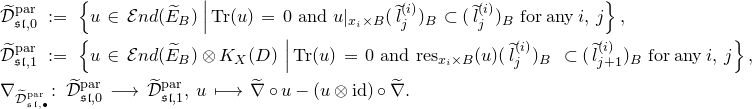 \begin{align*} &\widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},0} \,\,:=\,\, \left \{ u\,\in \, {\mathcal End}(\widetilde {E}_B)\, \middle | \: {\textrm{Tr}}(u)\,=\,0\ {\rm and}\ u|_{x_i\times B}(\,\widetilde {l}^{(i)}_j)_B\,\subset(\,\widetilde {l}^{(i)}_j)_B\ {\rm for \,any}\, i,\,j \right \}, \\ &\widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},1} \,\,:=\,\, \left \{ u\,\in \, {\mathcal End}(\widetilde {E}_B)\otimes K_X(D)\ \middle | \: {\textrm {Tr}}(u)\,=\,0\ {\rm and}\ \mathrm{res}_{x_i\times B}(u)(\,\widetilde {l}^{(i)}_j)_B\ \,\subset (\,\widetilde {l}^{(i)}_{j+1})_B\ {\rm for \,any} \,i, \,j \right \}, \\ &\nabla _{\widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},\bullet }} \colon \: \widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},0}\, \longrightarrow \, \widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},1},\, u\, \longmapsto \, \widetilde {\nabla }\circ u-(u\otimes {\rm id})\circ \widetilde {\nabla }. \end{align*}
\begin{align*} &\widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},0} \,\,:=\,\, \left \{ u\,\in \, {\mathcal End}(\widetilde {E}_B)\, \middle | \: {\textrm{Tr}}(u)\,=\,0\ {\rm and}\ u|_{x_i\times B}(\,\widetilde {l}^{(i)}_j)_B\,\subset(\,\widetilde {l}^{(i)}_j)_B\ {\rm for \,any}\, i,\,j \right \}, \\ &\widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},1} \,\,:=\,\, \left \{ u\,\in \, {\mathcal End}(\widetilde {E}_B)\otimes K_X(D)\ \middle | \: {\textrm {Tr}}(u)\,=\,0\ {\rm and}\ \mathrm{res}_{x_i\times B}(u)(\,\widetilde {l}^{(i)}_j)_B\ \,\subset (\,\widetilde {l}^{(i)}_{j+1})_B\ {\rm for \,any} \,i, \,j \right \}, \\ &\nabla _{\widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},\bullet }} \colon \: \widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},0}\, \longrightarrow \, \widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},1},\, u\, \longmapsto \, \widetilde {\nabla }\circ u-(u\otimes {\rm id})\circ \widetilde {\nabla }. \end{align*}
There is a canonically induced morphism
whose fiber over a point
![]() $z$
is an affine space isomorphic to
$z$
is an affine space isomorphic to
![]() $H^0\big (X,\, \widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},1} |_{X\times \{z\}}\big )$
. Set
$H^0\big (X,\, \widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},1} |_{X\times \{z\}}\big )$
. Set
Then there is a canonically induced morphism
By the construction, the complement
![]() $\mathcal{M}_{{\rm PC}}^{n_0{\rm -reg}}(\boldsymbol{\nu },\nabla _L) \setminus \mathcal{M}_{{\rm PC}}^{n_0{\rm -reg}}(\boldsymbol{\nu },\nabla _L)^{\circ }$
coincides with the image
$\mathcal{M}_{{\rm PC}}^{n_0{\rm -reg}}(\boldsymbol{\nu },\nabla _L) \setminus \mathcal{M}_{{\rm PC}}^{n_0{\rm -reg}}(\boldsymbol{\nu },\nabla _L)^{\circ }$
coincides with the image
![]() $q(B^{\circ })$
. So it suffices to show that for every irreducible component
$q(B^{\circ })$
. So it suffices to show that for every irreducible component
![]() $B'$
of
$B'$
of
![]() $B^{\circ }$
, the closure
$B^{\circ }$
, the closure
![]() $\overline {q(B')}$
has dimension at most
$\overline {q(B')}$
has dimension at most
![]() $2(r^2-1)(g-1)+r(r-1)n-2$
.
$2(r^2-1)(g-1)+r(r-1)n-2$
.
For each point
![]() $b\,\in \,B'$
, consider the group
$b\,\in \,B'$
, consider the group
![]() ${\rm Aut}((\widetilde {E},\,\widetilde {\boldsymbol{l}},\,\det \widetilde {E})|_{X\times \{b\}})$
of automorphisms of
${\rm Aut}((\widetilde {E},\,\widetilde {\boldsymbol{l}},\,\det \widetilde {E})|_{X\times \{b\}})$
of automorphisms of
![]() $\widetilde {E}|_{X\times \{b\}}$
preserving
$\widetilde {E}|_{X\times \{b\}}$
preserving
![]() $\widetilde {\boldsymbol{l}}_{D\times \{b\}}$
and
$\widetilde {\boldsymbol{l}}_{D\times \{b\}}$
and
![]() $\det \widetilde {E}|_{X\times \{b\}}$
. Then the tangent space of
$\det \widetilde {E}|_{X\times \{b\}}$
. Then the tangent space of
![]() ${\textrm { Aut}}((\widetilde {E},\,\widetilde {\boldsymbol{l}},\,\det \widetilde {E})|_{X\times \{b\}})$
is isomorphic to
${\textrm { Aut}}((\widetilde {E},\,\widetilde {\boldsymbol{l}},\,\det \widetilde {E})|_{X\times \{b\}})$
is isomorphic to
![]() $H^0(X,\, \widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},0} |_{X\times \{b\}})$
. For a point
$H^0(X,\, \widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},0} |_{X\times \{b\}})$
. For a point
![]() $b$
of
$b$
of
![]() $B'$
, there is the orbit map
$B'$
, there is the orbit map
whose differential
is injective because
![]() $(\widetilde {E},\,\widetilde {\nabla },\,\widetilde {\boldsymbol{l}})|_{X\times \{b\}}$
is simple. Since the fiber
$(\widetilde {E},\,\widetilde {\nabla },\,\widetilde {\boldsymbol{l}})|_{X\times \{b\}}$
is simple. Since the fiber
![]() $q^{-1}(x)$
over a point
$q^{-1}(x)$
over a point
![]() $x$
of
$x$
of
contains an orbit for the action of
![]() ${\rm Aut}((\widetilde {E},\,\widetilde {\boldsymbol{l}},\,\det \widetilde {E})|_{X\times \{b\}})$
, we have
${\rm Aut}((\widetilde {E},\,\widetilde {\boldsymbol{l}},\,\det \widetilde {E})|_{X\times \{b\}})$
, we have
Note that we have
![]() $\big (\widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},0}\big )^{\vee } \otimes K_X \,\cong \, \widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},1}$
, and
$\big (\widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},0}\big )^{\vee } \otimes K_X \,\cong \, \widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},1}$
, and
by the Riemann–Roch theorem. If we choose
![]() $x$
to be a generic point of
$x$
to be a generic point of
![]() $q(B')$
, then we have
$q(B')$
, then we have
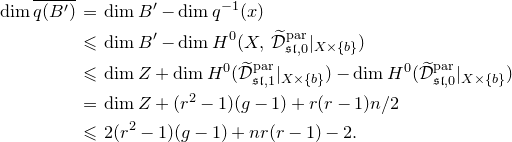 \begin{align*} \dim \overline {q(B')} \,&=\, \dim B'-\dim q^{-1}(x) \\ &\leqslant \, \dim B' -\dim H^0\big (X,\, \widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},0} |_{X\times \{b\}}\big ) \\ &\leqslant \, \dim Z +\dim H^0\big (\widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},1} |_{X\times \{b\}}\big ) -\dim H^0\big (\widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},0} |_{X\times \{b\}}\big ) \\ &=\,\dim Z +(r^2-1)(g-1)+r(r-1)n/2 \\ &\leqslant \, 2(r^2-1)(g-1)+nr(r-1)-2. \end{align*}
\begin{align*} \dim \overline {q(B')} \,&=\, \dim B'-\dim q^{-1}(x) \\ &\leqslant \, \dim B' -\dim H^0\big (X,\, \widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},0} |_{X\times \{b\}}\big ) \\ &\leqslant \, \dim Z +\dim H^0\big (\widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},1} |_{X\times \{b\}}\big ) -\dim H^0\big (\widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},0} |_{X\times \{b\}}\big ) \\ &=\,\dim Z +(r^2-1)(g-1)+r(r-1)n/2 \\ &\leqslant \, 2(r^2-1)(g-1)+nr(r-1)-2. \end{align*}
Since
![]() $q(B^{\circ })=\mathcal{M}_{{\rm PC}}^{n_0{\rm -reg}}(\boldsymbol{\nu },\nabla _L) \setminus \mathcal{M}_{{\rm PC}}^{n_0{\rm -reg}}(\boldsymbol{\nu },\nabla _L)^{\circ }$
is a union of the images
$q(B^{\circ })=\mathcal{M}_{{\rm PC}}^{n_0{\rm -reg}}(\boldsymbol{\nu },\nabla _L) \setminus \mathcal{M}_{{\rm PC}}^{n_0{\rm -reg}}(\boldsymbol{\nu },\nabla _L)^{\circ }$
is a union of the images
![]() $q(B')$
, the proof is completed.
$q(B')$
, the proof is completed.
Define the open subset
![]() $\mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L)^{\circ }$
of
$\mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L)^{\circ }$
of
![]() $\mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L)$
by
$\mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L)$
by
which consists of
![]() $\boldsymbol{\mu }$
-parabolic Higgs bundles
$\boldsymbol{\mu }$
-parabolic Higgs bundles
![]() $(E,\,\Phi ,\,\boldsymbol{l})$
with the determinant isomorphic to
$(E,\,\Phi ,\,\boldsymbol{l})$
with the determinant isomorphic to
![]() $(L,\Phi _L)$
such that the underlying quasi-parabolic bundle
$(L,\Phi _L)$
such that the underlying quasi-parabolic bundle
![]() $(E,\,\boldsymbol{l})$
is simple.
$(E,\,\boldsymbol{l})$
is simple.
The proof of the following proposition uses an argument similar to one in the proofs of Proposition 5.14.
Proposition 5.15. Let
![]() $X$
be a smooth projective curve of genus
$X$
be a smooth projective curve of genus
![]() $g$
over an algebraically closed field
$g$
over an algebraically closed field
![]() $k$
, and let
$k$
, and let
![]() $L$
be a line bundle on
$L$
be a line bundle on
![]() $X$
with a homomorphism
$X$
with a homomorphism
![]() $\Phi _L \,\colon \, L\,\longrightarrow \, L\otimes K_X(D)$
. Take positive integers
$\Phi _L \,\colon \, L\,\longrightarrow \, L\otimes K_X(D)$
. Take positive integers
![]() $r,n$
and a tuple
$r,n$
and a tuple
![]() $\boldsymbol{\mu }=(\mu ^{(i)}_j)^{1\leqslant i\leqslant n}_{0\leqslant j\leqslant r-1}\in \,k^{nr}$
such that
$\boldsymbol{\mu }=(\mu ^{(i)}_j)^{1\leqslant i\leqslant n}_{0\leqslant j\leqslant r-1}\in \,k^{nr}$
such that
![]() ${\sf res}_{x_i}(\Phi _L)\,=\,\sum _{j=0}^{r-1}\mu ^{(i)}_j$
for any
${\sf res}_{x_i}(\Phi _L)\,=\,\sum _{j=0}^{r-1}\mu ^{(i)}_j$
for any
![]() $i$
. Assume that
$i$
. Assume that
![]() $r$
is not divisible by the characteristic of
$r$
is not divisible by the characteristic of
![]() $k$
and one of the following holds:
$k$
and one of the following holds:
-
(a)
 $n\,\geqslant \, 1$
and
$n\,\geqslant \, 1$
and
 $r\,\geqslant \, 2$
are arbitrary if
$r\,\geqslant \, 2$
are arbitrary if
 $g\,\geqslant \, 2$
;
$g\,\geqslant \, 2$
; -
(b)
 $n\,\geqslant \, 2$
,
$n\,\geqslant \, 2$
,
 $r\geqslant 2$
and
$r\geqslant 2$
and
 $n+r\,\geqslant \, 5$
if
$n+r\,\geqslant \, 5$
if
 $g\,=\,1$
;
$g\,=\,1$
; -
(c)
 $n\,\geqslant \,3$
,
$n\,\geqslant \,3$
,
 $r\geqslant 2$
and
$r\geqslant 2$
and
 $n+r\,\geqslant \,7$
if
$n+r\,\geqslant \,7$
if
 $g\,=\,0$
.
$g\,=\,0$
.
Then
![]() ${\rm codim}_{\mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L)} \left ( \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L) \setminus \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L)^{\circ }\right ) \,\,\geqslant \,\, 2$
.
${\rm codim}_{\mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L)} \left ( \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L) \setminus \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L)^{\circ }\right ) \,\,\geqslant \,\, 2$
.
Proof. By Propositions 5.10, 5.11, 5.12, 5.13, there is a scheme
![]() $Z$
of finite type over
$Z$
of finite type over
![]() $\textrm { Spec}\, k$
and a flat family
$\textrm { Spec}\, k$
and a flat family
![]() $(\widetilde {E},\,\widetilde {\boldsymbol{l}})$
of quasi-parabolic bundles on
$(\widetilde {E},\,\widetilde {\boldsymbol{l}})$
of quasi-parabolic bundles on
![]() $X\times Z$
over
$X\times Z$
over
![]() $Z$
such that
$Z$
such that
-
(i)
 $\dim Z\,\leqslant \, (r^2-1)(g-1)+nr(r-1)/2-2$
;
$\dim Z\,\leqslant \, (r^2-1)(g-1)+nr(r-1)/2-2$
; -
(ii)
 $\dim \textrm { End}((\widetilde {E},\,\widetilde {\boldsymbol{l}})|_{X\times z})\,\geqslant \, 2$
for all
$\dim \textrm { End}((\widetilde {E},\,\widetilde {\boldsymbol{l}})|_{X\times z})\,\geqslant \, 2$
for all
 $z\,\in \, Z$
; and
$z\,\in \, Z$
; and -
(iii) each quasi-parabolic bundle in the complement
 $\left | {\mathcal N}^{n_0{\rm -reg}}_{{\rm par}}(L) \right | \setminus \left | {\mathcal N}^{n_0{\rm -reg}}_{{\rm par}}(L)^{\circ } \right |$
is isomorphic to
$\left | {\mathcal N}^{n_0{\rm -reg}}_{{\rm par}}(L) \right | \setminus \left | {\mathcal N}^{n_0{\rm -reg}}_{{\rm par}}(L)^{\circ } \right |$
is isomorphic to
 $(\widetilde {E},\,\widetilde {\boldsymbol{l}})|_{X\times \{z\}}$
for some
$(\widetilde {E},\,\widetilde {\boldsymbol{l}})|_{X\times \{z\}}$
for some
 $z\,\in \, Z$
.
$z\,\in \, Z$
.
Define
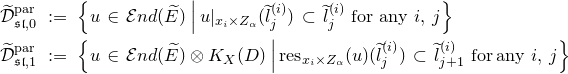 \begin{align*} &\widetilde {\mathcal{D}}^{{\rm par}}_{\mathfrak{sl},0} \,\,:=\,\, \left \{ u\,\in \, {\mathcal{E}}nd(\widetilde {E}) \, \Big | \: u|_{x_i\times Z_{\alpha }}(\widetilde {l}^{(i)}_j)\,\subset \, \widetilde {l}^{(i)}_j {\rm \ for\ any}\ i,\,j\right \} \\ &\widetilde {\mathcal{D}}^{{\rm par}}_{\mathfrak{sl},1} \,\,:=\,\, \left \{ u\,\in \, {\mathcal{E}}nd(\widetilde {E})\otimes K_X(D) \, \Big | \: {\rm res}_{x_i\times Z_{\alpha }}(u) (\widetilde {l}^{(i)}_j)\,\subset \, \widetilde {l}^{(i)}_{j+1} {\rm \ for\, any}\ i,\,j \right \} \end{align*}
\begin{align*} &\widetilde {\mathcal{D}}^{{\rm par}}_{\mathfrak{sl},0} \,\,:=\,\, \left \{ u\,\in \, {\mathcal{E}}nd(\widetilde {E}) \, \Big | \: u|_{x_i\times Z_{\alpha }}(\widetilde {l}^{(i)}_j)\,\subset \, \widetilde {l}^{(i)}_j {\rm \ for\ any}\ i,\,j\right \} \\ &\widetilde {\mathcal{D}}^{{\rm par}}_{\mathfrak{sl},1} \,\,:=\,\, \left \{ u\,\in \, {\mathcal{E}}nd(\widetilde {E})\otimes K_X(D) \, \Big | \: {\rm res}_{x_i\times Z_{\alpha }}(u) (\widetilde {l}^{(i)}_j)\,\subset \, \widetilde {l}^{(i)}_{j+1} {\rm \ for\, any}\ i,\,j \right \} \end{align*}
By [Reference GrothendieckGrot1, Theorem 7.7.6], there is a coherent sheaf
![]() $\mathcal H$
on
$\mathcal H$
on
![]() $Z$
together with a functorial isomorphism
$Z$
together with a functorial isomorphism
for any Noetherian scheme
![]() $S$
over
$S$
over
![]() $Z$
and any coherent sheaf
$Z$
and any coherent sheaf
![]() $Q$
on
$Q$
on
![]() $S$
. For
$S$
. For
![]() $\mathbb{V}({\mathcal H})\,\,:=\,\, \textrm {Spec} \big ( {\rm Sym}^*({\mathcal H})\big )$
, there is a universal family of Higgs fields
$\mathbb{V}({\mathcal H})\,\,:=\,\, \textrm {Spec} \big ( {\rm Sym}^*({\mathcal H})\big )$
, there is a universal family of Higgs fields
![]() $\widetilde {\Phi }\,\in \, H^0(X\times S,\,\widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},0} \otimes K_X(D)\otimes _{{\mathcal O}_Z} {\mathcal O}_{\mathbb{V}({\mathcal H})})$
on
$\widetilde {\Phi }\,\in \, H^0(X\times S,\,\widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},0} \otimes K_X(D)\otimes _{{\mathcal O}_Z} {\mathcal O}_{\mathbb{V}({\mathcal H})})$
on
![]() $(\widetilde {E},\,\widetilde {\boldsymbol{l}})\otimes {\mathcal O}_{\mathbb{V}({\mathcal H})}$
. We may assume that
$(\widetilde {E},\,\widetilde {\boldsymbol{l}})\otimes {\mathcal O}_{\mathbb{V}({\mathcal H})}$
. We may assume that
![]() $\det (\widetilde {E})\,\cong \, L\otimes {\mathcal P}$
for some line bundle
$\det (\widetilde {E})\,\cong \, L\otimes {\mathcal P}$
for some line bundle
![]() $\mathcal P$
on
$\mathcal P$
on
![]() $Z$
. Let
$Z$
. Let
![]() $B$
be the maximal locally closed subscheme of
$B$
be the maximal locally closed subscheme of
![]() $\mathbb{V}({\mathcal H})$
such that the composition of the homomorphisms
$\mathbb{V}({\mathcal H})$
such that the composition of the homomorphisms
coincides with
![]() $\nabla _L\otimes {\mathcal P}_B$
and
$\nabla _L\otimes {\mathcal P}_B$
and
![]() $({\sf res}_{x_i\times Z} (\widetilde {\Phi }) - \mu ^{(i)}_\ell ) (\widetilde {l}^{(i)}_\ell ) \,\subset \, \widetilde {l}^{(i)}_{\ell+1}$
for any
$({\sf res}_{x_i\times Z} (\widetilde {\Phi }) - \mu ^{(i)}_\ell ) (\widetilde {l}^{(i)}_\ell ) \,\subset \, \widetilde {l}^{(i)}_{\ell+1}$
for any
![]() $i,\,\ell$
and also
$i,\,\ell$
and also
![]() $(\widetilde {E},\,\widetilde {\boldsymbol{l}},\,\widetilde {\Phi })|_{X\times b}$
is simple for any
$(\widetilde {E},\,\widetilde {\boldsymbol{l}},\,\widetilde {\Phi })|_{X\times b}$
is simple for any
![]() $b\,\in \, B$
. Then the family
$b\,\in \, B$
. Then the family
![]() $(\widetilde {E},\,\widetilde {\boldsymbol{l}},\,\widetilde {\Phi })_{B}$
defines a morphism
$(\widetilde {E},\,\widetilde {\boldsymbol{l}},\,\widetilde {\Phi })_{B}$
defines a morphism
whose image coincides with
![]() $\mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L) \setminus \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L)^{\circ }$
. Note that the fibers of the morphism in (5.18) contain orbits of the action by the automorphism group of
$\mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L) \setminus \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L)^{\circ }$
. Note that the fibers of the morphism in (5.18) contain orbits of the action by the automorphism group of
![]() $(\widetilde {E},\,\widetilde {\boldsymbol{l}},\,\det (\widetilde {E}))_z$
whose dimension is that of
$(\widetilde {E},\,\widetilde {\boldsymbol{l}},\,\det (\widetilde {E}))_z$
whose dimension is that of
![]() $H^0(X,\,\widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},0}|_{X\times z})$
. So we have
$H^0(X,\,\widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},0}|_{X\times z})$
. So we have
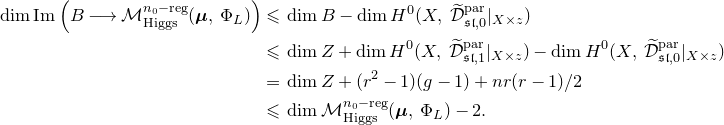 \begin{align*} \dim \textrm {Im}\left (B\longrightarrow \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L)\right ) &\leqslant \, \dim B- \dim H^0\big (X,\,\widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},0}|_{X\times z}\big ) \\ &\leqslant \, \dim Z+ \dim H^0 \big ( X,\,\widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},1}|_{X\times z}\big ) - \dim H^0\big (X,\,\widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},0}|_{X\times z}\big ) \\ &=\, \dim Z+ (r^2-1)(g-1)+nr(r-1)/2 \\ &\leqslant \, \dim \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L)-2. \end{align*}
\begin{align*} \dim \textrm {Im}\left (B\longrightarrow \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L)\right ) &\leqslant \, \dim B- \dim H^0\big (X,\,\widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},0}|_{X\times z}\big ) \\ &\leqslant \, \dim Z+ \dim H^0 \big ( X,\,\widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},1}|_{X\times z}\big ) - \dim H^0\big (X,\,\widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},0}|_{X\times z}\big ) \\ &=\, \dim Z+ (r^2-1)(g-1)+nr(r-1)/2 \\ &\leqslant \, \dim \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L)-2. \end{align*}
Since
![]() $\mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L) \setminus \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L)^{\circ }$
coincides with the image of the morphism in (5.18), the proof is complete.
$\mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L) \setminus \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L)^{\circ }$
coincides with the image of the morphism in (5.18), the proof is complete.
As a corollary of the above theorem, we can also get a result by Boden and Yokogawa [Reference Boden and YokogawaBoYo, Theorem 4.2(c)].
Corollary 5.16. Under the same assumption as in Propositions 5.14 and 5.15
, the moduli spaces
![]() $\mathcal{M}_{{\rm PC}}^{n_0{\rm -reg}}(\boldsymbol{\nu },\nabla _L)$
and
$\mathcal{M}_{{\rm PC}}^{n_0{\rm -reg}}(\boldsymbol{\nu },\nabla _L)$
and
![]() $\mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L)$
are irreducible.
$\mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L)$
are irreducible.
Proof. We only prove the irreducibility for
![]() $\mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L)$
as the proof is same for
$\mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L)$
as the proof is same for
![]() $\mathcal{M}_{{\rm PC}}^{n_0{\rm -reg}}(\boldsymbol{\nu },\nabla _L)$
. The open subspace
$\mathcal{M}_{{\rm PC}}^{n_0{\rm -reg}}(\boldsymbol{\nu },\nabla _L)$
. The open subspace
![]() $\mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L)^{\circ }$
is isomorphic to an affine space bundle over the moduli space
$\mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L)^{\circ }$
is isomorphic to an affine space bundle over the moduli space
![]() ${\mathcal N}_{\textrm { par}}^{n_0{\rm -reg}}(L)$
of
${\mathcal N}_{\textrm { par}}^{n_0{\rm -reg}}(L)$
of
![]() $n_0$
-regular simple quasi-parabolic bundles with the determinant
$n_0$
-regular simple quasi-parabolic bundles with the determinant
![]() $L$
. Since
$L$
. Since
![]() ${\mathcal N}_{\textrm { par}}^{n_0{\rm -reg}}(L)$
is irreducible, it follows that
${\mathcal N}_{\textrm { par}}^{n_0{\rm -reg}}(L)$
is irreducible, it follows that
![]() $\mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L)^{\circ }$
is also irreducible. Recall that the moduli space
$\mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L)^{\circ }$
is also irreducible. Recall that the moduli space
![]() $\mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L)$
is smooth of equi-dimension by Proposition 5.7. So
$\mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L)$
is smooth of equi-dimension by Proposition 5.7. So
![]() $\mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L)$
is connected and thus irreducible, because
$\mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L)$
is connected and thus irreducible, because
![]() $\dim \left ( \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L) \setminus \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L)^{\circ }\right ) \,\lt \,\dim \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L)$
by Proposition 5.15.
$\dim \left ( \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L) \setminus \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L)^{\circ }\right ) \,\lt \,\dim \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{\mu },\,\Phi _L)$
by Proposition 5.15.
Remark 5.17. The proof of Corollary 5.16 is in fact valid under a weaker assumption than that of Theorem 5.15. Indeed, it is valid under the same assumption as that of [Reference InabaIna, Theorem 2.2].
5.3 The moduli space is not affine
We use the notation of § 5.1. In this subsection,
![]() $k$
is assumed to be an algebraically closed field of arbitrary characteristic unless otherwise noted.
$k$
is assumed to be an algebraically closed field of arbitrary characteristic unless otherwise noted.
Let
![]() $X$
be a smooth projective curve over
$X$
be a smooth projective curve over
![]() $k$
of genus
$k$
of genus
![]() $g$
. Fix a line bundle
$g$
. Fix a line bundle
![]() $L$
of degree
$L$
of degree
![]() $d$
on
$d$
on
![]() $X$
equipped with a logarithmic connection
$X$
equipped with a logarithmic connection
![]() $\nabla _L\,\colon \, L \,\longrightarrow \, L\otimes K_X(D)$
, and also fix a string of local exponents
$\nabla _L\,\colon \, L \,\longrightarrow \, L\otimes K_X(D)$
, and also fix a string of local exponents
![]() $\boldsymbol{\nu }\,=\, (\nu ^{(i)}_j)\,\in \, k^{nr}$
such that
$\boldsymbol{\nu }\,=\, (\nu ^{(i)}_j)\,\in \, k^{nr}$
such that
![]() ${\sf res}_{x_i}(\nabla _L)\,=\,\sum _{j=0}^{r-1}\nu ^{(i)}_j$
for any
${\sf res}_{x_i}(\nabla _L)\,=\,\sum _{j=0}^{r-1}\nu ^{(i)}_j$
for any
![]() $i$
. We assume the following:
$i$
. We assume the following:
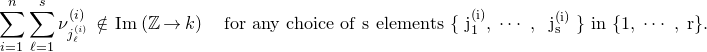 \begin{align} \sum _{i=1}^n\sum _{\ell=1}^s \nu ^{(i)}_{j^{(i)}_\ell } \,\notin \,{\rm Im}\left (\mathbb{Z}\rightarrow k\right ) \quad \rm for\ any\ choice\ of\ s\ elements\ \{\ j^{(i)}_1,\,\cdots\ ,\,\ j^{(i)}_s\ \}\ in\ \{1,\,\cdots\ ,\,r\}. \end{align}
\begin{align} \sum _{i=1}^n\sum _{\ell=1}^s \nu ^{(i)}_{j^{(i)}_\ell } \,\notin \,{\rm Im}\left (\mathbb{Z}\rightarrow k\right ) \quad \rm for\ any\ choice\ of\ s\ elements\ \{\ j^{(i)}_1,\,\cdots\ ,\,\ j^{(i)}_s\ \}\ in\ \{1,\,\cdots\ ,\,r\}. \end{align}
Under the assumption in (5.19), any
![]() $\boldsymbol{\nu }$
-parabolic connection is irreducible, and hence it is
$\boldsymbol{\nu }$
-parabolic connection is irreducible, and hence it is
![]() $\boldsymbol{\alpha }$
-stable for any parabolic weight
$\boldsymbol{\alpha }$
-stable for any parabolic weight
![]() $\boldsymbol{\alpha }$
. So we have
$\boldsymbol{\alpha }$
. So we have
![]() $\mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu },\,\nabla _L) \,=\,\mathcal{M}_{{\rm PC}}(\boldsymbol{\nu },\,\nabla _L)$
. In this subsection we will show that the moduli space
$\mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu },\,\nabla _L) \,=\,\mathcal{M}_{{\rm PC}}(\boldsymbol{\nu },\,\nabla _L)$
. In this subsection we will show that the moduli space
![]() $\mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu },\,\nabla _L)$
is not affine. This will be done by comparing the transcendence degree of the ring of global algebraic functions on the moduli space
$\mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu },\,\nabla _L)$
is not affine. This will be done by comparing the transcendence degree of the ring of global algebraic functions on the moduli space
![]() $\mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu },\nabla _L)$
of parabolic connections with the transcendence degree of the ring of global algebraic functions on the moduli space of parabolic Higgs bundles.
$\mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu },\nabla _L)$
of parabolic connections with the transcendence degree of the ring of global algebraic functions on the moduli space of parabolic Higgs bundles.
Consider the moduli space
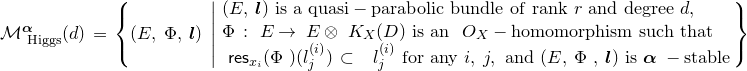 \begin{align*} {\mathcal M}^{\boldsymbol{\alpha }}_{\textrm { Higgs}}(d)\, =\, \left \{ (E,\,\Phi ,\,\boldsymbol{l})\,\, \middle |\, \begin{array}{l} (E,\,\boldsymbol{l})\ {\rm is\ a\ quasi-parabolic\ bundle\ of\ rank}\ r\ {\rm and\ degree}\ d, \\ \Phi\ \colon\ E\to\ E\otimes\ K_X(D)\ {\rm is\ an}\ {\mathcal\ O}_X-{\rm homomorphism\ such\ that} \\ {\sf\ res}_{x_i}(\Phi\ )(l^{(i)}_j)\,\subset\ \,\ l^{(i)}_j\ {\rm for\ any}\ i,\,j,\ {\rm and}\ (E,\,\Phi\ ,\,\boldsymbol{l})\ {\rm is}\ \boldsymbol{\alpha\ }-{\rm stable} \end{array} \right \} \end{align*}
\begin{align*} {\mathcal M}^{\boldsymbol{\alpha }}_{\textrm { Higgs}}(d)\, =\, \left \{ (E,\,\Phi ,\,\boldsymbol{l})\,\, \middle |\, \begin{array}{l} (E,\,\boldsymbol{l})\ {\rm is\ a\ quasi-parabolic\ bundle\ of\ rank}\ r\ {\rm and\ degree}\ d, \\ \Phi\ \colon\ E\to\ E\otimes\ K_X(D)\ {\rm is\ an}\ {\mathcal\ O}_X-{\rm homomorphism\ such\ that} \\ {\sf\ res}_{x_i}(\Phi\ )(l^{(i)}_j)\,\subset\ \,\ l^{(i)}_j\ {\rm for\ any}\ i,\,j,\ {\rm and}\ (E,\,\Phi\ ,\,\boldsymbol{l})\ {\rm is}\ \boldsymbol{\alpha\ }-{\rm stable} \end{array} \right \} \end{align*}
of
![]() $\boldsymbol{\alpha }$
-stable parabolic Higgs bundles. Setting
$\boldsymbol{\alpha }$
-stable parabolic Higgs bundles. Setting
 \begin{align*} \Lambda _{\textrm { Higgs}} = \Bigg \{ \boldsymbol{\mu }=(\mu ^{(i)}_j)^{1\leqslant i\leqslant n}_{0\leqslant j\leqslant r-1} \, \in \, k^{nr} \ \Bigg | \ \sum _{i=1}^n\sum _{j=0}^{r-1}\mu ^{(i)}_j=0 \Bigg \}, \end{align*}
\begin{align*} \Lambda _{\textrm { Higgs}} = \Bigg \{ \boldsymbol{\mu }=(\mu ^{(i)}_j)^{1\leqslant i\leqslant n}_{0\leqslant j\leqslant r-1} \, \in \, k^{nr} \ \Bigg | \ \sum _{i=1}^n\sum _{j=0}^{r-1}\mu ^{(i)}_j=0 \Bigg \}, \end{align*}
we have a canonical morphism
whose fiber over any
![]() $\boldsymbol{\mu }\,\in \, \Lambda _{\textrm { Higgs}}$
is the moduli space
$\boldsymbol{\mu }\,\in \, \Lambda _{\textrm { Higgs}}$
is the moduli space
![]() ${\mathcal M}^{\boldsymbol{\alpha }}_{\textrm { Higgs}}(\boldsymbol{\mu })$
of
${\mathcal M}^{\boldsymbol{\alpha }}_{\textrm { Higgs}}(\boldsymbol{\mu })$
of
![]() $\boldsymbol{\alpha }$
-stable
$\boldsymbol{\alpha }$
-stable
![]() $\boldsymbol{\mu }$
-parabolic Higgs bundles. For a parabolic Higgs bundle
$\boldsymbol{\mu }$
-parabolic Higgs bundles. For a parabolic Higgs bundle
![]() $(E,\,\Phi ,\,\boldsymbol{l})\,\in \, {\mathcal M}^{\boldsymbol{\alpha }}_{\textrm { Higgs}}(d)$
, consider the homomorphism
$(E,\,\Phi ,\,\boldsymbol{l})\,\in \, {\mathcal M}^{\boldsymbol{\alpha }}_{\textrm { Higgs}}(d)$
, consider the homomorphism
where
![]() $T$
is an indeterminate. We can write
$T$
is an indeterminate. We can write
with
![]() $s_j\,\in \, H^0(X,\,K_X^{\otimes j}(jD))$
. Note that
$s_j\,\in \, H^0(X,\,K_X^{\otimes j}(jD))$
. Note that
![]() $s_1\,=\,-{\textrm { Tr}}(\Phi )$
. Set
$s_1\,=\,-{\textrm { Tr}}(\Phi )$
. Set
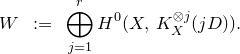 \begin{align*} W\,\,\,:=\,\,\,\bigoplus _{j=1}^r H^0(X,\,K_X^{\otimes j}(jD)). \end{align*}
\begin{align*} W\,\,\,:=\,\,\,\bigoplus _{j=1}^r H^0(X,\,K_X^{\otimes j}(jD)). \end{align*}
Using the above constructed
![]() $(s_1,\,\cdots ,\,s_r)$
, we get a morphism
$(s_1,\,\cdots ,\,s_r)$
, we get a morphism
which is called the Hitchin map. A remarkable property of the Hitchin map is that it is proper, which was proved by Hitchin, Simpson and Nitsure. We use the parabolic version of it, which was proved by Yokogawa.
Theorem 5.18 [Reference HitchinHi, Reference SimpsonSim3, Reference NitsureNit, Reference YokogawaYo].Under the assumption that
![]() $\boldsymbol{\alpha }$
-semistability implies
$\boldsymbol{\alpha }$
-semistability implies
![]() $\boldsymbol{\alpha }$
-stability, the Hitchin map
$\boldsymbol{\alpha }$
-stability, the Hitchin map
![]() $H\,\,\colon \, \,{\mathcal M}^{\boldsymbol{\alpha }}_{\textrm { Higgs}}(d)\,\, \longrightarrow \,\, W$
in (5.20) is a proper morphism.
$H\,\,\colon \, \,{\mathcal M}^{\boldsymbol{\alpha }}_{\textrm { Higgs}}(d)\,\, \longrightarrow \,\, W$
in (5.20) is a proper morphism.
Set
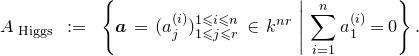 \begin{align*} A_{\textrm { Higgs}}\,\,\,:=\,\,\, \left \{ \boldsymbol{a}\,=\,(a^{(i)}_j)^{1\leqslant i\leqslant n}_{1\leqslant j\leqslant r} \, \in \, k^{nr} \ \middle | \ \sum _{i=1}^n a^{(i)}_1=0 \right \}. \end{align*}
\begin{align*} A_{\textrm { Higgs}}\,\,\,:=\,\,\, \left \{ \boldsymbol{a}\,=\,(a^{(i)}_j)^{1\leqslant i\leqslant n}_{1\leqslant j\leqslant r} \, \in \, k^{nr} \ \middle | \ \sum _{i=1}^n a^{(i)}_1=0 \right \}. \end{align*}
Using the correspondence
![]() $(s_\ell )_{1\leqslant \ell \leqslant r}\, \longmapsto \, ({\sf res}_{x_i}(s_\ell ))^{1\leqslant i\leqslant n}_{1\leqslant \ell \leqslant r}$
, we define a morphism
$(s_\ell )_{1\leqslant \ell \leqslant r}\, \longmapsto \, ({\sf res}_{x_i}(s_\ell ))^{1\leqslant i\leqslant n}_{1\leqslant \ell \leqslant r}$
, we define a morphism
which is a linear surjection under any of the following conditions:
-
(i)
 $n\,\geqslant \, 1$
when
$n\,\geqslant \, 1$
when
 $g\,\geqslant \, 2$
;
$g\,\geqslant \, 2$
; -
(ii)
 $n\,\geqslant \, 2$
when
$n\,\geqslant \, 2$
when
 $g\,=\,1$
;
$g\,=\,1$
; -
(iii)
 $n\,\geqslant \, 3$
when
$n\,\geqslant \, 3$
when
 $g\,=\,0$
.
$g\,=\,0$
.
There is also a morphism
that associates the coefficients of
![]() $\prod _{j=0}^{r-1}(t-\mu ^{(i)}_j)$
. Then the Hitchin map induces a morphism
$\prod _{j=0}^{r-1}(t-\mu ^{(i)}_j)$
. Then the Hitchin map induces a morphism
which is proper by Theorem5.18.
Fix a line bundle
![]() $L$
on
$L$
on
![]() $X$
of degree
$X$
of degree
![]() $d$
, and consider the closed subvariety
$d$
, and consider the closed subvariety
of
![]() ${\mathcal M}^{\boldsymbol{\alpha }}_{\textrm { Higgs}}(d)$
. Then the restriction of the map in (5.21)
${\mathcal M}^{\boldsymbol{\alpha }}_{\textrm { Higgs}}(d)$
. Then the restriction of the map in (5.21)
is also a proper morphism.
Generic fibers of the Hitchin map were investigated by Logares and Martens in [Reference Logares and MartensLaMa, Proposition 2.2]. The following result is likely to be well known to the experts. We give a proof of it using the arguments given by Alfaya and Gómez in [Reference Alfaya and GómezAlGo, Lemma 3.2].
Corollary 5.19. Assume that
![]() $\boldsymbol{\alpha }$
-semistability implies
$\boldsymbol{\alpha }$
-semistability implies
![]() $\boldsymbol{\alpha }$
-stability. Also, assume that one of the following statements holds:
$\boldsymbol{\alpha }$
-stability. Also, assume that one of the following statements holds:
-
(i)
 $n\,\geqslant \, 1$
if
$n\,\geqslant \, 1$
if
 $g\,\geqslant \, 2$
;
$g\,\geqslant \, 2$
; -
(ii)
 $n\,\geqslant \, 2$
if
$n\,\geqslant \, 2$
if
 $g\,=\,1$
;
$g\,=\,1$
; -
(iii)
 $n\,\geqslant \, 3$
if
$n\,\geqslant \, 3$
if
 $g\,=\,0$
.
$g\,=\,0$
.
Then the morphism
![]() ${\mathcal M}^{\boldsymbol{\alpha }}_{\textrm {Higgs}}(L) \ \longrightarrow \ W\times _{ A_{\textrm {Higgs}} } \Lambda _{\textrm { Higgs}}$
in (5.22) is surjective.
${\mathcal M}^{\boldsymbol{\alpha }}_{\textrm {Higgs}}(L) \ \longrightarrow \ W\times _{ A_{\textrm {Higgs}} } \Lambda _{\textrm { Higgs}}$
in (5.22) is surjective.
Proof. It suffices to prove that the morphism in (5.22) is dominant, because it is proper. Take any
![]() $(s\,=\,(s_\ell ),\,\boldsymbol{\mu })\,\in \, W\times _{ A_{\textrm { Higgs}} } \Lambda _{\textrm { Higgs}}$
. Consider the corresponding spectral curve
$(s\,=\,(s_\ell ),\,\boldsymbol{\mu })\,\in \, W\times _{ A_{\textrm { Higgs}} } \Lambda _{\textrm { Higgs}}$
. Consider the corresponding spectral curve
![]() $X_s\, \subset \, \mathbb{P}({\mathcal O}_X\oplus K_X(D))$
which is defined by the equation
$X_s\, \subset \, \mathbb{P}({\mathcal O}_X\oplus K_X(D))$
which is defined by the equation
where
![]() $y$
is the section of
$y$
is the section of
![]() ${\mathcal O}_{\mathbb{P}({\mathcal O}_X\oplus K_X(D))}(1)$
corresponding to the inclusion map
${\mathcal O}_{\mathbb{P}({\mathcal O}_X\oplus K_X(D))}(1)$
corresponding to the inclusion map
![]() ${\mathcal O}_X\,\hookrightarrow \, {\mathcal O}_X\oplus K_X(D)$
. Take a section
${\mathcal O}_X\,\hookrightarrow \, {\mathcal O}_X\oplus K_X(D)$
. Take a section
![]() $\tau \,\in \, H^0(X,\, K_X^{\otimes r}(rD))$
which has at most simple zeroes; since
$\tau \,\in \, H^0(X,\, K_X^{\otimes r}(rD))$
which has at most simple zeroes; since
![]() $K_X^{\otimes r}(rD)$
is very ample by the assumption in the corollary, such a section exists. Then the spectral curve
$K_X^{\otimes r}(rD)$
is very ample by the assumption in the corollary, such a section exists. Then the spectral curve
![]() $y^r-\tau \,=\,0$
has no singular points.
$y^r-\tau \,=\,0$
has no singular points.
Since the smoothness is an open condition, there is an open subset
![]() $U\,\subset \, W\times _{A_{\textrm { Higgs}}}\Lambda _{\textrm { Higgs}}$
such that the spectral curve
$U\,\subset \, W\times _{A_{\textrm { Higgs}}}\Lambda _{\textrm { Higgs}}$
such that the spectral curve
![]() $X_s$
is smooth for every
$X_s$
is smooth for every
![]() $s\,\in \,U$
. Take a line bundle
$s\,\in \,U$
. Take a line bundle
![]() $\mathcal L$
on
$\mathcal L$
on
![]() $X_s$
such that the locally free sheaf
$X_s$
such that the locally free sheaf
![]() $E\,\,:=\,\,\pi _*({\mathcal L})$
has its determinant
$E\,\,:=\,\,\pi _*({\mathcal L})$
has its determinant
![]() $\det (E)$
isomorphic to
$\det (E)$
isomorphic to
![]() $L$
, where
$L$
, where
![]() $\pi \,\colon \, X_s\, \longrightarrow \, X$
is the natural projection. By the Beauville–Narasimhan–Ramanan correspondence [Reference Beauville, Narasimhan and RamananBNR, Proposition 3.6], there is a Higgs field
$\pi \,\colon \, X_s\, \longrightarrow \, X$
is the natural projection. By the Beauville–Narasimhan–Ramanan correspondence [Reference Beauville, Narasimhan and RamananBNR, Proposition 3.6], there is a Higgs field
![]() $\Phi \,\colon \, E \,\longrightarrow \, E\otimes K_X(D)$
induced by the action of
$\Phi \,\colon \, E \,\longrightarrow \, E\otimes K_X(D)$
induced by the action of
![]() $y$
on
$y$
on
![]() $\mathcal L$
. Shrinking
$\mathcal L$
. Shrinking
![]() $U$
if necessary, we may further assume that
$U$
if necessary, we may further assume that
![]() $\mu ^{(i)}_0,\,\cdots ,\,\mu ^{(i)}_{r-1}$
are mutually distinct for any fixed
$\mu ^{(i)}_0,\,\cdots ,\,\mu ^{(i)}_{r-1}$
are mutually distinct for any fixed
![]() $i$
. Then we can associate a unique parabolic structure
$i$
. Then we can associate a unique parabolic structure
![]() $l$
on
$l$
on
![]() $E$
compatible with
$E$
compatible with
![]() $\Phi$
. Since
$\Phi$
. Since
![]() $(E,\,\Phi ,\,\boldsymbol{l})$
is irreducible by its construction, it is evidently
$(E,\,\Phi ,\,\boldsymbol{l})$
is irreducible by its construction, it is evidently
![]() $\boldsymbol{\alpha }$
-stable. So we have
$\boldsymbol{\alpha }$
-stable. So we have
![]() $(E,\,\Phi ,\,\boldsymbol{l})\,\in \, {\mathcal M}^{\boldsymbol{\alpha }}_{\textrm { Higgs}}(L)$
, which is sent to
$(E,\,\Phi ,\,\boldsymbol{l})\,\in \, {\mathcal M}^{\boldsymbol{\alpha }}_{\textrm { Higgs}}(L)$
, which is sent to
![]() $(s,\,\boldsymbol{\mu })$
under the morphism in (5.22). Thus, the morphism in (5.22) is dominant because its image contains the dense open subset
$(s,\,\boldsymbol{\mu })$
under the morphism in (5.22). Thus, the morphism in (5.22) is dominant because its image contains the dense open subset
![]() $U$
of
$U$
of
![]() $W\times _{ A_{\textrm { Higgs}} } \Lambda _{\textrm { Higgs}}$
.
$W\times _{ A_{\textrm { Higgs}} } \Lambda _{\textrm { Higgs}}$
.
As a consequence of Theorem5.18 and Corollary 5.19, we can determine the transcendence degree of the ring of global algebraic functions on the moduli space of parabolic Higgs bundles.
Corollary 5.20. Let
![]() $L$
be a line bundle on
$L$
be a line bundle on
![]() $X$
with a Higgs field
$X$
with a Higgs field
![]() $\Phi _L\,\colon \, L \,\longrightarrow \, L\otimes K_X(D)$
. Take
$\Phi _L\,\colon \, L \,\longrightarrow \, L\otimes K_X(D)$
. Take
![]() $\boldsymbol{\mu }\,=\,(\mu ^{(i)}_j)\,\in \,\Lambda _{\textrm { Higgs}}$
satisfying the condition
$\boldsymbol{\mu }\,=\,(\mu ^{(i)}_j)\,\in \,\Lambda _{\textrm { Higgs}}$
satisfying the condition
![]() ${\sf res}_{x_i}(\Phi _L)\,=\,\sum _{j=0}^{r-1} \mu ^{(i)}_j$
for all
${\sf res}_{x_i}(\Phi _L)\,=\,\sum _{j=0}^{r-1} \mu ^{(i)}_j$
for all
![]() $i$
. Then, under the same assumption as in Theorem 5.15, the transcendence degree of the ring of global algebraic functions on the moduli space of parabolic Higgs bundles is given by the following:
$i$
. Then, under the same assumption as in Theorem 5.15, the transcendence degree of the ring of global algebraic functions on the moduli space of parabolic Higgs bundles is given by the following:
Proof. The closed subvariety
of
![]() $W\times _{A_{\textrm { Higgs}}} \Lambda _{\textrm { Higgs}}$
is isomorphic to an affine space. Its inverse image
$W\times _{A_{\textrm { Higgs}}} \Lambda _{\textrm { Higgs}}$
is isomorphic to an affine space. Its inverse image
![]() ${\mathcal M}^{\boldsymbol{\alpha }}_{\textrm { Higgs}}(L) \times _{ W\times _{ A_{\textrm { Higgs}} } \Lambda _{\textrm { Higgs}} } Y$
for the morphism in (5.22) is nothing but the moduli space
${\mathcal M}^{\boldsymbol{\alpha }}_{\textrm { Higgs}}(L) \times _{ W\times _{ A_{\textrm { Higgs}} } \Lambda _{\textrm { Higgs}} } Y$
for the morphism in (5.22) is nothing but the moduli space
![]() ${\mathcal M}^{\boldsymbol{\alpha }}_{\textrm { Higgs}}(\boldsymbol{\mu }, \Phi _L)$
of
${\mathcal M}^{\boldsymbol{\alpha }}_{\textrm { Higgs}}(\boldsymbol{\mu }, \Phi _L)$
of
![]() $\boldsymbol{\alpha }$
-stable
$\boldsymbol{\alpha }$
-stable
![]() $\boldsymbol{\mu }$
-parabolic Higgs bundles with determinant
$\boldsymbol{\mu }$
-parabolic Higgs bundles with determinant
![]() $(L,\,\Phi _L)$
. By Corollary 5.19, the base change
$(L,\,\Phi _L)$
. By Corollary 5.19, the base change
is also a proper and surjective morphism. So the ring homomorphism
![]() ${\mathcal O}_Y\,\longrightarrow \, H'_*{\mathcal O}_{{\mathcal M}^{\boldsymbol{\alpha }}_{\textrm { Higgs}}(\boldsymbol{\mu },\Phi _L)}$
is injective, and
${\mathcal O}_Y\,\longrightarrow \, H'_*{\mathcal O}_{{\mathcal M}^{\boldsymbol{\alpha }}_{\textrm { Higgs}}(\boldsymbol{\mu },\Phi _L)}$
is injective, and
![]() $H'_*{\mathcal O}_{{\mathcal M}^{\boldsymbol{\alpha }}_{\textrm { Higgs}}(\boldsymbol{\mu },\Phi _L)}$
is a finite algebra over
$H'_*{\mathcal O}_{{\mathcal M}^{\boldsymbol{\alpha }}_{\textrm { Higgs}}(\boldsymbol{\mu },\Phi _L)}$
is a finite algebra over
![]() ${\mathcal O}_Y$
. Therefore,
${\mathcal O}_Y$
. Therefore,
is a finite algebra over
![]() $\Gamma (Y,\,{\mathcal O}_Y)$
whose Krull dimension is
$\Gamma (Y,\,{\mathcal O}_Y)$
whose Krull dimension is
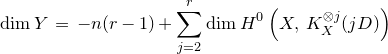 \begin{align*} \dim Y \, =\,-n(r-1)+\sum _{j=2}^r \dim H^0\left (X,\, K_X^{\otimes j}(jD)\right ) \end{align*}
\begin{align*} \dim Y \, =\,-n(r-1)+\sum _{j=2}^r \dim H^0\left (X,\, K_X^{\otimes j}(jD)\right ) \end{align*}
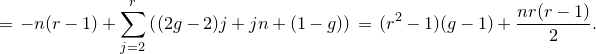 \begin{align*} =\, -n(r-1)+\sum _{j=2}^r \left ( (2g-2)j+jn+(1-g) \right ) \, =\,(r^2-1)(g-1)+\frac {nr(r-1)} {2}. \end{align*}
\begin{align*} =\, -n(r-1)+\sum _{j=2}^r \left ( (2g-2)j+jn+(1-g) \right ) \, =\,(r^2-1)(g-1)+\frac {nr(r-1)} {2}. \end{align*}
Since
![]() $\Gamma ({\mathcal M}^{\boldsymbol{\alpha }}_{\textrm { Higgs}}(\boldsymbol{\mu }, \Phi _L), \, {\mathcal O}_{{\mathcal M}^{\boldsymbol{\alpha }}_{\textrm { Higgs}}(\boldsymbol{\mu },\Phi _L)})$
is a finitely generated algebra over
$\Gamma ({\mathcal M}^{\boldsymbol{\alpha }}_{\textrm { Higgs}}(\boldsymbol{\mu }, \Phi _L), \, {\mathcal O}_{{\mathcal M}^{\boldsymbol{\alpha }}_{\textrm { Higgs}}(\boldsymbol{\mu },\Phi _L)})$
is a finitely generated algebra over
![]() $k$
, its transcendence degree over
$k$
, its transcendence degree over
![]() $k$
coincides with its Krull dimension.
$k$
coincides with its Krull dimension.
Proposition 5.21. There is a projective flat morphism
and an
![]() $\mathbb{A}^1$
-relative very ample divisor
$\mathbb{A}^1$
-relative very ample divisor
![]() $Y\,\subset \, \overline {\mathcal M'}$
such that the complement
$Y\,\subset \, \overline {\mathcal M'}$
such that the complement
![]() ${\mathcal M'}\,\,:=\,\,\overline {\mathcal M'}\setminus Y$
satisfies the following:
${\mathcal M'}\,\,:=\,\,\overline {\mathcal M'}\setminus Y$
satisfies the following:
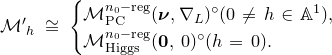 \begin{align*} {\mathcal M'}_h \ \cong \ \begin{cases} \mathcal{M}_{{\rm PC}}^{n_0{\rm -reg}}(\boldsymbol{\nu },\nabla _L)^{\circ } (0\,\neq \,h \,\in \,\mathbb{A}^1), \\ \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{0},\,0)^{\circ } (h\,=\,0). \end{cases} \end{align*}
\begin{align*} {\mathcal M'}_h \ \cong \ \begin{cases} \mathcal{M}_{{\rm PC}}^{n_0{\rm -reg}}(\boldsymbol{\nu },\nabla _L)^{\circ } (0\,\neq \,h \,\in \,\mathbb{A}^1), \\ \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{0},\,0)^{\circ } (h\,=\,0). \end{cases} \end{align*}
Proof. Let
![]() $\mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L)$
be the moduli space of simple
$\mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L)$
be the moduli space of simple
![]() $n_0$
-regular quasi-parabolic bundles
$n_0$
-regular quasi-parabolic bundles
![]() $(E,\,\boldsymbol{l})$
with
$(E,\,\boldsymbol{l})$
with
![]() $\det E\,\cong \, L$
. Let
$\det E\,\cong \, L$
. Let
![]() $(\widetilde {E},\,\widetilde {\boldsymbol{l}})$
be the universal family over
$(\widetilde {E},\,\widetilde {\boldsymbol{l}})$
be the universal family over
![]() $X\times \mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L)$
. As in the proof of Proposition 3.5, we can construct the relative Atiyah bundle
$X\times \mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L)$
. As in the proof of Proposition 3.5, we can construct the relative Atiyah bundle
![]() ${\rm At}_D(\widetilde {E})$
, which fits in the exact sequence
${\rm At}_D(\widetilde {E})$
, which fits in the exact sequence
Recall the construction of the homomorphism (3.4) in the proof of Proposition 3.5, which defines a surjection
Let
![]() ${\rm At}_D(\widetilde {E},\,\widetilde {\boldsymbol{l}}) \,\subset \, {\rm At}_D(\widetilde {E})$
be the pullback of the subsheaf
${\rm At}_D(\widetilde {E},\,\widetilde {\boldsymbol{l}}) \,\subset \, {\rm At}_D(\widetilde {E})$
be the pullback of the subsheaf
by the above surjection.
Since
![]() $\det (\widetilde {E})\,\cong \, L\otimes {\mathcal P}$
for a line bundle
$\det (\widetilde {E})\,\cong \, L\otimes {\mathcal P}$
for a line bundle
![]() $\mathcal P$
on
$\mathcal P$
on
![]() $\mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L)$
, it follows that
$\mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L)$
, it follows that
![]() ${\rm At}_D(\det (\widetilde {E}))\,\cong \, {\rm At}_D(L)\otimes {\mathcal O}_{X\times \mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L)}$
. There is an exact sequence
${\rm At}_D(\det (\widetilde {E}))\,\cong \, {\rm At}_D(L)\otimes {\mathcal O}_{X\times \mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L)}$
. There is an exact sequence
which admits a section
![]() $T_X(-D)\otimes {\mathcal O}_{X\times \mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L)} \,\longrightarrow \, {\rm At}_D(L)\otimes {\mathcal O}_{X\times \mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L)}$
induced by
$T_X(-D)\otimes {\mathcal O}_{X\times \mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L)} \,\longrightarrow \, {\rm At}_D(L)\otimes {\mathcal O}_{X\times \mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L)}$
induced by
![]() $\nabla _L$
. So its image determines a subbundle of
$\nabla _L$
. So its image determines a subbundle of
![]() ${\rm At}_D(L)\otimes {\mathcal O}_{X\times \mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L)}$
. Let
${\rm At}_D(L)\otimes {\mathcal O}_{X\times \mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L)}$
. Let
![]() ${\rm At}_D(\widetilde {E},\,\widetilde {\boldsymbol{l}},\,\nabla _L)$
be the pullback of this subbundle by the homomorphism
${\rm At}_D(\widetilde {E},\,\widetilde {\boldsymbol{l}},\,\nabla _L)$
be the pullback of this subbundle by the homomorphism
defined by
![]() $D\,\longmapsto \, D\wedge {\rm Id}\wedge \cdots \wedge {\rm Id}+\cdots + {\rm Id}\wedge \cdots \wedge {\rm Id}\wedge D$
. If we set
$D\,\longmapsto \, D\wedge {\rm Id}\wedge \cdots \wedge {\rm Id}+\cdots + {\rm Id}\wedge \cdots \wedge {\rm Id}\wedge D$
. If we set
then the subbundle
![]() ${\rm At}_D(\widetilde {E},\,\widetilde {\boldsymbol{l}},\,\nabla _L) \,\subset \, {\rm At}_D(\widetilde {E},\,\widetilde {\boldsymbol{l}})$
fits in the exact sequence
${\rm At}_D(\widetilde {E},\,\widetilde {\boldsymbol{l}},\,\nabla _L) \,\subset \, {\rm At}_D(\widetilde {E},\,\widetilde {\boldsymbol{l}})$
fits in the exact sequence
If we set
then, by Serre duality,
which in fact becomes zero because the underlying quasi-parabolic bundle
![]() $(\widetilde {E},\,\widetilde {\boldsymbol{l}})|_{X\times \{p\}}$
is simple. Let
$(\widetilde {E},\,\widetilde {\boldsymbol{l}})|_{X\times \{p\}}$
is simple. Let
be the projection. Then we have
![]() $R^1\pi _* \left (\widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},0} \otimes K_X(D) \right )\,=\,0$
, and get a short exact sequence
$R^1\pi _* \left (\widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},0} \otimes K_X(D) \right )\,=\,0$
, and get a short exact sequence
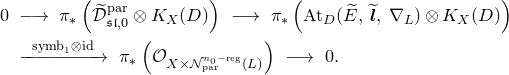 \begin{align*} 0 \,\, &\longrightarrow \,\, \pi _* \left ( \widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},0} \otimes K_X(D) \right ) \,\,\longrightarrow \,\, \pi _*\left ({\rm At}_D(\widetilde {E},\,\widetilde {\boldsymbol{l}},\,\nabla _L)\otimes K_X(D)\right ) \\ & \xrightarrow {\,\,\,{\rm symb}_1\otimes {\rm id}\,\,\,}\,\, \pi _* \left ( {\mathcal O}_{X\times \mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L)}\right ) \,\,\longrightarrow \,\,0. \end{align*}
\begin{align*} 0 \,\, &\longrightarrow \,\, \pi _* \left ( \widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},0} \otimes K_X(D) \right ) \,\,\longrightarrow \,\, \pi _*\left ({\rm At}_D(\widetilde {E},\,\widetilde {\boldsymbol{l}},\,\nabla _L)\otimes K_X(D)\right ) \\ & \xrightarrow {\,\,\,{\rm symb}_1\otimes {\rm id}\,\,\,}\,\, \pi _* \left ( {\mathcal O}_{X\times \mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L)}\right ) \,\,\longrightarrow \,\,0. \end{align*}
Note that
![]() $\pi _*\left ( {\mathcal O}_{X\times \mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L)}\right ) \,\cong \,{\mathcal O}_{\mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L)}$
. Consider the homomorphism
$\pi _*\left ( {\mathcal O}_{X\times \mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L)}\right ) \,\cong \,{\mathcal O}_{\mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L)}$
. Consider the homomorphism
on
![]() $\mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L)\times \textrm { Spec}\, k[t]$
defined by
$\mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L)\times \textrm { Spec}\, k[t]$
defined by
for
![]() $u\,\in \,\pi _*\left ({\rm At}_D(\widetilde {E},\,\widetilde {\boldsymbol{l}},\,\nabla _L)\otimes K_X(D)\right ) \otimes k[t]$
and
$u\,\in \,\pi _*\left ({\rm At}_D(\widetilde {E},\,\widetilde {\boldsymbol{l}},\,\nabla _L)\otimes K_X(D)\right ) \otimes k[t]$
and
![]() $f\,\in \, {\mathcal O}_{\mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L)}\otimes k[t]$
. Then
$f\,\in \, {\mathcal O}_{\mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L)}\otimes k[t]$
. Then
![]() $\ker \Psi _t$
is a locally free sheaf on
$\ker \Psi _t$
is a locally free sheaf on
![]() $\mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L)\times \textrm { Spec}\, k[t]$
, and we have
$\mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L)\times \textrm { Spec}\, k[t]$
, and we have
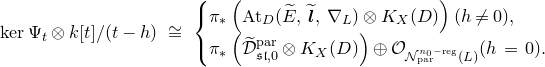 \begin{align*} \ker \Psi _t\otimes k[t]/(t-h)\,\,\cong \,\, \begin{cases} \pi _*\left ({\rm At}_D(\widetilde {E},\,\widetilde {\boldsymbol{l}},\,\nabla _L)\otimes K_X(D)\right ) (h\neq 0), \\ \pi _* \left (\widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},0} \otimes K_X(D) \right ) \oplus {\mathcal O}_{\mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L)} (h\,=\,0). \end{cases} \end{align*}
\begin{align*} \ker \Psi _t\otimes k[t]/(t-h)\,\,\cong \,\, \begin{cases} \pi _*\left ({\rm At}_D(\widetilde {E},\,\widetilde {\boldsymbol{l}},\,\nabla _L)\otimes K_X(D)\right ) (h\neq 0), \\ \pi _* \left (\widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},0} \otimes K_X(D) \right ) \oplus {\mathcal O}_{\mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L)} (h\,=\,0). \end{cases} \end{align*}
Define the projective bundle
over
![]() $\mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L)\times \textrm {Spec}\, k[t]$
. There is a tautological line-subbundle
$\mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L)\times \textrm {Spec}\, k[t]$
. There is a tautological line-subbundle
Consider the sections
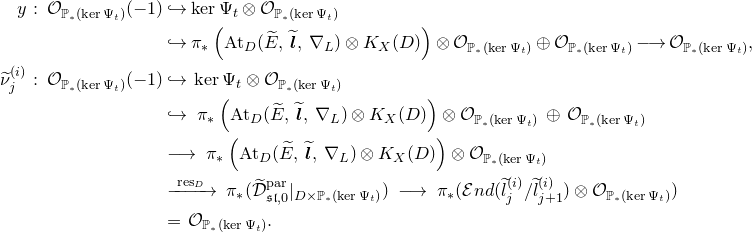 \begin{align*} y \,\colon \, {\mathcal O}_{\mathbb{P}_*(\ker \Psi _t)}(-1) &\hookrightarrow \ker \Psi _t\otimes {\mathcal O}_{\mathbb{P}_*(\ker \Psi _t)} \\& \hookrightarrow \pi _*\left ({\rm At}_D(\widetilde {E},\,\widetilde {\boldsymbol{l}},\,\nabla _L)\otimes K_X(D)\right ) \otimes {\mathcal O}_{\mathbb{P}_*(\ker \Psi _t)}\oplus{\mathcal O}_{\mathbb{P}_*(\ker \Psi _t)} \longrightarrow {\mathcal O}_{\mathbb{P}_*(\ker \Psi _t)}, \\ \widetilde {\nu }^{(i)}_j \,\colon \, {\mathcal O}_{\mathbb{P}_*(\ker \Psi _t)}(-1) &\hookrightarrow \, \ker \Psi _t\otimes {\mathcal O}_{\mathbb{P}_*(\ker \Psi _t)} \\ & \hookrightarrow \ \pi _*\left ({\rm At}_D(\widetilde {E},\,\widetilde {\boldsymbol{l}},\,\nabla _L)\otimes K_X(D)\right ) \otimes {\mathcal O}_{\mathbb{P}_*(\ker \Psi _t)} \, \oplus \, {\mathcal O}_{\mathbb{P}_*(\ker \Psi _t)} \\ & \longrightarrow \ \pi _*\left ({\rm At}_D(\widetilde {E},\,\widetilde {\boldsymbol{l}},\,\nabla _L)\otimes K_X(D)\right ) \otimes {\mathcal O}_{\mathbb{P}_*(\ker \Psi _t)} \\ &\xrightarrow {\,\,{\rm res}_D\,\,} \ \pi _*(\widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},0} |_{D\times {\mathbb{P}_*(\ker \Psi _t)}} ) \ \longrightarrow \ \pi _* ( {\mathcal End}(\widetilde {l}^{(i)}_j/\widetilde {l}^{(i)}_{j+1}) \otimes {\mathcal O}_{\mathbb{P}_*(\ker \Psi _t)} )\\ &=\,{\mathcal O}_{\mathbb{P}_*(\ker \Psi _t)}. \end{align*}
\begin{align*} y \,\colon \, {\mathcal O}_{\mathbb{P}_*(\ker \Psi _t)}(-1) &\hookrightarrow \ker \Psi _t\otimes {\mathcal O}_{\mathbb{P}_*(\ker \Psi _t)} \\& \hookrightarrow \pi _*\left ({\rm At}_D(\widetilde {E},\,\widetilde {\boldsymbol{l}},\,\nabla _L)\otimes K_X(D)\right ) \otimes {\mathcal O}_{\mathbb{P}_*(\ker \Psi _t)}\oplus{\mathcal O}_{\mathbb{P}_*(\ker \Psi _t)} \longrightarrow {\mathcal O}_{\mathbb{P}_*(\ker \Psi _t)}, \\ \widetilde {\nu }^{(i)}_j \,\colon \, {\mathcal O}_{\mathbb{P}_*(\ker \Psi _t)}(-1) &\hookrightarrow \, \ker \Psi _t\otimes {\mathcal O}_{\mathbb{P}_*(\ker \Psi _t)} \\ & \hookrightarrow \ \pi _*\left ({\rm At}_D(\widetilde {E},\,\widetilde {\boldsymbol{l}},\,\nabla _L)\otimes K_X(D)\right ) \otimes {\mathcal O}_{\mathbb{P}_*(\ker \Psi _t)} \, \oplus \, {\mathcal O}_{\mathbb{P}_*(\ker \Psi _t)} \\ & \longrightarrow \ \pi _*\left ({\rm At}_D(\widetilde {E},\,\widetilde {\boldsymbol{l}},\,\nabla _L)\otimes K_X(D)\right ) \otimes {\mathcal O}_{\mathbb{P}_*(\ker \Psi _t)} \\ &\xrightarrow {\,\,{\rm res}_D\,\,} \ \pi _*(\widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},0} |_{D\times {\mathbb{P}_*(\ker \Psi _t)}} ) \ \longrightarrow \ \pi _* ( {\mathcal End}(\widetilde {l}^{(i)}_j/\widetilde {l}^{(i)}_{j+1}) \otimes {\mathcal O}_{\mathbb{P}_*(\ker \Psi _t)} )\\ &=\,{\mathcal O}_{\mathbb{P}_*(\ker \Psi _t)}. \end{align*}
Let
![]() $I$
be the ideal sheaf of the graded algebra
$I$
be the ideal sheaf of the graded algebra
![]() ${\rm Sym} \left ( (\ker \Psi _t)^{\vee } \right )$
over
${\rm Sym} \left ( (\ker \Psi _t)^{\vee } \right )$
over
![]() $\mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L)$
, which is generated by
$\mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L)$
, which is generated by
![]() $\left \{ \widetilde {\nu }^{(i)}_j-\nu ^{(i)}_j ty \, \middle | \, 1\leqslant i\leqslant n , 0\leqslant j\leqslant r-1 \right \}$
. Set
$\left \{ \widetilde {\nu }^{(i)}_j-\nu ^{(i)}_j ty \, \middle | \, 1\leqslant i\leqslant n , 0\leqslant j\leqslant r-1 \right \}$
. Set
Then there is a canonical structure morphism
Let
![]() $Y\,\subset \,\overline {\mathcal M'}$
be the effective divisor defined by the equation
$Y\,\subset \,\overline {\mathcal M'}$
be the effective divisor defined by the equation
![]() $y\,=\,0$
. Setting
$y\,=\,0$
. Setting
![]() ${\mathcal M'}\,\,:=\,\,\overline {\mathcal M'}\setminus Y$
, we see by the construction that
${\mathcal M'}\,\,:=\,\,\overline {\mathcal M'}\setminus Y$
, we see by the construction that
![]() ${\mathcal M'}_h\,\cong \, \mathcal{M}_{{\rm PC}}^{n_0\textrm { -reg}}(\boldsymbol{\nu },\nabla _L)^{\circ }$
for
${\mathcal M'}_h\,\cong \, \mathcal{M}_{{\rm PC}}^{n_0\textrm { -reg}}(\boldsymbol{\nu },\nabla _L)^{\circ }$
for
![]() $h\,\neq \, 0$
and
$h\,\neq \, 0$
and
![]() ${\mathcal M'}_0\,\cong \, \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{0},\,0)^{\circ }$
.
${\mathcal M'}_0\,\cong \, \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{0},\,0)^{\circ }$
.
Theorem 5.22. Let
![]() $X$
be a smooth projective curve of genus
$X$
be a smooth projective curve of genus
![]() $g$
over an algebraically closed field
$g$
over an algebraically closed field
![]() $k$
of arbitrary characteristic, and let
$k$
of arbitrary characteristic, and let
![]() $D\,=\,\sum _{i=1}^n x_i$
be a reduced effective divisor on
$D\,=\,\sum _{i=1}^n x_i$
be a reduced effective divisor on
![]() $X$
. Fix a line bundle
$X$
. Fix a line bundle
![]() $L$
over
$L$
over
![]() $X$
with a connection
$X$
with a connection
![]() $\nabla _L \,\colon \, L\,\longrightarrow \, L\otimes K_X(D)$
. Take positive integers
$\nabla _L \,\colon \, L\,\longrightarrow \, L\otimes K_X(D)$
. Take positive integers
![]() $r$
and
$r$
and
![]() $d$
such that
$d$
such that
![]() $r\,\geqslant \, 2$
,
$r\,\geqslant \, 2$
,
![]() $n\,\geqslant \, 1$
and
$n\,\geqslant \, 1$
and
![]() $r$
is not divisible by the characteristic of
$r$
is not divisible by the characteristic of
![]() $k$
. Assume that one of the following statements holds:
$k$
. Assume that one of the following statements holds:
-
(a)
 $n\,\geqslant \, 1$
and
$n\,\geqslant \, 1$
and
 $r\,\geqslant \, 2$
are arbitrary if
$r\,\geqslant \, 2$
are arbitrary if
 $g\,\geqslant \,2$
;
$g\,\geqslant \,2$
; -
(b)
 $n\,\geqslant \, 2$
and
$n\,\geqslant \, 2$
and
 $n+r\,\geqslant \, 5$
if
$n+r\,\geqslant \, 5$
if
 $g\,=\,1$
;
$g\,=\,1$
; -
(c)
 $n\,\geqslant \, 3$
and
$n\,\geqslant \, 3$
and
 $n+r\,\geqslant \, 7$
if
$n+r\,\geqslant \, 7$
if
 $g\,=\,0$
.
$g\,=\,0$
.
Also, assume that the exponent
![]() $\boldsymbol{\nu }\,=\,(\nu ^{(i)}_j)^{1\leqslant i\leqslant n}_{0\leqslant j\leqslant r-1}$
satisfies the condition
$\boldsymbol{\nu }\,=\,(\nu ^{(i)}_j)^{1\leqslant i\leqslant n}_{0\leqslant j\leqslant r-1}$
satisfies the condition
![]() ${\sf res}_{x_i}(\nabla _L)\,=\,\sum _{j=0}^{r-1}\nu ^{(i)}_j$
for any
${\sf res}_{x_i}(\nabla _L)\,=\,\sum _{j=0}^{r-1}\nu ^{(i)}_j$
for any
![]() $i$
, and, furthermore,
$i$
, and, furthermore,
![]() $ \sum _{i=1}^n\sum _{\ell=1}^s \nu ^{(i)}_{j^{(i)}_\ell }$
is not contained in the image of
$ \sum _{i=1}^n\sum _{\ell=1}^s \nu ^{(i)}_{j^{(i)}_\ell }$
is not contained in the image of
![]() $\mathbb{Z}$
in
$\mathbb{Z}$
in
![]() $k$
for any integer
$k$
for any integer
![]() $1\,\leqslant \, s\,\lt \, r$
and any choice of
$1\,\leqslant \, s\,\lt \, r$
and any choice of
![]() $s$
elements
$s$
elements
![]() $\{j^{(i)}_1,\,\cdots ,\,j^{(i)}_s\}$
in
$\{j^{(i)}_1,\,\cdots ,\,j^{(i)}_s\}$
in
![]() $\{1,\,\ldots ,\,r\}$
for each
$\{1,\,\ldots ,\,r\}$
for each
![]() $1\,\leqslant \, i\,\leqslant \, n$
. Then, the transcendence degree of the global algebraic functions on the moduli space
$1\,\leqslant \, i\,\leqslant \, n$
. Then, the transcendence degree of the global algebraic functions on the moduli space
![]() $\mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu })$
of
$\mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu })$
of
![]() $\boldsymbol{\alpha }$
-stable
$\boldsymbol{\alpha }$
-stable
![]() $\boldsymbol{\nu }$
-parabolic connections satisfies the inequality
$\boldsymbol{\nu }$
-parabolic connections satisfies the inequality
Proof. Note that
by Proposition 5.15. Since we can extend the Hitchin map in (5.20) to a morphism
![]() $ \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{0},\,0) \,\longrightarrow \, W$
, we have the inclusion maps
$ \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{0},\,0) \,\longrightarrow \, W$
, we have the inclusion maps
where we take
![]() $\boldsymbol{\alpha '}$
generic so that
$\boldsymbol{\alpha '}$
generic so that
![]() $\boldsymbol{\alpha '}$
-semistability implies
$\boldsymbol{\alpha '}$
-semistability implies
![]() $\boldsymbol{\alpha '}$
-stability. Then, using Corollary 5.20, it follows that
$\boldsymbol{\alpha '}$
-stability. Then, using Corollary 5.20, it follows that
![]() $ \Gamma \left ( \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{0},\,0)^{\circ },\, {\mathcal O}_{ \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{0},\,0)^{\circ }}\right ) \,=\, \Gamma \left ( \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{0},\,0) ,\, {\mathcal O}_{ \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{0},\,0) } \right )$
is a finitely generated
$ \Gamma \left ( \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{0},\,0)^{\circ },\, {\mathcal O}_{ \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{0},\,0)^{\circ }}\right ) \,=\, \Gamma \left ( \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{0},\,0) ,\, {\mathcal O}_{ \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{0},\,0) } \right )$
is a finitely generated
![]() $k$
-algebra whose Krull dimension is
$k$
-algebra whose Krull dimension is
![]() $r^2(g-1)-g+1+nr(r-1)/2$
.
$r^2(g-1)-g+1+nr(r-1)/2$
.
We use the notation in the proof of Proposition 5.21. Note that
![]() $\mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{0},\,0)^{\circ }$
is isomorphic to the cotangent bundle over
$\mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{0},\,0)^{\circ }$
is isomorphic to the cotangent bundle over
![]() $\mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L)$
. So we have
$\mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L)$
. So we have
![]() $ \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{0},\,0)^{\circ } \,\cong \, {\rm Spec} \Big ( {\rm Sym}^* \Big ( \pi _* \big ( \widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},1}\big )^{\vee }\Big ) \Big )$
, which implies that
$ \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{0},\,0)^{\circ } \,\cong \, {\rm Spec} \Big ( {\rm Sym}^* \Big ( \pi _* \big ( \widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},1}\big )^{\vee }\Big ) \Big )$
, which implies that
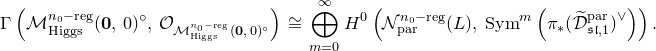 \begin{align*} \Gamma \left ( \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{0},\,0)^{\circ } ,\, {\mathcal O}_{ \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{0},\,0)^{\circ } } \right ) \,\cong \, \bigoplus _{m=0}^{\infty } H^0\left ( \mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L) ,\, {\rm Sym}^m \left ( \pi _* \big ( \widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},1} \big ) ^{\vee } \right ) \right ). \end{align*}
\begin{align*} \Gamma \left ( \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{0},\,0)^{\circ } ,\, {\mathcal O}_{ \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{0},\,0)^{\circ } } \right ) \,\cong \, \bigoplus _{m=0}^{\infty } H^0\left ( \mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L) ,\, {\rm Sym}^m \left ( \pi _* \big ( \widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},1} \big ) ^{\vee } \right ) \right ). \end{align*}
Note that there is a short exact sequence
We can see that the above homomorphism
![]() $q$
determines the equalities
$q$
determines the equalities
![]() $\big ( \widetilde {\nu }^{(i)}_j-\nu ^{(i)}_jty \big )|_{t=0}$
on the fiber
$\big ( \widetilde {\nu }^{(i)}_j-\nu ^{(i)}_jty \big )|_{t=0}$
on the fiber
![]() $\mathbb{P}(\ker \Psi _t^{\vee }\otimes \mathbb{C}[t]/(t))$
over
$\mathbb{P}(\ker \Psi _t^{\vee }\otimes \mathbb{C}[t]/(t))$
over
![]() $t\,=\,0$
. Taking the dual of the above exact sequence,
$t\,=\,0$
. Taking the dual of the above exact sequence,
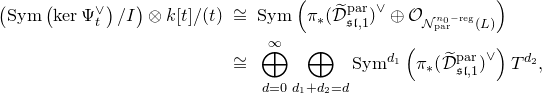 \begin{align*} \left ({\rm Sym}\left ( \ker \Psi _t ^{\vee }\right )/I\right ) \otimes k[t]/(t) \,\, &\cong \,\, {\rm Sym}\left (\pi _*\big ( \widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},1} \big )^{\vee } \oplus {\mathcal O}_{\mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L)} \right )\\& \cong \,\,\, \bigoplus _{d=0}^{\infty } \bigoplus _{d_1+d_2=d} {\rm Sym}^{d_1} \left (\pi _*\big ( \widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},1} \big )^{\vee }\right ) T^{d_2}, \end{align*}
\begin{align*} \left ({\rm Sym}\left ( \ker \Psi _t ^{\vee }\right )/I\right ) \otimes k[t]/(t) \,\, &\cong \,\, {\rm Sym}\left (\pi _*\big ( \widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},1} \big )^{\vee } \oplus {\mathcal O}_{\mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L)} \right )\\& \cong \,\,\, \bigoplus _{d=0}^{\infty } \bigoplus _{d_1+d_2=d} {\rm Sym}^{d_1} \left (\pi _*\big ( \widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},1} \big )^{\vee }\right ) T^{d_2}, \end{align*}
where
![]() $T$
is a variable corresponding to the second component of
$T$
is a variable corresponding to the second component of
![]() $\ker \Psi _t\otimes k[t]/(t) \,=\,\pi _*\big ( \widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},1} \big )^{\vee } \oplus {\mathcal O}_{{\mathcal N}^{n_0{\rm -reg}}_{{\rm par}}(L)}$
. So the ring of global sections of this sheaves of algebras over
$\ker \Psi _t\otimes k[t]/(t) \,=\,\pi _*\big ( \widetilde {\mathcal D}^{{\rm par}}_{\mathfrak{sl},1} \big )^{\vee } \oplus {\mathcal O}_{{\mathcal N}^{n_0{\rm -reg}}_{{\rm par}}(L)}$
. So the ring of global sections of this sheaves of algebras over
![]() $\mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L)$
becomes a polynomial ring
$\mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L)$
becomes a polynomial ring
over
![]() $\Gamma \left ( \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{0},\,0)^{\circ } ,\, {\mathcal O}_{ \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{0},\,0)^{\circ } } \right )$
. In particular,
$\Gamma \left ( \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{0},\,0)^{\circ } ,\, {\mathcal O}_{ \mathcal{M}^{n_0{\rm -reg}}_{{\rm Higgs}}(\boldsymbol{0},\,0)^{\circ } } \right )$
. In particular,
![]() $ \dim (({\rm Sym}^m (\ker \Phi _t^{\vee })/I_m)\otimes k[t]/(t))$
becomes a polynomial in
$ \dim (({\rm Sym}^m (\ker \Phi _t^{\vee })/I_m)\otimes k[t]/(t))$
becomes a polynomial in
![]() $m$
of degree
$m$
of degree
Let
![]() $\left ({\rm Sym}\left ( \ker \Psi _t^{\vee } \right )/I \right )_{(y)}$
be the subalgebra of the localized graded algebra
$\left ({\rm Sym}\left ( \ker \Psi _t^{\vee } \right )/I \right )_{(y)}$
be the subalgebra of the localized graded algebra
![]() $\left ({\rm Sym}\left ( \ker \Psi _t^{\vee } \right )/I \right )_y$
consisting of homogeneous elements of degree zero. Then we have
$\left ({\rm Sym}\left ( \ker \Psi _t^{\vee } \right )/I \right )_y$
consisting of homogeneous elements of degree zero. Then we have
for
![]() $h\,\neq \, 0$
. By the assumption in (5.19) on the choice of the exponent
$h\,\neq \, 0$
. By the assumption in (5.19) on the choice of the exponent
![]() $\boldsymbol{\nu }$
, and by Proposition 5.14, we have
$\boldsymbol{\nu }$
, and by Proposition 5.14, we have
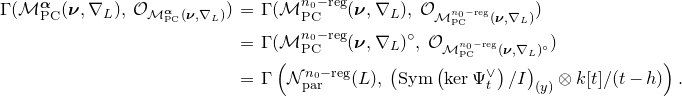 \begin{align*} \Gamma ( \mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu },\nabla _L),\, {\mathcal O}_{\mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu },\nabla _L)} ) \,&=\, \Gamma ( \mathcal{M}_{{\rm PC}}^{n_0{\rm -reg}}(\boldsymbol{\nu },\nabla _L),\, {\mathcal O}_{\mathcal{M}_{{\rm PC}}^{n_0{\rm -reg}}(\boldsymbol{\nu },\nabla _L)} ) \\ &=\, \Gamma ( \mathcal{M}_{{\rm PC}}^{n_0{\rm -reg}}(\boldsymbol{\nu },\nabla _L)^{\circ } ,\, {\mathcal O}_{\mathcal{M}_{{\rm PC}}^{n_0{\rm -reg}}(\boldsymbol{\nu },\nabla _L)^{\circ } }) \\ &=\, \Gamma \left (\mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L) , \, \left ({\rm Sym}\left ( \ker \Psi _t^{\vee } \right )/I \right )_{(y)} \otimes k[t]/(t-h) \right ). \end{align*}
\begin{align*} \Gamma ( \mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu },\nabla _L),\, {\mathcal O}_{\mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu },\nabla _L)} ) \,&=\, \Gamma ( \mathcal{M}_{{\rm PC}}^{n_0{\rm -reg}}(\boldsymbol{\nu },\nabla _L),\, {\mathcal O}_{\mathcal{M}_{{\rm PC}}^{n_0{\rm -reg}}(\boldsymbol{\nu },\nabla _L)} ) \\ &=\, \Gamma ( \mathcal{M}_{{\rm PC}}^{n_0{\rm -reg}}(\boldsymbol{\nu },\nabla _L)^{\circ } ,\, {\mathcal O}_{\mathcal{M}_{{\rm PC}}^{n_0{\rm -reg}}(\boldsymbol{\nu },\nabla _L)^{\circ } }) \\ &=\, \Gamma \left (\mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L) , \, \left ({\rm Sym}\left ( \ker \Psi _t^{\vee } \right )/I \right )_{(y)} \otimes k[t]/(t-h) \right ). \end{align*}
By Lemma A.1, which is proved later in § 6, the function
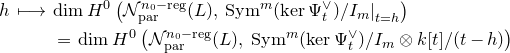 \begin{align*} &h\; \longmapsto \; \dim H^0\left (\mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L) , \, {\rm Sym}^m(\ker \Psi _t^{\vee })/I_m\big |_{t=h}\right ) \\ &\quad\qquad=\, \dim H^0\left (\mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L) , \, {\rm Sym}^m(\ker \Psi _t^{\vee })/I_m\otimes k[t]/(t-h)\right ) \end{align*}
\begin{align*} &h\; \longmapsto \; \dim H^0\left (\mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L) , \, {\rm Sym}^m(\ker \Psi _t^{\vee })/I_m\big |_{t=h}\right ) \\ &\quad\qquad=\, \dim H^0\left (\mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L) , \, {\rm Sym}^m(\ker \Psi _t^{\vee })/I_m\otimes k[t]/(t-h)\right ) \end{align*}
is upper semi-continuous in
![]() $h$
. So we have
$h$
. So we have
for
![]() $h\,\neq \, 0$
.
$h\,\neq \, 0$
.
Let
![]() $d$
be the transcendence degree of
$d$
be the transcendence degree of
![]() $\Gamma ( \mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu },\nabla _L),\, {\mathcal O}_{\mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu },\nabla _L)} )$
over
$\Gamma ( \mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu },\nabla _L),\, {\mathcal O}_{\mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu },\nabla _L)} )$
over
![]() $k$
. Then we have
$k$
. Then we have
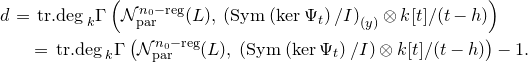 \begin{align*} d \,&=\, {\rm tr.deg}_{\,k}\Gamma \left ( \mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L), \, \left ({\rm Sym}\left ( \ker \Psi _t \right )/I\right )_{(y)} \otimes k[t]/(t-h) \right ) \\ &\quad=\, {\rm tr.deg}_{\,k} \Gamma \left ( \mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L),\, \left ({\rm Sym}\left ( \ker \Psi _t \right )/I\right ) \otimes k[t]/(t-h) \right ) -1. \end{align*}
\begin{align*} d \,&=\, {\rm tr.deg}_{\,k}\Gamma \left ( \mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L), \, \left ({\rm Sym}\left ( \ker \Psi _t \right )/I\right )_{(y)} \otimes k[t]/(t-h) \right ) \\ &\quad=\, {\rm tr.deg}_{\,k} \Gamma \left ( \mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L),\, \left ({\rm Sym}\left ( \ker \Psi _t \right )/I\right ) \otimes k[t]/(t-h) \right ) -1. \end{align*}
Take homogeneous elements
![]() $x_1,\,\cdots ,\,x_d$
of
$x_1,\,\cdots ,\,x_d$
of
such that
![]() $\{x_1,\,\cdots ,\,x_d,\,y\}$
is a transcendence basis of
$\{x_1,\,\cdots ,\,x_d,\,y\}$
is a transcendence basis of
![]() $\Gamma \left ( \mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L), \, \left ({\rm Sym}\left ( \ker \Psi _t \right )/I\right ) \big |_{t=h} \right )$
over
$\Gamma \left ( \mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L), \, \left ({\rm Sym}\left ( \ker \Psi _t \right )/I\right ) \big |_{t=h} \right )$
over
![]() $k$
. Let
$k$
. Let
![]() $S$
be the graded subalgebra of
$S$
be the graded subalgebra of
generated by
![]() $x_1,\,\cdots ,x_d,\,y$
. Then
$x_1,\,\cdots ,x_d,\,y$
. Then
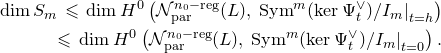 \begin{align*} \dim S_m \,\leqslant \, \dim H^0\left (\mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L), \, {\rm Sym}^m(\ker \Psi _t^{\vee })/I_m\big |_{t=h} \right ) \\ \leqslant \, \dim H^0\left (\mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L), \, {\rm Sym}^m(\ker \Psi _t^{\vee })/I_m\big |_{t=0} \right ). \end{align*}
\begin{align*} \dim S_m \,\leqslant \, \dim H^0\left (\mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L), \, {\rm Sym}^m(\ker \Psi _t^{\vee })/I_m\big |_{t=h} \right ) \\ \leqslant \, \dim H^0\left (\mathcal{N}^{n_0{\rm -reg}}_{{\rm par}}(L), \, {\rm Sym}^m(\ker \Psi _t^{\vee })/I_m\big |_{t=0} \right ). \end{align*}
Since
![]() $S_m$
is a polynomial in
$S_m$
is a polynomial in
![]() $m$
of degree
$m$
of degree
![]() $d$
for
$d$
for
![]() $m\,\gg \, 0$
, it follows that
$m\,\gg \, 0$
, it follows that
![]() $d\,\leqslant \, r^2(g-1)-g+1+nr(r-1)/2$
.
$d\,\leqslant \, r^2(g-1)-g+1+nr(r-1)/2$
.
Remark 5.23. A statement similar to Theorem 5.22 can be considered for connections without pole. When
![]() $X$
is a curve over the field of complex numbers whose genus is greater than
$X$
is a curve over the field of complex numbers whose genus is greater than
![]() $2$
, then there are only constant global algebraic functions on the de Rham moduli space of connections without pole by [Reference Biswas and RaghavendraBiRa, Corollary 4.4]. So the inequality similar to Theorem 5.22 becomes strict in that case. On the other hand, if
$2$
, then there are only constant global algebraic functions on the de Rham moduli space of connections without pole by [Reference Biswas and RaghavendraBiRa, Corollary 4.4]. So the inequality similar to Theorem 5.22 becomes strict in that case. On the other hand, if
![]() $X$
is defined over the base field of positive characteristic, it is proved in [Reference GroechenigGroe, Theorem 1.1] that the Hitchin map for the de Rham moduli space connections without pole is étale locally equivalent to that on the Dolbeault moduli space. So, the ring of global algebraic functions on the de Rham moduli space has the same transcendence degree as that of the ring of global algebraic functions on the Dolbeault moduli space in that case. The Hitchin map for the logarithmic de Rham moduli space over the base field of positive characteristic is introduced in [Reference de Cataldo, Herrero and ZhangdCHZ].
$X$
is defined over the base field of positive characteristic, it is proved in [Reference GroechenigGroe, Theorem 1.1] that the Hitchin map for the de Rham moduli space connections without pole is étale locally equivalent to that on the Dolbeault moduli space. So, the ring of global algebraic functions on the de Rham moduli space has the same transcendence degree as that of the ring of global algebraic functions on the Dolbeault moduli space in that case. The Hitchin map for the logarithmic de Rham moduli space over the base field of positive characteristic is introduced in [Reference de Cataldo, Herrero and ZhangdCHZ].
The following is an immediate consequence of Theorem5.22.
Corollary 5.24. The moduli space
![]() $\mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu },\nabla _L)$
of
$\mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu },\nabla _L)$
of
![]() $\boldsymbol{\alpha }$
-stable
$\boldsymbol{\alpha }$
-stable
![]() $\boldsymbol{\nu }$
-parabolic connections is not affine.
$\boldsymbol{\nu }$
-parabolic connections is not affine.
From now on, consider the case of
![]() $k\,=\,\mathbb{C}$
.
$k\,=\,\mathbb{C}$
.
Since the fundamental group
![]() $\pi _1(X\setminus D,\,*)$
is finitely presented, the space of representations
$\pi _1(X\setminus D,\,*)$
is finitely presented, the space of representations
can be realized as an affine variety. Take generators
![]() $\alpha _1,\,\beta _1,\,\cdots ,\,\alpha _g,\,\beta _g$
of the fundamental group
$\alpha _1,\,\beta _1,\,\cdots ,\,\alpha _g,\,\beta _g$
of the fundamental group
![]() $\pi _1(C,\, *)$
, and choose a loop
$\pi _1(C,\, *)$
, and choose a loop
![]() $\gamma _i$
around each
$\gamma _i$
around each
![]() $x_i$
with respect to the base point
$x_i$
with respect to the base point
![]() $*$
. Then the fundamental group
$*$
. Then the fundamental group
![]() $\pi _1(X\setminus D,\,*)$
is generated by
$\pi _1(X\setminus D,\,*)$
is generated by
![]() $\alpha _1,\,\beta _1,\,\cdots ,\,\alpha _g,\,\beta _g,\,\gamma _1,\,\cdots ,\,\gamma _n$
with the single relation
$\alpha _1,\,\beta _1,\,\cdots ,\,\alpha _g,\,\beta _g,\,\gamma _1,\,\cdots ,\,\gamma _n$
with the single relation
![]() $[\alpha _1,\,\beta _1]\cdots [\alpha _g,\,\beta _g]\gamma _1\cdots \gamma _n\,=\,1$
. The space of representations of
$[\alpha _1,\,\beta _1]\cdots [\alpha _g,\,\beta _g]\gamma _1\cdots \gamma _n\,=\,1$
. The space of representations of
![]() $\pi _1(X\setminus D,\,*)$
can be realized as the affine variety
$\pi _1(X\setminus D,\,*)$
can be realized as the affine variety
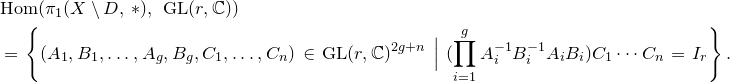 \begin{align*} &\textrm {Hom}(\pi _1(X\setminus D,\,*),\,\, {\rm GL}(r,\mathbb{C})) \\ & =\, \left \{ (A_1,B_1,\ldots ,A_g,B_g,C_1,\ldots ,C_n)\, \in \, {\rm GL}(r,\mathbb{C})^{2g+n} \,\, \Big |\,\, (\prod _{i=1}^g A_i^{-1}B_i^{-1}A_iB_i)C_1\cdots C_n\,=\,I_r \right \}. \end{align*}
\begin{align*} &\textrm {Hom}(\pi _1(X\setminus D,\,*),\,\, {\rm GL}(r,\mathbb{C})) \\ & =\, \left \{ (A_1,B_1,\ldots ,A_g,B_g,C_1,\ldots ,C_n)\, \in \, {\rm GL}(r,\mathbb{C})^{2g+n} \,\, \Big |\,\, (\prod _{i=1}^g A_i^{-1}B_i^{-1}A_iB_i)C_1\cdots C_n\,=\,I_r \right \}. \end{align*}
Note that the connection
![]() $\nabla _L$
on the line bundle
$\nabla _L$
on the line bundle
![]() $L$
induces a one-dimensional representation
$L$
induces a one-dimensional representation
![]() $\rho _{\nabla _L}$
of
$\rho _{\nabla _L}$
of
![]() $\pi _1(X\setminus D,\,*)$
. Define a tuple
$\pi _1(X\setminus D,\,*)$
. Define a tuple
![]() $(b^{(i)}_j)$
by
$(b^{(i)}_j)$
by
![]() $b^{(i)}_j\,\,:=\,\,e^{-2\pi \sqrt {-1}\nu ^{(i)}_j}$
, and consider the closed subvariety
$b^{(i)}_j\,\,:=\,\,e^{-2\pi \sqrt {-1}\nu ^{(i)}_j}$
, and consider the closed subvariety
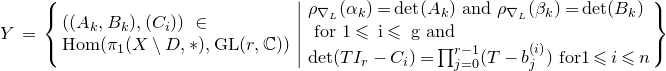 \begin{align*} Y\,=\, \left \{ \begin{array}{l} ((A_k,B_k),(C_i))\, \,\in \\ \textrm {Hom}(\pi _1(X\setminus D,*),{\rm GL}(r,\mathbb{C})) \end{array} \, \middle |\, \begin{array}{l} \rho _{\nabla _L}(\alpha _k)=\det (A_k)\ {\rm and}\ \rho _{\nabla _L}(\beta _k)=\det (B_k) \\ \rm \ for\ 1\leqslant\ i\leqslant\ g\ and \\ \det (TI_r-C_i)=\prod _{j=0}^{r-1} (T-b^{(i)}_j) \ {\rm for} 1\leqslant i \leqslant n \end{array}\right \} \end{align*}
\begin{align*} Y\,=\, \left \{ \begin{array}{l} ((A_k,B_k),(C_i))\, \,\in \\ \textrm {Hom}(\pi _1(X\setminus D,*),{\rm GL}(r,\mathbb{C})) \end{array} \, \middle |\, \begin{array}{l} \rho _{\nabla _L}(\alpha _k)=\det (A_k)\ {\rm and}\ \rho _{\nabla _L}(\beta _k)=\det (B_k) \\ \rm \ for\ 1\leqslant\ i\leqslant\ g\ and \\ \det (TI_r-C_i)=\prod _{j=0}^{r-1} (T-b^{(i)}_j) \ {\rm for} 1\leqslant i \leqslant n \end{array}\right \} \end{align*}
of
![]() $\textrm { Hom}(\pi _1(X\setminus D,\,*),\,{\rm GL}(r,\mathbb{C}))$
. There is a canonical action of
$\textrm { Hom}(\pi _1(X\setminus D,\,*),\,{\rm GL}(r,\mathbb{C}))$
. There is a canonical action of
![]() ${\rm GL}(r,\mathbb{C})$
on
${\rm GL}(r,\mathbb{C})$
on
![]() $Y$
given by the adjoint action of
$Y$
given by the adjoint action of
![]() ${\rm GL}(r,\mathbb{C})$
on itself, and we can take the corresponding categorical quotient
${\rm GL}(r,\mathbb{C})$
on itself, and we can take the corresponding categorical quotient
Under the genericity assumption in (5.19) of the eigenvalues of the residues, this quotient is in fact a geometric quotient, and we have a Riemann–Hilbert morphism
By [Reference InabaIna], the above Riemann–Hilbert morphism
![]() ${\rm RH}$
is a proper and surjective holomorphic map, which is generically an isomorphism. So
${\rm RH}$
is a proper and surjective holomorphic map, which is generically an isomorphism. So
![]() $\mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu },\nabla _L)$
gives an analytic resolution of singularities of
$\mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu },\nabla _L)$
gives an analytic resolution of singularities of
![]() ${\rm Ch}_{X\setminus D,(b^{(i)}_j)}$
. Since the character variety
${\rm Ch}_{X\setminus D,(b^{(i)}_j)}$
. Since the character variety
![]() ${\rm Ch}_{X\setminus D , (b^{(i)}_j)}$
is affine by its definition, it is evident that
${\rm Ch}_{X\setminus D , (b^{(i)}_j)}$
is affine by its definition, it is evident that
By Theorem5.22 and (5.25) (or by Corollary 5.24), we have the following.
Corollary 5.25. The Riemann–Hilbert morphism
![]() ${\rm RH}\,\colon \, \mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu },\nabla _L) \,\longrightarrow \, {\rm Ch}_{X\setminus D,(b^{(i)}_j)}$
is not an algebraic morphism.
${\rm RH}\,\colon \, \mathcal{M}_{{\rm PC}}^{\boldsymbol{\alpha }}(\boldsymbol{\nu },\nabla _L) \,\longrightarrow \, {\rm Ch}_{X\setminus D,(b^{(i)}_j)}$
is not an algebraic morphism.
Appendix
Let
![]() $k$
be an algebraically closed field of arbitrary characteristic. We will prove a lemma on the upper semi-continuity of the dimension of global sections of vector bundles on an algebraic space containing a projective variety over
$k$
be an algebraically closed field of arbitrary characteristic. We will prove a lemma on the upper semi-continuity of the dimension of global sections of vector bundles on an algebraic space containing a projective variety over
![]() $k$
.
$k$
.
Recall that an algebraic space
![]() $\mathcal X$
of finite type over
$\mathcal X$
of finite type over
![]() $\textrm { Spec}\, k$
is said to be locally separated over
$\textrm { Spec}\, k$
is said to be locally separated over
![]() $\textrm { Spec}\, k$
if there is a scheme
$\textrm { Spec}\, k$
if there is a scheme
![]() $U$
of finite type over
$U$
of finite type over
![]() $\textrm { Spec}\, k$
together with an étale surjective morphism
$\textrm { Spec}\, k$
together with an étale surjective morphism
![]() $U\,\longrightarrow \,{\mathcal X}$
such that
$U\,\longrightarrow \,{\mathcal X}$
such that
![]() $U\times _{\mathcal X}U$
is a locally closed subscheme of
$U\times _{\mathcal X}U$
is a locally closed subscheme of
![]() $U\times _{\textrm { Spec}\,\mathbb{C}}U$
. A locally separated algebraic space
$U\times _{\textrm { Spec}\,\mathbb{C}}U$
. A locally separated algebraic space
![]() $\mathcal X$
of finite type over
$\mathcal X$
of finite type over
![]() $\textrm { Spec}\, k$
is irreducible if the underlying topological space
$\textrm { Spec}\, k$
is irreducible if the underlying topological space
![]() $|{\mathcal X}|$
is irreducible. In other words, any two non-empty open subspaces
$|{\mathcal X}|$
is irreducible. In other words, any two non-empty open subspaces
![]() $U_1,\,U_2\,\subset \,{\mathcal X}$
intersect:
$U_1,\,U_2\,\subset \,{\mathcal X}$
intersect:
![]() $U_1\cap U_2\,\neq \,\emptyset$
.
$U_1\cap U_2\,\neq \,\emptyset$
.
Lemma A.1. Let
![]() $\mathcal X$
be a locally separated, smooth, irreducible algebraic space of finite type over
$\mathcal X$
be a locally separated, smooth, irreducible algebraic space of finite type over
![]() $\textrm { Spec}\, k$
. Assume that
$\textrm { Spec}\, k$
. Assume that
![]() $\overline {X}$
is an open subspace of
$\overline {X}$
is an open subspace of
![]() $\mathcal X$
such that
$\mathcal X$
such that
![]() $\overline {X}$
is isomorphic to a smooth projective variety over
$\overline {X}$
is isomorphic to a smooth projective variety over
![]() $k$
. Let
$k$
. Let
![]() $T$
be an affine variety, and let
$T$
be an affine variety, and let
![]() $\mathcal F$
be a locally free sheaf of finite rank on
$\mathcal F$
be a locally free sheaf of finite rank on
![]() ${\mathcal X}\times T$
. For each point
${\mathcal X}\times T$
. For each point
![]() $t\in T$
, denote by
$t\in T$
, denote by
![]() $\Gamma ({\mathcal X}\times \{t\} ,\, {\mathcal F}|_{{\mathcal X}\times \{t\}})$
the space of global sections of the restriction
$\Gamma ({\mathcal X}\times \{t\} ,\, {\mathcal F}|_{{\mathcal X}\times \{t\}})$
the space of global sections of the restriction
![]() ${\mathcal F}|_{{\mathcal X}\times \{t\}}$
. Then the function
${\mathcal F}|_{{\mathcal X}\times \{t\}}$
. Then the function
is upper semi-continuous.
Proof. Since the upper semi-continuity is a local property on
![]() $T$
, we may replace
$T$
, we may replace
![]() $T$
with a neighborhood at any point of
$T$
with a neighborhood at any point of
![]() $T$
. Take a finite number of smooth affine varieties
$T$
. Take a finite number of smooth affine varieties
![]() $\{U_i\}_{i=1}^n$
and an étale surjective morphism
$\{U_i\}_{i=1}^n$
and an étale surjective morphism
 \begin{align*} f\,\,\colon \,\, \overline {X} \sqcup \coprod _{i=1}^n U_i \ \longrightarrow \ {\mathcal X}, \end{align*}
\begin{align*} f\,\,\colon \,\, \overline {X} \sqcup \coprod _{i=1}^n U_i \ \longrightarrow \ {\mathcal X}, \end{align*}
whose restriction to
![]() $\overline {X}$
coincides with the given inclusion map
$\overline {X}$
coincides with the given inclusion map
![]() $f|_{\overline {X}}\,\,\colon \, \overline {X}\,\hookrightarrow \, {\mathcal X}$
. After shrinking
$f|_{\overline {X}}\,\,\colon \, \overline {X}\,\hookrightarrow \, {\mathcal X}$
. After shrinking
![]() $U_i$
and
$U_i$
and
![]() $T$
, we may assume that
$T$
, we may assume that
![]() ${\mathcal F}|_{U_i\times T}\,\cong \,{\mathcal O}_{U_i\times T}^{\oplus r}$
for every
${\mathcal F}|_{U_i\times T}\,\cong \,{\mathcal O}_{U_i\times T}^{\oplus r}$
for every
![]() $i$
. Since
$i$
. Since
![]() $\mathcal X$
is irreducible, we have
$\mathcal X$
is irreducible, we have
![]() $\overline {X}\cap (\bigcap _{i=1}^n f(U_i))\,\neq \,\emptyset$
. So there is a non-empty affine open subset
$\overline {X}\cap (\bigcap _{i=1}^n f(U_i))\,\neq \,\emptyset$
. So there is a non-empty affine open subset
![]() $V\,\subset \, \overline {X}\cap \bigcap _{i=1}^n f(U_i)$
. Take a non-empty smooth affine variety
$V\,\subset \, \overline {X}\cap \bigcap _{i=1}^n f(U_i)$
. Take a non-empty smooth affine variety
![]() $\widetilde {V}$
with étale morphisms
$\widetilde {V}$
with étale morphisms
![]() $\widetilde {V}\,\longrightarrow \, V$
and
$\widetilde {V}\,\longrightarrow \, V$
and
![]() $\widetilde {f}_i\,\colon \, \widetilde {V}\,\longrightarrow \, U_i$
for
$\widetilde {f}_i\,\colon \, \widetilde {V}\,\longrightarrow \, U_i$
for
![]() $1\,\leqslant \, i\,\leqslant \, n$
such that the diagram
$1\,\leqslant \, i\,\leqslant \, n$
such that the diagram
is commutative for every
![]() $1\,\leqslant \, i\,\leqslant \, n$
.
$1\,\leqslant \, i\,\leqslant \, n$
.
Let
![]() $\widetilde {X}$
be the normalization of
$\widetilde {X}$
be the normalization of
![]() $\overline {X}$
in the field
$\overline {X}$
in the field
![]() $K(\widetilde {V})$
of rational functions on
$K(\widetilde {V})$
of rational functions on
![]() $\widetilde {V}$
. Then
$\widetilde {V}$
. Then
![]() $\widetilde {X}$
is a projective variety with the following canonical commutative diagram.
$\widetilde {X}$
is a projective variety with the following canonical commutative diagram.
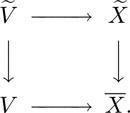
After shrinking
![]() $\widetilde {V}$
if necessary,
$\widetilde {V}$
if necessary,
![]() $\widetilde {V} \,\longrightarrow \,\widetilde {X}$
is an open immersion. We can take a very ample divisor
$\widetilde {V} \,\longrightarrow \,\widetilde {X}$
is an open immersion. We can take a very ample divisor
![]() $D\,\subset \, \overline {X}$
such that
$D\,\subset \, \overline {X}$
such that
![]() $\overline {X}\setminus V \,\subset \, D$
. Choose a very ample divisor
$\overline {X}\setminus V \,\subset \, D$
. Choose a very ample divisor
![]() $\widetilde {D}$
on
$\widetilde {D}$
on
![]() $\widetilde {X}$
such that the inclusion
$\widetilde {X}$
such that the inclusion
![]() $\widetilde {X}\setminus \widetilde {V}\,\subset \, \widetilde {D}$
holds set theoretically and that
$\widetilde {X}\setminus \widetilde {V}\,\subset \, \widetilde {D}$
holds set theoretically and that
![]() $D\times _{\overline {X}}\widetilde {X}\,\subset \, \widetilde {D}$
.
$D\times _{\overline {X}}\widetilde {X}\,\subset \, \widetilde {D}$
.
We can construct a projective variety
![]() $P_i$
with a very ample divisor
$P_i$
with a very ample divisor
![]() $D_i\,\subset \, P_i$
such that
$D_i\,\subset \, P_i$
such that
![]() $P_i\setminus D_i$
is isomorphic to
$P_i\setminus D_i$
is isomorphic to
![]() $U_i$
. We can also take a very ample divisor
$U_i$
. We can also take a very ample divisor
![]() $D'_i\,\subset \, P_i$
such that
$D'_i\,\subset \, P_i$
such that
![]() $P_i\setminus \widetilde {f}_i(\widetilde {V})\,\subset \, D'_i$
holds set theoretically and that
$P_i\setminus \widetilde {f}_i(\widetilde {V})\,\subset \, D'_i$
holds set theoretically and that
![]() $D'_i\,=\,D_i+B_i$
holds for a divisor
$D'_i\,=\,D_i+B_i$
holds for a divisor
![]() $B_i$
without any common component with
$B_i$
without any common component with
![]() $D_i$
.
$D_i$
.
For
![]() $i\,\lt \,j$
, the fiber product
$i\,\lt \,j$
, the fiber product
![]() $U_i \times _{\mathcal X}U_j$
is a smooth quasi-affine scheme over
$U_i \times _{\mathcal X}U_j$
is a smooth quasi-affine scheme over
![]() $\textrm { Spec}\, k$
. So we can construct a projective scheme
$\textrm { Spec}\, k$
. So we can construct a projective scheme
![]() $P_{ij}$
over
$P_{ij}$
over
![]() $\textrm { Spec}\, k$
that contains
$\textrm { Spec}\, k$
that contains
![]() $U_i\times _{\mathcal X}U_j$
as a Zariski open subscheme. Choose a very ample divisor
$U_i\times _{\mathcal X}U_j$
as a Zariski open subscheme. Choose a very ample divisor
![]() $D_{ij}\,\subset \, P_{ij}$
such that
$D_{ij}\,\subset \, P_{ij}$
such that
![]() $P_{ij}\setminus (U_i\times _{\mathcal X}U_j)\,\subset \, D_{ij}$
.
$P_{ij}\setminus (U_i\times _{\mathcal X}U_j)\,\subset \, D_{ij}$
.
Since
![]() $\overline {X}$
is projective and
$\overline {X}$
is projective and
![]() $D$
is very ample, we can take a sufficiently large integer
$D$
is very ample, we can take a sufficiently large integer
![]() $l$
such that
$l$
such that
![]() $H^p(\overline {X}\times \{t\},\, {\mathcal F}|_{\overline {X}\times \{t\}}(lD))\,=\,0$
for all
$H^p(\overline {X}\times \{t\},\, {\mathcal F}|_{\overline {X}\times \{t\}}(lD))\,=\,0$
for all
![]() $p\,\geqslant \, 1$
and
$p\,\geqslant \, 1$
and
![]() $t\,\in \, T$
. After shrinking
$t\,\in \, T$
. After shrinking
![]() $T$
, the space of sections
$T$
, the space of sections
![]() $\Gamma ({\mathcal F}|_{\overline {X}\times T}(lD))$
is a free
$\Gamma ({\mathcal F}|_{\overline {X}\times T}(lD))$
is a free
![]() $\Gamma ({\mathcal O}_T)$
–module of finite rank and the map
$\Gamma ({\mathcal O}_T)$
–module of finite rank and the map
![]() $\Gamma ({\mathcal F}|_{\overline {X}\times T}(lD))\otimes k(t) \,\longrightarrow \, \Gamma ({\mathcal F}|_{\overline {X}\times \{t\}}(lD))$
is bijective for any
$\Gamma ({\mathcal F}|_{\overline {X}\times T}(lD))\otimes k(t) \,\longrightarrow \, \Gamma ({\mathcal F}|_{\overline {X}\times \{t\}}(lD))$
is bijective for any
![]() $t\,\in \, T$
, where
$t\,\in \, T$
, where
![]() $k(t)$
is the residue field of
$k(t)$
is the residue field of
![]() ${\mathcal O}_{T,t}$
.
${\mathcal O}_{T,t}$
.
Choose generators
![]() $s_1,\,\cdots ,\,s_N$
of
$s_1,\,\cdots ,\,s_N$
of
![]() $\Gamma ({\mathcal F}|_{\overline {X}\times T}(lD))$
. Consider the pullbacks of these sections by the morphism
$\Gamma ({\mathcal F}|_{\overline {X}\times T}(lD))$
. Consider the pullbacks of these sections by the morphism
![]() $P_i\setminus D'_i\,\hookrightarrow \, \widetilde {f}_i(\widetilde {V})\,\xrightarrow {\,\,(f|_{U_i})|_{\widetilde {f}_i(\widetilde {V})}\,\,\,}\, V\,\hookrightarrow \, \overline {X}$
and denote them by
$P_i\setminus D'_i\,\hookrightarrow \, \widetilde {f}_i(\widetilde {V})\,\xrightarrow {\,\,(f|_{U_i})|_{\widetilde {f}_i(\widetilde {V})}\,\,\,}\, V\,\hookrightarrow \, \overline {X}$
and denote them by
There is a sufficiently large integer
![]() $l_i$
such that each
$l_i$
such that each
![]() $s_1|_{P_i\setminus D'_i},\,\cdots ,\,s_N|_{P_i\setminus D'_i}$
can be lifted to a section of
$s_1|_{P_i\setminus D'_i},\,\cdots ,\,s_N|_{P_i\setminus D'_i}$
can be lifted to a section of
![]() $\Gamma ({\mathcal O}_{P_i\times T}(l_iD'_i))$
.
$\Gamma ({\mathcal O}_{P_i\times T}(l_iD'_i))$
.
After shrinking
![]() $T$
, the space of sections
$T$
, the space of sections
![]() $\Gamma ({\mathcal O}_{P_i\times T}(l_iD_i))$
is a free
$\Gamma ({\mathcal O}_{P_i\times T}(l_iD_i))$
is a free
![]() $\Gamma ({\mathcal O}_T)$
–module of finite rank. Fix a basis
$\Gamma ({\mathcal O}_T)$
–module of finite rank. Fix a basis
![]() $t^{(i)}_1,\,\cdots ,\,t^{(i)}_{N_i}$
of it. Let
$t^{(i)}_1,\,\cdots ,\,t^{(i)}_{N_i}$
of it. Let
![]() $t^{(i)}_\ell \big |_{\widetilde {X}\setminus \widetilde {D}}$
be the pullback of
$t^{(i)}_\ell \big |_{\widetilde {X}\setminus \widetilde {D}}$
be the pullback of
![]() $t^{(i)}_\ell$
by the composition of the maps
$t^{(i)}_\ell$
by the composition of the maps
Then there is an integer
![]() $\widetilde {l}\,\geqslant \, l$
such that all
$\widetilde {l}\,\geqslant \, l$
such that all
![]() $t^{(i)}_1\big |_{\widetilde {X}\setminus \widetilde {D}},\, \cdots ,\, t^{(i)}_{N_i}\big |_{\widetilde {X}\setminus \widetilde {D}}$
can be lifted to sections
$t^{(i)}_1\big |_{\widetilde {X}\setminus \widetilde {D}},\, \cdots ,\, t^{(i)}_{N_i}\big |_{\widetilde {X}\setminus \widetilde {D}}$
can be lifted to sections
![]() $\widetilde {t}^{(i)}_1,\,\cdots , \,\widetilde {t}^{(i)}_{N_i}$
of
$\widetilde {t}^{(i)}_1,\,\cdots , \,\widetilde {t}^{(i)}_{N_i}$
of
![]() $\Gamma ({\mathcal F}_{\widetilde {X}\times T}(\widetilde {l}\,\widetilde {D}))$
for
$\Gamma ({\mathcal F}_{\widetilde {X}\times T}(\widetilde {l}\,\widetilde {D}))$
for
![]() $1\,\leqslant \,i\,\leqslant \, n$
.
$1\,\leqslant \,i\,\leqslant \, n$
.
Consider the pullback
![]() $t^{(i)}_{\gamma }\big |_{P_{ij}\setminus D_{ij}}$
of
$t^{(i)}_{\gamma }\big |_{P_{ij}\setminus D_{ij}}$
of
![]() $t^{(i)}_{\gamma }$
by the composition of maps
$t^{(i)}_{\gamma }$
by the composition of maps
If we choose
![]() $l_{ij}$
sufficiently large, all
$l_{ij}$
sufficiently large, all
![]() $t^{(i)}_1\big |_{P_{ij}\setminus D_{ij}},\,\cdots ,\,t^{(i)}_{N_i}\big |_{P_{ij}\setminus D_{ij}}$
can be lifted to sections
$t^{(i)}_1\big |_{P_{ij}\setminus D_{ij}},\,\cdots ,\,t^{(i)}_{N_i}\big |_{P_{ij}\setminus D_{ij}}$
can be lifted to sections
of
![]() $\Gamma ({\mathcal O}_{P_i\times T}(l_{ij}D_{ij})^{\oplus r})$
. We may also assume that all
$\Gamma ({\mathcal O}_{P_i\times T}(l_{ij}D_{ij})^{\oplus r})$
. We may also assume that all
![]() $t^{(j)}_1\big |_{P_{ij}\setminus D_{ij}},\,\cdots ,\,t^{(j)}_{N_j}\big |_{P_{ij}\setminus D_{ij}}$
can be lifted to sections
$t^{(j)}_1\big |_{P_{ij}\setminus D_{ij}},\,\cdots ,\,t^{(j)}_{N_j}\big |_{P_{ij}\setminus D_{ij}}$
can be lifted to sections
![]() $t^{(j)}_{i,1},\,\cdots ,\,t^{(j)}_{i,N_j}$
of
$t^{(j)}_{i,1},\,\cdots ,\,t^{(j)}_{i,N_j}$
of
![]() $\Gamma ({\mathcal O}_{P_i\times T}(l_{ij}D_{ij})^{\oplus r})$
.
$\Gamma ({\mathcal O}_{P_i\times T}(l_{ij}D_{ij})^{\oplus r})$
.
Take a resolution
where
![]() ${\mathcal L}_i\,=\, {\mathcal O}_{\overline {X}\times T}(-m_i)^{\oplus R_i}$
for
${\mathcal L}_i\,=\, {\mathcal O}_{\overline {X}\times T}(-m_i)^{\oplus R_i}$
for
![]() $i\,=\,1,\,2$
and
$i\,=\,1,\,2$
and
![]() $m_i\,\gg \, 1$
. After shrinking
$m_i\,\gg \, 1$
. After shrinking
![]() $T$
, both
$T$
, both
![]() $\Gamma ({\mathcal L}_i^{\vee })$
and
$\Gamma ({\mathcal L}_i^{\vee })$
and
![]() $\Gamma ({\mathcal L}_i^{\vee }(lD))$
are free
$\Gamma ({\mathcal L}_i^{\vee }(lD))$
are free
![]() $\Gamma ({\mathcal O}_T)$
–modules for
$\Gamma ({\mathcal O}_T)$
–modules for
![]() $i\,=\,1,\,2$
. Let
$i\,=\,1,\,2$
. Let
![]() ${\mathcal F}|_{\widetilde {X}\times T}$
and
${\mathcal F}|_{\widetilde {X}\times T}$
and
![]() ${\mathcal L}_i|_{\widetilde {X}\times T}$
respectively be the pullbacks of
${\mathcal L}_i|_{\widetilde {X}\times T}$
respectively be the pullbacks of
![]() ${\mathcal F}|_{\overline {X}\times T}$
and
${\mathcal F}|_{\overline {X}\times T}$
and
![]() ${\mathcal L}_i$
by the morphism
${\mathcal L}_i$
by the morphism
![]() $\widetilde {X}\times T\,\longrightarrow \,\overline {X}\times T$
. Then there is the following commutative diagram with exact rows.
$\widetilde {X}\times T\,\longrightarrow \,\overline {X}\times T$
. Then there is the following commutative diagram with exact rows.
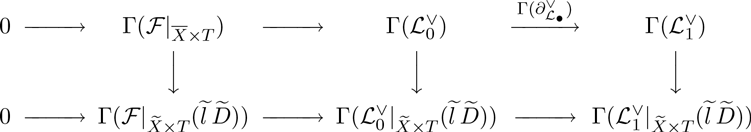
Consider the homomorphism
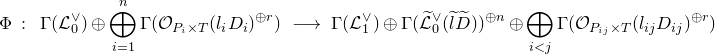 \begin{align*} \Phi \, \,\colon \,\, \Gamma ({\mathcal L}_0^{\vee }) \oplus \bigoplus _{i=1}^n \Gamma ({\mathcal O}_{P_i\times T}(l_iD_i)^{\oplus r}) \,\, \longrightarrow \,\, \Gamma ({\mathcal L}_1^{\vee })\oplus \Gamma (\widetilde {\mathcal L}_0^{\vee }(\widetilde {l}\widetilde {D}))^{\oplus n} \oplus \bigoplus _{i\lt j} \Gamma ({\mathcal O}_{P_{ij}\times T}(l_{ij}D_{ij})^{\oplus r}) \end{align*}
\begin{align*} \Phi \, \,\colon \,\, \Gamma ({\mathcal L}_0^{\vee }) \oplus \bigoplus _{i=1}^n \Gamma ({\mathcal O}_{P_i\times T}(l_iD_i)^{\oplus r}) \,\, \longrightarrow \,\, \Gamma ({\mathcal L}_1^{\vee })\oplus \Gamma (\widetilde {\mathcal L}_0^{\vee }(\widetilde {l}\widetilde {D}))^{\oplus n} \oplus \bigoplus _{i\lt j} \Gamma ({\mathcal O}_{P_{ij}\times T}(l_{ij}D_{ij})^{\oplus r}) \end{align*}
defined by
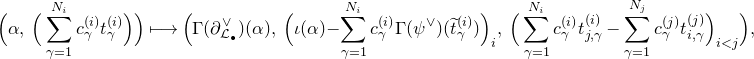 \begin{align*} \Big ( \alpha,\, \Big ( \sum _{\gamma=1}^{N_i} c^{(i)}_{\gamma } t^{(i)}_{\gamma } \Big ) \Big )\longmapsto \Big ( \Gamma (\partial _{{\mathcal L}_{\bullet }}^{\vee }) (\alpha ), \, \Big (\iota (\alpha) \!-\!\sum _{\gamma=1}^{N_i} c^{(i)}_{\gamma } \Gamma (\psi ^{\vee }) (\widetilde {t}^{(i)}_{\gamma }) \Big )_i , \, \Big ( \sum _{\gamma=1}^{N_i} c^{(i)}_{\gamma } t^{(i)}_{j,\gamma } -\sum _{\gamma=1}^{N_j} c^{(j)}_{\gamma } t^{(j)}_{i,\gamma } \Big )_{i\lt j} \Big ), \end{align*}
\begin{align*} \Big ( \alpha,\, \Big ( \sum _{\gamma=1}^{N_i} c^{(i)}_{\gamma } t^{(i)}_{\gamma } \Big ) \Big )\longmapsto \Big ( \Gamma (\partial _{{\mathcal L}_{\bullet }}^{\vee }) (\alpha ), \, \Big (\iota (\alpha) \!-\!\sum _{\gamma=1}^{N_i} c^{(i)}_{\gamma } \Gamma (\psi ^{\vee }) (\widetilde {t}^{(i)}_{\gamma }) \Big )_i , \, \Big ( \sum _{\gamma=1}^{N_i} c^{(i)}_{\gamma } t^{(i)}_{j,\gamma } -\sum _{\gamma=1}^{N_j} c^{(j)}_{\gamma } t^{(j)}_{i,\gamma } \Big )_{i\lt j} \Big ), \end{align*}
where
![]() $\iota \,\colon \, \Gamma ({\mathcal L}_0^{\vee }) \,\longrightarrow \, \Gamma ({\mathcal L}_0^{\vee }(\widetilde {l}\,\widetilde {D}))$
is the canonical inclusion map and
$\iota \,\colon \, \Gamma ({\mathcal L}_0^{\vee }) \,\longrightarrow \, \Gamma ({\mathcal L}_0^{\vee }(\widetilde {l}\,\widetilde {D}))$
is the canonical inclusion map and
is the map induced by
![]() $\psi$
.
$\psi$
.
Claim.
![]() $\Gamma ({{\mathcal X}\times \{t\},\,\, \mathcal F}|_{{\mathcal X}\times \{t\}}) \,\,=\,\, \ker (\Phi \otimes k(t))$
for any
$\Gamma ({{\mathcal X}\times \{t\},\,\, \mathcal F}|_{{\mathcal X}\times \{t\}}) \,\,=\,\, \ker (\Phi \otimes k(t))$
for any
![]() $t\,\in \,T$
.
$t\,\in \,T$
.
Proof of Claim. Take a section
![]() $s\,\in \, \Gamma ({{\mathcal X}\times \{t\},\, \mathcal F}|_{{\mathcal X}\times \{t\}})$
. Its restriction
$s\,\in \, \Gamma ({{\mathcal X}\times \{t\},\, \mathcal F}|_{{\mathcal X}\times \{t\}})$
. Its restriction
![]() $s|_{\overline {X}\times \{t\}}$
is a section of
$s|_{\overline {X}\times \{t\}}$
is a section of
![]() $\Gamma (\overline {X},\,{\mathcal F}|_{\overline {X}\times \{t\}}) \,\subset \, \Gamma (\overline {X},{\mathcal F}|_{\overline {X}\times \{t\}}(lD))$
. From the choice of
$\Gamma (\overline {X},\,{\mathcal F}|_{\overline {X}\times \{t\}}) \,\subset \, \Gamma (\overline {X},{\mathcal F}|_{\overline {X}\times \{t\}}(lD))$
. From the choice of
![]() $l_i$
, the pullback
$l_i$
, the pullback
![]() $(f|_{U_i\cap \widetilde {f}_i(\widetilde {V})})^*(s|_{\overline {X}\times \{t\}})$
can be lifted to a section
$(f|_{U_i\cap \widetilde {f}_i(\widetilde {V})})^*(s|_{\overline {X}\times \{t\}})$
can be lifted to a section
![]() $\sigma _i$
of
$\sigma _i$
of
![]() $\Gamma ({\mathcal O}_{P_i\times \{t\}}(l_iD'_i))$
. On the other hand, we have
$\Gamma ({\mathcal O}_{P_i\times \{t\}}(l_iD'_i))$
. On the other hand, we have
![]() $(s|_{U_i})|_{\widetilde {f}_i(\widetilde {V})} \,=\, (f|_{U_i\cap \widetilde {f}_i(\widetilde {V})})^*(s|_{\overline {X}\times \{t\}})$
. Since
$(s|_{U_i})|_{\widetilde {f}_i(\widetilde {V})} \,=\, (f|_{U_i\cap \widetilde {f}_i(\widetilde {V})})^*(s|_{\overline {X}\times \{t\}})$
. Since
![]() $s|_{U_i}$
does not have pole along
$s|_{U_i}$
does not have pole along
![]() $B_i$
, it follows that
$B_i$
, it follows that
![]() $\sigma _i$
belongs to
$\sigma _i$
belongs to
![]() $\Gamma ({\mathcal O}_{P_i\times \{t\}}(l_iD_i))$
. So we get an element
$\Gamma ({\mathcal O}_{P_i\times \{t\}}(l_iD_i))$
. So we get an element
![]() $\big ( \psi ^{\vee }\big (s|_{\overline {X}\times \{t\}}\big ) ,\, (\sigma _i)_i \big )$
of
$\big ( \psi ^{\vee }\big (s|_{\overline {X}\times \{t\}}\big ) ,\, (\sigma _i)_i \big )$
of
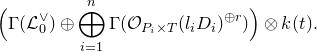 \begin{align*}\Big ( \Gamma ({\mathcal L}_0^{\vee }) \oplus \bigoplus _{i=1}^n \Gamma ({\mathcal O}_{P_i\times T}(l_iD_i)^{\oplus r}) \Big )\otimes k(t).\end{align*}
\begin{align*}\Big ( \Gamma ({\mathcal L}_0^{\vee }) \oplus \bigoplus _{i=1}^n \Gamma ({\mathcal O}_{P_i\times T}(l_iD_i)^{\oplus r}) \Big )\otimes k(t).\end{align*}
By the construction, we have
![]() $\Phi \big ( \psi ^{\vee }\big (s|_{\overline {X}\times \{t\}}\big ) ,\, (\sigma _i)_i \big ) \,=\,0$
. So we get the inclusion map
$\Phi \big ( \psi ^{\vee }\big (s|_{\overline {X}\times \{t\}}\big ) ,\, (\sigma _i)_i \big ) \,=\,0$
. So we get the inclusion map
![]() $\Gamma ({{\mathcal X}\times \{t\}, \,\mathcal F}|_{{\mathcal X}\times \{t\}}) \,\subset \, \ker (\Phi \otimes k(t))$
.
$\Gamma ({{\mathcal X}\times \{t\}, \,\mathcal F}|_{{\mathcal X}\times \{t\}}) \,\subset \, \ker (\Phi \otimes k(t))$
.
To prove the reverse direction, take a section
![]() $(\alpha ,\,(s_i))\,\in \, \ker (\Phi \otimes k(t))$
. Since
$(\alpha ,\,(s_i))\,\in \, \ker (\Phi \otimes k(t))$
. Since
![]() $\Gamma (\partial _{{\mathcal L}_{\bullet}}) (\alpha )\,=\,0$
, there is a section
$\Gamma (\partial _{{\mathcal L}_{\bullet}}) (\alpha )\,=\,0$
, there is a section
![]() $s\,\in \, \Gamma ({\mathcal F}|_{\overline {X}\times \{t\}})$
such that
$s\,\in \, \Gamma ({\mathcal F}|_{\overline {X}\times \{t\}})$
such that
![]() $\psi ^{\vee }(s)\,=\,\alpha$
. Considering the middle component of
$\psi ^{\vee }(s)\,=\,\alpha$
. Considering the middle component of
![]() $\Phi (\alpha ,\, (s_i))\,=\,0$
, we obtain the equality
$\Phi (\alpha ,\, (s_i))\,=\,0$
, we obtain the equality
![]() $s|_{\overline {X}\times _{\mathcal X}U_i}\,=\,s_i|_{\overline {X}\times _{\mathcal X}U_i}$
, because the maps
$s|_{\overline {X}\times _{\mathcal X}U_i}\,=\,s_i|_{\overline {X}\times _{\mathcal X}U_i}$
, because the maps
![]() $\Gamma ({\mathcal F}|_{\widetilde {X}\times T}(\widetilde {l}\widetilde {D})) \,\longrightarrow \, \Gamma ({\mathcal L}_0^{\vee }|_{\widetilde {X}\times T}(\widetilde {l}\widetilde {D}))$
and
$\Gamma ({\mathcal F}|_{\widetilde {X}\times T}(\widetilde {l}\widetilde {D})) \,\longrightarrow \, \Gamma ({\mathcal L}_0^{\vee }|_{\widetilde {X}\times T}(\widetilde {l}\widetilde {D}))$
and
![]() $\Gamma ({\mathcal F}|_{(\overline {X}\times _{\mathcal X}U_i)\times \{t\}}) \,\longrightarrow \, \Gamma ({\mathcal F}|_{(\widetilde {X}\setminus \widetilde {D})\times \{t\}})$
are injective. So
$\Gamma ({\mathcal F}|_{(\overline {X}\times _{\mathcal X}U_i)\times \{t\}}) \,\longrightarrow \, \Gamma ({\mathcal F}|_{(\widetilde {X}\setminus \widetilde {D})\times \{t\}})$
are injective. So
![]() $(s,\,(s_i))$
is in the kernel of
$(s,\,(s_i))$
is in the kernel of
which is in fact
![]() $\Gamma ({{\mathcal X}\times \{t\},\, \mathcal F}\big |_{{\mathcal X}\times \{t\}})$
. So we also have the inclusion
$\Gamma ({{\mathcal X}\times \{t\},\, \mathcal F}\big |_{{\mathcal X}\times \{t\}})$
. So we also have the inclusion
This proves the claim.
Since the claim holds, it suffices to show that
is Zariski closed for any
![]() $d\,\in \,\mathbb{Z}_{\geqslant 0}$
. Note that
$d\,\in \,\mathbb{Z}_{\geqslant 0}$
. Note that
 \begin{align*} \dim \ker (\Phi \otimes k(t)) \, =\,\textrm { rank}_{\Gamma ({\mathcal O}_T)} \Big ( \Gamma ({\mathcal L}_0^{\vee }) \oplus \bigoplus _{i=1}^n \Gamma ({\mathcal O}_{P_i\times T}(l_iD_i)^{\oplus r}) \Big ) -\textrm { rank} (\Phi \otimes k(t)). \end{align*}
\begin{align*} \dim \ker (\Phi \otimes k(t)) \, =\,\textrm { rank}_{\Gamma ({\mathcal O}_T)} \Big ( \Gamma ({\mathcal L}_0^{\vee }) \oplus \bigoplus _{i=1}^n \Gamma ({\mathcal O}_{P_i\times T}(l_iD_i)^{\oplus r}) \Big ) -\textrm { rank} (\Phi \otimes k(t)). \end{align*}
Since the subset of
![]() $T$
given by locus of all points satisfying the condition
$T$
given by locus of all points satisfying the condition
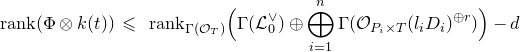 \begin{align*}\textrm { rank}(\Phi \otimes k(t))\,\leqslant \, \textrm { rank}_{\Gamma ({\mathcal O}_T)} \Big ( \Gamma ({\mathcal L}_0^{\vee }) \oplus \bigoplus _{i=1}^n \Gamma ({\mathcal O}_{P_i\times T}(l_iD_i)^{\oplus r}) \Big ) -d\end{align*}
\begin{align*}\textrm { rank}(\Phi \otimes k(t))\,\leqslant \, \textrm { rank}_{\Gamma ({\mathcal O}_T)} \Big ( \Gamma ({\mathcal L}_0^{\vee }) \oplus \bigoplus _{i=1}^n \Gamma ({\mathcal O}_{P_i\times T}(l_iD_i)^{\oplus r}) \Big ) -d\end{align*}
is Zariski closed, the proof of the lemma is complete.
Acknowledgements
We are very grateful to the referee for detailed comments to improve the exposition. The work was initiated during a visit of IB to Kobe University. He is grateful to Kobe University for its hospitality and great working conditions. During the conference The 13th MSJ-SI “Differential Geometry and Integrable Systems”, all of the authors fortunately had opportunities to meet together, which pushed the work to its completion. They are grateful to Professor Masashi Yasumoto for an excellent organization of the conference.
Financial Support
This work was partly supported by JSPS KAKENHI under grant numbers JP17H06127, JP19K03422, JP19K14506, JP22H00094 and JP22K18669. The first author is partially supported by a J. C. Bose Fellowship (JBR/2023/000003).
Conflicts of Interest
None.
Journal Information
Moduli is published as a joint venture of the Foundation Compositio Mathematica and the London Mathematical Society. As not-for-profit organisations, the Foundation and Society reinvest
![]() $100\%$
of any surplus generated from their publications back into mathematics through their charitable activities.
$100\%$
of any surplus generated from their publications back into mathematics through their charitable activities.











