We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 19 December 2019
Let 
$\mathfrak{o}$ be a complete discrete valuation ring of mixed characteristic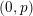 
$(0,p)$ and 
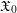$\mathfrak{X}_{0}$ a smooth formal 
$\mathfrak{o}$-scheme. Let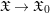 
$\mathfrak{X}\rightarrow \mathfrak{X}_{0}$ be an admissible blow-up. In the first part, we introduce sheaves of differential operators 
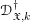$\mathscr{D}_{\mathfrak{X},k}^{\dagger }$ on 
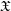$\mathfrak{X}$, for every sufficiently large positive integer 
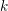$k$, generalizing Berthelot’s arithmetic differential operators on the smooth formal scheme 
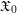$\mathfrak{X}_{0}$. The coherence of these sheaves and several other basic properties are proven. In the second part, we study the projective limit sheaf 
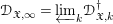$\mathscr{D}_{\mathfrak{X},\infty }=\mathop{\varprojlim }\nolimits_{k}\mathscr{D}_{\mathfrak{X},k}^{\dagger }$ and introduce its abelian category of coadmissible modules. The inductive limit of the sheaves 
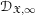$\mathscr{D}_{\mathfrak{X},\infty }$, over all admissible blow-ups 
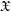$\mathfrak{X}$, is a sheaf 
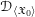$\mathscr{D}_{\langle \mathfrak{X}_{0}\rangle }$ on the Zariski–Riemann space of 
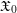$\mathfrak{X}_{0}$, which gives rise to an abelian category of coadmissible modules. Analogues of Theorems A and B are shown to hold in each of these settings, that is, for 
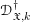$\mathscr{D}_{\mathfrak{X},k}^{\dagger }$, 
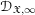$\mathscr{D}_{\mathfrak{X},\infty }$, and 
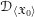$\mathscr{D}_{\langle \mathfrak{X}_{0}\rangle }$.
