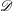Introduction
In this paper, we establish a theory of nearby/vanishing cycle functor in the framework of arithmetic
![]() $\mathscr{D}$
-modules and give some applications. Unipotent nearby/vanishing cycle formalism has already been established by the author together with Caro in [Reference Abe and CaroAC2] after the philosophy of Beilinson. Beilinson’s philosophy (cf. [Reference BeilinsonBei, Remark after Corollary 3.2]) also tells us how to go from unipotent nearby/vanishing cycle functors to the full ones, and in fact, this philosophy underlies the argument of [Reference AbeA2, Lemma 2.4.13]. The aim of this article is to carry this out more systematically so that the nearby/vanishing cycle formalism is also accessible in the
$\mathscr{D}$
-modules and give some applications. Unipotent nearby/vanishing cycle formalism has already been established by the author together with Caro in [Reference Abe and CaroAC2] after the philosophy of Beilinson. Beilinson’s philosophy (cf. [Reference BeilinsonBei, Remark after Corollary 3.2]) also tells us how to go from unipotent nearby/vanishing cycle functors to the full ones, and in fact, this philosophy underlies the argument of [Reference AbeA2, Lemma 2.4.13]. The aim of this article is to carry this out more systematically so that the nearby/vanishing cycle formalism is also accessible in the
![]() $p$
-adic cohomology theory.
$p$
-adic cohomology theory.
Now, let us clarify what properties make full nearby/vanishing cycle functors different from unipotent counterpart. Let
![]() $k$
be a perfect field of positive characteristic. Given a morphism of finite type
$k$
be a perfect field of positive characteristic. Given a morphism of finite type
![]() $f:X\rightarrow \mathbb{A}_{k}^{1}$
, and a “
$f:X\rightarrow \mathbb{A}_{k}^{1}$
, and a “
![]() $p$
-adic coefficient object”
$p$
-adic coefficient object”
![]() $\mathscr{M}$
on
$\mathscr{M}$
on
![]() $X$
, we have already defined unipotent nearby/vanishing cycles
$X$
, we have already defined unipotent nearby/vanishing cycles
![]() $\unicode[STIX]{x1D6F9}_{f}^{\text{un}}(\mathscr{M})$
and
$\unicode[STIX]{x1D6F9}_{f}^{\text{un}}(\mathscr{M})$
and
![]() $\unicode[STIX]{x1D6F7}_{f}^{\text{un}}(\mathscr{M})$
as objects on
$\unicode[STIX]{x1D6F7}_{f}^{\text{un}}(\mathscr{M})$
as objects on
![]() $X_{0}:=X\times _{\mathbb{A}^{1}}\{0\}$
. These functors are compatible with pushforward by proper morphisms and pullback by smooth morphisms. An important property of full nearby cycle functor is that it computes the “cohomology of the generic fiber” when
$X_{0}:=X\times _{\mathbb{A}^{1}}\{0\}$
. These functors are compatible with pushforward by proper morphisms and pullback by smooth morphisms. An important property of full nearby cycle functor is that it computes the “cohomology of the generic fiber” when
![]() $f$
is proper. However,
$f$
is proper. However,
![]() $\unicode[STIX]{x1D6F9}^{\text{un}}$
is not powerful enough to compute the cohomology. Let us explain what this means. Consider the simplest possible situation, namely
$\unicode[STIX]{x1D6F9}^{\text{un}}$
is not powerful enough to compute the cohomology. Let us explain what this means. Consider the simplest possible situation, namely
![]() $X=\mathbb{A}^{1}$
and
$X=\mathbb{A}^{1}$
and
![]() $f=\text{id}$
. Consider the
$f=\text{id}$
. Consider the
![]() $p$
-adic coefficient
$p$
-adic coefficient
![]() $\mathscr{M}$
defined by the differential equation
$\mathscr{M}$
defined by the differential equation
This differential equation has singularity at
![]() $0$
, and in fact, we may prove that the equation is trivialized by an Artin–Schreier type covering. The “cohomology” of
$0$
, and in fact, we may prove that the equation is trivialized by an Artin–Schreier type covering. The “cohomology” of
![]() $\mathscr{M}$
around the generic point of
$\mathscr{M}$
around the generic point of
![]() $\mathbb{A}^{1}$
is merely the “fiber” of
$\mathbb{A}^{1}$
is merely the “fiber” of
![]() $\mathscr{M}$
at the generic point because we are taking
$\mathscr{M}$
at the generic point because we are taking
![]() $f=\text{id}$
. Thus, this should be some vector space of dimension equal to the rank of
$f=\text{id}$
. Thus, this should be some vector space of dimension equal to the rank of
![]() $\mathscr{M}$
, which is
$\mathscr{M}$
, which is
![]() $1$
in this situation. In particular,
$1$
in this situation. In particular,
![]() $\unicode[STIX]{x1D6F9}_{\text{id}}(\mathscr{M})$
should not be zero. However, we may compute that
$\unicode[STIX]{x1D6F9}_{\text{id}}(\mathscr{M})$
should not be zero. However, we may compute that
![]() $\unicode[STIX]{x1D6F9}_{\text{id}}^{\text{un}}(\mathscr{M})=0$
. Thus,
$\unicode[STIX]{x1D6F9}_{\text{id}}^{\text{un}}(\mathscr{M})=0$
. Thus,
![]() $\unicode[STIX]{x1D6F9}_{\text{id}}^{\text{un}}(\mathscr{M})$
does not meet our need. Beilinson suggests to consider
$\unicode[STIX]{x1D6F9}_{\text{id}}^{\text{un}}(\mathscr{M})$
does not meet our need. Beilinson suggests to consider
![]() $\bigoplus _{\mathscr{L}}\unicode[STIX]{x1D6F9}^{\text{un}}(\mathscr{M}\,\otimes \,\mathscr{L})$
where
$\bigoplus _{\mathscr{L}}\unicode[STIX]{x1D6F9}^{\text{un}}(\mathscr{M}\,\otimes \,\mathscr{L})$
where
![]() $\mathscr{L}$
runs over all the irreducible “local system on a disk”. In the situation above,
$\mathscr{L}$
runs over all the irreducible “local system on a disk”. In the situation above,
![]() $\mathscr{M}^{\vee }$
(where
$\mathscr{M}^{\vee }$
(where
![]() $(-)^{\vee }$
denotes the dual) should be considered as an irreducible local system on the disk around
$(-)^{\vee }$
denotes the dual) should be considered as an irreducible local system on the disk around
![]() $0\in \mathbb{A}^{1}$
. Thus the contribution from
$0\in \mathbb{A}^{1}$
. Thus the contribution from
![]() $\unicode[STIX]{x1D6F9}^{\text{un}}(\mathscr{M}\,\otimes \,\mathscr{M}^{\vee })$
does not vanish, which gives us the correct computation of the cohomology of the generic fiber in terms of nearby cycle functor.
$\unicode[STIX]{x1D6F9}^{\text{un}}(\mathscr{M}\,\otimes \,\mathscr{M}^{\vee })$
does not vanish, which gives us the correct computation of the cohomology of the generic fiber in terms of nearby cycle functor.
Even though it is straightforward what to do philosophically, some technical issues come in. First of all, the unipotent nearby/vanishing cycle functors we have already defined a priori depend on the choice of “parameter”, whereas it should not be ideally. This issue is treated in Section 1. Second, it is not clear from the definition that
![]() $\unicode[STIX]{x1D6F9}_{f}$
and
$\unicode[STIX]{x1D6F9}_{f}$
and
![]() $\unicode[STIX]{x1D6F7}_{f}$
have certain finiteness property. We argue as Deligne to show the finiteness in Section 2. After constructing nearby/vanishing cycle functors, we give small applications. In Section 3, we define the category of smooth objects intrinsically, and show that this category coincides with the category of overconvergent isocrystals. We also show that this category is stable under taking pushforward by proper and smooth morphism. In the final section, Section 4, we propose a category over a Henselian trait which is an analogue of that of
$\unicode[STIX]{x1D6F7}_{f}$
have certain finiteness property. We argue as Deligne to show the finiteness in Section 2. After constructing nearby/vanishing cycle functors, we give small applications. In Section 3, we define the category of smooth objects intrinsically, and show that this category coincides with the category of overconvergent isocrystals. We also show that this category is stable under taking pushforward by proper and smooth morphism. In the final section, Section 4, we propose a category over a Henselian trait which is an analogue of that of
![]() $\ell$
-adic sheaves, and show that our nearby/vanishing cycle functors factor through this category.
$\ell$
-adic sheaves, and show that our nearby/vanishing cycle functors factor through this category.
Finally, it is my great pleasure to dedicate this article to Professor Shuji Saito, with deep respect to him and his mathematics, on the occasion of his 60th birthday. As a supervisor, Professor Saito taught me what it is to study mathematics. Even after I got Ph.D., he continuously encouraged me strongly in many occasions, advised me both on mathematics and on life. Without him, my life would not have been as rich.
1 Vanishing cycle functor
1.1
In the whole paper, we fix a (geometric) base tuple
![]() $(k,R,K,L)$
(cf. [Reference AbeA2, 1.4.10, 2.4.14]). This is a collection of data where
$(k,R,K,L)$
(cf. [Reference AbeA2, 1.4.10, 2.4.14]). This is a collection of data where
![]() $k$
is a perfect field of characteristic
$k$
is a perfect field of characteristic
![]() $p>0$
,
$p>0$
,
![]() $R$
is a discrete valuation ring whose residue field is
$R$
is a discrete valuation ring whose residue field is
![]() $k$
such that some power of Frobenius automorphism on
$k$
such that some power of Frobenius automorphism on
![]() $k$
lifts to
$k$
lifts to
![]() $R$
,
$R$
,
![]() $K:=\text{Frac}(R)$
, and
$K:=\text{Frac}(R)$
, and
![]() $L$
is an algebraic extension of
$L$
is an algebraic extension of
![]() $K$
. Once we fix these data, we are able to define the
$K$
. Once we fix these data, we are able to define the
![]() $L$
-linear triangulated category
$L$
-linear triangulated category
![]() $D(X)$
for a separated scheme
$D(X)$
for a separated scheme
![]() $X$
of finite type over
$X$
of finite type over
![]() $k$
. This triangulated category is denoted by
$k$
. This triangulated category is denoted by
![]() $D(X/L_{\emptyset })$
or
$D(X/L_{\emptyset })$
or
![]() $D(X/\mathfrak{T})$
where
$D(X/\mathfrak{T})$
where
![]() $\mathfrak{T}$
is the fixed base tuple to be more precise in [Reference AbeA2]. When
$\mathfrak{T}$
is the fixed base tuple to be more precise in [Reference AbeA2]. When
![]() $L=K$
and
$L=K$
and
![]() $X$
is quasi-projective (or more generally, realizable), we have a classical and more familiar description of
$X$
is quasi-projective (or more generally, realizable), we have a classical and more familiar description of
![]() $D(X)$
in terms of arithmetic
$D(X)$
in terms of arithmetic
![]() $\mathscr{D}$
-modules of Berthelot: Take an embedding
$\mathscr{D}$
-modules of Berthelot: Take an embedding
![]() $X{\hookrightarrow}\mathscr{P}$
where
$X{\hookrightarrow}\mathscr{P}$
where
![]() $\mathscr{P}$
is a proper smooth formal scheme over
$\mathscr{P}$
is a proper smooth formal scheme over
![]() $R$
. Then
$R$
. Then
![]() $D(X)$
is a full subcategory of
$D(X)$
is a full subcategory of
![]() $D_{\text{coh}}^{\text{b}}(\mathscr{D}_{\mathscr{P},\mathbb{Q}}^{\dagger })$
satisfying some finiteness condition called the overholonomicity and support condition. See [Reference AbeA2, 1.1.1] for more details.
$D_{\text{coh}}^{\text{b}}(\mathscr{D}_{\mathscr{P},\mathbb{Q}}^{\dagger })$
satisfying some finiteness condition called the overholonomicity and support condition. See [Reference AbeA2, 1.1.1] for more details.
The category
![]() $D(X)$
is equipped with a t-structure, called the holonomic t-structure, whose heart is denoted by
$D(X)$
is equipped with a t-structure, called the holonomic t-structure, whose heart is denoted by
![]() $\text{Hol}(X)$
. Philosophically, this category corresponds to the category of perverse sheaves in the
$\text{Hol}(X)$
. Philosophically, this category corresponds to the category of perverse sheaves in the
![]() $\ell$
-adic theory. Furthermore,
$\ell$
-adic theory. Furthermore,
![]() $D(X)$
is equipped with 6 functors. The category
$D(X)$
is equipped with 6 functors. The category
![]() $D(X)$
is a closed monoidal category, so we have 2 functors
$D(X)$
is a closed monoidal category, so we have 2 functors
![]() $\otimes$
and
$\otimes$
and
![]() ${\mathcal{H}}om$
. The unit object is denoted by
${\mathcal{H}}om$
. The unit object is denoted by
![]() $L_{X}$
. When
$L_{X}$
. When
![]() $X$
is smooth quasi-projective and
$X$
is smooth quasi-projective and
![]() $L=K$
,
$L=K$
,
![]() $L_{X}$
is, in fact, represented by the structure sheaf up to some shift. Given a morphism
$L_{X}$
is, in fact, represented by the structure sheaf up to some shift. Given a morphism
![]() $f:X\rightarrow Y$
between schemes of finite type, we have 4 more functors:
$f:X\rightarrow Y$
between schemes of finite type, we have 4 more functors:
We denote by
![]() $f_{\ast }$
and
$f_{\ast }$
and
![]() $f^{\ast }$
for normal pushforward and pullback in accordance with the
$f^{\ast }$
for normal pushforward and pullback in accordance with the
![]() $\ell$
-adic theory, and not
$\ell$
-adic theory, and not
![]() $f_{+}$
,
$f_{+}$
,
![]() $f^{+}$
as in [Reference AbeA2]. These functors enjoy a lot of standard properties. Some of the properties are summarized in [Reference AbeA2, 1.1.3], so we do not recall here. Finally, exclusively in Section 1.6, we consider Frobenius structure. In order to consider this extra structure, we remark that “arithmetic base tuple” (cf. [Reference AbeA2, 1.4.10, 2.4.14]) should be fixed, which contains some more information than geometric base tuple. We do not go into detail here.
$f^{+}$
as in [Reference AbeA2]. These functors enjoy a lot of standard properties. Some of the properties are summarized in [Reference AbeA2, 1.1.3], so we do not recall here. Finally, exclusively in Section 1.6, we consider Frobenius structure. In order to consider this extra structure, we remark that “arithmetic base tuple” (cf. [Reference AbeA2, 1.4.10, 2.4.14]) should be fixed, which contains some more information than geometric base tuple. We do not go into detail here.
Remark.
Since [Reference AbeA2, 1.1.3] is written only for realizable schemes, let us point out where in the paper the corresponding claim for separated schemes of finite type can be found. The functors
![]() $f_{\ast }$
,
$f_{\ast }$
,
![]() $f^{\ast }$
are defined in 2.3.7 and 2.3.10. The functor
$f^{\ast }$
are defined in 2.3.7 and 2.3.10. The functor
![]() $\otimes$
is defined in 2.3.14, and Proposition 2.3.15 implies the existence of
$\otimes$
is defined in 2.3.14, and Proposition 2.3.15 implies the existence of
![]() ${\mathcal{H}}om$
. The functor
${\mathcal{H}}om$
. The functor
![]() $f_{!}$
is defined in 2.3.21, and
$f_{!}$
is defined in 2.3.21, and
![]() $f^{!}$
in 2.3.32. The coincidence of
$f^{!}$
in 2.3.32. The coincidence of
![]() $f_{!}$
and
$f_{!}$
and
![]() $f_{\ast }$
when
$f_{\ast }$
when
![]() $f$
is proper follows by construction, and the base change is checked in 2.3.22. The projection formula is in 2.3.35, the Künneth formula is in 2.3.36, and the localization sequence is in 2.2.9. Duality results as well as trace formalism are also written in 2.3.
$f$
is proper follows by construction, and the base change is checked in 2.3.22. The projection formula is in 2.3.35, the Künneth formula is in 2.3.36, and the localization sequence is in 2.2.9. Duality results as well as trace formalism are also written in 2.3.
1.2
A projective system
![]() $\text{“}\varprojlim \text{”}_{i\in I}X_{i}$
, where
$\text{“}\varprojlim \text{”}_{i\in I}X_{i}$
, where
![]() $I$
is a filtered category which is said to be affine étale if all the morphisms
$I$
is a filtered category which is said to be affine étale if all the morphisms
![]() $X_{i}\rightarrow X_{j}$
are affine and étale. By [EGA IV, 8.2.3] as well as [SGA 4, Exp. I, Proposition 8.1.6], the projective limit is representable in the category of schemes over
$X_{i}\rightarrow X_{j}$
are affine and étale. By [EGA IV, 8.2.3] as well as [SGA 4, Exp. I, Proposition 8.1.6], the projective limit is representable in the category of schemes over
![]() $k$
. Let
$k$
. Let
![]() $\text{Sch}^{\text{ft}}(k)$
be the category of schemes separated of finite type over
$\text{Sch}^{\text{ft}}(k)$
be the category of schemes separated of finite type over
![]() $k$
. We denote by
$k$
. We denote by
![]() $\text{Sch}(k)$
the full subcategory of noetherian schemes over
$\text{Sch}(k)$
the full subcategory of noetherian schemes over
![]() $k$
which can be written as a projective limit of an affine étale inductive system in
$k$
which can be written as a projective limit of an affine étale inductive system in
![]() $\text{Sch}^{\text{ft}}(k)$
. From now on, we always mean an object of
$\text{Sch}^{\text{ft}}(k)$
. From now on, we always mean an object of
![]() $\text{Sch}(k)$
by simply saying schemes. In particular, schemes are assumed noetherian.
$\text{Sch}(k)$
by simply saying schemes. In particular, schemes are assumed noetherian.
Lemma 1.3.
(1) Any scheme in
 $\text{Sch}(k)$
is separated.
$\text{Sch}(k)$
is separated.(2) Let
 $S\in \text{Sch}(k)$
, and
$S\in \text{Sch}(k)$
, and
 $X\rightarrow S$
be a morphism of finite type. Then
$X\rightarrow S$
be a morphism of finite type. Then
 $X\in \text{Sch}(k)$
as well.
$X\in \text{Sch}(k)$
as well.(3) The category
 $\text{Sch}(k)$
is closed under taking Henselization (resp. strict Henselization).
$\text{Sch}(k)$
is closed under taking Henselization (resp. strict Henselization).
Proof. The first claim follows since, writing
![]() $X=\varprojlim \,X_{i}$
with
$X=\varprojlim \,X_{i}$
with
![]() $X_{i}\in \text{Sch}^{\text{ft}}(k)$
,
$X_{i}\in \text{Sch}^{\text{ft}}(k)$
,
![]() $X_{i}$
is assumed separated and
$X_{i}$
is assumed separated and
![]() $X\rightarrow X_{i}$
is affine. The second claim is [EGA IV, 8.8.2]. For the last claim, we only need to check that the Henselization and the strict Henselization of a point of a noetherian scheme are noetherian, but these are [EGA IV, 18.6.6, 18.8.8].◻
$X\rightarrow X_{i}$
is affine. The second claim is [EGA IV, 8.8.2]. For the last claim, we only need to check that the Henselization and the strict Henselization of a point of a noetherian scheme are noetherian, but these are [EGA IV, 18.6.6, 18.8.8].◻
1.4
Now, let us introduce the triangulated category of arithmetic
![]() $\mathscr{D}$
-modules for the schemes in
$\mathscr{D}$
-modules for the schemes in
![]() $\text{Sch}(k)$
. Let
$\text{Sch}(k)$
. Let
![]() $X\in \text{Sch}(k)$
. By definition, we may write
$X\in \text{Sch}(k)$
. By definition, we may write
![]() $X\cong \mathop{\varprojlim }\nolimits_{i\in I}X_{i}$
where
$X\cong \mathop{\varprojlim }\nolimits_{i\in I}X_{i}$
where
![]() $X_{i}\in \text{Sch}^{\text{ft}}(k)$
and
$X_{i}\in \text{Sch}^{\text{ft}}(k)$
and
![]() $\text{“}\varprojlim \text{”}_{i\in I}X_{i}$
is affine étale. Let
$\text{“}\varprojlim \text{”}_{i\in I}X_{i}$
is affine étale. Let
![]() $i\rightarrow j$
in
$i\rightarrow j$
in
![]() $I$
. Since the induced morphism
$I$
. Since the induced morphism
![]() $\unicode[STIX]{x1D719}:X_{i}\rightarrow X_{j}$
is étale, we have the isomorphism between pullback functors
$\unicode[STIX]{x1D719}:X_{i}\rightarrow X_{j}$
is étale, we have the isomorphism between pullback functors
![]() $\unicode[STIX]{x1D719}^{\ast }\cong \unicode[STIX]{x1D719}^{!}:D(X_{j})\rightarrow D(X_{i})$
. We define
$\unicode[STIX]{x1D719}^{\ast }\cong \unicode[STIX]{x1D719}^{!}:D(X_{j})\rightarrow D(X_{i})$
. We define
Since
![]() $\unicode[STIX]{x1D719}^{\ast }$
is t-exact with respect to the t-structure,
$\unicode[STIX]{x1D719}^{\ast }$
is t-exact with respect to the t-structure,
![]() $D(X)$
is also equipped with a t-structure, whose heart is still denoted by
$D(X)$
is also equipped with a t-structure, whose heart is still denoted by
![]() $\text{Hol}(X)$
. This category is independent of the choice of projective system up to canonical isomorphism, which justifies the notation
$\text{Hol}(X)$
. This category is independent of the choice of projective system up to canonical isomorphism, which justifies the notation
![]() $D(X)$
. Now, assume given any morphism
$D(X)$
. Now, assume given any morphism
![]() $f:X\rightarrow Y$
in
$f:X\rightarrow Y$
in
![]() $\text{Sch}(k)$
. Then we can find a morphism of affine étale projective systems
$\text{Sch}(k)$
. Then we can find a morphism of affine étale projective systems
![]() $\text{“}\varprojlim \text{”}_{i\in I}X_{i}\rightarrow \text{“}\varprojlim \text{”}_{j\in J}Y_{j}$
in
$\text{“}\varprojlim \text{”}_{i\in I}X_{i}\rightarrow \text{“}\varprojlim \text{”}_{j\in J}Y_{j}$
in
![]() $\text{Sch}^{\text{ft}}(k)$
which converges to
$\text{Sch}^{\text{ft}}(k)$
which converges to
![]() $f$
. This presentation makes it possible to extend the pullback and extraordinary pullback functor on
$f$
. This presentation makes it possible to extend the pullback and extraordinary pullback functor on
![]() $\text{Sch}^{\text{ft}}(k)$
to
$\text{Sch}^{\text{ft}}(k)$
to
Independence of presentation follows easily. Assume further that
![]() $f$
is of finite type. Then [EGA IV, 8.8.2] implies that by changing the projective system
$f$
is of finite type. Then [EGA IV, 8.8.2] implies that by changing the projective system
![]() $\text{“}\varprojlim \text{”}_{i\in I}X_{i}$
in
$\text{“}\varprojlim \text{”}_{i\in I}X_{i}$
in
![]() $\text{Sch}^{\text{ft}}(k)$
if necessary, we may assume that
$\text{Sch}^{\text{ft}}(k)$
if necessary, we may assume that
![]() $I=J$
and that for any
$I=J$
and that for any
![]() $i\rightarrow j$
in
$i\rightarrow j$
in
![]() $J$
the following diagram is cartesian:
$J$
the following diagram is cartesian:

Since
![]() $\unicode[STIX]{x1D719}_{Y}$
is étale, we have the canonical isomorphisms
$\unicode[STIX]{x1D719}_{Y}$
is étale, we have the canonical isomorphisms
![]() $\unicode[STIX]{x1D719}_{Y}^{\ast }\circ f_{j\ast }\cong f_{i\ast }\circ \unicode[STIX]{x1D719}_{X}^{\ast }$
,
$\unicode[STIX]{x1D719}_{Y}^{\ast }\circ f_{j\ast }\cong f_{i\ast }\circ \unicode[STIX]{x1D719}_{X}^{\ast }$
,
![]() $f_{i!}\circ \unicode[STIX]{x1D719}_{X}^{\ast }\cong \unicode[STIX]{x1D719}_{Y}^{\ast }\circ f_{j!}$
by base change and
$f_{i!}\circ \unicode[STIX]{x1D719}_{X}^{\ast }\cong \unicode[STIX]{x1D719}_{Y}^{\ast }\circ f_{j!}$
by base change and
![]() $\unicode[STIX]{x1D719}_{\star }^{\ast }\cong \unicode[STIX]{x1D719}_{\star }^{!}$
. Thus, we have the pushforward and extraordinary pushforward functor
$\unicode[STIX]{x1D719}_{\star }^{\ast }\cong \unicode[STIX]{x1D719}_{\star }^{!}$
. Thus, we have the pushforward and extraordinary pushforward functor
Lemma 1.5. For a scheme
![]() $X$
,
$X$
,
![]() $\text{Hol}(X)$
is a noetherian and artinian category.
$\text{Hol}(X)$
is a noetherian and artinian category.
Proof. Let
![]() $U$
be a scheme, and write
$U$
be a scheme, and write
![]() $U\cong \varprojlim \,U_{i}$
where
$U\cong \varprojlim \,U_{i}$
where
![]() $U_{i}\in \text{Sch}^{\text{ft}}(k)$
. Assume
$U_{i}\in \text{Sch}^{\text{ft}}(k)$
. Assume
![]() $U_{i}$
is smooth. We say that
$U_{i}$
is smooth. We say that
![]() $\mathscr{F}\in \text{Hol}(U)$
is smooth if there exists
$\mathscr{F}\in \text{Hol}(U)$
is smooth if there exists
![]() $i\in I$
and
$i\in I$
and
![]() $\mathscr{F}^{\prime }\in \text{Hol}(U_{i})$
whose pullback is
$\mathscr{F}^{\prime }\in \text{Hol}(U_{i})$
whose pullback is
![]() $\mathscr{F}$
such that
$\mathscr{F}$
such that
![]() $\mathscr{F}^{\prime }$
is smooth on
$\mathscr{F}^{\prime }$
is smooth on
![]() $U_{i}$
in the sense of [Reference AbeA2, 1.3.1]. It is easy to check that any smooth object is of finite length, and for any
$U_{i}$
in the sense of [Reference AbeA2, 1.3.1]. It is easy to check that any smooth object is of finite length, and for any
![]() $\mathscr{F}\in \text{Hol}(X)$
, there exists a smooth open dense subscheme
$\mathscr{F}\in \text{Hol}(X)$
, there exists a smooth open dense subscheme
![]() $U\subset \text{Supp}(\mathscr{F})$
such that
$U\subset \text{Supp}(\mathscr{F})$
such that
![]() $\mathscr{F}|_{U}$
is smooth on
$\mathscr{F}|_{U}$
is smooth on
![]() $U$
. Now, let
$U$
. Now, let
![]() $j:V{\hookrightarrow}X$
be an open immersion. It suffices to check that for an irreducible object
$j:V{\hookrightarrow}X$
be an open immersion. It suffices to check that for an irreducible object
![]() $\mathscr{F}_{V}\in \text{Hol}(V)$
,
$\mathscr{F}_{V}\in \text{Hol}(V)$
,
![]() $j_{!\ast }(\mathscr{F}_{V})$
remains to be irreducible. The verification is standard (see, for example, [Reference Abe and CaroAC, Proposition 1.4.7]).◻
$j_{!\ast }(\mathscr{F}_{V})$
remains to be irreducible. The verification is standard (see, for example, [Reference Abe and CaroAC, Proposition 1.4.7]).◻
1.6
Exclusively in this paragraph, we consider Frobenius structure for the future reference. The reader who does not need to consider Frobenius structure may simply ignore Tate twists appearing in this paragraph.
Let
![]() $\unicode[STIX]{x1D70B}:X\rightarrow \mathbb{A}_{k}^{1}$
be a morphism of finite type, and denote by
$\unicode[STIX]{x1D70B}:X\rightarrow \mathbb{A}_{k}^{1}$
be a morphism of finite type, and denote by
![]() $X_{0}$
the fiber over
$X_{0}$
the fiber over
![]() $0\in \mathbb{A}_{k}^{1}$
. Then the exact functors
$0\in \mathbb{A}_{k}^{1}$
. Then the exact functors
are defined.Footnote
1
Let us now recall the definition briefly. We put
![]() ${\mathcal{O}}_{\mathbb{G}_{\text{m}}}:={\mathcal{O}}_{\widehat{\mathbb{P}}_{R}^{1},\mathbb{Q}}(\text{}^{\dagger }\{0,\infty \})$
. We define
${\mathcal{O}}_{\mathbb{G}_{\text{m}}}:={\mathcal{O}}_{\widehat{\mathbb{P}}_{R}^{1},\mathbb{Q}}(\text{}^{\dagger }\{0,\infty \})$
. We define
![]() ${\mathcal{L}}og^{n}$
for an integer
${\mathcal{L}}og^{n}$
for an integer
![]() $n\geqslant 0$
as follows:
$n\geqslant 0$
as follows:
the free
![]() ${\mathcal{O}}_{\mathbb{G}_{\text{m}}}$
-module of rank
${\mathcal{O}}_{\mathbb{G}_{\text{m}}}$
-module of rank
![]() $n$
generated by the symbols
$n$
generated by the symbols
![]() $\log _{t}^{[k]}$
. For the later use, we denote
$\log _{t}^{[k]}$
. For the later use, we denote
![]() $k!\cdot \log _{t}^{[k]}$
by
$k!\cdot \log _{t}^{[k]}$
by
![]() $\log _{t}^{k}$
. There exists a unique
$\log _{t}^{k}$
. There exists a unique
![]() $\mathscr{D}_{\widehat{\mathbb{P}}^{1},\mathbb{Q}}^{\dagger }$
-module structure on
$\mathscr{D}_{\widehat{\mathbb{P}}^{1},\mathbb{Q}}^{\dagger }$
-module structure on
![]() ${\mathcal{L}}og^{n}$
so that for
${\mathcal{L}}og^{n}$
so that for
![]() $k\geqslant 0$
and
$k\geqslant 0$
and
![]() $g\in {\mathcal{O}}_{\mathbb{G}_{\text{m}}}$
,
$g\in {\mathcal{O}}_{\mathbb{G}_{\text{m}}}$
,
where
![]() $\log _{t}^{[j]}:=0$
for
$\log _{t}^{[j]}:=0$
for
![]() $j<0$
. There is a canonical Frobenius structure on
$j<0$
. There is a canonical Frobenius structure on
![]() ${\mathcal{L}}og^{n}$
. This defines an object of
${\mathcal{L}}og^{n}$
. This defines an object of
![]() $\text{Hol}(\mathbb{A}^{1})$
when
$\text{Hol}(\mathbb{A}^{1})$
when
![]() $L=K$
. If
$L=K$
. If
![]() $L\supsetneq K$
, we simply extend the scalar. We have the following exact sequence:
$L\supsetneq K$
, we simply extend the scalar. We have the following exact sequence:
where the first homomorphism sends
![]() $\log _{t}^{[i]}$
to
$\log _{t}^{[i]}$
to
![]() $\log _{t}^{[i]}$
and the second sends
$\log _{t}^{[i]}$
and the second sends
![]() $\log _{t}^{[i]}$
to
$\log _{t}^{[i]}$
to
![]() $\log _{t}^{[i-n]}$
. We follow the easy-to-describe definitions of various functors of Beilinson (cf. [Reference Abe and CaroAC2, Remark 2.6 (i)]).
$\log _{t}^{[i-n]}$
. We follow the easy-to-describe definitions of various functors of Beilinson (cf. [Reference Abe and CaroAC2, Remark 2.6 (i)]).
Recall we are given
![]() $\unicode[STIX]{x1D70B}:X\rightarrow \mathbb{A}^{1}$
, and put
$\unicode[STIX]{x1D70B}:X\rightarrow \mathbb{A}^{1}$
, and put
![]() $j:X\setminus X_{0}{\hookrightarrow}X$
, the open immersion, and
$j:X\setminus X_{0}{\hookrightarrow}X$
, the open immersion, and
![]() $i:X_{0}{\hookrightarrow}X$
, the closed immersion. Now, we put
$i:X_{0}{\hookrightarrow}X$
, the closed immersion. Now, we put
![]() ${\mathcal{L}}og_{\unicode[STIX]{x1D70B}}^{n}:=\unicode[STIX]{x1D70B}^{\ast }{\mathcal{L}}og^{n}$
. Using this we define for
${\mathcal{L}}og_{\unicode[STIX]{x1D70B}}^{n}:=\unicode[STIX]{x1D70B}^{\ast }{\mathcal{L}}og^{n}$
. Using this we define for
![]() $\mathscr{F}\in \text{Hol}(X)$
$\mathscr{F}\in \text{Hol}(X)$
and put
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}^{\text{un}}:=\unicode[STIX]{x1D6F1}_{!\ast }^{0,0}(1)$
,
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}^{\text{un}}:=\unicode[STIX]{x1D6F1}_{!\ast }^{0,0}(1)$
,
![]() $\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D70B}}:=\unicode[STIX]{x1D6F1}_{!\ast }^{0,1}$
. A key result of [Reference Abe and CaroAC2, Lemma 2.4] is that these limits are representable in
$\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D70B}}:=\unicode[STIX]{x1D6F1}_{!\ast }^{0,1}$
. A key result of [Reference Abe and CaroAC2, Lemma 2.4] is that these limits are representable in
![]() $\text{Hol}(X)$
. We have the following complex in
$\text{Hol}(X)$
. We have the following complex in
![]() $\text{Hol}(X)$
:
$\text{Hol}(X)$
:
and define
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70B}}^{\text{un}}(\mathscr{F})$
to be the cohomology of this complex. Here, the homomorphism
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70B}}^{\text{un}}(\mathscr{F})$
to be the cohomology of this complex. Here, the homomorphism
![]() $j_{!}\mathscr{F}\rightarrow \unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D70B}}(\mathscr{F})$
is the obvious one, and
$j_{!}\mathscr{F}\rightarrow \unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D70B}}(\mathscr{F})$
is the obvious one, and
![]() $\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D70B}}(\mathscr{F})\rightarrow j_{\ast }\mathscr{F}$
is the inductive limit of the connecting homomorphism of the following diagram, recalling
$\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D70B}}(\mathscr{F})\rightarrow j_{\ast }\mathscr{F}$
is the inductive limit of the connecting homomorphism of the following diagram, recalling
![]() ${\mathcal{L}}og_{\unicode[STIX]{x1D70B}}^{1}\cong L_{X\setminus X_{0}}$
:
${\mathcal{L}}og_{\unicode[STIX]{x1D70B}}^{1}\cong L_{X\setminus X_{0}}$
:

Moreover, this diagram induces the following exact sequence:
where the surjectivity of the last homomorphism is also a part of the key result of [Reference Abe and CaroAC2]. This short exact sequence together with the definition of the vanishing cycle functor yield the following fundamental exact triangle:
Remark.
(1) In [Reference Abe and CaroAC2], the object
 ${\mathcal{I}}^{a,b}$
is used instead of
${\mathcal{I}}^{a,b}$
is used instead of
 ${\mathcal{L}}og^{n}$
. We may check easily that there exists an isomorphism
${\mathcal{L}}og^{n}$
. We may check easily that there exists an isomorphism
 ${\mathcal{I}}^{a,b}\xrightarrow[{}]{{\sim}}{\mathcal{L}}og^{b-a}$
where
${\mathcal{I}}^{a,b}\xrightarrow[{}]{{\sim}}{\mathcal{L}}og^{b-a}$
where
 $s^{l}t^{s}$
, using the notation of [Reference Abe and CaroAC2, 2.3], is sent to
$s^{l}t^{s}$
, using the notation of [Reference Abe and CaroAC2, 2.3], is sent to
 $\log _{t}^{[l-a-1]}$
. The embedding
$\log _{t}^{[l-a-1]}$
. The embedding
 ${\mathcal{L}}og_{t}^{n}{\hookrightarrow}{\mathcal{L}}og_{t}^{n+1}$
is compatible with the embedding
${\mathcal{L}}og_{t}^{n}{\hookrightarrow}{\mathcal{L}}og_{t}^{n+1}$
is compatible with the embedding
 ${\mathcal{I}}^{a,b}{\hookrightarrow}{\mathcal{I}}^{a,b+1}$
. The description using
${\mathcal{I}}^{a,b}{\hookrightarrow}{\mathcal{I}}^{a,b+1}$
. The description using
 ${\mathcal{I}}^{a,b}$
is convenient to understand the relation with the dual functor, but in order to prove the theorem below,
${\mathcal{I}}^{a,b}$
is convenient to understand the relation with the dual functor, but in order to prove the theorem below,
 ${\mathcal{L}}og^{n}$
description reduces notation.
${\mathcal{L}}og^{n}$
description reduces notation.(2) We defined
 $\unicode[STIX]{x1D6F9}^{\text{un}}$
as
$\unicode[STIX]{x1D6F9}^{\text{un}}$
as
 $\unicode[STIX]{x1D6F1}_{!\ast }^{0,0}(1)$
, but in [Reference Abe and CaroAC2], following Beilinson, we did not put this Tate twist in the definition. This Tate twist is put in order that no Tate twist appears in (1.6.1). Since we do not consider Frobenius structure from the next paragraph, we may forget this confusing Tate twists.
$\unicode[STIX]{x1D6F1}_{!\ast }^{0,0}(1)$
, but in [Reference Abe and CaroAC2], following Beilinson, we did not put this Tate twist in the definition. This Tate twist is put in order that no Tate twist appears in (1.6.1). Since we do not consider Frobenius structure from the next paragraph, we may forget this confusing Tate twists.
1.7
Now, let
![]() $S$
be a scheme of finite type over
$S$
be a scheme of finite type over
![]() $k$
, and
$k$
, and
![]() $s\in S$
be a regular point of codimension
$s\in S$
be a regular point of codimension
![]() $1$
. Let
$1$
. Let
![]() $\unicode[STIX]{x1D70B}:X\rightarrow S$
be a morphism of finite type. For a dominant morphism
$\unicode[STIX]{x1D70B}:X\rightarrow S$
be a morphism of finite type. For a dominant morphism
![]() $h:S\rightarrow \mathbb{A}^{1}$
such that
$h:S\rightarrow \mathbb{A}^{1}$
such that
![]() $h(s)=0$
, the functor
$h(s)=0$
, the functor
![]() $\unicode[STIX]{x1D6F9}_{h\circ \unicode[STIX]{x1D70B}}^{\text{un}}$
is defined. Note that such
$\unicode[STIX]{x1D6F9}_{h\circ \unicode[STIX]{x1D70B}}^{\text{un}}$
is defined. Note that such
![]() $h$
exists Zariski locally around
$h$
exists Zariski locally around
![]() $s$
. In this paper, for a morphism of schemes
$s$
. In this paper, for a morphism of schemes
![]() $f:X\rightarrow Y$
and a point
$f:X\rightarrow Y$
and a point
![]() $y\in Y$
, the fiber
$y\in Y$
, the fiber
![]() $X\otimes _{Y}k(y)$
is denoted by
$X\otimes _{Y}k(y)$
is denoted by
![]() $X_{y}$
.
$X_{y}$
.
Theorem. The functors
![]() $\unicode[STIX]{x1D6F9}_{h\circ \unicode[STIX]{x1D70B}}^{\text{un}}|_{X_{s}}$
,
$\unicode[STIX]{x1D6F9}_{h\circ \unicode[STIX]{x1D70B}}^{\text{un}}|_{X_{s}}$
,
![]() $\unicode[STIX]{x1D6F7}_{h\circ \unicode[STIX]{x1D70B}}^{\text{un}}|_{X_{s}}$
does not depend on the choice of
$\unicode[STIX]{x1D6F7}_{h\circ \unicode[STIX]{x1D70B}}^{\text{un}}|_{X_{s}}$
does not depend on the choice of
![]() $h$
up to canonical equivalence. This justifies to denote these functors by
$h$
up to canonical equivalence. This justifies to denote these functors by
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B},s}^{\text{un}}$
and
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B},s}^{\text{un}}$
and
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70B},s}^{\text{un}}$
respectively.
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70B},s}^{\text{un}}$
respectively.
Proof. Let
![]() $\mathbb{A}_{(x,y)}^{2}\rightarrow \mathbb{A}_{t}^{1}$
be the morphism sending
$\mathbb{A}_{(x,y)}^{2}\rightarrow \mathbb{A}_{t}^{1}$
be the morphism sending
![]() $t$
to
$t$
to
![]() $xy$
. On
$xy$
. On
![]() $\mathbb{A}^{2}$
, we construct a homomorphism
$\mathbb{A}^{2}$
, we construct a homomorphism
by sending
![]() $(\log xy)^{k}$
to
$(\log xy)^{k}$
to
![]() $\sum _{i=0}^{k}\binom{k}{i}(\log x)^{i}\,\otimes \,(\log y)^{k-i}$
. It is easy to check that this defines a homomorphism of
$\sum _{i=0}^{k}\binom{k}{i}(\log x)^{i}\,\otimes \,(\log y)^{k-i}$
. It is easy to check that this defines a homomorphism of
![]() $\mathscr{D}^{\dagger }$
-modules. Now, shrink
$\mathscr{D}^{\dagger }$
-modules. Now, shrink
![]() $S$
around
$S$
around
![]() $s$
, which is allowed since we only need the equivalence after
$s$
, which is allowed since we only need the equivalence after
![]() $|_{X_{s}}$
, so that the closure of
$|_{X_{s}}$
, so that the closure of
![]() $s$
, is a smooth divisor denoted by
$s$
, is a smooth divisor denoted by
![]() $D$
. Let
$D$
. Let
![]() $u,v\in {\mathcal{O}}_{S}$
. These functions define a morphism
$u,v\in {\mathcal{O}}_{S}$
. These functions define a morphism
![]() $\unicode[STIX]{x1D70C}:S\rightarrow \mathbb{A}^{2}$
by sending
$\unicode[STIX]{x1D70C}:S\rightarrow \mathbb{A}^{2}$
by sending
![]() $x$
,
$x$
,
![]() $y$
to
$y$
to
![]() $u$
,
$u$
,
![]() $v$
respectively. Then we get a homomorphism in
$v$
respectively. Then we get a homomorphism in
![]() $\text{Hol}(S)$
$\text{Hol}(S)$
Given
![]() $u,v,w\in {\mathcal{O}}_{S}$
, the following diagram is commutative:
$u,v,w\in {\mathcal{O}}_{S}$
, the following diagram is commutative:
Now, for
![]() $h:S\rightarrow \mathbb{A}^{1}$
, we denote
$h:S\rightarrow \mathbb{A}^{1}$
, we denote
![]() $\unicode[STIX]{x1D6F9}_{h\unicode[STIX]{x1D70B}}^{\text{un}}$
,
$\unicode[STIX]{x1D6F9}_{h\unicode[STIX]{x1D70B}}^{\text{un}}$
,
![]() $\unicode[STIX]{x1D6F7}_{h\unicode[STIX]{x1D70B}}^{\text{un}}$
,
$\unicode[STIX]{x1D6F7}_{h\unicode[STIX]{x1D70B}}^{\text{un}}$
,
![]() $\unicode[STIX]{x1D6EF}_{h\unicode[STIX]{x1D70B}}^{\text{un}}$
by
$\unicode[STIX]{x1D6EF}_{h\unicode[STIX]{x1D70B}}^{\text{un}}$
by
![]() $\unicode[STIX]{x1D6F9}_{h}$
,
$\unicode[STIX]{x1D6F9}_{h}$
,
![]() $\unicode[STIX]{x1D6F7}_{h}$
,
$\unicode[STIX]{x1D6F7}_{h}$
,
![]() $\unicode[STIX]{x1D6EF}_{h}$
respectively. Take another dominant morphism
$\unicode[STIX]{x1D6EF}_{h}$
respectively. Take another dominant morphism
![]() $h^{\prime }:S\rightarrow \mathbb{A}^{1}$
such that
$h^{\prime }:S\rightarrow \mathbb{A}^{1}$
such that
![]() $h^{\prime }(s)=0$
. Possibly shrinking
$h^{\prime }(s)=0$
. Possibly shrinking
![]() $S$
around
$S$
around
![]() $s$
, we may assume that there exists
$s$
, we may assume that there exists
![]() $u\in {\mathcal{O}}_{S}^{\times }$
such that
$u\in {\mathcal{O}}_{S}^{\times }$
such that
![]() $h^{\prime }=uh$
. Because the image of the associated morphism
$h^{\prime }=uh$
. Because the image of the associated morphism
![]() $u:S\rightarrow \mathbb{A}^{1}$
is contained in
$u:S\rightarrow \mathbb{A}^{1}$
is contained in
![]() $\mathbb{G}_{\text{m}}$
, the object
$\mathbb{G}_{\text{m}}$
, the object
![]() ${\mathcal{L}}og_{u}^{n}$
is an iterated extension of the trivial object
${\mathcal{L}}og_{u}^{n}$
is an iterated extension of the trivial object
![]() $L_{S}$
. This implies that for
$L_{S}$
. This implies that for
![]() $\star \in \{!,\ast \}$
,
$\star \in \{!,\ast \}$
,
where
![]() $j:X\setminus (h\circ \unicode[STIX]{x1D70B})^{-1}(0){\hookrightarrow}X$
. Define
$j:X\setminus (h\circ \unicode[STIX]{x1D70B})^{-1}(0){\hookrightarrow}X$
. Define

and put
![]() $\unicode[STIX]{x1D6F9}_{u,h}:=\unicode[STIX]{x1D6F1}_{(u,h)!\ast }^{0,0}$
,
$\unicode[STIX]{x1D6F9}_{u,h}:=\unicode[STIX]{x1D6F1}_{(u,h)!\ast }^{0,0}$
,
![]() $\unicode[STIX]{x1D6EF}_{u,h}:=\unicode[STIX]{x1D6F1}_{(u,h)!\ast }^{0,1}$
as usual. Then (1.7.3) induces the canonical isomorphisms
$\unicode[STIX]{x1D6EF}_{u,h}:=\unicode[STIX]{x1D6F1}_{(u,h)!\ast }^{0,1}$
as usual. Then (1.7.3) induces the canonical isomorphisms
as Ind objects. We have a homomorphism
where
![]() $\text{pr}_{0}$
denotes the projection by the factor indexed by
$\text{pr}_{0}$
denotes the projection by the factor indexed by
![]() $\log _{u}^{[0]}$
. By taking the limit, we have a homomorphism
$\log _{u}^{[0]}$
. By taking the limit, we have a homomorphism
![]() $\text{pr}_{0}:\mathop{\varinjlim }\nolimits_{n}{\mathcal{L}}og_{u}^{n}|_{D}\rightarrow L_{D}$
. Composing everything, we have
$\text{pr}_{0}:\mathop{\varinjlim }\nolimits_{n}{\mathcal{L}}og_{u}^{n}|_{D}\rightarrow L_{D}$
. Composing everything, we have
We may check easily that
![]() $\unicode[STIX]{x1D719}_{h,h}=\text{id}$
. Using (1.7.2), it is also an easy exercise to show that
$\unicode[STIX]{x1D719}_{h,h}=\text{id}$
. Using (1.7.2), it is also an easy exercise to show that
![]() $\unicode[STIX]{x1D719}_{vuh,uh}\circ \unicode[STIX]{x1D719}_{uh,h}=\unicode[STIX]{x1D719}_{vuh,h}$
for
$\unicode[STIX]{x1D719}_{vuh,uh}\circ \unicode[STIX]{x1D719}_{uh,h}=\unicode[STIX]{x1D719}_{vuh,h}$
for
![]() $v\in {\mathcal{O}}_{S}^{\times }$
. Thus,
$v\in {\mathcal{O}}_{S}^{\times }$
. Thus,
![]() $\unicode[STIX]{x1D719}_{uh,h}$
is an isomorphism for any
$\unicode[STIX]{x1D719}_{uh,h}$
is an isomorphism for any
![]() $u\in {\mathcal{O}}_{S}^{\times }$
. In order to show the theorem for
$u\in {\mathcal{O}}_{S}^{\times }$
. In order to show the theorem for
![]() $\unicode[STIX]{x1D6F7}^{\text{un}}$
, we define
$\unicode[STIX]{x1D6F7}^{\text{un}}$
, we define
![]() $\unicode[STIX]{x1D6F7}_{u,h}$
by the cohomology of the following complex
$\unicode[STIX]{x1D6F7}_{u,h}$
by the cohomology of the following complex
and argue similarly.◻
1.8
Let
![]() $X\xrightarrow[{}]{\unicode[STIX]{x1D70B}}S\xrightarrow[{}]{h}S^{\prime }$
be morphisms of schemes of finite type over
$X\xrightarrow[{}]{\unicode[STIX]{x1D70B}}S\xrightarrow[{}]{h}S^{\prime }$
be morphisms of schemes of finite type over
![]() $k$
,
$k$
,
![]() $h$
is dominant, and
$h$
is dominant, and
![]() $s\in S$
,
$s\in S$
,
![]() $s^{\prime }\in S^{\prime }$
be codimension
$s^{\prime }\in S^{\prime }$
be codimension
![]() $1$
regular points such that
$1$
regular points such that
![]() $s$
is sent to
$s$
is sent to
![]() $s^{\prime }$
. We have the canonical morphism
$s^{\prime }$
. We have the canonical morphism
![]() $h^{\prime }:X_{s}\rightarrow X_{s^{\prime }}$
. Then by the construction of nearby/vanishing cycle functors, we have
$h^{\prime }:X_{s}\rightarrow X_{s^{\prime }}$
. Then by the construction of nearby/vanishing cycle functors, we have
By saying
![]() $(S,s,\unicode[STIX]{x1D702})$
is a Henselian trait, we mean
$(S,s,\unicode[STIX]{x1D702})$
is a Henselian trait, we mean
![]() $S$
is a scheme which is the spectrum of a Henselian discrete valuation ring with closed point
$S$
is a scheme which is the spectrum of a Henselian discrete valuation ring with closed point
![]() $s$
and generic point
$s$
and generic point
![]() $\unicode[STIX]{x1D702}$
, and a fixed separable closure
$\unicode[STIX]{x1D702}$
, and a fixed separable closure
![]() $\overline{k(\unicode[STIX]{x1D702})}$
of
$\overline{k(\unicode[STIX]{x1D702})}$
of
![]() $k(\unicode[STIX]{x1D702})$
often denoted by
$k(\unicode[STIX]{x1D702})$
often denoted by
![]() $\unicode[STIX]{x1D702}^{\text{sep}}$
. Let
$\unicode[STIX]{x1D702}^{\text{sep}}$
. Let
![]() $(S,s,\unicode[STIX]{x1D702})$
be a Henselian trait. Assume given a morphism
$(S,s,\unicode[STIX]{x1D702})$
be a Henselian trait. Assume given a morphism
![]() $\unicode[STIX]{x1D70B}:X\rightarrow S$
. Even if
$\unicode[STIX]{x1D70B}:X\rightarrow S$
. Even if
![]() $X$
and
$X$
and
![]() $S$
are not of finite type over
$S$
are not of finite type over
![]() $k$
, we may define exact functors
$k$
, we may define exact functors
Indeed, we can find a diagram using [EGA IV, 8.8.2]

Here,
![]() $\widetilde{\unicode[STIX]{x1D70B}}$
is a morphism of schemes of finite type over
$\widetilde{\unicode[STIX]{x1D70B}}$
is a morphism of schemes of finite type over
![]() $k$
,
$k$
,
![]() $\unicode[STIX]{x1D70C}(s)$
is a regular point
$\unicode[STIX]{x1D70C}(s)$
is a regular point
![]() $t\in {\mathcal{S}}$
of codimension
$t\in {\mathcal{S}}$
of codimension
![]() $1$
,
$1$
,
![]() $\unicode[STIX]{x1D6FE}$
is the limit of a projective system of affine étale
$\unicode[STIX]{x1D6FE}$
is the limit of a projective system of affine étale
![]() ${\mathcal{X}}\times _{{\mathcal{S}}}S$
-schemes. Let
${\mathcal{X}}\times _{{\mathcal{S}}}S$
-schemes. Let
![]() $\unicode[STIX]{x1D6FE}_{X}:X_{s}\rightarrow {\mathcal{X}}_{t}$
be the morphism induced by
$\unicode[STIX]{x1D6FE}_{X}:X_{s}\rightarrow {\mathcal{X}}_{t}$
be the morphism induced by
![]() $\unicode[STIX]{x1D6FE}$
. Then we define
$\unicode[STIX]{x1D6FE}$
. Then we define
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}^{\text{un}}:=\unicode[STIX]{x1D6FE}_{X}^{\ast }\unicode[STIX]{x1D6F9}_{\widetilde{\unicode[STIX]{x1D70B}},t}^{\text{un}}$
,
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}^{\text{un}}:=\unicode[STIX]{x1D6FE}_{X}^{\ast }\unicode[STIX]{x1D6F9}_{\widetilde{\unicode[STIX]{x1D70B}},t}^{\text{un}}$
,
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70B}}^{\text{un}}:=\unicode[STIX]{x1D6FE}_{X}^{\ast }\unicode[STIX]{x1D6F7}_{\widetilde{\unicode[STIX]{x1D70B}},t}^{\text{un}}$
. We claim that these do not depend on the choice of the diagram. Indeed, assume we are given another morphism
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70B}}^{\text{un}}:=\unicode[STIX]{x1D6FE}_{X}^{\ast }\unicode[STIX]{x1D6F7}_{\widetilde{\unicode[STIX]{x1D70B}},t}^{\text{un}}$
. We claim that these do not depend on the choice of the diagram. Indeed, assume we are given another morphism
![]() $\unicode[STIX]{x1D70C}^{\prime }:S\rightarrow {\mathcal{S}}^{\prime }$
such that
$\unicode[STIX]{x1D70C}^{\prime }:S\rightarrow {\mathcal{S}}^{\prime }$
such that
![]() $\unicode[STIX]{x1D70C}^{\prime }(s)$
is a regular point of codimension
$\unicode[STIX]{x1D70C}^{\prime }(s)$
is a regular point of codimension
![]() $1$
and also a morphism of finite type
$1$
and also a morphism of finite type
![]() $\widetilde{\unicode[STIX]{x1D70B}}^{\prime }:{\mathcal{X}}_{{\mathcal{S}}^{\prime }}^{\prime }\rightarrow {\mathcal{S}}^{\prime }$
having analogous properties as
$\widetilde{\unicode[STIX]{x1D70B}}^{\prime }:{\mathcal{X}}_{{\mathcal{S}}^{\prime }}^{\prime }\rightarrow {\mathcal{S}}^{\prime }$
having analogous properties as
![]() $\widetilde{\unicode[STIX]{x1D70B}}$
. We need to show that the resulting
$\widetilde{\unicode[STIX]{x1D70B}}$
. We need to show that the resulting
![]() $\unicode[STIX]{x1D6F9}^{\text{un}}$
and
$\unicode[STIX]{x1D6F9}^{\text{un}}$
and
![]() $\unicode[STIX]{x1D6F7}^{\text{un}}$
are canonically equivalent. By (1.8.4), we may change bases
$\unicode[STIX]{x1D6F7}^{\text{un}}$
are canonically equivalent. By (1.8.4), we may change bases
![]() ${\mathcal{S}}$
,
${\mathcal{S}}$
,
![]() ${\mathcal{S}}^{\prime }$
, and assume that there is a morphism
${\mathcal{S}}^{\prime }$
, and assume that there is a morphism
![]() ${\mathcal{S}}\rightarrow {\mathcal{S}}^{\prime }$
, and we may even assume that
${\mathcal{S}}\rightarrow {\mathcal{S}}^{\prime }$
, and we may even assume that
![]() ${\mathcal{S}}={\mathcal{S}}^{\prime }$
. Further changing the base, we may assume that there is a diagram of
${\mathcal{S}}={\mathcal{S}}^{\prime }$
. Further changing the base, we may assume that there is a diagram of
![]() ${\mathcal{S}}$
-schemes
${\mathcal{S}}$
-schemes

such that schemes on the 2nd row are of finite type over
![]() ${\mathcal{S}}$
and the vertical morphisms are étale. Since
${\mathcal{S}}$
and the vertical morphisms are étale. Since
![]() $\unicode[STIX]{x1D6F9}^{\text{un}}$
,
$\unicode[STIX]{x1D6F9}^{\text{un}}$
,
![]() $\unicode[STIX]{x1D6F7}^{\text{un}}$
are compatible with pullback by étale morphism, the independence follows.
$\unicode[STIX]{x1D6F7}^{\text{un}}$
are compatible with pullback by étale morphism, the independence follows.
1.9
Now, let
![]() $(S,s,\unicode[STIX]{x1D702})$
be a strict Henselian trait, and we define the category
$(S,s,\unicode[STIX]{x1D702})$
be a strict Henselian trait, and we define the category
![]() $\text{Hen}(S)$
to be the category of Henselian traits over
$\text{Hen}(S)$
to be the category of Henselian traits over
![]() $S$
which is generically étale, and the morphisms are morphisms of traits respecting the fixed separable closure. This is a filtered category. Morphisms are
$S$
which is generically étale, and the morphisms are morphisms of traits respecting the fixed separable closure. This is a filtered category. Morphisms are
![]() $S$
-morphisms. Given a morphism
$S$
-morphisms. Given a morphism
![]() $h:S^{\prime }\rightarrow S$
in
$h:S^{\prime }\rightarrow S$
in
![]() $\text{Hen}(S)$
, consider the following commutative diagram:
$\text{Hen}(S)$
, consider the following commutative diagram:

Now, assume given a morphism
![]() $f:X\rightarrow S$
. Let
$f:X\rightarrow S$
. Let
![]() $f^{\prime }:X\times _{S}S^{\prime }\rightarrow S^{\prime }$
. By abuse of notation, we use the same symbols for the base change from
$f^{\prime }:X\times _{S}S^{\prime }\rightarrow S^{\prime }$
. By abuse of notation, we use the same symbols for the base change from
![]() $S$
to
$S$
to
![]() $X$
, for example
$X$
, for example
![]() $h\times \text{id}:X\times _{S}S^{\prime }\rightarrow X$
is denoted by
$h\times \text{id}:X\times _{S}S^{\prime }\rightarrow X$
is denoted by
![]() $h$
. We have a canonical morphism
$h$
. We have a canonical morphism
where the isomorphism follows since
![]() $h$
is proper and
$h$
is proper and
![]() $s^{\prime }\rightarrow s\times _{S}S^{\prime }$
is a nilpotent immersion. Since
$s^{\prime }\rightarrow s\times _{S}S^{\prime }$
is a nilpotent immersion. Since
![]() $\unicode[STIX]{x1D6F9}_{f^{\prime }}^{\text{un}}\circ h^{\ast }\cong \unicode[STIX]{x1D6F9}_{f^{\prime }}^{\text{un}}\circ (j_{\ast }^{\prime }h_{\unicode[STIX]{x1D702}}^{\ast }j^{\ast })$
and the functor
$\unicode[STIX]{x1D6F9}_{f^{\prime }}^{\text{un}}\circ h^{\ast }\cong \unicode[STIX]{x1D6F9}_{f^{\prime }}^{\text{un}}\circ (j_{\ast }^{\prime }h_{\unicode[STIX]{x1D702}}^{\ast }j^{\ast })$
and the functor
![]() $j_{\ast }^{\prime }h_{\unicode[STIX]{x1D702}}^{\ast }j^{\ast }$
sends holonomic objects to holonomic objects, the exactness of
$j_{\ast }^{\prime }h_{\unicode[STIX]{x1D702}}^{\ast }j^{\ast }$
sends holonomic objects to holonomic objects, the exactness of
![]() $\unicode[STIX]{x1D6F9}^{\text{un}}$
implies that we have
$\unicode[STIX]{x1D6F9}^{\text{un}}$
implies that we have
![]() $\mathscr{H}^{i}(\unicode[STIX]{x1D6F9}_{f^{\prime }}^{\text{un}}\circ h^{\ast }(\mathscr{F}))=0$
for any
$\mathscr{H}^{i}(\unicode[STIX]{x1D6F9}_{f^{\prime }}^{\text{un}}\circ h^{\ast }(\mathscr{F}))=0$
for any
![]() $\mathscr{F}\in \text{Hol}(X)$
and
$\mathscr{F}\in \text{Hol}(X)$
and
![]() $i\neq 0$
. Now, we have the following diagram of exact sequences by (1.6.1).
$i\neq 0$
. Now, we have the following diagram of exact sequences by (1.6.1).

Here the middle homomorphism is an isomorphism since
![]() $h_{s}$
is an isomorphism, and the right vertical morphism is split injective since
$h_{s}$
is an isomorphism, and the right vertical morphism is split injective since
![]() $j^{\ast }\mathscr{F}$
is a direct factor of
$j^{\ast }\mathscr{F}$
is a direct factor of
![]() $h_{\unicode[STIX]{x1D702}\ast }h_{\unicode[STIX]{x1D702}}^{\ast }j^{\ast }\mathscr{F}$
. This implies that
$h_{\unicode[STIX]{x1D702}\ast }h_{\unicode[STIX]{x1D702}}^{\ast }j^{\ast }\mathscr{F}$
. This implies that
![]() $\mathscr{H}^{-1}(h_{s\ast }\unicode[STIX]{x1D6F7}_{f^{\prime }}^{\text{un}}(h^{\ast }\mathscr{F}))=0$
. Together with the other parts of the diagram of long exact sequences, we have
$\mathscr{H}^{-1}(h_{s\ast }\unicode[STIX]{x1D6F7}_{f^{\prime }}^{\text{un}}(h^{\ast }\mathscr{F}))=0$
. Together with the other parts of the diagram of long exact sequences, we have
![]() $\mathscr{H}^{i}(h_{s\ast }\unicode[STIX]{x1D6F7}_{f^{\prime }}^{\text{un}}(h^{\ast }\mathscr{F}))=0$
for
$\mathscr{H}^{i}(h_{s\ast }\unicode[STIX]{x1D6F7}_{f^{\prime }}^{\text{un}}(h^{\ast }\mathscr{F}))=0$
for
![]() $i\neq 0$
and
$i\neq 0$
and
![]() $\unicode[STIX]{x1D6F7}_{f}^{\text{un}}(\mathscr{F}){\hookrightarrow}h_{s\ast }\unicode[STIX]{x1D6F7}_{f^{\prime }}^{\text{un}}(h^{\ast }\mathscr{F})$
. This enables us to define exact functors
$\unicode[STIX]{x1D6F7}_{f}^{\text{un}}(\mathscr{F}){\hookrightarrow}h_{s\ast }\unicode[STIX]{x1D6F7}_{f^{\prime }}^{\text{un}}(h^{\ast }\mathscr{F})$
. This enables us to define exact functors
![]() $\text{Ind}\text{Hol}(X)\rightarrow \text{Ind}\text{Hol}(X_{s})$
as follows:
$\text{Ind}\text{Hol}(X)\rightarrow \text{Ind}\text{Hol}(X_{s})$
as follows:
For Ind-categories, see [Reference AbeA2, 1.2.2]. These are endowed with an action of
![]() $I:=\text{Gal}(\unicode[STIX]{x1D702}^{\text{sep}}/\unicode[STIX]{x1D702})$
where
$I:=\text{Gal}(\unicode[STIX]{x1D702}^{\text{sep}}/\unicode[STIX]{x1D702})$
where
![]() $\unicode[STIX]{x1D702}^{\text{sep}}$
is the separable closure of
$\unicode[STIX]{x1D702}^{\text{sep}}$
is the separable closure of
![]() $\unicode[STIX]{x1D702}$
. By construction, we have the homomorphism
$\unicode[STIX]{x1D702}$
. By construction, we have the homomorphism
![]() $c:\unicode[STIX]{x1D6F9}_{f}\rightarrow \unicode[STIX]{x1D6F7}_{f}$
compatible with the action of
$c:\unicode[STIX]{x1D6F9}_{f}\rightarrow \unicode[STIX]{x1D6F7}_{f}$
compatible with the action of
![]() $I$
. Moreover, for
$I$
. Moreover, for
![]() $\unicode[STIX]{x1D70E}\in I$
, we have the variation homomorphism
$\unicode[STIX]{x1D70E}\in I$
, we have the variation homomorphism
such that
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6F9}}=\text{id}+v(\unicode[STIX]{x1D70E})\circ c$
,
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6F9}}=\text{id}+v(\unicode[STIX]{x1D70E})\circ c$
,
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6F7}}=\text{id}+c\circ v(\unicode[STIX]{x1D70E})$
where
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6F7}}=\text{id}+c\circ v(\unicode[STIX]{x1D70E})$
where
![]() $\unicode[STIX]{x1D70E}_{-}$
is the action of
$\unicode[STIX]{x1D70E}_{-}$
is the action of
![]() $\unicode[STIX]{x1D70E}$
on
$\unicode[STIX]{x1D70E}$
on
![]() $(-)$
. The variation homomorphism is defined as follows: Let
$(-)$
. The variation homomorphism is defined as follows: Let
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}(\mathscr{F})$
. There exists
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}(\mathscr{F})$
. There exists
![]() $\unicode[STIX]{x1D6FC}^{\text{un}}\in \unicode[STIX]{x1D6F7}^{\text{un}}(\mathscr{F})\subset \unicode[STIX]{x1D6F7}(\mathscr{F})$
such that the images of
$\unicode[STIX]{x1D6FC}^{\text{un}}\in \unicode[STIX]{x1D6F7}^{\text{un}}(\mathscr{F})\subset \unicode[STIX]{x1D6F7}(\mathscr{F})$
such that the images of
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FC}^{\text{un}}$
in
$\unicode[STIX]{x1D6FC}^{\text{un}}$
in
![]() $\mathscr{H}^{0}i^{\ast }(\mathscr{F})$
coincide. Then there exists
$\mathscr{H}^{0}i^{\ast }(\mathscr{F})$
coincide. Then there exists
![]() $\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6F9}(\mathscr{F})$
so that
$\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6F9}(\mathscr{F})$
so that
![]() $c(\unicode[STIX]{x1D6FD})=\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FC}^{\text{un}}$
. We define
$c(\unicode[STIX]{x1D6FD})=\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FC}^{\text{un}}$
. We define
![]() $v(\unicode[STIX]{x1D70E})(\unicode[STIX]{x1D6FC}):=\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6F9}}(\unicode[STIX]{x1D6FD})-\unicode[STIX]{x1D6FD}$
. We leave the reader to check that this is well-defined, and satisfies the desired properties.
$v(\unicode[STIX]{x1D70E})(\unicode[STIX]{x1D6FC}):=\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6F9}}(\unicode[STIX]{x1D6FD})-\unicode[STIX]{x1D6FD}$
. We leave the reader to check that this is well-defined, and satisfies the desired properties.
Proposition 1.10. Let
![]() $(S,s,\unicode[STIX]{x1D702})$
,
$(S,s,\unicode[STIX]{x1D702})$
,
![]() $(S^{\prime },s^{\prime },\unicode[STIX]{x1D702}^{\prime })$
be strict Henselian traits, and
$(S^{\prime },s^{\prime },\unicode[STIX]{x1D702}^{\prime })$
be strict Henselian traits, and
![]() $\unicode[STIX]{x1D70B}:S^{\prime }\rightarrow S$
be a finite dominant morphism.
$\unicode[STIX]{x1D70B}:S^{\prime }\rightarrow S$
be a finite dominant morphism.
(1) For
 $\mathscr{F}\in \text{Hol}(\unicode[STIX]{x1D702}^{\prime })$
, the nearby cycles
$\mathscr{F}\in \text{Hol}(\unicode[STIX]{x1D702}^{\prime })$
, the nearby cycles
 $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{F})$
are representable in
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{F})$
are representable in
 $\text{Hol}(s^{\prime })$
.
$\text{Hol}(s^{\prime })$
.(2) For
 $\mathscr{F}\in \text{Hol}(\unicode[STIX]{x1D702}^{\prime })$
, we have
$\mathscr{F}\in \text{Hol}(\unicode[STIX]{x1D702}^{\prime })$
, we have
 $\text{rk}(\mathscr{F})=\text{rk}(\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{F}))$
.
$\text{rk}(\mathscr{F})=\text{rk}(\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{F}))$
.(3) The morphism
 $\unicode[STIX]{x1D70B}_{s}^{\ast }\circ \unicode[STIX]{x1D6F9}_{\text{id}}\xrightarrow[{}]{{\sim}}\unicode[STIX]{x1D6F9}_{\text{id}}\circ \unicode[STIX]{x1D70B}^{\ast }$
, where
$\unicode[STIX]{x1D70B}_{s}^{\ast }\circ \unicode[STIX]{x1D6F9}_{\text{id}}\xrightarrow[{}]{{\sim}}\unicode[STIX]{x1D6F9}_{\text{id}}\circ \unicode[STIX]{x1D70B}^{\ast }$
, where
 $\unicode[STIX]{x1D70B}_{s}:s^{\prime }\xrightarrow[{}]{{\sim}}s$
is the induced morphism, is isomorphic.
$\unicode[STIX]{x1D70B}_{s}:s^{\prime }\xrightarrow[{}]{{\sim}}s$
is the induced morphism, is isomorphic.
Proof. Let us check 3. Assume
![]() $\unicode[STIX]{x1D70B}$
is generically étale. Then
$\unicode[STIX]{x1D70B}$
is generically étale. Then
![]() $S^{\prime }\in \text{Hen}(S)$
. Thus we have the functor
$S^{\prime }\in \text{Hen}(S)$
. Thus we have the functor
![]() $\text{Hen}(S^{\prime })\rightarrow \text{Hen}(S)$
sending
$\text{Hen}(S^{\prime })\rightarrow \text{Hen}(S)$
sending
![]() $S^{\prime \prime }\rightarrow S^{\prime }$
to
$S^{\prime \prime }\rightarrow S^{\prime }$
to
![]() $S^{\prime \prime }\rightarrow S^{\prime }\rightarrow S$
. This functor is cofinal, and since
$S^{\prime \prime }\rightarrow S^{\prime }\rightarrow S$
. This functor is cofinal, and since
![]() $\unicode[STIX]{x1D70B}_{s}$
is an isomorphism, we get the claim in this case. If
$\unicode[STIX]{x1D70B}_{s}$
is an isomorphism, we get the claim in this case. If
![]() $\unicode[STIX]{x1D70B}$
is not generically étale, the morphism
$\unicode[STIX]{x1D70B}$
is not generically étale, the morphism
![]() $\unicode[STIX]{x1D702}^{\prime }\rightarrow \unicode[STIX]{x1D702}$
breaks up into
$\unicode[STIX]{x1D702}^{\prime }\rightarrow \unicode[STIX]{x1D702}$
breaks up into
![]() $\unicode[STIX]{x1D702}^{\prime }\xrightarrow[{}]{a}\unicode[STIX]{x1D702}^{\text{sep}}\xrightarrow[{}]{b}\unicode[STIX]{x1D702}$
where
$\unicode[STIX]{x1D702}^{\prime }\xrightarrow[{}]{a}\unicode[STIX]{x1D702}^{\text{sep}}\xrightarrow[{}]{b}\unicode[STIX]{x1D702}$
where
![]() $a$
is purely inseparable and
$a$
is purely inseparable and
![]() $b$
is étale. By the generically étale case we have already treated, it suffices to check the claim for the case where
$b$
is étale. By the generically étale case we have already treated, it suffices to check the claim for the case where
![]() $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D702}}$
is purely inseparable. In this case,
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D702}}$
is purely inseparable. In this case,
![]() $\unicode[STIX]{x1D70B}$
is universally homeomorphic, thus the functors do not see the difference between
$\unicode[STIX]{x1D70B}$
is universally homeomorphic, thus the functors do not see the difference between
![]() $S$
and
$S$
and
![]() $S^{\prime }$
(cf. [Reference AbeA2, Lemma 1.1.3]).
$S^{\prime }$
(cf. [Reference AbeA2, Lemma 1.1.3]).
Let us check the other two claims. By 3, we may assume that
![]() $\unicode[STIX]{x1D70B}=\text{id}$
. Let
$\unicode[STIX]{x1D70B}=\text{id}$
. Let
![]() $Y$
be a scheme and
$Y$
be a scheme and
![]() $y$
be a point such that
$y$
be a point such that
![]() $S$
is a strict Henselization of
$S$
is a strict Henselization of
![]() $Y$
at
$Y$
at
![]() $y$
. By [EGA IV, 18.8.13], by replacing
$y$
. By [EGA IV, 18.8.13], by replacing
![]() $Y$
by a neighborhood of
$Y$
by a neighborhood of
![]() $y$
, we may assume that
$y$
, we may assume that
![]() $Y$
is smooth. Moreover, by [EGA IV, 18.8.12 (ii), 6.1.3],
$Y$
is smooth. Moreover, by [EGA IV, 18.8.12 (ii), 6.1.3],
![]() ${\mathcal{O}}_{Y,y}$
is of dimension
${\mathcal{O}}_{Y,y}$
is of dimension
![]() $1$
. Thus, we may assume that
$1$
. Thus, we may assume that
![]() $y$
is a generic point
$y$
is a generic point
![]() $\unicode[STIX]{x1D702}_{D}$
of a smooth divisor
$\unicode[STIX]{x1D702}_{D}$
of a smooth divisor
![]() $D$
in
$D$
in
![]() $Y$
. By Kedlaya’s semistable reduction theorem [Reference KedlayaK2], at the cost of shrinking
$Y$
. By Kedlaya’s semistable reduction theorem [Reference KedlayaK2], at the cost of shrinking
![]() $Y$
further, there exists a surjective morphism
$Y$
further, there exists a surjective morphism
![]() $g:Y^{\prime }\rightarrow Y$
such that
$g:Y^{\prime }\rightarrow Y$
such that
![]() $Y^{\prime }$
is smooth,
$Y^{\prime }$
is smooth,
![]() $g$
is étale outside of
$g$
is étale outside of
![]() $D$
, and the pullback of
$D$
, and the pullback of
![]() $\mathscr{F}$
to
$\mathscr{F}$
to
![]() $Y^{\prime }$
is log-extendable along the smooth irreducible divisor
$Y^{\prime }$
is log-extendable along the smooth irreducible divisor
![]() $D^{\prime }:=g^{-1}(D)$
with generic point
$D^{\prime }:=g^{-1}(D)$
with generic point
![]() $\unicode[STIX]{x1D702}_{D^{\prime }}$
. Replacing
$\unicode[STIX]{x1D702}_{D^{\prime }}$
. Replacing
![]() $Y$
by its étale neighborhood around
$Y$
by its étale neighborhood around
![]() $\unicode[STIX]{x1D702}_{D}$
, we may assume that
$\unicode[STIX]{x1D702}_{D}$
, we may assume that
![]() $\unicode[STIX]{x1D702}_{D^{\prime }}\rightarrow \unicode[STIX]{x1D702}_{D}$
is an isomorphism. Take any function
$\unicode[STIX]{x1D702}_{D^{\prime }}\rightarrow \unicode[STIX]{x1D702}_{D}$
is an isomorphism. Take any function
![]() $h\in {\mathcal{O}}_{Y^{\prime }}$
such that the zero locus is equal to
$h\in {\mathcal{O}}_{Y^{\prime }}$
such that the zero locus is equal to
![]() $D^{\prime }$
. In this situation, the computation of [Reference Abe and CaroAC2, Lemma 2.4] shows that
$D^{\prime }$
. In this situation, the computation of [Reference Abe and CaroAC2, Lemma 2.4] shows that
![]() $\unicode[STIX]{x1D6F9}_{h}^{\text{un}}(g^{\ast }\mathscr{F})$
is a smooth object on
$\unicode[STIX]{x1D6F9}_{h}^{\text{un}}(g^{\ast }\mathscr{F})$
is a smooth object on
![]() $D^{\prime }$
of rank equal to that of
$D^{\prime }$
of rank equal to that of
![]() $\mathscr{F}$
. Now, take a finite morphism
$\mathscr{F}$
. Now, take a finite morphism
![]() $\unicode[STIX]{x1D6FC}:Y^{\prime \prime }\rightarrow Y^{\prime }$
which is étale outside of
$\unicode[STIX]{x1D6FC}:Y^{\prime \prime }\rightarrow Y^{\prime }$
which is étale outside of
![]() $D^{\prime }$
. Then
$D^{\prime }$
. Then
![]() $g^{\ast }\mathscr{F}|_{Y^{\prime }\setminus D^{\prime }}$
is a direct factor of
$g^{\ast }\mathscr{F}|_{Y^{\prime }\setminus D^{\prime }}$
is a direct factor of
![]() $\unicode[STIX]{x1D6FC}_{\ast }\unicode[STIX]{x1D6FC}^{\ast }g^{\ast }\mathscr{F}|_{Y^{\prime }\setminus D^{\prime }}$
, so we get that the canonical homomorphism
$\unicode[STIX]{x1D6FC}_{\ast }\unicode[STIX]{x1D6FC}^{\ast }g^{\ast }\mathscr{F}|_{Y^{\prime }\setminus D^{\prime }}$
, so we get that the canonical homomorphism
is a split injective homomorphism. Since
![]() $\unicode[STIX]{x1D6FC}^{\ast }g^{\ast }\mathscr{F}$
is also log-extendable, the rank is the same as that of
$\unicode[STIX]{x1D6FC}^{\ast }g^{\ast }\mathscr{F}$
is also log-extendable, the rank is the same as that of
![]() $\mathscr{F}$
. This implies that the canonical map (1.10.5) is an isomorphism. Thus,
$\mathscr{F}$
. This implies that the canonical map (1.10.5) is an isomorphism. Thus,
![]() $\unicode[STIX]{x1D6F9}_{\text{id}}^{\text{un}}(\mathscr{F})$
is the same as the pullback of
$\unicode[STIX]{x1D6F9}_{\text{id}}^{\text{un}}(\mathscr{F})$
is the same as the pullback of
![]() $g_{\ast }\unicode[STIX]{x1D6F9}_{h}^{\text{un}}(\mathscr{F})$
. ◻
$g_{\ast }\unicode[STIX]{x1D6F9}_{h}^{\text{un}}(\mathscr{F})$
. ◻
2 Finiteness of nearby cycle
Throughout this section, we fix a strict Henselian trait
![]() $(S,s,\unicode[STIX]{x1D702})$
.
$(S,s,\unicode[STIX]{x1D702})$
.
2.1
First, we need a preparation. Let
![]() $f:X\rightarrow Y$
be a morphism of finite type. We put
$f:X\rightarrow Y$
be a morphism of finite type. We put
![]() $f_{\ast }^{i}:=\mathscr{H}^{i}f_{\ast }:\text{Hol}(X)\rightarrow \text{Hol}(Y)$
. This extends canonically to Ind-categories (cf. [Reference AbeA2, after (4) of 1.2.2]), and defines a functor
$f_{\ast }^{i}:=\mathscr{H}^{i}f_{\ast }:\text{Hol}(X)\rightarrow \text{Hol}(Y)$
. This extends canonically to Ind-categories (cf. [Reference AbeA2, after (4) of 1.2.2]), and defines a functor
![]() $If_{\ast }^{i}:\text{Ind}\text{Hol}(X)\rightarrow \text{Ind}\text{Hol}(Y)$
, which we still denote by
$If_{\ast }^{i}:\text{Ind}\text{Hol}(X)\rightarrow \text{Ind}\text{Hol}(Y)$
, which we still denote by
![]() $f_{\ast }^{i}$
. If
$f_{\ast }^{i}$
. If
![]() $f$
is smooth of codimension
$f$
is smooth of codimension
![]() $d$
, we have the exact functor
$d$
, we have the exact functor
![]() $f^{\ast }[d]:\text{Hol}(Y)\rightarrow \text{Hol}(X)$
. This functor also extends to Ind-categories, and is denoted by
$f^{\ast }[d]:\text{Hol}(Y)\rightarrow \text{Hol}(X)$
. This functor also extends to Ind-categories, and is denoted by
![]() $f^{\circledast }$
.
$f^{\circledast }$
.
Lemma. Let
![]() $S$
be a strict Henselian trait, and
$S$
be a strict Henselian trait, and
![]() $f:X\rightarrow Y$
be a morphism of
$f:X\rightarrow Y$
be a morphism of
![]() $S$
-schemes.
$S$
-schemes.
(1) If
 $f$
is proper, then there exists a canonical isomorphism
$f$
is proper, then there exists a canonical isomorphism
 $\unicode[STIX]{x1D6F9}\circ f_{\ast }^{i}\cong f_{\ast }^{i}\circ \unicode[STIX]{x1D6F9}$
in
$\unicode[STIX]{x1D6F9}\circ f_{\ast }^{i}\cong f_{\ast }^{i}\circ \unicode[STIX]{x1D6F9}$
in
 $\text{Ind}\text{Hol}(Y)$
for each
$\text{Ind}\text{Hol}(Y)$
for each
 $i$
.
$i$
.(2) If
 $f$
is smooth, then there exists a canonical isomorphism
$f$
is smooth, then there exists a canonical isomorphism
 $f^{\circledast }\circ \unicode[STIX]{x1D6F9}\cong \unicode[STIX]{x1D6F9}\circ f^{\circledast }$
in
$f^{\circledast }\circ \unicode[STIX]{x1D6F9}\cong \unicode[STIX]{x1D6F9}\circ f^{\circledast }$
in
 $\text{Ind}\text{Hol}(X)$
.
$\text{Ind}\text{Hol}(X)$
.
Proof. These are exercise of six-functor formalism, so we leave the verification to the reader.
Theorem 2.2. If
![]() $\unicode[STIX]{x1D70B}:X\rightarrow S$
is of finite type, the functors
$\unicode[STIX]{x1D70B}:X\rightarrow S$
is of finite type, the functors
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}$
and
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}$
and
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70B}}$
define functors from
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70B}}$
define functors from
![]() $\text{Hol}(X)$
to
$\text{Hol}(X)$
to
![]() $\text{Hol}(X_{s})$
.
$\text{Hol}(X_{s})$
.
By the fundamental exact triangle
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}^{\text{un}}\rightarrow \unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70B}}^{\text{un}}\rightarrow i^{\ast }\xrightarrow[{}]{+}$
, where
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}^{\text{un}}\rightarrow \unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70B}}^{\text{un}}\rightarrow i^{\ast }\xrightarrow[{}]{+}$
, where
![]() $i:X_{s}\rightarrow X$
, it suffices to check the theorem just for
$i:X_{s}\rightarrow X$
, it suffices to check the theorem just for
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}$
. The idea of the proof is essentially the same as [Reference DeligneD, Théorème 3.2]. The proof is divided into several parts. We prove the theorem by induction on the dimension of
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}$
. The idea of the proof is essentially the same as [Reference DeligneD, Théorème 3.2]. The proof is divided into several parts. We prove the theorem by induction on the dimension of
![]() $X_{\unicode[STIX]{x1D702}}$
. The case where
$X_{\unicode[STIX]{x1D702}}$
. The case where
![]() $\dim (X_{\unicode[STIX]{x1D702}})=0$
has already been treated in Proposition 1.10. We assume that the theorem holds for
$\dim (X_{\unicode[STIX]{x1D702}})=0$
has already been treated in Proposition 1.10. We assume that the theorem holds for
![]() $X$
such that
$X$
such that
![]() $\dim (X_{\unicode[STIX]{x1D702}})<n$
. From now on, we assume that
$\dim (X_{\unicode[STIX]{x1D702}})<n$
. From now on, we assume that
![]() $\dim (X_{\unicode[STIX]{x1D702}})=n$
.
$\dim (X_{\unicode[STIX]{x1D702}})=n$
.
Lemma 2.3. [Reference DeligneD, Lemme 3.5]
Let
![]() $K$
be a field containing
$K$
be a field containing
![]() $k$
. Let
$k$
. Let
![]() $X\subset \mathbb{A}_{K}^{n}$
be a closed subscheme,
$X\subset \mathbb{A}_{K}^{n}$
be a closed subscheme,
![]() $\mathscr{F}\in \text{Ind}\text{Hol}(X)$
, and
$\mathscr{F}\in \text{Ind}\text{Hol}(X)$
, and
![]() $\overline{\unicode[STIX]{x1D702}}$
be a geometric generic point of
$\overline{\unicode[STIX]{x1D702}}$
be a geometric generic point of
![]() $\mathbb{A}_{K}^{1}$
. Let
$\mathbb{A}_{K}^{1}$
. Let
![]() $X_{\overline{\unicode[STIX]{x1D702}},i}$
be the geometric generic fiber of the morphism
$X_{\overline{\unicode[STIX]{x1D702}},i}$
be the geometric generic fiber of the morphism
![]() $X\subset \mathbb{A}^{n}\xrightarrow[{}]{\text{pr}_{i}}\mathbb{A}^{1}$
, where
$X\subset \mathbb{A}^{n}\xrightarrow[{}]{\text{pr}_{i}}\mathbb{A}^{1}$
, where
![]() $\text{pr}_{i}$
denotes the
$\text{pr}_{i}$
denotes the
![]() $i$
th projection, and
$i$
th projection, and
![]() $\mathscr{F}_{\overline{\unicode[STIX]{x1D702}},i}$
denotes the pullback of
$\mathscr{F}_{\overline{\unicode[STIX]{x1D702}},i}$
denotes the pullback of
![]() $\mathscr{F}$
to
$\mathscr{F}$
to
![]() $X_{\overline{\unicode[STIX]{x1D702}},i}$
. Assume
$X_{\overline{\unicode[STIX]{x1D702}},i}$
. Assume
![]() $\mathscr{F}_{\overline{\unicode[STIX]{x1D702}},i}\in \text{Hol}(X_{\overline{\unicode[STIX]{x1D702}},i})$
for all
$\mathscr{F}_{\overline{\unicode[STIX]{x1D702}},i}\in \text{Hol}(X_{\overline{\unicode[STIX]{x1D702}},i})$
for all
![]() $i$
. Then there exists
$i$
. Then there exists
![]() $\mathscr{F}^{\prime }\in \text{Hol}(X)$
contained in
$\mathscr{F}^{\prime }\in \text{Hol}(X)$
contained in
![]() $\mathscr{F}$
such that the local sections of
$\mathscr{F}$
such that the local sections of
![]() $\mathscr{F}/\mathscr{F}^{\prime }$
are supported on finitely many points, namely it is isomorphic to
$\mathscr{F}/\mathscr{F}^{\prime }$
are supported on finitely many points, namely it is isomorphic to
![]() $\bigoplus _{x\in |\mathbb{A}^{n}|}\mathscr{G}_{x}$
where
$\bigoplus _{x\in |\mathbb{A}^{n}|}\mathscr{G}_{x}$
where
![]() $\mathscr{G}_{x}$
is supported on
$\mathscr{G}_{x}$
is supported on
![]() $x$
.
$x$
.
Proof. Let
![]() $\unicode[STIX]{x1D70B}:\mathbb{A}^{n}\rightarrow \mathbb{A}^{1}$
be a projection. For each
$\unicode[STIX]{x1D70B}:\mathbb{A}^{n}\rightarrow \mathbb{A}^{1}$
be a projection. For each
![]() $x\in \mathbb{A}^{1}$
, denote by
$x\in \mathbb{A}^{1}$
, denote by
![]() $i_{x}:\mathbb{A}_{x}:=\unicode[STIX]{x1D70B}^{-1}(x){\hookrightarrow}\mathbb{A}^{n}$
and by
$i_{x}:\mathbb{A}_{x}:=\unicode[STIX]{x1D70B}^{-1}(x){\hookrightarrow}\mathbb{A}^{n}$
and by
![]() $\unicode[STIX]{x1D702}$
the generic point of
$\unicode[STIX]{x1D702}$
the generic point of
![]() $\mathbb{A}^{1}$
. Assume given
$\mathbb{A}^{1}$
. Assume given
![]() $\mathscr{G}\in \text{Ind}\text{Hol}(\mathbb{A}^{n})$
such that the pullback to
$\mathscr{G}\in \text{Ind}\text{Hol}(\mathbb{A}^{n})$
such that the pullback to
![]() $\mathbb{A}_{\unicode[STIX]{x1D702}}$
is
$\mathbb{A}_{\unicode[STIX]{x1D702}}$
is
![]() $0$
. Then
$0$
. Then
Indeed, since
![]() $\text{Hol}(\mathbb{A}^{n})$
is a noetherian category by Lemma 1.5, we may write
$\text{Hol}(\mathbb{A}^{n})$
is a noetherian category by Lemma 1.5, we may write
![]() $\mathscr{G}\cong \mathop{\varinjlim }\nolimits_{i}\mathscr{G}_{i}$
where
$\mathscr{G}\cong \mathop{\varinjlim }\nolimits_{i}\mathscr{G}_{i}$
where
![]() $\mathscr{G}_{i}{\hookrightarrow}\mathscr{G}$
and
$\mathscr{G}_{i}{\hookrightarrow}\mathscr{G}$
and
![]() $\mathscr{G}_{i}\in \text{Hol}(\mathbb{A}^{n})$
. Since the pullback by
$\mathscr{G}_{i}\in \text{Hol}(\mathbb{A}^{n})$
. Since the pullback by
![]() $\mathbb{A}_{\unicode[STIX]{x1D702}}\rightarrow \mathbb{A}^{n}$
is exact, by assumption,
$\mathbb{A}_{\unicode[STIX]{x1D702}}\rightarrow \mathbb{A}^{n}$
is exact, by assumption,
![]() $\mathscr{G}_{i}$
becomes
$\mathscr{G}_{i}$
becomes
![]() $0$
on
$0$
on
![]() $\mathbb{A}_{\unicode[STIX]{x1D702}}$
. This implies that
$\mathbb{A}_{\unicode[STIX]{x1D702}}$
. This implies that
![]() $\mathscr{G}_{i}$
is supported on
$\mathscr{G}_{i}$
is supported on
![]() $\coprod _{i=1}^{n}\mathbb{A}_{x_{i}}$
where
$\coprod _{i=1}^{n}\mathbb{A}_{x_{i}}$
where
![]() $x_{i}$
are closed points of
$x_{i}$
are closed points of
![]() $\mathbb{A}^{1}$
, and the claim follows.
$\mathbb{A}^{1}$
, and the claim follows.
Fix
![]() $i$
. There exists an étale neighborhood
$i$
. There exists an étale neighborhood
![]() $U$
of
$U$
of
![]() $\overline{\unicode[STIX]{x1D702}}$
and
$\overline{\unicode[STIX]{x1D702}}$
and
![]() $\mathscr{H}_{i}\in \text{Hol}(X_{U,i})$
, where
$\mathscr{H}_{i}\in \text{Hol}(X_{U,i})$
, where
![]() $j_{i}:X_{U,i}:=X\times _{\text{pr}_{i},\mathbb{A}^{1}}U{\hookrightarrow}X$
, such that its pullback to
$j_{i}:X_{U,i}:=X\times _{\text{pr}_{i},\mathbb{A}^{1}}U{\hookrightarrow}X$
, such that its pullback to
![]() $X_{\overline{\unicode[STIX]{x1D702}},i}$
is
$X_{\overline{\unicode[STIX]{x1D702}},i}$
is
![]() $\mathscr{F}_{\overline{\unicode[STIX]{x1D702}},i}$
. By shrinking
$\mathscr{F}_{\overline{\unicode[STIX]{x1D702}},i}$
. By shrinking
![]() $U$
if necessary, we may assume that the isomorphism
$U$
if necessary, we may assume that the isomorphism
![]() $\mathscr{H}_{i,\overline{\unicode[STIX]{x1D702}},i}\xrightarrow[{}]{{\sim}}\mathscr{F}_{\overline{\unicode[STIX]{x1D702}},i}$
is induced by a homomorphism
$\mathscr{H}_{i,\overline{\unicode[STIX]{x1D702}},i}\xrightarrow[{}]{{\sim}}\mathscr{F}_{\overline{\unicode[STIX]{x1D702}},i}$
is induced by a homomorphism
![]() $\mathscr{H}_{i}\rightarrow \mathscr{F}_{U,i}$
where
$\mathscr{H}_{i}\rightarrow \mathscr{F}_{U,i}$
where
![]() $\mathscr{F}_{U,i}$
denotes the pullback of
$\mathscr{F}_{U,i}$
denotes the pullback of
![]() $\mathscr{F}$
to
$\mathscr{F}$
to
![]() $X_{U,i}$
. Now, put
$X_{U,i}$
. Now, put
By construction,
![]() $\mathscr{F}^{\prime }\in \text{Hol}(X)$
and
$\mathscr{F}^{\prime }\in \text{Hol}(X)$
and
![]() $(\mathscr{F}/\mathscr{F}^{\prime })_{\overline{\unicode[STIX]{x1D702}},i}=0$
for any
$(\mathscr{F}/\mathscr{F}^{\prime })_{\overline{\unicode[STIX]{x1D702}},i}=0$
for any
![]() $n$
. Thus, using the observation above, any local section of
$n$
. Thus, using the observation above, any local section of
![]() $\mathscr{F}/\mathscr{F}^{\prime }$
is supported on finitely many points.◻
$\mathscr{F}/\mathscr{F}^{\prime }$
is supported on finitely many points.◻
2.4
Let
![]() $s^{\prime }$
be the generic point of
$s^{\prime }$
be the generic point of
![]() $\mathbb{A}_{s}^{1}$
, and let
$\mathbb{A}_{s}^{1}$
, and let
![]() $(S^{\prime },s^{\prime },\unicode[STIX]{x1D702}^{\prime })$
be the strict Henselization of
$(S^{\prime },s^{\prime },\unicode[STIX]{x1D702}^{\prime })$
be the strict Henselization of
![]() $\mathbb{A}_{S}^{1}$
at the generic point
$\mathbb{A}_{S}^{1}$
at the generic point
![]() $s^{\prime }$
of the divisor
$s^{\prime }$
of the divisor
![]() $\mathbb{A}_{s}^{1}$
. Let
$\mathbb{A}_{s}^{1}$
. Let
![]() $h:S^{\prime }\rightarrow S$
be the morphism. Deligne constructed the following diagram in the proof of [Reference DeligneD, Lemme 3.3]:
$h:S^{\prime }\rightarrow S$
be the morphism. Deligne constructed the following diagram in the proof of [Reference DeligneD, Lemme 3.3]:
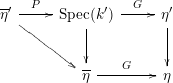
where horizontal maps are algebraic extensions of fields, and
![]() $P$
,
$P$
,
![]() $G$
denote the Galois groups of the extension. The group
$G$
denote the Galois groups of the extension. The group
![]() $P$
is a pro-
$P$
is a pro-
![]() $p$
-group. Now, let
$p$
-group. Now, let
![]() $\unicode[STIX]{x1D70B}^{\prime }:X^{\prime }\rightarrow S^{\prime }$
be a morphism, and let
$\unicode[STIX]{x1D70B}^{\prime }:X^{\prime }\rightarrow S^{\prime }$
be a morphism, and let
![]() $\mathscr{F}\in \text{Hol}(X_{\unicode[STIX]{x1D702}^{\prime }}^{\prime })$
. Note that
$\mathscr{F}\in \text{Hol}(X_{\unicode[STIX]{x1D702}^{\prime }}^{\prime })$
. Note that
![]() $X_{\unicode[STIX]{x1D702}}^{\prime }=X_{\unicode[STIX]{x1D702}^{\prime }}^{\prime }$
and
$X_{\unicode[STIX]{x1D702}}^{\prime }=X_{\unicode[STIX]{x1D702}^{\prime }}^{\prime }$
and
![]() $X_{s}^{\prime }=X_{s^{\prime }}^{\prime }$
. Then we have
$X_{s}^{\prime }=X_{s^{\prime }}^{\prime }$
. Then we have
![]() $\unicode[STIX]{x1D6F9}_{h\circ \unicode[STIX]{x1D70B}^{\prime }}(\mathscr{F})\cong \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}^{\prime }}(\mathscr{F})^{P}$
.
$\unicode[STIX]{x1D6F9}_{h\circ \unicode[STIX]{x1D70B}^{\prime }}(\mathscr{F})\cong \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}^{\prime }}(\mathscr{F})^{P}$
.
2.5 Proof of Theorem 2.2
Now, let
![]() $\unicode[STIX]{x1D70B}:X\rightarrow S$
be a morphism of finite type. We first assume
$\unicode[STIX]{x1D70B}:X\rightarrow S$
be a morphism of finite type. We first assume
![]() $X$
affine, and take a closed immersion
$X$
affine, and take a closed immersion
![]() $X{\hookrightarrow}\mathbb{A}_{S}^{n}$
, and let
$X{\hookrightarrow}\mathbb{A}_{S}^{n}$
, and let
![]() $f:X\subset \mathbb{A}_{S}^{n}\rightarrow \mathbb{A}_{S}^{1}$
where the second morphism is a projection. Recall from the previous paragraph that
$f:X\subset \mathbb{A}_{S}^{n}\rightarrow \mathbb{A}_{S}^{1}$
where the second morphism is a projection. Recall from the previous paragraph that
![]() $\unicode[STIX]{x1D706}:S^{\prime }{\hookrightarrow}\mathbb{A}_{S}^{1}$
is a strict Henselization of
$\unicode[STIX]{x1D706}:S^{\prime }{\hookrightarrow}\mathbb{A}_{S}^{1}$
is a strict Henselization of
![]() $\mathbb{A}_{S}^{1}$
. Consider the following diagram:
$\mathbb{A}_{S}^{1}$
. Consider the following diagram:

Let
![]() $\mathscr{F}^{\prime }$
be the pullback of
$\mathscr{F}^{\prime }$
be the pullback of
![]() $\mathscr{F}$
to
$\mathscr{F}$
to
![]() $X^{\prime }$
. Then we have
$X^{\prime }$
. Then we have
where the first isomorphism follows by Lemma 2.1, and the second by 2.4. Now, the induction hypothesis tells us that
![]() $\unicode[STIX]{x1D6F9}_{f^{\prime }}(\mathscr{F})^{P}\in \text{Hol}(X_{s^{\prime }}^{\prime })$
, and by construction
$\unicode[STIX]{x1D6F9}_{f^{\prime }}(\mathscr{F})^{P}\in \text{Hol}(X_{s^{\prime }}^{\prime })$
, and by construction
![]() $X_{s^{\prime }}^{\prime }=X_{s}^{\prime }$
. This implies that
$X_{s^{\prime }}^{\prime }=X_{s}^{\prime }$
. This implies that
![]() $\unicode[STIX]{x1D706}_{X}^{\circledast }\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{F})\in \text{Hol}(X_{s}^{\prime })$
. Lemma 2.3 ensures the existence of
$\unicode[STIX]{x1D706}_{X}^{\circledast }\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{F})\in \text{Hol}(X_{s}^{\prime })$
. Lemma 2.3 ensures the existence of
![]() $\mathscr{G}\in \text{Hol}(X_{s})$
contained in
$\mathscr{G}\in \text{Hol}(X_{s})$
contained in
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{F})$
such that the local sections of
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{F})$
such that the local sections of
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{F})/\mathscr{G}$
are supported on finitely many points. Now, if
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{F})/\mathscr{G}$
are supported on finitely many points. Now, if
![]() $X$
is not affine, we take a finite affine open covering
$X$
is not affine, we take a finite affine open covering
![]() $\{U_{i}\}$
and we can get such
$\{U_{i}\}$
and we can get such
![]() $\mathscr{G}_{i}$
for each subscheme. Then
$\mathscr{G}_{i}$
for each subscheme. Then
![]() $\mathscr{G}:=\text{Im}(\bigoplus \mathscr{H}^{0}\mathscr{G}_{i,!}\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{F}))$
, where
$\mathscr{G}:=\text{Im}(\bigoplus \mathscr{H}^{0}\mathscr{G}_{i,!}\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{F}))$
, where
![]() $\mathscr{G}_{i,!}$
denotes the extension by zero of
$\mathscr{G}_{i,!}$
denotes the extension by zero of
![]() $\mathscr{G}_{i}$
to
$\mathscr{G}_{i}$
to
![]() $X$
, is in
$X$
, is in
![]() $\text{Hol}(X_{s})$
and the local sections of
$\text{Hol}(X_{s})$
and the local sections of
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{F})/\mathscr{G}$
are supported on finitely many points.
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{F})/\mathscr{G}$
are supported on finitely many points.
In order to show the finiteness of
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{F})$
, we may assume
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{F})$
, we may assume
![]() $X$
is proper over
$X$
is proper over
![]() $S$
. Take
$S$
. Take
![]() $\mathscr{G}$
as above, and we may write
$\mathscr{G}$
as above, and we may write
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{F})/\mathscr{G}\cong \bigoplus _{x\in |X_{s}|}\mathscr{G}_{x}$
where
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{F})/\mathscr{G}\cong \bigoplus _{x\in |X_{s}|}\mathscr{G}_{x}$
where
![]() $\mathscr{G}_{x}$
is supported on
$\mathscr{G}_{x}$
is supported on
![]() $x$
. We have the following long exact sequence:
$x$
. We have the following long exact sequence:

where the vertical isomorphism follows by Lemma 2.1. Since we already know that the objects with ![]() are in
are in
![]() $\text{Hol}(s)$
, we have
$\text{Hol}(s)$
, we have
This implies that
![]() $\bigoplus _{x\in |X_{s}|}\mathscr{G}_{x}\in \text{Hol}(X_{s})$
, and thus
$\bigoplus _{x\in |X_{s}|}\mathscr{G}_{x}\in \text{Hol}(X_{s})$
, and thus
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{F})\in \text{Hol}(X_{s})$
as required.◻
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{F})\in \text{Hol}(X_{s})$
as required.◻
Corollary 2.6. Let
![]() $\unicode[STIX]{x1D70B}:X\rightarrow S$
be a morphism of finite type, and
$\unicode[STIX]{x1D70B}:X\rightarrow S$
be a morphism of finite type, and
![]() $f:X\rightarrow Y$
be a morphism of
$f:X\rightarrow Y$
be a morphism of
![]() $S$
-schemes of finite type.
$S$
-schemes of finite type.
(1) If
 $f$
is proper, then there exists a canonical isomorphism
$f$
is proper, then there exists a canonical isomorphism
 $\unicode[STIX]{x1D6F9}\circ f_{\ast }\cong f_{\ast }\circ \unicode[STIX]{x1D6F9}$
in
$\unicode[STIX]{x1D6F9}\circ f_{\ast }\cong f_{\ast }\circ \unicode[STIX]{x1D6F9}$
in
 $D(Y)$
.
$D(Y)$
.(2) If
 $f$
is smooth, then there exists a canonical isomorphism
$f$
is smooth, then there exists a canonical isomorphism
 $f^{\ast }\circ \unicode[STIX]{x1D6F9}\cong \unicode[STIX]{x1D6F9}\circ f^{\ast }$
in
$f^{\ast }\circ \unicode[STIX]{x1D6F9}\cong \unicode[STIX]{x1D6F9}\circ f^{\ast }$
in
 $D(X)$
.
$D(X)$
.(3) We have the exact triangle of functors
 $i^{\ast }[-1]\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}\rightarrow \unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70B}}\xrightarrow[{}]{+}$
.
$i^{\ast }[-1]\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}\rightarrow \unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70B}}\xrightarrow[{}]{+}$
.
Remark.
Let
![]() $R\unicode[STIX]{x1D713}$
and
$R\unicode[STIX]{x1D713}$
and
![]() $R\unicode[STIX]{x1D719}$
be the nearby and vanishing cycle functors for
$R\unicode[STIX]{x1D719}$
be the nearby and vanishing cycle functors for
![]() $\ell$
-adic sheaves. The exact triangle for nearby/vanishing cycle functor usually goes
$\ell$
-adic sheaves. The exact triangle for nearby/vanishing cycle functor usually goes
![]() $i^{\ast }\rightarrow R\unicode[STIX]{x1D713}\rightarrow R\unicode[STIX]{x1D719}\xrightarrow[{}]{+}$
. This difference arises because in the spirit of Riemann–Hilbert correspondence,
$i^{\ast }\rightarrow R\unicode[STIX]{x1D713}\rightarrow R\unicode[STIX]{x1D719}\xrightarrow[{}]{+}$
. This difference arises because in the spirit of Riemann–Hilbert correspondence,
![]() $\unicode[STIX]{x1D6F9}=R\unicode[STIX]{x1D713}[-1]$
,
$\unicode[STIX]{x1D6F9}=R\unicode[STIX]{x1D713}[-1]$
,
![]() $\unicode[STIX]{x1D6F7}=R\unicode[STIX]{x1D719}[-1]$
. We could have employed this normalization, but in order to be consistent with [Reference Abe and CaroAC2], we decided not to take the shift.
$\unicode[STIX]{x1D6F7}=R\unicode[STIX]{x1D719}[-1]$
. We could have employed this normalization, but in order to be consistent with [Reference Abe and CaroAC2], we decided not to take the shift.
3 Smooth objects
3.1
Let
![]() $X$
be a scheme of finite type over
$X$
be a scheme of finite type over
![]() $k$
. Then
$k$
. Then
![]() $D(X)$
is equipped with two t-structures; the holonomic t-structure whose heart is
$D(X)$
is equipped with two t-structures; the holonomic t-structure whose heart is
![]() $\text{Hol}(X)$
, and the constructible t-structure defined in [Reference AbeA2, §1.3]. The heart of constructible t-structure is denoted by
$\text{Hol}(X)$
, and the constructible t-structure defined in [Reference AbeA2, §1.3]. The heart of constructible t-structure is denoted by
![]() $\text{Con}(X)$
. Given a morphism of finite type
$\text{Con}(X)$
. Given a morphism of finite type
![]() $f:X\rightarrow Y$
, the pullback
$f:X\rightarrow Y$
, the pullback
![]() $f^{\ast }$
is exact with respect to constructible t-structure by [Reference AbeA2, 1.3.4]. Thus constructible t-structure extends to a t-structure on
$f^{\ast }$
is exact with respect to constructible t-structure by [Reference AbeA2, 1.3.4]. Thus constructible t-structure extends to a t-structure on
![]() $D(X)$
for any scheme
$D(X)$
for any scheme
![]() $X$
. The cohomology functor for holonomic t-structure is denoted by
$X$
. The cohomology functor for holonomic t-structure is denoted by
![]() $\mathscr{H}^{\ast }$
, as we have already used several times, and the constructible t-structure by
$\mathscr{H}^{\ast }$
, as we have already used several times, and the constructible t-structure by
![]() $\text{}^{\text{c}}\!\mathscr{H}^{\ast }$
.
$\text{}^{\text{c}}\!\mathscr{H}^{\ast }$
.
Definition 3.2. Let
![]() $X$
be a scheme. Then
$X$
be a scheme. Then
![]() $\mathscr{F}\in \text{Con}(X)$
is said to be smooth if for any morphism
$\mathscr{F}\in \text{Con}(X)$
is said to be smooth if for any morphism
![]() $\unicode[STIX]{x1D719}:S\rightarrow X$
from a strict Henselian trait,
$\unicode[STIX]{x1D719}:S\rightarrow X$
from a strict Henselian trait,
![]() $\unicode[STIX]{x1D6F7}_{\text{id}}(\unicode[STIX]{x1D719}^{\ast }\mathscr{F})=0$
. The full subcategory of smooth objects in
$\unicode[STIX]{x1D6F7}_{\text{id}}(\unicode[STIX]{x1D719}^{\ast }\mathscr{F})=0$
. The full subcategory of smooth objects in
![]() $\text{Con}(X)$
is denoted by
$\text{Con}(X)$
is denoted by
![]() $\text{Sm}(X)$
.
$\text{Sm}(X)$
.
By Theorem 3.8, we can see that this definition is in fact a generalization of smoothness defined in [Reference AbeA2, 1.3.1]. To be more precise, when
![]() $X$
is a realizable scheme over
$X$
is a realizable scheme over
![]() $k$
such that
$k$
such that
![]() $X_{\text{red}}$
is smooth,
$X_{\text{red}}$
is smooth,
![]() $\text{Sm}(X)$
is the same as the category introduced in [Reference AbeA2, 1.1.3 (12)].
$\text{Sm}(X)$
is the same as the category introduced in [Reference AbeA2, 1.1.3 (12)].
Lemma 3.3. Let
![]() $f:Y\rightarrow X$
be a proper surjective morphism, and
$f:Y\rightarrow X$
be a proper surjective morphism, and
![]() $\mathscr{F}\in \text{Con}(X)$
. If
$\mathscr{F}\in \text{Con}(X)$
. If
![]() $f^{\ast }\mathscr{F}$
is smooth, then
$f^{\ast }\mathscr{F}$
is smooth, then
![]() $\mathscr{F}$
is smooth.
$\mathscr{F}$
is smooth.
Proof. Let
![]() $f:S^{\prime }\rightarrow S$
be a finite morphism between strict Henselian traits. In this case, we have an isomorphism
$f:S^{\prime }\rightarrow S$
be a finite morphism between strict Henselian traits. In this case, we have an isomorphism
![]() $f_{s}^{\ast }\unicode[STIX]{x1D6F9}_{\text{id}}(\mathscr{F})\cong \unicode[STIX]{x1D6F9}_{\text{id}}(f^{\ast }\mathscr{F})$
by Proposition 1.10.3. Since
$f_{s}^{\ast }\unicode[STIX]{x1D6F9}_{\text{id}}(\mathscr{F})\cong \unicode[STIX]{x1D6F9}_{\text{id}}(f^{\ast }\mathscr{F})$
by Proposition 1.10.3. Since
![]() $f_{s}^{\ast }$
is an isomorphism, the claim follows. Consider the general case. Given a morphism
$f_{s}^{\ast }$
is an isomorphism, the claim follows. Consider the general case. Given a morphism
![]() $\unicode[STIX]{x1D719}:S\rightarrow X$
from a strict Henselian trait, the fiber
$\unicode[STIX]{x1D719}:S\rightarrow X$
from a strict Henselian trait, the fiber
![]() $Y\times _{X}\unicode[STIX]{x1D702}$
is nonempty since
$Y\times _{X}\unicode[STIX]{x1D702}$
is nonempty since
![]() $f$
is assumed surjective. There exists a finite extension
$f$
is assumed surjective. There exists a finite extension
![]() $\unicode[STIX]{x1D702}^{\prime }$
of
$\unicode[STIX]{x1D702}^{\prime }$
of
![]() $\unicode[STIX]{x1D702}$
and a morphism
$\unicode[STIX]{x1D702}$
and a morphism
![]() $\unicode[STIX]{x1D702}^{\prime }\rightarrow Y$
compatible with
$\unicode[STIX]{x1D702}^{\prime }\rightarrow Y$
compatible with
![]() $\unicode[STIX]{x1D702}\rightarrow X$
, thus, by valuative criterion of properness, we have a commutative diagram
$\unicode[STIX]{x1D702}\rightarrow X$
, thus, by valuative criterion of properness, we have a commutative diagram

where
![]() $S^{\prime }$
is a strict Henselian trait, and
$S^{\prime }$
is a strict Henselian trait, and
![]() $f^{\prime }$
is dominant. By the finite morphism case we have already treated, it suffices to check that
$f^{\prime }$
is dominant. By the finite morphism case we have already treated, it suffices to check that
![]() $f^{\prime \ast }\unicode[STIX]{x1D719}^{\ast }\mathscr{F}$
is smooth, which follows by assumption.◻
$f^{\prime \ast }\unicode[STIX]{x1D719}^{\ast }\mathscr{F}$
is smooth, which follows by assumption.◻
3.4
Let us recall briefly some basics of the theory of descent. Let
![]() $\unicode[STIX]{x1D6E5}$
be the category of three objects
$\unicode[STIX]{x1D6E5}$
be the category of three objects
![]() $[0],[1],[2]$
where
$[0],[1],[2]$
where
![]() $[i]=\{0,\ldots ,i\}$
. The morphism
$[i]=\{0,\ldots ,i\}$
. The morphism
![]() $[i]\rightarrow [j]$
is a nondecreasing map. We denote by
$[i]\rightarrow [j]$
is a nondecreasing map. We denote by
![]() $\unicode[STIX]{x1D6FF}_{j}^{n}:[n-1]\rightarrow [n]$
the map skipping
$\unicode[STIX]{x1D6FF}_{j}^{n}:[n-1]\rightarrow [n]$
the map skipping
![]() $j$
and
$j$
and
![]() $\unicode[STIX]{x1D70E}_{j}^{n}:[n+1]\rightarrow [n]$
be the map such that
$\unicode[STIX]{x1D70E}_{j}^{n}:[n+1]\rightarrow [n]$
be the map such that
![]() $(\unicode[STIX]{x1D70E}_{j}^{n})^{-1}(j)=\{j,j+1\}$
. A simplicial scheme
$(\unicode[STIX]{x1D70E}_{j}^{n})^{-1}(j)=\{j,j+1\}$
. A simplicial scheme
![]() $X_{\bullet }$
is a contravariant functor
$X_{\bullet }$
is a contravariant functor
![]() $\unicode[STIX]{x1D6E5}^{\circ }\rightarrow \text{Sch}(k)$
. Usually, this type of simplicial scheme is called
$\unicode[STIX]{x1D6E5}^{\circ }\rightarrow \text{Sch}(k)$
. Usually, this type of simplicial scheme is called
![]() $2$
-truncated simplicial scheme, but since we only use these, we abbreviate the word “
$2$
-truncated simplicial scheme, but since we only use these, we abbreviate the word “
![]() $2$
-truncated”. We put
$2$
-truncated”. We put
![]() $X_{i}:=X_{\bullet }([i])$
, and
$X_{i}:=X_{\bullet }([i])$
, and
![]() $d_{j}^{n}:=X_{\bullet }(\unicode[STIX]{x1D6FF}_{j}^{n})$
and
$d_{j}^{n}:=X_{\bullet }(\unicode[STIX]{x1D6FF}_{j}^{n})$
and
![]() $s_{j}^{n}:=X_{\bullet }(\unicode[STIX]{x1D70E}_{j}^{n})$
. The category of descent data for
$s_{j}^{n}:=X_{\bullet }(\unicode[STIX]{x1D70E}_{j}^{n})$
. The category of descent data for
![]() $X_{\bullet }$
denoted by
$X_{\bullet }$
denoted by
![]() $\text{Con}(X_{\bullet })$
consists of the following data as objects:
$\text{Con}(X_{\bullet })$
consists of the following data as objects:
∙ an object
 $\mathscr{F}\in \text{Con}(X_{0})$
;
$\mathscr{F}\in \text{Con}(X_{0})$
;∙ an isomorphism
 $\unicode[STIX]{x1D719}:d_{0}^{1\ast }\mathscr{F}\xrightarrow[{}]{{\sim}}d_{1}^{1\ast }\mathscr{F}$
;
$\unicode[STIX]{x1D719}:d_{0}^{1\ast }\mathscr{F}\xrightarrow[{}]{{\sim}}d_{1}^{1\ast }\mathscr{F}$
;
which satisfies the cocycle condition
![]() $d_{2}^{2\ast }(\unicode[STIX]{x1D719})\circ d_{0}^{2\ast }(\unicode[STIX]{x1D719})=d_{1}^{2\ast }(\unicode[STIX]{x1D719})$
on
$d_{2}^{2\ast }(\unicode[STIX]{x1D719})\circ d_{0}^{2\ast }(\unicode[STIX]{x1D719})=d_{1}^{2\ast }(\unicode[STIX]{x1D719})$
on
![]() $X_{2}$
and
$X_{2}$
and
![]() $s_{0}^{0\ast }\unicode[STIX]{x1D719}=\text{id}$
on
$s_{0}^{0\ast }\unicode[STIX]{x1D719}=\text{id}$
on
![]() $X_{0}$
. Given an augmentation
$X_{0}$
. Given an augmentation
![]() $f:X_{\bullet }\rightarrow X$
, namely a morphism of simplicial schemes considering
$f:X_{\bullet }\rightarrow X$
, namely a morphism of simplicial schemes considering
![]() $X$
as the constant simplicial scheme, we say that
$X$
as the constant simplicial scheme, we say that
![]() $\text{Con}(X)$
satisfies the descent with respect to
$\text{Con}(X)$
satisfies the descent with respect to
![]() $f$
if the canonical functor
$f$
if the canonical functor
![]() $\text{Con}(X)\rightarrow \text{Con}(X_{\bullet })$
is an equivalence of categories. An augmentation
$\text{Con}(X)\rightarrow \text{Con}(X_{\bullet })$
is an equivalence of categories. An augmentation
![]() $X_{\bullet }\rightarrow X$
is a proper hypercovering if the canonical morphisms
$X_{\bullet }\rightarrow X$
is a proper hypercovering if the canonical morphisms
![]() $X_{0}\rightarrow X$
,
$X_{0}\rightarrow X$
,
![]() $X_{0}\times _{X}X_{0}\rightarrow X_{1}$
, and
$X_{0}\times _{X}X_{0}\rightarrow X_{1}$
, and
![]() $X_{2}\rightarrow \text{cosk}_{1}\text{sk}_{1}(X_{\bullet })_{2}$
are proper surjective. For the functors
$X_{2}\rightarrow \text{cosk}_{1}\text{sk}_{1}(X_{\bullet })_{2}$
are proper surjective. For the functors
![]() $\text{sk}_{1}$
and
$\text{sk}_{1}$
and
![]() $\text{cosk}_{1}$
, one can refer, for example, to [St, Tag 0AMA].
$\text{cosk}_{1}$
, one can refer, for example, to [St, Tag 0AMA].
Lemma 3.5. Let
![]() $f:Y\rightarrow X$
be a proper surjective morphism. Then the hypercovering
$f:Y\rightarrow X$
be a proper surjective morphism. Then the hypercovering
![]() $Y_{\bullet }:=\text{cosk}_{1}(Y\times _{X}Y\rightrightarrows Y)\rightarrow X$
satisfies the descent.
$Y_{\bullet }:=\text{cosk}_{1}(Y\times _{X}Y\rightrightarrows Y)\rightarrow X$
satisfies the descent.
Proof. We have the natural functor
![]() $\unicode[STIX]{x1D6FC}:\text{Con}(X)\rightarrow \text{Con}(Y_{\bullet })$
, and we need to show that this is an equivalence. Let us construct the quasi-inverse. Let
$\unicode[STIX]{x1D6FC}:\text{Con}(X)\rightarrow \text{Con}(Y_{\bullet })$
, and we need to show that this is an equivalence. Let us construct the quasi-inverse. Let
![]() $(\mathscr{F},d_{0}^{1\ast }\mathscr{F}\cong d_{1}^{1\ast }\mathscr{F})$
where
$(\mathscr{F},d_{0}^{1\ast }\mathscr{F}\cong d_{1}^{1\ast }\mathscr{F})$
where
![]() $\mathscr{F}\in \text{Con}(Y)$
is a descent data. This is sent to
$\mathscr{F}\in \text{Con}(Y)$
is a descent data. This is sent to
where
![]() $g_{\ast }^{0}$
denotes
$g_{\ast }^{0}$
denotes
![]() $\text{}^{\text{c}}\!\mathscr{H}^{0}g_{\ast }$
for a morphism
$\text{}^{\text{c}}\!\mathscr{H}^{0}g_{\ast }$
for a morphism
![]() $g$
. This functor is denoted by
$g$
. This functor is denoted by
![]() $\unicode[STIX]{x1D6FD}$
. By adjunction, we have functors
$\unicode[STIX]{x1D6FD}$
. By adjunction, we have functors
![]() $\text{id}\rightarrow \unicode[STIX]{x1D6FD}\circ \unicode[STIX]{x1D6FC}$
and
$\text{id}\rightarrow \unicode[STIX]{x1D6FD}\circ \unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FC}\circ \unicode[STIX]{x1D6FD}\rightarrow \text{id}$
, and it remains to check that these functors are equivalent. Since
$\unicode[STIX]{x1D6FC}\circ \unicode[STIX]{x1D6FD}\rightarrow \text{id}$
, and it remains to check that these functors are equivalent. Since
![]() $f$
is assumed proper, by proper base change and [Reference AbeA2, 1.3.7 (i)], we may assume that
$f$
is assumed proper, by proper base change and [Reference AbeA2, 1.3.7 (i)], we may assume that
![]() $X$
is a point. Further, by replacing
$X$
is a point. Further, by replacing
![]() $X$
by its finite extension, we may assume that
$X$
by its finite extension, we may assume that
![]() $f$
has a section
$f$
has a section
![]() $s:X\rightarrow Y$
. In this case, the argument is standard.◻
$s:X\rightarrow Y$
. In this case, the argument is standard.◻
Corollary 3.6. Any proper hypercovering satisfies the descent.
Proof. Although the argument is very standard (for example, see [St, Tag 0D8D]), we give a proof for the convenience of the reader. Let
![]() $Y_{\bullet }\rightarrow X$
be a hypercovering of
$Y_{\bullet }\rightarrow X$
be a hypercovering of
![]() $X$
. If the hypercovering is
$X$
. If the hypercovering is
![]() $\text{cosk}_{1}(Y_{0}\times _{X}Y_{0}\rightrightarrows Y_{0})$
, then we already know the result by the lemma. The lemma also tells us that for a proper surjective morphism
$\text{cosk}_{1}(Y_{0}\times _{X}Y_{0}\rightrightarrows Y_{0})$
, then we already know the result by the lemma. The lemma also tells us that for a proper surjective morphism
![]() $W\rightarrow Z$
, the pullback
$W\rightarrow Z$
, the pullback
![]() $\text{Con}(Z)\rightarrow \text{Con}(W)$
is faithful. Thus, giving a descent data on
$\text{Con}(Z)\rightarrow \text{Con}(W)$
is faithful. Thus, giving a descent data on
![]() $Y_{\bullet }$
is equivalent to giving a descent data on
$Y_{\bullet }$
is equivalent to giving a descent data on
![]() $\text{cosk}_{1}(Y_{1}\rightrightarrows Y_{0})$
. From now on, we assume that
$\text{cosk}_{1}(Y_{1}\rightrightarrows Y_{0})$
. From now on, we assume that
![]() $Y_{\bullet }=\text{cosk}_{1}(Y_{1}\rightrightarrows Y_{0})$
.
$Y_{\bullet }=\text{cosk}_{1}(Y_{1}\rightrightarrows Y_{0})$
.
Given a proper hypercovering
![]() $Y_{\bullet }$
, a descent data for
$Y_{\bullet }$
, a descent data for
![]() $Y_{\bullet }$
is
$Y_{\bullet }$
is
![]() $\mathscr{F}\in \text{Con}(Y_{0})$
and an isomorphism
$\mathscr{F}\in \text{Con}(Y_{0})$
and an isomorphism
![]() $\unicode[STIX]{x1D719}:d_{0}^{1\ast }\mathscr{F}\cong d_{1}^{1\ast }\mathscr{F}$
satisfying some conditions. In order to define a descent data for
$\unicode[STIX]{x1D719}:d_{0}^{1\ast }\mathscr{F}\cong d_{1}^{1\ast }\mathscr{F}$
satisfying some conditions. In order to define a descent data for
![]() $\text{cosk}_{1}(Y_{0}\times _{X}Y_{0}\rightrightarrows Y_{0})$
, we only need to descent
$\text{cosk}_{1}(Y_{0}\times _{X}Y_{0}\rightrightarrows Y_{0})$
, we only need to descent
![]() $\unicode[STIX]{x1D719}$
to
$\unicode[STIX]{x1D719}$
to
![]() $Y_{0}\times _{X}Y_{0}$
. Now, we have the following morphism
$Y_{0}\times _{X}Y_{0}$
. Now, we have the following morphism
This defines the following diagram of simplicial schemes:

where
![]() $d_{i}^{\prime 2}:=\text{pr}_{i}\circ \unicode[STIX]{x1D6FC}$
. By the universal property of
$d_{i}^{\prime 2}:=\text{pr}_{i}\circ \unicode[STIX]{x1D6FC}$
. By the universal property of
![]() $\text{cosk}$
, we have the dotted vertical arrow so that they form a morphism of simplicial schemes. The cocycle condition for
$\text{cosk}$
, we have the dotted vertical arrow so that they form a morphism of simplicial schemes. The cocycle condition for
![]() $\unicode[STIX]{x1D719}$
on
$\unicode[STIX]{x1D719}$
on
![]() $Y_{2}$
pulled back to
$Y_{2}$
pulled back to
![]() $Y_{1}\times _{(Y_{0}\times _{X}Y_{0})}Y_{1}$
by the dotted arrow gives us the following commutative diagram:
$Y_{1}\times _{(Y_{0}\times _{X}Y_{0})}Y_{1}$
by the dotted arrow gives us the following commutative diagram:

Thus, the isomorphism
![]() $\unicode[STIX]{x1D719}$
descends to
$\unicode[STIX]{x1D719}$
descends to
![]() $Y_{0}\times _{X}Y_{0}$
, and defines a descent data on
$Y_{0}\times _{X}Y_{0}$
, and defines a descent data on
![]() $\text{cosk}_{1}(Y_{0}\times _{X}Y_{0}\rightrightarrows Y_{0})$
. Finally, use Lemma 3.5 to conclude.◻
$\text{cosk}_{1}(Y_{0}\times _{X}Y_{0}\rightrightarrows Y_{0})$
. Finally, use Lemma 3.5 to conclude.◻
Lemma 3.7. Let
![]() $X$
be a scheme, and
$X$
be a scheme, and
![]() $\mathscr{F}\in D^{{\leqslant}0}(X)$
. Then
$\mathscr{F}\in D^{{\leqslant}0}(X)$
. Then
![]() $\mathscr{H}^{0}(\mathscr{F})=0$
if and only if for any closed immersion
$\mathscr{H}^{0}(\mathscr{F})=0$
if and only if for any closed immersion
![]() $i:Z{\hookrightarrow}X$
, there exists a dense subscheme
$i:Z{\hookrightarrow}X$
, there exists a dense subscheme
![]() $U\subset Z$
such that
$U\subset Z$
such that
![]() $\mathscr{H}^{0}(i^{\ast }\mathscr{F})|_{U}=0$
.
$\mathscr{H}^{0}(i^{\ast }\mathscr{F})|_{U}=0$
.
Proof. Only if part follows since
![]() $i^{\ast }$
is right exact by [Reference Abe and CaroAC, Proposition 1.3.13]. Assume
$i^{\ast }$
is right exact by [Reference Abe and CaroAC, Proposition 1.3.13]. Assume
![]() $\mathscr{H}^{0}\mathscr{F}$
is supported on a reduced scheme
$\mathscr{H}^{0}\mathscr{F}$
is supported on a reduced scheme
![]() $Z$
. Consider the triangle
$Z$
. Consider the triangle
Since
![]() $i^{\ast }$
is right exact,
$i^{\ast }$
is right exact,
![]() $\mathscr{H}^{i}i_{Z}^{\ast }\unicode[STIX]{x1D70F}_{{<}0}\mathscr{F}=0$
for
$\mathscr{H}^{i}i_{Z}^{\ast }\unicode[STIX]{x1D70F}_{{<}0}\mathscr{F}=0$
for
![]() $i\geqslant 0$
, which implies that
$i\geqslant 0$
, which implies that
![]() $\mathscr{H}^{0}i_{Z}^{\ast }(\mathscr{F})\cong \mathscr{H}^{0}i_{Z}^{\ast }\mathscr{H}^{0}(\mathscr{F})$
. Since we assumed that
$\mathscr{H}^{0}i_{Z}^{\ast }(\mathscr{F})\cong \mathscr{H}^{0}i_{Z}^{\ast }\mathscr{H}^{0}(\mathscr{F})$
. Since we assumed that
![]() $Z$
is the support of
$Z$
is the support of
![]() $\mathscr{H}^{0}\mathscr{F}$
, we have
$\mathscr{H}^{0}\mathscr{F}$
, we have
![]() $i_{Z\ast }\mathscr{H}^{0}i_{Z}^{\ast }\mathscr{H}^{0}(\mathscr{F})\cong \mathscr{H}^{0}(\mathscr{F})$
. Combining these, we have
$i_{Z\ast }\mathscr{H}^{0}i_{Z}^{\ast }\mathscr{H}^{0}(\mathscr{F})\cong \mathscr{H}^{0}(\mathscr{F})$
. Combining these, we have
![]() $i_{Z\ast }\mathscr{H}^{0}i_{Z}^{\ast }(\mathscr{F})\cong \mathscr{H}^{0}(\mathscr{F})$
, and this vanishes generically on
$i_{Z\ast }\mathscr{H}^{0}i_{Z}^{\ast }(\mathscr{F})\cong \mathscr{H}^{0}(\mathscr{F})$
, and this vanishes generically on
![]() $Z$
by assumption. This can happen only when
$Z$
by assumption. This can happen only when
![]() $Z=\emptyset$
.◻
$Z=\emptyset$
.◻
3.8
Let us compare smooth objects with isocrystals. For a scheme
![]() $X$
of finite type over
$X$
of finite type over
![]() $k$
, we denote by
$k$
, we denote by
![]() $\text{Isoc}^{\dagger }(X)$
the subcategory of the category of overconvergent isocrystals on
$\text{Isoc}^{\dagger }(X)$
the subcategory of the category of overconvergent isocrystals on
![]() $X$
consisting of isocrystals whose constituents can be endowed with Frobenius structure (see right after [Reference AbeA2, 1.1.3 (11)]). Caution that
$X$
consisting of isocrystals whose constituents can be endowed with Frobenius structure (see right after [Reference AbeA2, 1.1.3 (11)]). Caution that
![]() $\text{Isoc}^{\dagger }(X)$
is slightly smaller than the category of overconvergent isocrystals on
$\text{Isoc}^{\dagger }(X)$
is slightly smaller than the category of overconvergent isocrystals on
![]() $X$
.
$X$
.
Theorem. Let
![]() $X$
be a scheme of finite type over
$X$
be a scheme of finite type over
![]() $k$
. Then we have a canonical equivalence of categories
$k$
. Then we have a canonical equivalence of categories
![]() $\text{Isoc}^{\dagger }(X)\xrightarrow[{}]{{\sim}}\text{Sm}(X)$
. This equivalence is compatible with pullback.
$\text{Isoc}^{\dagger }(X)\xrightarrow[{}]{{\sim}}\text{Sm}(X)$
. This equivalence is compatible with pullback.
Proof. First, let us construct the functor in the case where
![]() $X$
is smooth. In this situation, Caro [Reference CaroC1] (cf. [Reference AbeA2, 2.4.15] for a summary) defines a fully faithful functor
$X$
is smooth. In this situation, Caro [Reference CaroC1] (cf. [Reference AbeA2, 2.4.15] for a summary) defines a fully faithful functor
Note that this functor is compatible with pullback. All we need to show is that the essential image of this functor is
![]() $\text{Sm}(X)$
. First, let us check this claim when
$\text{Sm}(X)$
. First, let us check this claim when
![]() $X$
is a curve. In this case, the inclusion
$X$
is a curve. In this case, the inclusion
![]() $\text{Im}(\unicode[STIX]{x1D70C}_{X})\subset \text{Sm}(X)$
follows easily, and the other inclusion follows by [Reference AbeA2, Lemma 2.4.11]. We note that in [Reference AbeA2],
$\text{Im}(\unicode[STIX]{x1D70C}_{X})\subset \text{Sm}(X)$
follows easily, and the other inclusion follows by [Reference AbeA2, Lemma 2.4.11]. We note that in [Reference AbeA2],
![]() $\mathscr{M}\in D(X)$
being smooth means
$\mathscr{M}\in D(X)$
being smooth means
![]() $\mathscr{M}$
is in the essential image of
$\mathscr{M}$
is in the essential image of
![]() $\unicode[STIX]{x1D70C}_{X}$
. Now assume
$\unicode[STIX]{x1D70C}_{X}$
. Now assume
![]() $X$
is smooth but not necessarily a curve. We show by using the induction on the dimension of
$X$
is smooth but not necessarily a curve. We show by using the induction on the dimension of
![]() $X$
. We assume the equivalence is known for any smooth
$X$
. We assume the equivalence is known for any smooth
![]() $X$
of dimension
$X$
of dimension
![]() ${<}n$
. Assume
${<}n$
. Assume
![]() $X$
is of dimension
$X$
is of dimension
![]() $n$
. Let
$n$
. Let
![]() $E\in \text{Isoc}^{\dagger }(X)$
, and let us check that
$E\in \text{Isoc}^{\dagger }(X)$
, and let us check that
![]() $\unicode[STIX]{x1D70C}_{X}(E)$
is smooth. By definition and some limit argument, it suffices to check that for any morphism
$\unicode[STIX]{x1D70C}_{X}(E)$
is smooth. By definition and some limit argument, it suffices to check that for any morphism
![]() $c:C\rightarrow X$
from a smooth curve
$c:C\rightarrow X$
from a smooth curve
![]() $C$
,
$C$
,
![]() $c^{\ast }\unicode[STIX]{x1D70C}_{X}(E)$
is smooth. However, since
$c^{\ast }\unicode[STIX]{x1D70C}_{X}(E)$
is smooth. However, since
![]() $c^{\ast }\unicode[STIX]{x1D70C}_{X}(E)\cong \unicode[STIX]{x1D70C}_{X}(c^{\ast }E)$
by the compatibility of pullback and we have already checked the claim for curves,
$c^{\ast }\unicode[STIX]{x1D70C}_{X}(E)\cong \unicode[STIX]{x1D70C}_{X}(c^{\ast }E)$
by the compatibility of pullback and we have already checked the claim for curves,
![]() $\unicode[STIX]{x1D70C}_{X}(c^{\ast }E)$
is smooth, thus
$\unicode[STIX]{x1D70C}_{X}(c^{\ast }E)$
is smooth, thus
![]() $\unicode[STIX]{x1D70C}_{X}(E)\in \text{Sm}(X)$
. Let
$\unicode[STIX]{x1D70C}_{X}(E)\in \text{Sm}(X)$
. Let
![]() $\mathscr{L}\in \text{Sm}(X)$
, and let us show that
$\mathscr{L}\in \text{Sm}(X)$
, and let us show that
![]() $\mathscr{L}$
comes from an isocrystal. There exists an open dense subscheme
$\mathscr{L}$
comes from an isocrystal. There exists an open dense subscheme
![]() $j:U\subset X$
such that
$j:U\subset X$
such that
![]() $\mathscr{L}|_{U}\cong \unicode[STIX]{x1D70C}_{U}(E_{U})$
. We claim that
$\mathscr{L}|_{U}\cong \unicode[STIX]{x1D70C}_{U}(E_{U})$
. We claim that
![]() $E_{U}$
extends to an isocrystal
$E_{U}$
extends to an isocrystal
![]() $E$
on
$E$
on
![]() $X$
. Indeed, let
$X$
. Indeed, let
![]() $c:C\rightarrow X$
be a morphism from a smooth curve
$c:C\rightarrow X$
be a morphism from a smooth curve
![]() $C$
. By the compatibility of pullback and the equivalence of
$C$
. By the compatibility of pullback and the equivalence of
![]() $\unicode[STIX]{x1D70C}_{C}$
we have already checked,
$\unicode[STIX]{x1D70C}_{C}$
we have already checked,
![]() $c^{\ast }E_{U}$
does extend to an isocrystal on
$c^{\ast }E_{U}$
does extend to an isocrystal on
![]() $C$
. Now, let
$C$
. Now, let
![]() $W\subset X$
be a closed subscheme of codimension
$W\subset X$
be a closed subscheme of codimension
![]() ${\geqslant}2$
such that
${\geqslant}2$
such that
![]() $(X\setminus U)\setminus W$
is smooth. By Shiho’s cut-by-curve theorem [Reference ShihoS, Theorem 0.1] (see footnote of [Reference AbeA2, 2.4.13] when the base field
$(X\setminus U)\setminus W$
is smooth. By Shiho’s cut-by-curve theorem [Reference ShihoS, Theorem 0.1] (see footnote of [Reference AbeA2, 2.4.13] when the base field
![]() $k$
is not uncountable for some explanation),
$k$
is not uncountable for some explanation),
![]() $E_{U}$
extends to an isocrystal on
$E_{U}$
extends to an isocrystal on
![]() $X\setminus W$
. Finally, by Kedlaya’s purity result [Reference KedlayaK1, Proposition 5.3.3],
$X\setminus W$
. Finally, by Kedlaya’s purity result [Reference KedlayaK1, Proposition 5.3.3],
![]() $E_{U}$
extends even to
$E_{U}$
extends even to
![]() $X$
, and the claim follows. To conclude the proof, we need to show that the isomorphism
$X$
, and the claim follows. To conclude the proof, we need to show that the isomorphism
![]() $\mathscr{L}|_{U}\cong \unicode[STIX]{x1D70C}_{U}(E_{U})$
extends uniquely to an isomorphism
$\mathscr{L}|_{U}\cong \unicode[STIX]{x1D70C}_{U}(E_{U})$
extends uniquely to an isomorphism
![]() $\mathscr{L}\cong \unicode[STIX]{x1D70C}_{X}(E)$
.
$\mathscr{L}\cong \unicode[STIX]{x1D70C}_{X}(E)$
.
Let
![]() $i:Z\rightarrow X$
be the complement of
$i:Z\rightarrow X$
be the complement of
![]() $U$
. Let us show that
$U$
. Let us show that
![]() $\mathscr{H}^{n}(i^{\ast }\mathscr{L})=0$
. In order to show this, it suffices to check that for any closed immersion
$\mathscr{H}^{n}(i^{\ast }\mathscr{L})=0$
. In order to show this, it suffices to check that for any closed immersion
![]() $i_{W}:W{\hookrightarrow}Z$
,
$i_{W}:W{\hookrightarrow}Z$
,
![]() $\mathscr{H}^{n}(i_{W}^{\ast }i^{\ast }\mathscr{L})$
vanishes generically on
$\mathscr{H}^{n}(i_{W}^{\ast }i^{\ast }\mathscr{L})$
vanishes generically on
![]() $W$
by Lemma 3.7. Since the associated reduced scheme of
$W$
by Lemma 3.7. Since the associated reduced scheme of
![]() $W$
is generically smooth,
$W$
is generically smooth,
![]() $i_{W}^{\ast }i^{\ast }\mathscr{L}$
is smooth on
$i_{W}^{\ast }i^{\ast }\mathscr{L}$
is smooth on
![]() $W$
, and by induction hypothesis,
$W$
, and by induction hypothesis,
![]() $i_{W}^{\ast }i^{\ast }\mathscr{L}$
generically comes from an isocrystal. Since isocrystals concentrate on degree
$i_{W}^{\ast }i^{\ast }\mathscr{L}$
generically comes from an isocrystal. Since isocrystals concentrate on degree
![]() ${\leqslant}\dim (W)<n$
, we get the claim. Now, since
${\leqslant}\dim (W)<n$
, we get the claim. Now, since
![]() $\mathscr{L}$
is constructible,
$\mathscr{L}$
is constructible,
![]() $\mathscr{H}^{i}\mathscr{L}=0$
for
$\mathscr{H}^{i}\mathscr{L}=0$
for
![]() $i>n$
. Considering the exact triangle
$i>n$
. Considering the exact triangle
![]() $j_{!}\mathscr{L}\rightarrow \mathscr{L}\rightarrow i^{\ast }\mathscr{L}\xrightarrow[{}]{+}$
, the homomorphism
$j_{!}\mathscr{L}\rightarrow \mathscr{L}\rightarrow i^{\ast }\mathscr{L}\xrightarrow[{}]{+}$
, the homomorphism
![]() $\mathscr{H}^{n}j_{!}\mathscr{L}\rightarrow \mathscr{H}^{n}\mathscr{L}$
is surjective because we have checked that
$\mathscr{H}^{n}j_{!}\mathscr{L}\rightarrow \mathscr{H}^{n}\mathscr{L}$
is surjective because we have checked that
![]() $\mathscr{H}^{n}i^{\ast }\mathscr{L}=0$
. Thus, we have a canonical homomorphism
$\mathscr{H}^{n}i^{\ast }\mathscr{L}=0$
. Thus, we have a canonical homomorphism
![]() $\mathscr{L}\rightarrow j_{!\ast }(\mathscr{L})$
. This induces
$\mathscr{L}\rightarrow j_{!\ast }(\mathscr{L})$
. This induces
![]() $\mathscr{L}\rightarrow j_{!\ast }\mathscr{L}\cong j_{!\ast }\unicode[STIX]{x1D70C}_{U}(E_{U})\cong \unicode[STIX]{x1D70C}_{X}(E)$
whose restriction to
$\mathscr{L}\rightarrow j_{!\ast }\mathscr{L}\cong j_{!\ast }\unicode[STIX]{x1D70C}_{U}(E_{U})\cong \unicode[STIX]{x1D70C}_{X}(E)$
whose restriction to
![]() $U$
is the given map. The compatibility of pullback and induction hypothesis implies that this is in fact an isomorphism and is a unique homomorphism extending the given
$U$
is the given map. The compatibility of pullback and induction hypothesis implies that this is in fact an isomorphism and is a unique homomorphism extending the given
![]() $\mathscr{L}|_{U}\cong \unicode[STIX]{x1D70C}_{U}(E_{U})$
.
$\mathscr{L}|_{U}\cong \unicode[STIX]{x1D70C}_{U}(E_{U})$
.
In the general case, by using de Jong’s alteration, we can take a proper hypercovering
![]() $Y_{\bullet }$
of
$Y_{\bullet }$
of
![]() $X$
such that
$X$
such that
![]() $Y_{i}$
is smooth for any
$Y_{i}$
is smooth for any
![]() $i$
. By Corollary 3.6, proper descent of isocrystals [Reference ShihoS, Proposition 7.3], and the compatibility of pullback, we have a functor
$i$
. By Corollary 3.6, proper descent of isocrystals [Reference ShihoS, Proposition 7.3], and the compatibility of pullback, we have a functor
![]() $\text{Isoc}^{\dagger }(X)\rightarrow \text{Con}(X)$
. It is easy to check that this functor does not depend on the choice of
$\text{Isoc}^{\dagger }(X)\rightarrow \text{Con}(X)$
. It is easy to check that this functor does not depend on the choice of
![]() $Y_{0}$
,
$Y_{0}$
,
![]() $Y_{1}$
up to canonical isomorphism. The essential image coincides with
$Y_{1}$
up to canonical isomorphism. The essential image coincides with
![]() $\text{Sm}(X)$
since smooth objects are preserved by pullback and Lemma 3.3.◻
$\text{Sm}(X)$
since smooth objects are preserved by pullback and Lemma 3.3.◻
Corollary 3.9. Let
![]() $X$
be a scheme,
$X$
be a scheme,
![]() $j:U{\hookrightarrow}X$
an open immersion, and
$j:U{\hookrightarrow}X$
an open immersion, and
![]() $\mathscr{L}\in \text{Sm}(X)$
. For any
$\mathscr{L}\in \text{Sm}(X)$
. For any
![]() $\mathscr{G}\in D(X)$
, we have a canonical isomorphism
$\mathscr{G}\in D(X)$
, we have a canonical isomorphism
Proof. By limit argument, we may assume
![]() $X$
is of finite type over
$X$
is of finite type over
![]() $k$
. The homomorphism is defined by adjunctions. Since it is an isomorphism on
$k$
. The homomorphism is defined by adjunctions. Since it is an isomorphism on
![]() $U$
, it suffices to check that
$U$
, it suffices to check that
![]() $i^{!}(\mathscr{L}\,\otimes \,j_{\ast }(\mathscr{G}))=0$
where
$i^{!}(\mathscr{L}\,\otimes \,j_{\ast }(\mathscr{G}))=0$
where
![]() $i:X\setminus U\rightarrow X$
. Let us show the claim using the induction on the dimension of the support of
$i:X\setminus U\rightarrow X$
. Let us show the claim using the induction on the dimension of the support of
![]() $\mathscr{G}$
. When the dimension is
$\mathscr{G}$
. When the dimension is
![]() $0$
, there is nothing to show. Take an alteration
$0$
, there is nothing to show. Take an alteration
![]() $g:X^{\prime }\rightarrow X$
such that
$g:X^{\prime }\rightarrow X$
such that
![]() $X^{\prime }$
is smooth, and let
$X^{\prime }$
is smooth, and let
![]() $j_{UV}:V\subset U$
be an open dense subscheme such that
$j_{UV}:V\subset U$
be an open dense subscheme such that
![]() $g_{V}:g^{-1}(V)\rightarrow V$
is finite étale. By induction hypothesis, we may assume that
$g_{V}:g^{-1}(V)\rightarrow V$
is finite étale. By induction hypothesis, we may assume that
![]() $\mathscr{G}=j_{UV\ast }\mathscr{G}_{V}$
for some
$\mathscr{G}=j_{UV\ast }\mathscr{G}_{V}$
for some
![]() $\mathscr{G}_{V}$
. Since
$\mathscr{G}_{V}$
. Since
![]() $g_{V}$
is finite étale,
$g_{V}$
is finite étale,
![]() $\mathscr{G}_{V}$
is a direct factor of
$\mathscr{G}_{V}$
is a direct factor of
![]() $g_{V\ast }g_{V}^{\ast }\mathscr{G}_{V}$
. Consider the following diagram
$g_{V\ast }g_{V}^{\ast }\mathscr{G}_{V}$
. Consider the following diagram

Using the projection formula and the commutation of
![]() $g_{\ast }$
and
$g_{\ast }$
and
![]() $i^{!}$
, we have
$i^{!}$
, we have
Thus, it suffices to check that
![]() $i^{\prime !}(g^{\ast }\mathscr{L}\,\otimes \,j_{V\ast }^{\prime }g_{V}^{\ast }(\mathscr{G}_{V}))=0$
, and may assume that
$i^{\prime !}(g^{\ast }\mathscr{L}\,\otimes \,j_{V\ast }^{\prime }g_{V}^{\ast }(\mathscr{G}_{V}))=0$
, and may assume that
![]() $X$
is smooth. Then we use Theorem 3.8 and [Reference AbeA1, Proposition 5.8] to conclude.
$X$
is smooth. Then we use Theorem 3.8 and [Reference AbeA1, Proposition 5.8] to conclude.
Corollary 3.10. Let
![]() $(S,s,\unicode[STIX]{x1D702})$
be a Henselian trait. Let
$(S,s,\unicode[STIX]{x1D702})$
be a Henselian trait. Let
![]() $\unicode[STIX]{x1D70B}:X\rightarrow S$
be a morphism of finite type and
$\unicode[STIX]{x1D70B}:X\rightarrow S$
be a morphism of finite type and
![]() $\mathscr{L}\in \text{Sm}(X)$
. Then for any
$\mathscr{L}\in \text{Sm}(X)$
. Then for any
![]() $\mathscr{G}\in \text{Hol}(X)$
, we have a canonical isomorphism
$\mathscr{G}\in \text{Hol}(X)$
, we have a canonical isomorphism
Theorem 3.11. Let
![]() $f:X\rightarrow Y$
be a morphism of schemes.
$f:X\rightarrow Y$
be a morphism of schemes.
(1) The functor
 $f^{\ast }$
preserves smooth objects. In particular, it induces a functor
$f^{\ast }$
preserves smooth objects. In particular, it induces a functor
 $f^{\ast }:\text{Sm}(Y)\rightarrow \text{Sm}(X)$
.
$f^{\ast }:\text{Sm}(Y)\rightarrow \text{Sm}(X)$
.(2) Assume that
 $f$
is proper and smooth. Then
$f$
is proper and smooth. Then
 $f_{\ast }$
preserves smooth objects.
$f_{\ast }$
preserves smooth objects.
Proof. The preservation under pullback follows directly by definition, and we write it just for the future reference. Let us check the second claim. Take a strict Henselian trait
![]() $S$
and a morphism
$S$
and a morphism
![]() $\unicode[STIX]{x1D719}:S\rightarrow Y$
. Using 1 and the commutation of
$\unicode[STIX]{x1D719}:S\rightarrow Y$
. Using 1 and the commutation of
![]() $f_{\ast }$
and
$f_{\ast }$
and
![]() $\unicode[STIX]{x1D719}^{\ast }$
because
$\unicode[STIX]{x1D719}^{\ast }$
because
![]() $f$
is assumed proper, it suffices to check the claim when
$f$
is assumed proper, it suffices to check the claim when
![]() $Y$
is strict Henselian trait. Let
$Y$
is strict Henselian trait. Let
![]() $\mathscr{L}$
be a smooth object on
$\mathscr{L}$
be a smooth object on
![]() $X$
. We have
$X$
. We have
where the first isomorphism follows by Corollary 2.6.1, and the second by Corollary 3.10. Finally, since
![]() $f$
is assumed smooth, we have
$f$
is assumed smooth, we have
![]() $\unicode[STIX]{x1D6F7}_{f}(L_{X})\cong f^{\ast }\unicode[STIX]{x1D6F7}_{\text{id}}(L_{Y})$
by Corollary 2.6.2. Since
$\unicode[STIX]{x1D6F7}_{f}(L_{X})\cong f^{\ast }\unicode[STIX]{x1D6F7}_{\text{id}}(L_{Y})$
by Corollary 2.6.2. Since
![]() $Y$
is assumed strict Henselian trait,
$Y$
is assumed strict Henselian trait,
![]() $\text{rk}(\unicode[STIX]{x1D6F9}_{\text{id}}(L_{Y}))=1$
by Proposition 1.10. Thus, the exact triangle 2.6.3 tells us that
$\text{rk}(\unicode[STIX]{x1D6F9}_{\text{id}}(L_{Y}))=1$
by Proposition 1.10. Thus, the exact triangle 2.6.3 tells us that
![]() $\unicode[STIX]{x1D6F7}_{\text{id}}(L_{Y})=0$
, and the theorem follows.◻
$\unicode[STIX]{x1D6F7}_{\text{id}}(L_{Y})=0$
, and the theorem follows.◻
Remark.
One can think part 2 of the theorem above as a
![]() $\mathscr{D}$
-module theoretic version of Berthelot’s conjecture [Reference BerthelotBer, (4.3)]. This variant has already been considered by Caro in [Reference CaroC2, Théorème 4.4.2] when
$\mathscr{D}$
-module theoretic version of Berthelot’s conjecture [Reference BerthelotBer, (4.3)]. This variant has already been considered by Caro in [Reference CaroC2, Théorème 4.4.2] when
![]() $X$
,
$X$
,
![]() $Y$
are realizable schemes. In that case, he proved without the existence of Frobenius structure, whereas we assume the existence implicitly in the construction of the category
$Y$
are realizable schemes. In that case, he proved without the existence of Frobenius structure, whereas we assume the existence implicitly in the construction of the category
![]() $\text{Hol}(X)$
. However, our theorem is stronger in the sense that the schemes need not be realizable. In order to deduce the original Berthelot’s conjecture from our result, one might need to compare our pushforward and relative rigid cohomology (cf. [Reference AbeA2, 2.4.16]). This will be addressed in future works.
$\text{Hol}(X)$
. However, our theorem is stronger in the sense that the schemes need not be realizable. In order to deduce the original Berthelot’s conjecture from our result, one might need to compare our pushforward and relative rigid cohomology (cf. [Reference AbeA2, 2.4.16]). This will be addressed in future works.
Question 3.12. Assume
![]() $X$
is smooth. For any object
$X$
is smooth. For any object
![]() $\mathscr{M}\in D(X)$
, the characteristic variety
$\mathscr{M}\in D(X)$
, the characteristic variety
![]() $\text{Car}(\mathscr{M})$
is defined as a closed subscheme of codimension
$\text{Car}(\mathscr{M})$
is defined as a closed subscheme of codimension
![]() $\dim (X)$
in
$\dim (X)$
in
![]() $T^{\ast }X$
by Berthelot. We expect that this characteristic variety has the following characterization: for any
$T^{\ast }X$
by Berthelot. We expect that this characteristic variety has the following characterization: for any
![]() $X\supset U\xrightarrow[{}]{f}\mathbb{A}^{1}$
such that
$X\supset U\xrightarrow[{}]{f}\mathbb{A}^{1}$
such that
![]() $U$
is an open subscheme of
$U$
is an open subscheme of
![]() $X$
and
$X$
and
![]() $df(U)\cap \text{Car}(\mathscr{M})=\emptyset$
we have
$df(U)\cap \text{Car}(\mathscr{M})=\emptyset$
we have
![]() $\unicode[STIX]{x1D6F7}_{f}(\mathscr{M})=0$
, and
$\unicode[STIX]{x1D6F7}_{f}(\mathscr{M})=0$
, and
![]() $\text{Car}(\mathscr{M})$
is the smallest closed subscheme of
$\text{Car}(\mathscr{M})$
is the smallest closed subscheme of
![]() $T^{\ast }X$
having possessing such a property.
$T^{\ast }X$
having possessing such a property.
4 Toward a local theory
Definition 4.1.
(1) Let
 $S$
be a Henselian local scheme (i.e., it is a scheme which is the spectrum of a Henselian local ring), and let
$S$
be a Henselian local scheme (i.e., it is a scheme which is the spectrum of a Henselian local ring), and let
 $i:s{\hookrightarrow}S$
be the closed immersion from the closed point. The category
$i:s{\hookrightarrow}S$
be the closed immersion from the closed point. The category
 $\text{Loc}(S)$
is defined as follows: The object is the same as
$\text{Loc}(S)$
is defined as follows: The object is the same as
 $\text{Hol}(S)$
. For
$\text{Hol}(S)$
. For
 $\mathscr{F}\in \text{Hol}(S)$
the corresponding object in
$\mathscr{F}\in \text{Hol}(S)$
the corresponding object in
 $\text{Loc}(S)$
is denoted by
$\text{Loc}(S)$
is denoted by
 $\mathscr{F}^{\text{loc}}$
. Then where
$\mathscr{F}^{\text{loc}}$
. Then where $$\begin{eqnarray}\text{Hom}_{\text{Loc}(S)}(\mathscr{F}^{\text{loc}},\mathscr{G}^{\text{loc}}):=H^{0}(s,i^{\ast }{\mathcal{H}}om_{S}(\mathscr{F},\mathscr{G})),\end{eqnarray}$$
$$\begin{eqnarray}\text{Hom}_{\text{Loc}(S)}(\mathscr{F}^{\text{loc}},\mathscr{G}^{\text{loc}}):=H^{0}(s,i^{\ast }{\mathcal{H}}om_{S}(\mathscr{F},\mathscr{G})),\end{eqnarray}$$
 $H^{i}(s,\mathscr{H}):=\text{Hom}_{D(s)}(L_{s},\mathscr{H}[i])$
. The object
$H^{i}(s,\mathscr{H}):=\text{Hom}_{D(s)}(L_{s},\mathscr{H}[i])$
. The object
 $L_{S}^{\text{loc}}$
is denoted by
$L_{S}^{\text{loc}}$
is denoted by
 $L_{S}$
for simplicity.
$L_{S}$
for simplicity.(2) Let
 $S$
be a local Henselian scheme, and
$S$
be a local Henselian scheme, and
 $f:X\rightarrow S$
be a morphism of finite type. Then
$f:X\rightarrow S$
be a morphism of finite type. Then
 $\text{Loc}(X/S)$
is defined as follows. The objects are the same as
$\text{Loc}(X/S)$
is defined as follows. The objects are the same as
 $\text{Hol}(X)$
. For
$\text{Hol}(X)$
. For
 $\mathscr{F},\mathscr{G}\in \text{Hol}(X)$
, we define
$\mathscr{F},\mathscr{G}\in \text{Hol}(X)$
, we define  $$\begin{eqnarray}\text{Hom}_{\text{Loc}(X/S)}(\mathscr{F},\mathscr{G}):=\text{Hom}_{\text{Loc}(S)}(L_{S},f_{\ast }{\mathcal{H}}om(\mathscr{F},\mathscr{G})).\end{eqnarray}$$
$$\begin{eqnarray}\text{Hom}_{\text{Loc}(X/S)}(\mathscr{F},\mathscr{G}):=\text{Hom}_{\text{Loc}(S)}(L_{S},f_{\ast }{\mathcal{H}}om(\mathscr{F},\mathscr{G})).\end{eqnarray}$$
Remark 4.2.
(1) The category
 $\text{Loc}(X/S)$
is certainly an additive category. However, we do not know if this is abelian or not.
$\text{Loc}(X/S)$
is certainly an additive category. However, we do not know if this is abelian or not.(2) We assume we are in the situation of 4.1.1. We remark that
for $$\begin{eqnarray}H^{i}(s,i^{\ast }{\mathcal{H}}om_{S}(\mathscr{F},\mathscr{G}))=0\end{eqnarray}$$
$$\begin{eqnarray}H^{i}(s,i^{\ast }{\mathcal{H}}om_{S}(\mathscr{F},\mathscr{G}))=0\end{eqnarray}$$
 $i<0$
. Indeed, let us check first that for any scheme
$i<0$
. Indeed, let us check first that for any scheme
 $X$
and
$X$
and
 $\mathscr{F},\mathscr{G}\in \text{Hol}(X)$
,
$\mathscr{F},\mathscr{G}\in \text{Hol}(X)$
,
 $\text{}^{\text{c}}\!\mathscr{H}^{i}{\mathcal{H}}om_{X}(\mathscr{F},\mathscr{G})=0$
for
$\text{}^{\text{c}}\!\mathscr{H}^{i}{\mathcal{H}}om_{X}(\mathscr{F},\mathscr{G})=0$
for
 $i<0$
. We may assume
$i<0$
. We may assume
 $X$
is smooth. For
$X$
is smooth. For
 $\mathscr{F}\in D^{{\leqslant}0}(X)$
,
$\mathscr{F}\in D^{{\leqslant}0}(X)$
,
 $\mathscr{G}\in D^{{\geqslant}0}(X)$
, we may check as [Reference Beilinson, Bernstein and DeligneBBD, 2.1.20] that
$\mathscr{G}\in D^{{\geqslant}0}(X)$
, we may check as [Reference Beilinson, Bernstein and DeligneBBD, 2.1.20] that
 ${\mathcal{H}}om(\mathscr{F},\mathscr{G})\in ^{\text{c}}D^{{\geqslant}0}(X)$
. Thus,
${\mathcal{H}}om(\mathscr{F},\mathscr{G})\in ^{\text{c}}D^{{\geqslant}0}(X)$
. Thus,
 $\text{}^{\text{c}}\!\mathscr{H}^{i}{\mathcal{H}}om(\mathscr{F},\mathscr{G})=0$
for
$\text{}^{\text{c}}\!\mathscr{H}^{i}{\mathcal{H}}om(\mathscr{F},\mathscr{G})=0$
for
 $i<0$
. Since
$i<0$
. Since
 $i^{\ast }$
is c-t-exact and
$i^{\ast }$
is c-t-exact and
 $L_{s}$
is constructible object, we get the claim.
$L_{s}$
is constructible object, we get the claim.(3) Ultimately, we expect a triangulated category
 $D_{\text{loc}}(X/S)$
with the following properties: First, we have a functor
$D_{\text{loc}}(X/S)$
with the following properties: First, we have a functor
 $\unicode[STIX]{x1D70C}:D(X)\rightarrow D_{\text{loc}}(X/S)$
. For
$\unicode[STIX]{x1D70C}:D(X)\rightarrow D_{\text{loc}}(X/S)$
. For
 $\mathscr{F},\mathscr{G}\in D(X)$
, we should have Second, we have a t-structure on
$\mathscr{F},\mathscr{G}\in D(X)$
, we should have Second, we have a t-structure on $$\begin{eqnarray}\text{Hom}_{D_{\text{loc}}(X/S)}(\unicode[STIX]{x1D70C}(\mathscr{F}),\unicode[STIX]{x1D70C}(\mathscr{G}))\cong \text{Hom}_{D(s)}(L_{s},i^{\ast }f_{\ast }{\mathcal{H}}om(\mathscr{F},\mathscr{G})).\end{eqnarray}$$
$$\begin{eqnarray}\text{Hom}_{D_{\text{loc}}(X/S)}(\unicode[STIX]{x1D70C}(\mathscr{F}),\unicode[STIX]{x1D70C}(\mathscr{G}))\cong \text{Hom}_{D(s)}(L_{s},i^{\ast }f_{\ast }{\mathcal{H}}om(\mathscr{F},\mathscr{G})).\end{eqnarray}$$
 $D_{\text{loc}}(X/S)$
whose heart contains
$D_{\text{loc}}(X/S)$
whose heart contains
 $\unicode[STIX]{x1D70C}(\text{Hol}(X))$
. The computation of part 2 above shows that the “higher homotopies” of
$\unicode[STIX]{x1D70C}(\text{Hol}(X))$
. The computation of part 2 above shows that the “higher homotopies” of
 $\unicode[STIX]{x1D70C}(\text{Hol}(X))$
vanish in the category
$\unicode[STIX]{x1D70C}(\text{Hol}(X))$
vanish in the category
 $D_{\text{loc}}(X/S)$
. This gives us an evidence of the existence of such t-structure. The category
$D_{\text{loc}}(X/S)$
. This gives us an evidence of the existence of such t-structure. The category
 $\text{Loc}(X/S)$
should be a full subcategory of this heart.
$\text{Loc}(X/S)$
should be a full subcategory of this heart.This category should be an analogue of the derived category of constructible sheaves for
 $\ell$
-adic sheaves of a scheme of separated of finite type over a local Henselian scheme as in [Reference Ekedahl, Cartier, Katz, Manin, Illusie, Laumon and RibetE, Theorem 6.3]. The following Theorem 4.6 gives an evidence for this philosophy.
$\ell$
-adic sheaves of a scheme of separated of finite type over a local Henselian scheme as in [Reference Ekedahl, Cartier, Katz, Manin, Illusie, Laumon and RibetE, Theorem 6.3]. The following Theorem 4.6 gives an evidence for this philosophy.
4.3
Let
![]() $S$
be a strict Henselian trait, and
$S$
be a strict Henselian trait, and
![]() $\unicode[STIX]{x1D70B}:X\rightarrow S$
be a morphism of finite type. The nearby cycle formalism extends to that on
$\unicode[STIX]{x1D70B}:X\rightarrow S$
be a morphism of finite type. The nearby cycle formalism extends to that on
![]() $\text{Loc}(X)$
. For
$\text{Loc}(X)$
. For
![]() $\mathscr{F},\mathscr{G}\in D(X)$
, we have the canonical homomorphism
$\mathscr{F},\mathscr{G}\in D(X)$
, we have the canonical homomorphism
On the other hand, the adjunction induces a map
for any
![]() $\mathscr{H}\in D(X_{s})$
. Combining these, we obtain a homomorphism
$\mathscr{H}\in D(X_{s})$
. Combining these, we obtain a homomorphism
Thus, we have a homomorphism
If
![]() $\mathscr{F}=\mathscr{G}$
, then the identity is sent to the identity, and the map is compatible with the composition. Thus,
$\mathscr{F}=\mathscr{G}$
, then the identity is sent to the identity, and the map is compatible with the composition. Thus,
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}$
is defined also on the level of the category
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}$
is defined also on the level of the category
![]() $\text{Loc}(X)$
.
$\text{Loc}(X)$
.
4.4
Let us describe the category
![]() $\text{Loc}(S)$
when
$\text{Loc}(S)$
when
![]() $S$
is a Henselian trait in terms of the theory on a formal unit disk after Crew. Let
$S$
is a Henselian trait in terms of the theory on a formal unit disk after Crew. Let
![]() $\mathscr{S}:=k[\![t]\!]$
, a formal disk. For this disk, he constructed the category
$\mathscr{S}:=k[\![t]\!]$
, a formal disk. For this disk, he constructed the category
![]() $\text{Coh}^{\text{an}}({\mathcal{D}}^{\dagger })$
in [Reference CrewCr1, 5.2]. Crew defined a category of holonomic objects in
$\text{Coh}^{\text{an}}({\mathcal{D}}^{\dagger })$
in [Reference CrewCr1, 5.2]. Crew defined a category of holonomic objects in
![]() $\text{Coh}^{\text{an}}({\mathcal{D}}^{\dagger })$
with Frobenius structure, and denote it by
$\text{Coh}^{\text{an}}({\mathcal{D}}^{\dagger })$
with Frobenius structure, and denote it by
![]() $\text{Hol}^{\text{an}}(F{\mathcal{D}}^{\dagger })$
. As usual, we consider the full subcategory of
$\text{Hol}^{\text{an}}(F{\mathcal{D}}^{\dagger })$
. As usual, we consider the full subcategory of
![]() $\text{Coh}^{\text{an}}({\mathcal{D}}^{\dagger })$
consisting of objects which are of finite length and whose constituent can be endowed with a Frobenius structure with which the constituent is in
$\text{Coh}^{\text{an}}({\mathcal{D}}^{\dagger })$
consisting of objects which are of finite length and whose constituent can be endowed with a Frobenius structure with which the constituent is in
![]() $\text{Hol}^{\text{an}}(F{\mathcal{D}}^{\dagger })$
. We denote this category by
$\text{Hol}^{\text{an}}(F{\mathcal{D}}^{\dagger })$
. We denote this category by
![]() $\text{Hol}^{\text{an}}({\mathcal{D}}^{\dagger })$
, or
$\text{Hol}^{\text{an}}({\mathcal{D}}^{\dagger })$
, or
![]() $\text{Hol}^{\text{an}}({\mathcal{D}}_{\mathscr{S},\mathbb{Q}}^{\dagger })$
if we want to emphasize the formal disk. In this situation, the functors
$\text{Hol}^{\text{an}}({\mathcal{D}}_{\mathscr{S},\mathbb{Q}}^{\dagger })$
if we want to emphasize the formal disk. In this situation, the functors
![]() $j_{+}$
,
$j_{+}$
,
![]() $j^{+}$
$j^{+}$
![]() $i_{+}$
,
$i_{+}$
,
![]() $i^{+}$
,
$i^{+}$
,
![]() $i^{!}$
are defined (cf. [Reference CrewCr1, 5.2]). Even though the definition seems to be a bit involved,
$i^{!}$
are defined (cf. [Reference CrewCr1, 5.2]). Even though the definition seems to be a bit involved,
![]() $\text{Hol}^{\text{an}}({\mathcal{D}}^{\dagger })$
is very close to the category which has already appeared in the theory of
$\text{Hol}^{\text{an}}({\mathcal{D}}^{\dagger })$
is very close to the category which has already appeared in the theory of
![]() $p$
-adic differential equation. In fact, the category
$p$
-adic differential equation. In fact, the category
![]() $\text{MLS}({\mathcal{R}},\mathbf{F},\mathbf{pot})$
appearing in [Reference Christol and MebkhoutCM, Définition 6.0-19] is contained full faithfully in
$\text{MLS}({\mathcal{R}},\mathbf{F},\mathbf{pot})$
appearing in [Reference Christol and MebkhoutCM, Définition 6.0-19] is contained full faithfully in
![]() $\text{Hol}^{\text{an}}({\mathcal{D}}^{\dagger })$
, and it is easy to characterize this subcategory: it consists of the objects
$\text{Hol}^{\text{an}}({\mathcal{D}}^{\dagger })$
, and it is easy to characterize this subcategory: it consists of the objects
![]() ${\mathcal{M}}\in \text{Hol}^{\text{an}}({\mathcal{D}}^{\dagger })$
such that
${\mathcal{M}}\in \text{Hol}^{\text{an}}({\mathcal{D}}^{\dagger })$
such that
![]() $i^{!}{\mathcal{M}}=0$
. The verification of this characterization is left to the reader.
$i^{!}{\mathcal{M}}=0$
. The verification of this characterization is left to the reader.
4.5
Let
![]() $S$
be the Henselization of
$S$
be the Henselization of
![]() $\mathbb{A}_{k}^{1}$
at
$\mathbb{A}_{k}^{1}$
at
![]() $0$
. Recall that Crew constructed a canonical functor
$0$
. Recall that Crew constructed a canonical functor
![]() $\text{An}:\text{Hol}(S)\rightarrow \text{Hol}^{\text{an}}({\mathcal{D}}^{\dagger })$
sending an object
$\text{An}:\text{Hol}(S)\rightarrow \text{Hol}^{\text{an}}({\mathcal{D}}^{\dagger })$
sending an object
![]() $\mathscr{F}\in \text{Hol}(S)$
to
$\mathscr{F}\in \text{Hol}(S)$
to
![]() $\mathscr{F}^{\text{an}}$
in [Reference CrewCr1, (5.2.3)]. Since
$\mathscr{F}^{\text{an}}$
in [Reference CrewCr1, (5.2.3)]. Since
![]() ${\mathcal{D}}^{\text{an}}$
is flat over
${\mathcal{D}}^{\text{an}}$
is flat over
![]() ${\mathcal{D}}^{\dagger }$
, this functor extends to
${\mathcal{D}}^{\dagger }$
, this functor extends to
![]() $\text{An}:D(S)\rightarrow D({\mathcal{D}}_{\mathscr{S},\mathbb{Q}}^{\text{an}})$
by simply considering
$\text{An}:D(S)\rightarrow D({\mathcal{D}}_{\mathscr{S},\mathbb{Q}}^{\text{an}})$
by simply considering
![]() ${\mathcal{D}}^{\text{an}}\otimes _{{\mathcal{D}}^{\dagger }}$
.
${\mathcal{D}}^{\text{an}}\otimes _{{\mathcal{D}}^{\dagger }}$
.
Lemma. For
![]() $\mathscr{F},\mathscr{G}\in \text{Hol}(S)$
, we define
$\mathscr{F},\mathscr{G}\in \text{Hol}(S)$
, we define
![]() $\mathscr{F}\otimes ^{\text{an}}\mathscr{G}$
to be
$\mathscr{F}\otimes ^{\text{an}}\mathscr{G}$
to be
![]() ${\mathcal{D}}^{\text{an}}\otimes _{{\mathcal{D}}^{\dagger }}(\mathscr{F}\otimes ^{\dagger }\mathscr{G})$
in
${\mathcal{D}}^{\text{an}}\otimes _{{\mathcal{D}}^{\dagger }}(\mathscr{F}\otimes ^{\dagger }\mathscr{G})$
in
![]() $D^{\text{b}}({\mathcal{D}}^{\text{an}})$
. Then this functor factors through
$D^{\text{b}}({\mathcal{D}}^{\text{an}})$
. Then this functor factors through
![]() $\text{Hol}^{\text{an}}({\mathcal{D}}^{\dagger })$
.
$\text{Hol}^{\text{an}}({\mathcal{D}}^{\dagger })$
.
Proof. Let
![]() $X$
be an étale neighborhood of
$X$
be an étale neighborhood of
![]() $\mathbb{A}^{1}$
at
$\mathbb{A}^{1}$
at
![]() $0$
so that
$0$
so that
![]() $\mathscr{F}$
,
$\mathscr{F}$
,
![]() $\mathscr{G}$
are defined in
$\mathscr{G}$
are defined in
![]() $\text{Hol}(X)$
. Let
$\text{Hol}(X)$
. Let
![]() $\mathscr{X}$
be a smooth lifting of
$\mathscr{X}$
be a smooth lifting of
![]() $X$
. We have the functor
$X$
. We have the functor
![]() $\otimes ^{\dagger }:\underset{\longrightarrow }{LD}_{\mathbb{Q}}^{\text{b}}(\widehat{\mathscr{D}}_{\mathscr{X}}^{(\bullet )})\,\otimes \,\underset{\longrightarrow }{LD}_{\mathbb{Q}}^{\text{b}}(\widehat{\mathscr{D}}_{\mathscr{X}}^{(\bullet )})\rightarrow \underset{\longrightarrow }{LD}_{\mathbb{Q}}^{\text{b}}(\widehat{\mathscr{D}}_{\mathscr{X}}^{(\bullet )})$
. This functor is isomorphic to
$\otimes ^{\dagger }:\underset{\longrightarrow }{LD}_{\mathbb{Q}}^{\text{b}}(\widehat{\mathscr{D}}_{\mathscr{X}}^{(\bullet )})\,\otimes \,\underset{\longrightarrow }{LD}_{\mathbb{Q}}^{\text{b}}(\widehat{\mathscr{D}}_{\mathscr{X}}^{(\bullet )})\rightarrow \underset{\longrightarrow }{LD}_{\mathbb{Q}}^{\text{b}}(\widehat{\mathscr{D}}_{\mathscr{X}}^{(\bullet )})$
. This functor is isomorphic to
![]() $\unicode[STIX]{x1D6E5}^{!}(-\boxtimes ^{\dagger }-)$
up to some shift. Thus, by [Reference CaroC3, Theorem 3.4.9],
$\unicode[STIX]{x1D6E5}^{!}(-\boxtimes ^{\dagger }-)$
up to some shift. Thus, by [Reference CaroC3, Theorem 3.4.9],
![]() $\otimes ^{\dagger }$
sends
$\otimes ^{\dagger }$
sends
![]() $\underset{\longrightarrow }{LD}_{\mathbb{Q},\text{coh}}^{\text{b}}\times \underset{\longrightarrow }{LD}_{\mathbb{Q},\text{coh}}^{\text{b}}$
to
$\underset{\longrightarrow }{LD}_{\mathbb{Q},\text{coh}}^{\text{b}}\times \underset{\longrightarrow }{LD}_{\mathbb{Q},\text{coh}}^{\text{b}}$
to
![]() $\underset{\longrightarrow }{LD}_{\mathbb{Q},\text{coh}}^{\text{b}}$
. Let
$\underset{\longrightarrow }{LD}_{\mathbb{Q},\text{coh}}^{\text{b}}$
. Let
![]() $\mathscr{F}=\mathscr{F}^{(\bullet )}$
,
$\mathscr{F}=\mathscr{F}^{(\bullet )}$
,
![]() $\mathscr{G}=\mathscr{G}^{(\bullet )}$
in
$\mathscr{G}=\mathscr{G}^{(\bullet )}$
in
![]() $\underset{\longrightarrow }{LD}_{\mathbb{Q},\text{coh}}^{\text{b}}$
. For
$\underset{\longrightarrow }{LD}_{\mathbb{Q},\text{coh}}^{\text{b}}$
. For
![]() $\mathscr{H}_{\mathbb{Q}}$
in
$\mathscr{H}_{\mathbb{Q}}$
in
![]() $D_{\text{coh}}^{\text{b}}(\widehat{\mathscr{D}}_{\mathscr{X},\mathbb{Q}}^{(m)})$
, we denote by
$D_{\text{coh}}^{\text{b}}(\widehat{\mathscr{D}}_{\mathscr{X},\mathbb{Q}}^{(m)})$
, we denote by
![]() $\mathscr{H}_{\mathbb{Q}}^{(m)\text{an}}$
the complex
$\mathscr{H}_{\mathbb{Q}}^{(m)\text{an}}$
the complex
![]() $R\,\mathop{\varprojlim }\nolimits_{r}(R\,\mathop{\varprojlim }\nolimits_{n}({\mathcal{O}}_{r,n}\otimes _{{\mathcal{O}}}^{L}\mathscr{H}))\,\otimes \,\mathbb{Q}$
where
$R\,\mathop{\varprojlim }\nolimits_{r}(R\,\mathop{\varprojlim }\nolimits_{n}({\mathcal{O}}_{r,n}\otimes _{{\mathcal{O}}}^{L}\mathscr{H}))\,\otimes \,\mathbb{Q}$
where
![]() $\mathscr{H}$
is a complex in
$\mathscr{H}$
is a complex in
![]() $D_{\text{coh}}^{\text{b}}(\widehat{\mathscr{D}}_{\mathscr{X}}^{(m)})$
such that
$D_{\text{coh}}^{\text{b}}(\widehat{\mathscr{D}}_{\mathscr{X}}^{(m)})$
such that
![]() $\mathscr{H}\,\otimes \,\mathbb{Q}\cong \mathscr{H}_{\mathbb{Q}}$
, using the notation appearing in [Reference CrewCr1, (4.1.8)]. Then Caro’s finiteness above together with [Reference CrewCr1, Theorem 4.1.1] implies that
$\mathscr{H}\,\otimes \,\mathbb{Q}\cong \mathscr{H}_{\mathbb{Q}}$
, using the notation appearing in [Reference CrewCr1, (4.1.8)]. Then Caro’s finiteness above together with [Reference CrewCr1, Theorem 4.1.1] implies that
This description implies that the functor factors through
![]() $\text{Hol}^{\text{an}}({\mathcal{D}}^{\dagger })$
.◻
$\text{Hol}^{\text{an}}({\mathcal{D}}^{\dagger })$
.◻
For
![]() ${\mathcal{M}},{\mathcal{N}}\in \text{Hol}^{\text{an}}({\mathcal{D}}^{\dagger })$
, we define
${\mathcal{M}},{\mathcal{N}}\in \text{Hol}^{\text{an}}({\mathcal{D}}^{\dagger })$
, we define
![]() ${\mathcal{H}}om({\mathcal{M}},{\mathcal{N}}):=(\mathbb{D}({\mathcal{M}})\otimes ^{\text{an}}{\mathcal{N}})[-1]$
. The definition of
${\mathcal{H}}om({\mathcal{M}},{\mathcal{N}}):=(\mathbb{D}({\mathcal{M}})\otimes ^{\text{an}}{\mathcal{N}})[-1]$
. The definition of
![]() $\otimes ^{\text{an}}$
implies that for
$\otimes ^{\text{an}}$
implies that for
![]() $\mathscr{F},\mathscr{G}$
in
$\mathscr{F},\mathscr{G}$
in
![]() $\text{Hol}(S)$
, we have
$\text{Hol}(S)$
, we have
This implies
Theorem 4.6. Let
![]() $S$
be a Henselian trait such that the closed point is of finite type over
$S$
be a Henselian trait such that the closed point is of finite type over
![]() $k$
. Let
$k$
. Let
![]() $\mathscr{S}$
be the formal completion of
$\mathscr{S}$
be the formal completion of
![]() $S$
with respect to the closed point. Then we have the canonical equivalence of categories
$S$
with respect to the closed point. Then we have the canonical equivalence of categories
![]() $\text{Loc}(S)\cong \text{Hol}^{\text{an}}({\mathcal{D}}_{\mathscr{S},\mathbb{Q}}^{\dagger })$
.
$\text{Loc}(S)\cong \text{Hol}^{\text{an}}({\mathcal{D}}_{\mathscr{S},\mathbb{Q}}^{\dagger })$
.
Proof. Let us show that the functor
![]() $\text{An}$
factors through
$\text{An}$
factors through
![]() $\text{Hol}(S)\rightarrow \text{Loc}(S)$
. Recall that we have the Crew–Matsuda canonical extension
$\text{Hol}(S)\rightarrow \text{Loc}(S)$
. Recall that we have the Crew–Matsuda canonical extension
which is fully faithful and
![]() $\text{An}\circ \text{Can}\cong \text{id}$
(cf. [Reference CrewCr1, Theorem 8.2.1]). Consider the canonical homomorphism
$\text{An}\circ \text{Can}\cong \text{id}$
(cf. [Reference CrewCr1, Theorem 8.2.1]). Consider the canonical homomorphism
![]() $\text{Hom}(\mathscr{F},\mathscr{G})\rightarrow \mathscr{H}^{0}i^{\ast }{\mathcal{H}}om(\mathscr{F},\mathscr{G})$
for
$\text{Hom}(\mathscr{F},\mathscr{G})\rightarrow \mathscr{H}^{0}i^{\ast }{\mathcal{H}}om(\mathscr{F},\mathscr{G})$
for
![]() $\mathscr{F},\mathscr{G}\in D(\mathbb{A}^{1})$
. Let us show that this is an isomorphism if
$\mathscr{F},\mathscr{G}\in D(\mathbb{A}^{1})$
. Let us show that this is an isomorphism if
![]() $\mathscr{F}$
and
$\mathscr{F}$
and
![]() $\mathscr{G}$
are canonical extensions. Denote by
$\mathscr{G}$
are canonical extensions. Denote by
![]() $i:0{\hookrightarrow}\mathbb{A}^{1}$
the closed immersion and
$i:0{\hookrightarrow}\mathbb{A}^{1}$
the closed immersion and
![]() $j$
the complement. If
$j$
the complement. If
![]() $\mathscr{F}$
or
$\mathscr{F}$
or
![]() $\mathscr{G}$
is of the form
$\mathscr{G}$
is of the form
![]() $i_{\ast }\mathscr{H}\cong i_{!}\mathscr{H}$
, then the claim follows by adjunction. Considering the localization sequence, this implies that we may assume that
$i_{\ast }\mathscr{H}\cong i_{!}\mathscr{H}$
, then the claim follows by adjunction. Considering the localization sequence, this implies that we may assume that
![]() $\mathscr{G}=j_{\ast }j^{\ast }\mathscr{G}$
. In this case, we have
$\mathscr{G}=j_{\ast }j^{\ast }\mathscr{G}$
. In this case, we have
![]() ${\mathcal{H}}om(\mathscr{F},\mathscr{G})\cong j_{\ast }{\mathcal{H}}om(j^{\ast }\mathscr{F},j^{\ast }\mathscr{G})$
by adjunction. If
${\mathcal{H}}om(\mathscr{F},\mathscr{G})\cong j_{\ast }{\mathcal{H}}om(j^{\ast }\mathscr{F},j^{\ast }\mathscr{G})$
by adjunction. If
![]() $\mathscr{F}$
,
$\mathscr{F}$
,
![]() $\mathscr{G}$
are canonical extensions, we get that
$\mathscr{G}$
are canonical extensions, we get that
![]() ${\mathcal{H}}om(\mathscr{F},\mathscr{G})$
is a canonical extension as well. Thus, it remains to check that if
${\mathcal{H}}om(\mathscr{F},\mathscr{G})$
is a canonical extension as well. Thus, it remains to check that if
![]() $\mathscr{H}$
is a canonical extension and
$\mathscr{H}$
is a canonical extension and
![]() $\mathscr{H}\cong j_{\ast }j^{\ast }\mathscr{H}$
, then the restriction
$\mathscr{H}\cong j_{\ast }j^{\ast }\mathscr{H}$
, then the restriction
![]() $H^{0}(\mathbb{A}^{1},\mathscr{H})\rightarrow \mathscr{H}^{0}i^{\ast }\mathscr{H}$
is an isomorphism. The source is isomorphic to
$H^{0}(\mathbb{A}^{1},\mathscr{H})\rightarrow \mathscr{H}^{0}i^{\ast }\mathscr{H}$
is an isomorphism. The source is isomorphic to
![]() $H^{0}(\mathscr{S},\mathscr{H}^{\text{an}})$
since the canonical extension is fully faithful, and the claim follows by the proof of [Reference Abe and MarmoraAM, Lemma 3.1.10] where we showed
$H^{0}(\mathscr{S},\mathscr{H}^{\text{an}})$
since the canonical extension is fully faithful, and the claim follows by the proof of [Reference Abe and MarmoraAM, Lemma 3.1.10] where we showed
![]() $H^{n}(\mathscr{S},\mathscr{H}^{\text{an}})\cong \mathscr{H}^{n}i^{+}\mathscr{H}^{\text{an}}$
. Now, we have
$H^{n}(\mathscr{S},\mathscr{H}^{\text{an}})\cong \mathscr{H}^{n}i^{+}\mathscr{H}^{\text{an}}$
. Now, we have
 $$\begin{eqnarray}\displaystyle \text{Hom}(\mathscr{F}^{\text{loc}},\mathscr{G}^{\text{loc}}) & := & \displaystyle H^{0}(s,i^{\ast }{\mathcal{H}}om(\mathscr{F},\mathscr{G}))\nonumber\\ \displaystyle & \cong & \displaystyle H^{0}(s,i^{\ast }{\mathcal{H}}om(\text{Can}(\mathscr{F}^{\text{an}}),\text{Can}(\mathscr{G}^{\text{an}})))\nonumber\\ \displaystyle & \xleftarrow[{}]{{\sim}} & \displaystyle \text{Hom}(\text{Can}(\mathscr{F}^{\text{an}}),\text{Can}(\mathscr{G}^{\text{an}}))\cong \text{Hom}(\mathscr{F}^{\text{an}},\mathscr{G}^{\text{an}}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{Hom}(\mathscr{F}^{\text{loc}},\mathscr{G}^{\text{loc}}) & := & \displaystyle H^{0}(s,i^{\ast }{\mathcal{H}}om(\mathscr{F},\mathscr{G}))\nonumber\\ \displaystyle & \cong & \displaystyle H^{0}(s,i^{\ast }{\mathcal{H}}om(\text{Can}(\mathscr{F}^{\text{an}}),\text{Can}(\mathscr{G}^{\text{an}})))\nonumber\\ \displaystyle & \xleftarrow[{}]{{\sim}} & \displaystyle \text{Hom}(\text{Can}(\mathscr{F}^{\text{an}}),\text{Can}(\mathscr{G}^{\text{an}}))\cong \text{Hom}(\mathscr{F}^{\text{an}},\mathscr{G}^{\text{an}}),\nonumber\end{eqnarray}$$
where the 2nd isomorphism follows by (4.5.6) and the 3rd by the isomorphism we have just proven, and the last by full faithfulness of
![]() $\text{Can}$
. It is easy to check that this isomorphism is compatible with composition, and we have the desired functor
$\text{Can}$
. It is easy to check that this isomorphism is compatible with composition, and we have the desired functor
![]() $\text{Loc}(S)\rightarrow \text{Hol}^{\text{an}}({\mathcal{D}}^{\dagger })$
, which is moreover fully faithful. To check the equivalence, it remains to check that the functor is essentially surjective. This follows by Crew–Matsuda canonical extension. ◻
$\text{Loc}(S)\rightarrow \text{Hol}^{\text{an}}({\mathcal{D}}^{\dagger })$
, which is moreover fully faithful. To check the equivalence, it remains to check that the functor is essentially surjective. This follows by Crew–Matsuda canonical extension. ◻
Remark 4.7.
(1) It might be possible to reprove [Reference Abe and MarmoraAM] without using microlocal technique by using the foundation of this paper instead.
(2) It would be interesting to compare the theory developed here and recent works of Lazda–Pal [Reference Lazda and PalLP], Caro–Vauclair [Reference Caro and VauclairCV], or Crew [Reference CrewCr2] on the theory of
 $p$
-adic cohomology theory for formal schemes or schemes over Laurent series field.
$p$
-adic cohomology theory for formal schemes or schemes over Laurent series field.
Acknowledgments
The author is grateful to the referee for his careful job, especially finding a gap in the proof of Theorem 4.6 of the earlier version. This research is supported by Grant-in-Aid for Young Scientists (A) 16H05993.