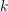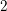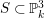1 Introduction
This paper continues our study of the maximum number of lines on smooth quartic surfaces in
![]() $\mathbb{P}^{3}$
initiated in [Reference Rams and Schütt9, Reference Rams and Schütt10]. Starting from Segre’s original ideas and claims in [Reference Segre16], we proved in [Reference Rams and Schütt9] that a smooth quartic surface outside characteristics
$\mathbb{P}^{3}$
initiated in [Reference Rams and Schütt9, Reference Rams and Schütt10]. Starting from Segre’s original ideas and claims in [Reference Segre16], we proved in [Reference Rams and Schütt9] that a smooth quartic surface outside characteristics
![]() $2$
and
$2$
and
![]() $3$
contains at most 64 lines, with the maximum attained by Schur’s quartic [Reference Schur12]. In characteristic
$3$
contains at most 64 lines, with the maximum attained by Schur’s quartic [Reference Schur12]. In characteristic
![]() $3$
, this specializes to the Fermat quartic which contains 112 lines, the maximum by [Reference Rams and Schütt10]. In characteristic
$3$
, this specializes to the Fermat quartic which contains 112 lines, the maximum by [Reference Rams and Schütt10]. In characteristic
![]() $2$
, however, both these quartics degenerate which opens the way to new phenomena. In this paper we study these phenomena and give a geometric proof that the maximum number of lines still cannot exceed 64:
$2$
, however, both these quartics degenerate which opens the way to new phenomena. In this paper we study these phenomena and give a geometric proof that the maximum number of lines still cannot exceed 64:
Theorem 1.1. Let
![]() $k$
be a field of characteristic
$k$
be a field of characteristic
![]() $p=2$
. Then any smooth quartic surface over
$p=2$
. Then any smooth quartic surface over
![]() $k$
contains at most 64 lines.
$k$
contains at most 64 lines.
After this paper was written, Degtyarev stated in [Reference Degtyarev2], partly based on machine-aided calculations from [Reference Degtyarev, Itenberg and Sertöz3], that the bound of Theorem 1.1 can be improved to 60 in characteristic
![]() $2$
. The record is attained by a quartic with
$2$
. The record is attained by a quartic with
![]() $S_{5}$
-action which we shall exhibit explicitly in Section 8. We point out that unlike in other characteristics (by work of us and Veniani [Reference Rams and Schütt9, Reference Rams and Schütt10, Reference Veniani19]), there exist nonsmooth quartic K3 surfaces with more lines than in the smooth case, in fact with as many as 68 lines in characteristic
$S_{5}$
-action which we shall exhibit explicitly in Section 8. We point out that unlike in other characteristics (by work of us and Veniani [Reference Rams and Schütt9, Reference Rams and Schütt10, Reference Veniani19]), there exist nonsmooth quartic K3 surfaces with more lines than in the smooth case, in fact with as many as 68 lines in characteristic
![]() $2$
(see Remark 2.3), indicating how special this situation is.
$2$
(see Remark 2.3), indicating how special this situation is.
We emphasize that originally we were expecting the bound from characteristics
![]() $\neq 2,3$
to go up in characteristic
$\neq 2,3$
to go up in characteristic
![]() $2$
, since just like in characteristic
$2$
, since just like in characteristic
![]() $3$
, there may be quasi-elliptic fibrations and the flecnodal divisor may degenerate. With this in mind, our previous best bound ended up at
$3$
, there may be quasi-elliptic fibrations and the flecnodal divisor may degenerate. With this in mind, our previous best bound ended up at
![]() $84$
in [Reference Rams and Schütt10, Proposition 1.3]. In contrast, this paper will show that quasi-elliptic fibrations in characteristic
$84$
in [Reference Rams and Schütt10, Proposition 1.3]. In contrast, this paper will show that quasi-elliptic fibrations in characteristic
![]() $2$
cannot arise from lines on smooth quartics (see Proposition 2.1). Then we make particular use of special features of elliptic fibrations in characteristic 2, and of the Hessian, to preserve the original bound of
$2$
cannot arise from lines on smooth quartics (see Proposition 2.1). Then we make particular use of special features of elliptic fibrations in characteristic 2, and of the Hessian, to preserve the original bound of
![]() $64$
.
$64$
.
The paper is organized as follows. Section 2 reviews genus one fibrations for smooth quartics with lines with a special view toward quasi-elliptic fibrations. In Section 3, we discuss ramification types and the Hessian of a cubic in characteristic
![]() $2$
to derive Segre’s upper bound for the number of lines met by a line of the so-called first kind on a smooth quartic surface. Lines of the second kind are analyzed in Section 4, much in the spirit of [Reference Rams and Schütt9]. The proof of Theorem 1.1 is given in Sections 5–7 by distinguishing which basic configurations of lines occur on the quartic. The paper concludes with an example of a smooth quartic over
$2$
to derive Segre’s upper bound for the number of lines met by a line of the so-called first kind on a smooth quartic surface. Lines of the second kind are analyzed in Section 4, much in the spirit of [Reference Rams and Schütt9]. The proof of Theorem 1.1 is given in Sections 5–7 by distinguishing which basic configurations of lines occur on the quartic. The paper concludes with an example of a smooth quartic over
![]() $\mathbb{F}_{4}$
containing 60 lines over
$\mathbb{F}_{4}$
containing 60 lines over
![]() $\mathbb{F}_{16}$
.
$\mathbb{F}_{16}$
.
Convention 1.2. Throughout this note we work over an algebraically closed field
![]() $k$
of characteristic
$k$
of characteristic
![]() $p=2$
, since base change does not affect the validity of Theorem 1.1.
$p=2$
, since base change does not affect the validity of Theorem 1.1.
2 Genus one fibration
Let
![]() $S$
be a smooth quartic surface over an algebraically closed field
$S$
be a smooth quartic surface over an algebraically closed field
![]() $k$
of characteristic
$k$
of characteristic
![]() $2$
. Assuming that
$2$
. Assuming that
![]() $S$
contains a line
$S$
contains a line
![]() $\ell$
, the linear system
$\ell$
, the linear system
![]() $|{\mathcal{O}}_{S}(1)-\ell |$
gives a pencil of cubic curves; explicitly these are obtained as residual cubics
$|{\mathcal{O}}_{S}(1)-\ell |$
gives a pencil of cubic curves; explicitly these are obtained as residual cubics
![]() $C_{t}$
when
$C_{t}$
when
![]() $S$
is intersected with the pencil of planes
$S$
is intersected with the pencil of planes
![]() $H_{t}$
containing
$H_{t}$
containing
![]() $\ell$
. In particular, we obtain a fibration
$\ell$
. In particular, we obtain a fibration
whose fibers are reduced curves of arithmetic genus one. Note that in general there need not be a section, and due to the special characteristic, the general fiber need not be smooth, that is, the fibration may a priori be quasi-elliptic. In fact, we shall instantly rule this latter special behavior out, but before doing so, we note the limited types of singular fibers (in Kodaira’s notation [Reference Kodaira5]) which may arise from a plane curve of degree
![]() $3$
:
$3$
:
Table 1. Possible singular fibers of
![]() $\unicode[STIX]{x1D70B}$
.
$\unicode[STIX]{x1D70B}$
.

While this is already quite restrictive for any genus one fibration, it determines the singular fibers of a quasi-elliptic fibration in characteristic
![]() $2$
completely: the general fiber has Kodaira type
$2$
completely: the general fiber has Kodaira type
![]() $\text{II}$
, and for Euler–Poincaré characteristic reasons, there are exactly 20 reducible fibers, all of type
$\text{II}$
, and for Euler–Poincaré characteristic reasons, there are exactly 20 reducible fibers, all of type
![]() $\text{III}$
. It turns out that this together with the theory of Mordell–Weil lattices provides enough information to rule out quasi-elliptic fibrations in our characteristic
$\text{III}$
. It turns out that this together with the theory of Mordell–Weil lattices provides enough information to rule out quasi-elliptic fibrations in our characteristic
![]() $2$
set-up:
$2$
set-up:
Proposition 2.1. The fibration
![]() $\unicode[STIX]{x1D70B}$
cannot be quasi-elliptic.
$\unicode[STIX]{x1D70B}$
cannot be quasi-elliptic.
Proof. Assume to the contrary that
![]() $\unicode[STIX]{x1D70B}$
is quasi-elliptic. Then
$\unicode[STIX]{x1D70B}$
is quasi-elliptic. Then
![]() $S$
automatically is unirational, and thus supersingular, that is, the Néron–Severi group
$S$
automatically is unirational, and thus supersingular, that is, the Néron–Severi group
![]() $\operatorname{NS}(S)$
has rank
$\operatorname{NS}(S)$
has rank
![]() $22$
equaling the second Betti number; endowed with the intersection pairing, the Néron–Severi lattice has discriminant
$22$
equaling the second Betti number; endowed with the intersection pairing, the Néron–Severi lattice has discriminant
by [Reference Artin1]. We use the following basic result whose proof resembles that of [Reference Elkies and Schütt4, Theorem 2].
Lemma 2.2. If
![]() $\unicode[STIX]{x1D70B}$
is quasi-elliptic, then it admits a section.
$\unicode[STIX]{x1D70B}$
is quasi-elliptic, then it admits a section.
Proof of Lemma 2.2.
If there were no section, then
![]() $\unicode[STIX]{x1D70B}$
would have multisection index
$\unicode[STIX]{x1D70B}$
would have multisection index
![]() $3$
, thanks to the trisection
$3$
, thanks to the trisection
![]() $\ell$
. Hence we can define an auxiliary integral lattice
$\ell$
. Hence we can define an auxiliary integral lattice
![]() $L$
of the same rank by dividing the general fiber
$L$
of the same rank by dividing the general fiber
![]() $F$
by
$F$
by
![]() $3$
:
$3$
:
Since
![]() $L$
can be interpreted as index
$L$
can be interpreted as index
![]() $3$
overlattice of
$3$
overlattice of
![]() $\operatorname{NS}(S)$
, we obtain
$\operatorname{NS}(S)$
, we obtain
By (2), this is not an integer, despite
![]() $L$
being integral, giving the desired contradiction.◻
$L$
being integral, giving the desired contradiction.◻
We continue the proof of Proposition 2.1 by picking a section of
![]() $\unicode[STIX]{x1D70B}$
and denoting it by
$\unicode[STIX]{x1D70B}$
and denoting it by
![]() $O$
. Then
$O$
. Then
![]() $\ell$
induces a section
$\ell$
induces a section
![]() $P$
of
$P$
of
![]() $\unicode[STIX]{x1D70B}$
which is obtained fiberwise (or on the generic fiber) from
$\unicode[STIX]{x1D70B}$
which is obtained fiberwise (or on the generic fiber) from
![]() $\ell$
by Abel’s theorem. By the theory of Mordell–Weil lattices [Reference Shioda17] (which also applies to quasi-elliptic fibrations), the class of
$\ell$
by Abel’s theorem. By the theory of Mordell–Weil lattices [Reference Shioda17] (which also applies to quasi-elliptic fibrations), the class of
![]() $P$
in
$P$
in
![]() $\operatorname{NS}(S)$
is computed as follows. Let
$\operatorname{NS}(S)$
is computed as follows. Let
![]() $r$
be the number of reducible fibers which are intersected by
$r$
be the number of reducible fibers which are intersected by
![]() $O$
in the linear component, and denote the respective component by
$O$
in the linear component, and denote the respective component by
![]() $\ell _{i}$
. Let
$\ell _{i}$
. Let
![]() $\ell \cdot O=s$
. We claim that
$\ell \cdot O=s$
. We claim that
To see this, it suffices to verify the following properties, using the fact that
![]() $P\equiv \ell$
modulo the trivial lattice generated by
$P\equiv \ell$
modulo the trivial lattice generated by
![]() $O$
and fiber components:
$O$
and fiber components:
∙
 $P$
meets every fiber with multiplicity one in a single component (the linear component; this is assured by subtracting
$P$
meets every fiber with multiplicity one in a single component (the linear component; this is assured by subtracting
 $2O$
and the
$2O$
and the
 $\ell _{i}$
);
$\ell _{i}$
);∙
 $P^{2}=-2$
(giving the coefficient of
$P^{2}=-2$
(giving the coefficient of
 $F$
in the representation of
$F$
in the representation of
 $P$
).
$P$
).
But then the Mordell–Weil group of a Jacobian quasi-elliptic fibration is always finite (compare [Reference Rudakov and Shafarevich11, Section 4]), so
![]() $P$
has height zero. Using
$P$
has height zero. Using
![]() $P.O=8+3s-r$
and the correction terms
$P.O=8+3s-r$
and the correction terms
![]() $1/2$
from each of the
$1/2$
from each of the
![]() $20-r$
reducible fibers where
$20-r$
reducible fibers where
![]() $O$
meets the conic while
$O$
meets the conic while
![]() $P$
always meets the line, we find
$P$
always meets the line, we find
Since the equation
![]() $h(P)=0$
has no integer solution (reduce modulo
$h(P)=0$
has no integer solution (reduce modulo
![]() $3$
!), we arrive at the required contradiction.◻
$3$
!), we arrive at the required contradiction.◻
Remark 2.3. Once quasi-elliptic fibrations are excluded, one can adopt the techniques from [Reference Rams and Schütt9, Reference Rams and Schütt10] to prove without too much difficulty that
![]() $S$
cannot contain more than 68 lines. While this is still a few lines away from Theorem 1.1, it is an interesting coincidence that there exists a one-dimensional family of nonsmooth quartic K3 surfaces (parameterized by
$S$
cannot contain more than 68 lines. While this is still a few lines away from Theorem 1.1, it is an interesting coincidence that there exists a one-dimensional family of nonsmooth quartic K3 surfaces (parameterized by
![]() $\unicode[STIX]{x1D706}$
), that is, admitting only isolated ordinary double points as singularities, which contain as many as 68 lines:
$\unicode[STIX]{x1D706}$
), that is, admitting only isolated ordinary double points as singularities, which contain as many as 68 lines:
We found this family experimentally during our search for smooth quartics with many lines (see Section 8). Generically, there is only a single (isolated) singularity; it is located at
![]() $[0,0,0,1]$
and has type
$[0,0,0,1]$
and has type
![]() $A_{3}$
. The minimal resolution of a general member of the family is a supersingular K3 surface of Artin invariant
$A_{3}$
. The minimal resolution of a general member of the family is a supersingular K3 surface of Artin invariant
![]() $\unicode[STIX]{x1D70E}=2$
.
$\unicode[STIX]{x1D70E}=2$
.
Recently, Veniani proved in [Reference Veniani20] that 68 is indeed the maximum for the number of lines on quartic surfaces with at worst isolated ordinary double point singularities in characteristic
![]() $2$
, and every surface attaining this maximum is projectively equivalent to a member of the above family.
$2$
, and every surface attaining this maximum is projectively equivalent to a member of the above family.
3 Ramification and Hessian
In this section, we introduce two of the main tools for the proof of Theorem 1.1. It is instructive that both of them have different features in characteristic
![]() $2$
than usual.
$2$
than usual.
3.1 Ramification
First we consider the ramification of the restriction of the morphism
![]() $\unicode[STIX]{x1D70B}$
to the line
$\unicode[STIX]{x1D70B}$
to the line
![]() $\ell$
:
$\ell$
:
Since this morphism has degree
![]() $3$
, it always has exactly 1 or 2 ramification points in characteristic
$3$
, it always has exactly 1 or 2 ramification points in characteristic
![]() $2$
(because of Riemann–Hurwitz and wild ramification). We distinguish the ramification type of
$2$
(because of Riemann–Hurwitz and wild ramification). We distinguish the ramification type of
![]() $\ell$
according to the ramification points as follows:
$\ell$
according to the ramification points as follows:
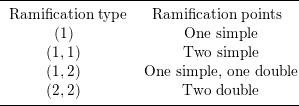
The ramification type is relevant for our purposes because often one studies the base change of
![]() $S$
over
$S$
over
![]() $k(\ell )$
where by definition the fibration corresponding to
$k(\ell )$
where by definition the fibration corresponding to
![]() $\unicode[STIX]{x1D70B}$
attains a section. In fact, we usually extend the base field to the Galois closure of
$\unicode[STIX]{x1D70B}$
attains a section. In fact, we usually extend the base field to the Galois closure of
![]() $k(\ell )/k(\mathbb{P}^{1})$
where
$k(\ell )/k(\mathbb{P}^{1})$
where
![]() $\ell$
splits into three sections. Note that the field extension
$\ell$
splits into three sections. Note that the field extension
![]() $k(\ell )/k(\mathbb{P}^{1})$
itself is Galois if and only if
$k(\ell )/k(\mathbb{P}^{1})$
itself is Galois if and only if
![]() $\ell$
has ramification type
$\ell$
has ramification type
![]() $(2,2)$
. Encoded in the ramification, one finds how the singular fibers behave under the base change, and more importantly, how they are intersected by the sections obtained from
$(2,2)$
. Encoded in the ramification, one finds how the singular fibers behave under the base change, and more importantly, how they are intersected by the sections obtained from
![]() $\ell$
.
$\ell$
.
3.2 Hessian
We now introduce the Hessian of the residual cubics
![]() $C_{\unicode[STIX]{x1D706}}$
. To this end, we apply a projective transformation, so that
$C_{\unicode[STIX]{x1D706}}$
. To this end, we apply a projective transformation, so that
Then the pencil of hyperplanes in
![]() $\mathbb{P}^{3}$
containing
$\mathbb{P}^{3}$
containing
![]() $\ell$
is given by
$\ell$
is given by
(including the hyperplane
![]() $\{x_{3}=0\}$
at
$\{x_{3}=0\}$
at
![]() $\unicode[STIX]{x1D706}=\infty$
, so everything in what follows can be understood in homogeneous coordinates of
$\unicode[STIX]{x1D706}=\infty$
, so everything in what follows can be understood in homogeneous coordinates of
![]() $\mathbb{P}^{1}$
parametrizing
$\mathbb{P}^{1}$
parametrizing
![]() $H_{\unicode[STIX]{x1D706}}$
; we decided to opt for the affine notation for simplicity). The residual cubics
$H_{\unicode[STIX]{x1D706}}$
; we decided to opt for the affine notation for simplicity). The residual cubics
![]() $C_{\unicode[STIX]{x1D706}}$
of
$C_{\unicode[STIX]{x1D706}}$
of
![]() $S\cap H_{\unicode[STIX]{x1D706}}$
are given by a homogeneous cubic polynomial
$S\cap H_{\unicode[STIX]{x1D706}}$
are given by a homogeneous cubic polynomial
which is obtained from the homogeneous quartic polynomial
![]() $f\in k[x_{1},x_{2},x_{3},x_{4}]$
defining
$f\in k[x_{1},x_{2},x_{3},x_{4}]$
defining
![]() $S$
by substituting
$S$
by substituting
![]() $H_{\unicode[STIX]{x1D706}}$
for
$H_{\unicode[STIX]{x1D706}}$
for
![]() $x_{4}$
and factoring out
$x_{4}$
and factoring out
![]() $x_{3}$
. Outside characteristic
$x_{3}$
. Outside characteristic
![]() $2$
, the points of inflection of
$2$
, the points of inflection of
![]() $C_{\unicode[STIX]{x1D706}}$
(which are often used to define a group structure on
$C_{\unicode[STIX]{x1D706}}$
(which are often used to define a group structure on
![]() $C_{\unicode[STIX]{x1D706}}$
, at least when one of them is rational) are given by the Hessian
$C_{\unicode[STIX]{x1D706}}$
, at least when one of them is rational) are given by the Hessian
In characteristic
![]() $2$
, however, some extra divisibilities in the coefficients force us to modify the Hessian formally using the
$2$
, however, some extra divisibilities in the coefficients force us to modify the Hessian formally using the
![]() $x_{1}x_{2}x_{3}$
-coefficient
$x_{1}x_{2}x_{3}$
-coefficient
![]() $\unicode[STIX]{x1D6FC}$
of
$\unicode[STIX]{x1D6FC}$
of
![]() $g$
until it takes the following shape (understood algebraically over
$g$
until it takes the following shape (understood algebraically over
![]() $\mathbb{Z}$
in terms of the generic coefficients of
$\mathbb{Z}$
in terms of the generic coefficients of
![]() $g$
before reducing modulo
$g$
before reducing modulo
![]() $2$
and substituting):
$2$
and substituting):
(These manipulations must be known to the experts as they amount to the saturation of the ideal generated by
![]() $g$
and its Hessian over
$g$
and its Hessian over
![]() $\mathbb{Z}[\unicode[STIX]{x1D706}][x_{1},x_{2},x_{3}]$
.) In order to use the Hessian for considerations of lines on
$\mathbb{Z}[\unicode[STIX]{x1D706}][x_{1},x_{2},x_{3}]$
.) In order to use the Hessian for considerations of lines on
![]() $S$
, Segre’s key insight from [Reference Segre16] was that
$S$
, Segre’s key insight from [Reference Segre16] was that
![]() $h$
vanishes on each linear component of a given residual cubic
$h$
vanishes on each linear component of a given residual cubic
![]() $C_{\unicode[STIX]{x1D706}_{0}}$
(or, if
$C_{\unicode[STIX]{x1D706}_{0}}$
(or, if
![]() $C_{\unicode[STIX]{x1D706}_{0}}$
is singular, but irreducible, in its singularity). That is, any line in a fiber of
$C_{\unicode[STIX]{x1D706}_{0}}$
is singular, but irreducible, in its singularity). That is, any line in a fiber of
![]() $\unicode[STIX]{x1D70B}$
(i.e., intersecting
$\unicode[STIX]{x1D70B}$
(i.e., intersecting
![]() $\ell$
) gives a zero of the following polynomial
$\ell$
) gives a zero of the following polynomial
![]() $R$
, obtained by intersecting
$R$
, obtained by intersecting
![]() $g$
and
$g$
and
![]() $h$
with
$h$
with
![]() $\ell$
(i.e., substituting
$\ell$
(i.e., substituting
![]() $x_{3}=0$
) and taking the resultant with respect to either remaining homogeneous variable:
$x_{3}=0$
) and taking the resultant with respect to either remaining homogeneous variable:
More precisely, one computes that
![]() $R$
has generically degree
$R$
has generically degree
![]() $18$
, and that each line contributes to the zeroes of
$18$
, and that each line contributes to the zeroes of
![]() $R$
on its own, that is, if some fiber contains three lines, then
$R$
on its own, that is, if some fiber contains three lines, then
![]() $R$
attains a triple root:
$R$
attains a triple root:
Lemma 3.1. In the above set-up, assume that
![]() $\unicode[STIX]{x1D70B}$
has:
$\unicode[STIX]{x1D70B}$
has:
(1) a fiber of type
 $\text{I}_{3}$
or
$\text{I}_{3}$
or
 $\text{IV}$
at
$\text{IV}$
at
 $\unicode[STIX]{x1D706}_{0}$
, then
$\unicode[STIX]{x1D706}_{0}$
, then
 $(\unicode[STIX]{x1D706}-\unicode[STIX]{x1D706}_{0})^{3}\mid R$
;
$(\unicode[STIX]{x1D706}-\unicode[STIX]{x1D706}_{0})^{3}\mid R$
;(2) a fiber of type
 $\text{I}_{2}$
or
$\text{I}_{2}$
or
 $\text{III}$
with double ramification at
$\text{III}$
with double ramification at
 $\unicode[STIX]{x1D706}_{0}$
, then
$\unicode[STIX]{x1D706}_{0}$
, then
 $(\unicode[STIX]{x1D706}-\unicode[STIX]{x1D706}_{0})^{2}\mid R$
.
$(\unicode[STIX]{x1D706}-\unicode[STIX]{x1D706}_{0})^{2}\mid R$
.
For degree reasons, one directly obtains the following upper bound, originally due to Segre over
![]() $\mathbb{C}$
, for the valency
$\mathbb{C}$
, for the valency
![]() $v(\ell )$
of the line
$v(\ell )$
of the line
![]() $\ell$
, that is, the number of other lines on
$\ell$
, that is, the number of other lines on
![]() $S$
met by
$S$
met by
![]() $\ell$
:
$\ell$
:
Corollary 3.2. If
![]() $R\not \equiv 0$
, then
$R\not \equiv 0$
, then
![]() $v(\ell )\leqslant 18$
.
$v(\ell )\leqslant 18$
.
This makes clear that we have to carefully distinguish whether
![]() $R$
vanishes identically or not. Recall from [Reference Rams and Schütt9, Reference Segre16] how this leads to the following terminology:
$R$
vanishes identically or not. Recall from [Reference Rams and Schütt9, Reference Segre16] how this leads to the following terminology:
Definition 3.3. The line
![]() $\ell$
is said to be of the second kind if
$\ell$
is said to be of the second kind if
![]() $R\equiv 0$
. Otherwise, we call
$R\equiv 0$
. Otherwise, we call
![]() $\ell$
a line of the first kind.
$\ell$
a line of the first kind.
We next show that lines of the second kind behave essentially as in characteristic
![]() $\neq 2,3$
. For lines of the first kind, the different quality of ramification changes the situation substantially, but it is not clear (to us) whether the valency bound from Corollary 3.2 is still sharp. (The lines on the record surface from Section 8 have all valency 17.)
$\neq 2,3$
. For lines of the first kind, the different quality of ramification changes the situation substantially, but it is not clear (to us) whether the valency bound from Corollary 3.2 is still sharp. (The lines on the record surface from Section 8 have all valency 17.)
4 Lines of the second kind
Since lines of the second kind in characteristic
![]() $2$
turn out to behave mostly like in characteristics
$2$
turn out to behave mostly like in characteristics
![]() $\neq 2,3$
, we will be somewhat sketchy in this section. That is, while trying to keep the exposition as self-contained as possible, we refer the reader back to [Reference Rams and Schütt9] for the details whenever possible.
$\neq 2,3$
, we will be somewhat sketchy in this section. That is, while trying to keep the exposition as self-contained as possible, we refer the reader back to [Reference Rams and Schütt9] for the details whenever possible.
Let
![]() $\ell$
be a line of the second kind. Then, by definition,
$\ell$
be a line of the second kind. Then, by definition,
![]() $\ell$
is contained in the closure of the flex locus on the smooth fibers. This severely limits the way how
$\ell$
is contained in the closure of the flex locus on the smooth fibers. This severely limits the way how
![]() $\ell$
may intersect the singular fibers. As in characteristics
$\ell$
may intersect the singular fibers. As in characteristics
![]() $\neq 2,3$
in [Reference Rams and Schütt9], one obtains the following configurations depending on the ramification:
$\neq 2,3$
in [Reference Rams and Schütt9], one obtains the following configurations depending on the ramification:
Lemma 4.1. A line of the second kind may intersect the singular fibers of
![]() $\unicode[STIX]{x1D70B}$
depending on the ramification as follows:
$\unicode[STIX]{x1D70B}$
depending on the ramification as follows:

We emphasize that fibers of types
![]() $\text{II}$
and
$\text{II}$
and
![]() $\text{III}$
necessarily come with wild ramification in characteristic
$\text{III}$
necessarily come with wild ramification in characteristic
![]() $2$
; in fact they impose on the discriminant a zero of multiplicity at least 4 by [Reference Schütt and Schweizer14]. (In mixed characteristic, i.e., when specializing from characteristic zero to characteristic
$2$
; in fact they impose on the discriminant a zero of multiplicity at least 4 by [Reference Schütt and Schweizer14]. (In mixed characteristic, i.e., when specializing from characteristic zero to characteristic
![]() $2$
, this can often be explained as some fiber of type
$2$
, this can often be explained as some fiber of type
![]() $\text{II}$
absorbing other irreducible singular fibers without changing its type, compare Lemma 4.2 with the results valid in characteristic zero from [Reference Rams and Schütt9, Lemma 4.3].)
$\text{II}$
absorbing other irreducible singular fibers without changing its type, compare Lemma 4.2 with the results valid in characteristic zero from [Reference Rams and Schütt9, Lemma 4.3].)
As in [Reference Rams and Schütt9] we continue to argue with the base change of
![]() $S$
to the Galois closure of
$S$
to the Galois closure of
![]() $k(\ell )/k(\mathbb{P}^{1})$
. By construction, this sees
$k(\ell )/k(\mathbb{P}^{1})$
. By construction, this sees
![]() $\ell$
split into three sections; taking one as zero for the group law, the others necessarily become
$\ell$
split into three sections; taking one as zero for the group law, the others necessarily become
![]() $3$
-torsion. In practice, this implies that fibers of types
$3$
-torsion. In practice, this implies that fibers of types
![]() $\text{I}_{1}$
and
$\text{I}_{1}$
and
![]() $\text{I}_{3}$
have to even out—including two possible degenerations:
$\text{I}_{3}$
have to even out—including two possible degenerations:
∙ a pair of fibers
 $\text{I}_{1},\text{I}_{3}$
might merge to type
$\text{I}_{1},\text{I}_{3}$
might merge to type
 $\text{IV}$
;
$\text{IV}$
;∙ two fibers of type
 $\text{I}_{1}$
might merge to
$\text{I}_{1}$
might merge to
 $\text{I}_{2}$
, still paired with two
$\text{I}_{2}$
, still paired with two
 $\text{I}_{3}$
fibers.
$\text{I}_{3}$
fibers.
In the next table, we thus group the fibers according to their Kodaira type in single entries
![]() $\text{II},\text{IV}$
, pairs
$\text{II},\text{IV}$
, pairs
![]() $(\text{I}_{1},\text{I}_{3})$
and triples
$(\text{I}_{1},\text{I}_{3})$
and triples
![]() $(\text{I}_{2},\text{I}_{3},\text{I}_{3})$
. Since fiber type
$(\text{I}_{2},\text{I}_{3},\text{I}_{3})$
. Since fiber type
![]() $\text{I}_{2}$
automatically comes with double ramification by Lemma 4.1, we can bound the possible configurations of singular fibers (where the precise numbers depend on the index of wild ramification of the
$\text{I}_{2}$
automatically comes with double ramification by Lemma 4.1, we can bound the possible configurations of singular fibers (where the precise numbers depend on the index of wild ramification of the
![]() $\text{II}$
fibers):
$\text{II}$
fibers):
Lemma 4.2. For a line of the second kind, the singular fibers of
![]() $\unicode[STIX]{x1D70B}$
can be configured as follows:
$\unicode[STIX]{x1D70B}$
can be configured as follows:

Corollary 4.3. Unless the line
![]() $\ell$
of the second kind has ramification type
$\ell$
of the second kind has ramification type
![]() $(2,2)$
, it has valency
$(2,2)$
, it has valency
Otherwise one has
![]() $v(\ell )\leqslant 20$
.
$v(\ell )\leqslant 20$
.
It is due to this result that we will have to pay particular attention to lines of the second kind with ramification type
![]() $(2,2)$
. As it happens, quartics containing such a line are not hard to parametrize; in fact, a comparison with the proof of [Reference Rams and Schütt9, Lemma 4.5] shows that exactly the same argument as in characteristics
$(2,2)$
. As it happens, quartics containing such a line are not hard to parametrize; in fact, a comparison with the proof of [Reference Rams and Schütt9, Lemma 4.5] shows that exactly the same argument as in characteristics
![]() $\neq 2,3$
goes through:
$\neq 2,3$
goes through:
Lemma 4.4. Let
![]() $\ell$
be a line of the second kind on a smooth quartic
$\ell$
be a line of the second kind on a smooth quartic
![]() $S$
with ramification type
$S$
with ramification type
![]() $(2,2)$
. Then
$(2,2)$
. Then
![]() $S$
is projectively equivalent to a quartic in the family
$S$
is projectively equivalent to a quartic in the family
![]() ${\mathcal{Z}}$
given by the homogeneous polynomials
${\mathcal{Z}}$
given by the homogeneous polynomials
where
![]() $\ell =\{x_{3}=x_{4}=0\}$
,
$\ell =\{x_{3}=x_{4}=0\}$
,
![]() $q_{2}\in k[x_{3},x_{4}]_{(2)}$
and
$q_{2}\in k[x_{3},x_{4}]_{(2)}$
and
![]() $q_{4}\in k[x_{3},x_{4}]_{(4)}$
.
$q_{4}\in k[x_{3},x_{4}]_{(4)}$
.
We will not need the precise location of all singular fibers of
![]() $\unicode[STIX]{x1D70B}$
in what follows, but we would like to highlight the ramified singular fibers of Kodaira type
$\unicode[STIX]{x1D70B}$
in what follows, but we would like to highlight the ramified singular fibers of Kodaira type
![]() $\text{I}_{1}$
at
$\text{I}_{1}$
at
![]() $\unicode[STIX]{x1D706}=0,\infty$
. These degenerate to type
$\unicode[STIX]{x1D706}=0,\infty$
. These degenerate to type
![]() $\text{I}_{2}$
if and only if
$\text{I}_{2}$
if and only if
![]() $x_{3}$
respectively
$x_{3}$
respectively
![]() $x_{4}$
divides
$x_{4}$
divides
![]() $q_{4}$
(unless the surface attains singularities, for instance if
$q_{4}$
(unless the surface attains singularities, for instance if
![]() $q_{4}$
has a square factor). Note that if
$q_{4}$
has a square factor). Note that if
![]() $S$
is smooth and taken as in Lemma 4.4, then
$S$
is smooth and taken as in Lemma 4.4, then
For the record, we also note the following easy consequence of our considerations which we use occasionally to specialize to Jacobian elliptic fibrations:
Corollary 4.5. If
![]() $\unicode[STIX]{x1D70B}$
admits no section, or if no two lines on
$\unicode[STIX]{x1D70B}$
admits no section, or if no two lines on
![]() $S$
intersect, then
$S$
intersect, then
![]() $S$
contains at most 21 lines.
$S$
contains at most 21 lines.
Proof. In the first case, since any line disjoint from
![]() $\ell$
would give a section of
$\ell$
would give a section of
![]() $\unicode[STIX]{x1D70B}$
, we know that all lines on
$\unicode[STIX]{x1D70B}$
, we know that all lines on
![]() $S$
meet
$S$
meet
![]() $\ell$
. Hence the corollary follows from the combination of Corollaries 3.2 and 4.3.
$\ell$
. Hence the corollary follows from the combination of Corollaries 3.2 and 4.3.
In the second case, the lines give orthogonal
![]() $(-2)$
classes in
$(-2)$
classes in
![]() $\operatorname{NS}(X)$
. Since the latter has signature
$\operatorname{NS}(X)$
. Since the latter has signature
![]() $(1,\unicode[STIX]{x1D70C}(X)-1)$
with
$(1,\unicode[STIX]{x1D70C}(X)-1)$
with
![]() $\unicode[STIX]{x1D70C}(X)\leqslant b_{2}(X)=22$
, the claim follows.◻
$\unicode[STIX]{x1D70C}(X)\leqslant b_{2}(X)=22$
, the claim follows.◻
5 Proof of Theorem 1.1 in the triangle case
We break the proof of Theorem 1.1 into three cases, depending on which configurations of lines the smooth quartic
![]() $S$
admits. They will be treated separately in this and the next two sections. Throughout this section, we work with a smooth quartic
$S$
admits. They will be treated separately in this and the next two sections. Throughout this section, we work with a smooth quartic
![]() $S$
satisfying the following assumption:
$S$
satisfying the following assumption:
Assumption 5.1.
![]() $S$
contains a triangle (or a star) composed of 3 lines.
$S$
contains a triangle (or a star) composed of 3 lines.
Equivalently (since
![]() $S$
is assumed to be smooth), there is a hyperplane
$S$
is assumed to be smooth), there is a hyperplane
![]() $H$
containing the three said lines and thus splitting completely into lines on
$H$
containing the three said lines and thus splitting completely into lines on
![]() $S$
:
$S$
:
5.1
If neither of the lines
![]() $\ell _{1},\ldots ,\ell _{4}$
is of the second kind, then each of them meets at most
$\ell _{1},\ldots ,\ell _{4}$
is of the second kind, then each of them meets at most
![]() $18$
lines on
$18$
lines on
![]() $S$
by Corollary 3.2. Since any line on
$S$
by Corollary 3.2. Since any line on
![]() $S$
meets
$S$
meets
![]() $H$
, we find that
$H$
, we find that
![]() $S$
contains at most 64 lines as claimed.
$S$
contains at most 64 lines as claimed.
5.2
If the lines are allowed to be of the second kind, but not of ramification type
![]() $(2,2)$
, then Corollary 4.3 implies again that
$(2,2)$
, then Corollary 4.3 implies again that
![]() $S$
contains at most 64 lines.
$S$
contains at most 64 lines.
5.3
To complete the proof of Theorem 1.1 in the triangle case, it thus suffices to consider the case where one of the lines, say
![]() $\ell _{1}$
, is of the second kind with ramification type
$\ell _{1}$
, is of the second kind with ramification type
![]() $(2,2)$
. Hence
$(2,2)$
. Hence
![]() $X$
can be given as in Lemma 4.4; in particular, it admits a symplectic automorphism
$X$
can be given as in Lemma 4.4; in particular, it admits a symplectic automorphism
![]() $\unicode[STIX]{x1D711}$
of order 3 acting by
$\unicode[STIX]{x1D711}$
of order 3 acting by
for some primitive root of unity
![]() $\unicode[STIX]{x1D714}$
. Note that
$\unicode[STIX]{x1D714}$
. Note that
![]() $\unicode[STIX]{x1D711}$
permutes the lines
$\unicode[STIX]{x1D711}$
permutes the lines
![]() $\ell _{2},\ell _{3},\ell _{4}$
(or of any triangle coplanar with
$\ell _{2},\ell _{3},\ell _{4}$
(or of any triangle coplanar with
![]() $\ell _{1}$
). In particular, these three lines are of the same type. As before, we continue to distinguish three cases:
$\ell _{1}$
). In particular, these three lines are of the same type. As before, we continue to distinguish three cases:
5.3.1
If
![]() $\ell _{2}$
is of the first kind, then consider the degree 18 polynomial
$\ell _{2}$
is of the first kind, then consider the degree 18 polynomial
![]() $R\in k[\unicode[STIX]{x1D706}]$
associated to the flex points of the genus one fibration induced by
$R\in k[\unicode[STIX]{x1D706}]$
associated to the flex points of the genus one fibration induced by
![]() $\ell _{2}$
. Locate the singular fiber
$\ell _{2}$
. Locate the singular fiber
![]() $\ell _{1}+\ell _{3}+\ell _{4}$
(of type
$\ell _{1}+\ell _{3}+\ell _{4}$
(of type
![]() $\text{I}_{3}$
or
$\text{I}_{3}$
or
![]() $\text{IV}$
) at
$\text{IV}$
) at
![]() $\unicode[STIX]{x1D706}=0$
. Then an explicit computation shows that
$\unicode[STIX]{x1D706}=0$
. Then an explicit computation shows that
Since this divisibility exceeds the lower bound from Lemma 3.1, we infer from the arguments laid out in Section 3 that
![]() $\ell _{2}$
meets at most 14 lines outside the fiber at
$\ell _{2}$
meets at most 14 lines outside the fiber at
![]() $\unicode[STIX]{x1D706}=0$
. In total, this gives
$\unicode[STIX]{x1D706}=0$
. In total, this gives
Together with Corollary 4.3, this shows that
![]() $S$
contains at most 63 lines.
$S$
contains at most 63 lines.
5.3.2
Similarly, if
![]() $\ell _{2}$
is of the second kind, but not of ramification type
$\ell _{2}$
is of the second kind, but not of ramification type
![]() $(2,2)$
, then by Corollary 4.3, there are no more than 60 lines on
$(2,2)$
, then by Corollary 4.3, there are no more than 60 lines on
![]() $S$
.
$S$
.
5.3.3
We conclude the proof of Theorem 1.1 in the triangle case by ruling out that
![]() $\ell _{2}$
is of the second kind with ramification type
$\ell _{2}$
is of the second kind with ramification type
![]() $(2,2)$
. (Over
$(2,2)$
. (Over
![]() $\mathbb{C}$
this case leads either to Schur’s quartic (containing 64 lines) or to
$\mathbb{C}$
this case leads either to Schur’s quartic (containing 64 lines) or to
![]() $S$
being singular [Reference Rams and Schütt9, Lemma 6.2].) But presently the situation differs substantially since there can only be two ramification points anyway. Rescaling
$S$
being singular [Reference Rams and Schütt9, Lemma 6.2].) But presently the situation differs substantially since there can only be two ramification points anyway. Rescaling
![]() $x_{3},x_{4}$
, we can assume that the given line lies in the fiber at
$x_{3},x_{4}$
, we can assume that the given line lies in the fiber at
![]() $\unicode[STIX]{x1D706}=1$
; this determines the
$\unicode[STIX]{x1D706}=1$
; this determines the
![]() $x_{4}^{4}$
-coefficient of
$x_{4}^{4}$
-coefficient of
![]() $q_{4}$
, say. Then, up to the action of
$q_{4}$
, say. Then, up to the action of
![]() $\unicode[STIX]{x1D711}$
, it is given by
$\unicode[STIX]{x1D711}$
, it is given by
One checks that
![]() $\ell _{2}$
has generically ramification type
$\ell _{2}$
has generically ramification type
![]() $(1,1)$
; this degenerates to type
$(1,1)$
; this degenerates to type
![]() $(2,2)$
with
$(2,2)$
with
![]() $S$
continuing to be smooth if and only if
$S$
continuing to be smooth if and only if
where the prime indicates the formal derivative with respect to either
![]() $x_{3}$
or
$x_{3}$
or
![]() $x_{4}$
. Substituting for a coefficient of
$x_{4}$
. Substituting for a coefficient of
![]() $q_{4}$
, this directly implies
$q_{4}$
, this directly implies
where we have located the
![]() $\text{I}_{3}$
or
$\text{I}_{3}$
or
![]() $\text{IV}$
fiber
$\text{IV}$
fiber
![]() $\ell _{1}+\ell _{3}+\ell _{4}$
at
$\ell _{1}+\ell _{3}+\ell _{4}$
at
![]() $\unicode[STIX]{x1D706}=0$
as in 5.3.1. Solving for
$\unicode[STIX]{x1D706}=0$
as in 5.3.1. Solving for
![]() $R\equiv 0$
, we inspect the first few coefficients of
$R\equiv 0$
, we inspect the first few coefficients of
![]() $R$
. Starting with the coefficient of
$R$
. Starting with the coefficient of
![]() $\unicode[STIX]{x1D706}^{7}$
, a simple case-by-case analysis yields that
$\unicode[STIX]{x1D706}^{7}$
, a simple case-by-case analysis yields that
![]() $R$
can only vanish identically if
$R$
can only vanish identically if
![]() $S$
is singular. This completes the proof of Theorem 1.1 in the triangle case.◻
$S$
is singular. This completes the proof of Theorem 1.1 in the triangle case.◻
6 Proof of Theorem 1.1 in the square case
Throughout this section, we work with a smooth quartic
![]() $S$
satisfying the following assumption:
$S$
satisfying the following assumption:
Assumption 6.1.
![]() $S$
contains neither a triangle nor a star composed of 3 lines, but it does contain a square comprising 4 lines.
$S$
contains neither a triangle nor a star composed of 3 lines, but it does contain a square comprising 4 lines.
We shall refer to this situation as the square case. Our arguments are inspired by an approach due to Degtyarev and Veniani (see [Reference Veniani19]).
Lemma 6.2. If
![]() $S$
contains no triangles or stars, then each line
$S$
contains no triangles or stars, then each line
![]() $\ell$
on
$\ell$
on
![]() $S$
has valency
$S$
has valency
Proof. Since the genus one fibration
![]() $\unicode[STIX]{x1D70B}$
induced by
$\unicode[STIX]{x1D70B}$
induced by
![]() $\ell$
cannot be quasi-elliptic by Proposition 2.1, the proof of Lemma 6.2 amounts to a simple Euler–Poincaré characteristic computation as the contributions of the singular fibers (including wild ramification) have to sum up to
$\ell$
cannot be quasi-elliptic by Proposition 2.1, the proof of Lemma 6.2 amounts to a simple Euler–Poincaré characteristic computation as the contributions of the singular fibers (including wild ramification) have to sum up to
![]() $24$
. Presently, since
$24$
. Presently, since
![]() $S$
admits no triangles and stars by assumption,
$S$
admits no triangles and stars by assumption,
![]() $\unicode[STIX]{x1D70B}$
can only have singular fibers of Kodaira types
$\unicode[STIX]{x1D70B}$
can only have singular fibers of Kodaira types
![]() $\text{I}_{1},\text{I}_{2},\text{II},\text{III}$
. Hence there can be at most 12 fibers containing a line.◻
$\text{I}_{1},\text{I}_{2},\text{II},\text{III}$
. Hence there can be at most 12 fibers containing a line.◻
Denote any 4 lines forming a square on
![]() $S$
by
$S$
by
![]() $\ell _{1},\ldots ,\ell _{4}$
. Order the lines such that
$\ell _{1},\ldots ,\ell _{4}$
. Order the lines such that
![]() $\ell _{i}.\ell _{j}=1$
if and only if
$\ell _{i}.\ell _{j}=1$
if and only if
![]() $i\not \equiv j\;\text{mod}\;2$
. Consider the two residual (irreducible) conics
$i\not \equiv j\;\text{mod}\;2$
. Consider the two residual (irreducible) conics
![]() $Q_{12},Q_{34}$
such that the hyperplane class
$Q_{12},Q_{34}$
such that the hyperplane class
![]() $H$
decomposes on
$H$
decomposes on
![]() $S$
as
$S$
as
Then the linear system
![]() $|2H-Q_{12}-Q_{34}|$
induces a genus one fibration
$|2H-Q_{12}-Q_{34}|$
induces a genus one fibration
with fibers of degree
![]() $4$
– one of them is exactly the square
$4$
– one of them is exactly the square
![]() $D=\ell _{1}+\cdots +\ell _{4}$
of Kodaira type
$D=\ell _{1}+\cdots +\ell _{4}$
of Kodaira type
![]() $\text{I}_{4}$
. Any line on
$\text{I}_{4}$
. Any line on
![]() $S$
is either orthogonal to
$S$
is either orthogonal to
![]() $D$
and thus a fiber component of
$D$
and thus a fiber component of
![]() $\unicode[STIX]{x1D713}$
, or it gives a section or bisection for
$\unicode[STIX]{x1D713}$
, or it gives a section or bisection for
![]() $\unicode[STIX]{x1D713}$
, thus contributing to the valency of one or two of the lines
$\unicode[STIX]{x1D713}$
, thus contributing to the valency of one or two of the lines
![]() $\ell _{i}$
. In total, this gives the upper bound
$\ell _{i}$
. In total, this gives the upper bound
 $$\begin{eqnarray}\displaystyle \#\{\text{lines on }S\} & {\leqslant} & \displaystyle \#\{\text{lines in fibers of }\unicode[STIX]{x1D713}\}+\mathop{\sum }_{i=1}^{4}(v(\ell _{i})-2)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \#\{\text{lines in fibers of }\unicode[STIX]{x1D713}\}+40\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \#\{\text{lines on }S\} & {\leqslant} & \displaystyle \#\{\text{lines in fibers of }\unicode[STIX]{x1D713}\}+\mathop{\sum }_{i=1}^{4}(v(\ell _{i})-2)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \#\{\text{lines in fibers of }\unicode[STIX]{x1D713}\}+40\nonumber\end{eqnarray}$$
where the second equality follows from Lemma 6.2. We shall now study the possible fiber configurations to derive the following upper bound for the number of lines on
![]() $S$
which will prove Theorem 1.1 in the square case.
$S$
which will prove Theorem 1.1 in the square case.
Proposition 6.3. Under Assumption 6.1, the smooth quartic
![]() $S$
contains at most 60 lines.
$S$
contains at most 60 lines.
Before starting the proof of Proposition 6.3 properly, we note the possible reducible fibers of
![]() $\unicode[STIX]{x1D713}$
:
$\unicode[STIX]{x1D713}$
:
Table 2. Possible reducible fibers of
![]() $\unicode[STIX]{x1D713}$
.
$\unicode[STIX]{x1D713}$
.

Using the fact that additive fibers necessarily come with wild ramification (so that they contribute at least 4 to the Euler–Poincaré characteristic, see [Reference Schütt and Schweizer14, Proposition 5.1]), one can easily work out all fiber configurations possibly admitting more than 20 lines as fiber components:

To rule out all these configurations, we employ structural Weierstrass form arguments specific to characteristic
![]() $2$
(which apply since we can always switch to the Jacobian of
$2$
(which apply since we can always switch to the Jacobian of
![]() $\unicode[STIX]{x1D713}$
). Similar arguments have been applied to the particular problem of maximal singular fibers of elliptic K3 surfaces in [Reference Schütt and Schweizer14].
$\unicode[STIX]{x1D713}$
). Similar arguments have been applied to the particular problem of maximal singular fibers of elliptic K3 surfaces in [Reference Schütt and Schweizer14].
6.1 General set-up
In characteristic
![]() $2$
, an elliptic curve with given nonzero
$2$
, an elliptic curve with given nonzero
![]() $j$
-invariant
$j$
-invariant
![]() $j$
can be defined by a Weierstrass form over a given field
$j$
can be defined by a Weierstrass form over a given field
![]() $K$
by
$K$
by
As usual, this is unique up to quadratic twist, but here twists occur in terms of an extra summand
![]() $Dx^{2}$
, with
$Dx^{2}$
, with
![]() $K$
-isomorphic surfaces connected by the Artin–Schreier map
$K$
-isomorphic surfaces connected by the Artin–Schreier map
![]() $z\mapsto z^{2}+z$
over
$z\mapsto z^{2}+z$
over
![]() $K$
:
$K$
:
The main approach now consists in substituting a conjectural
![]() $j$
-invariant, given as quotient
$j$
-invariant, given as quotient
associated to the usual integral Weierstrass form
Converting the twisted form of (3) with
![]() $j$
-invariant from (5) to an integral model
$j$
-invariant from (5) to an integral model
![]() $E$
, we arrive at the Weierstrass form
$E$
, we arrive at the Weierstrass form
Which, outside very special cases, will be nonminimal at the zeroes of
![]() $a_{1}$
. Then minimalizing is achieved by running Tate’s algorithm [Reference Tate18] which consequently gives relations between the coefficients of
$a_{1}$
. Then minimalizing is achieved by running Tate’s algorithm [Reference Tate18] which consequently gives relations between the coefficients of
![]() $a_{1},D^{\prime }$
and
$a_{1},D^{\prime }$
and
![]() $\unicode[STIX]{x1D6E5}$
, or in some cases like ours leads to a contradiction. By inspection of (6), the polynomial
$\unicode[STIX]{x1D6E5}$
, or in some cases like ours leads to a contradiction. By inspection of (6), the polynomial
![]() $a_{1}$
encodes singular or supersingular fibers. For immediate use, we record the following criterion which is borrowed from [Reference Schweizer15, Lemma 2.4(a)]:
$a_{1}$
encodes singular or supersingular fibers. For immediate use, we record the following criterion which is borrowed from [Reference Schweizer15, Lemma 2.4(a)]:
Lemma 6.4. Assume that there is a supersingular place which is not singular. Locating it at
![]() $t=0$
, the
$t=0$
, the
![]() $t$
-coefficient of
$t$
-coefficient of
![]() $\unicode[STIX]{x1D6E5}$
has to vanish.
$\unicode[STIX]{x1D6E5}$
has to vanish.
Proof. By assumption,
![]() $a_{1}=ta_{1}^{\prime }$
, so the integral Weierstrass form (6) reads
$a_{1}=ta_{1}^{\prime }$
, so the integral Weierstrass form (6) reads
Writing
![]() $\unicode[STIX]{x1D6E5}=d_{0}+d_{1}t+\cdots \,$
, the fiber of the affine Weierstrass form at
$\unicode[STIX]{x1D6E5}=d_{0}+d_{1}t+\cdots \,$
, the fiber of the affine Weierstrass form at
![]() $t=0$
has a singular point at
$t=0$
has a singular point at
![]() $(0,\sqrt{d_{0}})$
. Since
$(0,\sqrt{d_{0}})$
. Since
![]() $t=0$
is a place of good reduction, the Weierstrass form is nonminimal. From Tate’s algorithm [Reference Tate18], this translates as
$t=0$
is a place of good reduction, the Weierstrass form is nonminimal. From Tate’s algorithm [Reference Tate18], this translates as
![]() $(0,\sqrt{d_{0}})$
being in fact a surface singularity. Equivalently,
$(0,\sqrt{d_{0}})$
being in fact a surface singularity. Equivalently,
![]() $d_{1}=0$
by Jacobi’s criterion.◻
$d_{1}=0$
by Jacobi’s criterion.◻
Example 6.5. There cannot be a rational elliptic surface in characteristic
![]() $2$
with singular fibers
$2$
with singular fibers
![]() $5\text{I}_{2},2\text{I}_{1}$
. Otherwise,
$5\text{I}_{2},2\text{I}_{1}$
. Otherwise,
![]() $\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}_{5}^{2}(t^{2}+at+b)$
for some squarefree degree 5 polynomial
$\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}_{5}^{2}(t^{2}+at+b)$
for some squarefree degree 5 polynomial
![]() $\unicode[STIX]{x1D6E5}_{5}$
and with
$\unicode[STIX]{x1D6E5}_{5}$
and with
![]() $a\neq 0$
. Since the surface is semistable, Lemma 6.4 kicks in to show that
$a\neq 0$
. Since the surface is semistable, Lemma 6.4 kicks in to show that
![]() $a=0$
, contradiction.
$a=0$
, contradiction.
Remark 6.6. Note that the criterion of Lemma 6.4 applies after any Möbius transformation fixing
![]() $0$
, and to any supersingular place that is not singular. Tracing the nonminimality argument further through Tate’s algorithm, one can, for instance, show that there do not exist elliptic fibrations in characteristic
$0$
, and to any supersingular place that is not singular. Tracing the nonminimality argument further through Tate’s algorithm, one can, for instance, show that there do not exist elliptic fibrations in characteristic
![]() $2$
with configuration of singular fibers
$2$
with configuration of singular fibers
![]() $4\text{I}_{3}+6\text{I}_{2}$
(as occurring on Schur’s quartic over
$4\text{I}_{3}+6\text{I}_{2}$
(as occurring on Schur’s quartic over
![]() $\mathbb{C}$
).
$\mathbb{C}$
).
6.2 Nonexistence of the configurations
 $6\text{I}_{4},5\text{I}_{4}+2\text{I}_{2},5\text{I}_{4}+\text{IV},5\text{I}_{4}+\text{III}$
$6\text{I}_{4},5\text{I}_{4}+2\text{I}_{2},5\text{I}_{4}+\text{IV},5\text{I}_{4}+\text{III}$
In each of the said cases, the
![]() $j$
-invariant (5) is a perfect square. Equivalently,
$j$
-invariant (5) is a perfect square. Equivalently,
![]() $\unicode[STIX]{x1D713}$
arises from another elliptic fibration by a purely inseparable base change. (To see this, apply the variable transformation
$\unicode[STIX]{x1D713}$
arises from another elliptic fibration by a purely inseparable base change. (To see this, apply the variable transformation
![]() $y\mapsto y+Dx$
to (4).) In the first two cases, this would lead to a rational elliptic surface with five
$y\mapsto y+Dx$
to (4).) In the first two cases, this would lead to a rational elliptic surface with five
![]() $\text{I}_{2}$
fibers; this cannot exist by [Reference Lang6] (which can be checked independently as in Example 6.5 or 6.3). Similarly, the configuration
$\text{I}_{2}$
fibers; this cannot exist by [Reference Lang6] (which can be checked independently as in Example 6.5 or 6.3). Similarly, the configuration
![]() $5\text{I}_{4}+\text{IV}$
cannot arise at all because fibers of type
$5\text{I}_{4}+\text{IV}$
cannot arise at all because fibers of type
![]() $\text{IV}$
are only related to type
$\text{IV}$
are only related to type
![]() $\text{IV}^{\ast }$
by inseparable base change, so that the Euler–Poincaré characteristics would not sum up to a multiple of
$\text{IV}^{\ast }$
by inseparable base change, so that the Euler–Poincaré characteristics would not sum up to a multiple of
![]() $12$
.
$12$
.
For the last configuration, since the fiber of type
![]() $\text{III}$
comes with wild ramification of index
$\text{III}$
comes with wild ramification of index
![]() $1$
(by the Euler–Poincaré characteristic formula), it can only arise from a singular fiber of the same ramification index and total contribution to the discriminant congruent to
$1$
(by the Euler–Poincaré characteristic formula), it can only arise from a singular fiber of the same ramification index and total contribution to the discriminant congruent to
![]() $2$
mod
$2$
mod
![]() $6$
. By [Reference Schütt and Schweizer14, Proposition 5.1], this uniquely leads to Kodaira type
$6$
. By [Reference Schütt and Schweizer14, Proposition 5.1], this uniquely leads to Kodaira type
![]() $\text{I}_{1}^{\ast }$
, but then again with the five
$\text{I}_{1}^{\ast }$
, but then again with the five
![]() $\text{I}_{2}$
fibers the Euler–Poincaré characteristics do not sum up to a multiple of
$\text{I}_{2}$
fibers the Euler–Poincaré characteristics do not sum up to a multiple of
![]() $12$
.
$12$
.
6.3 Nonexistence of the configurations
 $5\text{I}_{4}+\text{I}_{3}+\text{I}_{1},5\text{I}_{4}+\text{I}_{2}+2\text{I}_{1},4\text{I}_{4}+2\text{I}_{3}+\text{I}_{2}$
$5\text{I}_{4}+\text{I}_{3}+\text{I}_{1},5\text{I}_{4}+\text{I}_{2}+2\text{I}_{1},4\text{I}_{4}+2\text{I}_{3}+\text{I}_{2}$
Each of these configurations is semistable, so Lemma 6.4 applies with supersingular (smooth) place at
![]() $t=0$
. In the first case, for instance, we can locate the
$t=0$
. In the first case, for instance, we can locate the
![]() $\text{I}_{3}$
fiber at
$\text{I}_{3}$
fiber at
![]() $\infty$
and write affinely
$\infty$
and write affinely
for some squarefree polynomial
![]() $\unicode[STIX]{x1D6E5}$
of degree
$\unicode[STIX]{x1D6E5}$
of degree
![]() $5$
. But then
$5$
. But then
![]() $t\mid \unicode[STIX]{x1D6E5}_{5}$
by Lemma 6.4, contradiction. The other two configurations can be ruled out completely analogously.
$t\mid \unicode[STIX]{x1D6E5}_{5}$
by Lemma 6.4, contradiction. The other two configurations can be ruled out completely analogously.
Proof of Proposition 6.3.
Altogether it follows from Sections 6.2 and 6.3 that the fibers of
![]() $\unicode[STIX]{x1D713}$
may contain at most 20 lines. In view of the upper bound
$\unicode[STIX]{x1D713}$
may contain at most 20 lines. In view of the upper bound
this completes the proof of Proposition 6.3. ◻
7 Proof of Theorem 1.1 in the squarefree case
Throughout this section, we work with a smooth quartic
![]() $S$
satisfying the following assumption:
$S$
satisfying the following assumption:
Assumption 7.1.
![]() $S$
contains neither a triangle nor a star composed of 3 lines nor a square comprising 4 lines.
$S$
contains neither a triangle nor a star composed of 3 lines nor a square comprising 4 lines.
In short, we also call
![]() $S$
squarefree (meaning also trianglefree). In the sequel of this paper we use the following stronger version of [Reference Rams and Schütt10, Theorem 1.1].
$S$
squarefree (meaning also trianglefree). In the sequel of this paper we use the following stronger version of [Reference Rams and Schütt10, Theorem 1.1].
Lemma 7.2. Let
![]() $Q\subset S$
be an irreducible conic which is coplanar with two lines on
$Q\subset S$
be an irreducible conic which is coplanar with two lines on
![]() $S$
. Then
$S$
. Then
![]() $Q$
is met by at most
$Q$
is met by at most
![]() $46$
lines on
$46$
lines on
![]() $S$
.
$S$
.
Proof. The proof of the claim forms the last section of the proof of [Reference Rams and Schütt10, Proposition 1.3]. ◻
Proposition 7.3. If
![]() $S$
is squarefree, then
$S$
is squarefree, then
![]() $S$
contains at most
$S$
contains at most
![]() $60$
lines.
$60$
lines.
Proof. By Corollary 4.5 we can assume that
![]() $S$
contains a pair of lines
$S$
contains a pair of lines
![]() $\ell _{1}\neq \ell _{2}$
that intersect. Let
$\ell _{1}\neq \ell _{2}$
that intersect. Let
![]() $\ell _{2},\ell _{3},\ell _{4},\ldots ,\ell _{k_{1}+1}$
be the lines on
$\ell _{2},\ell _{3},\ell _{4},\ldots ,\ell _{k_{1}+1}$
be the lines on
![]() $S$
that meet
$S$
that meet
![]() $\ell _{1}$
, and let
$\ell _{1}$
, and let
![]() $\ell _{i,1},\ldots ,\ell _{i,k_{i}}$
be the lines that intersect
$\ell _{i,1},\ldots ,\ell _{i,k_{i}}$
be the lines that intersect
![]() $\ell _{i}$
for
$\ell _{i}$
for
![]() $i\geqslant 2$
. After reordering the lines, we assume
$i\geqslant 2$
. After reordering the lines, we assume
![]() $\ell _{1}=\ell _{i,1}$
.
$\ell _{1}=\ell _{i,1}$
.
Suppose that
![]() $(k_{1}+k_{i})\leqslant 16$
for an
$(k_{1}+k_{i})\leqslant 16$
for an
![]() $i\in \{2,\ldots ,k_{1}+1\}$
. Then, by Lemma 7.2 the irreducible conic in
$i\in \{2,\ldots ,k_{1}+1\}$
. Then, by Lemma 7.2 the irreducible conic in
![]() $|{\mathcal{O}}_{S}(1)-\ell _{1}-\ell _{i}|$
is met by at most
$|{\mathcal{O}}_{S}(1)-\ell _{1}-\ell _{i}|$
is met by at most
![]() $44$
lines on
$44$
lines on
![]() $S$
other than
$S$
other than
![]() $\ell _{1},\ell _{i}$
, and the claim of the proposition follows immediately, because every line on
$\ell _{1},\ell _{i}$
, and the claim of the proposition follows immediately, because every line on
![]() $S$
meets either
$S$
meets either
![]() $\ell _{1}$
or
$\ell _{1}$
or
![]() $\ell _{i}$
or the conic.
$\ell _{i}$
or the conic.
Otherwise, we assume to the contrary that
![]() $S$
contains more than 60 lines. After exchanging
$S$
contains more than 60 lines. After exchanging
![]() $\ell _{1},\ell _{i}$
, if necessary, and iterating the above process, we may assume using Lemma 6.2 that
$\ell _{1},\ell _{i}$
, if necessary, and iterating the above process, we may assume using Lemma 6.2 that
In particular, we always have the lines
![]() $\ell _{2},\ldots ,\ell _{6}$
on
$\ell _{2},\ldots ,\ell _{6}$
on
![]() $S$
, and
$S$
, and
![]() $k_{i}\geqslant 9$
for
$k_{i}\geqslant 9$
for
![]() $i\geqslant 2$
. Assumption 7.1 guarantees that
$i\geqslant 2$
. Assumption 7.1 guarantees that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \ell _{j_{1}}.\ell _{j_{2}}=0\quad \text{whenever }2\leqslant j_{1}<j_{2}\nonumber\\ \displaystyle & & \displaystyle \ell _{i,j_{1}}.\ell _{i,j_{2}}=0\quad \text{whenever }1\leqslant j_{1}<j_{2}\text{ and }i\geqslant 2\nonumber\\ \displaystyle & & \displaystyle \ell _{i,j}\text{ meets at most one of the }\ell _{m,n}\quad \forall i,j,m\geqslant 2.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \ell _{j_{1}}.\ell _{j_{2}}=0\quad \text{whenever }2\leqslant j_{1}<j_{2}\nonumber\\ \displaystyle & & \displaystyle \ell _{i,j_{1}}.\ell _{i,j_{2}}=0\quad \text{whenever }1\leqslant j_{1}<j_{2}\text{ and }i\geqslant 2\nonumber\\ \displaystyle & & \displaystyle \ell _{i,j}\text{ meets at most one of the }\ell _{m,n}\quad \forall i,j,m\geqslant 2.\end{eqnarray}$$
Consider the divisor
![]() $D=2\ell _{2}+\ell _{2,2}+\cdots +\ell _{2,5}$
of Kodaira type
$D=2\ell _{2}+\ell _{2,2}+\cdots +\ell _{2,5}$
of Kodaira type
![]() $\text{I}_{0}^{\ast }$
. Then
$\text{I}_{0}^{\ast }$
. Then
![]() $|D|$
induces a genus one fibration
$|D|$
induces a genus one fibration
with
![]() $D$
as fiber. Naturally,
$D$
as fiber. Naturally,
![]() $\ell _{3},\ldots ,\ell _{k_{1}+1}$
, being perpendicular to
$\ell _{3},\ldots ,\ell _{k_{1}+1}$
, being perpendicular to
![]() $D$
, also appear as fiber components, but we can say a little more. Namely, by (8), each
$D$
, also appear as fiber components, but we can say a little more. Namely, by (8), each
![]() $\ell _{j}$
(for
$\ell _{j}$
(for
![]() $2<j\leqslant k_{1}+1$
) comes with at least
$2<j\leqslant k_{1}+1$
) comes with at least
![]() $(k_{j}-5)$
adjacent lines, say
$(k_{j}-5)$
adjacent lines, say
![]() $\ell _{j,6},\ldots ,\ell _{j,k_{j}}$
which are also perpendicular to
$\ell _{j,6},\ldots ,\ell _{j,k_{j}}$
which are also perpendicular to
![]() $D$
. Since
$D$
. Since
![]() $k_{j}\geqslant 9$
, the divisor
$k_{j}\geqslant 9$
, the divisor
![]() $2\ell _{j}+\ell _{j,6}+\cdots +\ell _{j,9}$
gives another
$2\ell _{j}+\ell _{j,6}+\cdots +\ell _{j,9}$
gives another
![]() $\text{I}_{0}^{\ast }$
fiber of
$\text{I}_{0}^{\ast }$
fiber of
![]() $\unicode[STIX]{x1D713}$
; in particular, there is no space for any further fiber components, that is,
$\unicode[STIX]{x1D713}$
; in particular, there is no space for any further fiber components, that is,
![]() $k_{j}=9$
for all
$k_{j}=9$
for all
![]() $j=3,\ldots ,k_{1}+1$
. Therefore, we obtain
$j=3,\ldots ,k_{1}+1$
. Therefore, we obtain
![]() $k_{1}\geqslant 8$
from (7), so
$k_{1}\geqslant 8$
from (7), so
![]() $\unicode[STIX]{x1D713}$
admits at least
$\unicode[STIX]{x1D713}$
admits at least
![]() $8$
fibers of type
$8$
fibers of type
![]() $\text{I}_{0}^{\ast }$
. The sum of their contributions to the Euler–Poincaré characteristic of
$\text{I}_{0}^{\ast }$
. The sum of their contributions to the Euler–Poincaré characteristic of
![]() $S$
clearly exceeds
$S$
clearly exceeds
![]() $e(S)=24$
, even if
$e(S)=24$
, even if
![]() $\unicode[STIX]{x1D713}$
were to be quasi-elliptic. This gives the desired contradiction and thus concludes the proof of Proposition 7.3.◻
$\unicode[STIX]{x1D713}$
were to be quasi-elliptic. This gives the desired contradiction and thus concludes the proof of Proposition 7.3.◻
8 Example with 60 lines
This section gives an explicit example of a smooth quartic surface defined over the finite field
![]() $\mathbb{F}_{4}$
which contains 60 lines over
$\mathbb{F}_{4}$
which contains 60 lines over
![]() $\mathbb{F}_{16}$
. Motivated by [Reference Rams and Schütt8] where a pencil of quintic surfaces going back to Barth was studied, we consider geometrically irreducible quartic surfaces with an action by the symmetric group
$\mathbb{F}_{16}$
. Motivated by [Reference Rams and Schütt8] where a pencil of quintic surfaces going back to Barth was studied, we consider geometrically irreducible quartic surfaces with an action by the symmetric group
![]() $S_{5}$
of order
$S_{5}$
of order
![]() $120$
. These come in a one-dimensional pencil which can be expressed in elementary symmetric polynomials
$120$
. These come in a one-dimensional pencil which can be expressed in elementary symmetric polynomials
![]() $s_{i}$
of degree
$s_{i}$
of degree
![]() $i$
in the homogeneous coordinates of
$i$
in the homogeneous coordinates of
![]() $\mathbb{P}^{4}$
as
$\mathbb{P}^{4}$
as
There are 60 lines at the primitive third roots of unity as follows. Let
![]() $\unicode[STIX]{x1D6FC}\in \mathbb{F}_{16}$
be a fifth root of unity, that is,
$\unicode[STIX]{x1D6FC}\in \mathbb{F}_{16}$
be a fifth root of unity, that is,
![]() $\unicode[STIX]{x1D6FC}^{4}+\unicode[STIX]{x1D6FC}^{3}+\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FC}+1=0$
. Then
$\unicode[STIX]{x1D6FC}^{4}+\unicode[STIX]{x1D6FC}^{3}+\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FC}+1=0$
. Then
![]() $\unicode[STIX]{x1D707}_{0}=1+\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FC}^{3}$
is a cube root of unity, and
$\unicode[STIX]{x1D707}_{0}=1+\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FC}^{3}$
is a cube root of unity, and
![]() $S_{\unicode[STIX]{x1D707}_{0}}$
contains the line
$S_{\unicode[STIX]{x1D707}_{0}}$
contains the line
![]() $\ell$
given by
$\ell$
given by
The
![]() $S_{5}$
-orbit of
$S_{5}$
-orbit of
![]() $\ell$
consists of exactly 60 lines which span
$\ell$
consists of exactly 60 lines which span
![]() $\operatorname{NS}(S_{\unicode[STIX]{x1D707}_{0}})$
of rank
$\operatorname{NS}(S_{\unicode[STIX]{x1D707}_{0}})$
of rank
![]() $20$
and discriminant
$20$
and discriminant
![]() $-55$
. We are not aware of any other smooth quartic surface in
$-55$
. We are not aware of any other smooth quartic surface in
![]() $\mathbb{P}_{\bar{\mathbb{F}}_{2}}^{2}$
with 60 or more lines.
$\mathbb{P}_{\bar{\mathbb{F}}_{2}}^{2}$
with 60 or more lines.
In fact, the surface
![]() $S_{\unicode[STIX]{x1D707}_{0}}$
can be shown to lift to characteristic zero together with all its 60 lines at
$S_{\unicode[STIX]{x1D707}_{0}}$
can be shown to lift to characteristic zero together with all its 60 lines at
![]() $\hat{\unicode[STIX]{x1D707}}=-\frac{3}{10}\pm \frac{\sqrt{-11}}{10}$
(although proving this is not as easy as it might seem). The lines are then defined over the Hilbert class field
$\hat{\unicode[STIX]{x1D707}}=-\frac{3}{10}\pm \frac{\sqrt{-11}}{10}$
(although proving this is not as easy as it might seem). The lines are then defined over the Hilbert class field
![]() $H(-55)$
as follows. Let
$H(-55)$
as follows. Let
![]() $\unicode[STIX]{x1D6FC}\in \bar{\mathbb{Q}}$
satisfy
$\unicode[STIX]{x1D6FC}\in \bar{\mathbb{Q}}$
satisfy
The quartic at
![]() $\hat{\unicode[STIX]{x1D707}}$
contains the line
$\hat{\unicode[STIX]{x1D707}}$
contains the line
where
As before, its
![]() $S_{5}$
-orbit comprises all 60 lines on
$S_{5}$
-orbit comprises all 60 lines on
![]() $S_{\hat{\unicode[STIX]{x1D707}}}$
.
$S_{\hat{\unicode[STIX]{x1D707}}}$
.
Acknowledgments
We thank Davide Veniani for helpful comments and discussions, and the anonymous referee for valuable suggestions. This paper was completed at the workshop on K3 surfaces and related topics at KIAS in November 2015. We thank the organizers JongHae Keum and Shigeyuki Kondō for their great hospitality.