Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hu, Zejun
and
Li, Deying
2007.
Möbius isoparametric hypersurfaces with three distinct principal curvatures.
Pacific Journal of Mathematics,
Vol. 232,
Issue. 2,
p.
289.
Hu, Zejun
Li, Haizhong
and
Wang, Changping
2007.
Classification of Möbius Isoparametric Hypersurfaces in ${\Bbb S}^5$.
Monatshefte für Mathematik,
Vol. 151,
Issue. 3,
p.
201.
Li, Xing Xiao
and
Zhang, Feng Yun
2007.
Immersed Hypersurfaces in the Unit Sphere S m+1 with Constant Blaschke Eigenvalues.
Acta Mathematica Sinica, English Series,
Vol. 23,
Issue. 3,
p.
533.
Riveros, Carlos
Rodrigues, Luciana
and
Tenenblat, Keti
2008.
On Dupin hypersurfaces with constant Möbius curvature.
Pacific Journal of Mathematics,
Vol. 236,
Issue. 1,
p.
89.
Hu, Zejun
and
Zhai, Shujie
2008.
Classification of Möbius isoparametric hypersurfaces in the unit six-sphere.
Tohoku Mathematical Journal,
Vol. 60,
Issue. 4,
Rodrigues, L. A.
and
Tenenblat, K.
2009.
A characterization of Moebius isoparametric hypersurfaces of the sphere.
Monatshefte für Mathematik,
Vol. 158,
Issue. 3,
p.
321.
Li, Xing Xiao
and
Zhang, Feng Yun
2009.
On the Blaschke isoparametric hypersurfaces in the unit sphere.
Acta Mathematica Sinica, English Series,
Vol. 25,
Issue. 4,
p.
657.
Hu, Ze Jun
and
Tian, Xiao Li
2009.
On Möbius form and Möbius isoparametric hypersurfaces.
Acta Mathematica Sinica, English Series,
Vol. 25,
Issue. 12,
p.
2077.
Li, Xingxiao
and
Peng, Yejuan
2010.
Classification of the Blaschke Isoparametric Hypersurfaces with Three Distinct Blaschke Eigenvalues.
Results in Mathematics,
Vol. 58,
Issue. 1-2,
p.
145.
Hu, ZeJun
Li, XingXiao
and
Zhai, ShuJie
2011.
On the Blaschke isoparametric hypersurfaces in the unit sphere with three distinct Blaschke eigenvalues.
Science China Mathematics,
Vol. 54,
Issue. 10,
p.
2171.
Li, TongZhu
Li, HaiZhong
and
Wang, ChangPing
2011.
Classification of hypersurfaces with constant Laguerre eigenvalues in ℝ n.
Science China Mathematics,
Vol. 54,
Issue. 6,
p.
1129.
Hu, Zejun
and
Zhai, Shujie
2011.
Möbius isoparametric hypersurfaces with three distinct principal curvatures, II.
Pacific Journal of Mathematics,
Vol. 249,
Issue. 2,
p.
343.
Brasil, Aldir
and
de Araujo Costa, Ezio
2011.
On Hypersurfaces of Spheres with Two Principal Curvatures.
Results in Mathematics,
Vol. 60,
Issue. 1-4,
p.
287.
Shu, Shichang
and
Su, Bianping
2012.
Conformal isoparametric spacelike hypersurfaces in conformal spaces $ \mathbb{Q}_1^4 $ and $ \mathbb{Q}_1^5 $.
Ukrainian Mathematical Journal,
Vol. 64,
Issue. 4,
p.
634.
Li, Tongzhu
and
Wang, Changping
2014.
A note on Blaschke isoparametric hypersurfaces.
International Journal of Mathematics,
Vol. 25,
Issue. 12,
p.
1450117.
Fang, Jian Bo
and
Zhang, Kun
2014.
Hypersurfaces with isotropic para-Blaschke tensor.
Acta Mathematica Sinica, English Series,
Vol. 30,
Issue. 7,
p.
1195.
Cecil, Thomas E.
and
Ryan, Patrick J.
2015.
Geometry of Hypersurfaces.
p.
233.
Fang, Jian Bo
2015.
On Laguerre form and Laguerre isoparametric hypersurfaces.
Acta Mathematica Sinica, English Series,
Vol. 31,
Issue. 3,
p.
501.
Li, Feng Jiang
and
Fang, Jian Bo
2016.
Complete hypersurfaces with constant Möbius scalar curvature.
International Journal of Mathematics,
Vol. 27,
Issue. 08,
p.
1650063.
Fang, Jian Bo
and
Li, Feng Jiang
2016.
Complete hypersurfaces with constant laguerre scalar curvature in ℝ n.
Acta Mathematica Sinica, English Series,
Vol. 32,
Issue. 6,
p.
715.
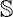 4
4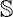 n+1, then Mn is associated with a so-called Möbius metric g, a Möbius second fundamental form B and a Möbius form Φ which are invariants of Mn under the Möbius transformation group of
n+1, then Mn is associated with a so-called Möbius metric g, a Möbius second fundamental form B and a Möbius form Φ which are invariants of Mn under the Möbius transformation group of 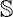 n+1. A classical theorem of Möbius geometry states that Mn (n ≥ 3) is in fact characterized by g and B up to Möbius equivalence. A Möbius isoparametric hypersurface is defined by satisfying two conditions: (1) Φ ≡ 0; (2) All the eigenvalues of B with respect to g are constants. Note that Euclidean isoparametric hyper-surfaces are automatically Möbius isoparametric, whereas the latter are Dupin hypersurfaces.
n+1. A classical theorem of Möbius geometry states that Mn (n ≥ 3) is in fact characterized by g and B up to Möbius equivalence. A Möbius isoparametric hypersurface is defined by satisfying two conditions: (1) Φ ≡ 0; (2) All the eigenvalues of B with respect to g are constants. Note that Euclidean isoparametric hyper-surfaces are automatically Möbius isoparametric, whereas the latter are Dupin hypersurfaces.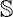 4 is either of parallel Möbius second fundamental form or Möbius equivalent to a tube of constant radius over a standard Veronese embedding of ℝP 2 into
4 is either of parallel Möbius second fundamental form or Möbius equivalent to a tube of constant radius over a standard Veronese embedding of ℝP 2 into 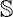 4. The classification of hypersurfaces in
4. The classification of hypersurfaces in 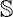 n+1 (n ≥ 2) with parallel Möbius second fundamental form has been accomplished in our previous paper [6]. The present result is a counterpart of Pinkall’s classification for Dupin hypersurfaces in
n+1 (n ≥ 2) with parallel Möbius second fundamental form has been accomplished in our previous paper [6]. The present result is a counterpart of Pinkall’s classification for Dupin hypersurfaces in 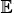 4 up to Lie equivalence.
4 up to Lie equivalence.
