Article contents
THE GAMMA CONSTRUCTION AND ASYMPTOTIC INVARIANTS OF LINE BUNDLES OVER ARBITRARY FIELDS
Published online by Cambridge University Press: 23 September 2019
Abstract
We extend results on asymptotic invariants of line bundles on complex projective varieties to projective varieties over arbitrary fields. To do so over imperfect fields, we prove a scheme-theoretic version of the gamma construction of Hochster and Huneke to reduce to the setting where the ground field is  $F$-finite. Our main result uses the gamma construction to extend the ampleness criterion of de Fernex, Küronya, and Lazarsfeld using asymptotic cohomological functions to projective varieties over arbitrary fields, which was previously known only for complex projective varieties. We also extend Nakayama’s description of the restricted base locus to klt or strongly
$F$-finite. Our main result uses the gamma construction to extend the ampleness criterion of de Fernex, Küronya, and Lazarsfeld using asymptotic cohomological functions to projective varieties over arbitrary fields, which was previously known only for complex projective varieties. We also extend Nakayama’s description of the restricted base locus to klt or strongly 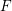 $F$-regular varieties over arbitrary fields.
$F$-regular varieties over arbitrary fields.
Information
- Type
- Article
- Information
- Copyright
- © 2019 Foundation Nagoya Mathematical Journal
Footnotes
This material is based upon work supported by the National Science Foundation under grant nos. DMS-1501461 and DMS-1701622.
References
- 4
- Cited by


