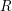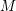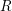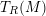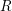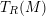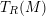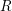1 Introduction
Let
![]() $R$
be a two-sided Noetherian ring. In Gorenstein homological algebra, the following Gorenstein homological properties of
$R$
be a two-sided Noetherian ring. In Gorenstein homological algebra, the following Gorenstein homological properties of
![]() $R$
are the main concerns: the Gorensteinness of the ring
$R$
are the main concerns: the Gorensteinness of the ring
![]() $R$
, the (stable) category of Gorenstein projective
$R$
, the (stable) category of Gorenstein projective
![]() $R$
-modules, and the Gorenstein projective dimensions and resolutions of
$R$
-modules, and the Gorenstein projective dimensions and resolutions of
![]() $R$
-modules.
$R$
-modules.
Let
![]() $M$
be an
$M$
be an
![]() $R$
-bimodule, which is finitely generated on both sides. The classical homological properties of the tensor ring
$R$
-bimodule, which is finitely generated on both sides. The classical homological properties of the tensor ring
![]() $T_{R}(M)$
are studied in [Reference Cohn7, Reference Minamoto17, Reference Roganov19]. In general, the tensor ring
$T_{R}(M)$
are studied in [Reference Cohn7, Reference Minamoto17, Reference Roganov19]. In general, the tensor ring
![]() $T_{R}(M)$
is not Noetherian. Hence, we require that
$T_{R}(M)$
is not Noetherian. Hence, we require that
![]() $M$
is nilpotent, that is, its
$M$
is nilpotent, that is, its
![]() $n$
th tensor power vanishes for
$n$
th tensor power vanishes for
![]() $n$
large enough, in which case
$n$
large enough, in which case
![]() $T_{R}(M)$
is two-sided Noetherian.
$T_{R}(M)$
is two-sided Noetherian.
We are concerned with the Gorenstein homological properties of the tensor ring
![]() $T_{R}(M)$
for a nilpotent
$T_{R}(M)$
for a nilpotent
![]() $R$
-bimodule
$R$
-bimodule
![]() $M$
. The motivation is the example in [Reference Geiss, Leclerc and Schroer9], which is a tensor ring and is
$M$
. The motivation is the example in [Reference Geiss, Leclerc and Schroer9], which is a tensor ring and is
![]() $1$
-Gorenstein, that is, the regular module has self-injective dimension at most one on each side. More precisely, the ring
$1$
-Gorenstein, that is, the regular module has self-injective dimension at most one on each side. More precisely, the ring
![]() $R$
considered in [Reference Geiss, Leclerc and Schroer9] is a certain self-injective algebra and the nilpotent
$R$
considered in [Reference Geiss, Leclerc and Schroer9] is a certain self-injective algebra and the nilpotent
![]() $R$
-bimodule
$R$
-bimodule
![]() $M$
is projective on each side; see also [Reference Geuenich10]. Then the tensor ring
$M$
is projective on each side; see also [Reference Geuenich10]. Then the tensor ring
![]() $T_{R}(M)$
is
$T_{R}(M)$
is
![]() $1$
-Gorenstein, whose modules yield a characteristic-free categorification of the root system. We mention other related examples in [Reference Li and Ye15, Reference Wang20, Reference Xiong and Zhang21].
$1$
-Gorenstein, whose modules yield a characteristic-free categorification of the root system. We mention other related examples in [Reference Li and Ye15, Reference Wang20, Reference Xiong and Zhang21].
The main result of this paper is a vast generalization of the mentioned examples. An
![]() $R$
-bimodule
$R$
-bimodule
![]() $M$
is said to be perfect provided that it has finite projective dimension on each side and satisfies the following Tor-vanishing conditions:
$M$
is said to be perfect provided that it has finite projective dimension on each side and satisfies the following Tor-vanishing conditions:
![]() $\text{Tor}_{j}^{R}(M,M^{\otimes _{R}i})=0$
for each
$\text{Tor}_{j}^{R}(M,M^{\otimes _{R}i})=0$
for each
![]() $i,j\geqslant 1$
, where
$i,j\geqslant 1$
, where
![]() $M^{\otimes _{R}i}$
is the
$M^{\otimes _{R}i}$
is the
![]() $i$
th tensor power of
$i$
th tensor power of
![]() $M$
.
$M$
.
Theorem. Let
![]() $R$
be a two-sided Noetherian ring, and let
$R$
be a two-sided Noetherian ring, and let
![]() $M$
be a nilpotent perfect
$M$
be a nilpotent perfect
![]() $R$
-bimodule. Then the ring
$R$
-bimodule. Then the ring
![]() $R$
is Gorenstein if and only if so is the tensor ring
$R$
is Gorenstein if and only if so is the tensor ring
![]() $T_{R}(M)$
.
$T_{R}(M)$
.
We give an inequality between the Gorenstein dimensions of
![]() $R$
and
$R$
and
![]() $T_{R}(M)$
. For details, we refer the reader to Theorem 4.7.
$T_{R}(M)$
. For details, we refer the reader to Theorem 4.7.
We characterize Gorenstein projective
![]() $T_{R}(M)$
-modules in terms of
$T_{R}(M)$
-modules in terms of
![]() $R$
-modules; see Theorem 3.9. This extends the corresponding description in [Reference Geiss, Leclerc and Schroer9, Theorem 10.9]. It is well known that the study of Gorenstein projective modules is intimately related to that of Frobenius categories; compare [Reference Beligiannis4, Reference Chen6]. The characterization of Gorenstein projective
$R$
-modules; see Theorem 3.9. This extends the corresponding description in [Reference Geiss, Leclerc and Schroer9, Theorem 10.9]. It is well known that the study of Gorenstein projective modules is intimately related to that of Frobenius categories; compare [Reference Beligiannis4, Reference Chen6]. The characterization of Gorenstein projective
![]() $T_{R}(M)$
-modules relies on an explicit construction of a new Frobenius category; see Theorem 2.5. It seems that this construction might be of independent interest.
$T_{R}(M)$
-modules relies on an explicit construction of a new Frobenius category; see Theorem 2.5. It seems that this construction might be of independent interest.
The paper is structured as follows. In Section 2, we construct a new Frobenius category, using the category of representations of a nilpotent endofunctor on an abelian category. In Section 3, we characterize Gorenstein projective
![]() $T_{R}(M)$
-modules for a certain nilpotent
$T_{R}(M)$
-modules for a certain nilpotent
![]() $R$
-bimodule
$R$
-bimodule
![]() $M$
. We also study the Gorenstein projective dimensions of
$M$
. We also study the Gorenstein projective dimensions of
![]() $T_{R}(M)$
-modules. In Section 4, we introduce the notion of a perfect bimodule and prove Theorem 4.7. Some (non-)examples are studied in the end.
$T_{R}(M)$
-modules. In Section 4, we introduce the notion of a perfect bimodule and prove Theorem 4.7. Some (non-)examples are studied in the end.
2 The construction of a new Frobenius category
In this section, we construct a new Frobenius category, which is an exact subcategory in the category of representations of a certain nilpotent endofunctor on an abelian category. For exact categories, we refer the reader to [Reference Keller12, Appendix A].
2.1 The category of representations
Let
![]() ${\mathcal{A}}$
be an additive category with an additive endofunctor
${\mathcal{A}}$
be an additive category with an additive endofunctor
![]() $F:{\mathcal{A}}\rightarrow {\mathcal{A}}$
. By a representation of
$F:{\mathcal{A}}\rightarrow {\mathcal{A}}$
. By a representation of
![]() $F$
, we mean a pair
$F$
, we mean a pair
![]() $(X,u)$
with
$(X,u)$
with
![]() $X$
an object and
$X$
an object and
![]() $u:F(X)\rightarrow X$
a morphism in
$u:F(X)\rightarrow X$
a morphism in
![]() ${\mathcal{A}}$
. A morphism
${\mathcal{A}}$
. A morphism
![]() $f:(X,u)\rightarrow (Y,v)$
between two representations is a morphism
$f:(X,u)\rightarrow (Y,v)$
between two representations is a morphism
![]() $f:X\rightarrow Y$
in
$f:X\rightarrow Y$
in
![]() ${\mathcal{A}}$
satisfying
${\mathcal{A}}$
satisfying
![]() $f\circ u=v\circ F(f)$
. This defines the category
$f\circ u=v\circ F(f)$
. This defines the category
![]() $\text{rep}(F)$
of representations of
$\text{rep}(F)$
of representations of
![]() $F$
. We have a forgetful functor
$F$
. We have a forgetful functor
sending
![]() $(X,u)$
to the underlying object
$(X,u)$
to the underlying object
![]() $X$
.
$X$
.
We assume that
![]() $F$
is nilpotent, that is,
$F$
is nilpotent, that is,
![]() $F^{N+1}=0$
for some
$F^{N+1}=0$
for some
![]() $N\geqslant 0$
. For each object
$N\geqslant 0$
. For each object
![]() $A$
, we define
$A$
, we define
![]() $\text{Ind}(A)=\bigoplus _{i=0}^{N}F^{i}(A)$
with
$\text{Ind}(A)=\bigoplus _{i=0}^{N}F^{i}(A)$
with
![]() $F^{0}=\text{Id}_{{\mathcal{A}}}$
, and a morphism
$F^{0}=\text{Id}_{{\mathcal{A}}}$
, and a morphism
![]() $c_{A}:F\text{Ind}(A)\rightarrow \text{Ind}(A)$
such that its restriction to
$c_{A}:F\text{Ind}(A)\rightarrow \text{Ind}(A)$
such that its restriction to
![]() $F(F^{i}(A))=F^{i+1}(A)$
is the inclusion into
$F(F^{i}(A))=F^{i+1}(A)$
is the inclusion into
![]() $\text{Ind}(A)$
. This defines a representation
$\text{Ind}(A)$
. This defines a representation
![]() $(\text{Ind}(A),c_{A})$
of
$(\text{Ind}(A),c_{A})$
of
![]() $F$
. Moreover, we have the induction functor
$F$
. Moreover, we have the induction functor
sending
![]() $A$
to
$A$
to
![]() $(\text{Ind}(A),c_{A})$
, and a morphism
$(\text{Ind}(A),c_{A})$
, and a morphism
![]() $f$
to
$f$
to
![]() $\bigoplus _{i=0}^{N}F^{i}(f)$
.
$\bigoplus _{i=0}^{N}F^{i}(f)$
.
Lemma 2.1. Keep the notation as above. Then the pair
![]() $(\text{Ind},U)$
is adjoint.
$(\text{Ind},U)$
is adjoint.
Proof. The natural isomorphism
sends
![]() $f$
to the restriction
$f$
to the restriction
![]() $f|_{A}$
. The inverse map sends
$f|_{A}$
. The inverse map sends
![]() $g:A\rightarrow X$
to
$g:A\rightarrow X$
to
![]() $g^{\prime }:(\text{Ind}(A),c_{A})\rightarrow (X,u)$
, such that the restriction of
$g^{\prime }:(\text{Ind}(A),c_{A})\rightarrow (X,u)$
, such that the restriction of
![]() $g^{\prime }$
to
$g^{\prime }$
to
![]() $F^{0}(A)=A$
is
$F^{0}(A)=A$
is
![]() $g$
, and to
$g$
, and to
![]() $F^{i}(A)$
is given by
$F^{i}(A)$
is given by
![]() $u\circ F(u)\circ \cdots \circ F^{i-1}(u)\circ F^{i}(g)$
for
$u\circ F(u)\circ \cdots \circ F^{i-1}(u)\circ F^{i}(g)$
for
![]() $i\geqslant 1$
.◻
$i\geqslant 1$
.◻
We refer the reader to [Reference Mac Lane14, Chapter VI] for monads and monadic adjoint pairs.
Remark 2.2. The nilpotent endofunctor
![]() $F$
defines a monad
$F$
defines a monad
![]() $M$
on
$M$
on
![]() ${\mathcal{A}}$
, which, as a functor, equals
${\mathcal{A}}$
, which, as a functor, equals
![]() $\bigoplus _{i=0}^{N}F^{i}$
and whose multiplication is induced by the composition of functors. There is an isomorphism of categories between
$\bigoplus _{i=0}^{N}F^{i}$
and whose multiplication is induced by the composition of functors. There is an isomorphism of categories between
![]() $\text{rep}(F)$
and
$\text{rep}(F)$
and
![]() $M\text{-}\text{Mod}_{{\mathcal{A}}}$
, the category of
$M\text{-}\text{Mod}_{{\mathcal{A}}}$
, the category of
![]() $M$
-modules in
$M$
-modules in
![]() ${\mathcal{A}}$
. In other words, the adjoint pair
${\mathcal{A}}$
. In other words, the adjoint pair
![]() $(\text{Ind},U)$
is strictly monadic.
$(\text{Ind},U)$
is strictly monadic.
We characterize the essential image of the induction functor.
Lemma 2.3. A representation
![]() $(X,u)$
is isomorphic to
$(X,u)$
is isomorphic to
![]() $(\text{Ind}(A),c_{A})$
for some object
$(\text{Ind}(A),c_{A})$
for some object
![]() $A$
if and only if
$A$
if and only if
![]() $u$
is a split monomorphism, which has a cokernel in
$u$
is a split monomorphism, which has a cokernel in
![]() ${\mathcal{A}}$
.
${\mathcal{A}}$
.
Proof. For the “only if” part, we just observe that the cokernel of
![]() $c_{A}$
is the natural projection on
$c_{A}$
is the natural projection on
![]() $A$
.
$A$
.
For the “if” part, we assume that the cokernel of
![]() $u$
is
$u$
is
![]() $\unicode[STIX]{x1D70B}:X\rightarrow A$
. Take a section
$\unicode[STIX]{x1D70B}:X\rightarrow A$
. Take a section
![]() $\unicode[STIX]{x1D704}:A\rightarrow X$
of
$\unicode[STIX]{x1D704}:A\rightarrow X$
of
![]() $\unicode[STIX]{x1D70B}$
. Then
$\unicode[STIX]{x1D70B}$
. Then
![]() $X$
is isomorphic to
$X$
is isomorphic to
![]() $A\oplus F(X)$
, which is further isomorphic to
$A\oplus F(X)$
, which is further isomorphic to
![]() $A\oplus F(A\oplus F(X))$
. Using induction and the nilpotency of
$A\oplus F(A\oplus F(X))$
. Using induction and the nilpotency of
![]() $F$
, we infer that
$F$
, we infer that
![]() $X$
is isomorphic to
$X$
is isomorphic to
![]() $\text{Ind}(A)=A\oplus F(A)\oplus \cdots \oplus F^{N}(A)$
; moreover, the corresponding inclusion map
$\text{Ind}(A)=A\oplus F(A)\oplus \cdots \oplus F^{N}(A)$
; moreover, the corresponding inclusion map
![]() $F^{i}(A)\rightarrow X$
is given by
$F^{i}(A)\rightarrow X$
is given by
![]() $u\circ F(u)\circ \cdots \circ F^{i-1}(u)\circ F^{i}(\unicode[STIX]{x1D704})$
. In other words, this gives rise to an isomorphism
$u\circ F(u)\circ \cdots \circ F^{i-1}(u)\circ F^{i}(\unicode[STIX]{x1D704})$
. In other words, this gives rise to an isomorphism
![]() $(\text{Ind}(A),c_{A})\rightarrow (X,u)$
, which corresponds to
$(\text{Ind}(A),c_{A})\rightarrow (X,u)$
, which corresponds to
![]() $\unicode[STIX]{x1D704}:A\rightarrow X$
in the adjoint pair
$\unicode[STIX]{x1D704}:A\rightarrow X$
in the adjoint pair
![]() $(\text{Ind},U)$
; compare the proof of Lemma 2.1.◻
$(\text{Ind},U)$
; compare the proof of Lemma 2.1.◻
We assume now that
![]() ${\mathcal{A}}$
is abelian and that the endofunctor
${\mathcal{A}}$
is abelian and that the endofunctor
![]() $F$
is right exact. Then
$F$
is right exact. Then
![]() $\text{rep}(F)$
is an abelian category. Moreover, a sequence
$\text{rep}(F)$
is an abelian category. Moreover, a sequence
![]() $(X,u)\stackrel{f}{\rightarrow }(Y,v)\stackrel{g}{\rightarrow }(Z,w)$
is exact in
$(X,u)\stackrel{f}{\rightarrow }(Y,v)\stackrel{g}{\rightarrow }(Z,w)$
is exact in
![]() $\text{rep}(F)$
if and only if the underlying sequence
$\text{rep}(F)$
if and only if the underlying sequence
![]() $X\stackrel{f}{\rightarrow }Y\stackrel{g}{\rightarrow }Z$
is exact in
$X\stackrel{f}{\rightarrow }Y\stackrel{g}{\rightarrow }Z$
is exact in
![]() ${\mathcal{A}}$
. In particular, the forgetful functor
${\mathcal{A}}$
. In particular, the forgetful functor
![]() $U:\text{rep}(F)\rightarrow {\mathcal{A}}$
is exact.
$U:\text{rep}(F)\rightarrow {\mathcal{A}}$
is exact.
For each representation
![]() $(X,u)$
, there is an exact sequence in
$(X,u)$
, there is an exact sequence in
![]() $\text{rep}(F)$
$\text{rep}(F)$
Here, we view
![]() $\unicode[STIX]{x1D719}_{(X,u)}$
as a formal matrix; the only possibly nonzero entries are
$\unicode[STIX]{x1D719}_{(X,u)}$
as a formal matrix; the only possibly nonzero entries are
![]() $\text{Id}_{F^{i}(X)}:F^{i}(X)\rightarrow F^{i}(X)$
and
$\text{Id}_{F^{i}(X)}:F^{i}(X)\rightarrow F^{i}(X)$
and
![]() $-F^{i-1}(u):F^{i}(X)\rightarrow F^{i-1}(X)$
for
$-F^{i-1}(u):F^{i}(X)\rightarrow F^{i-1}(X)$
for
![]() $i\geqslant 1$
. The morphism
$i\geqslant 1$
. The morphism
![]() $\unicode[STIX]{x1D702}_{(X,u)}$
is given by the counit of the adjoint pair
$\unicode[STIX]{x1D702}_{(X,u)}$
is given by the counit of the adjoint pair
![]() $(\text{Ind},U)$
. More precisely, the restriction of
$(\text{Ind},U)$
. More precisely, the restriction of
![]() $\unicode[STIX]{x1D702}_{(X,u)}$
on
$\unicode[STIX]{x1D702}_{(X,u)}$
on
![]() $X$
is
$X$
is
![]() $\text{Id}_{X}$
, and on
$\text{Id}_{X}$
, and on
![]() $F^{i}(X)$
is
$F^{i}(X)$
is
![]() $u\circ F(u)\circ \cdots \circ F^{i-1}(u)$
for
$u\circ F(u)\circ \cdots \circ F^{i-1}(u)$
for
![]() $i\geqslant 1$
. The above exact sequence is a categorical version of that in [Reference Roganov19, Lemma].
$i\geqslant 1$
. The above exact sequence is a categorical version of that in [Reference Roganov19, Lemma].
2.2 A new Frobenius category
Let
![]() ${\mathcal{A}}$
be an abelian category. A full additive subcategory
${\mathcal{A}}$
be an abelian category. A full additive subcategory
![]() ${\mathcal{E}}$
is exact provided that it is closed under extensions. In this case,
${\mathcal{E}}$
is exact provided that it is closed under extensions. In this case,
![]() ${\mathcal{E}}$
becomes naturally an exact category in the sense of Quillen, whose conflations are given by short exact sequences with terms in
${\mathcal{E}}$
becomes naturally an exact category in the sense of Quillen, whose conflations are given by short exact sequences with terms in
![]() ${\mathcal{E}}$
.
${\mathcal{E}}$
.
Recall that an exact category
![]() ${\mathcal{E}}$
is Frobenius provided that it has enough projective objects and enough injective objects, and the class of projective objects coincides with the class of injective objects. Frobenius categories are important, since their stable categories modulo projective objects have natural triangulated structures; see [Reference Happel11, Section I.2].
${\mathcal{E}}$
is Frobenius provided that it has enough projective objects and enough injective objects, and the class of projective objects coincides with the class of injective objects. Frobenius categories are important, since their stable categories modulo projective objects have natural triangulated structures; see [Reference Happel11, Section I.2].
We will consider the following conditions for the triple
![]() $({\mathcal{A}},{\mathcal{A}}^{\prime },F)$
.
$({\mathcal{A}},{\mathcal{A}}^{\prime },F)$
.
(F1) The category
 ${\mathcal{A}}$
is abelian, and
${\mathcal{A}}$
is abelian, and
 ${\mathcal{A}}^{\prime }\subseteq {\mathcal{A}}$
is an exact subcategory, which is Frobenius as an exact category. Denote by
${\mathcal{A}}^{\prime }\subseteq {\mathcal{A}}$
is an exact subcategory, which is Frobenius as an exact category. Denote by
 ${\mathcal{P}}\subseteq {\mathcal{A}}^{\prime }$
the subcategory of projective objects.
${\mathcal{P}}\subseteq {\mathcal{A}}^{\prime }$
the subcategory of projective objects.(F2) For every epimorphism
 $f:A\rightarrow X$
with
$f:A\rightarrow X$
with
 $X\in {\mathcal{A}}^{\prime }$
, there is an epimorphism
$X\in {\mathcal{A}}^{\prime }$
, there is an epimorphism
 $g:Y\rightarrow A$
with
$g:Y\rightarrow A$
with
 $Y\in {\mathcal{A}}^{\prime }$
and
$Y\in {\mathcal{A}}^{\prime }$
and
 $\text{Ker}(f\circ g)\in {\mathcal{A}}^{\prime }$
.
$\text{Ker}(f\circ g)\in {\mathcal{A}}^{\prime }$
.(F3) The endofunctor
 $F:{\mathcal{A}}\rightarrow {\mathcal{A}}$
is right exact and nilpotent, satisfying that
$F:{\mathcal{A}}\rightarrow {\mathcal{A}}$
is right exact and nilpotent, satisfying that
 $\text{Ext}_{{\mathcal{A}}}^{1}(X,F^{i}(P))=0=\text{Ext}_{{\mathcal{A}}}^{1}(P,F^{i}(X))$
for any
$\text{Ext}_{{\mathcal{A}}}^{1}(X,F^{i}(P))=0=\text{Ext}_{{\mathcal{A}}}^{1}(P,F^{i}(X))$
for any
 $X\in {\mathcal{A}}^{\prime }$
,
$X\in {\mathcal{A}}^{\prime }$
,
 $P\in {\mathcal{P}}$
and
$P\in {\mathcal{P}}$
and
 $i\geqslant 1$
.
$i\geqslant 1$
.(F4) For any exact sequence
 $\unicode[STIX]{x1D702}:0\rightarrow A\rightarrow B\rightarrow X\rightarrow 0$
in
$\unicode[STIX]{x1D702}:0\rightarrow A\rightarrow B\rightarrow X\rightarrow 0$
in
 ${\mathcal{A}}$
, we have that
${\mathcal{A}}$
, we have that
 $F(\unicode[STIX]{x1D702})$
is exact, provided that
$F(\unicode[STIX]{x1D702})$
is exact, provided that
 $X$
admits a monomorphism
$X$
admits a monomorphism
 $u:F(X)\rightarrow X$
with
$u:F(X)\rightarrow X$
with
 $\text{Cok}\,u\in {\mathcal{A}}^{\prime }$
.
$\text{Cok}\,u\in {\mathcal{A}}^{\prime }$
.
Lemma 2.4. Assume that the triple
![]() $({\mathcal{A}},{\mathcal{A}}^{\prime },F)$
satisfies (F1)–(F4). Then the following statements hold.
$({\mathcal{A}},{\mathcal{A}}^{\prime },F)$
satisfies (F1)–(F4). Then the following statements hold.
(1) For every epimorphism
 $f:A\rightarrow X$
with
$f:A\rightarrow X$
with
 $X\in {\mathcal{A}}^{\prime }$
, there is an epimorphism
$X\in {\mathcal{A}}^{\prime }$
, there is an epimorphism
 $g^{\prime }:P\rightarrow A$
with
$g^{\prime }:P\rightarrow A$
with
 $P\in {\mathcal{P}}$
and
$P\in {\mathcal{P}}$
and
 $\text{Ker}(f\circ g^{\prime })\in {\mathcal{A}}^{\prime }$
.
$\text{Ker}(f\circ g^{\prime })\in {\mathcal{A}}^{\prime }$
.(2) For an exact sequence
 $0\rightarrow A\stackrel{f}{\rightarrow }B\rightarrow X\rightarrow 0$
with
$0\rightarrow A\stackrel{f}{\rightarrow }B\rightarrow X\rightarrow 0$
with
 $X\in {\mathcal{A}}^{\prime }$
and a morphism
$X\in {\mathcal{A}}^{\prime }$
and a morphism
 $a:A\rightarrow F^{i}(P)$
for some
$a:A\rightarrow F^{i}(P)$
for some
 $P\in {\mathcal{P}}$
and
$P\in {\mathcal{P}}$
and
 $i\geqslant 0$
, there is a morphism
$i\geqslant 0$
, there is a morphism
 $b:B\rightarrow F^{i}(P)$
with
$b:B\rightarrow F^{i}(P)$
with
 $a=b\circ f$
.
$a=b\circ f$
.(3) For an exact sequence
 $\unicode[STIX]{x1D702}:0\rightarrow A\rightarrow B\rightarrow F^{i}(X)\rightarrow 0$
with
$\unicode[STIX]{x1D702}:0\rightarrow A\rightarrow B\rightarrow F^{i}(X)\rightarrow 0$
with
 $X\in {\mathcal{A}}^{\prime }$
and
$X\in {\mathcal{A}}^{\prime }$
and
 $i\geqslant 0$
, we have that
$i\geqslant 0$
, we have that
 $F(\unicode[STIX]{x1D702})$
is exact.
$F(\unicode[STIX]{x1D702})$
is exact.(4) For any monomorphism
 $f:A\rightarrow B$
with cokernel in
$f:A\rightarrow B$
with cokernel in
 ${\mathcal{A}}^{\prime }$
, we have that
${\mathcal{A}}^{\prime }$
, we have that
 $F^{i}(f)$
is mono for any
$F^{i}(f)$
is mono for any
 $i\geqslant 1$
.
$i\geqslant 1$
.(5) Assume that
 $u:F(X)\rightarrow X$
is a monomorphism with
$u:F(X)\rightarrow X$
is a monomorphism with
 $\text{Cok}\,u\in {\mathcal{A}}^{\prime }$
. Then
$\text{Cok}\,u\in {\mathcal{A}}^{\prime }$
. Then
 $\text{Ext}_{{\mathcal{A}}}^{1}(P,X)=0$
for each
$\text{Ext}_{{\mathcal{A}}}^{1}(P,X)=0$
for each
 $P\in {\mathcal{P}}^{\prime }$
.
$P\in {\mathcal{P}}^{\prime }$
.
Proof. For (1), we just compose the morphism
![]() $g$
in (F2) with an epimorphism
$g$
in (F2) with an epimorphism
![]() $P\rightarrow Y$
, whose kernel lies in
$P\rightarrow Y$
, whose kernel lies in
![]() ${\mathcal{A}}^{\prime }$
.
${\mathcal{A}}^{\prime }$
.
If
![]() $i=0$
in (2), we use the fact that
$i=0$
in (2), we use the fact that
![]() $\text{Ext}_{{\mathcal{A}}}^{1}(X,P)=0$
, since
$\text{Ext}_{{\mathcal{A}}}^{1}(X,P)=0$
, since
![]() $P$
is also injective in
$P$
is also injective in
![]() ${\mathcal{A}}^{\prime }$
. If
${\mathcal{A}}^{\prime }$
. If
![]() $i\geqslant 1$
, we just apply
$i\geqslant 1$
, we just apply
![]() $\text{Ext}_{{\mathcal{A}}}^{1}(X,F^{i}(P))=0$
in (F3).
$\text{Ext}_{{\mathcal{A}}}^{1}(X,F^{i}(P))=0$
in (F3).
For (3), we may assume that
![]() $i\leqslant N$
. By adding a trivial direct summand, we may replace
$i\leqslant N$
. By adding a trivial direct summand, we may replace
![]() $\unicode[STIX]{x1D702}$
by
$\unicode[STIX]{x1D702}$
by
![]() $\unicode[STIX]{x1D702}^{\prime }:0\rightarrow A\rightarrow B^{\prime }\rightarrow \text{Ind}(X)\rightarrow 0$
with
$\unicode[STIX]{x1D702}^{\prime }:0\rightarrow A\rightarrow B^{\prime }\rightarrow \text{Ind}(X)\rightarrow 0$
with
![]() $B^{\prime }=B\oplus (\bigoplus _{j\neq i}F^{j}(X))$
. By the exact sequence
$B^{\prime }=B\oplus (\bigoplus _{j\neq i}F^{j}(X))$
. By the exact sequence
we might apply (F4) to
![]() $\unicode[STIX]{x1D702}^{\prime }$
. The exactness of
$\unicode[STIX]{x1D702}^{\prime }$
. The exactness of
![]() $F(\unicode[STIX]{x1D702}^{\prime })$
implies that for
$F(\unicode[STIX]{x1D702}^{\prime })$
implies that for
![]() $F(\unicode[STIX]{x1D702})$
. Statement (4) follows from (3) and by induction.
$F(\unicode[STIX]{x1D702})$
. Statement (4) follows from (3) and by induction.
For the last statement, we apply (4) to obtain that
![]() $F^{i}(u)$
is mono for each
$F^{i}(u)$
is mono for each
![]() $i\geqslant 1$
. The cokernel of
$i\geqslant 1$
. The cokernel of
![]() $F^{i}(u)$
is isomorphic to
$F^{i}(u)$
is isomorphic to
![]() $F^{i}(\text{Cok}\,u)$
. By the nilpotency of
$F^{i}(\text{Cok}\,u)$
. By the nilpotency of
![]() $F$
, we infer that
$F$
, we infer that
![]() $X$
is an iterated extension of the objects
$X$
is an iterated extension of the objects
![]() $F^{i}(\text{Cok}\,u)$
for
$F^{i}(\text{Cok}\,u)$
for
![]() $0\leqslant i\leqslant N$
. By
$0\leqslant i\leqslant N$
. By
![]() $\text{Ext}_{{\mathcal{A}}}^{1}(P,F^{i}(\text{Cok}\,u))=0$
in (F3), we deduce the required statement.◻
$\text{Ext}_{{\mathcal{A}}}^{1}(P,F^{i}(\text{Cok}\,u))=0$
in (F3), we deduce the required statement.◻
The following consideration is inspired by [Reference Luo and Zhang16, Reference Xiong and Zhang21]. We consider the following full subcategory of
![]() $\text{rep}(F)$
:
$\text{rep}(F)$
:
Theorem 2.5. Assume that the triple
![]() $({\mathcal{A}},{\mathcal{A}}^{\prime },F)$
satisfies (F1)–(F4). Then
$({\mathcal{A}},{\mathcal{A}}^{\prime },F)$
satisfies (F1)–(F4). Then
![]() ${\mathcal{B}}\subseteq \text{rep}(F)$
is an exact subcategory, which is a Frobenius category. Moreover, its projective objects are precisely of the form
${\mathcal{B}}\subseteq \text{rep}(F)$
is an exact subcategory, which is a Frobenius category. Moreover, its projective objects are precisely of the form
![]() $(\text{Ind}(P),c_{P})$
for
$(\text{Ind}(P),c_{P})$
for
![]() $P\in {\mathcal{P}}$
.
$P\in {\mathcal{P}}$
.
Proof.
Step 1. To show that
![]() ${\mathcal{B}}\subseteq \text{rep}(F)$
is closed under extensions, we take an exact sequence
${\mathcal{B}}\subseteq \text{rep}(F)$
is closed under extensions, we take an exact sequence
![]() $0\rightarrow (X,u)\rightarrow (Y,v)\rightarrow (Z,w)\rightarrow 0$
with
$0\rightarrow (X,u)\rightarrow (Y,v)\rightarrow (Z,w)\rightarrow 0$
with
![]() $(X,u)$
and
$(X,u)$
and
![]() $(Z,w)$
in
$(Z,w)$
in
![]() ${\mathcal{B}}$
. Since the sequence
${\mathcal{B}}$
. Since the sequence
![]() $0\rightarrow F(X)\rightarrow F(Y)\rightarrow F(Z)\rightarrow 0$
is exact by (F4), we infer by the five lemma that
$0\rightarrow F(X)\rightarrow F(Y)\rightarrow F(Z)\rightarrow 0$
is exact by (F4), we infer by the five lemma that
![]() $v$
is a monomorphism, whose cokernel is an extension of
$v$
is a monomorphism, whose cokernel is an extension of
![]() $\text{Cok}\,w$
by
$\text{Cok}\,w$
by
![]() $\text{Cok}\,u$
. Since
$\text{Cok}\,u$
. Since
![]() ${\mathcal{A}}^{\prime }\subseteq {\mathcal{A}}$
is closed under extensions, the cokernel of
${\mathcal{A}}^{\prime }\subseteq {\mathcal{A}}$
is closed under extensions, the cokernel of
![]() $v$
lies in
$v$
lies in
![]() ${\mathcal{A}}^{\prime }$
. This proves that
${\mathcal{A}}^{\prime }$
. This proves that
![]() $(Y,v)$
lies in
$(Y,v)$
lies in
![]() ${\mathcal{B}}$
.
${\mathcal{B}}$
.
Step 2. We claim that
![]() $(\text{Ind}(P),c_{P})$
is projective in
$(\text{Ind}(P),c_{P})$
is projective in
![]() ${\mathcal{B}}$
for
${\mathcal{B}}$
for
![]() $P\in {\mathcal{P}}$
. Take an exact sequence
$P\in {\mathcal{P}}$
. Take an exact sequence
![]() $\unicode[STIX]{x1D709}:0\rightarrow (X,u)\rightarrow (Y,v)\rightarrow (Z,w)\rightarrow 0$
in
$\unicode[STIX]{x1D709}:0\rightarrow (X,u)\rightarrow (Y,v)\rightarrow (Z,w)\rightarrow 0$
in
![]() ${\mathcal{B}}$
. By the adjoint pair in Lemma 2.1, the sequence
${\mathcal{B}}$
. By the adjoint pair in Lemma 2.1, the sequence
![]() $\text{Hom}_{\text{rep}(F)}((\text{Ind}(P),c_{P}),\unicode[STIX]{x1D709})$
is isomorphic to
$\text{Hom}_{\text{rep}(F)}((\text{Ind}(P),c_{P}),\unicode[STIX]{x1D709})$
is isomorphic to
![]() $\text{Hom}_{{\mathcal{A}}}(P,U(\unicode[STIX]{x1D709}))$
. The latter is exact by
$\text{Hom}_{{\mathcal{A}}}(P,U(\unicode[STIX]{x1D709}))$
. The latter is exact by
![]() $\text{Ext}_{{\mathcal{A}}}^{1}(P,X)=0$
in Lemma 2.4(5). This proves the claim.
$\text{Ext}_{{\mathcal{A}}}^{1}(P,X)=0$
in Lemma 2.4(5). This proves the claim.
Let
![]() $(X,u)$
be an object in
$(X,u)$
be an object in
![]() ${\mathcal{B}}$
. Denote by
${\mathcal{B}}$
. Denote by
![]() $\unicode[STIX]{x1D70B}:X\rightarrow \text{Cok}\,u$
the projection. Then by Lemma 2.4(1), there is an epimorphism
$\unicode[STIX]{x1D70B}:X\rightarrow \text{Cok}\,u$
the projection. Then by Lemma 2.4(1), there is an epimorphism
![]() $f:P\rightarrow X$
with
$f:P\rightarrow X$
with
![]() $P\in {\mathcal{P}}$
and
$P\in {\mathcal{P}}$
and
![]() $\text{Ker}(\unicode[STIX]{x1D70B}\circ f)\in {\mathcal{A}}^{\prime }$
. By the adjoint pair in Lemma 2.1, the morphism
$\text{Ker}(\unicode[STIX]{x1D70B}\circ f)\in {\mathcal{A}}^{\prime }$
. By the adjoint pair in Lemma 2.1, the morphism
![]() $f$
corresponds to a morphism
$f$
corresponds to a morphism
![]() $f^{\prime }:(\text{Ind}(P),c_{P})\rightarrow (X,u)$
, which is clearly epic. Then we have an exact sequence in
$f^{\prime }:(\text{Ind}(P),c_{P})\rightarrow (X,u)$
, which is clearly epic. Then we have an exact sequence in
![]() $\text{rep}(F)$
$\text{rep}(F)$
By (F4), we have that
![]() $0\rightarrow F(Y)\rightarrow F\text{Ind}(P)\rightarrow F(X)\rightarrow 0$
is exact. Using the five lemma, we infer that
$0\rightarrow F(Y)\rightarrow F\text{Ind}(P)\rightarrow F(X)\rightarrow 0$
is exact. Using the five lemma, we infer that
![]() $v$
is mono, whose cokernel is isomorphic to
$v$
is mono, whose cokernel is isomorphic to
![]() $\text{Ker}(\unicode[STIX]{x1D70B}\circ f)$
and thus lies in
$\text{Ker}(\unicode[STIX]{x1D70B}\circ f)$
and thus lies in
![]() ${\mathcal{A}}^{\prime }$
. Hence
${\mathcal{A}}^{\prime }$
. Hence
![]() $(Y,v)$
lies in
$(Y,v)$
lies in
![]() ${\mathcal{B}}$
. The above exact sequence shows that
${\mathcal{B}}$
. The above exact sequence shows that
![]() ${\mathcal{B}}$
has enough projective objects. Moreover, each projective object is a direct summand of
${\mathcal{B}}$
has enough projective objects. Moreover, each projective object is a direct summand of
![]() $(\text{Ind}(P),c_{P})$
for some
$(\text{Ind}(P),c_{P})$
for some
![]() $P\in {\mathcal{P}}$
. Using Lemma 2.3, we infer that any projective object is of the form
$P\in {\mathcal{P}}$
. Using Lemma 2.3, we infer that any projective object is of the form
![]() $(\text{Ind}(Q),c_{Q})$
for
$(\text{Ind}(Q),c_{Q})$
for
![]() $Q\in {\mathcal{P}}$
.
$Q\in {\mathcal{P}}$
.
Step 3. We claim that
![]() $(\text{Ind}(P),c_{P})$
is injective for each
$(\text{Ind}(P),c_{P})$
is injective for each
![]() $P\in {\mathcal{P}}$
. For this, we take an arbitrary exact sequence
$P\in {\mathcal{P}}$
. For this, we take an arbitrary exact sequence
![]() $0\rightarrow (X,u)\stackrel{f}{\rightarrow }(Y,v)\stackrel{g}{\rightarrow }(Z,w)\rightarrow 0$
in
$0\rightarrow (X,u)\stackrel{f}{\rightarrow }(Y,v)\stackrel{g}{\rightarrow }(Z,w)\rightarrow 0$
in
![]() ${\mathcal{B}}$
. Then we have the following exact commutative diagram
${\mathcal{B}}$
. Then we have the following exact commutative diagram

Take any morphism
where “
![]() $t$
” denotes the transpose and
$t$
” denotes the transpose and
![]() $a_{i}:X\rightarrow F^{i}(P)$
. We observe that
$a_{i}:X\rightarrow F^{i}(P)$
. We observe that
![]() $a_{0}\circ u=0$
and
$a_{0}\circ u=0$
and
![]() $a_{i}\circ u=F(a_{i-1})$
for
$a_{i}\circ u=F(a_{i-1})$
for
![]() $i\geqslant 1$
. Then there exists a morphism
$i\geqslant 1$
. Then there exists a morphism
![]() $\bar{a}_{0}:\text{Cok}\,u\rightarrow P$
with
$\bar{a}_{0}:\text{Cok}\,u\rightarrow P$
with
![]() $a_{0}=\bar{a}_{0}\circ \unicode[STIX]{x1D70B}_{1}$
. By Lemma 2.4(2) we have a morphism
$a_{0}=\bar{a}_{0}\circ \unicode[STIX]{x1D70B}_{1}$
. By Lemma 2.4(2) we have a morphism
![]() $\bar{b}_{0}:\text{Cok}\,v\rightarrow P$
with
$\bar{b}_{0}:\text{Cok}\,v\rightarrow P$
with
![]() $\bar{a}_{0}=\bar{b}_{0}\circ \bar{f}$
. We set
$\bar{a}_{0}=\bar{b}_{0}\circ \bar{f}$
. We set
![]() $b_{0}=\bar{b}_{0}\circ \unicode[STIX]{x1D70B}_{2}:Y\rightarrow P$
. Hence, we have
$b_{0}=\bar{b}_{0}\circ \unicode[STIX]{x1D70B}_{2}:Y\rightarrow P$
. Hence, we have
![]() $a_{0}=b_{0}\circ f$
and
$a_{0}=b_{0}\circ f$
and
![]() $b_{0}\circ v=0$
.
$b_{0}\circ v=0$
.
Since
![]() $\text{Cok}\,v$
lies in
$\text{Cok}\,v$
lies in
![]() ${\mathcal{A}}^{\prime }$
, by Lemma 2.4(2) we have a morphism
${\mathcal{A}}^{\prime }$
, by Lemma 2.4(2) we have a morphism
![]() $b_{1}^{\prime }:Y\rightarrow F(P)$
satisfying
$b_{1}^{\prime }:Y\rightarrow F(P)$
satisfying
![]() $F(b_{0})=b_{1}^{\prime }\circ v$
. We have
$F(b_{0})=b_{1}^{\prime }\circ v$
. We have
There exists
![]() $x:\text{Cok}\,u\rightarrow F(P)$
satisfying
$x:\text{Cok}\,u\rightarrow F(P)$
satisfying
![]() $a_{1}-b_{1}^{\prime }\circ f=x\circ \unicode[STIX]{x1D70B}_{1}$
. Applying Lemma 2.4(2) again, we have a morphism
$a_{1}-b_{1}^{\prime }\circ f=x\circ \unicode[STIX]{x1D70B}_{1}$
. Applying Lemma 2.4(2) again, we have a morphism
![]() $y:\text{Cok}\,v\rightarrow F(P)$
with
$y:\text{Cok}\,v\rightarrow F(P)$
with
![]() $x=y\circ \bar{f}$
. Set
$x=y\circ \bar{f}$
. Set
![]() $b_{1}=b_{1}^{\prime }+y\circ \unicode[STIX]{x1D70B}_{2}$
. Then we have
$b_{1}=b_{1}^{\prime }+y\circ \unicode[STIX]{x1D70B}_{2}$
. Then we have
![]() $a_{1}=b_{1}\circ f$
and
$a_{1}=b_{1}\circ f$
and
![]() $b_{1}\circ v=F(b_{0})$
.
$b_{1}\circ v=F(b_{0})$
.
We iterate the above argument to construct
![]() $b_{i}:Y\rightarrow F^{i}(P)$
such that
$b_{i}:Y\rightarrow F^{i}(P)$
such that
![]() $a_{i}=b_{i}\circ f$
and
$a_{i}=b_{i}\circ f$
and
![]() $b_{i}\circ v=F(b_{i-1})$
hold for
$b_{i}\circ v=F(b_{i-1})$
hold for
![]() $i\geqslant 2$
. Then we have the morphism
$i\geqslant 2$
. Then we have the morphism
which makes
![]() $(a_{0},a_{1},\ldots ,a_{N})^{t}$
factor though
$(a_{0},a_{1},\ldots ,a_{N})^{t}$
factor though
![]() $f:(X,u)\rightarrow (Y,v)$
, as required.
$f:(X,u)\rightarrow (Y,v)$
, as required.
Step 4. For the final step, we construct for each object
![]() $(X,u)$
in
$(X,u)$
in
![]() ${\mathcal{B}}$
an exact sequence
${\mathcal{B}}$
an exact sequence
in
![]() ${\mathcal{B}}$
with
${\mathcal{B}}$
with
![]() $P\in {\mathcal{P}}$
. Then we are done with the whole proof.
$P\in {\mathcal{P}}$
. Then we are done with the whole proof.
Denote by
![]() $\unicode[STIX]{x1D70B}:X\rightarrow \text{Cok}\,u$
the cokernel of
$\unicode[STIX]{x1D70B}:X\rightarrow \text{Cok}\,u$
the cokernel of
![]() $u$
. We observe that for each
$u$
. We observe that for each
![]() $i\geqslant 1$
,
$i\geqslant 1$
,
![]() $F^{i-1}(u)$
is mono by Lemma 2.4(4). In what follows, we view
$F^{i-1}(u)$
is mono by Lemma 2.4(4). In what follows, we view
![]() $F^{i}(X)$
as a subobject of
$F^{i}(X)$
as a subobject of
![]() $X$
.
$X$
.
Since
![]() ${\mathcal{A}}^{\prime }$
is Frobenius, we take a monomorphism
${\mathcal{A}}^{\prime }$
is Frobenius, we take a monomorphism
![]() $\unicode[STIX]{x1D704}:\text{Cok}\,u\rightarrow P$
with its cokernel in
$\unicode[STIX]{x1D704}:\text{Cok}\,u\rightarrow P$
with its cokernel in
![]() ${\mathcal{A}}^{\prime }$
. Set
${\mathcal{A}}^{\prime }$
. Set
![]() $a_{0}=\unicode[STIX]{x1D704}\circ \unicode[STIX]{x1D70B}$
. Then
$a_{0}=\unicode[STIX]{x1D704}\circ \unicode[STIX]{x1D70B}$
. Then
![]() $\text{Ker}\,a_{0}=\text{Im}\,u$
. Since
$\text{Ker}\,a_{0}=\text{Im}\,u$
. Since
![]() $F^{i}(\unicode[STIX]{x1D704})$
is mono by Lemma 2.4(4), we infer that
$F^{i}(\unicode[STIX]{x1D704})$
is mono by Lemma 2.4(4), we infer that
![]() $\text{Ker}\,F^{i}(a_{0})=\text{Im}\,F^{i}(u)$
for all
$\text{Ker}\,F^{i}(a_{0})=\text{Im}\,F^{i}(u)$
for all
![]() $i\geqslant 1$
.
$i\geqslant 1$
.
By Lemma 2.4(2), we have a morphism
![]() $a_{1}:X\rightarrow F(P)$
with
$a_{1}:X\rightarrow F(P)$
with
![]() $F(a_{0})=a_{1}\circ u$
. Then we have
$F(a_{0})=a_{1}\circ u$
. Then we have
Similarly, we have a morphism
![]() $a_{2}:X\rightarrow F^{2}(P)$
with
$a_{2}:X\rightarrow F^{2}(P)$
with
![]() $F(a_{1})=a_{2}\circ u$
. Then we have
$F(a_{1})=a_{2}\circ u$
. Then we have
 $$\begin{eqnarray}\displaystyle \text{Ker}\,a_{2}\cap \text{Im}\,u\cap \text{Im}\,F(u) & = & \displaystyle \text{Ker}\,F(a_{1})\cap \text{Im}\,F(u)\nonumber\\ \displaystyle & = & \displaystyle \text{Ker}\,F^{2}(a_{0})\nonumber\\ \displaystyle & = & \displaystyle \text{Im}\,F^{2}(u).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{Ker}\,a_{2}\cap \text{Im}\,u\cap \text{Im}\,F(u) & = & \displaystyle \text{Ker}\,F(a_{1})\cap \text{Im}\,F(u)\nonumber\\ \displaystyle & = & \displaystyle \text{Ker}\,F^{2}(a_{0})\nonumber\\ \displaystyle & = & \displaystyle \text{Im}\,F^{2}(u).\nonumber\end{eqnarray}$$
Here, the first and second equalities follow from
![]() $F(a_{1})=a_{2}\circ u$
and
$F(a_{1})=a_{2}\circ u$
and
![]() $F(a_{0})=a_{1}\circ u$
, respectively. We observe that the above identities actually prove the following ones:
$F(a_{0})=a_{1}\circ u$
, respectively. We observe that the above identities actually prove the following ones:
We proceed in the same way to construct
![]() $a_{i}:X\rightarrow F^{i}(P)$
. We observe that
$a_{i}:X\rightarrow F^{i}(P)$
. We observe that
This gives rise to a monomorphism
which induces
![]() $\unicode[STIX]{x1D704}$
by taking the cokernels. Denote its cokernel by
$\unicode[STIX]{x1D704}$
by taking the cokernels. Denote its cokernel by
![]() $(Y,v)$
. By the snake lemma and the injectivity of
$(Y,v)$
. By the snake lemma and the injectivity of
![]() $\unicode[STIX]{x1D704}$
, we infer that
$\unicode[STIX]{x1D704}$
, we infer that
![]() $v$
is mono, whose cokernel coincides with that of
$v$
is mono, whose cokernel coincides with that of
![]() $\unicode[STIX]{x1D704}$
and thus lies in
$\unicode[STIX]{x1D704}$
and thus lies in
![]() ${\mathcal{A}}^{\prime }$
. This proves the desired short exact sequence.◻
${\mathcal{A}}^{\prime }$
. This proves the desired short exact sequence.◻
3 Gorenstein projective modules and admissible bimodules
In this section, we study Gorenstein projective modules over a tensor ring. The main reference for Gorenstein homological algebra is [Reference Enochs and Jenda8].
Throughout
![]() $R$
is a two-sided Noetherian ring. We denote by
$R$
is a two-sided Noetherian ring. We denote by
![]() $R\text{-}\text{mod}$
the abelian category of finitely generated left
$R\text{-}\text{mod}$
the abelian category of finitely generated left
![]() $R$
-modules, and by
$R$
-modules, and by
![]() $R\text{-}\text{proj}$
the full subcategory of projective modules. We identify right
$R\text{-}\text{proj}$
the full subcategory of projective modules. We identify right
![]() $R$
-modules with left
$R$
-modules with left
![]() $R^{\text{op}}$
-modules, where
$R^{\text{op}}$
-modules, where
![]() $R^{\text{op}}$
is the opposite ring. Hence,
$R^{\text{op}}$
is the opposite ring. Hence,
![]() $R^{\text{op}}\text{-}\text{mod}$
denotes the category of finitely generated right
$R^{\text{op}}\text{-}\text{mod}$
denotes the category of finitely generated right
![]() $R$
-modules.
$R$
-modules.
An unbounded complex
![]() $P^{\bullet }$
of projective
$P^{\bullet }$
of projective
![]() $R$
-modules is totally acyclic provided that it is acyclic and that its dual
$R$
-modules is totally acyclic provided that it is acyclic and that its dual
![]() $(P^{\bullet })^{\ast }=\text{Hom}_{R}(P^{\bullet },R)$
is also acyclic. Recall that an
$(P^{\bullet })^{\ast }=\text{Hom}_{R}(P^{\bullet },R)$
is also acyclic. Recall that an
![]() $R$
-module
$R$
-module
![]() $G$
is Gorenstein projective provided that there exists a totally acyclic complex
$G$
is Gorenstein projective provided that there exists a totally acyclic complex
![]() $P^{\bullet }$
with its zeroth cocycle
$P^{\bullet }$
with its zeroth cocycle
![]() $Z^{0}(P^{\bullet })\simeq G$
. The complex
$Z^{0}(P^{\bullet })\simeq G$
. The complex
![]() $P^{\bullet }$
is called a complete resolution of
$P^{\bullet }$
is called a complete resolution of
![]() $G$
.
$G$
.
We denote by
![]() $R\text{-}\text{Gproj}$
the full subcategory of Gorenstein projective modules. We observe that
$R\text{-}\text{Gproj}$
the full subcategory of Gorenstein projective modules. We observe that
![]() $R\text{-}\text{proj}\subseteq R\text{-}\text{Gproj}$
. It is well known that
$R\text{-}\text{proj}\subseteq R\text{-}\text{Gproj}$
. It is well known that
![]() $R\text{-}\text{Gproj}\subseteq R\text{-}\text{mod}$
is closed under extensions. Moreover, as an exact category, it is Frobenius, whose projective objects are precisely projective
$R\text{-}\text{Gproj}\subseteq R\text{-}\text{mod}$
is closed under extensions. Moreover, as an exact category, it is Frobenius, whose projective objects are precisely projective
![]() $R$
-modules; compare [Reference Beligiannis4, Proposition 3.8].
$R$
-modules; compare [Reference Beligiannis4, Proposition 3.8].
The following fact is standard; compare [Reference Chen6, Theorem 4.2].
Proposition 3.1. Let
![]() ${\mathcal{C}}$
be an exact subcategory of
${\mathcal{C}}$
be an exact subcategory of
![]() $R\text{-}\text{mod}$
containing
$R\text{-}\text{mod}$
containing
![]() $R\text{-}\text{proj}$
. Assume that
$R\text{-}\text{proj}$
. Assume that
![]() ${\mathcal{C}}$
is Frobenius, whose projective objects are precisely projective
${\mathcal{C}}$
is Frobenius, whose projective objects are precisely projective
![]() $R$
-modules. Then
$R$
-modules. Then
![]() ${\mathcal{C}}\subseteq R\text{-}\text{Gproj}$
.
${\mathcal{C}}\subseteq R\text{-}\text{Gproj}$
.
Proof. For a module
![]() $C\in {\mathcal{C}}$
, we construct its complete resolution by gluing the projective resolution and injective resolution of
$C\in {\mathcal{C}}$
, we construct its complete resolution by gluing the projective resolution and injective resolution of
![]() $C$
inside
$C$
inside
![]() ${\mathcal{C}}$
.◻
${\mathcal{C}}$
.◻
For a left
![]() $R$
-module
$R$
-module
![]() $X$
, we denote by
$X$
, we denote by
![]() $\text{pd}_{R}X$
,
$\text{pd}_{R}X$
,
![]() $\text{id}_{R}X$
, and
$\text{id}_{R}X$
, and
![]() $\text{Gpd}_{R}X$
the projective dimension, injective dimension, and Gorenstein projective dimension of
$\text{Gpd}_{R}X$
the projective dimension, injective dimension, and Gorenstein projective dimension of
![]() $X$
, respectively. Recall that
$X$
, respectively. Recall that
![]() $\text{Gpd}_{R}X\leqslant n$
if and only if there is an exact sequence
$\text{Gpd}_{R}X\leqslant n$
if and only if there is an exact sequence
![]() $0\rightarrow G^{-n}\rightarrow \cdots \rightarrow G^{-1}\rightarrow G^{0}\rightarrow X\rightarrow 0$
with each
$0\rightarrow G^{-n}\rightarrow \cdots \rightarrow G^{-1}\rightarrow G^{0}\rightarrow X\rightarrow 0$
with each
![]() $G^{-i}\in R\text{-}\text{Gproj}$
.
$G^{-i}\in R\text{-}\text{Gproj}$
.
Recall that a two-sided Noetherian ring
![]() $R$
is Gorenstein provided that
$R$
is Gorenstein provided that
![]() $\text{id}_{R}R<\infty$
and
$\text{id}_{R}R<\infty$
and
![]() $\text{id}_{R^{\text{op}}}R<\infty$
. In this case, we have
$\text{id}_{R^{\text{op}}}R<\infty$
. In this case, we have
![]() $\text{id}_{R}R=\text{id}_{R^{\text{op}}}R$
by [Reference Zaks22, Lemma A]. This common value is denoted by
$\text{id}_{R}R=\text{id}_{R^{\text{op}}}R$
by [Reference Zaks22, Lemma A]. This common value is denoted by
![]() $\text{G.dim}\,R$
. If
$\text{G.dim}\,R$
. If
![]() $\text{G.dim}\,R\leqslant d$
, we call
$\text{G.dim}\,R\leqslant d$
, we call
![]() $R$
a
$R$
a
![]() $d$
-Gorenstein ring. For example,
$d$
-Gorenstein ring. For example,
![]() $0$
-Gorenstein rings are precisely quasi-Frobenius rings.
$0$
-Gorenstein rings are precisely quasi-Frobenius rings.
Lemma 3.2. Let
![]() $R$
be a two-sided Noetherian ring, and let
$R$
be a two-sided Noetherian ring, and let
![]() $d,d_{1},d_{2}$
be integers. Then the following statements hold.
$d,d_{1},d_{2}$
be integers. Then the following statements hold.
(1) If
 $R$
is
$R$
is
 $d$
-Gorenstein, then
$d$
-Gorenstein, then
 $\text{Gpd}_{R}X\leqslant d$
and
$\text{Gpd}_{R}X\leqslant d$
and
 $\text{Gpd}_{R^{\text{op}}}Y\leqslant d$
for each left
$\text{Gpd}_{R^{\text{op}}}Y\leqslant d$
for each left
 $R$
-module
$R$
-module
 $X$
and right
$X$
and right
 $R$
-module
$R$
-module
 $Y$
.
$Y$
.(2) If
 $\text{Gpd}_{R}X\leqslant d_{1}$
and
$\text{Gpd}_{R}X\leqslant d_{1}$
and
 $\text{Gpd}_{R^{\text{op}}}Y\leqslant d_{2}$
for each left
$\text{Gpd}_{R^{\text{op}}}Y\leqslant d_{2}$
for each left
 $R$
-module
$R$
-module
 $X$
and right
$X$
and right
 $R$
-module
$R$
-module
 $Y$
, then
$Y$
, then
 $R$
is
$R$
is
 $\text{min}\{d_{1},d_{2}\}$
-Gorenstein.
$\text{min}\{d_{1},d_{2}\}$
-Gorenstein.
Proof. We refer the reader to [Reference Enochs and Jenda8, Theorem 12.3.1] for a detailed proof. For (2), we just note that
![]() $\text{Ext}_{R}^{i}(X,R)=0$
for
$\text{Ext}_{R}^{i}(X,R)=0$
for
![]() $i>\text{Gpd}_{R}X$
. Hence, the assumptions imply that
$i>\text{Gpd}_{R}X$
. Hence, the assumptions imply that
![]() $\text{id}_{R}R\leqslant d_{1}$
and
$\text{id}_{R}R\leqslant d_{1}$
and
![]() $\text{id}_{R^{\text{op}}}R\leqslant d_{2}$
. Then we are done by using the fact
$\text{id}_{R^{\text{op}}}R\leqslant d_{2}$
. Then we are done by using the fact
![]() $\text{id}_{R}R=\text{id}_{R^{\text{op}}}R$
for any Gorenstein ring
$\text{id}_{R}R=\text{id}_{R^{\text{op}}}R$
for any Gorenstein ring
![]() $R$
.◻
$R$
.◻
Let
![]() $M$
be an
$M$
be an
![]() $R$
-bimodule, which is finitely generated on both sides. Write
$R$
-bimodule, which is finitely generated on both sides. Write
![]() $M^{\otimes _{R}0}=R$
and
$M^{\otimes _{R}0}=R$
and
![]() $M^{\otimes _{R}(j+1)}=M\otimes _{R}(M^{\otimes _{R}j})$
for
$M^{\otimes _{R}(j+1)}=M\otimes _{R}(M^{\otimes _{R}j})$
for
![]() $j\geqslant 0$
. We say that
$j\geqslant 0$
. We say that
![]() $M$
is nilpotent, if
$M$
is nilpotent, if
![]() $M^{\otimes _{R}(N+1)}=0$
for some
$M^{\otimes _{R}(N+1)}=0$
for some
![]() $N\geqslant 0$
. This is equivalent to the condition that the endofunctor
$N\geqslant 0$
. This is equivalent to the condition that the endofunctor
![]() $M\otimes _{R}-$
on
$M\otimes _{R}-$
on
![]() $R\text{-}\text{mod}$
is nilpotent.
$R\text{-}\text{mod}$
is nilpotent.
Let
![]() $M$
be a nilpotent bimodule. We denote by
$M$
be a nilpotent bimodule. We denote by
![]() $T_{R}(M)=\bigoplus _{i=0}^{\infty }M^{\otimes _{R}i}$
the tensor ring, which is also two-sided Noetherian. There is an isomorphism of categories
$T_{R}(M)=\bigoplus _{i=0}^{\infty }M^{\otimes _{R}i}$
the tensor ring, which is also two-sided Noetherian. There is an isomorphism of categories
which identifies a representation
![]() $(X,u)$
of
$(X,u)$
of
![]() $M\otimes _{R}-$
with a left
$M\otimes _{R}-$
with a left
![]() $T_{R}(M)$
-module
$T_{R}(M)$
-module
![]() $X$
such that
$X$
such that
![]() $m\cdot x=u(m\otimes x)$
for
$m\cdot x=u(m\otimes x)$
for
![]() $m\in M$
and
$m\in M$
and
![]() $x\in X$
. In particular, projective
$x\in X$
. In particular, projective
![]() $T_{R}(M)$
-modules correspond to the representations
$T_{R}(M)$
-modules correspond to the representations
![]() $(\text{Ind}(P),c_{P})$
for projective
$(\text{Ind}(P),c_{P})$
for projective
![]() $R$
-modules
$R$
-modules
![]() $P$
, which might also be viewed as the scalar extension
$P$
, which might also be viewed as the scalar extension
![]() $T_{R}(M)\otimes _{R}P$
. Indeed, for each left
$T_{R}(M)\otimes _{R}P$
. Indeed, for each left
![]() $R$
-module
$R$
-module
![]() $Z$
,
$Z$
,
![]() $(\text{Ind}(Z),c_{Z})$
corresponds to
$(\text{Ind}(Z),c_{Z})$
corresponds to
![]() $T_{R}(M)\otimes _{R}Z$
.
$T_{R}(M)\otimes _{R}Z$
.
In what follows, we will identify the two categories in (3.1). The following results are standard.
Lemma 3.3. Keep the assumptions as above. Let
![]() $Z$
be a left
$Z$
be a left
![]() $R$
-module. Then the following statements hold.
$R$
-module. Then the following statements hold.
(1) The
 $R$
-module
$R$
-module
 $Z$
is projective if and only if
$Z$
is projective if and only if
 $T_{R}(M)\otimes _{R}Z$
is projective as a
$T_{R}(M)\otimes _{R}Z$
is projective as a
 $T_{R}(M)$
-module
.
$T_{R}(M)$
-module
.(2) If
 $\text{Tor}_{i}^{R}(T_{R}(M),Z)=0$
for each
$\text{Tor}_{i}^{R}(T_{R}(M),Z)=0$
for each
 $i\geqslant 1$
, then we have
$i\geqslant 1$
, then we have  $$\begin{eqnarray}\text{pd}_{R}Z=\text{pd}_{T_{R}(M)}T_{R}(M)\otimes _{R}Z.\end{eqnarray}$$
$$\begin{eqnarray}\text{pd}_{R}Z=\text{pd}_{T_{R}(M)}T_{R}(M)\otimes _{R}Z.\end{eqnarray}$$
Proof. For (1), it suffices to show the “if” part. Recall the identification of
![]() $(\text{Ind}(Z),c_{Z})$
and
$(\text{Ind}(Z),c_{Z})$
and
![]() $T_{R}(M)\otimes _{R}Z$
. Assume that
$T_{R}(M)\otimes _{R}Z$
. Assume that
![]() $T_{R}(M)\otimes _{R}Z$
is projective. Hence,
$T_{R}(M)\otimes _{R}Z$
is projective. Hence,
![]() $(\text{Ind}(Z),c_{Z})$
is a direct summand of
$(\text{Ind}(Z),c_{Z})$
is a direct summand of
![]() $(\text{Ind}(R^{n}),c_{R^{n}})$
for some
$(\text{Ind}(R^{n}),c_{R^{n}})$
for some
![]() $n\geqslant 1$
. It follows that
$n\geqslant 1$
. It follows that
![]() $Z$
is projective, since it is isomorphic to the cokernel of
$Z$
is projective, since it is isomorphic to the cokernel of
![]() $c_{Z}$
.
$c_{Z}$
.
For (2), we take an exact sequence
of
![]() $R$
-modules with each
$R$
-modules with each
![]() $P^{-i}$
projective. Applying
$P^{-i}$
projective. Applying
![]() $T_{R}(M)\otimes _{R}-$
to it, we get an exact sequence starting at
$T_{R}(M)\otimes _{R}-$
to it, we get an exact sequence starting at
![]() $T_{R}(M)\otimes _{R}Y$
, with middle terms projective
$T_{R}(M)\otimes _{R}Y$
, with middle terms projective
![]() $T_{R}(M)$
-modules. We apply (1) to
$T_{R}(M)$
-modules. We apply (1) to
![]() $Y$
. Then we are done.◻
$Y$
. Then we are done.◻
We also consider the category
![]() $\text{rep}(-\otimes _{R}M)$
of representations of the endofunctor
$\text{rep}(-\otimes _{R}M)$
of representations of the endofunctor
![]() $-\otimes _{R}M$
on
$-\otimes _{R}M$
on
![]() $R^{\text{op}}\text{-}\text{mod}$
. Similar to (3.1), we have the following isomorphism of categories
$R^{\text{op}}\text{-}\text{mod}$
. Similar to (3.1), we have the following isomorphism of categories
We identify these categories.
Lemma 3.4. We have a natural isomorphism
of
![]() $T_{R}(M)^{\text{op}}$
-modules for each
$T_{R}(M)^{\text{op}}$
-modules for each
![]() $P\in R\text{-}\text{proj}$
.
$P\in R\text{-}\text{proj}$
.
Proof. We are done by the following canonical isomorphisms
 $$\begin{eqnarray}\displaystyle (\text{Ind}(P),c_{P})^{\ast } & = & \displaystyle \text{Hom}_{T_{R}(M)}(T_{R}(M)\otimes _{R}P,T_{R}(M))\nonumber\\ \displaystyle & \simeq & \displaystyle \text{Hom}_{R}(P,T_{R}(M))\nonumber\\ \displaystyle & \simeq & \displaystyle \text{Hom}_{R}(P,R)\otimes _{R}T_{R}(M)\nonumber\\ \displaystyle & \simeq & \displaystyle (\text{Ind}(P^{\ast }),c_{P^{\ast }}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\text{Ind}(P),c_{P})^{\ast } & = & \displaystyle \text{Hom}_{T_{R}(M)}(T_{R}(M)\otimes _{R}P,T_{R}(M))\nonumber\\ \displaystyle & \simeq & \displaystyle \text{Hom}_{R}(P,T_{R}(M))\nonumber\\ \displaystyle & \simeq & \displaystyle \text{Hom}_{R}(P,R)\otimes _{R}T_{R}(M)\nonumber\\ \displaystyle & \simeq & \displaystyle (\text{Ind}(P^{\ast }),c_{P^{\ast }}).\nonumber\end{eqnarray}$$
As mentioned above, we identify
![]() $(\text{Ind}(P),c_{P})$
with
$(\text{Ind}(P),c_{P})$
with
![]() $T_{R}(M)\otimes _{R}P$
via (3.1), and
$T_{R}(M)\otimes _{R}P$
via (3.1), and
![]() $(\text{Ind}(P^{\ast }),c_{P^{\ast }})$
with
$(\text{Ind}(P^{\ast }),c_{P^{\ast }})$
with
![]() $P^{\ast }\otimes _{R}T_{R}(M)$
via (3.2).◻
$P^{\ast }\otimes _{R}T_{R}(M)$
via (3.2).◻
Definition 3.5. An
![]() $R$
-bimodule
$R$
-bimodule
![]() $M$
is left-admissible provided that
$M$
is left-admissible provided that
for each
![]() $G\in R\text{-}\text{Gproj}$
and
$G\in R\text{-}\text{Gproj}$
and
![]() $i\geqslant 0$
. Dually, it is right-admissible if
$i\geqslant 0$
. Dually, it is right-admissible if
![]() $M$
is left-admissible replacing
$M$
is left-admissible replacing
![]() $R$
by its opposite. We say that
$R$
by its opposite. We say that
![]() $M$
is admissible if it is both left- and right-admissible.
$M$
is admissible if it is both left- and right-admissible.
Lemma 3.6. Let
![]() $M$
be an
$M$
be an
![]() $R$
-bimodule. Then the triple
$R$
-bimodule. Then the triple
satisfies (F1)–(F4) if and only if
![]() $M$
is nilpotent and left-admissible.
$M$
is nilpotent and left-admissible.
Proof. For the “only if” part, it suffices to infer
from Lemma 2.4(3).
For the “if” part, we have that (F2) holds, since
![]() $R\text{-}\text{Gproj}$
is closed under kernels of epimorphisms. It remains to verify (F4). Assume that an
$R\text{-}\text{Gproj}$
is closed under kernels of epimorphisms. It remains to verify (F4). Assume that an
![]() $R$
-module
$R$
-module
![]() $X$
fits into a short exact sequence
$X$
fits into a short exact sequence
![]() $\unicode[STIX]{x1D702}:0\rightarrow M\otimes _{R}X\rightarrow X\rightarrow G\rightarrow 0$
with
$\unicode[STIX]{x1D702}:0\rightarrow M\otimes _{R}X\rightarrow X\rightarrow G\rightarrow 0$
with
![]() $G$
Gorenstein projective. By assumption, we infer that
$G$
Gorenstein projective. By assumption, we infer that
![]() $(M^{\otimes _{R}i})\otimes _{R}\unicode[STIX]{x1D702}$
is exact for each
$(M^{\otimes _{R}i})\otimes _{R}\unicode[STIX]{x1D702}$
is exact for each
![]() $i$
. Recall that
$i$
. Recall that
![]() $M$
is nilpotent. It follows that
$M$
is nilpotent. It follows that
![]() $X$
is an iterated extension of the modules
$X$
is an iterated extension of the modules
![]() $M^{\otimes _{R}i}\otimes _{R}G$
. By the Tor-vanishing assumption, we infer that
$M^{\otimes _{R}i}\otimes _{R}G$
. By the Tor-vanishing assumption, we infer that
![]() $\text{Tor}_{1}^{R}(M,X)=0$
. This proves (F4).◻
$\text{Tor}_{1}^{R}(M,X)=0$
. This proves (F4).◻
Recall identifications (3.1) and (3.2). We introduce the following full subcategories of
![]() $T_{R}(M)\text{-}\text{mod}$
and
$T_{R}(M)\text{-}\text{mod}$
and
![]() $T_{R}(M)^{\text{op}}\text{-}\text{mod}$
, respectively:
$T_{R}(M)^{\text{op}}\text{-}\text{mod}$
, respectively:
and
Lemma 3.7. Let
![]() $R$
be a two-sided Noetherian ring. Assume that
$R$
be a two-sided Noetherian ring. Assume that
![]() $M$
is a nilpotent left-admissible
$M$
is a nilpotent left-admissible
![]() $R$
-bimodule. Then we have
$R$
-bimodule. Then we have
![]() $\text{Gmon}(M\otimes _{R}-)\subseteq T_{R}(M)\text{-}\text{Gproj}$
.
$\text{Gmon}(M\otimes _{R}-)\subseteq T_{R}(M)\text{-}\text{Gproj}$
.
Proof. Recall isomorphism (3.1), where projective
![]() $T_{R}(M)$
-modules are identified with
$T_{R}(M)$
-modules are identified with
![]() $(\text{Ind}(P),c_{P})$
for projective
$(\text{Ind}(P),c_{P})$
for projective
![]() $R$
-modules
$R$
-modules
![]() $P$
. By Theorem 2.5 and Lemma 3.6, the category
$P$
. By Theorem 2.5 and Lemma 3.6, the category
![]() $\text{Gmon}(M\otimes _{R}-)$
is Frobenius. Then the required inclusion follows from Proposition 3.1.◻
$\text{Gmon}(M\otimes _{R}-)$
is Frobenius. Then the required inclusion follows from Proposition 3.1.◻
Proposition 3.8. Let
![]() $R$
be a two-sided Noetherian ring, and let
$R$
be a two-sided Noetherian ring, and let
![]() $M$
be a nilpotent
$M$
be a nilpotent
![]() $R$
-bimodule. Then the following two statements are equivalent:
$R$
-bimodule. Then the following two statements are equivalent:
(1) We have
 $T_{R}(M)\text{-}\text{Gproj}\subseteq \text{Gmon}(M\otimes _{R}-)$
and
$T_{R}(M)\text{-}\text{Gproj}\subseteq \text{Gmon}(M\otimes _{R}-)$
and
 $T_{R}(M)^{\text{op}}\text{-}\text{Gproj}\subseteq \text{Gmon}(-\otimes _{R}M)$
.
$T_{R}(M)^{\text{op}}\text{-}\text{Gproj}\subseteq \text{Gmon}(-\otimes _{R}M)$
.(2) For any totally acyclic complex
 $Q^{\bullet }$
of
$Q^{\bullet }$
of
 $T_{R}(M)$
-modules and its dual
$T_{R}(M)$
-modules and its dual
 $(Q^{\bullet })^{\ast }=\text{Hom}_{T_{R}(M)}(Q^{\bullet },T_{R}(M))$
, both the complexes
$(Q^{\bullet })^{\ast }=\text{Hom}_{T_{R}(M)}(Q^{\bullet },T_{R}(M))$
, both the complexes
 $M\otimes _{R}Q^{\bullet }$
and
$M\otimes _{R}Q^{\bullet }$
and
 $(Q^{\bullet })^{\ast }\otimes _{R}M$
are acyclic.
$(Q^{\bullet })^{\ast }\otimes _{R}M$
are acyclic.
Proof. For “
![]() $(1)\Rightarrow (2)$
,” we take a totally acyclic complex
$(1)\Rightarrow (2)$
,” we take a totally acyclic complex
![]() $Q^{\bullet }$
of
$Q^{\bullet }$
of
![]() $T_{R}(M)$
-modules. We assume that
$T_{R}(M)$
-modules. We assume that
![]() $Q^{i}=(\text{Ind}(P^{i}),c_{P^{i}})$
for
$Q^{i}=(\text{Ind}(P^{i}),c_{P^{i}})$
for
![]() $P^{i}\in R\text{-}\text{proj}$
. The
$P^{i}\in R\text{-}\text{proj}$
. The
![]() $i$
th cocycle of
$i$
th cocycle of
![]() $Q^{\bullet }$
is denoted by
$Q^{\bullet }$
is denoted by
![]() $(Z^{i},u^{i})$
, which is Gorenstein projective. In particular,
$(Z^{i},u^{i})$
, which is Gorenstein projective. In particular,
![]() $u^{i}$
is mono by assumption. It follows that the upper row of the following commutative diagram is exact.
$u^{i}$
is mono by assumption. It follows that the upper row of the following commutative diagram is exact.

Then we infer that
![]() $M\otimes _{R}Q^{\bullet }$
is acyclic. Since
$M\otimes _{R}Q^{\bullet }$
is acyclic. Since
![]() $(Q^{\bullet })^{\ast }$
is also totally acyclic, the same argument proves that
$(Q^{\bullet })^{\ast }$
is also totally acyclic, the same argument proves that
![]() $(Q^{\bullet })^{\ast }\otimes _{R}M$
is acyclic.
$(Q^{\bullet })^{\ast }\otimes _{R}M$
is acyclic.
To prove “
![]() $(2)\Rightarrow (1)$
,” we only prove the first inclusion. Take
$(2)\Rightarrow (1)$
,” we only prove the first inclusion. Take
![]() $(X,u)\in T_{R}(M)\text{-}\text{Gproj}$
. Assume that its complete resolution is
$(X,u)\in T_{R}(M)\text{-}\text{Gproj}$
. Assume that its complete resolution is
![]() $Q^{\bullet }$
, where
$Q^{\bullet }$
, where
![]() $Q^{i}=(\text{Ind}(P^{i}),c_{P^{i}})$
for projective
$Q^{i}=(\text{Ind}(P^{i}),c_{P^{i}})$
for projective
![]() $R$
-modules
$R$
-modules
![]() $P^{i}$
. We consider the monomorphism
$P^{i}$
. We consider the monomorphism
![]() $\unicode[STIX]{x1D704}:(X,u)\rightarrow Q^{0}=(\text{Ind}(P^{0}),c_{P^{0}})$
. By the acyclicity of
$\unicode[STIX]{x1D704}:(X,u)\rightarrow Q^{0}=(\text{Ind}(P^{0}),c_{P^{0}})$
. By the acyclicity of
![]() $M\otimes _{R}Q^{\bullet }$
, we infer that
$M\otimes _{R}Q^{\bullet }$
, we infer that
![]() $M\otimes _{R}\unicode[STIX]{x1D704}$
is mono. By
$M\otimes _{R}\unicode[STIX]{x1D704}$
is mono. By
![]() $c_{P^{0}}\circ (M\otimes _{R}\unicode[STIX]{x1D704})=\unicode[STIX]{x1D704}\circ u$
and the monomorphism
$c_{P^{0}}\circ (M\otimes _{R}\unicode[STIX]{x1D704})=\unicode[STIX]{x1D704}\circ u$
and the monomorphism
![]() $c_{P^{0}}$
, we infer that
$c_{P^{0}}$
, we infer that
![]() $u$
is mono. We have the following commutative exact diagram.
$u$
is mono. We have the following commutative exact diagram.

The bottom row
![]() $P^{\bullet }$
is acyclic, whose zeroth cocycle is isomorphic to
$P^{\bullet }$
is acyclic, whose zeroth cocycle is isomorphic to
![]() $\text{Cok}\,u$
.
$\text{Cok}\,u$
.
We consider the dual complex
![]() $(Q^{\bullet })^{\ast }$
, whose components are isomorphic to
$(Q^{\bullet })^{\ast }$
, whose components are isomorphic to
![]() $(\text{Ind}(P^{i})^{\ast },c_{(P^{i})^{\ast }})$
by Lemma 3.4. Applying the same argument to
$(\text{Ind}(P^{i})^{\ast },c_{(P^{i})^{\ast }})$
by Lemma 3.4. Applying the same argument to
![]() $(Q^{\bullet })^{\ast }$
, we obtain a commutative exact diagram in
$(Q^{\bullet })^{\ast }$
, we obtain a commutative exact diagram in
![]() $R^{\text{op}}\text{-}\text{mod}$
, whose bottom row is exact. However, the bottom row is isomorphic to
$R^{\text{op}}\text{-}\text{mod}$
, whose bottom row is exact. However, the bottom row is isomorphic to
![]() $(P^{\bullet })^{\ast }$
, proving the total acyclicity of
$(P^{\bullet })^{\ast }$
, proving the total acyclicity of
![]() $P^{\bullet }$
. Consequently,
$P^{\bullet }$
. Consequently,
![]() $\text{Cok}\,u$
is Gorenstein projective. It follows that
$\text{Cok}\,u$
is Gorenstein projective. It follows that
![]() $(X,u)\in \text{Gmon}(M\otimes _{R}-)$
, as required.◻
$(X,u)\in \text{Gmon}(M\otimes _{R}-)$
, as required.◻
We summarize the results in this section. Recall that a two-sided Noetherian ring
![]() $R$
is CM-free provided that
$R$
is CM-free provided that
![]() $R\text{-}\text{Gproj}=R\text{-}\text{proj}$
. We mention that Gorenstein projective modules are also called maximal Cohen–Macaulay modules. Here, CM stands for Cohen–Macaulay.
$R\text{-}\text{Gproj}=R\text{-}\text{proj}$
. We mention that Gorenstein projective modules are also called maximal Cohen–Macaulay modules. Here, CM stands for Cohen–Macaulay.
Theorem 3.9. Let
![]() $R$
be a two-sided Noetherian ring, and
$R$
be a two-sided Noetherian ring, and
![]() $M$
be a nilpotent admissible
$M$
be a nilpotent admissible
![]() $R$
-bimodule satisfying the following condition: for any totally acyclic complex
$R$
-bimodule satisfying the following condition: for any totally acyclic complex
![]() $Q^{\bullet }$
of
$Q^{\bullet }$
of
![]() $T_{R}(M)$
-modules, the complexes
$T_{R}(M)$
-modules, the complexes
![]() $M\otimes _{R}Q^{\bullet }$
and
$M\otimes _{R}Q^{\bullet }$
and
![]() $\text{Hom}_{T_{R}(M)}(Q^{\bullet },T_{R}(M))\otimes _{R}M$
are both acyclic. Then we have
$\text{Hom}_{T_{R}(M)}(Q^{\bullet },T_{R}(M))\otimes _{R}M$
are both acyclic. Then we have
Consequently, for any left
![]() $R$
-module
$R$
-module
![]() $Z$
, the following statements hold.
$Z$
, the following statements hold.
(1) The module
 $Z$
lies in
$Z$
lies in
 $R\text{-}\text{Gproj}$
if and only if
$R\text{-}\text{Gproj}$
if and only if
 $T_{R}(M)\otimes _{R}Z$
lies in
$T_{R}(M)\otimes _{R}Z$
lies in
 $T_{R}(M)\text{-}\text{Gproj}$
.
$T_{R}(M)\text{-}\text{Gproj}$
.(2) If
 $\text{Tor}_{i}^{R}(T_{R}(M),Z)=0$
for each
$\text{Tor}_{i}^{R}(T_{R}(M),Z)=0$
for each
 $i\geqslant 1$
, then we have
$i\geqslant 1$
, then we have  $$\begin{eqnarray}\text{Gpd}_{R}Z=\text{Gpd}_{T_{R}(M)}T_{R}(M)\otimes _{R}Z.\end{eqnarray}$$
$$\begin{eqnarray}\text{Gpd}_{R}Z=\text{Gpd}_{T_{R}(M)}T_{R}(M)\otimes _{R}Z.\end{eqnarray}$$
(3) The ring
 $R$
is CM-free if and only if so is
$R$
is CM-free if and only if so is
 $T_{R}(M)$
.
$T_{R}(M)$
.
Proof. We just prove the consequences. Recall isomorphism (3.1), which identifies
![]() $T_{R}(M)\otimes _{R}Z$
with the induced representation
$T_{R}(M)\otimes _{R}Z$
with the induced representation
![]() $(\text{Ind}(Z),c_{Z})$
. The cokernel of
$(\text{Ind}(Z),c_{Z})$
. The cokernel of
![]() $c_{Z}$
is isomorphic to
$c_{Z}$
is isomorphic to
![]() $Z$
. Then (1) follows immediately.
$Z$
. Then (1) follows immediately.
For (2), we take an exact sequence
of
![]() $R$
-modules with each
$R$
-modules with each
![]() $P^{-i}$
projective. Applying
$P^{-i}$
projective. Applying
![]() $T_{R}(M)\otimes _{R}-$
to it, we get an exact sequence starting at
$T_{R}(M)\otimes _{R}-$
to it, we get an exact sequence starting at
![]() $T_{R}(M)\otimes _{R}Y$
, with middle terms projective
$T_{R}(M)\otimes _{R}Y$
, with middle terms projective
![]() $T_{R}(M)$
-modules. Recall that
$T_{R}(M)$
-modules. Recall that
![]() $\text{Gpd}_{R}Z\leqslant n+1$
if and only if
$\text{Gpd}_{R}Z\leqslant n+1$
if and only if
![]() $Y$
is Gorenstein projective. A similar remark holds for
$Y$
is Gorenstein projective. A similar remark holds for
![]() $T_{R}(M)\otimes _{R}Z$
. Then we are done by (1), applied to
$T_{R}(M)\otimes _{R}Z$
. Then we are done by (1), applied to
![]() $Y$
.
$Y$
.
For the “only if” part of (3), we assume that
![]() $R$
is CM-free. Gorenstein projective
$R$
is CM-free. Gorenstein projective
![]() $T_{R}(M)$
-modules are of the form
$T_{R}(M)$
-modules are of the form
![]() $(X,u)$
with
$(X,u)$
with
![]() $u$
a monomorphism and
$u$
a monomorphism and
![]() $\text{Cok}\,u\in R\text{-}\text{Gproj}$
. Hence
$\text{Cok}\,u\in R\text{-}\text{Gproj}$
. Hence
![]() $\text{Cok}\,u=P$
is projective. By Lemma 2.3 and its proof, we infer that
$\text{Cok}\,u=P$
is projective. By Lemma 2.3 and its proof, we infer that
![]() $(X,u)$
is isomorphic to
$(X,u)$
is isomorphic to
![]() $(\text{Ind}(P),c_{P})$
, which is identified with a projective
$(\text{Ind}(P),c_{P})$
, which is identified with a projective
![]() $T_{R}(M)$
-module. For the “if” part, we take any Gorenstein projective
$T_{R}(M)$
-module. For the “if” part, we take any Gorenstein projective
![]() $R$
-module
$R$
-module
![]() $G$
. Then
$G$
. Then
![]() $T_{R}(M)\otimes _{R}G$
is Gorenstein projective and thus projective. Then we are done by Lemma 3.3(1).◻
$T_{R}(M)\otimes _{R}G$
is Gorenstein projective and thus projective. Then we are done by Lemma 3.3(1).◻
4 Perfect bimodules
In this section, we study homological conditions, under which Theorem 3.9 applies. For this, we introduce the notion of a perfect bimodule; see Definition 4.4.
Let
![]() $R$
be a two-sided Noetherian ring. We only consider finitely generated
$R$
be a two-sided Noetherian ring. We only consider finitely generated
![]() $R$
-modules. The following result is well known.
$R$
-modules. The following result is well known.
Lemma 4.1. Let
![]() $Y$
be a right
$Y$
be a right
![]() $R$
-module. Suppose that we are given an exact sequence in
$R$
-module. Suppose that we are given an exact sequence in
![]() $R\text{-}\text{mod}$
$R\text{-}\text{mod}$
with
![]() $\text{Tor}_{i}^{R}(Y,E^{-j})=0$
for each
$\text{Tor}_{i}^{R}(Y,E^{-j})=0$
for each
![]() $i\geqslant 1$
and
$i\geqslant 1$
and
![]() $j\geqslant 0$
. Denote its
$j\geqslant 0$
. Denote its
![]() $(-i)$
th cocycle by
$(-i)$
th cocycle by
![]() $Z^{-i}$
. Then the following statements hold.
$Z^{-i}$
. Then the following statements hold.
(1) The complex
 $Y\otimes _{R}E^{\bullet }$
computes
$Y\otimes _{R}E^{\bullet }$
computes
 $\text{Tor}_{i}^{R}(Y,X)$
, that is,
$\text{Tor}_{i}^{R}(Y,X)$
, that is,
 $H^{-i}(Y\otimes _{R}E^{\bullet })\simeq \text{Tor}_{i}^{R}(Y,X)$
for
$H^{-i}(Y\otimes _{R}E^{\bullet })\simeq \text{Tor}_{i}^{R}(Y,X)$
for
 $i\geqslant 0$
.
$i\geqslant 0$
.(2) There is an isomorphism
 $\text{Tor}_{i}^{R}(Y,Z^{-j})=\text{Tor}_{i+j+1}^{R}(Y,X)$
for each
$\text{Tor}_{i}^{R}(Y,Z^{-j})=\text{Tor}_{i+j+1}^{R}(Y,X)$
for each
 $i\geqslant 1$
and
$i\geqslant 1$
and
 $j\geqslant 0$
.
$j\geqslant 0$
.(3) Assume that
 $\text{pd}_{R^{\text{op}}}Y<\infty$
and that
$\text{pd}_{R^{\text{op}}}Y<\infty$
and that
 $F^{\bullet }$
is an acyclic complex with
$F^{\bullet }$
is an acyclic complex with
 $\text{Tor}_{i}^{R}(Y,F^{j})=0$
for each
$\text{Tor}_{i}^{R}(Y,F^{j})=0$
for each
 $i\geqslant 1$
and
$i\geqslant 1$
and
 $j\in \mathbb{Z}$
. Then the complex
$j\in \mathbb{Z}$
. Then the complex
 $Y\otimes _{R}F^{\bullet }$
is acyclic.
$Y\otimes _{R}F^{\bullet }$
is acyclic.
Proof. Statements (1) and (2) are classical. Statement (3) follows from (1) and (2). ◻
The following consideration is related to that in [Reference Minamoto and Yamaura18]. Let
![]() $M$
be an
$M$
be an
![]() $R$
-bimodule, which is finitely generated on both sides. We will consider the following Tor-vanishing conditions:
$R$
-bimodule, which is finitely generated on both sides. We will consider the following Tor-vanishing conditions:
Lemma 4.2. We assume that the
![]() $R$
-bimodule
$R$
-bimodule
![]() $M$
satisfies condition (P). Then the following statements are equivalent for each left
$M$
satisfies condition (P). Then the following statements are equivalent for each left
![]() $R$
-module
$R$
-module
![]() $Y$
:
$Y$
:
(1)
 $\text{Tor}_{i}^{R}(M,M^{\otimes _{R}j}\otimes _{R}Y)=0$
for any
$\text{Tor}_{i}^{R}(M,M^{\otimes _{R}j}\otimes _{R}Y)=0$
for any
 $i\geqslant 1$
and
$i\geqslant 1$
and
 $j\geqslant 0$
;
$j\geqslant 0$
;(2)
 $\text{Tor}_{i}^{R}(M^{\otimes _{R}s},M^{\otimes _{R}j}\otimes _{R}Y)=0$
for any
$\text{Tor}_{i}^{R}(M^{\otimes _{R}s},M^{\otimes _{R}j}\otimes _{R}Y)=0$
for any
 $i,s\geqslant 1$
and
$i,s\geqslant 1$
and
 $j\geqslant 0$
;
$j\geqslant 0$
;(3)
 $\text{Tor}_{i}^{R}(M^{\otimes _{R}s},Y)=0$
for any
$\text{Tor}_{i}^{R}(M^{\otimes _{R}s},Y)=0$
for any
 $i,s\geqslant 1$
.
$i,s\geqslant 1$
.
We will say that an
![]() $R$
-module
$R$
-module
![]() $Y$
is
$Y$
is
![]() $M$
-flat, provided that it satisfies one of the above equivalent conditions.
$M$
-flat, provided that it satisfies one of the above equivalent conditions.
Proof. To show “(1)
![]() $\Rightarrow$
(2),” we fix
$\Rightarrow$
(2),” we fix
![]() $j\geqslant 0$
and
$j\geqslant 0$
and
![]() $s\geqslant 2$
. Take a projective resolution
$s\geqslant 2$
. Take a projective resolution
![]() $P^{\bullet }$
of
$P^{\bullet }$
of
![]() $M^{\otimes _{R}j}\otimes _{R}Y$
. It follows from (1) that
$M^{\otimes _{R}j}\otimes _{R}Y$
. It follows from (1) that
![]() $M\otimes _{R}P^{\bullet }$
is quasi-isomorphic to
$M\otimes _{R}P^{\bullet }$
is quasi-isomorphic to
![]() $M^{\otimes _{R}(j+1)}\otimes _{R}Y$
. By Lemma 4.1(1), the complex
$M^{\otimes _{R}(j+1)}\otimes _{R}Y$
. By Lemma 4.1(1), the complex
![]() $M\otimes _{R}(M\otimes _{R}P^{\bullet })$
is quasi-isomorphic to
$M\otimes _{R}(M\otimes _{R}P^{\bullet })$
is quasi-isomorphic to
![]() $M^{\otimes _{R}(j+2)}\otimes _{R}Y$
, using the condition
$M^{\otimes _{R}(j+2)}\otimes _{R}Y$
, using the condition
![]() $\text{Tor}_{i}^{R}(M,M^{\otimes _{R}(j+1)}\otimes _{R}Y)=0$
for each
$\text{Tor}_{i}^{R}(M,M^{\otimes _{R}(j+1)}\otimes _{R}Y)=0$
for each
![]() $i\geqslant 1$
. Iterating this argument, we infer that
$i\geqslant 1$
. Iterating this argument, we infer that
![]() $M^{\otimes _{R}s}\otimes _{R}P^{\bullet }$
is quasi-isomorphic to
$M^{\otimes _{R}s}\otimes _{R}P^{\bullet }$
is quasi-isomorphic to
![]() $M^{\otimes _{R}(j+s)}\otimes _{R}Y$
. This proves (2). The implications “(2)
$M^{\otimes _{R}(j+s)}\otimes _{R}Y$
. This proves (2). The implications “(2)
![]() $\Rightarrow$
(1)” and “(2)
$\Rightarrow$
(1)” and “(2)
![]() $\Rightarrow$
(3)” are clear.
$\Rightarrow$
(3)” are clear.
It remains to show “(3)
![]() $\Rightarrow$
(1).” For this, we fix
$\Rightarrow$
(1).” For this, we fix
![]() $j\geqslant 1$
. Take a projective resolution
$j\geqslant 1$
. Take a projective resolution
![]() $P^{\bullet }$
of
$P^{\bullet }$
of
![]() $Y$
. Then by (3), the complex
$Y$
. Then by (3), the complex
![]() $M^{\otimes _{R}j}\otimes _{R}P^{\bullet }$
is quasi-isomorphic to
$M^{\otimes _{R}j}\otimes _{R}P^{\bullet }$
is quasi-isomorphic to
![]() $M^{\otimes _{R}j}\otimes _{R}Y$
. Applying Lemma 4.1(1), we infer that
$M^{\otimes _{R}j}\otimes _{R}Y$
. Applying Lemma 4.1(1), we infer that
![]() $M\otimes _{R}(M^{\otimes _{R}j}\otimes _{R}P^{\bullet })$
computes
$M\otimes _{R}(M^{\otimes _{R}j}\otimes _{R}P^{\bullet })$
computes
![]() $\text{Tor}_{i}^{R}(M,M^{\otimes _{R}j}\otimes _{R}Y)$
. But the complex is isomorphic to
$\text{Tor}_{i}^{R}(M,M^{\otimes _{R}j}\otimes _{R}Y)$
. But the complex is isomorphic to
![]() $M^{\otimes _{R}(j+1)}\otimes _{R}P^{\bullet }$
, which is quasi-isomorphic to
$M^{\otimes _{R}(j+1)}\otimes _{R}P^{\bullet }$
, which is quasi-isomorphic to
![]() $M^{\otimes _{R}(j+1)}\otimes _{R}Y$
by (3). It follows that
$M^{\otimes _{R}(j+1)}\otimes _{R}Y$
by (3). It follows that
![]() $\text{Tor}_{i}^{R}(M,M^{\otimes _{R}j}\otimes _{R}Y)=0$
for
$\text{Tor}_{i}^{R}(M,M^{\otimes _{R}j}\otimes _{R}Y)=0$
for
![]() $i\geqslant 1$
.◻
$i\geqslant 1$
.◻
The following consequence implies that condition (P) is symmetric.
Corollary 4.3. Let
![]() $M$
be an
$M$
be an
![]() $R$
-bimodule. Then
$R$
-bimodule. Then
![]() $M$
satisfies condition (P) if and only if
$M$
satisfies condition (P) if and only if
![]() $\text{Tor}_{i}^{R}(M^{\otimes _{R}s},M^{\otimes _{R}j})=0$
for each
$\text{Tor}_{i}^{R}(M^{\otimes _{R}s},M^{\otimes _{R}j})=0$
for each
![]() $i,s,j\geqslant 1$
, if and only if
$i,s,j\geqslant 1$
, if and only if
![]() $\text{Tor}_{i}^{R}(M^{\otimes _{R}s},M)=0$
for each
$\text{Tor}_{i}^{R}(M^{\otimes _{R}s},M)=0$
for each
![]() $i,s\geqslant 1$
.
$i,s\geqslant 1$
.
Proof. By duality, it suffices to show the first “if and only if.” For this, we just take
![]() $Y=M$
in the previous lemma.◻
$Y=M$
in the previous lemma.◻
Definition 4.4. We call an
![]() $R$
-bimodule
$R$
-bimodule
![]() $M$
perfect, provided that it satisfies
$M$
perfect, provided that it satisfies
![]() $\text{pd}_{R}M<\infty$
,
$\text{pd}_{R}M<\infty$
,
![]() $\text{pd}_{R^{\text{op}}}M<\infty$
, and condition (P).
$\text{pd}_{R^{\text{op}}}M<\infty$
, and condition (P).
Lemma 4.5. Let
![]() $M$
be a perfect bimodule, and
$M$
be a perfect bimodule, and
![]() $Y\in R\text{-}\text{mod}$
. Then the following statements hold.
$Y\in R\text{-}\text{mod}$
. Then the following statements hold.
(1) If
 $\text{Tor}_{i}^{R}(M,Y)=0$
for each
$\text{Tor}_{i}^{R}(M,Y)=0$
for each
 $i\geqslant 1$
, then we have
$i\geqslant 1$
, then we have
 $\text{pd}_{R}(M\otimes _{R}Y)\leqslant \text{pd}_{R}M+\text{pd}_{R}Y$
.
$\text{pd}_{R}(M\otimes _{R}Y)\leqslant \text{pd}_{R}M+\text{pd}_{R}Y$
.(2) For each
 $i\geqslant 0$
, we have
$i\geqslant 0$
, we have
 $\text{pd}_{R}M^{\otimes _{R}i}\leqslant i\text{pd}_{R}M$
and
$\text{pd}_{R}M^{\otimes _{R}i}\leqslant i\text{pd}_{R}M$
and
 $\text{pd}_{R^{\text{op}}}M^{\otimes _{R}i}\leqslant i\text{pd}_{R^{\text{op}}}M$
.
$\text{pd}_{R^{\text{op}}}M^{\otimes _{R}i}\leqslant i\text{pd}_{R^{\text{op}}}M$
.(3) Assume further that
 $M^{\otimes _{R}(N+1)}=0$
for
$M^{\otimes _{R}(N+1)}=0$
for
 $N\geqslant 0$
. Then
$N\geqslant 0$
. Then
 $\text{pd}_{R}T_{R}(M)\leqslant N\text{pd}_{R}M$
and
$\text{pd}_{R}T_{R}(M)\leqslant N\text{pd}_{R}M$
and
 $\text{pd}_{R^{\text{op}}}T_{R}(M)\leqslant N\text{pd}_{R^{\text{op}}}M$
.
$\text{pd}_{R^{\text{op}}}T_{R}(M)\leqslant N\text{pd}_{R^{\text{op}}}M$
.
Proof. For (1), we assume that
![]() $\text{pd}_{R}Y=n<\infty$
. Take a projective resolution
$\text{pd}_{R}Y=n<\infty$
. Take a projective resolution
![]() $P^{\bullet }$
of
$P^{\bullet }$
of
![]() $Y$
, which has length
$Y$
, which has length
![]() $n$
. Then by assumption, the complex
$n$
. Then by assumption, the complex
![]() $M\otimes _{R}P^{\bullet }$
is quasi-isomorphic to
$M\otimes _{R}P^{\bullet }$
is quasi-isomorphic to
![]() $M\otimes _{R}Y$
. We observe that each component of
$M\otimes _{R}Y$
. We observe that each component of
![]() $M\otimes _{R}P^{\bullet }$
has projective dimension at most
$M\otimes _{R}P^{\bullet }$
has projective dimension at most
![]() $\text{pd}_{R}M$
. Then (1) follows immediately. (2) follows from (1) by induction, and (3) follows from (2).◻
$\text{pd}_{R}M$
. Then (1) follows immediately. (2) follows from (1) by induction, and (3) follows from (2).◻
We observe that Theorem 3.9 applies to nilpotent perfect bimodules.
Proposition 4.6. Let
![]() $R$
be a two-sided Noetherian ring, and let
$R$
be a two-sided Noetherian ring, and let
![]() $M$
be a nilpotent perfect
$M$
be a nilpotent perfect
![]() $R$
-bimodule. Then the conditions in Theorem 3.9 are fulfilled.
$R$
-bimodule. Then the conditions in Theorem 3.9 are fulfilled.
Proof. Let
![]() $G$
be a Gorenstein projective
$G$
be a Gorenstein projective
![]() $R$
-module. We recall that
$R$
-module. We recall that
![]() $\text{Ext}_{R}^{i}(G,X)=0=\text{Tor}_{j}^{R}(Y,G)$
for each
$\text{Ext}_{R}^{i}(G,X)=0=\text{Tor}_{j}^{R}(Y,G)$
for each
![]() $i,j\geqslant 1$
, provided that
$i,j\geqslant 1$
, provided that
![]() $\text{pd}_{R}X<\infty$
and
$\text{pd}_{R}X<\infty$
and
![]() $\text{pd}_{R^{\text{op}}}Y<\infty$
. Hence, by Lemma 4.5(2), we have
$\text{pd}_{R^{\text{op}}}Y<\infty$
. Hence, by Lemma 4.5(2), we have
![]() $\text{Ext}_{R}^{1}(G,M^{\otimes _{R}i})=0$
for
$\text{Ext}_{R}^{1}(G,M^{\otimes _{R}i})=0$
for
![]() $i\geqslant 0$
. Moreover, it follows that
$i\geqslant 0$
. Moreover, it follows that
![]() $G$
is
$G$
is
![]() $M$
-flat. Hence, by Lemma 4.2(2),
$M$
-flat. Hence, by Lemma 4.2(2),
![]() $M^{\otimes _{R}i}\otimes _{R}G$
is
$M^{\otimes _{R}i}\otimes _{R}G$
is
![]() $M$
-flat for each
$M$
-flat for each
![]() $i\geqslant 0$
. In particular, we have
$i\geqslant 0$
. In particular, we have
![]() $\text{Tor}_{1}^{R}(M,M^{\otimes _{R}i}\otimes _{R}G)=0$
. Hence,
$\text{Tor}_{1}^{R}(M,M^{\otimes _{R}i}\otimes _{R}G)=0$
. Hence,
![]() $M$
is left-admissible. Similarly, it is right-admissible. The last condition follows from Lemma 4.1(3), since each projective
$M$
is left-admissible. Similarly, it is right-admissible. The last condition follows from Lemma 4.1(3), since each projective
![]() $T_{R}(M)$
-module, as an
$T_{R}(M)$
-module, as an
![]() $R$
-module, is
$R$
-module, is
![]() $M$
-flat.◻
$M$
-flat.◻
Theorem 4.7. Let
![]() $R$
be a two-sided Noetherian ring, and let
$R$
be a two-sided Noetherian ring, and let
![]() $M$
be a nilpotent perfect
$M$
be a nilpotent perfect
![]() $R$
-bimodule. Then
$R$
-bimodule. Then
![]() $R$
is Gorenstein if and only if so is
$R$
is Gorenstein if and only if so is
![]() $T_{R}(M)$
. In this case, we have the following equalities
$T_{R}(M)$
. In this case, we have the following equalities
where
![]() $\unicode[STIX]{x1D6FF}=\text{min}\{\text{pd}_{R}T_{R}(M),\text{pd}_{R^{\text{op}}}T_{R}(M)\}$
.
$\unicode[STIX]{x1D6FF}=\text{min}\{\text{pd}_{R}T_{R}(M),\text{pd}_{R^{\text{op}}}T_{R}(M)\}$
.
Proof. Set
![]() $l=\text{pd}_{R}T_{R}(M)$
and
$l=\text{pd}_{R}T_{R}(M)$
and
![]() $r=\text{pd}_{R^{\text{op}}}T_{R}(M)$
. For the “only if” part, we assume that
$r=\text{pd}_{R^{\text{op}}}T_{R}(M)$
. For the “only if” part, we assume that
![]() $R$
is
$R$
is
![]() $d$
-Gorenstein with
$d$
-Gorenstein with
![]() $d=\text{G.dim}\,R$
. We claim that
$d=\text{G.dim}\,R$
. We claim that
![]() $\text{Gpd}_{T_{R}(M)}X\leqslant r+d+1$
for any left
$\text{Gpd}_{T_{R}(M)}X\leqslant r+d+1$
for any left
![]() $T_{R}(M)$
-module
$T_{R}(M)$
-module
![]() $X$
.
$X$
.
For the claim, we take an exact sequence in
![]() $T_{R}(M)\text{-}\text{mod}$
$T_{R}(M)\text{-}\text{mod}$
with each
![]() $Q^{-i}$
projective. In case that
$Q^{-i}$
projective. In case that
![]() $r=0$
, we set
$r=0$
, we set
![]() $Y=X$
. Since
$Y=X$
. Since
![]() $M$
is perfect, we infer that
$M$
is perfect, we infer that
![]() $\text{Tor}_{j}^{R}(T_{R}(M),Q^{-i})=0$
for
$\text{Tor}_{j}^{R}(T_{R}(M),Q^{-i})=0$
for
![]() $j\geqslant 1$
and
$j\geqslant 1$
and
![]() $0\leqslant i<r$
. By Lemma 4.1(2), we infer that
$0\leqslant i<r$
. By Lemma 4.1(2), we infer that
![]() $\text{Tor}_{j}^{R}(T_{R}(M),Y)=0$
for
$\text{Tor}_{j}^{R}(T_{R}(M),Y)=0$
for
![]() $j\geqslant 1$
. Hence, as
$j\geqslant 1$
. Hence, as
![]() $R$
-modules,
$R$
-modules,
![]() $Y$
and thus
$Y$
and thus
![]() $M\otimes _{R}Y$
are
$M\otimes _{R}Y$
are
![]() $M$
-flat. Recall isomorphism (3.1). Then by (2.1), we have an exact sequence in
$M$
-flat. Recall isomorphism (3.1). Then by (2.1), we have an exact sequence in
![]() $T_{R}(M)\text{-}\text{mod}$
$T_{R}(M)\text{-}\text{mod}$
Since
![]() $\text{Gpd}_{R}Y\leqslant d$
and
$\text{Gpd}_{R}Y\leqslant d$
and
![]() $\text{Gpd}_{R}(M\otimes _{R}Y)\leqslant d$
, we infer from Theorem 3.9(2) that
$\text{Gpd}_{R}(M\otimes _{R}Y)\leqslant d$
, we infer from Theorem 3.9(2) that
![]() $\text{Gpd}_{T_{R}(M)}T_{R}(M)\otimes _{R}Y\leqslant d$
and
$\text{Gpd}_{T_{R}(M)}T_{R}(M)\otimes _{R}Y\leqslant d$
and
![]() $\text{Gpd}_{T_{R}(M)}T_{R}(M)\otimes _{R}(M\otimes _{R}Y)\leqslant d$
. Therefore, the exact sequence implies that
$\text{Gpd}_{T_{R}(M)}T_{R}(M)\otimes _{R}(M\otimes _{R}Y)\leqslant d$
. Therefore, the exact sequence implies that
![]() $\text{Gpd}_{T_{R}(M)}Y\leqslant d+1$
, which implies the claim.
$\text{Gpd}_{T_{R}(M)}Y\leqslant d+1$
, which implies the claim.
Similarly, we prove that
![]() $\text{Gpd}_{T_{R}(M)^{\text{op}}}X\leqslant l+d+1$
for any right
$\text{Gpd}_{T_{R}(M)^{\text{op}}}X\leqslant l+d+1$
for any right
![]() $T_{R}(M)$
-module
$T_{R}(M)$
-module
![]() $X$
. Then we are done by Lemma 3.2(2).
$X$
. Then we are done by Lemma 3.2(2).
For the “if” part, we assume that
![]() $T_{R}(M)$
is
$T_{R}(M)$
is
![]() $d^{\prime }$
-Gorenstein. For any left
$d^{\prime }$
-Gorenstein. For any left
![]() $R$
-module
$R$
-module
![]() $Z$
, we consider the exact sequence of
$Z$
, we consider the exact sequence of
![]() $R$
-modules
$R$
-modules
with each
![]() $P^{-i}$
projective. If
$P^{-i}$
projective. If
![]() $r=0$
, we set
$r=0$
, we set
![]() $K=Z$
. By a dimension shift, we infer that
$K=Z$
. By a dimension shift, we infer that
![]() $\text{Tor}_{j}^{R}(T_{R}(M),K)=0$
for each
$\text{Tor}_{j}^{R}(T_{R}(M),K)=0$
for each
![]() $j\geqslant 1$
. Hence
$j\geqslant 1$
. Hence
![]() $K$
is
$K$
is
![]() $M$
-flat. By Theorem 3.9(2), we have
$M$
-flat. By Theorem 3.9(2), we have
![]() $\text{Gpd}_{R}K=\text{Gpd}_{T_{R}(M)}T_{R}(M)\otimes _{R}K\leqslant d^{\prime }$
. Hence, we have
$\text{Gpd}_{R}K=\text{Gpd}_{T_{R}(M)}T_{R}(M)\otimes _{R}K\leqslant d^{\prime }$
. Hence, we have
![]() $\text{Gpd}_{R}Z\leqslant r+d^{\prime }$
. By a similar statement for right
$\text{Gpd}_{R}Z\leqslant r+d^{\prime }$
. By a similar statement for right
![]() $R$
-modules and Lemma 3.2(2), we complete the proof.◻
$R$
-modules and Lemma 3.2(2), we complete the proof.◻
The global dimension of a ring
![]() $S$
is denoted by
$S$
is denoted by
![]() $\text{gl.dim}\,S$
. Then we have the following immediate consequence. We refer the reader to [Reference Minamoto17, Theorem A.1] for a related result.
$\text{gl.dim}\,S$
. Then we have the following immediate consequence. We refer the reader to [Reference Minamoto17, Theorem A.1] for a related result.
Corollary 4.8. Keep the same assumptions as in Theorem 4.7. Then
![]() $R$
has finite global dimension if and only if so does
$R$
has finite global dimension if and only if so does
![]() $T_{R}(M)$
, in which case we have
$T_{R}(M)$
, in which case we have
where
![]() $\unicode[STIX]{x1D6FF}=\text{min}\{\text{pd}_{R}T_{R}(M),\text{pd}_{R^{\text{op}}}T_{R}(M)\}$
.
$\unicode[STIX]{x1D6FF}=\text{min}\{\text{pd}_{R}T_{R}(M),\text{pd}_{R^{\text{op}}}T_{R}(M)\}$
.
Proof. Recall that a two-sided Noetherian ring
![]() $S$
has finite global dimension if and only if it is Gorenstein and CM-free, in which case we have
$S$
has finite global dimension if and only if it is Gorenstein and CM-free, in which case we have
![]() $\text{G.dim}\,S=\text{gl.dim}\,S$
. Then we are done by Theorem 3.9(3).◻
$\text{G.dim}\,S=\text{gl.dim}\,S$
. Then we are done by Theorem 3.9(3).◻
The following result is analogous to [Reference Geiss, Leclerc and Schroer9, Theorem 1.2]; compare Example 4.10(1).
Proposition 4.9. Keep the same assumptions as in Theorem 4.7. Let
![]() $X$
be a left
$X$
be a left
![]() $T_{R}(M)$
-module. Then
$T_{R}(M)$
-module. Then
![]() $\text{pd}_{T_{R}(M)}X<\infty$
if and only if
$\text{pd}_{T_{R}(M)}X<\infty$
if and only if
![]() $\text{pd}_{R}X<\infty$
.
$\text{pd}_{R}X<\infty$
.
Proof. The “only if” part is trivial, since
![]() $\text{pd}_{R}T_{R}(M)<\infty$
.
$\text{pd}_{R}T_{R}(M)<\infty$
.
For the “if” part, we assume that
![]() $\text{pd}_{R}X<\infty$
. Take the exact sequence (4.1) as above. Hence, as
$\text{pd}_{R}X<\infty$
. Take the exact sequence (4.1) as above. Hence, as
![]() $R$
-modules,
$R$
-modules,
![]() $Y$
and
$Y$
and
![]() $M\otimes _{R}Y$
are
$M\otimes _{R}Y$
are
![]() $M$
-flat. We observe that
$M$
-flat. We observe that
![]() $\text{pd}_{R}Y<\infty$
and by Lemma 4.5(1)
$\text{pd}_{R}Y<\infty$
and by Lemma 4.5(1)
![]() $\text{pd}_{R}(M\otimes _{R}Y)<\infty$
. Hence, we obtain by Lemma 3.3(2) that the left two terms in (4.2) have finite projective dimension. Then so does
$\text{pd}_{R}(M\otimes _{R}Y)<\infty$
. Hence, we obtain by Lemma 3.3(2) that the left two terms in (4.2) have finite projective dimension. Then so does
![]() $Y$
. We deduce from (4.1) that the
$Y$
. We deduce from (4.1) that the
![]() $T_{R}(M)$
-module
$T_{R}(M)$
-module
![]() $X$
has finite projective dimension.◻
$X$
has finite projective dimension.◻
Let
![]() $k$
be a field. We denote by
$k$
be a field. We denote by
![]() $D=\text{Hom}_{k}(-,k)$
the
$D=\text{Hom}_{k}(-,k)$
the
![]() $k$
-dual. For quivers, we refer the reader to [Reference Auslander, Reiten and Smalø3].
$k$
-dual. For quivers, we refer the reader to [Reference Auslander, Reiten and Smalø3].
Example 4.10. (1) Let
![]() $M$
be a nilpotent
$M$
be a nilpotent
![]() $R$
-bimodule, which is finitely generated projective on both sides. Then
$R$
-bimodule, which is finitely generated projective on both sides. Then
![]() $M$
is perfect. Indeed, the tensor ring
$M$
is perfect. Indeed, the tensor ring
![]() $T_{R}(M)$
is a projective left and right
$T_{R}(M)$
is a projective left and right
![]() $R$
-module. It follows from Theorem 4.7 that if
$R$
-module. It follows from Theorem 4.7 that if
![]() $R$
is
$R$
is
![]() $d$
-Gorenstein, then
$d$
-Gorenstein, then
![]() $T_{R}(M)$
is
$T_{R}(M)$
is
![]() $(d+1)$
-Gorenstein. Taking
$(d+1)$
-Gorenstein. Taking
![]() $d=0$
, we recover the examples in [Reference Geiss, Leclerc and Schroer9, Section 6] and [Reference Geuenich10, Reference Li and Ye15, Reference Wang20].
$d=0$
, we recover the examples in [Reference Geiss, Leclerc and Schroer9, Section 6] and [Reference Geuenich10, Reference Li and Ye15, Reference Wang20].
Let
![]() $R$
be the
$R$
be the
![]() $k$
-algebra given by the following quiver
$k$
-algebra given by the following quiver
subject to relations
![]() $\{\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{3}\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{3}\}$
. Then it is a self-injective algebra. We denote by
$\{\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{3}\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{3}\}$
. Then it is a self-injective algebra. We denote by
![]() $e_{i}$
the idempotent corresponding to the vertex
$e_{i}$
the idempotent corresponding to the vertex
![]() $i$
. Take
$i$
. Take
![]() $M=Re_{1}\otimes _{k}e_{3}R$
, which is an
$M=Re_{1}\otimes _{k}e_{3}R$
, which is an
![]() $R$
-bimodule, projective on both sides. We observe that
$R$
-bimodule, projective on both sides. We observe that
![]() $M\otimes _{R}M=0$
. It follows that
$M\otimes _{R}M=0$
. It follows that
![]() $T_{R}(M)=R\ltimes M$
, the trivial extension of
$T_{R}(M)=R\ltimes M$
, the trivial extension of
![]() $R$
by
$R$
by
![]() $M$
. By Theorem 4.7, we infer that
$M$
. By Theorem 4.7, we infer that
![]() $T_{R}(M)$
is
$T_{R}(M)$
is
![]() $1$
-Gorenstein. Indeed, the algebra
$1$
-Gorenstein. Indeed, the algebra
![]() $T_{R}(M)$
is a gentle algebra.
$T_{R}(M)$
is a gentle algebra.
(2) Let
![]() $R_{1}$
and
$R_{1}$
and
![]() $R_{2}$
be two-sided Noetherian rings, and let
$R_{2}$
be two-sided Noetherian rings, and let
![]() $M$
be an
$M$
be an
![]() $R_{1}$
-
$R_{1}$
-
![]() $R_{2}$
-bimodule, which is finitely generated on both sides. Set
$R_{2}$
-bimodule, which is finitely generated on both sides. Set
![]() $R=R_{1}\times R_{2}$
. Then
$R=R_{1}\times R_{2}$
. Then
![]() $M$
becomes naturally an
$M$
becomes naturally an
![]() $R$
-module. Then the tensor ring
$R$
-module. Then the tensor ring
![]() $T_{R}(M)$
is isomorphic to the formal matrix ring
$T_{R}(M)$
is isomorphic to the formal matrix ring
![]() $\left(\begin{array}{@{}cc@{}}R_{1} & M\\ 0 & R_{2}\end{array}\right)$
. We observe that
$\left(\begin{array}{@{}cc@{}}R_{1} & M\\ 0 & R_{2}\end{array}\right)$
. We observe that
![]() $M$
is a perfect
$M$
is a perfect
![]() $R$
-module if and only if
$R$
-module if and only if
![]() $M$
has finite projective dimension as a left
$M$
has finite projective dimension as a left
![]() $R_{1}$
-module and a right
$R_{1}$
-module and a right
![]() $R_{2}$
-module. Then Theorem 4.7 recovers [Reference Xiong and Zhang21, Theorem 2.2(iii)]; compare [Reference Chen5, Theorem 3.3]. It is of interest to compare the conditions in Theorem 3.9 with the compatible bimodule in [Reference Zhang23, Definition 1.1].
$R_{2}$
-module. Then Theorem 4.7 recovers [Reference Xiong and Zhang21, Theorem 2.2(iii)]; compare [Reference Chen5, Theorem 3.3]. It is of interest to compare the conditions in Theorem 3.9 with the compatible bimodule in [Reference Zhang23, Definition 1.1].
(3) We mention that the perfectness assumption in Corollary 4.8 is necessary. Let
![]() $Q$
be the quiver
$Q$
be the quiver
![]() $1\rightarrow 2$
of type
$1\rightarrow 2$
of type
![]() $A_{2}$
, and let
$A_{2}$
, and let
![]() $R=kQ$
be the path algebra. Let
$R=kQ$
be the path algebra. Let
![]() $S$
be the nonprojective simple left
$S$
be the nonprojective simple left
![]() $R$
-module, let
$R$
-module, let
![]() $T$
be the nonprojective simple right
$T$
be the nonprojective simple right
![]() $R$
-module, and let
$R$
-module, and let
![]() $M=S\otimes _{k}T$
be the tensor product. Then we have
$M=S\otimes _{k}T$
be the tensor product. Then we have
![]() $M\otimes _{R}M=0$
and
$M\otimes _{R}M=0$
and
![]() $T_{R}(M)=R\ltimes M$
is
$T_{R}(M)=R\ltimes M$
is
![]() $1$
-Gorenstein of infinite global dimension. Indeed, the algebra
$1$
-Gorenstein of infinite global dimension. Indeed, the algebra
![]() $T_{R}(M)$
is self-injective and Nakayama. We observe an isomorphism
$T_{R}(M)$
is self-injective and Nakayama. We observe an isomorphism
![]() $\text{Tor}_{1}^{R}(M,M)\simeq M$
. Hence, the
$\text{Tor}_{1}^{R}(M,M)\simeq M$
. Hence, the
![]() $R$
-bimodule
$R$
-bimodule
![]() $M$
is not perfect.
$M$
is not perfect.
(4) Let
![]() $Q$
be a finite acyclic quiver, and let
$Q$
be a finite acyclic quiver, and let
![]() ${\mathcal{C}}_{Q}$
be the associated cluster category. Let
${\mathcal{C}}_{Q}$
be the associated cluster category. Let
![]() $T$
be a tilting module of the path algebra
$T$
be a tilting module of the path algebra
![]() $kQ$
. Denote by
$kQ$
. Denote by
![]() $R=\text{End}_{kQ}(T)$
the tilted algebra, and by
$R=\text{End}_{kQ}(T)$
the tilted algebra, and by
![]() $B=\text{End}_{{\mathcal{C}}_{Q}}(T)$
the cluster-tilted algebra, respectively. In particular, the global dimension of
$B=\text{End}_{{\mathcal{C}}_{Q}}(T)$
the cluster-tilted algebra, respectively. In particular, the global dimension of
![]() $R$
is at most two. Denote
$R$
is at most two. Denote
![]() $M=\text{Ext}_{R}^{2}(DR,R)$
, which is naturally an
$M=\text{Ext}_{R}^{2}(DR,R)$
, which is naturally an
![]() $R$
-bimodule. Then we have
$R$
-bimodule. Then we have
![]() $B\cong T_{R}(M)$
; see [Reference Amiot1, Proposition 4.7]. On the other hand, we have
$B\cong T_{R}(M)$
; see [Reference Amiot1, Proposition 4.7]. On the other hand, we have
![]() $B\cong R\ltimes M$
by [Reference Assem, Brustle and Schiffler2, Theorem 3.4]. Therefore, we infer that
$B\cong R\ltimes M$
by [Reference Assem, Brustle and Schiffler2, Theorem 3.4]. Therefore, we infer that
![]() $M\otimes _{R}M=0$
. Recall from [Reference Keller and Reiten13] that a cluster-tilted algebra is
$M\otimes _{R}M=0$
. Recall from [Reference Keller and Reiten13] that a cluster-tilted algebra is
![]() $1$
-Gorenstein, which usually has infinite global dimension. Hence, the
$1$
-Gorenstein, which usually has infinite global dimension. Hence, the
![]() $R$
-bimodule
$R$
-bimodule
![]() $M$
is not perfect in general.
$M$
is not perfect in general.
We mention that Gorenstein homological properties of trivial extensions are studied in [Reference Minamoto and Yamaura18].
Acknowledgments
The project was initiated when both authors were visiting the University of Bielefeld. We thank Henning Krause for his hospitality. We thank the referee for helpful comments and Example 4.10(3). The authors are supported by the National Natural Science Foundation of China (Nos. 11522113, 11671245, 11401401, and 11601441).