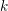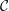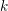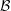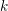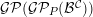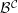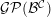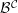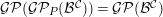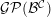1 Introduction
In homological algebra the projective and injective modules play a central role. The analogues in Gorenstein homological algebra are the Gorenstein projective and Gorenstein injective modules. These were defined by Auslander and Bridger in [Reference Auslander and Bridger1] for a two sided Noetherian ring, and were later extended to a general ring in [Reference Enochs and Jenda15]. Nowadays, the field of Gorenstein homological algebra has turned into a well-developed subject and an active area of research, see [Reference Enochs and Jenda16, Reference Enochs and Jenda17]. Some examples of other papers are [Reference Avramov and Martsinkovsky3, Reference Beligiannis6–Reference Bennis and Mahdou10, Reference Enochs, Estrada and Garcia-Rozas13, Reference Holm19, Reference Jørgensen24, Reference Jørgensen and Zhang26]. It has also found applications in other areas, see for example [Reference Dell’Ambrogio, Stevenson and Stovicek12]. In particular, the Gorenstein projective modules are used when categorifying cluster algebras [Reference Jensen, King and Su23, Reference Nájera Chávez32, Reference Pressland35], and being able to describe them is therefore important.
Let ![]() $k$ be a commutative ring, let
$k$ be a commutative ring, let ![]() ${\mathcal{B}}$ be a
${\mathcal{B}}$ be a ![]() $k$-linear abelian category with enough projectives, and let
$k$-linear abelian category with enough projectives, and let ![]() ${\mathcal{C}}$ be a small
${\mathcal{C}}$ be a small ![]() $k$-linear category. Furthermore, let
$k$-linear category. Furthermore, let ![]() ${\mathcal{B}}^{{\mathcal{C}}}$ denote the category of
${\mathcal{B}}^{{\mathcal{C}}}$ denote the category of ![]() $k$-linear functors from
$k$-linear functors from ![]() ${\mathcal{C}}$ to
${\mathcal{C}}$ to ![]() ${\mathcal{B}}$.
${\mathcal{B}}$.
Example 1. Let ![]() ${\mathcal{C}}=k\mathbb{A}_{2}$ where
${\mathcal{C}}=k\mathbb{A}_{2}$ where ![]() $k\mathbb{A}_{2}$ is the
$k\mathbb{A}_{2}$ is the ![]() $k$-linearization of the category
$k$-linearization of the category ![]() $\bullet \rightarrow \bullet$. The category
$\bullet \rightarrow \bullet$. The category ![]() ${\mathcal{B}}^{k\mathbb{A}_{2}}$ can then be identified with the morphism category
${\mathcal{B}}^{k\mathbb{A}_{2}}$ can then be identified with the morphism category ![]() $\operatorname{Mor}({\mathcal{B}})$ of
$\operatorname{Mor}({\mathcal{B}})$ of ![]() ${\mathcal{B}}$. Since
${\mathcal{B}}$. Since ![]() $\operatorname{Mor}({\mathcal{B}})$ is abelian and has enough projectives, it also has Gorenstein projective objects. By [Reference Jørgensen and Kato25, Corollary 3.6], a morphism
$\operatorname{Mor}({\mathcal{B}})$ is abelian and has enough projectives, it also has Gorenstein projective objects. By [Reference Jørgensen and Kato25, Corollary 3.6], a morphism ![]() $B_{1}\xrightarrow[{}]{f}B_{2}$ is Gorenstein projective in
$B_{1}\xrightarrow[{}]{f}B_{2}$ is Gorenstein projective in ![]() $\operatorname{Mor}({\mathcal{B}})$ if and only if
$\operatorname{Mor}({\mathcal{B}})$ if and only if ![]() $f$ is a monomorphism and
$f$ is a monomorphism and ![]() $\operatorname{Coker}f$,
$\operatorname{Coker}f$, ![]() $B_{1}$, and
$B_{1}$, and ![]() $B_{2}$ are Gorenstein projective in
$B_{2}$ are Gorenstein projective in ![]() ${\mathcal{B}}$. Since Gorenstein projective objects are closed under kernels of epimorphisms, this is equivalent to only requiring
${\mathcal{B}}$. Since Gorenstein projective objects are closed under kernels of epimorphisms, this is equivalent to only requiring ![]() $\operatorname{Coker}f$ and
$\operatorname{Coker}f$ and ![]() $B_{2}$ to be Gorenstein projective.
$B_{2}$ to be Gorenstein projective.
Motivated by this example, one can hope to describe the Gorenstein projective objects in ![]() ${\mathcal{B}}^{{\mathcal{C}}}$ more generally. Several authors [Reference Enochs, Estrada and Garcia-Rozas14, Reference Eshraghi, Hafezi and Salarian18, Reference Hu, Luo, Xiong and Zhou21, Reference Luo and Zhang29, Reference Luo and Zhang30, Reference Shen36] have studied this problem. However, their descriptions only hold in special cases. In [Reference Hu, Luo, Xiong and Zhou21, Reference Luo and Zhang29, Reference Luo and Zhang30, Reference Shen36] they assume
${\mathcal{B}}^{{\mathcal{C}}}$ more generally. Several authors [Reference Enochs, Estrada and Garcia-Rozas14, Reference Eshraghi, Hafezi and Salarian18, Reference Hu, Luo, Xiong and Zhou21, Reference Luo and Zhang29, Reference Luo and Zhang30, Reference Shen36] have studied this problem. However, their descriptions only hold in special cases. In [Reference Hu, Luo, Xiong and Zhou21, Reference Luo and Zhang29, Reference Luo and Zhang30, Reference Shen36] they assume ![]() $k$ is a field and
$k$ is a field and ![]() ${\mathcal{C}}$ is either
${\mathcal{C}}$ is either ![]() $kQ$ where
$kQ$ where ![]() $Q$ is a finite acyclic quiver,
$Q$ is a finite acyclic quiver, ![]() $kQ/I$ where
$kQ/I$ where ![]() $I$ is generated by monomial relations, or a finite-dimensional Iwanaga–Gorenstein algebra, while in [Reference Enochs, Estrada and Garcia-Rozas14, Reference Eshraghi, Hafezi and Salarian18] they assume
$I$ is generated by monomial relations, or a finite-dimensional Iwanaga–Gorenstein algebra, while in [Reference Enochs, Estrada and Garcia-Rozas14, Reference Eshraghi, Hafezi and Salarian18] they assume ![]() $k=\mathbb{Z}$ and
$k=\mathbb{Z}$ and ![]() ${\mathcal{C}}=\mathbb{Z}Q$ for a left rooted quiver
${\mathcal{C}}=\mathbb{Z}Q$ for a left rooted quiver ![]() $Q$. The latter results have motivated Holm and Jørgensen to give a description of cotorsion pairs in
$Q$. The latter results have motivated Holm and Jørgensen to give a description of cotorsion pairs in ![]() ${\mathcal{B}}^{\mathbb{Z}Q}$ from cotorsion pairs in
${\mathcal{B}}^{\mathbb{Z}Q}$ from cotorsion pairs in ![]() ${\mathcal{B}}$, see [Reference Henrik and Jørgensen20].
${\mathcal{B}}$, see [Reference Henrik and Jørgensen20].
We give a more systematic description of the Gorenstein projective objects in ![]() ${\mathcal{B}}^{{\mathcal{C}}}$, which works for any commutative base ring
${\mathcal{B}}^{{\mathcal{C}}}$, which works for any commutative base ring ![]() $k$. Since
$k$. Since ![]() $({\mathcal{B}}^{{\mathcal{C}}})^{\text{op}}=({\mathcal{B}}^{\text{op}})^{{\mathcal{C}}^{\text{op}}}$, the dual results for Gorenstein injective objects are obtained by considering the opposite category. We leave the explicit statements of these results to the reader.
$({\mathcal{B}}^{{\mathcal{C}}})^{\text{op}}=({\mathcal{B}}^{\text{op}})^{{\mathcal{C}}^{\text{op}}}$, the dual results for Gorenstein injective objects are obtained by considering the opposite category. We leave the explicit statements of these results to the reader.
The first step is to give a suitable generalization of what it means for ![]() $f$ to be a monomorphism in Example 1. For this we need to assume that
$f$ to be a monomorphism in Example 1. For this we need to assume that ![]() ${\mathcal{C}}$ is a locally bounded and Hom-finite category, see Definition 52. The evaluation functor
${\mathcal{C}}$ is a locally bounded and Hom-finite category, see Definition 52. The evaluation functor
then has a left adjoint ![]() $i_{!}:\prod _{c\in {\mathcal{C}}}{\mathcal{B}}\rightarrow {\mathcal{B}}^{{\mathcal{C}}}$. In [Reference Kvamme28] it was shown that there exists a Nakayama functor
$i_{!}:\prod _{c\in {\mathcal{C}}}{\mathcal{B}}\rightarrow {\mathcal{B}}^{{\mathcal{C}}}$. In [Reference Kvamme28] it was shown that there exists a Nakayama functor ![]() $\unicode[STIX]{x1D708}:{\mathcal{B}}^{{\mathcal{C}}}\rightarrow {\mathcal{B}}^{{\mathcal{C}}}$relative to
$\unicode[STIX]{x1D708}:{\mathcal{B}}^{{\mathcal{C}}}\rightarrow {\mathcal{B}}^{{\mathcal{C}}}$relative to ![]() $i_{!}\dashv i^{\ast }$, see Definition 15. This means that the following holds:
$i_{!}\dashv i^{\ast }$, see Definition 15. This means that the following holds:
(i)
 $\unicode[STIX]{x1D708}$ has a right adjoint
$\unicode[STIX]{x1D708}$ has a right adjoint  $\unicode[STIX]{x1D708}^{-}$;
$\unicode[STIX]{x1D708}^{-}$;(ii) The composite
 $\unicode[STIX]{x1D708}\circ i_{!}$ is right adjoint to
$\unicode[STIX]{x1D708}\circ i_{!}$ is right adjoint to  $i^{\ast }$;
$i^{\ast }$;(iii) The unit
 $\unicode[STIX]{x1D706}$ of the adjunction
$\unicode[STIX]{x1D706}$ of the adjunction  $\unicode[STIX]{x1D708}\dashv \unicode[STIX]{x1D708}^{-}$ induces an isomorphism for all objects
$\unicode[STIX]{x1D708}\dashv \unicode[STIX]{x1D708}^{-}$ induces an isomorphism for all objects $$\begin{eqnarray}\unicode[STIX]{x1D706}_{i_{!}((B_{c})_{c\in {\mathcal{C}}})}:i_{!}((B_{c})_{c\in {\mathcal{C}}})\rightarrow \unicode[STIX]{x1D708}^{-}\unicode[STIX]{x1D708}i_{!}((B_{c})_{c\in {\mathcal{C}}})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}_{i_{!}((B_{c})_{c\in {\mathcal{C}}})}:i_{!}((B_{c})_{c\in {\mathcal{C}}})\rightarrow \unicode[STIX]{x1D708}^{-}\unicode[STIX]{x1D708}i_{!}((B_{c})_{c\in {\mathcal{C}}})\end{eqnarray}$$ $(B_{c})_{c\in {\mathcal{C}}}\in \prod _{c\in {\mathcal{C}}}{\mathcal{B}}$.
$(B_{c})_{c\in {\mathcal{C}}}\in \prod _{c\in {\mathcal{C}}}{\mathcal{B}}$.
Explicitly, the Nakayama functor is given by the weighted colimit
and in Example 1 it is just the cokernel functor ![]() $\unicode[STIX]{x1D708}(B_{1}\xrightarrow[{}]{f}B_{2})=B_{2}\rightarrow \operatorname{Coker}f$. We give another example to illustrate this definition.
$\unicode[STIX]{x1D708}(B_{1}\xrightarrow[{}]{f}B_{2})=B_{2}\rightarrow \operatorname{Coker}f$. We give another example to illustrate this definition.
Example 2. [Reference Kvamme28, Example 3.2.6]
Let ![]() $k$ be a commutative ring, let
$k$ be a commutative ring, let ![]() $\unicode[STIX]{x1D6EC}_{1}$ be a
$\unicode[STIX]{x1D6EC}_{1}$ be a ![]() $k$-algebra which is finitely generated projective as a
$k$-algebra which is finitely generated projective as a ![]() $k$-module, and let
$k$-module, and let ![]() $\unicode[STIX]{x1D6EC}_{2}$ be a
$\unicode[STIX]{x1D6EC}_{2}$ be a ![]() $k$-algebra. If we consider
$k$-algebra. If we consider ![]() $\unicode[STIX]{x1D6EC}_{1}$ as a
$\unicode[STIX]{x1D6EC}_{1}$ as a ![]() $k$-linear category with one object and with endomorphism ring
$k$-linear category with one object and with endomorphism ring ![]() $\unicode[STIX]{x1D6EC}_{1}$, we get the identification
$\unicode[STIX]{x1D6EC}_{1}$, we get the identification
In particular, we have an adjoint pair ![]() $i_{!}\dashv i^{\ast }$ on
$i_{!}\dashv i^{\ast }$ on ![]() $(\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{Mod}$ and a Nakayama functor
$(\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{Mod}$ and a Nakayama functor ![]() $\unicode[STIX]{x1D708}$ relative to
$\unicode[STIX]{x1D708}$ relative to ![]() $i_{!}\dashv i^{\ast }$. Explicitly,
$i_{!}\dashv i^{\ast }$. Explicitly,
 $$\begin{eqnarray}\displaystyle & & \displaystyle i^{\ast }:(\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{Mod}\rightarrow \unicode[STIX]{x1D6EC}_{2}\text{-}\!\operatorname{Mod}\quad i^{\ast }(M)=_{\unicode[STIX]{x1D6EC}_{2}}M\nonumber\\ \displaystyle & & \displaystyle i_{!}:\unicode[STIX]{x1D6EC}_{2}\text{-}\!\operatorname{Mod}\rightarrow (\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{Mod}\quad i_{!}(M)=\unicode[STIX]{x1D6EC}_{1}\otimes _{k}M\nonumber\\ \displaystyle & & \displaystyle \unicode[STIX]{x1D708}:(\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{Mod}\rightarrow (\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{Mod}\quad \unicode[STIX]{x1D708}(M)=\operatorname{Hom}_{k}(\unicode[STIX]{x1D6EC}_{1},k)\otimes _{\unicode[STIX]{x1D6EC}_{1}}M.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle i^{\ast }:(\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{Mod}\rightarrow \unicode[STIX]{x1D6EC}_{2}\text{-}\!\operatorname{Mod}\quad i^{\ast }(M)=_{\unicode[STIX]{x1D6EC}_{2}}M\nonumber\\ \displaystyle & & \displaystyle i_{!}:\unicode[STIX]{x1D6EC}_{2}\text{-}\!\operatorname{Mod}\rightarrow (\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{Mod}\quad i_{!}(M)=\unicode[STIX]{x1D6EC}_{1}\otimes _{k}M\nonumber\\ \displaystyle & & \displaystyle \unicode[STIX]{x1D708}:(\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{Mod}\rightarrow (\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{Mod}\quad \unicode[STIX]{x1D708}(M)=\operatorname{Hom}_{k}(\unicode[STIX]{x1D6EC}_{1},k)\otimes _{\unicode[STIX]{x1D6EC}_{1}}M.\nonumber\end{eqnarray}$$ Note that if ![]() $k$ is a field and
$k$ is a field and ![]() $\unicode[STIX]{x1D6EC}_{2}=k$, then we just obtain the classical Nakayama functor for a finite-dimensional algebra.
$\unicode[STIX]{x1D6EC}_{2}=k$, then we just obtain the classical Nakayama functor for a finite-dimensional algebra.
We can now apply the machinery developed in [Reference Kvamme28]. In particular, we can define the category ![]() ${\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{B}}^{{\mathcal{C}}})$ of Gorenstein
${\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{B}}^{{\mathcal{C}}})$ of Gorenstein ![]() $P$-projective objects where
$P$-projective objects where ![]() $P=i_{!}\circ i^{\ast }$. Explicitly,
$P=i_{!}\circ i^{\ast }$. Explicitly, ![]() $A\in {\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{B}}^{{\mathcal{C}}})$ if and only if
$A\in {\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{B}}^{{\mathcal{C}}})$ if and only if
(i) The
 $i$th left derived functor
$i$th left derived functor  $L_{i}\unicode[STIX]{x1D708}(A)$ is
$L_{i}\unicode[STIX]{x1D708}(A)$ is  $0$ for all
$0$ for all  $i>0$;
$i>0$;(ii) The
 $i$th right derived functor
$i$th right derived functor  $R^{i}\unicode[STIX]{x1D708}^{-}(\unicode[STIX]{x1D708}(A))$ is
$R^{i}\unicode[STIX]{x1D708}^{-}(\unicode[STIX]{x1D708}(A))$ is  $0$ for all
$0$ for all  $i>0$;
$i>0$;(iii) the unit
 $\unicode[STIX]{x1D706}_{A}:A\rightarrow \unicode[STIX]{x1D708}^{-}\unicode[STIX]{x1D708}(A)$ of the adjunction
$\unicode[STIX]{x1D706}_{A}:A\rightarrow \unicode[STIX]{x1D708}^{-}\unicode[STIX]{x1D708}(A)$ of the adjunction  $\unicode[STIX]{x1D708}\dashv \unicode[STIX]{x1D708}^{-}$ is an isomorphism on
$\unicode[STIX]{x1D708}\dashv \unicode[STIX]{x1D708}^{-}$ is an isomorphism on  $A$.
$A$.
See Definition 16 and Theorem 20. In Example 2 with ![]() $k$ a field and
$k$ a field and ![]() $\unicode[STIX]{x1D6EC}_{2}=k$ the objects in
$\unicode[STIX]{x1D6EC}_{2}=k$ the objects in ![]() ${\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{B}}^{{\mathcal{C}}})$ are precisely the ordinary Gorenstein projective modules. Also, it turns out that for
${\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{B}}^{{\mathcal{C}}})$ are precisely the ordinary Gorenstein projective modules. Also, it turns out that for ![]() ${\mathcal{C}}=k\mathbb{A}_{2}$ the Gorenstein
${\mathcal{C}}=k\mathbb{A}_{2}$ the Gorenstein ![]() $P$-projective objects are precisely the monomorphisms. More generally, for
$P$-projective objects are precisely the monomorphisms. More generally, for ![]() ${\mathcal{C}}=kQ$ where
${\mathcal{C}}=kQ$ where ![]() $Q$ is a locally bounded acyclic quiver, the Gorenstein
$Q$ is a locally bounded acyclic quiver, the Gorenstein ![]() $P$-projective objects are precisely the monic representations, see Definition 59 and Proposition 60 part (ii).
$P$-projective objects are precisely the monic representations, see Definition 59 and Proposition 60 part (ii).
The next step is to generalize the requirement in Example 1 that ![]() $B_{2}$ and
$B_{2}$ and ![]() $\operatorname{Coker}f$ are Gorenstein projective. Since
$\operatorname{Coker}f$ are Gorenstein projective. Since ![]() $i^{\ast }\unicode[STIX]{x1D708}(B_{1}\xrightarrow[{}]{f}B_{2})=(B_{2},\operatorname{Coker}f)$, a natural guess would be that the image of
$i^{\ast }\unicode[STIX]{x1D708}(B_{1}\xrightarrow[{}]{f}B_{2})=(B_{2},\operatorname{Coker}f)$, a natural guess would be that the image of ![]() $i^{\ast }\circ \unicode[STIX]{x1D708}$ must be Gorenstein projective, that is, that we should consider the category
$i^{\ast }\circ \unicode[STIX]{x1D708}$ must be Gorenstein projective, that is, that we should consider the category
which we denote by ![]() ${\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{B}}^{{\mathcal{C}}}))$. We obtain the following result for this subcategory.
${\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{B}}^{{\mathcal{C}}}))$. We obtain the following result for this subcategory.
Theorem 3. (Theorem 36)
Assume ![]() ${\mathcal{B}}$ is a
${\mathcal{B}}$ is a ![]() $k$-linear abelian category with enough projectives and
$k$-linear abelian category with enough projectives and ![]() ${\mathcal{C}}$ is a small,
${\mathcal{C}}$ is a small, ![]() $k$-linear, locally bounded, and Hom-finite category. Then the subcategory
$k$-linear, locally bounded, and Hom-finite category. Then the subcategory ![]() ${\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{B}}^{{\mathcal{C}}}))$ is an admissible subcategory of
${\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{B}}^{{\mathcal{C}}}))$ is an admissible subcategory of ![]() ${\mathcal{G}}{\mathcal{P}}({\mathcal{B}}^{{\mathcal{C}}})$.
${\mathcal{G}}{\mathcal{P}}({\mathcal{B}}^{{\mathcal{C}}})$.
We refer to Definition 9 for our definition of admissible subcategory. It implies that
where ![]() ${\mathcal{G}}{\mathcal{P}}({\mathcal{B}}^{{\mathcal{C}}})$ denotes the category of Gorenstein projective objects in
${\mathcal{G}}{\mathcal{P}}({\mathcal{B}}^{{\mathcal{C}}})$ denotes the category of Gorenstein projective objects in ![]() ${\mathcal{B}}^{{\mathcal{C}}}$. It also implies that
${\mathcal{B}}^{{\mathcal{C}}}$. It also implies that ![]() ${\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{B}}^{{\mathcal{C}}}))$ is a Frobenius exact subcategory of
${\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{B}}^{{\mathcal{C}}}))$ is a Frobenius exact subcategory of ![]() ${\mathcal{B}}^{{\mathcal{C}}}$. In fact, Theorem 36 holds more generally for any admissible subcategory of
${\mathcal{B}}^{{\mathcal{C}}}$. In fact, Theorem 36 holds more generally for any admissible subcategory of ![]() $\prod _{c\in {\mathcal{C}}}{\mathcal{G}}{\mathcal{P}}({\mathcal{B}})$ and any
$\prod _{c\in {\mathcal{C}}}{\mathcal{G}}{\mathcal{P}}({\mathcal{B}})$ and any ![]() $P$-admissible subcategory of
$P$-admissible subcategory of ![]() ${\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{B}}^{{\mathcal{C}}})$, see Definition 23. This gives examples of other Frobenius exact categories, see Example 37 and 38.
${\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{B}}^{{\mathcal{C}}})$, see Definition 23. This gives examples of other Frobenius exact categories, see Example 37 and 38.
It remains to determine when ![]() ${\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{B}}^{{\mathcal{C}}}))={\mathcal{G}}{\mathcal{P}}({\mathcal{B}}^{{\mathcal{C}}})$. In general, this is not true, see Example 49. However, under some mild conditions the equality holds.
${\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{B}}^{{\mathcal{C}}}))={\mathcal{G}}{\mathcal{P}}({\mathcal{B}}^{{\mathcal{C}}})$. In general, this is not true, see Example 49. However, under some mild conditions the equality holds.
Theorem 4. (Theorem 42)
Assume ![]() ${\mathcal{B}}$ is a
${\mathcal{B}}$ is a ![]() $k$-linear abelian category with enough projectives and
$k$-linear abelian category with enough projectives and ![]() ${\mathcal{C}}$ is a small,
${\mathcal{C}}$ is a small, ![]() $k$-linear, locally bounded and Hom-finite category. If either of the following conditions hold, then we have an equality
$k$-linear, locally bounded and Hom-finite category. If either of the following conditions hold, then we have an equality ![]() ${\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{B}}^{{\mathcal{C}}}))={\mathcal{G}}{\mathcal{P}}({\mathcal{B}}^{{\mathcal{C}}})$:
${\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{B}}^{{\mathcal{C}}}))={\mathcal{G}}{\mathcal{P}}({\mathcal{B}}^{{\mathcal{C}}})$:
(i) For any long exact sequence in
 ${\mathcal{B}}^{{\mathcal{C}}}$with
${\mathcal{B}}^{{\mathcal{C}}}$with $$\begin{eqnarray}0\rightarrow K\rightarrow Q_{0}\rightarrow Q_{1}\rightarrow \cdots\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow K\rightarrow Q_{0}\rightarrow Q_{1}\rightarrow \cdots\end{eqnarray}$$ $Q_{i}$ projective for
$Q_{i}$ projective for  $i\geqslant 0$, we have
$i\geqslant 0$, we have  $K\in {\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{B}}^{{\mathcal{C}}})$;
$K\in {\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{B}}^{{\mathcal{C}}})$;(ii) If
 $B\in {\mathcal{B}}$ satisfy
$B\in {\mathcal{B}}$ satisfy  $\operatorname{Ext}_{{\mathcal{B}}}^{1}(B,B^{\prime })=0$ for all
$\operatorname{Ext}_{{\mathcal{B}}}^{1}(B,B^{\prime })=0$ for all  $B^{\prime }$ of finite projective dimension, then
$B^{\prime }$ of finite projective dimension, then  $B\in {\mathcal{G}}{\mathcal{P}}({\mathcal{B}})$.
$B\in {\mathcal{G}}{\mathcal{P}}({\mathcal{B}})$.
Condition (i) holds when ![]() $P$ is Iwanaga–Gorenstein, see Definition 18 and Corollary 43. In this case
$P$ is Iwanaga–Gorenstein, see Definition 18 and Corollary 43. In this case
and ![]() ${\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{B}}^{{\mathcal{C}}})$ is therefore particularly easy to compute.
${\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{B}}^{{\mathcal{C}}})$ is therefore particularly easy to compute.
Example 5. Consider ![]() ${\mathcal{C}}=k\mathbb{A}_{2}$ as in Example 1. In this case,
${\mathcal{C}}=k\mathbb{A}_{2}$ as in Example 1. In this case, ![]() $P$ is Iwanaga–Gorenstein of dimension
$P$ is Iwanaga–Gorenstein of dimension ![]() $1$. This implies that
$1$. This implies that ![]() $L_{i}\unicode[STIX]{x1D708}(A)=0$ for
$L_{i}\unicode[STIX]{x1D708}(A)=0$ for ![]() $i>1$, and hence
$i>1$, and hence ![]() $A\in {\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{B}}^{k\mathbb{A}_{2}})$ if and only if
$A\in {\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{B}}^{k\mathbb{A}_{2}})$ if and only if ![]() $L_{1}\unicode[STIX]{x1D708}(A)=0$. If we let
$L_{1}\unicode[STIX]{x1D708}(A)=0$. If we let ![]() $A=(B_{1}\xrightarrow[{}]{f}B_{2})$, then a simple computation shows that
$A=(B_{1}\xrightarrow[{}]{f}B_{2})$, then a simple computation shows that
In particular, ![]() $(B_{1}\xrightarrow[{}]{f}B_{2})\in {\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{B}}^{k\mathbb{A}_{2}})$ if and only if
$(B_{1}\xrightarrow[{}]{f}B_{2})\in {\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{B}}^{k\mathbb{A}_{2}})$ if and only if ![]() $f$ is a monomorphism. Since
$f$ is a monomorphism. Since ![]() $\unicode[STIX]{x1D708}(B_{1}\xrightarrow[{}]{f}B_{2})=B_{2}\rightarrow \operatorname{Coker}f$, we recover the description in Example 1
$\unicode[STIX]{x1D708}(B_{1}\xrightarrow[{}]{f}B_{2})=B_{2}\rightarrow \operatorname{Coker}f$, we recover the description in Example 1
More generally, for any locally bounded quiver, ![]() $P$ is Iwanaga–Gorenstein of dimension less than or equal
$P$ is Iwanaga–Gorenstein of dimension less than or equal ![]() $1$. Using this, we recover the description in [Reference Eshraghi, Hafezi and Salarian18] and [Reference Luo and Zhang29], see Proposition 65. We also illustrate how to compute the Gorenstein projectives for quivers with relations in Examples 66, 67 and 70. Finally, note that Condition (ii) of Theorem 4 holds when
$1$. Using this, we recover the description in [Reference Eshraghi, Hafezi and Salarian18] and [Reference Luo and Zhang29], see Proposition 65. We also illustrate how to compute the Gorenstein projectives for quivers with relations in Examples 66, 67 and 70. Finally, note that Condition (ii) of Theorem 4 holds when ![]() $\operatorname{G.pdim}B<\infty$ for all
$\operatorname{G.pdim}B<\infty$ for all ![]() $B\in {\mathcal{B}}$, see Lemma 44. In particular,
$B\in {\mathcal{B}}$, see Lemma 44. In particular, ![]() ${\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{B}}^{{\mathcal{C}}}))={\mathcal{G}}{\mathcal{P}}({\mathcal{B}}^{{\mathcal{C}}})$ if
${\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{B}}^{{\mathcal{C}}}))={\mathcal{G}}{\mathcal{P}}({\mathcal{B}}^{{\mathcal{C}}})$ if ![]() ${\mathcal{B}}=\operatorname{mod}\!\text{-}\unicode[STIX]{x1D6EC}$ or
${\mathcal{B}}=\operatorname{mod}\!\text{-}\unicode[STIX]{x1D6EC}$ or ![]() $\operatorname{Mod}\!\text{-}\unicode[STIX]{x1D6EC}$ for an Iwanaga–Gorenstein algebra
$\operatorname{Mod}\!\text{-}\unicode[STIX]{x1D6EC}$ for an Iwanaga–Gorenstein algebra ![]() $\unicode[STIX]{x1D6EC}$.
$\unicode[STIX]{x1D6EC}$.
Applying Theorem 4 to Example 2 with ![]() $k$ a field, we obtain the following result.
$k$ a field, we obtain the following result.
Theorem 6. (Example 47)
Let ![]() $k$ be a field, let
$k$ be a field, let ![]() $\unicode[STIX]{x1D6EC}_{1}$ be a finite-dimensional
$\unicode[STIX]{x1D6EC}_{1}$ be a finite-dimensional ![]() $k$-algebra, and let
$k$-algebra, and let ![]() $\unicode[STIX]{x1D6EC}_{2}$ be a
$\unicode[STIX]{x1D6EC}_{2}$ be a ![]() $k$-algebra. If
$k$-algebra. If ![]() $\unicode[STIX]{x1D6FA}^{\infty }(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod})\subset {\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod})$ or
$\unicode[STIX]{x1D6FA}^{\infty }(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod})\subset {\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod})$ or
then
Hence, this equality holds in particular if ![]() $\unicode[STIX]{x1D6EC}_{1}$ or
$\unicode[STIX]{x1D6EC}_{1}$ or ![]() $\unicode[STIX]{x1D6EC}_{2}$ is Iwanaga–Gorenstein.
$\unicode[STIX]{x1D6EC}_{2}$ is Iwanaga–Gorenstein.
We have an analogous statement for finitely presented modules, see Example 46. Finally, using the explicit description of the Gorenstein projective objects in Theorem 4 we also obtain a partly generalization of [Reference Dell’Ambrogio, Stevenson and Stovicek12, Theorem 4.6], see Theorem 57 and Remark 58.
The paper is organized as follows. In Section 2 we recall the notion of Nakayama functors relative to adjoint pairs and the necessary notions in Gorenstein homological algebra. We introduce ![]() $P$-admissible subcategories of
$P$-admissible subcategories of ![]() ${\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$ in Section 3.1. In Section 3.2 we show that adjoint pairs with Nakayama functor lift admissible subcategories of Gorenstein projectives, see Theorem 36. In Section 3.3 we use Theorem 36 to lift Gorenstein projective objects, and we provide sufficient criteria for when all Gorenstein projective objects are obtained, see Theorem 42. In Section 4 we study the functor category
${\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$ in Section 3.1. In Section 3.2 we show that adjoint pairs with Nakayama functor lift admissible subcategories of Gorenstein projectives, see Theorem 36. In Section 3.3 we use Theorem 36 to lift Gorenstein projective objects, and we provide sufficient criteria for when all Gorenstein projective objects are obtained, see Theorem 42. In Section 4 we study the functor category ![]() ${\mathcal{B}}^{{\mathcal{C}}}$ in detail. In Section 4.3 we use Theorem 42 to recover the known description of
${\mathcal{B}}^{{\mathcal{C}}}$ in detail. In Section 4.3 we use Theorem 42 to recover the known description of ![]() ${\mathcal{G}}{\mathcal{P}}({\mathcal{B}}^{kQ})$ for
${\mathcal{G}}{\mathcal{P}}({\mathcal{B}}^{kQ})$ for ![]() $Q$ a finite acyclic quiver, and in Section 4.4 we compute
$Q$ a finite acyclic quiver, and in Section 4.4 we compute ![]() ${\mathcal{G}}{\mathcal{P}}({\mathcal{B}}^{{\mathcal{C}}})$ for other examples of
${\mathcal{G}}{\mathcal{P}}({\mathcal{B}}^{{\mathcal{C}}})$ for other examples of ![]() ${\mathcal{C}}$.
${\mathcal{C}}$.
1.1 Conventions
For a ring ![]() $\unicode[STIX]{x1D6EC}$ we let
$\unicode[STIX]{x1D6EC}$ we let ![]() $\unicode[STIX]{x1D6EC}\text{-}\!\operatorname{Mod}$ (
$\unicode[STIX]{x1D6EC}\text{-}\!\operatorname{Mod}$ (![]() $\unicode[STIX]{x1D6EC}\text{-}\!\operatorname{mod}$) denote the category of (finitely presented) left
$\unicode[STIX]{x1D6EC}\text{-}\!\operatorname{mod}$) denote the category of (finitely presented) left ![]() $\unicode[STIX]{x1D6EC}$-modules. We fix
$\unicode[STIX]{x1D6EC}$-modules. We fix ![]() $k$ to be a commutative ring. All categories are assumed to be preadditive and all functors are assumed to be additive.
$k$ to be a commutative ring. All categories are assumed to be preadditive and all functors are assumed to be additive. ![]() ${\mathcal{A}}$ and
${\mathcal{A}}$ and ![]() ${\mathcal{B}}$ always denote abelian categories, and
${\mathcal{B}}$ always denote abelian categories, and ![]() ${\mathcal{D}}$ and
${\mathcal{D}}$ and ![]() ${\mathcal{E}}$ always denote additive categories. We let
${\mathcal{E}}$ always denote additive categories. We let ![]() $\operatorname{Proj}({\mathcal{A}})$ denote the category of projective objects in
$\operatorname{Proj}({\mathcal{A}})$ denote the category of projective objects in ![]() ${\mathcal{A}}$. The projective dimension of an object
${\mathcal{A}}$. The projective dimension of an object ![]() $A\in {\mathcal{A}}$ is denoted by
$A\in {\mathcal{A}}$ is denoted by ![]() $\operatorname{pdim}A$. If
$\operatorname{pdim}A$. If ![]() ${\mathcal{B}}$ and
${\mathcal{B}}$ and ![]() ${\mathcal{C}}$ are
${\mathcal{C}}$ are ![]() $k$-linear categories, then
$k$-linear categories, then ![]() ${\mathcal{B}}^{{\mathcal{C}}}$ denotes the category of
${\mathcal{B}}^{{\mathcal{C}}}$ denotes the category of ![]() $k$-linear functors from
$k$-linear functors from ![]() ${\mathcal{C}}$ to
${\mathcal{C}}$ to ![]() ${\mathcal{B}}$. We write
${\mathcal{B}}$. We write ![]() $F\dashv G:{\mathcal{D}}\rightarrow {\mathcal{E}}$ to denote that we have a functor
$F\dashv G:{\mathcal{D}}\rightarrow {\mathcal{E}}$ to denote that we have a functor ![]() $F:{\mathcal{D}}\rightarrow {\mathcal{E}}$ with right adjoint
$F:{\mathcal{D}}\rightarrow {\mathcal{E}}$ with right adjoint ![]() $G:{\mathcal{E}}\rightarrow {\mathcal{D}}$. In this case we let
$G:{\mathcal{E}}\rightarrow {\mathcal{D}}$. In this case we let ![]() $\unicode[STIX]{x1D6FC}^{F\dashv G}$ and
$\unicode[STIX]{x1D6FC}^{F\dashv G}$ and ![]() $\unicode[STIX]{x1D6FD}^{F\dashv G}$ denote the unit and counit of the adjunction, respectively. Furthermore,
$\unicode[STIX]{x1D6FD}^{F\dashv G}$ denote the unit and counit of the adjunction, respectively. Furthermore, ![]() $\unicode[STIX]{x1D719}^{F\dashv G}:{\mathcal{E}}(F(D),E)\rightarrow {\mathcal{D}}(D,G(E))$ denotes the adjunction isomorphism. If
$\unicode[STIX]{x1D719}^{F\dashv G}:{\mathcal{E}}(F(D),E)\rightarrow {\mathcal{D}}(D,G(E))$ denotes the adjunction isomorphism. If ![]() $\unicode[STIX]{x1D70E}:F_{1}\rightarrow F_{2}$ is a natural transformation, then
$\unicode[STIX]{x1D70E}:F_{1}\rightarrow F_{2}$ is a natural transformation, then ![]() $\unicode[STIX]{x1D70E}_{G}:F_{1}\circ G\rightarrow F_{2}\circ G$ denotes the natural transformation obtained by precomposing with
$\unicode[STIX]{x1D70E}_{G}:F_{1}\circ G\rightarrow F_{2}\circ G$ denotes the natural transformation obtained by precomposing with ![]() $G$.
$G$.
2 Preliminaries
2.1 Gorenstein projective objects
Let ![]() ${\mathcal{A}}$ be an abelian category. We say that
${\mathcal{A}}$ be an abelian category. We say that ![]() ${\mathcal{A}}$ has enough projectives if for any object
${\mathcal{A}}$ has enough projectives if for any object ![]() $A\in {\mathcal{A}}$ there exists an object
$A\in {\mathcal{A}}$ there exists an object ![]() $Q\in \operatorname{Proj}({\mathcal{A}})$ and an epimorphism
$Q\in \operatorname{Proj}({\mathcal{A}})$ and an epimorphism ![]() $Q\rightarrow A$.
$Q\rightarrow A$.
Definition 7. Assume ![]() ${\mathcal{A}}$ has enough projectives:
${\mathcal{A}}$ has enough projectives:
(i) An acyclic complex of projective objects in
 ${\mathcal{A}}$is called totally acyclic if the complex
${\mathcal{A}}$is called totally acyclic if the complex is acyclic for all
is acyclic for all
 $Q\in \operatorname{Proj}({\mathcal{A}})$.
$Q\in \operatorname{Proj}({\mathcal{A}})$.(ii) An object
 $A\in {\mathcal{A}}$ is called Gorenstein projective if there exists a totally acyclic complex
$A\in {\mathcal{A}}$ is called Gorenstein projective if there exists a totally acyclic complex  $Q_{\bullet }$ with
$Q_{\bullet }$ with  $A=Z_{0}(Q_{\bullet })=\operatorname{Ker}f_{0}$. We denote the full subcategory of Gorenstein projective objects in
$A=Z_{0}(Q_{\bullet })=\operatorname{Ker}f_{0}$. We denote the full subcategory of Gorenstein projective objects in  ${\mathcal{A}}$ by
${\mathcal{A}}$ by  ${\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$.
${\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$.
Lemma 8. If ![]() ${\mathcal{A}}$ has enough projectives, then the subcategory
${\mathcal{A}}$ has enough projectives, then the subcategory ![]() ${\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$ is closed under extensions and direct summands.
${\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$ is closed under extensions and direct summands.
Proof. The fact that ![]() ${\mathcal{A}}$ is closed under direct summands follows from [Reference Huang22, Theorem 1.4(2)]. The fact that
${\mathcal{A}}$ is closed under direct summands follows from [Reference Huang22, Theorem 1.4(2)]. The fact that ![]() ${\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$ is closed under extensions follows from [Reference Beligiannis5, Proposition 2.13(1)].
${\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$ is closed under extensions follows from [Reference Beligiannis5, Proposition 2.13(1)].
Definition 9. Assume ![]() ${\mathcal{A}}$ has enough projectives. A full subcategory
${\mathcal{A}}$ has enough projectives. A full subcategory ![]() ${\mathcal{F}}\subset {\mathcal{A}}$ is called an admissible subcategory of
${\mathcal{F}}\subset {\mathcal{A}}$ is called an admissible subcategory of ![]() ${\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$ if it is closed under extensions, direct summands, and satisfies the following properties:
${\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$ if it is closed under extensions, direct summands, and satisfies the following properties:
(i)
 ${\mathcal{F}}$ contains the projective objects in
${\mathcal{F}}$ contains the projective objects in  ${\mathcal{A}}$;
${\mathcal{A}}$;(ii)
 $\operatorname{Ext}^{1}(A,Q)=0$ for all
$\operatorname{Ext}^{1}(A,Q)=0$ for all  $A\in {\mathcal{F}}$ and
$A\in {\mathcal{F}}$ and  $Q\in \operatorname{Proj}({\mathcal{A}})$;
$Q\in \operatorname{Proj}({\mathcal{A}})$;(iii) For all
 $A\in {\mathcal{F}}$ there exists an exact sequence
$A\in {\mathcal{F}}$ there exists an exact sequence  $0\rightarrow A^{\prime }\rightarrow Q\rightarrow A\rightarrow 0$ with
$0\rightarrow A^{\prime }\rightarrow Q\rightarrow A\rightarrow 0$ with  $A^{\prime }\in {\mathcal{F}}$ and
$A^{\prime }\in {\mathcal{F}}$ and  $Q\in \operatorname{Proj}({\mathcal{A}})$;
$Q\in \operatorname{Proj}({\mathcal{A}})$;(iv) For all
 $A\in {\mathcal{F}}$ there exists an exact sequence
$A\in {\mathcal{F}}$ there exists an exact sequence  $0\rightarrow A\rightarrow Q\rightarrow A^{\prime }\rightarrow 0$ with
$0\rightarrow A\rightarrow Q\rightarrow A^{\prime }\rightarrow 0$ with  $A^{\prime }\in {\mathcal{F}}$ and
$A^{\prime }\in {\mathcal{F}}$ and  $Q\in \operatorname{Proj}({\mathcal{A}})$.
$Q\in \operatorname{Proj}({\mathcal{A}})$.
Assume ![]() ${\mathcal{F}}$ is an admissible subcategory of
${\mathcal{F}}$ is an admissible subcategory of ![]() ${\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$. Since
${\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$. Since ![]() ${\mathcal{F}}$ is closed under extensions, it inherits an exact structure from
${\mathcal{F}}$ is closed under extensions, it inherits an exact structure from ![]() ${\mathcal{A}}$ (see [Reference Bühler11] for the theory of exact categories). In fact, under this exact structure
${\mathcal{A}}$ (see [Reference Bühler11] for the theory of exact categories). In fact, under this exact structure ![]() ${\mathcal{F}}$ becomes a Frobenius exact category, and the projective objects in
${\mathcal{F}}$ becomes a Frobenius exact category, and the projective objects in ![]() ${\mathcal{F}}$ are precisely the projective objects in
${\mathcal{F}}$ are precisely the projective objects in ![]() ${\mathcal{A}}$.
${\mathcal{A}}$.
The following result is immediate from the definition.
Proposition 10. Assume ![]() ${\mathcal{A}}$ has enough projectives. The following holds:
${\mathcal{A}}$ has enough projectives. The following holds:
(i)
 ${\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$ is an admissible subcategory of
${\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$ is an admissible subcategory of  ${\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$;
${\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$;(ii)
 $\operatorname{Proj}({\mathcal{A}})$ is an admissible subcategory of
$\operatorname{Proj}({\mathcal{A}})$ is an admissible subcategory of  ${\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$;
${\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$;(iii) Assume
 ${\mathcal{F}}$ is an admissible subcategory of
${\mathcal{F}}$ is an admissible subcategory of  ${\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$. Then
${\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$. Then  ${\mathcal{F}}\subset {\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$.
${\mathcal{F}}\subset {\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$.
Recall that a full subcategory ![]() ${\mathcal{X}}\subset {\mathcal{A}}$ is called generating if for any
${\mathcal{X}}\subset {\mathcal{A}}$ is called generating if for any ![]() $A\in {\mathcal{A}}$ there exists an object
$A\in {\mathcal{A}}$ there exists an object ![]() $X\in {\mathcal{X}}$ and an epimorphism
$X\in {\mathcal{X}}$ and an epimorphism ![]() $X\rightarrow A$. A full subcategory
$X\rightarrow A$. A full subcategory ![]() ${\mathcal{X}}\subset {\mathcal{A}}$ is called resolving if it is generating and closed under direct summands, extensions, and kernels of epimorphisms. Here we follow the same conventions as in [Reference Stovicek37]. Note that a resolving subcategory contains all the projective objects in
${\mathcal{X}}\subset {\mathcal{A}}$ is called resolving if it is generating and closed under direct summands, extensions, and kernels of epimorphisms. Here we follow the same conventions as in [Reference Stovicek37]. Note that a resolving subcategory contains all the projective objects in ![]() ${\mathcal{A}}$.
${\mathcal{A}}$.
Lemma 11. Assume ![]() ${\mathcal{A}}$ has enough projectives, and let
${\mathcal{A}}$ has enough projectives, and let ![]() ${\mathcal{F}}$ be an admissible subcategory of
${\mathcal{F}}$ be an admissible subcategory of ![]() ${\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$. Then
${\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$. Then ![]() ${\mathcal{F}}$ is a resolving subcategory of
${\mathcal{F}}$ is a resolving subcategory of ![]() ${\mathcal{A}}$.
${\mathcal{A}}$.
Proof. We only need to check that it is closed under kernels of epimorphisms. Let ![]() $0\rightarrow A_{3}\xrightarrow[{}]{f}A_{2}\xrightarrow[{}]{g}A_{1}\rightarrow 0$ be an exact sequence in
$0\rightarrow A_{3}\xrightarrow[{}]{f}A_{2}\xrightarrow[{}]{g}A_{1}\rightarrow 0$ be an exact sequence in ![]() ${\mathcal{A}}$ with
${\mathcal{A}}$ with ![]() $A_{2}\in {\mathcal{F}}$ and
$A_{2}\in {\mathcal{F}}$ and ![]() $A_{1}\in {\mathcal{F}}$. Choose an exact sequence
$A_{1}\in {\mathcal{F}}$. Choose an exact sequence ![]() $0\rightarrow A\xrightarrow[{}]{i}Q\xrightarrow[{}]{p}A_{1}\rightarrow 0$ in
$0\rightarrow A\xrightarrow[{}]{i}Q\xrightarrow[{}]{p}A_{1}\rightarrow 0$ in ![]() ${\mathcal{A}}$ with
${\mathcal{A}}$ with ![]() $Q$ projective and
$Q$ projective and ![]() $A\in {\mathcal{F}}$. Since
$A\in {\mathcal{F}}$. Since ![]() $Q$ is projective, there exists a morphism
$Q$ is projective, there exists a morphism ![]() $s:Q\rightarrow A_{2}$ satisfying
$s:Q\rightarrow A_{2}$ satisfying ![]() $g\circ s=p$. This gives a commutative diagram
$g\circ s=p$. This gives a commutative diagram

with exact rows, where the morphism ![]() $A\rightarrow A_{3}$ is induced from the commutativity of the right square. By [Reference Popescu34, Lemma 5.2] the left square is a pushforward and a pullback square, and hence we get an exact sequence
$A\rightarrow A_{3}$ is induced from the commutativity of the right square. By [Reference Popescu34, Lemma 5.2] the left square is a pushforward and a pullback square, and hence we get an exact sequence
Since ![]() ${\mathcal{F}}$ is closed under extensions and direct summands, it follows that
${\mathcal{F}}$ is closed under extensions and direct summands, it follows that ![]() $A_{3}\in {\mathcal{F}}$.
$A_{3}\in {\mathcal{F}}$.
In particular, it follows that ![]() ${\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$ is a resolving subcategory of
${\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$ is a resolving subcategory of ![]() ${\mathcal{A}}$.
${\mathcal{A}}$.
One can define the resolution dimension ![]() $\dim _{{\mathcal{X}}}(A)$ of any object
$\dim _{{\mathcal{X}}}(A)$ of any object ![]() $A\in {\mathcal{A}}$ with respect to a resolving subcategory
$A\in {\mathcal{A}}$ with respect to a resolving subcategory ![]() ${\mathcal{X}}$ of
${\mathcal{X}}$ of ![]() ${\mathcal{A}}$, see [Reference Stovicek37]. It is the smallest integer
${\mathcal{A}}$, see [Reference Stovicek37]. It is the smallest integer ![]() $n\geqslant 0$ such that there exists an exact sequence
$n\geqslant 0$ such that there exists an exact sequence
where ![]() $X_{i}\in {\mathcal{X}}$ for
$X_{i}\in {\mathcal{X}}$ for ![]() $0\leqslant i\leqslant n$. In this case, if
$0\leqslant i\leqslant n$. In this case, if
is another exact sequence with ![]() $X_{i}^{\prime }\in {\mathcal{X}}$ for all
$X_{i}^{\prime }\in {\mathcal{X}}$ for all ![]() $0\leqslant i\leqslant n-1$, then
$0\leqslant i\leqslant n-1$, then ![]() $X_{n}^{\prime }\in {\mathcal{X}}$, see [Reference Stovicek37, Proposition 2.3]. We write
$X_{n}^{\prime }\in {\mathcal{X}}$, see [Reference Stovicek37, Proposition 2.3]. We write ![]() $\dim _{{\mathcal{X}}}(A)=\infty$ if there does not exist such an
$\dim _{{\mathcal{X}}}(A)=\infty$ if there does not exist such an ![]() $n$. The global resolution dimension
$n$. The global resolution dimension ![]() $\dim _{{\mathcal{X}}}({\mathcal{A}})$ of
$\dim _{{\mathcal{X}}}({\mathcal{A}})$ of ![]() ${\mathcal{A}}$ with respect to
${\mathcal{A}}$ with respect to ![]() ${\mathcal{X}}$ is the supremum of
${\mathcal{X}}$ is the supremum of ![]() $\dim _{{\mathcal{X}}}(A)$ over all
$\dim _{{\mathcal{X}}}(A)$ over all ![]() $A\in {\mathcal{A}}$. Putting
$A\in {\mathcal{A}}$. Putting ![]() ${\mathcal{X}}={\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$ we get the Gorenstein projective dimension
${\mathcal{X}}={\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$ we get the Gorenstein projective dimension
and the global Gorenstein projective dimension
We need the following lemma later.
Lemma 12. Let ![]() $A_{2}\xrightarrow[{}]{f}A_{1}$ be a morphism in
$A_{2}\xrightarrow[{}]{f}A_{1}$ be a morphism in ![]() ${\mathcal{A}}$ with
${\mathcal{A}}$ with ![]() $A_{2}\in {\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$. Assume
$A_{2}\in {\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$. Assume
is an epimorphism for all projective objects ![]() $Q\in {\mathcal{A}}$. Then
$Q\in {\mathcal{A}}$. Then ![]() $f$ is a monomorphism.
$f$ is a monomorphism.
Proof. Let ![]() $A_{2}\xrightarrow[{}]{i}Q$ be a monomorphism into a projective object
$A_{2}\xrightarrow[{}]{i}Q$ be a monomorphism into a projective object ![]() $Q$. By assumption, there exists a morphism
$Q$. By assumption, there exists a morphism ![]() $h:A_{1}\rightarrow Q$ such that
$h:A_{1}\rightarrow Q$ such that ![]() $i=h\circ f$. This implies that
$i=h\circ f$. This implies that ![]() $f$ is a monomorphism, and we are done.
$f$ is a monomorphism, and we are done.
2.2 Derived functors
For a functor ![]() $F:{\mathcal{D}}\rightarrow {\mathcal{E}}$, we let
$F:{\mathcal{D}}\rightarrow {\mathcal{E}}$, we let ![]() $\operatorname{im}F$ denote the full subcategory of
$\operatorname{im}F$ denote the full subcategory of ![]() ${\mathcal{E}}$ consisting of the objects
${\mathcal{E}}$ consisting of the objects ![]() $F(D)$ for
$F(D)$ for ![]() $D\in {\mathcal{D}}$.
$D\in {\mathcal{D}}$.
Proposition 13. [Reference Kvamme28, Proposition 3.1.4]
Let ![]() ${\mathcal{A}}$ and
${\mathcal{A}}$ and ![]() ${\mathcal{B}}$ be abelian categories, and let
${\mathcal{B}}$ be abelian categories, and let ![]() $G:{\mathcal{A}}\rightarrow {\mathcal{B}}$ be a functor.
$G:{\mathcal{A}}\rightarrow {\mathcal{B}}$ be a functor.
(i) Assume
 $G$ is left exact,
$G$ is left exact,  $L\dashv R:{\mathcal{A}}\rightarrow {\mathcal{D}}$ is an adjunction, and
$L\dashv R:{\mathcal{A}}\rightarrow {\mathcal{D}}$ is an adjunction, and  $\operatorname{im}R$ is a cogenerating subcategory of
$\operatorname{im}R$ is a cogenerating subcategory of  ${\mathcal{A}}$. If
${\mathcal{A}}$. If  $R\circ L$ and
$R\circ L$ and  $G\circ R\circ L$ are exact functors, then the
$G\circ R\circ L$ are exact functors, then the  $i$th right derived functor
$i$th right derived functor  $R^{i}G$ of G exists for all
$R^{i}G$ of G exists for all  $i>0$, and
$i>0$, and  $R^{i}G(X)=0$ for all
$R^{i}G(X)=0$ for all  $i>0$ and
$i>0$ and  $X\in \operatorname{im}R$;
$X\in \operatorname{im}R$;(ii) Assume
 $G$ is right exact,
$G$ is right exact,  $L^{\prime }\dashv R^{\prime }:{\mathcal{D}}\rightarrow {\mathcal{A}}$ is an adjunction, and
$L^{\prime }\dashv R^{\prime }:{\mathcal{D}}\rightarrow {\mathcal{A}}$ is an adjunction, and  $\operatorname{im}L^{\prime }$ is a generating subcategory of
$\operatorname{im}L^{\prime }$ is a generating subcategory of  ${\mathcal{A}}$. If
${\mathcal{A}}$. If  $L^{\prime }\circ R^{\prime }$ and
$L^{\prime }\circ R^{\prime }$ and  $G\circ L^{\prime }\circ R^{\prime }$ are exact functors, then the
$G\circ L^{\prime }\circ R^{\prime }$ are exact functors, then the  $i$th left derived functor
$i$th left derived functor  $L_{i}G$ of G exists for all
$L_{i}G$ of G exists for all  $i>0$, and
$i>0$, and  $L_{i}G(X)=0$ for all
$L_{i}G(X)=0$ for all  $i>0$ and
$i>0$ and  $X\in \operatorname{im}L^{\prime }$.
$X\in \operatorname{im}L^{\prime }$.
We say that ![]() $R$is adapted to
$R$is adapted to ![]() $G$ or
$G$ or ![]() $L^{\prime }$is adapted to
$L^{\prime }$is adapted to ![]() $G$ in these two cases, respectively. Note that
$G$ in these two cases, respectively. Note that ![]() $\operatorname{im}R$ is cogenerating if and only the unit of the adjunction
$\operatorname{im}R$ is cogenerating if and only the unit of the adjunction ![]() $L\dashv R$ is a monomorphism. By the dual of [Reference Mac Lane31, Theorem IV.3.1] this is equivalent to
$L\dashv R$ is a monomorphism. By the dual of [Reference Mac Lane31, Theorem IV.3.1] this is equivalent to ![]() $L$ being faithful. Dually,
$L$ being faithful. Dually, ![]() $\operatorname{im}L^{\prime }$ is generating if and only if the counit of
$\operatorname{im}L^{\prime }$ is generating if and only if the counit of ![]() $L^{\prime }\dashv R^{\prime }$ is an epimorphism, and by [Reference Mac Lane31, Theorem IV.3.1] this is equivalent to
$L^{\prime }\dashv R^{\prime }$ is an epimorphism, and by [Reference Mac Lane31, Theorem IV.3.1] this is equivalent to ![]() $R^{\prime }$ being faithful.
$R^{\prime }$ being faithful.
We need the following result.
Lemma 14. Let ![]() ${\mathcal{A}}$ and
${\mathcal{A}}$ and ![]() ${\mathcal{B}}$ be abelian categories, and let
${\mathcal{B}}$ be abelian categories, and let ![]() $\unicode[STIX]{x1D702}:G_{1}\rightarrow G_{2}$ and
$\unicode[STIX]{x1D702}:G_{1}\rightarrow G_{2}$ and ![]() $\unicode[STIX]{x1D716}:G_{2}\rightarrow G_{3}$ be two natural transformations between functors
$\unicode[STIX]{x1D716}:G_{2}\rightarrow G_{3}$ be two natural transformations between functors ![]() ${\mathcal{A}}\rightarrow {\mathcal{B}}$.
${\mathcal{A}}\rightarrow {\mathcal{B}}$.
(i) Assume
 $G_{i}$ is left exact for all
$G_{i}$ is left exact for all  $i$. Furthermore, assume there exists an adjunction
$i$. Furthermore, assume there exists an adjunction  $L\dashv R:{\mathcal{A}}\rightarrow {\mathcal{D}}$ such that
$L\dashv R:{\mathcal{A}}\rightarrow {\mathcal{D}}$ such that  $R$ is adapted to
$R$ is adapted to  $G_{i}$ for all
$G_{i}$ for all  $i$. If the sequence is exact, then there exists a long exact sequence
$i$. If the sequence is exact, then there exists a long exact sequence $$\begin{eqnarray}0\rightarrow G_{1}\circ R\circ L\xrightarrow[{}]{\unicode[STIX]{x1D702}_{R\circ L}}G_{2}\circ R\circ L\xrightarrow[{}]{\unicode[STIX]{x1D716}_{R\circ L}}G_{3}\circ R\circ L\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow G_{1}\circ R\circ L\xrightarrow[{}]{\unicode[STIX]{x1D702}_{R\circ L}}G_{2}\circ R\circ L\xrightarrow[{}]{\unicode[STIX]{x1D716}_{R\circ L}}G_{3}\circ R\circ L\rightarrow 0\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle 0\rightarrow G_{1}\xrightarrow[{}]{\unicode[STIX]{x1D702}}G_{2}\xrightarrow[{}]{\unicode[STIX]{x1D716}}G_{3}\rightarrow L_{1}G_{1}\rightarrow L_{1}G_{2}\rightarrow L_{1}G_{3}\rightarrow L_{2}G_{1}\rightarrow \cdots & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0\rightarrow G_{1}\xrightarrow[{}]{\unicode[STIX]{x1D702}}G_{2}\xrightarrow[{}]{\unicode[STIX]{x1D716}}G_{3}\rightarrow L_{1}G_{1}\rightarrow L_{1}G_{2}\rightarrow L_{1}G_{3}\rightarrow L_{2}G_{1}\rightarrow \cdots & & \displaystyle \nonumber\end{eqnarray}$$(ii) Assume
 $G_{i}$ is right exact for all
$G_{i}$ is right exact for all  $i$. Furthermore, assume there exists an adjunction
$i$. Furthermore, assume there exists an adjunction  $L^{\prime }\dashv R^{\prime }:{\mathcal{D}}\rightarrow {\mathcal{A}}$ such that
$L^{\prime }\dashv R^{\prime }:{\mathcal{D}}\rightarrow {\mathcal{A}}$ such that  $L^{\prime }$ is adapted to
$L^{\prime }$ is adapted to  $G_{i}$ for
$G_{i}$ for  $1\leqslant i\leqslant 3$. If the sequence is exact, then there exists a long exact sequence
$1\leqslant i\leqslant 3$. If the sequence is exact, then there exists a long exact sequence $$\begin{eqnarray}0\rightarrow G_{1}\circ L^{\prime }\circ R^{\prime }\xrightarrow[{}]{\unicode[STIX]{x1D702}_{L^{\prime }\circ R^{\prime }}}G_{2}\circ L^{\prime }\circ R^{\prime }\xrightarrow[{}]{\unicode[STIX]{x1D716}_{L^{\prime }\circ R^{\prime }}}G_{3}\circ L^{\prime }\circ R^{\prime }\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow G_{1}\circ L^{\prime }\circ R^{\prime }\xrightarrow[{}]{\unicode[STIX]{x1D702}_{L^{\prime }\circ R^{\prime }}}G_{2}\circ L^{\prime }\circ R^{\prime }\xrightarrow[{}]{\unicode[STIX]{x1D716}_{L^{\prime }\circ R^{\prime }}}G_{3}\circ L^{\prime }\circ R^{\prime }\rightarrow 0\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle \cdots \rightarrow L_{2}G_{3}\rightarrow L_{1}G_{1}\rightarrow L_{1}G_{2}\rightarrow L_{1}G_{3}\rightarrow G_{1}\xrightarrow[{}]{\unicode[STIX]{x1D702}}G_{2}\xrightarrow[{}]{\unicode[STIX]{x1D716}}G_{3}\rightarrow 0. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \cdots \rightarrow L_{2}G_{3}\rightarrow L_{1}G_{1}\rightarrow L_{1}G_{2}\rightarrow L_{1}G_{3}\rightarrow G_{1}\xrightarrow[{}]{\unicode[STIX]{x1D702}}G_{2}\xrightarrow[{}]{\unicode[STIX]{x1D716}}G_{3}\rightarrow 0. & & \displaystyle \nonumber\end{eqnarray}$$
Proof. We prove part (ii), part (i) follows dually. Let ![]() $\mathsf{S}$ be the induced comonad on
$\mathsf{S}$ be the induced comonad on ![]() ${\mathcal{A}}$ from the adjunction
${\mathcal{A}}$ from the adjunction ![]() $L^{\prime }\dashv R^{\prime }$. There is an obvious natural isomorphism
$L^{\prime }\dashv R^{\prime }$. There is an obvious natural isomorphism ![]() $L_{n}G_{i}\cong H_{n}(-,G_{i})$ and
$L_{n}G_{i}\cong H_{n}(-,G_{i})$ and ![]() $G_{i}\cong H_{0}(-,G_{i})$ where
$G_{i}\cong H_{0}(-,G_{i})$ where ![]() $H_{i}(-,G_{i})$ is the comonad homology relative to
$H_{i}(-,G_{i})$ is the comonad homology relative to ![]() $\mathsf{S}$ as defined in [Reference Barr and Beck4, Section 1]. The claim follows now from [Reference Barr and Beck4, Section 3.2].
$\mathsf{S}$ as defined in [Reference Barr and Beck4, Section 1]. The claim follows now from [Reference Barr and Beck4, Section 3.2].
2.3 Nakayama functor
We need the notion of Nakayama functor relative to adjoint pairs which was introduced in [Reference Kvamme28].
Definition 15. Let ![]() $f^{\ast }:{\mathcal{A}}\rightarrow {\mathcal{D}}$ be a faithful functor with left adjoint
$f^{\ast }:{\mathcal{A}}\rightarrow {\mathcal{D}}$ be a faithful functor with left adjoint ![]() $f_{!}:{\mathcal{D}}\rightarrow {\mathcal{A}}$. A Nakayama functor relative to the adjunction
$f_{!}:{\mathcal{D}}\rightarrow {\mathcal{A}}$. A Nakayama functor relative to the adjunction ![]() $f_{!}\dashv f^{\ast }$ is a functor
$f_{!}\dashv f^{\ast }$ is a functor ![]() $\unicode[STIX]{x1D708}:{\mathcal{A}}\rightarrow {\mathcal{A}}$ with a right adjoint
$\unicode[STIX]{x1D708}:{\mathcal{A}}\rightarrow {\mathcal{A}}$ with a right adjoint ![]() $\unicode[STIX]{x1D708}^{-}$ satisfying:
$\unicode[STIX]{x1D708}^{-}$ satisfying:
(i)
 $\unicode[STIX]{x1D708}\circ f_{!}$ is right adjoint to
$\unicode[STIX]{x1D708}\circ f_{!}$ is right adjoint to  $f^{\ast }$;
$f^{\ast }$;(ii) The unit of
 $\unicode[STIX]{x1D708}\dashv \unicode[STIX]{x1D708}^{-}$ induces an isomorphism
$\unicode[STIX]{x1D708}\dashv \unicode[STIX]{x1D708}^{-}$ induces an isomorphism  $f_{!}\xrightarrow[{}]{\cong }\unicode[STIX]{x1D708}^{-}\circ \unicode[STIX]{x1D708}\circ f_{!}$ when precomposed with
$f_{!}\xrightarrow[{}]{\cong }\unicode[STIX]{x1D708}^{-}\circ \unicode[STIX]{x1D708}\circ f_{!}$ when precomposed with  $f_{!}$.
$f_{!}$.
We let ![]() $\unicode[STIX]{x1D706}:1_{{\mathcal{A}}}\rightarrow \unicode[STIX]{x1D708}^{-}\circ \unicode[STIX]{x1D708}$ and
$\unicode[STIX]{x1D706}:1_{{\mathcal{A}}}\rightarrow \unicode[STIX]{x1D708}^{-}\circ \unicode[STIX]{x1D708}$ and ![]() $\unicode[STIX]{x1D70E}:\unicode[STIX]{x1D708}\circ \unicode[STIX]{x1D708}^{-}\rightarrow 1_{{\mathcal{A}}}$ denote the unit and counit of the adjunction
$\unicode[STIX]{x1D70E}:\unicode[STIX]{x1D708}\circ \unicode[STIX]{x1D708}^{-}\rightarrow 1_{{\mathcal{A}}}$ denote the unit and counit of the adjunction ![]() $\unicode[STIX]{x1D708}\dashv \unicode[STIX]{x1D708}^{-}$. We also fix the notation
$\unicode[STIX]{x1D708}\dashv \unicode[STIX]{x1D708}^{-}$. We also fix the notation ![]() $f_{\ast }:=\unicode[STIX]{x1D708}\circ f_{!}$,
$f_{\ast }:=\unicode[STIX]{x1D708}\circ f_{!}$, ![]() $P:=f_{!}\circ f^{\ast }$ and
$P:=f_{!}\circ f^{\ast }$ and ![]() $I:=f_{\ast }\circ f^{\ast }$. Note that we have adjunctions
$I:=f_{\ast }\circ f^{\ast }$. Note that we have adjunctions
We call summands of objects ![]() $P(A)$ for
$P(A)$ for ![]() $P$-projective and summands of objects
$P$-projective and summands of objects ![]() $I(A)$ for
$I(A)$ for ![]() $I$-injective. By the triangle identities the
$I$-injective. By the triangle identities the ![]() $P$-projectives and
$P$-projectives and ![]() $I$-injectives are precisely the summands of objects of the form
$I$-injectives are precisely the summands of objects of the form ![]() $f_{!}(D)$ and
$f_{!}(D)$ and ![]() $f_{\ast }(D)$ for
$f_{\ast }(D)$ for ![]() $D\in {\mathcal{D}}$, respectively. Since
$D\in {\mathcal{D}}$, respectively. Since ![]() $P$,
$P$, ![]() $\unicode[STIX]{x1D708}\circ P=I$, and
$\unicode[STIX]{x1D708}\circ P=I$, and ![]() $\unicode[STIX]{x1D708}^{-}\circ I\cong P$ are exact, it follows from Proposition 13 that
$\unicode[STIX]{x1D708}^{-}\circ I\cong P$ are exact, it follows from Proposition 13 that ![]() $f_{!}$ is adapted to
$f_{!}$ is adapted to ![]() $\unicode[STIX]{x1D708}$ and
$\unicode[STIX]{x1D708}$ and ![]() $f_{\ast }$ is adapted to
$f_{\ast }$ is adapted to ![]() $\unicode[STIX]{x1D708}^{-}$. In particular, the derived functors
$\unicode[STIX]{x1D708}^{-}$. In particular, the derived functors ![]() $L_{i}\unicode[STIX]{x1D708}$ and
$L_{i}\unicode[STIX]{x1D708}$ and ![]() $R^{i}\unicode[STIX]{x1D708}^{-}$ exist for all
$R^{i}\unicode[STIX]{x1D708}^{-}$ exist for all ![]() $i>0$.
$i>0$.
Definition 16. [Reference Kvamme28, Definition 4.1.1]
Assume ![]() $\unicode[STIX]{x1D708}$ is a Nakayama functor relative to the adjunction
$\unicode[STIX]{x1D708}$ is a Nakayama functor relative to the adjunction ![]() $f_{!}\dashv f^{\ast }:{\mathcal{D}}\rightarrow {\mathcal{A}}$. An object
$f_{!}\dashv f^{\ast }:{\mathcal{D}}\rightarrow {\mathcal{A}}$. An object ![]() $X\in {\mathcal{A}}$ is called Gorenstein
$X\in {\mathcal{A}}$ is called Gorenstein ![]() $P$-projective if there exists an exact sequence
$P$-projective if there exists an exact sequence
with ![]() $A_{i}\in {\mathcal{A}}$ being
$A_{i}\in {\mathcal{A}}$ being ![]() $P$-projective for all
$P$-projective for all ![]() $i\in \mathbb{Z}$, such that the sequence
$i\in \mathbb{Z}$, such that the sequence
is exact, and with ![]() $Z_{0}(A_{\bullet })=\operatorname{Ker}f_{0}=X$. The subcategory of
$Z_{0}(A_{\bullet })=\operatorname{Ker}f_{0}=X$. The subcategory of ![]() ${\mathcal{A}}$ consisting of all Gorenstein
${\mathcal{A}}$ consisting of all Gorenstein ![]() $P$-projective objects is denoted by
$P$-projective objects is denoted by ![]() ${\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$.
${\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$.
Proposition 17. Assume ![]() $\unicode[STIX]{x1D708}$ is a Nakayama functor relative to the adjunction
$\unicode[STIX]{x1D708}$ is a Nakayama functor relative to the adjunction ![]() $f_{!}\dashv f^{\ast }:{\mathcal{D}}\rightarrow {\mathcal{A}}$. The following holds:
$f_{!}\dashv f^{\ast }:{\mathcal{D}}\rightarrow {\mathcal{A}}$. The following holds:
(i)
 ${\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$ is a resolving subcategory of
${\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$ is a resolving subcategory of  ${\mathcal{A}}$;
${\mathcal{A}}$;(ii) Assume
 $i:A_{2}\rightarrow A_{1}$ is a morphism such that
$i:A_{2}\rightarrow A_{1}$ is a morphism such that  $\unicode[STIX]{x1D708}(i)$ is a monomorphism and
$\unicode[STIX]{x1D708}(i)$ is a monomorphism and  $A_{1},A_{2}\in {\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$. Then
$A_{1},A_{2}\in {\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$. Then  $i$ is a monomorphism and
$i$ is a monomorphism and  $\operatorname{Coker}i\in {\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$.
$\operatorname{Coker}i\in {\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$.
Proof. This follows from [Reference Kvamme28, Proposition 4.1.5] and [Reference Kvamme28, Lemma 4.1.6].
Definition 18. [Reference Kvamme28, Definition 4.2.1]
Assume ![]() $\unicode[STIX]{x1D708}$ is a Nakayama functor relative to the adjunction
$\unicode[STIX]{x1D708}$ is a Nakayama functor relative to the adjunction ![]() $f_{!}\dashv f^{\ast }:{\mathcal{D}}\rightarrow {\mathcal{A}}$. We say that
$f_{!}\dashv f^{\ast }:{\mathcal{D}}\rightarrow {\mathcal{A}}$. We say that ![]() $P$ is Iwanaga–Gorenstein if there exists an integer
$P$ is Iwanaga–Gorenstein if there exists an integer ![]() $n\geqslant 0$ such that
$n\geqslant 0$ such that ![]() $L_{i}\unicode[STIX]{x1D708}=0$ and
$L_{i}\unicode[STIX]{x1D708}=0$ and ![]() $R^{i}\unicode[STIX]{x1D708}^{-}=0$ for all
$R^{i}\unicode[STIX]{x1D708}^{-}=0$ for all ![]() $i>n$.
$i>n$.
Theorem 19. [Reference Kvamme28, Theorem 4.2.6]
Assume ![]() $\unicode[STIX]{x1D708}$ is a Nakayama functor relative to the adjunction
$\unicode[STIX]{x1D708}$ is a Nakayama functor relative to the adjunction ![]() $f_{!}\dashv f^{\ast }:{\mathcal{D}}\rightarrow {\mathcal{A}}$, and that
$f_{!}\dashv f^{\ast }:{\mathcal{D}}\rightarrow {\mathcal{A}}$, and that ![]() $P$ is Iwanaga–Gorenstein. Then the following numbers coincide:
$P$ is Iwanaga–Gorenstein. Then the following numbers coincide:
(i)
 $\dim _{{\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})}({\mathcal{A}})$;
$\dim _{{\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})}({\mathcal{A}})$;(ii) The smallest integer
 $r$ such that
$r$ such that  $L_{i}\unicode[STIX]{x1D708}=0$ for all
$L_{i}\unicode[STIX]{x1D708}=0$ for all  $i>r$;
$i>r$;(iii) The smallest integer
 $s$ such that
$s$ such that  $R^{i}\unicode[STIX]{x1D708}^{-}=0$ for all
$R^{i}\unicode[STIX]{x1D708}^{-}=0$ for all  $i>s$.
$i>s$.
If this common number is ![]() $n$ we say that
$n$ we say that ![]() $P$ is
$P$ is ![]() $n$-Gorenstein. We also say that
$n$-Gorenstein. We also say that ![]() $n$ is the Gorenstein dimension of
$n$ is the Gorenstein dimension of ![]() $P$.
$P$.
The following theorem is useful for computing examples.
Theorem 20. Assume ![]() $\unicode[STIX]{x1D708}$ is a Nakayama functor relative to the adjunction
$\unicode[STIX]{x1D708}$ is a Nakayama functor relative to the adjunction ![]() $f_{!}\dashv f^{\ast }:{\mathcal{D}}\rightarrow {\mathcal{A}}$. The following holds:
$f_{!}\dashv f^{\ast }:{\mathcal{D}}\rightarrow {\mathcal{A}}$. The following holds:
(i)
 $A\in {\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$ if and only if
$A\in {\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$ if and only if(a)
 $L_{i}\unicode[STIX]{x1D708}(A)=0$ for all
$L_{i}\unicode[STIX]{x1D708}(A)=0$ for all  $i>0$;
$i>0$;(b)
 $R^{i}\unicode[STIX]{x1D708}^{-}(\unicode[STIX]{x1D708}(A))=0$ for all
$R^{i}\unicode[STIX]{x1D708}^{-}(\unicode[STIX]{x1D708}(A))=0$ for all  $i>0$;
$i>0$;(c)
 $\unicode[STIX]{x1D706}_{A}:A\rightarrow \unicode[STIX]{x1D708}^{-}\unicode[STIX]{x1D708}(A)$ is an isomorphism.
$\unicode[STIX]{x1D706}_{A}:A\rightarrow \unicode[STIX]{x1D708}^{-}\unicode[STIX]{x1D708}(A)$ is an isomorphism.
(ii) If
 $P$ is Iwanaga–Gorenstein, then
$P$ is Iwanaga–Gorenstein, then  $$\begin{eqnarray}{\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})=\{A\in {\mathcal{A}}\mid L_{i}\unicode[STIX]{x1D708}(A)=0\text{ for all }i>0\}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})=\{A\in {\mathcal{A}}\mid L_{i}\unicode[STIX]{x1D708}(A)=0\text{ for all }i>0\}.\end{eqnarray}$$
Proof. This is [Reference Kvamme28, Proposition 4.1.3] and [Reference Kvamme28, Theorem 4.2.2].
Example 21. [Reference Kvamme28, Example 3.2.6]
Let ![]() $k$ be a commutative ring, and let
$k$ be a commutative ring, and let ![]() $\unicode[STIX]{x1D6EC}_{1}$ and
$\unicode[STIX]{x1D6EC}_{1}$ and ![]() $\unicode[STIX]{x1D6EC}_{2}$ be
$\unicode[STIX]{x1D6EC}_{2}$ be ![]() $k$-algebras. Consider the adjoint pair
$k$-algebras. Consider the adjoint pair ![]() $f_{!}\dashv f^{\ast }$ where
$f_{!}\dashv f^{\ast }$ where ![]() $f^{\ast }$ is the restriction functor
$f^{\ast }$ is the restriction functor
and ![]() $f_{!}:=\unicode[STIX]{x1D6EC}_{1}\otimes _{k}-:\unicode[STIX]{x1D6EC}_{2}\text{-}\!\operatorname{Mod}\rightarrow (\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{Mod}$. If
$f_{!}:=\unicode[STIX]{x1D6EC}_{1}\otimes _{k}-:\unicode[STIX]{x1D6EC}_{2}\text{-}\!\operatorname{Mod}\rightarrow (\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{Mod}$. If ![]() $\unicode[STIX]{x1D6EC}_{1}$ is finitely generated projective as a
$\unicode[STIX]{x1D6EC}_{1}$ is finitely generated projective as a ![]() $k$-module, then the functor
$k$-module, then the functor
is a Nakayama functor relative to ![]() $f_{!}\dashv f^{\ast }$.
$f_{!}\dashv f^{\ast }$.
Example 22. Assume ![]() $k$,
$k$, ![]() $\unicode[STIX]{x1D6EC}_{1}$ and
$\unicode[STIX]{x1D6EC}_{1}$ and ![]() $\unicode[STIX]{x1D6EC}_{2}$ are as in Example 21. If in addition
$\unicode[STIX]{x1D6EC}_{2}$ are as in Example 21. If in addition ![]() $\unicode[STIX]{x1D6EC}_{2}$ is left coherent, then the categories
$\unicode[STIX]{x1D6EC}_{2}$ is left coherent, then the categories ![]() $\unicode[STIX]{x1D6EC}_{2}\text{-}\!\operatorname{mod}$ and
$\unicode[STIX]{x1D6EC}_{2}\text{-}\!\operatorname{mod}$ and ![]() $(\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}$ of finitely presented left modules are abelian. In this case
$(\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}$ of finitely presented left modules are abelian. In this case ![]() $f^{\ast }$,
$f^{\ast }$, ![]() $f_{!}$ and
$f_{!}$ and ![]() $\unicode[STIX]{x1D708}$ restrict to functors
$\unicode[STIX]{x1D708}$ restrict to functors
 $$\begin{eqnarray}\displaystyle & & \displaystyle f^{\ast }:=\operatorname{res}_{\unicode[STIX]{x1D6EC}_{2}}^{\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2}}:(\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}\rightarrow \unicode[STIX]{x1D6EC}_{2}\text{-}\!\operatorname{mod}\nonumber\\ \displaystyle & & \displaystyle f_{!}:=\unicode[STIX]{x1D6EC}_{1}\otimes _{k}-:\unicode[STIX]{x1D6EC}_{2}\text{-}\!\operatorname{mod}\rightarrow (\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}\nonumber\\ \displaystyle & & \displaystyle \unicode[STIX]{x1D708}:=\operatorname{Hom}_{k}(\unicode[STIX]{x1D6EC}_{1},k)\otimes _{\unicode[STIX]{x1D6EC}_{1}}-:(\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}\rightarrow (\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}\!.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle f^{\ast }:=\operatorname{res}_{\unicode[STIX]{x1D6EC}_{2}}^{\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2}}:(\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}\rightarrow \unicode[STIX]{x1D6EC}_{2}\text{-}\!\operatorname{mod}\nonumber\\ \displaystyle & & \displaystyle f_{!}:=\unicode[STIX]{x1D6EC}_{1}\otimes _{k}-:\unicode[STIX]{x1D6EC}_{2}\text{-}\!\operatorname{mod}\rightarrow (\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}\nonumber\\ \displaystyle & & \displaystyle \unicode[STIX]{x1D708}:=\operatorname{Hom}_{k}(\unicode[STIX]{x1D6EC}_{1},k)\otimes _{\unicode[STIX]{x1D6EC}_{1}}-:(\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}\rightarrow (\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}\!.\nonumber\end{eqnarray}$$ and ![]() $\unicode[STIX]{x1D708}$ is still a Nakayama functor relative to
$\unicode[STIX]{x1D708}$ is still a Nakayama functor relative to ![]() $f_{!}\dashv f^{\ast }$ in this case.
$f_{!}\dashv f^{\ast }$ in this case.
3 Lifting Frobenius exact subcategories
In this section we fix abelian categories ![]() ${\mathcal{A}}$ and
${\mathcal{A}}$ and ![]() ${\mathcal{B}}$, a faithful functor
${\mathcal{B}}$, a faithful functor ![]() $f^{\ast }:{\mathcal{A}}\rightarrow {\mathcal{B}}$ with left adjoint
$f^{\ast }:{\mathcal{A}}\rightarrow {\mathcal{B}}$ with left adjoint ![]() $f_{!}:{\mathcal{B}}\rightarrow {\mathcal{A}}$, and we assume
$f_{!}:{\mathcal{B}}\rightarrow {\mathcal{A}}$, and we assume ![]() $f_{!}\dashv f^{\ast }$ has a Nakayama functor
$f_{!}\dashv f^{\ast }$ has a Nakayama functor ![]() $\unicode[STIX]{x1D708}:{\mathcal{A}}\rightarrow {\mathcal{A}}$. Our goal is to investigate when the subcategory
$\unicode[STIX]{x1D708}:{\mathcal{A}}\rightarrow {\mathcal{A}}$. Our goal is to investigate when the subcategory ![]() $(f^{\ast }\circ \unicode[STIX]{x1D708})^{-1}({\mathcal{G}}{\mathcal{P}}({\mathcal{B}}))\cap {\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$ is equal to
$(f^{\ast }\circ \unicode[STIX]{x1D708})^{-1}({\mathcal{G}}{\mathcal{P}}({\mathcal{B}}))\cap {\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$ is equal to ![]() ${\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$ if
${\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$ if ![]() ${\mathcal{A}}$ and
${\mathcal{A}}$ and ![]() ${\mathcal{B}}$ have enough projectives. In the first part we show that
${\mathcal{B}}$ have enough projectives. In the first part we show that ![]() $(f^{\ast }\circ \unicode[STIX]{x1D708})^{-1}({\mathcal{F}})\cap {\mathcal{X}}$ is an admissible subcategory of
$(f^{\ast }\circ \unicode[STIX]{x1D708})^{-1}({\mathcal{F}})\cap {\mathcal{X}}$ is an admissible subcategory of ![]() ${\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$ if
${\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$ if ![]() ${\mathcal{X}}$ is a
${\mathcal{X}}$ is a ![]() $P$-admissible subcategory of
$P$-admissible subcategory of ![]() ${\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$ and
${\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$ and ![]() ${\mathcal{F}}$ is an admissible subcategory of
${\mathcal{F}}$ is an admissible subcategory of ![]() ${\mathcal{G}}{\mathcal{P}}({\mathcal{B}})$.
${\mathcal{G}}{\mathcal{P}}({\mathcal{B}})$.
3.1  $P$-admissible subcategories of
$P$-admissible subcategories of  ${\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$
${\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$
Definition 23. A full subcategory ![]() ${\mathcal{X}}\subset {\mathcal{A}}$ is called a
${\mathcal{X}}\subset {\mathcal{A}}$ is called a ![]() $P$-admissible subcategory of
$P$-admissible subcategory of ![]() ${\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$ if it is closed under extensions, direct summands, and satisfies the following properties:
${\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$ if it is closed under extensions, direct summands, and satisfies the following properties:
(i)
 ${\mathcal{X}}$ contains all the
${\mathcal{X}}$ contains all the  $P$-projective objects of
$P$-projective objects of  ${\mathcal{A}}$;
${\mathcal{A}}$;(ii)
 $L_{1}\unicode[STIX]{x1D708}(X)=0$ for all
$L_{1}\unicode[STIX]{x1D708}(X)=0$ for all  $X\in {\mathcal{X}}$;
$X\in {\mathcal{X}}$;(iii) For all
 $X\in {\mathcal{X}}$ there exists a short exact sequence
$X\in {\mathcal{X}}$ there exists a short exact sequence  $0\rightarrow X^{\prime }\xrightarrow[{}]{}A\xrightarrow[{}]{}X\rightarrow 0$ with
$0\rightarrow X^{\prime }\xrightarrow[{}]{}A\xrightarrow[{}]{}X\rightarrow 0$ with  $A$ being
$A$ being  $P$-projective and
$P$-projective and  $X^{\prime }\in {\mathcal{X}}$;
$X^{\prime }\in {\mathcal{X}}$;(iv) For all
 $X\in {\mathcal{X}}$ there exists a short exact sequence
$X\in {\mathcal{X}}$ there exists a short exact sequence  $0\rightarrow X\xrightarrow[{}]{}A\xrightarrow[{}]{}X^{\prime }\rightarrow 0$ with
$0\rightarrow X\xrightarrow[{}]{}A\xrightarrow[{}]{}X^{\prime }\rightarrow 0$ with  $A$ being
$A$ being  $P$-projective and
$P$-projective and  $X^{\prime }\in {\mathcal{X}}$.
$X^{\prime }\in {\mathcal{X}}$.
The following result is immediate from the definition.
Proposition 24. The following hold:
(i)
 ${\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$ is a
${\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$ is a  $P$-admissible subcategory of
$P$-admissible subcategory of  ${\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$;
${\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$;(ii) Assume
 ${\mathcal{X}}$ is a
${\mathcal{X}}$ is a  $P$-admissible subcategory of
$P$-admissible subcategory of  ${\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$. Then
${\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$. Then  ${\mathcal{X}}\subset {\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$.
${\mathcal{X}}\subset {\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$.
Example 25. Let ![]() $\unicode[STIX]{x1D6EC}$ be a finite-dimensional algebra over a field
$\unicode[STIX]{x1D6EC}$ be a finite-dimensional algebra over a field ![]() $k$. Furthermore, let
$k$. Furthermore, let ![]() $g^{\ast }:\unicode[STIX]{x1D6EC}\text{-}\!\operatorname{Mod}\rightarrow k\text{-}\!\operatorname{Mod}$ be the restriction functor and
$g^{\ast }:\unicode[STIX]{x1D6EC}\text{-}\!\operatorname{Mod}\rightarrow k\text{-}\!\operatorname{Mod}$ be the restriction functor and ![]() $g_{!}=\unicode[STIX]{x1D6EC}\otimes _{k}-:k\text{-}\!\operatorname{Mod}\rightarrow \unicode[STIX]{x1D6EC}\text{-}\!\operatorname{Mod}$ its left adjoint. As stated in Example 21, the adjoint pair
$g_{!}=\unicode[STIX]{x1D6EC}\otimes _{k}-:k\text{-}\!\operatorname{Mod}\rightarrow \unicode[STIX]{x1D6EC}\text{-}\!\operatorname{Mod}$ its left adjoint. As stated in Example 21, the adjoint pair ![]() $g_{!}\dashv g^{\ast }$ has Nakayama functor
$g_{!}\dashv g^{\ast }$ has Nakayama functor
In this case the ![]() $P^{\prime }$-projective objects are just the projective
$P^{\prime }$-projective objects are just the projective ![]() $\unicode[STIX]{x1D6EC}$-modules, where
$\unicode[STIX]{x1D6EC}$-modules, where ![]() $P^{\prime }:=g_{!}\circ g^{\ast }$. Also,
$P^{\prime }:=g_{!}\circ g^{\ast }$. Also, ![]() $L_{1}\unicode[STIX]{x1D708}^{\prime }(M)=\operatorname{Tor}_{1}^{\unicode[STIX]{x1D6EC}}(\operatorname{Hom}_{k}(\unicode[STIX]{x1D6EC},k),M)=0$ if and only if
$L_{1}\unicode[STIX]{x1D708}^{\prime }(M)=\operatorname{Tor}_{1}^{\unicode[STIX]{x1D6EC}}(\operatorname{Hom}_{k}(\unicode[STIX]{x1D6EC},k),M)=0$ if and only if
In this case ![]() $\operatorname{Ext}_{\unicode[STIX]{x1D6EC}}^{1}(M,\prod \unicode[STIX]{x1D6EC})\cong \prod \operatorname{Ext}_{\unicode[STIX]{x1D6EC}}^{1}(M,\unicode[STIX]{x1D6EC})=0$. Since any projective
$\operatorname{Ext}_{\unicode[STIX]{x1D6EC}}^{1}(M,\prod \unicode[STIX]{x1D6EC})\cong \prod \operatorname{Ext}_{\unicode[STIX]{x1D6EC}}^{1}(M,\unicode[STIX]{x1D6EC})=0$. Since any projective ![]() $\unicode[STIX]{x1D6EC}$-module is a direct summand of a product
$\unicode[STIX]{x1D6EC}$-module is a direct summand of a product ![]() $\prod \unicode[STIX]{x1D6EC}$ when
$\prod \unicode[STIX]{x1D6EC}$ when ![]() $\unicode[STIX]{x1D6EC}$ is finite-dimensional, it follows that
$\unicode[STIX]{x1D6EC}$ is finite-dimensional, it follows that ![]() $L_{1}\unicode[STIX]{x1D708}^{\prime }(M)=0$ if and only if
$L_{1}\unicode[STIX]{x1D708}^{\prime }(M)=0$ if and only if ![]() $\operatorname{Ext}_{\unicode[STIX]{x1D6EC}}^{1}(M,Q)=0$ for any
$\operatorname{Ext}_{\unicode[STIX]{x1D6EC}}^{1}(M,Q)=0$ for any ![]() $Q\in \operatorname{Proj}(\unicode[STIX]{x1D6EC}\text{-}\!\operatorname{Mod})$. Hence, the
$Q\in \operatorname{Proj}(\unicode[STIX]{x1D6EC}\text{-}\!\operatorname{Mod})$. Hence, the ![]() $P^{\prime }$-admissible subcategories of
$P^{\prime }$-admissible subcategories of ![]() ${\mathcal{G}}{\mathcal{P}}_{P^{\prime }}(\unicode[STIX]{x1D6EC}\text{-}\!\operatorname{Mod})$ are precisely the admissible subcategories of
${\mathcal{G}}{\mathcal{P}}_{P^{\prime }}(\unicode[STIX]{x1D6EC}\text{-}\!\operatorname{Mod})$ are precisely the admissible subcategories of ![]() ${\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}\text{-}\!\operatorname{Mod})$. In particular, it follows that
${\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}\text{-}\!\operatorname{Mod})$. In particular, it follows that
In the following we consider the adjunctions
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D719}^{f^{\ast }\circ \unicode[STIX]{x1D708}\dashv f_{!}}:{\mathcal{B}}(f^{\ast }\unicode[STIX]{x1D708}(A),B)\xrightarrow[{}]{\cong }{\mathcal{A}}(A,f_{!}(B))\nonumber\\ \displaystyle & & \displaystyle \unicode[STIX]{x1D719}^{f_{!}\dashv f^{\ast }}:{\mathcal{A}}(f_{!}(B),A)\xrightarrow[{}]{\cong }{\mathcal{B}}(B,f^{\ast }(A))\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D719}^{f^{\ast }\circ \unicode[STIX]{x1D708}\dashv f_{!}}:{\mathcal{B}}(f^{\ast }\unicode[STIX]{x1D708}(A),B)\xrightarrow[{}]{\cong }{\mathcal{A}}(A,f_{!}(B))\nonumber\\ \displaystyle & & \displaystyle \unicode[STIX]{x1D719}^{f_{!}\dashv f^{\ast }}:{\mathcal{A}}(f_{!}(B),A)\xrightarrow[{}]{\cong }{\mathcal{B}}(B,f^{\ast }(A))\nonumber\end{eqnarray}$$with units and counits
Since ![]() $f^{\ast }$ is faithful, it follows that
$f^{\ast }$ is faithful, it follows that ![]() $\unicode[STIX]{x1D6FD}^{f_{!}\dashv f^{\ast }}$ is an epimorphism.
$\unicode[STIX]{x1D6FD}^{f_{!}\dashv f^{\ast }}$ is an epimorphism.
Lemma 26. Let ![]() ${\mathcal{X}}$ be a
${\mathcal{X}}$ be a ![]() $P$-admissible subcategory of
$P$-admissible subcategory of ![]() ${\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$, and let
${\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$, and let ![]() $X\in {\mathcal{X}}$. The following holds:
$X\in {\mathcal{X}}$. The following holds:
(i)
 $\unicode[STIX]{x1D6FC}_{X}^{f^{\ast }\circ \unicode[STIX]{x1D708}\dashv f_{!}}$ is a monomorphism and
$\unicode[STIX]{x1D6FC}_{X}^{f^{\ast }\circ \unicode[STIX]{x1D708}\dashv f_{!}}$ is a monomorphism and  $\operatorname{Coker}\unicode[STIX]{x1D6FC}_{X}^{f^{\ast }\circ \unicode[STIX]{x1D708}\dashv f_{!}}\in {\mathcal{X}}$;
$\operatorname{Coker}\unicode[STIX]{x1D6FC}_{X}^{f^{\ast }\circ \unicode[STIX]{x1D708}\dashv f_{!}}\in {\mathcal{X}}$;(ii)
 $\operatorname{Ker}\unicode[STIX]{x1D6FD}_{X}^{f_{!}\dashv f^{\ast }}\in {\mathcal{X}}$.
$\operatorname{Ker}\unicode[STIX]{x1D6FD}_{X}^{f_{!}\dashv f^{\ast }}\in {\mathcal{X}}$.
Proof. We prove (i). Since ![]() $X\in {\mathcal{X}}$ there exists an exact sequence
$X\in {\mathcal{X}}$ there exists an exact sequence ![]() $0\rightarrow X\xrightarrow[{}]{i}f_{!}(B)\xrightarrow[{}]{}X^{\prime }\rightarrow 0$ with
$0\rightarrow X\xrightarrow[{}]{i}f_{!}(B)\xrightarrow[{}]{}X^{\prime }\rightarrow 0$ with ![]() $X^{\prime }\in {\mathcal{X}}$ and
$X^{\prime }\in {\mathcal{X}}$ and ![]() $B\in {\mathcal{B}}$. Since
$B\in {\mathcal{B}}$. Since ![]() $i=f_{!}((\unicode[STIX]{x1D719}^{f^{\ast }\circ \unicode[STIX]{x1D708}\dashv f_{!}})^{-1}(i))\circ \unicode[STIX]{x1D6FC}_{X}^{f^{\ast }\circ \unicode[STIX]{x1D708}\dashv f_{!}}$, it follows that
$i=f_{!}((\unicode[STIX]{x1D719}^{f^{\ast }\circ \unicode[STIX]{x1D708}\dashv f_{!}})^{-1}(i))\circ \unicode[STIX]{x1D6FC}_{X}^{f^{\ast }\circ \unicode[STIX]{x1D708}\dashv f_{!}}$, it follows that ![]() $\unicode[STIX]{x1D6FC}_{X}^{f^{\ast }\circ \unicode[STIX]{x1D708}\dashv f_{!}}$ is a monomorphism. We therefore have a commutative diagram
$\unicode[STIX]{x1D6FC}_{X}^{f^{\ast }\circ \unicode[STIX]{x1D708}\dashv f_{!}}$ is a monomorphism. We therefore have a commutative diagram

where the rows are short exact sequences. By the dual of [Reference Popescu34, Lemma 5.2] it follows that the right square is a pushforward and a pullback square. Hence we get a short exact sequence
Since ![]() ${\mathcal{X}}$ is closed under extensions and direct summands, it follows that
${\mathcal{X}}$ is closed under extensions and direct summands, it follows that ![]() $\operatorname{Coker}\unicode[STIX]{x1D6FC}_{X}^{f^{\ast }\circ \unicode[STIX]{x1D708}\dashv f_{!}}\in {\mathcal{X}}$.
$\operatorname{Coker}\unicode[STIX]{x1D6FC}_{X}^{f^{\ast }\circ \unicode[STIX]{x1D708}\dashv f_{!}}\in {\mathcal{X}}$.
For (ii), choose an exact sequence ![]() $0\rightarrow X^{\prime \prime }\xrightarrow[{}]{}f_{!}(B^{\prime })\xrightarrow[{}]{p}X\rightarrow 0$ with
$0\rightarrow X^{\prime \prime }\xrightarrow[{}]{}f_{!}(B^{\prime })\xrightarrow[{}]{p}X\rightarrow 0$ with ![]() $X^{\prime \prime }\in {\mathcal{X}}$ and
$X^{\prime \prime }\in {\mathcal{X}}$ and ![]() $B^{\prime }\in {\mathcal{B}}$. We then get a commutative diagram
$B^{\prime }\in {\mathcal{B}}$. We then get a commutative diagram

where the rows are short exact sequences. The left square is a pushforward and a pullback square, and therefore gives rise to an exact sequence
Since ![]() ${\mathcal{X}}$ is closed under extensions and direct summands, it follows that
${\mathcal{X}}$ is closed under extensions and direct summands, it follows that ![]() $\operatorname{Ker}\unicode[STIX]{x1D6FD}_{X}^{f_{!}\dashv f^{\ast }}\in {\mathcal{X}}$.
$\operatorname{Ker}\unicode[STIX]{x1D6FD}_{X}^{f_{!}\dashv f^{\ast }}\in {\mathcal{X}}$.
Lemma 27. Let ![]() ${\mathcal{X}}$ be a
${\mathcal{X}}$ be a ![]() $P$-admissible subcategory of
$P$-admissible subcategory of ![]() ${\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$. The following holds:
${\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$. The following holds:
(i) Let
 $s:X\rightarrow f_{!}(B)$ be a morphism in
$s:X\rightarrow f_{!}(B)$ be a morphism in  ${\mathcal{A}}$ with
${\mathcal{A}}$ with  $X\in {\mathcal{X}}$ and
$X\in {\mathcal{X}}$ and  $B\in {\mathcal{B}}$. Assume
$B\in {\mathcal{B}}$. Assume  $(\unicode[STIX]{x1D719}^{f^{\ast }\circ \unicode[STIX]{x1D708}\dashv f_{!}})^{-1}(s):f^{\ast }\unicode[STIX]{x1D708}(X)\rightarrow B$ is a monomorphism. Then
$(\unicode[STIX]{x1D719}^{f^{\ast }\circ \unicode[STIX]{x1D708}\dashv f_{!}})^{-1}(s):f^{\ast }\unicode[STIX]{x1D708}(X)\rightarrow B$ is a monomorphism. Then  $s$ is a monomorphism and
$s$ is a monomorphism and  $\operatorname{Coker}s\in {\mathcal{X}}$;
$\operatorname{Coker}s\in {\mathcal{X}}$;(ii) Let
 $s^{\prime }:f_{!}(B)\rightarrow X$ be a morphism in
$s^{\prime }:f_{!}(B)\rightarrow X$ be a morphism in  ${\mathcal{A}}$ with
${\mathcal{A}}$ with  $X\in {\mathcal{X}}$ and
$X\in {\mathcal{X}}$ and  $B\in {\mathcal{B}}$. Assume that
$B\in {\mathcal{B}}$. Assume that  $\unicode[STIX]{x1D719}^{f_{!}\dashv f^{\ast }}(s^{\prime }):B\rightarrow f^{\ast }(X)$ is an epimorphism. Then
$\unicode[STIX]{x1D719}^{f_{!}\dashv f^{\ast }}(s^{\prime }):B\rightarrow f^{\ast }(X)$ is an epimorphism. Then  $s^{\prime }$ is an epimorphism and
$s^{\prime }$ is an epimorphism and  $\operatorname{Ker}s^{\prime }\in {\mathcal{X}}$.
$\operatorname{Ker}s^{\prime }\in {\mathcal{X}}$.
Proof. We only prove part (i), part (ii) is proved dually. Consider the commutative diagram

where ![]() $t$ is induced from the commutativity of the left square. Since
$t$ is induced from the commutativity of the left square. Since ![]() $\unicode[STIX]{x1D6FC}_{X}^{f^{\ast }\circ \unicode[STIX]{x1D708}\dashv f_{!}}$ is a monomorphism by Lemma 26, we get that
$\unicode[STIX]{x1D6FC}_{X}^{f^{\ast }\circ \unicode[STIX]{x1D708}\dashv f_{!}}$ is a monomorphism by Lemma 26, we get that ![]() $s$ is a monomorphism. Hence, the upper and lower rows are short exact sequences. Therefore, by the snake lemma
$s$ is a monomorphism. Hence, the upper and lower rows are short exact sequences. Therefore, by the snake lemma ![]() $t$ is a monomorphism and
$t$ is a monomorphism and
Hence, we get an exact sequence
Since ![]() ${\mathcal{X}}$ is closed under extensions,
${\mathcal{X}}$ is closed under extensions, ![]() $f_{!}(\operatorname{Coker}(\unicode[STIX]{x1D719}^{f^{\ast }\circ \unicode[STIX]{x1D708}\dashv f_{!}})^{-1}(s))$ is
$f_{!}(\operatorname{Coker}(\unicode[STIX]{x1D719}^{f^{\ast }\circ \unicode[STIX]{x1D708}\dashv f_{!}})^{-1}(s))$ is ![]() $P$-projective, and
$P$-projective, and ![]() $\operatorname{Coker}\unicode[STIX]{x1D6FC}_{X}^{f^{\ast }\circ \unicode[STIX]{x1D708}\dashv f_{!}}\in {\mathcal{X}}$ by Lemma 26, we get that
$\operatorname{Coker}\unicode[STIX]{x1D6FC}_{X}^{f^{\ast }\circ \unicode[STIX]{x1D708}\dashv f_{!}}\in {\mathcal{X}}$ by Lemma 26, we get that ![]() $\operatorname{Coker}s\in {\mathcal{X}}$.
$\operatorname{Coker}s\in {\mathcal{X}}$.
Example 28. Let ![]() $k$ be a field, let
$k$ be a field, let ![]() $\unicode[STIX]{x1D6EC}_{1}$ be a finite-dimensional
$\unicode[STIX]{x1D6EC}_{1}$ be a finite-dimensional ![]() $k$-algebra, and let
$k$-algebra, and let ![]() $\unicode[STIX]{x1D6EC}_{2}$ be a
$\unicode[STIX]{x1D6EC}_{2}$ be a ![]() $k$-algebra which is left coherent. Let
$k$-algebra which is left coherent. Let ![]() $f_{!}\dashv f^{\ast }$ be the adjoint pair with Nakayama functor
$f_{!}\dashv f^{\ast }$ be the adjoint pair with Nakayama functor ![]() $\unicode[STIX]{x1D708}$ as in Example 22. Let
$\unicode[STIX]{x1D708}$ as in Example 22. Let ![]() ${\mathcal{F}}\subset {\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod})$ be an admissible subcategory. We claim that the category
${\mathcal{F}}\subset {\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod})$ be an admissible subcategory. We claim that the category
is a ![]() $P$-admissible subcategory of
$P$-admissible subcategory of ![]() ${\mathcal{G}}{\mathcal{P}}_{P}((\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod})$, where
${\mathcal{G}}{\mathcal{P}}_{P}((\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod})$, where ![]() $P:=f_{!}\circ f^{\ast }$: Indeed, the
$P:=f_{!}\circ f^{\ast }$: Indeed, the ![]() $P$-projective objects are summands of modules of the form
$P$-projective objects are summands of modules of the form ![]() $\unicode[STIX]{x1D6EC}_{1}\otimes _{k}M$. Since they are projective when restricted to
$\unicode[STIX]{x1D6EC}_{1}\otimes _{k}M$. Since they are projective when restricted to ![]() $\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod}$, they are contained in
$\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod}$, they are contained in ![]() ${\mathcal{X}}$, which shows (i). Furthermore, for
${\mathcal{X}}$, which shows (i). Furthermore, for ![]() $M\in {\mathcal{X}}$ we have
$M\in {\mathcal{X}}$ we have ![]() $L_{1}\unicode[STIX]{x1D708}(M)=\operatorname{Tor}_{1}^{\unicode[STIX]{x1D6EC}_{1}}(\operatorname{Hom}_{k}(\unicode[STIX]{x1D6EC}_{1},k),M)$, and this is
$L_{1}\unicode[STIX]{x1D708}(M)=\operatorname{Tor}_{1}^{\unicode[STIX]{x1D6EC}_{1}}(\operatorname{Hom}_{k}(\unicode[STIX]{x1D6EC}_{1},k),M)$, and this is ![]() $0$ since
$0$ since ![]() $_{\unicode[STIX]{x1D6EC}_{1}}M\in {\mathcal{F}}\subset {\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod})$ and
$_{\unicode[STIX]{x1D6EC}_{1}}M\in {\mathcal{F}}\subset {\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod})$ and ![]() $\operatorname{Hom}_{k}(\operatorname{Tor}_{1}^{\unicode[STIX]{x1D6EC}_{1}}(\operatorname{Hom}_{k}(\unicode[STIX]{x1D6EC}_{1},k),M),k)\cong \operatorname{Ext}_{\unicode[STIX]{x1D6EC}_{1}}^{1}(M,\unicode[STIX]{x1D6EC}_{1})$. This shows (ii). Also,
$\operatorname{Hom}_{k}(\operatorname{Tor}_{1}^{\unicode[STIX]{x1D6EC}_{1}}(\operatorname{Hom}_{k}(\unicode[STIX]{x1D6EC}_{1},k),M),k)\cong \operatorname{Ext}_{\unicode[STIX]{x1D6EC}_{1}}^{1}(M,\unicode[STIX]{x1D6EC}_{1})$. This shows (ii). Also, ![]() ${\mathcal{X}}$ is closed under kernels of epimorphisms by Lemma 11, and hence it satisfies (iii). It only remains to show (iv): By Example 25 we know that
${\mathcal{X}}$ is closed under kernels of epimorphisms by Lemma 11, and hence it satisfies (iii). It only remains to show (iv): By Example 25 we know that ![]() ${\mathcal{F}}$ is a
${\mathcal{F}}$ is a ![]() $P^{\prime }$-admissible subcategory of
$P^{\prime }$-admissible subcategory of ![]() ${\mathcal{G}}{\mathcal{P}}_{P^{\prime }}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod})$, where
${\mathcal{G}}{\mathcal{P}}_{P^{\prime }}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod})$, where ![]() $P^{\prime }=g_{!}\circ g^{\ast }$ and
$P^{\prime }=g_{!}\circ g^{\ast }$ and ![]() $g^{\ast }:\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod}\rightarrow k\text{-}\!\operatorname{Mod}$ is the restriction with left adjoint
$g^{\ast }:\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod}\rightarrow k\text{-}\!\operatorname{Mod}$ is the restriction with left adjoint ![]() $g_{!}=\unicode[STIX]{x1D6EC}_{1}\otimes _{k}-:k\text{-}\!\operatorname{Mod}\rightarrow \unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod}$. Consider the exact sequence
$g_{!}=\unicode[STIX]{x1D6EC}_{1}\otimes _{k}-:k\text{-}\!\operatorname{Mod}\rightarrow \unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod}$. Consider the exact sequence
of ![]() $\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2}$-modules. Restricting to
$\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2}$-modules. Restricting to ![]() $\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod}$ gives the exact sequence
$\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod}$ gives the exact sequence
It follows from Lemma 26 that ![]() $\operatorname{Coker}\unicode[STIX]{x1D6FC}_{_{\unicode[STIX]{x1D6EC}_{1}}M}^{g^{\ast }\circ \unicode[STIX]{x1D708}^{\prime }\dashv g_{!}}\in {\mathcal{F}}$. Therefore, we have that
$\operatorname{Coker}\unicode[STIX]{x1D6FC}_{_{\unicode[STIX]{x1D6EC}_{1}}M}^{g^{\ast }\circ \unicode[STIX]{x1D708}^{\prime }\dashv g_{!}}\in {\mathcal{F}}$. Therefore, we have that ![]() $\operatorname{Coker}\unicode[STIX]{x1D6FC}_{M}^{f^{\ast }\circ \unicode[STIX]{x1D708}\dashv f_{!}}\in {\mathcal{X}}$. This implies that
$\operatorname{Coker}\unicode[STIX]{x1D6FC}_{M}^{f^{\ast }\circ \unicode[STIX]{x1D708}\dashv f_{!}}\in {\mathcal{X}}$. This implies that ![]() ${\mathcal{X}}$ satisfies (iv), which proves the claim. In particular,
${\mathcal{X}}$ satisfies (iv), which proves the claim. In particular, ![]() ${\mathcal{X}}$ is a
${\mathcal{X}}$ is a ![]() $P$-admissible subcategory of
$P$-admissible subcategory of ![]() ${\mathcal{G}}{\mathcal{P}}_{P}((\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod})$ when
${\mathcal{G}}{\mathcal{P}}_{P}((\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod})$ when ![]() ${\mathcal{F}}={\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod})$ or
${\mathcal{F}}={\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod})$ or ![]() ${\mathcal{F}}=\operatorname{Proj}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod})$.
${\mathcal{F}}=\operatorname{Proj}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod})$.
Now assume ![]() ${\mathcal{F}}={\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod})$. We claim that the equality
${\mathcal{F}}={\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod})$. We claim that the equality ![]() ${\mathcal{X}}={\mathcal{G}}{\mathcal{P}}_{P}((\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod})$ holds. By the argument above we know that
${\mathcal{X}}={\mathcal{G}}{\mathcal{P}}_{P}((\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod})$ holds. By the argument above we know that ![]() ${\mathcal{X}}\subset {\mathcal{G}}{\mathcal{P}}_{P}((\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod})$, so we only need to show the other inclusion. Assume
${\mathcal{X}}\subset {\mathcal{G}}{\mathcal{P}}_{P}((\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod})$, so we only need to show the other inclusion. Assume ![]() $M\in {\mathcal{G}}{\mathcal{P}}_{P}((\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod})$, and let
$M\in {\mathcal{G}}{\mathcal{P}}_{P}((\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod})$, and let ![]() $A_{\bullet }$ be an exact sequence in
$A_{\bullet }$ be an exact sequence in ![]() $(\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}$ with
$(\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}$ with ![]() $Z_{0}(A_{\bullet })=M$ as in Definition 16. Note that the components of
$Z_{0}(A_{\bullet })=M$ as in Definition 16. Note that the components of ![]() $_{\unicode[STIX]{x1D6EC}_{1}}A_{\bullet }$ are projective
$_{\unicode[STIX]{x1D6EC}_{1}}A_{\bullet }$ are projective ![]() $\unicode[STIX]{x1D6EC}_{1}$-modules. Furthermore, since the sequence
$\unicode[STIX]{x1D6EC}_{1}$-modules. Furthermore, since the sequence ![]() $\unicode[STIX]{x1D708}(A_{\bullet })$ is exact, the sequence
$\unicode[STIX]{x1D708}(A_{\bullet })$ is exact, the sequence
is exact. Since any projective ![]() $\unicode[STIX]{x1D6EC}_{1}$-module is a summand of a product of
$\unicode[STIX]{x1D6EC}_{1}$-module is a summand of a product of ![]() $\unicode[STIX]{x1D6EC}_{1}$, and
$\unicode[STIX]{x1D6EC}_{1}$, and ![]() $\operatorname{Hom}_{\unicode[STIX]{x1D6EC}_{1}}(A_{\bullet },\prod \unicode[STIX]{x1D6EC}_{1})\cong \prod \operatorname{Hom}_{\unicode[STIX]{x1D6EC}_{1}}(A_{\bullet },\unicode[STIX]{x1D6EC}_{1})$ is exact, it follows that
$\operatorname{Hom}_{\unicode[STIX]{x1D6EC}_{1}}(A_{\bullet },\prod \unicode[STIX]{x1D6EC}_{1})\cong \prod \operatorname{Hom}_{\unicode[STIX]{x1D6EC}_{1}}(A_{\bullet },\unicode[STIX]{x1D6EC}_{1})$ is exact, it follows that ![]() $_{\unicode[STIX]{x1D6EC}_{1}}A_{\bullet }$ is a totally acyclic complex of
$_{\unicode[STIX]{x1D6EC}_{1}}A_{\bullet }$ is a totally acyclic complex of ![]() $\unicode[STIX]{x1D6EC}_{1}$-modules. This shows that
$\unicode[STIX]{x1D6EC}_{1}$-modules. This shows that ![]() $_{\unicode[STIX]{x1D6EC}_{1}}M\in {\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod})$, and the claim follows.
$_{\unicode[STIX]{x1D6EC}_{1}}M\in {\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod})$, and the claim follows.
Example 29. Let ![]() $k$ be a field, let
$k$ be a field, let ![]() $\unicode[STIX]{x1D6EC}_{1}$ be a finite-dimensional
$\unicode[STIX]{x1D6EC}_{1}$ be a finite-dimensional ![]() $k$-algebra, and let
$k$-algebra, and let ![]() $\unicode[STIX]{x1D6EC}_{2}$ be a
$\unicode[STIX]{x1D6EC}_{2}$ be a ![]() $k$-algebra. Let
$k$-algebra. Let ![]() $f_{!}\dashv f^{\ast }$ be the adjoint pair with Nakayama functor
$f_{!}\dashv f^{\ast }$ be the adjoint pair with Nakayama functor ![]() $\unicode[STIX]{x1D708}$ as in Example 21. By a similar argument as in Example 28 we get that if
$\unicode[STIX]{x1D708}$ as in Example 21. By a similar argument as in Example 28 we get that if ![]() ${\mathcal{F}}\subset \unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod}$ is an admissible subcategory of
${\mathcal{F}}\subset \unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod}$ is an admissible subcategory of ![]() ${\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod})$, then
${\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod})$, then
is a ![]() $P$-admissible subcategory of
$P$-admissible subcategory of ![]() ${\mathcal{G}}{\mathcal{P}}_{P}((\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{Mod})$, where
${\mathcal{G}}{\mathcal{P}}_{P}((\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{Mod})$, where ![]() $P=f_{!}\circ f^{\ast }$. Also, we get that
$P=f_{!}\circ f^{\ast }$. Also, we get that
3.2 Lifting admissible subcategories
Note that ![]() $f_{!}$ preserves projective objects since it has an exact right adjoint. In fact, we have the following result.
$f_{!}$ preserves projective objects since it has an exact right adjoint. In fact, we have the following result.
Lemma 30. Assume ![]() ${\mathcal{B}}$ has enough projectives. Then the full subcategory
${\mathcal{B}}$ has enough projectives. Then the full subcategory
is generating in ![]() ${\mathcal{A}}$. In particular,
${\mathcal{A}}$. In particular, ![]() ${\mathcal{A}}$ has enough projectives.
${\mathcal{A}}$ has enough projectives.
Proof. For ![]() $A\in {\mathcal{A}}$ choose an epimorphism
$A\in {\mathcal{A}}$ choose an epimorphism ![]() $Q\xrightarrow[{}]{p}f^{\ast }(A)$ in
$Q\xrightarrow[{}]{p}f^{\ast }(A)$ in ![]() ${\mathcal{B}}$ with
${\mathcal{B}}$ with ![]() $Q$ projective. The composition
$Q$ projective. The composition ![]() $f_{!}(Q)\xrightarrow[{}]{f_{!}(p)}f_{!}f^{\ast }(A)\xrightarrow[{}]{\unicode[STIX]{x1D6FD}_{A}^{f_{!}\dashv f^{\ast }}}A$ is then an epimorphism in
$f_{!}(Q)\xrightarrow[{}]{f_{!}(p)}f_{!}f^{\ast }(A)\xrightarrow[{}]{\unicode[STIX]{x1D6FD}_{A}^{f_{!}\dashv f^{\ast }}}A$ is then an epimorphism in ![]() ${\mathcal{A}}$. This proves the claim.
${\mathcal{A}}$. This proves the claim.
For the remainder of this section we assume ![]() ${\mathcal{B}}$ has enough projective objects. Furthermore, we fix a
${\mathcal{B}}$ has enough projective objects. Furthermore, we fix a ![]() $P$-admissible subcategory
$P$-admissible subcategory ![]() ${\mathcal{X}}$ of
${\mathcal{X}}$ of ![]() ${\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$ and an admissible subcategory
${\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$ and an admissible subcategory ![]() ${\mathcal{F}}$ of
${\mathcal{F}}$ of ![]() ${\mathcal{G}}{\mathcal{P}}({\mathcal{B}})$. Let
${\mathcal{G}}{\mathcal{P}}({\mathcal{B}})$. Let
Our goal is to show that ![]() $(f^{\ast }\circ \unicode[STIX]{x1D708})^{-1}({\mathcal{F}})\cap {\mathcal{X}}$ is an admissible subcategory of
$(f^{\ast }\circ \unicode[STIX]{x1D708})^{-1}({\mathcal{F}})\cap {\mathcal{X}}$ is an admissible subcategory of ![]() ${\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$.
${\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$.
Lemma 31. The category ![]() $(f^{\ast }\circ \unicode[STIX]{x1D708})^{-1}({\mathcal{F}})\cap {\mathcal{X}}$ is closed under extensions and direct summands in
$(f^{\ast }\circ \unicode[STIX]{x1D708})^{-1}({\mathcal{F}})\cap {\mathcal{X}}$ is closed under extensions and direct summands in ![]() ${\mathcal{A}}$.
${\mathcal{A}}$.
Proof. It is immediate that ![]() $(f^{\ast }\circ \unicode[STIX]{x1D708})^{-1}({\mathcal{F}})\cap {\mathcal{X}}$ is closed under direct summands. We show that it is closed under extensions. Let
$(f^{\ast }\circ \unicode[STIX]{x1D708})^{-1}({\mathcal{F}})\cap {\mathcal{X}}$ is closed under direct summands. We show that it is closed under extensions. Let ![]() $0\rightarrow A_{1}\xrightarrow[{}]{s}A_{2}\xrightarrow[{}]{t}A_{3}\rightarrow 0$ be an exact sequence in
$0\rightarrow A_{1}\xrightarrow[{}]{s}A_{2}\xrightarrow[{}]{t}A_{3}\rightarrow 0$ be an exact sequence in ![]() ${\mathcal{A}}$ with
${\mathcal{A}}$ with ![]() $A_{1},A_{3}\in (f^{\ast }\circ \unicode[STIX]{x1D708})^{-1}({\mathcal{F}})\cap {\mathcal{X}}$. Since
$A_{1},A_{3}\in (f^{\ast }\circ \unicode[STIX]{x1D708})^{-1}({\mathcal{F}})\cap {\mathcal{X}}$. Since ![]() ${\mathcal{X}}$ is closed under extensions, it follows that
${\mathcal{X}}$ is closed under extensions, it follows that ![]() $A_{2}\in {\mathcal{X}}$. Also, since
$A_{2}\in {\mathcal{X}}$. Also, since ![]() $L_{1}\unicode[STIX]{x1D708}(A_{3})=0$, we have an exact sequence
$L_{1}\unicode[STIX]{x1D708}(A_{3})=0$, we have an exact sequence
in ![]() ${\mathcal{B}}$. Since
${\mathcal{B}}$. Since ![]() ${\mathcal{F}}$ is closed under extensions, it follows that
${\mathcal{F}}$ is closed under extensions, it follows that ![]() $f^{\ast }\unicode[STIX]{x1D708}(A_{2})\in {\mathcal{F}}$. This proves the claim.
$f^{\ast }\unicode[STIX]{x1D708}(A_{2})\in {\mathcal{F}}$. This proves the claim.
Since ![]() $(f^{\ast }\circ \unicode[STIX]{x1D708})^{-1}({\mathcal{F}})\cap {\mathcal{X}}$ is closed under extensions, it inherits an exact structure from
$(f^{\ast }\circ \unicode[STIX]{x1D708})^{-1}({\mathcal{F}})\cap {\mathcal{X}}$ is closed under extensions, it inherits an exact structure from ![]() ${\mathcal{A}}$.
${\mathcal{A}}$.
Lemma 32. The category ![]() $(f^{\ast }\circ \unicode[STIX]{x1D708})^{-1}({\mathcal{F}})\cap {\mathcal{X}}$ contains the projective objects in
$(f^{\ast }\circ \unicode[STIX]{x1D708})^{-1}({\mathcal{F}})\cap {\mathcal{X}}$ contains the projective objects in ![]() ${\mathcal{A}}$.
${\mathcal{A}}$.
Proof. Let ![]() $Q\in {\mathcal{B}}$ be projective. Then
$Q\in {\mathcal{B}}$ be projective. Then ![]() $f^{\ast }\unicode[STIX]{x1D708}f_{!}(Q)$ is projective since the functor
$f^{\ast }\unicode[STIX]{x1D708}f_{!}(Q)$ is projective since the functor ![]() ${\mathcal{B}}(f^{\ast }\unicode[STIX]{x1D708}f_{!}(Q),-)\cong {\mathcal{B}}(Q,f^{\ast }f_{!}(-))$ is exact. Since
${\mathcal{B}}(f^{\ast }\unicode[STIX]{x1D708}f_{!}(Q),-)\cong {\mathcal{B}}(Q,f^{\ast }f_{!}(-))$ is exact. Since ![]() ${\mathcal{X}}$ contains all the
${\mathcal{X}}$ contains all the ![]() $P$-projective objects of
$P$-projective objects of ![]() ${\mathcal{A}}$ and
${\mathcal{A}}$ and ![]() ${\mathcal{F}}$ contains all the projective objects of
${\mathcal{F}}$ contains all the projective objects of ![]() ${\mathcal{B}}$, it follows that
${\mathcal{B}}$, it follows that ![]() $f_{!}(Q)\in (f^{\ast }\circ \unicode[STIX]{x1D708})^{-1}({\mathcal{F}})\cap {\mathcal{X}}$. Since any projective object in
$f_{!}(Q)\in (f^{\ast }\circ \unicode[STIX]{x1D708})^{-1}({\mathcal{F}})\cap {\mathcal{X}}$. Since any projective object in ![]() ${\mathcal{A}}$ is a summand of an object of the form
${\mathcal{A}}$ is a summand of an object of the form ![]() $f_{!}(Q)$, the claim follows.
$f_{!}(Q)$, the claim follows.
Lemma 33. We have ![]() $\operatorname{Ext}_{{\mathcal{A}}}^{i}(A,Q)=0$ for all
$\operatorname{Ext}_{{\mathcal{A}}}^{i}(A,Q)=0$ for all ![]() $i>0$,
$i>0$, ![]() $A\in (f^{\ast }\circ \unicode[STIX]{x1D708})^{-1}({\mathcal{F}})\cap {\mathcal{X}}$, and
$A\in (f^{\ast }\circ \unicode[STIX]{x1D708})^{-1}({\mathcal{F}})\cap {\mathcal{X}}$, and ![]() $Q\in {\mathcal{A}}$ projective.
$Q\in {\mathcal{A}}$ projective.
Proof. We only need to show the statement for ![]() $Q=f_{!}(Q^{\prime })$ where
$Q=f_{!}(Q^{\prime })$ where ![]() $Q^{\prime }\in {\mathcal{B}}$ is projective. Note first that any exact sequence
$Q^{\prime }\in {\mathcal{B}}$ is projective. Note first that any exact sequence ![]() $0\rightarrow f_{!}(Q^{\prime })\rightarrow \cdots \rightarrow A\rightarrow 0$ stays exact under the functor
$0\rightarrow f_{!}(Q^{\prime })\rightarrow \cdots \rightarrow A\rightarrow 0$ stays exact under the functor ![]() $f^{\ast }\circ \unicode[STIX]{x1D708}$ since
$f^{\ast }\circ \unicode[STIX]{x1D708}$ since ![]() $L_{i}\unicode[STIX]{x1D708}(A)=0$ for all
$L_{i}\unicode[STIX]{x1D708}(A)=0$ for all ![]() $i>0$ and as
$i>0$ and as ![]() $f^{\ast }$ is exact. Since we have an adjunction
$f^{\ast }$ is exact. Since we have an adjunction ![]() $f^{\ast }\circ \unicode[STIX]{x1D708}\dashv f_{!}$ and the functor
$f^{\ast }\circ \unicode[STIX]{x1D708}\dashv f_{!}$ and the functor ![]() $f_{!}$ is exact it follows that
$f_{!}$ is exact it follows that ![]() $\operatorname{Ext}_{{\mathcal{A}}}^{i}(A,f_{!}(Q^{\prime }))\cong \operatorname{Ext}_{{\mathcal{B}}}^{i}(f^{\ast }\unicode[STIX]{x1D708}(A),Q^{\prime })$ by [Reference Henrik and Jørgensen20, Lemma 6.1]. Since the latter is
$\operatorname{Ext}_{{\mathcal{A}}}^{i}(A,f_{!}(Q^{\prime }))\cong \operatorname{Ext}_{{\mathcal{B}}}^{i}(f^{\ast }\unicode[STIX]{x1D708}(A),Q^{\prime })$ by [Reference Henrik and Jørgensen20, Lemma 6.1]. Since the latter is ![]() $0$ by the assumption on
$0$ by the assumption on ![]() $A$, the claim follows.
$A$, the claim follows.
Lemma 34. If ![]() $A\in (f^{\ast }\circ \unicode[STIX]{x1D708})^{-1}({\mathcal{F}})\cap {\mathcal{X}}$, then there exists a projective object
$A\in (f^{\ast }\circ \unicode[STIX]{x1D708})^{-1}({\mathcal{F}})\cap {\mathcal{X}}$, then there exists a projective object ![]() $Q\in {\mathcal{A}}$ and an epimorphism
$Q\in {\mathcal{A}}$ and an epimorphism ![]() $p:Q\rightarrow A$ such that
$p:Q\rightarrow A$ such that ![]() $\operatorname{Ker}p\in (f^{\ast }\circ \unicode[STIX]{x1D708})^{-1}({\mathcal{F}})\cap {\mathcal{X}}$.
$\operatorname{Ker}p\in (f^{\ast }\circ \unicode[STIX]{x1D708})^{-1}({\mathcal{F}})\cap {\mathcal{X}}$.
Proof. Let ![]() $A\in (f^{\ast }\circ \unicode[STIX]{x1D708})^{-1}({\mathcal{F}})\cap {\mathcal{X}}$ be arbitrary, and choose an epimorphism
$A\in (f^{\ast }\circ \unicode[STIX]{x1D708})^{-1}({\mathcal{F}})\cap {\mathcal{X}}$ be arbitrary, and choose an epimorphism ![]() $q:Q^{\prime }\rightarrow f^{\ast }(A)$ in
$q:Q^{\prime }\rightarrow f^{\ast }(A)$ in ![]() ${\mathcal{B}}$ with
${\mathcal{B}}$ with ![]() $Q^{\prime }$ projective. By Lemma 27 part (ii) the morphism
$Q^{\prime }$ projective. By Lemma 27 part (ii) the morphism ![]() $(\unicode[STIX]{x1D719}^{f_{!}\dashv f^{\ast }})^{-1}(q):f_{!}(Q^{\prime })\rightarrow A$ is an epimorphism and
$(\unicode[STIX]{x1D719}^{f_{!}\dashv f^{\ast }})^{-1}(q):f_{!}(Q^{\prime })\rightarrow A$ is an epimorphism and
Since ![]() $f_{!}(Q^{\prime })$ is projective, it only remains to show
$f_{!}(Q^{\prime })$ is projective, it only remains to show ![]() $\operatorname{Ker}(\unicode[STIX]{x1D719}^{f_{!}\dashv f^{\ast }})^{-1}(q)\in (f^{\ast }\circ \unicode[STIX]{x1D708})^{-1}({\mathcal{F}})$. To this end, note that applying
$\operatorname{Ker}(\unicode[STIX]{x1D719}^{f_{!}\dashv f^{\ast }})^{-1}(q)\in (f^{\ast }\circ \unicode[STIX]{x1D708})^{-1}({\mathcal{F}})$. To this end, note that applying ![]() $f^{\ast }\circ \unicode[STIX]{x1D708}$ to
$f^{\ast }\circ \unicode[STIX]{x1D708}$ to
gives an exact sequence
in ![]() ${\mathcal{B}}$ since
${\mathcal{B}}$ since ![]() $L_{1}\unicode[STIX]{x1D708}(A)=0$. By Lemma 11 we have that
$L_{1}\unicode[STIX]{x1D708}(A)=0$. By Lemma 11 we have that ![]() ${\mathcal{F}}$ is resolving, and therefore
${\mathcal{F}}$ is resolving, and therefore ![]() $f^{\ast }\unicode[STIX]{x1D708}(\operatorname{Ker}(\unicode[STIX]{x1D719}^{f_{!}\dashv f^{\ast }})^{-1}(q))\in {\mathcal{F}}$. This proves the claim.
$f^{\ast }\unicode[STIX]{x1D708}(\operatorname{Ker}(\unicode[STIX]{x1D719}^{f_{!}\dashv f^{\ast }})^{-1}(q))\in {\mathcal{F}}$. This proves the claim.
Lemma 35. If ![]() $A\in (f^{\ast }\circ \unicode[STIX]{x1D708})^{-1}({\mathcal{F}})\cap {\mathcal{X}}$, then there exists a projective object
$A\in (f^{\ast }\circ \unicode[STIX]{x1D708})^{-1}({\mathcal{F}})\cap {\mathcal{X}}$, then there exists a projective object ![]() $Q\in {\mathcal{A}}$ and a monomorphism
$Q\in {\mathcal{A}}$ and a monomorphism ![]() $j:A\rightarrow Q$ such that
$j:A\rightarrow Q$ such that ![]() $\operatorname{Coker}j\in (f^{\ast }\circ \unicode[STIX]{x1D708})^{-1}({\mathcal{F}})\cap {\mathcal{X}}$.
$\operatorname{Coker}j\in (f^{\ast }\circ \unicode[STIX]{x1D708})^{-1}({\mathcal{F}})\cap {\mathcal{X}}$.
Proof. Let ![]() $A\in (f^{\ast }\circ \unicode[STIX]{x1D708})^{-1}({\mathcal{F}})\cap {\mathcal{X}}$ be arbitrary. Choose a projective object
$A\in (f^{\ast }\circ \unicode[STIX]{x1D708})^{-1}({\mathcal{F}})\cap {\mathcal{X}}$ be arbitrary. Choose a projective object ![]() $Q^{\prime }\in {\mathcal{B}}$ and an exact sequence
$Q^{\prime }\in {\mathcal{B}}$ and an exact sequence
with ![]() $B\in {\mathcal{F}}$. By Lemma 27 we get that
$B\in {\mathcal{F}}$. By Lemma 27 we get that ![]() $j:=\unicode[STIX]{x1D719}^{f^{\ast }\circ \unicode[STIX]{x1D708}\dashv f_{!}}(i):A\rightarrow f_{!}(Q^{\prime })$ is a monomorphism and
$j:=\unicode[STIX]{x1D719}^{f^{\ast }\circ \unicode[STIX]{x1D708}\dashv f_{!}}(i):A\rightarrow f_{!}(Q^{\prime })$ is a monomorphism and ![]() $\operatorname{Coker}j\in {\mathcal{X}}$. Since
$\operatorname{Coker}j\in {\mathcal{X}}$. Since ![]() $f_{!}(Q^{\prime })$ is projective, it only remains to show that
$f_{!}(Q^{\prime })$ is projective, it only remains to show that ![]() $\operatorname{Coker}j\in (f^{\ast }\circ \unicode[STIX]{x1D708})^{-1}({\mathcal{F}})$. To this end, note that we have a commutative diagram
$\operatorname{Coker}j\in (f^{\ast }\circ \unicode[STIX]{x1D708})^{-1}({\mathcal{F}})$. To this end, note that we have a commutative diagram

where the rows are short exact sequences. Hence, the right square is a pullback and a pushout square. Therefore, we get an exact sequence
We know that ![]() $B\in {\mathcal{F}}$,
$B\in {\mathcal{F}}$, ![]() $f^{\ast }\unicode[STIX]{x1D708}f_{!}(Q^{\prime })$ is projective, and
$f^{\ast }\unicode[STIX]{x1D708}f_{!}(Q^{\prime })$ is projective, and ![]() ${\mathcal{F}}$ is closed under extensions and direct summands. Therefore, it follows that
${\mathcal{F}}$ is closed under extensions and direct summands. Therefore, it follows that ![]() $f^{\ast }\unicode[STIX]{x1D708}(\operatorname{Coker}j)\in {\mathcal{F}}$. This proves the claim.
$f^{\ast }\unicode[STIX]{x1D708}(\operatorname{Coker}j)\in {\mathcal{F}}$. This proves the claim.
Theorem 36. The category ![]() $(f^{\ast }\circ \unicode[STIX]{x1D708})^{-1}({\mathcal{F}})\cap {\mathcal{X}}$ is an admissible subcategory of
$(f^{\ast }\circ \unicode[STIX]{x1D708})^{-1}({\mathcal{F}})\cap {\mathcal{X}}$ is an admissible subcategory of ![]() ${\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$.
${\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$.
Example 37. Let ![]() $k$ be a field, let
$k$ be a field, let ![]() $\unicode[STIX]{x1D6EC}_{1}$ be a finite-dimensional algebra over
$\unicode[STIX]{x1D6EC}_{1}$ be a finite-dimensional algebra over ![]() $k$, and let
$k$, and let ![]() $\unicode[STIX]{x1D6EC}_{2}$ be a left coherent
$\unicode[STIX]{x1D6EC}_{2}$ be a left coherent ![]() $k$-algebra. Theorem 36 together with Example 28 show that the categories
$k$-algebra. Theorem 36 together with Example 28 show that the categories
(i)
 $\{\!M\in (\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}\mid \text{}_{\unicode[STIX]{x1D6EC}_{1}}M\in {\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod})\text{ and }_{\unicode[STIX]{x1D6EC}_{2}}(\operatorname{Hom}_{k}(\unicode[STIX]{x1D6EC}_{1},k)\otimes _{\unicode[STIX]{x1D6EC}_{1}}M)\in {\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{2}\text{-}\!\operatorname{mod})\!\}$
$\{\!M\in (\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}\mid \text{}_{\unicode[STIX]{x1D6EC}_{1}}M\in {\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod})\text{ and }_{\unicode[STIX]{x1D6EC}_{2}}(\operatorname{Hom}_{k}(\unicode[STIX]{x1D6EC}_{1},k)\otimes _{\unicode[STIX]{x1D6EC}_{1}}M)\in {\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{2}\text{-}\!\operatorname{mod})\!\}$(ii)
 $\{\!M\in (\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}\mid \text{}_{\unicode[STIX]{x1D6EC}_{1}}M\in {\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod})\text{ and }_{\unicode[STIX]{x1D6EC}_{2}}(\operatorname{Hom}_{k}(\unicode[STIX]{x1D6EC}_{1},k)\otimes _{\unicode[STIX]{x1D6EC}_{1}}M)\in \operatorname{Proj}(\unicode[STIX]{x1D6EC}_{2}\text{-}\!\operatorname{mod})\!\}$
$\{\!M\in (\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}\mid \text{}_{\unicode[STIX]{x1D6EC}_{1}}M\in {\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod})\text{ and }_{\unicode[STIX]{x1D6EC}_{2}}(\operatorname{Hom}_{k}(\unicode[STIX]{x1D6EC}_{1},k)\otimes _{\unicode[STIX]{x1D6EC}_{1}}M)\in \operatorname{Proj}(\unicode[STIX]{x1D6EC}_{2}\text{-}\!\operatorname{mod})\!\}$(iii)
 $\{\!M\in (\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}\mid \text{}_{\unicode[STIX]{x1D6EC}_{1}}M\in \operatorname{Proj}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod})\text{ and }_{\unicode[STIX]{x1D6EC}_{2}}(\operatorname{Hom}_{k}(\unicode[STIX]{x1D6EC}_{1},k)\otimes _{\unicode[STIX]{x1D6EC}_{1}}M)\in {\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{2}\text{-}\!\operatorname{mod})\!\}$
$\{\!M\in (\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}\mid \text{}_{\unicode[STIX]{x1D6EC}_{1}}M\in \operatorname{Proj}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod})\text{ and }_{\unicode[STIX]{x1D6EC}_{2}}(\operatorname{Hom}_{k}(\unicode[STIX]{x1D6EC}_{1},k)\otimes _{\unicode[STIX]{x1D6EC}_{1}}M)\in {\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{2}\text{-}\!\operatorname{mod})\!\}$(iv)
 $\{\!M\in (\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}\mid \text{}_{\unicode[STIX]{x1D6EC}_{1}}M\in \operatorname{Proj}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod})\text{ and }_{\unicode[STIX]{x1D6EC}_{2}}(\operatorname{Hom}_{k}(\unicode[STIX]{x1D6EC}_{1},k)\otimes _{\unicode[STIX]{x1D6EC}_{1}}M)\in \operatorname{Proj}(\unicode[STIX]{x1D6EC}_{2}\text{-}\!\operatorname{mod})\!\}$
$\{\!M\in (\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}\mid \text{}_{\unicode[STIX]{x1D6EC}_{1}}M\in \operatorname{Proj}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod})\text{ and }_{\unicode[STIX]{x1D6EC}_{2}}(\operatorname{Hom}_{k}(\unicode[STIX]{x1D6EC}_{1},k)\otimes _{\unicode[STIX]{x1D6EC}_{1}}M)\in \operatorname{Proj}(\unicode[STIX]{x1D6EC}_{2}\text{-}\!\operatorname{mod})\!\}$
are admissible subcategories of ![]() ${\mathcal{G}}{\mathcal{P}}((\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod})$.
${\mathcal{G}}{\mathcal{P}}((\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod})$.
Example 38. Let ![]() $k$ be a field, let
$k$ be a field, let ![]() $\unicode[STIX]{x1D6EC}_{1}$ be a finite-dimensional algebra over
$\unicode[STIX]{x1D6EC}_{1}$ be a finite-dimensional algebra over ![]() $k$, and let
$k$, and let ![]() $\unicode[STIX]{x1D6EC}_{2}$ be a
$\unicode[STIX]{x1D6EC}_{2}$ be a ![]() $k$-algebra. Example 29 together with Theorem 36 show that the categories
$k$-algebra. Example 29 together with Theorem 36 show that the categories
(i)
 $\{\!M\in (\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{Mod}\mid \text{}_{\unicode[STIX]{x1D6EC}_{1}}M\in {\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod})\text{ and }_{\unicode[STIX]{x1D6EC}_{2}}(\operatorname{Hom}_{k}(\unicode[STIX]{x1D6EC}_{1},k)\otimes _{\unicode[STIX]{x1D6EC}_{1}}M)\in {\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{2}\text{-}\!\operatorname{Mod})\!\}$
$\{\!M\in (\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{Mod}\mid \text{}_{\unicode[STIX]{x1D6EC}_{1}}M\in {\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod})\text{ and }_{\unicode[STIX]{x1D6EC}_{2}}(\operatorname{Hom}_{k}(\unicode[STIX]{x1D6EC}_{1},k)\otimes _{\unicode[STIX]{x1D6EC}_{1}}M)\in {\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{2}\text{-}\!\operatorname{Mod})\!\}$(ii)
 $\{\!M\in (\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{Mod}\mid \text{}_{\unicode[STIX]{x1D6EC}_{1}}M\in {\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod})\text{ and }_{\unicode[STIX]{x1D6EC}_{2}}(\operatorname{Hom}_{k}(\unicode[STIX]{x1D6EC}_{1},k)\otimes _{\unicode[STIX]{x1D6EC}_{1}}M)\in \operatorname{Proj}(\unicode[STIX]{x1D6EC}_{2}\text{-}\!\operatorname{Mod})\!\}$
$\{\!M\in (\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{Mod}\mid \text{}_{\unicode[STIX]{x1D6EC}_{1}}M\in {\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod})\text{ and }_{\unicode[STIX]{x1D6EC}_{2}}(\operatorname{Hom}_{k}(\unicode[STIX]{x1D6EC}_{1},k)\otimes _{\unicode[STIX]{x1D6EC}_{1}}M)\in \operatorname{Proj}(\unicode[STIX]{x1D6EC}_{2}\text{-}\!\operatorname{Mod})\!\}$(iii)
 $\{\!M\in (\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{Mod}\mid \text{}_{\unicode[STIX]{x1D6EC}_{1}}M\in \operatorname{Proj}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod})\text{ and }_{\unicode[STIX]{x1D6EC}_{2}}(\operatorname{Hom}_{k}(\unicode[STIX]{x1D6EC}_{1},k)\otimes _{\unicode[STIX]{x1D6EC}_{1}}M)\in {\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{2}\text{-}\!\operatorname{Mod})\!\}$
$\{\!M\in (\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{Mod}\mid \text{}_{\unicode[STIX]{x1D6EC}_{1}}M\in \operatorname{Proj}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod})\text{ and }_{\unicode[STIX]{x1D6EC}_{2}}(\operatorname{Hom}_{k}(\unicode[STIX]{x1D6EC}_{1},k)\otimes _{\unicode[STIX]{x1D6EC}_{1}}M)\in {\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{2}\text{-}\!\operatorname{Mod})\!\}$(iv)
 $\{\!M\in (\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{Mod}\mid \text{}_{\unicode[STIX]{x1D6EC}_{1}}M\in \operatorname{Proj}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod})\text{ and }_{\unicode[STIX]{x1D6EC}_{2}}(\operatorname{Hom}_{k}(\unicode[STIX]{x1D6EC}_{1},k)\otimes _{\unicode[STIX]{x1D6EC}_{1}}M)\in \operatorname{Proj}(\unicode[STIX]{x1D6EC}_{2}\text{-}\!\operatorname{Mod})\!\}$
$\{\!M\in (\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{Mod}\mid \text{}_{\unicode[STIX]{x1D6EC}_{1}}M\in \operatorname{Proj}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{Mod})\text{ and }_{\unicode[STIX]{x1D6EC}_{2}}(\operatorname{Hom}_{k}(\unicode[STIX]{x1D6EC}_{1},k)\otimes _{\unicode[STIX]{x1D6EC}_{1}}M)\in \operatorname{Proj}(\unicode[STIX]{x1D6EC}_{2}\text{-}\!\operatorname{Mod})\!\}$
are admissible subcategories of ![]() ${\mathcal{G}}{\mathcal{P}}((\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{Mod})$.
${\mathcal{G}}{\mathcal{P}}((\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{Mod})$.
3.3 Lifting Gorenstein projectives
Now assume ![]() ${\mathcal{X}}={\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$ and
${\mathcal{X}}={\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$ and ![]() ${\mathcal{F}}={\mathcal{G}}{\mathcal{P}}({\mathcal{B}})$. We define
${\mathcal{F}}={\mathcal{G}}{\mathcal{P}}({\mathcal{B}})$. We define
By Theorem 36 we know that ![]() ${\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}}))$ is an admissible subcategory of
${\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}}))$ is an admissible subcategory of ![]() ${\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$, and therefore
${\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$, and therefore
We want to investigate when this inclusion is an equality. We first give a different description of the objects in ![]() ${\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}}))$.
${\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}}))$.
Proposition 39. Let ![]() $A\in {\mathcal{A}}$ be arbitrary. Then
$A\in {\mathcal{A}}$ be arbitrary. Then ![]() $A\in {\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}}))$ if and only if there exists a totally acyclic complex
$A\in {\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}}))$ if and only if there exists a totally acyclic complex
in ![]() ${\mathcal{A}}$, such that
${\mathcal{A}}$, such that ![]() $Z_{i}(Q_{\bullet })\in {\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$ for all
$Z_{i}(Q_{\bullet })\in {\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$ for all ![]() $i\in \mathbb{Z}$, and such that
$i\in \mathbb{Z}$, and such that ![]() $Z_{0}(Q_{\bullet })=A$.
$Z_{0}(Q_{\bullet })=A$.
Proof. Assume ![]() $A\in {\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}}))$. Since
$A\in {\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}}))$. Since ![]() ${\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}}))$ is an admissible subcategory of
${\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}}))$ is an admissible subcategory of ![]() ${\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$, we can find a long exact sequence
${\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$, we can find a long exact sequence
with ![]() $Q_{i}\in {\mathcal{A}}$ projective,
$Q_{i}\in {\mathcal{A}}$ projective, ![]() $Z_{0}(Q_{\bullet })=A$, and
$Z_{0}(Q_{\bullet })=A$, and ![]() $Z_{i}(Q_{\bullet })\in {\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}}))$ for all
$Z_{i}(Q_{\bullet })\in {\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}}))$ for all ![]() $i\in \mathbb{Z}$. Furthermore,
$i\in \mathbb{Z}$. Furthermore, ![]() $\operatorname{Ext}_{{\mathcal{A}}}^{1}(A^{\prime },Q^{\prime })=0$ for all
$\operatorname{Ext}_{{\mathcal{A}}}^{1}(A^{\prime },Q^{\prime })=0$ for all ![]() $A^{\prime }\in {\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}}))$ and
$A^{\prime }\in {\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}}))$ and ![]() $Q^{\prime }\in \operatorname{Proj}({\mathcal{A}})$ since
$Q^{\prime }\in \operatorname{Proj}({\mathcal{A}})$ since ![]() ${\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}}))$ is admissible. This shows that
${\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}}))$ is admissible. This shows that ![]() $Q_{\bullet }$ is totally acyclic.
$Q_{\bullet }$ is totally acyclic.
For the converse, assume ![]() $Q_{\bullet }$ is totally acyclic,
$Q_{\bullet }$ is totally acyclic, ![]() $Z_{i}(Q_{\bullet })\in {\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$ for all
$Z_{i}(Q_{\bullet })\in {\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$ for all ![]() $i\in \mathbb{Z}$, and
$i\in \mathbb{Z}$, and ![]() $A=Z_{0}(Q_{\bullet })$. The sequence
$A=Z_{0}(Q_{\bullet })$. The sequence
is then exact since ![]() $L_{1}\unicode[STIX]{x1D708}(A^{\prime })=0$ for all
$L_{1}\unicode[STIX]{x1D708}(A^{\prime })=0$ for all ![]() $A^{\prime }\in {\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$. Furthermore, the objects
$A^{\prime }\in {\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$. Furthermore, the objects ![]() $f^{\ast }\unicode[STIX]{x1D708}(Q_{i})\in {\mathcal{B}}$ are projective since
$f^{\ast }\unicode[STIX]{x1D708}(Q_{i})\in {\mathcal{B}}$ are projective since ![]() $f^{\ast }\circ \unicode[STIX]{x1D708}$ preserves projectives. Applying
$f^{\ast }\circ \unicode[STIX]{x1D708}$ preserves projectives. Applying ![]() ${\mathcal{B}}(-,Q)$ for
${\mathcal{B}}(-,Q)$ for ![]() $Q\in {\mathcal{B}}$ projective and using the isomorphism
$Q\in {\mathcal{B}}$ projective and using the isomorphism ![]() ${\mathcal{B}}(f^{\ast }\unicode[STIX]{x1D708}(Q_{i}),Q)\cong {\mathcal{A}}(Q_{i},f_{!}(Q))$ gives us the sequence
${\mathcal{B}}(f^{\ast }\unicode[STIX]{x1D708}(Q_{i}),Q)\cong {\mathcal{A}}(Q_{i},f_{!}(Q))$ gives us the sequence
which is exact since ![]() $Q_{\bullet }$ is totally acyclic. Hence,
$Q_{\bullet }$ is totally acyclic. Hence, ![]() $f^{\ast }\unicode[STIX]{x1D708}(Q_{\bullet })$ is totally acyclic, and therefore
$f^{\ast }\unicode[STIX]{x1D708}(Q_{\bullet })$ is totally acyclic, and therefore ![]() $f^{\ast }\unicode[STIX]{x1D708}(A)=Z_{0}(f^{\ast }\unicode[STIX]{x1D708}(Q_{\bullet }))\in {\mathcal{G}}{\mathcal{P}}({\mathcal{B}})$. This shows that
$f^{\ast }\unicode[STIX]{x1D708}(A)=Z_{0}(f^{\ast }\unicode[STIX]{x1D708}(Q_{\bullet }))\in {\mathcal{G}}{\mathcal{P}}({\mathcal{B}})$. This shows that ![]() $A\in {\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}}))$, and we are done.
$A\in {\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}}))$, and we are done.
Remark 40. Proposition 39 shows that ![]() $A\in {\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}}))$ if and only if
$A\in {\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}}))$ if and only if ![]() $A$ is Gorenstein projective inside the exact category
$A$ is Gorenstein projective inside the exact category ![]() ${\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$. This is the reason for the notation
${\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$. This is the reason for the notation ![]() ${\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}}))$.
${\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}}))$.
Proposition 41. The following statements are equivalent:
(i)
 ${\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}}))={\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$;
${\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}}))={\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$;(ii)
 ${\mathcal{G}}{\mathcal{P}}({\mathcal{A}})\subset {\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$;
${\mathcal{G}}{\mathcal{P}}({\mathcal{A}})\subset {\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$;(iii)
 $f^{\ast }\circ \unicode[STIX]{x1D708}:{\mathcal{A}}\rightarrow {\mathcal{B}}$ preserves Gorenstein projectives.
$f^{\ast }\circ \unicode[STIX]{x1D708}:{\mathcal{A}}\rightarrow {\mathcal{B}}$ preserves Gorenstein projectives.
Proof. Obviously, (i)![]() $\;\Longrightarrow \;$ (ii) and (i)
$\;\Longrightarrow \;$ (ii) and (i)![]() $\;\Longrightarrow \;$ (iii). Also, if (ii) holds then any totally acyclic complex satisfies the assumptions in Proposition 39, and therefore (i) holds. We show the implication (iii)
$\;\Longrightarrow \;$ (iii). Also, if (ii) holds then any totally acyclic complex satisfies the assumptions in Proposition 39, and therefore (i) holds. We show the implication (iii)![]() $\;\Longrightarrow \;$ (i). Assume
$\;\Longrightarrow \;$ (i). Assume ![]() $f^{\ast }\circ \unicode[STIX]{x1D708}$ preserves Gorenstein projectives, and let
$f^{\ast }\circ \unicode[STIX]{x1D708}$ preserves Gorenstein projectives, and let ![]() $A\in {\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$ be arbitrary. We only need to show that
$A\in {\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$ be arbitrary. We only need to show that ![]() $L_{1}\unicode[STIX]{x1D708}(A)=0$ since this implies that if
$L_{1}\unicode[STIX]{x1D708}(A)=0$ since this implies that if ![]() $Q_{\bullet }$ is totally acyclic, then
$Q_{\bullet }$ is totally acyclic, then ![]() $\unicode[STIX]{x1D708}(Q_{\bullet })$ is exact, and hence
$\unicode[STIX]{x1D708}(Q_{\bullet })$ is exact, and hence ![]() $Z_{0}(Q_{\bullet })\in {\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$ by definition since projective objects are
$Z_{0}(Q_{\bullet })\in {\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$ by definition since projective objects are ![]() $P$-projective. Let
$P$-projective. Let
be an exact sequence in ![]() ${\mathcal{A}}$ with
${\mathcal{A}}$ with ![]() $Q$ projective and
$Q$ projective and ![]() $A^{\prime }\in {\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$. Applying
$A^{\prime }\in {\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$. Applying ![]() $\unicode[STIX]{x1D708}$ gives an exact sequence
$\unicode[STIX]{x1D708}$ gives an exact sequence
Hence, ![]() $L_{1}\unicode[STIX]{x1D708}(A)=0$ if and only if
$L_{1}\unicode[STIX]{x1D708}(A)=0$ if and only if ![]() $\unicode[STIX]{x1D708}(s)$ is a monomorphism. Let
$\unicode[STIX]{x1D708}(s)$ is a monomorphism. Let ![]() $Q^{\prime }\in {\mathcal{B}}$ be a projective object. We know that the map
$Q^{\prime }\in {\mathcal{B}}$ be a projective object. We know that the map ![]() ${\mathcal{A}}(Q,f_{!}(Q^{\prime }))\xrightarrow[{}]{-\circ s}{\mathcal{A}}(A^{\prime },f_{!}(Q^{\prime }))$ is an epimorphism since
${\mathcal{A}}(Q,f_{!}(Q^{\prime }))\xrightarrow[{}]{-\circ s}{\mathcal{A}}(A^{\prime },f_{!}(Q^{\prime }))$ is an epimorphism since ![]() $\operatorname{Ext}_{{\mathcal{A}}}^{1}(A,f_{!}(Q^{\prime }))=0$. Hence, from the adjunction
$\operatorname{Ext}_{{\mathcal{A}}}^{1}(A,f_{!}(Q^{\prime }))=0$. Hence, from the adjunction ![]() $f^{\ast }\circ \unicode[STIX]{x1D708}\dashv f_{!}$ we get that
$f^{\ast }\circ \unicode[STIX]{x1D708}\dashv f_{!}$ we get that
is an epimorphism. It follows therefore from Lemma 12 that ![]() $f^{\ast }\unicode[STIX]{x1D708}(s)$ is a monomorphism. Since
$f^{\ast }\unicode[STIX]{x1D708}(s)$ is a monomorphism. Since ![]() $f^{\ast }$ is faithful, we get that
$f^{\ast }$ is faithful, we get that ![]() $\unicode[STIX]{x1D708}(s)$ is a monomorphism. This proves the claim.
$\unicode[STIX]{x1D708}(s)$ is a monomorphism. This proves the claim.
The following result gives sufficient criteria for when ![]() ${\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}}))={\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$.
${\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}}))={\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$.
Theorem 42. We have that ![]() ${\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}}))={\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$ if either of the following conditions hold:
${\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}}))={\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$ if either of the following conditions hold:
(i) For any long exact sequence
with $$\begin{eqnarray}0\rightarrow K\rightarrow Q_{0}\rightarrow Q_{-1}\rightarrow \cdots\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow K\rightarrow Q_{0}\rightarrow Q_{-1}\rightarrow \cdots\end{eqnarray}$$ $Q_{i}\in {\mathcal{A}}$ projective for
$Q_{i}\in {\mathcal{A}}$ projective for  $i\leqslant 0$, we have
$i\leqslant 0$, we have  $K\in {\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$;
$K\in {\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$;(ii) If
 $B\in {\mathcal{B}}$ satisfy
$B\in {\mathcal{B}}$ satisfy  $\operatorname{Ext}_{{\mathcal{B}}}^{1}(B,B^{\prime })=0$ for all
$\operatorname{Ext}_{{\mathcal{B}}}^{1}(B,B^{\prime })=0$ for all  $B^{\prime }$ of
$B^{\prime }$ of  $\operatorname{pdim}B^{\prime }<\infty$, then
$\operatorname{pdim}B^{\prime }<\infty$, then  $B\in {\mathcal{G}}{\mathcal{P}}({\mathcal{B}})$.
$B\in {\mathcal{G}}{\mathcal{P}}({\mathcal{B}})$.
Proof. Proposition 41 part (ii) shows that condition (i) is sufficient. Assume condition (ii) holds. By Proposition 41 part (iii) it is sufficient to show that ![]() $f^{\ast }\unicode[STIX]{x1D708}(A)\in {\mathcal{G}}{\mathcal{P}}({\mathcal{B}})$ for all
$f^{\ast }\unicode[STIX]{x1D708}(A)\in {\mathcal{G}}{\mathcal{P}}({\mathcal{B}})$ for all ![]() $A\in {\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$. Fix
$A\in {\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$. Fix ![]() $A\in {\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$, and let
$A\in {\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$, and let ![]() $0\rightarrow A^{\prime }\xrightarrow[{}]{s}Q\xrightarrow[{}]{t}A\rightarrow 0$ be an exact sequence in
$0\rightarrow A^{\prime }\xrightarrow[{}]{s}Q\xrightarrow[{}]{t}A\rightarrow 0$ be an exact sequence in ![]() ${\mathcal{A}}$ with
${\mathcal{A}}$ with ![]() $Q\in \operatorname{Proj}({\mathcal{A}})$. Applying
$Q\in \operatorname{Proj}({\mathcal{A}})$. Applying ![]() $f^{\ast }\circ \unicode[STIX]{x1D708}$ gives an exact sequence
$f^{\ast }\circ \unicode[STIX]{x1D708}$ gives an exact sequence ![]() $f^{\ast }\unicode[STIX]{x1D708}(A^{\prime })\xrightarrow[{}]{f^{\ast }\unicode[STIX]{x1D708}(s)}f^{\ast }\unicode[STIX]{x1D708}(Q)\xrightarrow[{}]{f^{\ast }\unicode[STIX]{x1D708}(t)}f^{\ast }\unicode[STIX]{x1D708}(A)\rightarrow 0$ in
$f^{\ast }\unicode[STIX]{x1D708}(A^{\prime })\xrightarrow[{}]{f^{\ast }\unicode[STIX]{x1D708}(s)}f^{\ast }\unicode[STIX]{x1D708}(Q)\xrightarrow[{}]{f^{\ast }\unicode[STIX]{x1D708}(t)}f^{\ast }\unicode[STIX]{x1D708}(A)\rightarrow 0$ in ![]() ${\mathcal{B}}$. Let
${\mathcal{B}}$. Let ![]() $i:K\rightarrow f^{\ast }\unicode[STIX]{x1D708}(Q)$ be the inclusion of the kernel of
$i:K\rightarrow f^{\ast }\unicode[STIX]{x1D708}(Q)$ be the inclusion of the kernel of ![]() $f^{\ast }\unicode[STIX]{x1D708}(t)$, let
$f^{\ast }\unicode[STIX]{x1D708}(t)$, let ![]() $p:f^{\ast }\unicode[STIX]{x1D708}(A^{\prime })\rightarrow K$ be the surjection induced from
$p:f^{\ast }\unicode[STIX]{x1D708}(A^{\prime })\rightarrow K$ be the surjection induced from ![]() $f^{\ast }\unicode[STIX]{x1D708}(s)$, and let
$f^{\ast }\unicode[STIX]{x1D708}(s)$, and let ![]() $B^{\prime }\in {\mathcal{B}}$ be an arbitrary object. Applying
$B^{\prime }\in {\mathcal{B}}$ be an arbitrary object. Applying ![]() ${\mathcal{B}}(-,B)$ gives an exact sequence
${\mathcal{B}}(-,B)$ gives an exact sequence
where ![]() $\operatorname{Ext}_{{\mathcal{B}}}^{1}(f^{\ast }\unicode[STIX]{x1D708}(Q),B^{\prime })=0$ since
$\operatorname{Ext}_{{\mathcal{B}}}^{1}(f^{\ast }\unicode[STIX]{x1D708}(Q),B^{\prime })=0$ since ![]() $f^{\ast }\unicode[STIX]{x1D708}$ preserves projective objects. Hence, we only need to show that
$f^{\ast }\unicode[STIX]{x1D708}$ preserves projective objects. Hence, we only need to show that ![]() $-\circ i:{\mathcal{B}}(f^{\ast }\unicode[STIX]{x1D708}(Q),B^{\prime })\rightarrow {\mathcal{B}}(K,B^{\prime })$ is an epimorphism if
$-\circ i:{\mathcal{B}}(f^{\ast }\unicode[STIX]{x1D708}(Q),B^{\prime })\rightarrow {\mathcal{B}}(K,B^{\prime })$ is an epimorphism if ![]() $\operatorname{pdim}B^{\prime }<\infty$. To this end, note that
$\operatorname{pdim}B^{\prime }<\infty$. To this end, note that ![]() $\operatorname{Ext}_{{\mathcal{A}}}^{1}(A,f_{!}(B))=0$ if
$\operatorname{Ext}_{{\mathcal{A}}}^{1}(A,f_{!}(B))=0$ if ![]() $\operatorname{pdim}B^{\prime }<\infty$ since
$\operatorname{pdim}B^{\prime }<\infty$ since ![]() $A\in {\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$ and
$A\in {\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$ and ![]() $f_{!}$ preserves objects of finite projective dimension. Therefore, we have an exact sequence
$f_{!}$ preserves objects of finite projective dimension. Therefore, we have an exact sequence
Via the adjunction ![]() ${\mathcal{A}}(-,f_{!})\cong {\mathcal{B}}(f^{\ast }\circ \unicode[STIX]{x1D708},-)$ the map
${\mathcal{A}}(-,f_{!})\cong {\mathcal{B}}(f^{\ast }\circ \unicode[STIX]{x1D708},-)$ the map
corresponds to
which is therefore also an epimorphism. But ![]() $-\circ f^{\ast }\unicode[STIX]{x1D708}(s)$ factors as
$-\circ f^{\ast }\unicode[STIX]{x1D708}(s)$ factors as
Since ![]() ${\mathcal{B}}(K,B^{\prime })\xrightarrow[{}]{-\circ p}{\mathcal{B}}(f^{\ast }\unicode[STIX]{x1D708}(A^{\prime }),B^{\prime })$ is a monomorphism, it follows that
${\mathcal{B}}(K,B^{\prime })\xrightarrow[{}]{-\circ p}{\mathcal{B}}(f^{\ast }\unicode[STIX]{x1D708}(A^{\prime }),B^{\prime })$ is a monomorphism, it follows that
is an epimorphism. This proves the claim.
Corollary 43. If ![]() $P$ is Iwanaga–Gorenstein, then
$P$ is Iwanaga–Gorenstein, then
Proof. This follows from condition (i) in Theorem 42 and the fact that ![]() $\dim _{{\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})}({\mathcal{A}})<\infty$ when
$\dim _{{\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})}({\mathcal{A}})<\infty$ when ![]() $P$ is Iwanaga–Gorenstein.
$P$ is Iwanaga–Gorenstein.
Recall that ![]() ${\mathcal{B}}$ is
${\mathcal{B}}$ is ![]() $\operatorname{Proj}({\mathcal{B}})$-Gorenstein if
$\operatorname{Proj}({\mathcal{B}})$-Gorenstein if ![]() $\operatorname{G.pdim}(B)<\infty$ for all
$\operatorname{G.pdim}(B)<\infty$ for all ![]() $B\in {\mathcal{B}}$ [Reference Beligiannis5, Corollary 4.13].
$B\in {\mathcal{B}}$ [Reference Beligiannis5, Corollary 4.13].
Lemma 44. If ![]() ${\mathcal{B}}$ is
${\mathcal{B}}$ is ![]() $\operatorname{Proj}({\mathcal{B}})$-Gorenstein, then
$\operatorname{Proj}({\mathcal{B}})$-Gorenstein, then
Proof. Assume ![]() $\operatorname{Ext}_{{\mathcal{B}}}^{1}(B,B^{\prime })=0$ for all
$\operatorname{Ext}_{{\mathcal{B}}}^{1}(B,B^{\prime })=0$ for all ![]() $B^{\prime }$ satisfying
$B^{\prime }$ satisfying ![]() $\operatorname{pdim}B<\infty ^{\prime }$. Since
$\operatorname{pdim}B<\infty ^{\prime }$. Since ![]() $\operatorname{G.pdim}(B)<\infty$, there exists an exact sequence
$\operatorname{G.pdim}(B)<\infty$, there exists an exact sequence ![]() $0\rightarrow B_{2}\rightarrow B_{1}\rightarrow B\rightarrow 0$ such that
$0\rightarrow B_{2}\rightarrow B_{1}\rightarrow B\rightarrow 0$ such that ![]() $B_{1}\in {\mathcal{G}}{\mathcal{P}}({\mathcal{B}})$ and
$B_{1}\in {\mathcal{G}}{\mathcal{P}}({\mathcal{B}})$ and ![]() $\operatorname{pdim}B_{2}<\infty$ by [Reference Auslander and Buchweitz2, Theorem 1.1]. Since
$\operatorname{pdim}B_{2}<\infty$ by [Reference Auslander and Buchweitz2, Theorem 1.1]. Since ![]() $\operatorname{Ext}_{{\mathcal{B}}}^{1}(B,B_{2})=0$ by assumption, the sequence is split. Hence,
$\operatorname{Ext}_{{\mathcal{B}}}^{1}(B,B_{2})=0$ by assumption, the sequence is split. Hence, ![]() $B$ is a direct summand of
$B$ is a direct summand of ![]() $B_{1}$, and therefore
$B_{1}$, and therefore ![]() $B\in {\mathcal{G}}{\mathcal{P}}({\mathcal{B}})$. This proves the claim.
$B\in {\mathcal{G}}{\mathcal{P}}({\mathcal{B}})$. This proves the claim.
Corollary 45. If ![]() ${\mathcal{B}}$ is
${\mathcal{B}}$ is ![]() $\operatorname{Proj}({\mathcal{B}})$-Gorenstein, then
$\operatorname{Proj}({\mathcal{B}})$-Gorenstein, then
In particular, this holds if ![]() ${\mathcal{B}}=\unicode[STIX]{x1D6EC}\text{-}\!\operatorname{mod}$ or
${\mathcal{B}}=\unicode[STIX]{x1D6EC}\text{-}\!\operatorname{mod}$ or ![]() ${\mathcal{B}}=\unicode[STIX]{x1D6EC}\text{-}\!\operatorname{Mod}$ for an Iwanaga–Gorenstein ring
${\mathcal{B}}=\unicode[STIX]{x1D6EC}\text{-}\!\operatorname{Mod}$ for an Iwanaga–Gorenstein ring ![]() $\unicode[STIX]{x1D6EC}$.
$\unicode[STIX]{x1D6EC}$.
For an abelian category ![]() ${\mathcal{A}}$ we let
${\mathcal{A}}$ we let ![]() $\unicode[STIX]{x1D6FA}^{\infty }({\mathcal{A}})$ denote the collection of objects
$\unicode[STIX]{x1D6FA}^{\infty }({\mathcal{A}})$ denote the collection of objects ![]() $A\in {\mathcal{A}}$ such that there exists an exact sequence
$A\in {\mathcal{A}}$ such that there exists an exact sequence ![]() $0\rightarrow A\rightarrow Q_{0}\rightarrow Q_{-1}\rightarrow \cdots \,$ with
$0\rightarrow A\rightarrow Q_{0}\rightarrow Q_{-1}\rightarrow \cdots \,$ with ![]() $Q_{i}\in {\mathcal{A}}$ projective for all
$Q_{i}\in {\mathcal{A}}$ projective for all ![]() $i\leqslant 0$.
$i\leqslant 0$.
Example 46. Let ![]() $k$ be a field, let
$k$ be a field, let ![]() $\unicode[STIX]{x1D6EC}_{1}$ be a finite-dimensional algebra over
$\unicode[STIX]{x1D6EC}_{1}$ be a finite-dimensional algebra over ![]() $k$, and let
$k$, and let ![]() $\unicode[STIX]{x1D6EC}_{2}$ be a left coherent
$\unicode[STIX]{x1D6EC}_{2}$ be a left coherent ![]() $k$-algebra. From Example 28 we have that
$k$-algebra. From Example 28 we have that
If ![]() $\unicode[STIX]{x1D6FA}^{\infty }(\unicode[STIX]{x1D6EC}\text{-}\!\operatorname{Mod})\subset {\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}\text{-}\!\operatorname{Mod})$ or
$\unicode[STIX]{x1D6FA}^{\infty }(\unicode[STIX]{x1D6EC}\text{-}\!\operatorname{Mod})\subset {\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}\text{-}\!\operatorname{Mod})$ or
then by Theorem 42 we have
In particular, the equality holds if ![]() $\unicode[STIX]{x1D6EC}_{1}$ or
$\unicode[STIX]{x1D6EC}_{1}$ or ![]() $\unicode[STIX]{x1D6EC}_{2}$ is Iwanaga–Gorenstein. This description of
$\unicode[STIX]{x1D6EC}_{2}$ is Iwanaga–Gorenstein. This description of ![]() ${\mathcal{G}}{\mathcal{P}}((\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod})$ has previously been obtained in [Reference Shen36], but it was only shown to hold under the assumption that
${\mathcal{G}}{\mathcal{P}}((\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod})$ has previously been obtained in [Reference Shen36], but it was only shown to hold under the assumption that ![]() $\unicode[STIX]{x1D6EC}_{1}$ is Iwanaga–Gorenstein.
$\unicode[STIX]{x1D6EC}_{1}$ is Iwanaga–Gorenstein.
Example 47. Let ![]() $k$ be a field, let
$k$ be a field, let ![]() $\unicode[STIX]{x1D6EC}_{1}$ be a finite-dimensional algebra over
$\unicode[STIX]{x1D6EC}_{1}$ be a finite-dimensional algebra over ![]() $k$, and let
$k$, and let ![]() $\unicode[STIX]{x1D6EC}_{2}$ be a
$\unicode[STIX]{x1D6EC}_{2}$ be a ![]() $k$-algebra. From Example 29 we get that if
$k$-algebra. From Example 29 we get that if ![]() $\unicode[STIX]{x1D6FA}^{\infty }(\unicode[STIX]{x1D6EC}\text{-}\!\operatorname{Mod})\subset {\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}\text{-}\!\operatorname{Mod})$ or
$\unicode[STIX]{x1D6FA}^{\infty }(\unicode[STIX]{x1D6EC}\text{-}\!\operatorname{Mod})\subset {\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}\text{-}\!\operatorname{Mod})$ or
then the criteria in Theorem 42 hold, and therefore
In particular, this equality holds if ![]() $\unicode[STIX]{x1D6EC}_{1}$ or
$\unicode[STIX]{x1D6EC}_{1}$ or ![]() $\unicode[STIX]{x1D6EC}_{2}$ are Iwanaga–Gorenstein.
$\unicode[STIX]{x1D6EC}_{2}$ are Iwanaga–Gorenstein.
Since ![]() ${\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}}))$ is closed under direct summands and contains all the projective objects, the projectively stable category
${\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}}))$ is closed under direct summands and contains all the projective objects, the projectively stable category ![]() $\text{}\underline{{\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}}))}$ is a thick triangulated subcategory of
$\text{}\underline{{\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}}))}$ is a thick triangulated subcategory of ![]() $\text{}\underline{{\mathcal{G}}{\mathcal{P}}({\mathcal{A}})}$.
$\text{}\underline{{\mathcal{G}}{\mathcal{P}}({\mathcal{A}})}$.
Definition 48. We define the Gorenstein discrepancy category of ![]() $P$ to be the Verdier quotient
$P$ to be the Verdier quotient ![]() $\operatorname{Discr}_{P}({\mathcal{A}})=\text{}\underline{{\mathcal{G}}{\mathcal{P}}({\mathcal{A}})}/\text{}\underline{{\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}}))}$.
$\operatorname{Discr}_{P}({\mathcal{A}})=\text{}\underline{{\mathcal{G}}{\mathcal{P}}({\mathcal{A}})}/\text{}\underline{{\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}}))}$.
The triangulated category ![]() $\operatorname{Discr}_{P}({\mathcal{A}})$ measures how far
$\operatorname{Discr}_{P}({\mathcal{A}})$ measures how far ![]() ${\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}}))$ is from
${\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}}))$ is from ![]() ${\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$. The following example shows that the Gorenstein discrepancy category can be nonzero.
${\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$. The following example shows that the Gorenstein discrepancy category can be nonzero.
Example 49. Let ![]() $k$ be a field, and let
$k$ be a field, and let ![]() $\unicode[STIX]{x1D6EC}_{1}$ be the path algebra of the quiver
$\unicode[STIX]{x1D6EC}_{1}$ be the path algebra of the quiver

with relations ![]() $\unicode[STIX]{x1D6FD}^{2}=\unicode[STIX]{x1D6FD}\circ \unicode[STIX]{x1D6FC}=0$. Let
$\unicode[STIX]{x1D6FD}^{2}=\unicode[STIX]{x1D6FD}\circ \unicode[STIX]{x1D6FC}=0$. Let ![]() $e_{1}$ and
$e_{1}$ and ![]() $e_{2}$ be the two primitive idempotents of
$e_{2}$ be the two primitive idempotents of ![]() $\unicode[STIX]{x1D6EC}_{1}$. Note that
$\unicode[STIX]{x1D6EC}_{1}$. Note that ![]() ${\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{mod})=\operatorname{Proj}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{mod})$. In fact, up to isomorphism the only indecomposable
${\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{mod})=\operatorname{Proj}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{mod})$. In fact, up to isomorphism the only indecomposable ![]() $\unicode[STIX]{x1D6EC}_{1}$-modules are the two simple modules
$\unicode[STIX]{x1D6EC}_{1}$-modules are the two simple modules ![]() $S_{1}$ and
$S_{1}$ and ![]() $S_{2}$ concentrated in vertex
$S_{2}$ concentrated in vertex ![]() $1$ and
$1$ and ![]() $2$, the two projective modules
$2$, the two projective modules ![]() $P_{1}=\unicode[STIX]{x1D6EC}e_{1}$ and
$P_{1}=\unicode[STIX]{x1D6EC}e_{1}$ and ![]() $P_{2}=\unicode[STIX]{x1D6EC}e_{2}$, and the two injective modules
$P_{2}=\unicode[STIX]{x1D6EC}e_{2}$, and the two injective modules ![]() $I_{1}=\operatorname{Hom}_{k}(e_{1}\unicode[STIX]{x1D6EC},k)$ and
$I_{1}=\operatorname{Hom}_{k}(e_{1}\unicode[STIX]{x1D6EC},k)$ and ![]() $I_{2}=\operatorname{Hom}_{k}(e_{2}\unicode[STIX]{x1D6EC},k)$. Furthermore, we have an equality
$I_{2}=\operatorname{Hom}_{k}(e_{2}\unicode[STIX]{x1D6EC},k)$. Furthermore, we have an equality ![]() $I_{2}=S_{1}$. Now since
$I_{2}=S_{1}$. Now since ![]() $I_{1}$ and
$I_{1}$ and ![]() $I_{2}$ are injective but not projective, they cannot be Gorenstein projective. Also,
$I_{2}$ are injective but not projective, they cannot be Gorenstein projective. Also, ![]() $S_{2}$ is not Gorenstein projective since there exists a nonsplit exact sequence
$S_{2}$ is not Gorenstein projective since there exists a nonsplit exact sequence
This shows that ![]() ${\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{mod})=\operatorname{Proj}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{mod})$. Now let
${\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{mod})=\operatorname{Proj}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{mod})$. Now let ![]() $\unicode[STIX]{x1D6EC}_{2}$ be a finite-dimensional
$\unicode[STIX]{x1D6EC}_{2}$ be a finite-dimensional ![]() $k$-algebra. A module
$k$-algebra. A module ![]() $M\in (\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}$ can be identified with a representation
$M\in (\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}$ can be identified with a representation

where ![]() $M_{1},M_{2}\in \unicode[STIX]{x1D6EC}_{2}\text{-}\!\operatorname{mod}$ and
$M_{1},M_{2}\in \unicode[STIX]{x1D6EC}_{2}\text{-}\!\operatorname{mod}$ and ![]() $u,v$ are morphisms of
$u,v$ are morphisms of ![]() $\unicode[STIX]{x1D6EC}_{2}$-modules satisfying
$\unicode[STIX]{x1D6EC}_{2}$-modules satisfying ![]() $v^{2}=0$ and
$v^{2}=0$ and ![]() $v\circ u=0$. Let
$v\circ u=0$. Let
 $$\begin{eqnarray}\displaystyle & & \displaystyle f^{\ast }:=\operatorname{res}_{\unicode[STIX]{x1D6EC}_{2}}^{\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2}}:(\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}\rightarrow \unicode[STIX]{x1D6EC}_{2}\text{-}\!\operatorname{mod}\nonumber\\ \displaystyle & & \displaystyle f_{!}:=\unicode[STIX]{x1D6EC}_{1}\otimes _{k}-:\unicode[STIX]{x1D6EC}_{2}\text{-}\!\operatorname{mod}\rightarrow (\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}\nonumber\\ \displaystyle & & \displaystyle \unicode[STIX]{x1D708}_{1}:=\operatorname{Hom}_{k}(\unicode[STIX]{x1D6EC}_{1},k)\otimes _{\unicode[STIX]{x1D6EC}_{1}}-:(\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}\rightarrow (\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle f^{\ast }:=\operatorname{res}_{\unicode[STIX]{x1D6EC}_{2}}^{\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2}}:(\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}\rightarrow \unicode[STIX]{x1D6EC}_{2}\text{-}\!\operatorname{mod}\nonumber\\ \displaystyle & & \displaystyle f_{!}:=\unicode[STIX]{x1D6EC}_{1}\otimes _{k}-:\unicode[STIX]{x1D6EC}_{2}\text{-}\!\operatorname{mod}\rightarrow (\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}\nonumber\\ \displaystyle & & \displaystyle \unicode[STIX]{x1D708}_{1}:=\operatorname{Hom}_{k}(\unicode[STIX]{x1D6EC}_{1},k)\otimes _{\unicode[STIX]{x1D6EC}_{1}}-:(\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}\rightarrow (\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}\nonumber\end{eqnarray}$$and
 $$\begin{eqnarray}\displaystyle & & \displaystyle g^{\ast }:=\operatorname{res}_{\unicode[STIX]{x1D6EC}_{1}}^{\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2}}:(\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}\rightarrow \unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{mod}\nonumber\\ \displaystyle & & \displaystyle g_{!}:=\unicode[STIX]{x1D6EC}_{2}\otimes _{k}-:\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{mod}\rightarrow (\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}\nonumber\\ \displaystyle & & \displaystyle \unicode[STIX]{x1D708}_{2}:=\operatorname{Hom}_{k}(\unicode[STIX]{x1D6EC}_{2},k)\otimes _{\unicode[STIX]{x1D6EC}_{2}}-:(\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}\rightarrow (\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle g^{\ast }:=\operatorname{res}_{\unicode[STIX]{x1D6EC}_{1}}^{\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2}}:(\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}\rightarrow \unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{mod}\nonumber\\ \displaystyle & & \displaystyle g_{!}:=\unicode[STIX]{x1D6EC}_{2}\otimes _{k}-:\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{mod}\rightarrow (\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}\nonumber\\ \displaystyle & & \displaystyle \unicode[STIX]{x1D708}_{2}:=\operatorname{Hom}_{k}(\unicode[STIX]{x1D6EC}_{2},k)\otimes _{\unicode[STIX]{x1D6EC}_{2}}-:(\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}\rightarrow (\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}\nonumber\end{eqnarray}$$ be two adjoint pairs with Nakayama functors as in Example 22. Let ![]() $P_{1}:=f_{!}\circ f^{\ast }$ and
$P_{1}:=f_{!}\circ f^{\ast }$ and ![]() $P_{2}:=g_{!}\circ g^{\ast }$. We have that
$P_{2}:=g_{!}\circ g^{\ast }$. We have that
and
as in Example 46. Note that ![]() $_{\unicode[STIX]{x1D6EC}_{1}}M\in {\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{mod})=\operatorname{Proj}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{mod})$ if and only if the following holds:
$_{\unicode[STIX]{x1D6EC}_{1}}M\in {\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{mod})=\operatorname{Proj}(\unicode[STIX]{x1D6EC}_{1}\text{-}\!\operatorname{mod})$ if and only if the following holds:
(i)
 $u$ is a monomorphism;
$u$ is a monomorphism;(ii)
 $\operatorname{im}u\cap \operatorname{im}v=(0)$;
$\operatorname{im}u\cap \operatorname{im}v=(0)$;(iii)
 $\operatorname{im}u\oplus \operatorname{im}v=\operatorname{Ker}v$.
$\operatorname{im}u\oplus \operatorname{im}v=\operatorname{Ker}v$.
Also, a simple computation shows that
Hence, ![]() $M\in {\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P_{1}}((\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}))$ if and only the following holds:
$M\in {\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P_{1}}((\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}))$ if and only the following holds:
(i)
 $u:M_{1}\rightarrow M_{2}$ is a monomorphism;
$u:M_{1}\rightarrow M_{2}$ is a monomorphism;(ii)
 $\operatorname{im}u\cap \operatorname{im}v=(0)$;
$\operatorname{im}u\cap \operatorname{im}v=(0)$;(iii)
 $\operatorname{im}u\oplus \operatorname{im}v=\operatorname{Ker}v$;
$\operatorname{im}u\oplus \operatorname{im}v=\operatorname{Ker}v$;(iv)
 $\operatorname{Coker}u,\operatorname{Coker}v\in {\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{2}\text{-}\!\operatorname{mod})$.
$\operatorname{Coker}u,\operatorname{Coker}v\in {\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{2}\text{-}\!\operatorname{mod})$.
Also, ![]() $M\in {\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P_{2}}((\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}))$ if and only the following holds:
$M\in {\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P_{2}}((\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}))$ if and only the following holds:
(i)
 $M_{1},M_{2}\in {\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{2}\operatorname{mod})$;
$M_{1},M_{2}\in {\mathcal{G}}{\mathcal{P}}(\unicode[STIX]{x1D6EC}_{2}\operatorname{mod})$;(ii)
 $1\otimes _{}u$ is a monomorphism;
$1\otimes _{}u$ is a monomorphism;(iii)
 $\operatorname{im}(1\otimes _{}u)\cap \operatorname{im}(1\otimes _{}v)=(0)$;
$\operatorname{im}(1\otimes _{}u)\cap \operatorname{im}(1\otimes _{}v)=(0)$;(iv)
 $\operatorname{im}(1\otimes _{}u)\oplus \operatorname{im}(1\otimes _{}v)=\operatorname{Ker}(1\otimes _{}v)$.
$\operatorname{im}(1\otimes _{}u)\oplus \operatorname{im}(1\otimes _{}v)=\operatorname{Ker}(1\otimes _{}v)$.
where
Now set ![]() $\unicode[STIX]{x1D6EC}_{2}:=\unicode[STIX]{x1D6EC}_{1}^{\text{op}}$, and let
$\unicode[STIX]{x1D6EC}_{2}:=\unicode[STIX]{x1D6EC}_{1}^{\text{op}}$, and let ![]() $Q_{2}=\unicode[STIX]{x1D6EC}_{2}e_{2}$ and
$Q_{2}=\unicode[STIX]{x1D6EC}_{2}e_{2}$ and ![]() $J_{2}=\operatorname{Hom}_{k}(e_{2}\unicode[STIX]{x1D6EC}_{2},k)$ be the projective and injective left
$J_{2}=\operatorname{Hom}_{k}(e_{2}\unicode[STIX]{x1D6EC}_{2},k)$ be the projective and injective left ![]() $\unicode[STIX]{x1D6EC}_{2}$-module corresponding to vertex 2. Furthermore, let
$\unicode[STIX]{x1D6EC}_{2}$-module corresponding to vertex 2. Furthermore, let ![]() $s:Q_{2}\rightarrow Q_{2}$ be a nonzero morphism satisfying
$s:Q_{2}\rightarrow Q_{2}$ be a nonzero morphism satisfying ![]() $s^{2}=0$ (there exists a unique one up to scalars). Let
$s^{2}=0$ (there exists a unique one up to scalars). Let ![]() $M\in \unicode[STIX]{x1D6EC}_{1}\otimes \unicode[STIX]{x1D6EC}_{2}\text{-}\!\operatorname{mod}$ be given by
$M\in \unicode[STIX]{x1D6EC}_{1}\otimes \unicode[STIX]{x1D6EC}_{2}\text{-}\!\operatorname{mod}$ be given by ![]() $M_{1}=0$,
$M_{1}=0$, ![]() $M_{2}=Q_{2}$ and
$M_{2}=Q_{2}$ and ![]() $v=s$. Under the isomorphism
$v=s$. Under the isomorphism ![]() $\operatorname{Hom}_{k}(\unicode[STIX]{x1D6EC}_{2},k)\otimes _{\unicode[STIX]{x1D6EC}_{2}}Q_{2}\cong J_{2}$ the map
$\operatorname{Hom}_{k}(\unicode[STIX]{x1D6EC}_{2},k)\otimes _{\unicode[STIX]{x1D6EC}_{2}}Q_{2}\cong J_{2}$ the map ![]() $s$ corresponds to a nonzero map
$s$ corresponds to a nonzero map ![]() $t:J_{2}\rightarrow J_{2}$ satisfying
$t:J_{2}\rightarrow J_{2}$ satisfying ![]() $t^{2}=0$. There exists a unique such map up to scalars, and it also satisfies
$t^{2}=0$. There exists a unique such map up to scalars, and it also satisfies ![]() $\operatorname{im}t=\ker t$. This shows that
$\operatorname{im}t=\ker t$. This shows that ![]() $M\in {\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P_{2}}((\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}))$, and
$M\in {\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P_{2}}((\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}))$, and ![]() $M$ is therefore Gorenstein projective in
$M$ is therefore Gorenstein projective in ![]() $(\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}$. On the other hand, we have that
$(\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}$. On the other hand, we have that ![]() $\operatorname{im}s\neq \operatorname{Ker}s$, and hence
$\operatorname{im}s\neq \operatorname{Ker}s$, and hence ![]() $M\notin {\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P_{1}}((\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}))$. This shows that the discrepancy category corresponding to
$M\notin {\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P_{1}}((\unicode[STIX]{x1D6EC}_{1}\otimes _{k}\unicode[STIX]{x1D6EC}_{2})\text{-}\!\operatorname{mod}))$. This shows that the discrepancy category corresponding to ![]() $P_{1}$ is nonzero.
$P_{1}$ is nonzero.
We end this section with a result on the Gorenstein projective dimension of ![]() ${\mathcal{A}}$.
${\mathcal{A}}$.
Proposition 51. We have the inequality
Proof. It is obviously true if ![]() $\operatorname{gl.Gpdim}{\mathcal{B}}=\infty$ or
$\operatorname{gl.Gpdim}{\mathcal{B}}=\infty$ or ![]() $\dim _{{\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})}{\mathcal{A}}=\infty$. We therefore assume
$\dim _{{\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})}{\mathcal{A}}=\infty$. We therefore assume ![]() $\operatorname{gl.Gpdim}{\mathcal{B}}=n<\infty$ and
$\operatorname{gl.Gpdim}{\mathcal{B}}=n<\infty$ and ![]() $\dim _{{\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})}{\mathcal{A}}=m<\infty$. Let
$\dim _{{\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})}{\mathcal{A}}=m<\infty$. Let ![]() $A\in {\mathcal{A}}$ be arbitrary, and let
$A\in {\mathcal{A}}$ be arbitrary, and let
be an exact sequence in ![]() ${\mathcal{A}}$ with
${\mathcal{A}}$ with ![]() $Q_{j}$ projective for
$Q_{j}$ projective for ![]() $1\leqslant j\leqslant n+m$. Since
$1\leqslant j\leqslant n+m$. Since ![]() $Q_{j}$ is in
$Q_{j}$ is in ![]() ${\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$ and
${\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$ and ![]() $\dim _{{\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})}A\leqslant m$, we get that
$\dim _{{\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})}A\leqslant m$, we get that ![]() $\operatorname{Ker}s_{j}\in {\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$ for
$\operatorname{Ker}s_{j}\in {\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}})$ for ![]() $j\geqslant m$. In particular, this implies that the sequence
$j\geqslant m$. In particular, this implies that the sequence
 $$\begin{eqnarray}\displaystyle 0\rightarrow f^{\ast }\unicode[STIX]{x1D708}(K)\xrightarrow[{}]{f^{\ast }\unicode[STIX]{x1D708}(i)}f^{\ast }\unicode[STIX]{x1D708}(Q_{n+m})\xrightarrow[{}]{f^{\ast }\unicode[STIX]{x1D708}(s_{n+m})}\cdots & & \displaystyle \nonumber\\ \displaystyle \xrightarrow[{}]{f^{\ast }\unicode[STIX]{x1D708}(s_{m+2})}f^{\ast }\unicode[STIX]{x1D708}(Q_{m+1})\xrightarrow[{}]{}f^{\ast }\unicode[STIX]{x1D708}(\operatorname{Ker}s_{m})\rightarrow 0 & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0\rightarrow f^{\ast }\unicode[STIX]{x1D708}(K)\xrightarrow[{}]{f^{\ast }\unicode[STIX]{x1D708}(i)}f^{\ast }\unicode[STIX]{x1D708}(Q_{n+m})\xrightarrow[{}]{f^{\ast }\unicode[STIX]{x1D708}(s_{n+m})}\cdots & & \displaystyle \nonumber\\ \displaystyle \xrightarrow[{}]{f^{\ast }\unicode[STIX]{x1D708}(s_{m+2})}f^{\ast }\unicode[STIX]{x1D708}(Q_{m+1})\xrightarrow[{}]{}f^{\ast }\unicode[STIX]{x1D708}(\operatorname{Ker}s_{m})\rightarrow 0 & & \displaystyle \nonumber\end{eqnarray}$$ is exact. Since ![]() $f^{\ast }\unicode[STIX]{x1D708}(Q_{j})$ is projective in
$f^{\ast }\unicode[STIX]{x1D708}(Q_{j})$ is projective in ![]() ${\mathcal{B}}$ and
${\mathcal{B}}$ and ![]() $\operatorname{G.pdim}f^{\ast }\unicode[STIX]{x1D708}(\operatorname{Ker}s_{m})\leqslant n$, we get that
$\operatorname{G.pdim}f^{\ast }\unicode[STIX]{x1D708}(\operatorname{Ker}s_{m})\leqslant n$, we get that ![]() $f^{\ast }\unicode[STIX]{x1D708}(K)\in {\mathcal{G}}{\mathcal{P}}({\mathcal{B}})$. Hence,
$f^{\ast }\unicode[STIX]{x1D708}(K)\in {\mathcal{G}}{\mathcal{P}}({\mathcal{B}})$. Hence, ![]() $K\in {\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}}))={\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$, and the claim follows.
$K\in {\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{A}}))={\mathcal{G}}{\mathcal{P}}({\mathcal{A}})$, and the claim follows.
4 Application to functor categories
Our goal in this section is to compute ![]() ${\mathcal{G}}{\mathcal{P}}({\mathcal{B}}^{{\mathcal{C}}})$ in examples using the theory we have developed.
${\mathcal{G}}{\mathcal{P}}({\mathcal{B}}^{{\mathcal{C}}})$ in examples using the theory we have developed.
4.1 Preliminaries
Let ![]() $k$ be a commutative ring, and let
$k$ be a commutative ring, and let ![]() ${\mathcal{C}}$ be a small
${\mathcal{C}}$ be a small ![]() $k$-linear category. Recall that a right
$k$-linear category. Recall that a right ![]() ${\mathcal{C}}$-module is a
${\mathcal{C}}$-module is a ![]() $k$-linear functor
$k$-linear functor ![]() ${\mathcal{C}}^{\text{op}}\rightarrow k\text{-}\!\operatorname{Mod}$. We let
${\mathcal{C}}^{\text{op}}\rightarrow k\text{-}\!\operatorname{Mod}$. We let ![]() $\operatorname{Mod}\!\text{-}{\mathcal{C}}$ denote the categories of right
$\operatorname{Mod}\!\text{-}{\mathcal{C}}$ denote the categories of right ![]() ${\mathcal{C}}$-modules. A right
${\mathcal{C}}$-modules. A right ![]() ${\mathcal{C}}$-module
${\mathcal{C}}$-module ![]() $M$ is called finitely presented if there exists an exact sequence
$M$ is called finitely presented if there exists an exact sequence
in ![]() $\operatorname{Mod}\!\text{-}{\mathcal{C}}$ for objects
$\operatorname{Mod}\!\text{-}{\mathcal{C}}$ for objects ![]() $c_{i},d_{j}\in {\mathcal{C}}$. The category of finitely presented right
$c_{i},d_{j}\in {\mathcal{C}}$. The category of finitely presented right ![]() ${\mathcal{C}}$-modules is denoted by
${\mathcal{C}}$-modules is denoted by ![]() $\operatorname{mod}\!\text{-}{\mathcal{C}}$. Dually, the category of left
$\operatorname{mod}\!\text{-}{\mathcal{C}}$. Dually, the category of left ![]() ${\mathcal{C}}$-modules and finitely presented left
${\mathcal{C}}$-modules and finitely presented left ![]() ${\mathcal{C}}$-modules are
${\mathcal{C}}$-modules are ![]() $\operatorname{Mod}\!\text{-}{\mathcal{C}}^{\text{op}}$ and
$\operatorname{Mod}\!\text{-}{\mathcal{C}}^{\text{op}}$ and ![]() $\operatorname{mod}\!\text{-}{\mathcal{C}}^{\text{op}}$, respectively.
$\operatorname{mod}\!\text{-}{\mathcal{C}}^{\text{op}}$, respectively.
Let ![]() ${\mathcal{B}}$ be a
${\mathcal{B}}$ be a ![]() $k$-linear abelian category, and let
$k$-linear abelian category, and let ![]() ${\mathcal{B}}^{{\mathcal{C}}}$ denote the category of
${\mathcal{B}}^{{\mathcal{C}}}$ denote the category of ![]() $k$-linear functors from
$k$-linear functors from ![]() ${\mathcal{C}}$ to
${\mathcal{C}}$ to ![]() ${\mathcal{B}}$. Up to isomorphism there exists a unique functor
${\mathcal{B}}$. Up to isomorphism there exists a unique functor
such that ![]() ${\mathcal{C}}(c,-)\otimes _{{\mathcal{C}}}F=F(c)$ and the induced functor
${\mathcal{C}}(c,-)\otimes _{{\mathcal{C}}}F=F(c)$ and the induced functor ![]() $-\otimes _{{\mathcal{C}}}F:\operatorname{mod}\!\text{-}{\mathcal{C}}\rightarrow {\mathcal{B}}$ is right exact for all
$-\otimes _{{\mathcal{C}}}F:\operatorname{mod}\!\text{-}{\mathcal{C}}\rightarrow {\mathcal{B}}$ is right exact for all ![]() $F\in {\mathcal{B}}^{{\mathcal{C}}}$, see [Reference Kelly27, chapter 3] or [Reference Oberst and Röhrl33] for details. If
$F\in {\mathcal{B}}^{{\mathcal{C}}}$, see [Reference Kelly27, chapter 3] or [Reference Oberst and Röhrl33] for details. If ![]() ${\mathcal{C}}=k$ we get a functor
${\mathcal{C}}=k$ we get a functor
For ![]() $N\in {\mathcal{C}}\text{-}\!\operatorname{mod}$ and
$N\in {\mathcal{C}}\text{-}\!\operatorname{mod}$ and ![]() $B\in {\mathcal{B}}$ we have a functor
$B\in {\mathcal{B}}$ we have a functor ![]() $N\otimes _{k}B\in {\mathcal{B}}^{{\mathcal{C}}}$ given by
$N\otimes _{k}B\in {\mathcal{B}}^{{\mathcal{C}}}$ given by ![]() $c\mapsto N(c)\otimes _{k}B$. If furthermore
$c\mapsto N(c)\otimes _{k}B$. If furthermore ![]() $M\in \operatorname{mod}\!\text{-}{\mathcal{C}}$ then we get a natural isomorphism
$M\in \operatorname{mod}\!\text{-}{\mathcal{C}}$ then we get a natural isomorphism
see [Reference Kelly27, (3.23)].
We use the same terminology as in [Reference Dell’Ambrogio, Stevenson and Stovicek12] in the following definition.
Definition 52. Let ![]() ${\mathcal{C}}$ be a small
${\mathcal{C}}$ be a small ![]() $k$-linear category.
$k$-linear category.
(i)
 ${\mathcal{C}}$ is locally bounded if for any object
${\mathcal{C}}$ is locally bounded if for any object  $c\in {\mathcal{C}}$ there are only finitely many objects in
$c\in {\mathcal{C}}$ there are only finitely many objects in  ${\mathcal{C}}$ mapping nontrivially in and out of
${\mathcal{C}}$ mapping nontrivially in and out of  $c$. This means that for each
$c$. This means that for each  $c\in {\mathcal{C}}$ we have
$c\in {\mathcal{C}}$ we have  $$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{C}}(c,c^{\prime })\neq 0\quad \text{for only finitely many }c^{\prime }\in {\mathcal{C}}\nonumber\\ \displaystyle & & \displaystyle {\mathcal{C}}(c^{\prime \prime },c)\neq 0\quad \text{for only finitely many }c^{\prime \prime }\in {\mathcal{C}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{C}}(c,c^{\prime })\neq 0\quad \text{for only finitely many }c^{\prime }\in {\mathcal{C}}\nonumber\\ \displaystyle & & \displaystyle {\mathcal{C}}(c^{\prime \prime },c)\neq 0\quad \text{for only finitely many }c^{\prime \prime }\in {\mathcal{C}}.\nonumber\end{eqnarray}$$(ii)
 ${\mathcal{C}}$ is Hom-finite if
${\mathcal{C}}$ is Hom-finite if  ${\mathcal{C}}(c,c^{\prime })$ is a finitely generated projective
${\mathcal{C}}(c,c^{\prime })$ is a finitely generated projective  $k$-module for all
$k$-module for all  $c,c^{\prime }\in {\mathcal{C}}$.
$c,c^{\prime }\in {\mathcal{C}}$.
If ![]() ${\mathcal{C}}$ is locally bounded and Hom-finite, and
${\mathcal{C}}$ is locally bounded and Hom-finite, and ![]() $M\in \operatorname{Mod}\!\text{-}{\mathcal{C}}$ satisfies
$M\in \operatorname{Mod}\!\text{-}{\mathcal{C}}$ satisfies
(i)
 $M(c)$ is a finitely generated projective
$M(c)$ is a finitely generated projective  $k$-module for all
$k$-module for all  $c\in {\mathcal{C}}$
$c\in {\mathcal{C}}$(ii)
 $M(c)\neq 0$ for only finitely many
$M(c)\neq 0$ for only finitely many  $c\in {\mathcal{C}}$
$c\in {\mathcal{C}}$
then it follows from [Reference Kvamme28, Lemma 5.2.2] that ![]() $M\in \operatorname{mod}\!\text{-}{\mathcal{C}}$.
$M\in \operatorname{mod}\!\text{-}{\mathcal{C}}$.
Let ![]() $k(\operatorname{ob}\text{-}{\mathcal{C}})$ be the category with the same objects as
$k(\operatorname{ob}\text{-}{\mathcal{C}})$ be the category with the same objects as ![]() ${\mathcal{C}}$, and with morphisms
${\mathcal{C}}$, and with morphisms
The functor category ![]() ${\mathcal{B}}^{k(\operatorname{ob}\text{-}{\mathcal{C}})}$ is just a product of copies of
${\mathcal{B}}^{k(\operatorname{ob}\text{-}{\mathcal{C}})}$ is just a product of copies of ![]() ${\mathcal{B}}$, indexed over the objects of
${\mathcal{B}}$, indexed over the objects of ![]() ${\mathcal{C}}$. Let
${\mathcal{C}}$. Let ![]() $i:k(\operatorname{ob}\text{-}{\mathcal{C}})\rightarrow {\mathcal{C}}$ be the inclusion. We have functors
$i:k(\operatorname{ob}\text{-}{\mathcal{C}})\rightarrow {\mathcal{C}}$ be the inclusion. We have functors
 $$\begin{eqnarray}\displaystyle & & \displaystyle i_{!}:{\mathcal{B}}^{k(\operatorname{ob}\text{-}{\mathcal{C}})}\rightarrow {\mathcal{B}}^{{\mathcal{C}}}\quad i_{!}((B^{c})_{c\in {\mathcal{C}}})=\bigoplus _{c\in {\mathcal{C}}}{\mathcal{C}}(c,-)\otimes _{k}B^{c}\nonumber\\ \displaystyle & & \displaystyle i^{\ast }:{\mathcal{B}}^{{\mathcal{C}}}\rightarrow {\mathcal{B}}^{k(\operatorname{ob}\text{-}{\mathcal{C}})}\quad i^{\ast }(F)=(F(c))_{c\in {\mathcal{C}}}\nonumber\\ \displaystyle & & \displaystyle \unicode[STIX]{x1D708}:{\mathcal{B}}^{{\mathcal{C}}}\rightarrow {\mathcal{B}}^{{\mathcal{C}}}\quad \unicode[STIX]{x1D708}(F)=D({\mathcal{C}})\otimes _{{\mathcal{C}}}F\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle i_{!}:{\mathcal{B}}^{k(\operatorname{ob}\text{-}{\mathcal{C}})}\rightarrow {\mathcal{B}}^{{\mathcal{C}}}\quad i_{!}((B^{c})_{c\in {\mathcal{C}}})=\bigoplus _{c\in {\mathcal{C}}}{\mathcal{C}}(c,-)\otimes _{k}B^{c}\nonumber\\ \displaystyle & & \displaystyle i^{\ast }:{\mathcal{B}}^{{\mathcal{C}}}\rightarrow {\mathcal{B}}^{k(\operatorname{ob}\text{-}{\mathcal{C}})}\quad i^{\ast }(F)=(F(c))_{c\in {\mathcal{C}}}\nonumber\\ \displaystyle & & \displaystyle \unicode[STIX]{x1D708}:{\mathcal{B}}^{{\mathcal{C}}}\rightarrow {\mathcal{B}}^{{\mathcal{C}}}\quad \unicode[STIX]{x1D708}(F)=D({\mathcal{C}})\otimes _{{\mathcal{C}}}F\nonumber\end{eqnarray}$$ where ![]() $D=\operatorname{Hom}_{k}(-,k)$ and
$D=\operatorname{Hom}_{k}(-,k)$ and ![]() $(D({\mathcal{C}})\otimes _{{\mathcal{C}}}F)(c)=D({\mathcal{C}}(c,-))\otimes _{{\mathcal{C}}}F$, see [Reference Kvamme28, Section 5.3] for details.
$(D({\mathcal{C}})\otimes _{{\mathcal{C}}}F)(c)=D({\mathcal{C}}(c,-))\otimes _{{\mathcal{C}}}F$, see [Reference Kvamme28, Section 5.3] for details.
Theorem 53. [Reference Kvamme28, Theorem 5.3.3]
Let ![]() ${\mathcal{C}}$ be a small,
${\mathcal{C}}$ be a small, ![]() $k$-linear, locally bounded and Hom-finite category, let
$k$-linear, locally bounded and Hom-finite category, let ![]() ${\mathcal{B}}$ be a
${\mathcal{B}}$ be a ![]() $k$-linear abelian category, and let
$k$-linear abelian category, and let ![]() $i_{!}$,
$i_{!}$, ![]() $i^{\ast }$ and
$i^{\ast }$ and ![]() $\unicode[STIX]{x1D708}$ be as above. Then
$\unicode[STIX]{x1D708}$ be as above. Then ![]() $\unicode[STIX]{x1D708}$ is a Nakayama functor relative to
$\unicode[STIX]{x1D708}$ is a Nakayama functor relative to ![]() $i_{!}\dashv i^{\ast }$.
$i_{!}\dashv i^{\ast }$.
Theorem 54. [Reference Kvamme28, Theorem 5.3.4]
Let ![]() ${\mathcal{C}}$ be a small,
${\mathcal{C}}$ be a small, ![]() $k$-linear, locally bounded, and Hom-finite category, and let
$k$-linear, locally bounded, and Hom-finite category, and let ![]() $i_{!}$,
$i_{!}$, ![]() $i^{\ast }$ and
$i^{\ast }$ and ![]() $\unicode[STIX]{x1D708}$ be as above with
$\unicode[STIX]{x1D708}$ be as above with ![]() ${\mathcal{B}}=k\text{-}\!\operatorname{Mod}$. Then
${\mathcal{B}}=k\text{-}\!\operatorname{Mod}$. Then
if and only if the endofunctor ![]() $P=i_{!}\circ i^{\ast }:{\mathcal{C}}\text{-}\!\operatorname{Mod}\rightarrow {\mathcal{C}}\text{-}\!\operatorname{Mod}$ is Iwanaga–Gorenstein. In this case we have that
$P=i_{!}\circ i^{\ast }:{\mathcal{C}}\text{-}\!\operatorname{Mod}\rightarrow {\mathcal{C}}\text{-}\!\operatorname{Mod}$ is Iwanaga–Gorenstein. In this case we have that
and this number is equal to the Gorenstein dimension of the functor ![]() $P$.
$P$.
4.2 Properties of locally bounded and Hom-finite categories
In this subsection we fix a small, ![]() $k$-linear, locally bounded and Hom-finite category
$k$-linear, locally bounded and Hom-finite category ![]() ${\mathcal{C}}$ and a
${\mathcal{C}}$ and a ![]() $k$-linear abelian category
$k$-linear abelian category ![]() ${\mathcal{B}}$. Let
${\mathcal{B}}$. Let ![]() $M$ be a finitely presented right
$M$ be a finitely presented right ![]() ${\mathcal{C}}$-module. Since
${\mathcal{C}}$-module. Since
it follows that the functor ![]() $(M\otimes _{{\mathcal{C}}}-)\circ i_{!}\circ i^{\ast }:{\mathcal{B}}^{{\mathcal{C}}}\rightarrow {\mathcal{B}}^{{\mathcal{C}}}$ is exact if
$(M\otimes _{{\mathcal{C}}}-)\circ i_{!}\circ i^{\ast }:{\mathcal{B}}^{{\mathcal{C}}}\rightarrow {\mathcal{B}}^{{\mathcal{C}}}$ is exact if ![]() $M(c)$ is a finitely generated projective
$M(c)$ is a finitely generated projective ![]() $k$-module for all
$k$-module for all ![]() $c\in {\mathcal{C}}$. By Proposition 13 part (ii) we have that
$c\in {\mathcal{C}}$. By Proposition 13 part (ii) we have that ![]() $i_{!}$ is adapted to
$i_{!}$ is adapted to ![]() $M\otimes _{{\mathcal{C}}}-$, and hence the left derived functor
$M\otimes _{{\mathcal{C}}}-$, and hence the left derived functor
exists.
Lemma 55. Let ![]() $0\rightarrow M_{3}\xrightarrow[{}]{f}M_{2}\xrightarrow[{}]{g}M_{1}\rightarrow 0$ be an exact sequence of finitely presented right
$0\rightarrow M_{3}\xrightarrow[{}]{f}M_{2}\xrightarrow[{}]{g}M_{1}\rightarrow 0$ be an exact sequence of finitely presented right ![]() ${\mathcal{C}}$-modules, and assume
${\mathcal{C}}$-modules, and assume ![]() $M_{i}(c)$ is a finitely generated projective
$M_{i}(c)$ is a finitely generated projective ![]() $k$-module for all
$k$-module for all ![]() $i$ and all
$i$ and all ![]() $c\in {\mathcal{C}}$. Then there exists a long exact sequence of functors
$c\in {\mathcal{C}}$. Then there exists a long exact sequence of functors
 $$\begin{eqnarray}\displaystyle \cdots \rightarrow \operatorname{Tor}_{i+1}^{{\mathcal{C}}}(M_{1},-)\rightarrow \operatorname{Tor}_{i}^{{\mathcal{C}}}(M_{3},-)\rightarrow \operatorname{Tor}_{i}^{{\mathcal{C}}}(M_{2},-)\rightarrow \operatorname{Tor}_{i}^{{\mathcal{C}}}(M_{1},-)\rightarrow & & \displaystyle \nonumber\\ \displaystyle \cdots \rightarrow \operatorname{Tor}_{1}^{{\mathcal{C}}}(M_{1},-)\rightarrow (M_{3}\otimes _{{\mathcal{C}}}-)\xrightarrow[{}]{f\otimes 1}(M_{2}\otimes _{{\mathcal{C}}}-)\xrightarrow[{}]{g\otimes 1}(M_{1}\otimes _{{\mathcal{C}}}-)\rightarrow 0. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \cdots \rightarrow \operatorname{Tor}_{i+1}^{{\mathcal{C}}}(M_{1},-)\rightarrow \operatorname{Tor}_{i}^{{\mathcal{C}}}(M_{3},-)\rightarrow \operatorname{Tor}_{i}^{{\mathcal{C}}}(M_{2},-)\rightarrow \operatorname{Tor}_{i}^{{\mathcal{C}}}(M_{1},-)\rightarrow & & \displaystyle \nonumber\\ \displaystyle \cdots \rightarrow \operatorname{Tor}_{1}^{{\mathcal{C}}}(M_{1},-)\rightarrow (M_{3}\otimes _{{\mathcal{C}}}-)\xrightarrow[{}]{f\otimes 1}(M_{2}\otimes _{{\mathcal{C}}}-)\xrightarrow[{}]{g\otimes 1}(M_{1}\otimes _{{\mathcal{C}}}-)\rightarrow 0. & & \displaystyle \nonumber\end{eqnarray}$$Proof. Consider the sequence
of functors. Evaluating at the object ![]() $i_{!}i^{\ast }(F)=\bigoplus _{c\in {\mathcal{C}}}{\mathcal{C}}(c,-)\otimes _{k}F(c)$ gives the exact sequence
$i_{!}i^{\ast }(F)=\bigoplus _{c\in {\mathcal{C}}}{\mathcal{C}}(c,-)\otimes _{k}F(c)$ gives the exact sequence
 $$\begin{eqnarray}\displaystyle & & \displaystyle 0\rightarrow \bigoplus _{c\in {\mathcal{C}}}M_{3}(c)\otimes _{k}F(c)\xrightarrow[{}]{f\otimes 1}\bigoplus _{c\in {\mathcal{C}}}M_{2}(c)\otimes _{k}F(c)\xrightarrow[{}]{g\otimes 1}\nonumber\\ \displaystyle & & \displaystyle \qquad \bigoplus _{c\in {\mathcal{C}}}M_{1}(c)\otimes _{k}F(c)\rightarrow 0.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle 0\rightarrow \bigoplus _{c\in {\mathcal{C}}}M_{3}(c)\otimes _{k}F(c)\xrightarrow[{}]{f\otimes 1}\bigoplus _{c\in {\mathcal{C}}}M_{2}(c)\otimes _{k}F(c)\xrightarrow[{}]{g\otimes 1}\nonumber\\ \displaystyle & & \displaystyle \qquad \bigoplus _{c\in {\mathcal{C}}}M_{1}(c)\otimes _{k}F(c)\rightarrow 0.\nonumber\end{eqnarray}$$The claim follows therefore by Lemma 14.
From now on we let ![]() $P_{{\mathcal{B}}^{{\mathcal{C}}}}=i_{!}\circ i^{\ast }$ denote the endofunctor on
$P_{{\mathcal{B}}^{{\mathcal{C}}}}=i_{!}\circ i^{\ast }$ denote the endofunctor on ![]() ${\mathcal{B}}^{{\mathcal{C}}}$ and
${\mathcal{B}}^{{\mathcal{C}}}$ and ![]() $P_{{\mathcal{C}}\text{-}\!\operatorname{Mod}}$ the endofunctor on
$P_{{\mathcal{C}}\text{-}\!\operatorname{Mod}}$ the endofunctor on ![]() ${\mathcal{C}}\text{-}\!\operatorname{Mod}$ in Theorem 54.
${\mathcal{C}}\text{-}\!\operatorname{Mod}$ in Theorem 54.
Lemma 56. Assume ![]() $P_{{\mathcal{C}}\text{-}\!\operatorname{Mod}}$ is
$P_{{\mathcal{C}}\text{-}\!\operatorname{Mod}}$ is ![]() $n$-Gorenstein. Then
$n$-Gorenstein. Then ![]() $P_{{\mathcal{B}}^{{\mathcal{C}}}}$ is
$P_{{\mathcal{B}}^{{\mathcal{C}}}}$ is ![]() $m$-Gorenstein where
$m$-Gorenstein where ![]() $m\leqslant n$.
$m\leqslant n$.
Proof. Let ![]() $c\in {\mathcal{C}}$ be arbitrary. By Theorem 54 there exists an exact sequence
$c\in {\mathcal{C}}$ be arbitrary. By Theorem 54 there exists an exact sequence
in ![]() $\operatorname{mod}\!\text{-}{\mathcal{C}}$ where
$\operatorname{mod}\!\text{-}{\mathcal{C}}$ where ![]() $M_{i}$ are projective. By Lemma 55 and dimension shifting we get that
$M_{i}$ are projective. By Lemma 55 and dimension shifting we get that
is ![]() $0$ for all
$0$ for all ![]() $j\geqslant n+1$. Since
$j\geqslant n+1$. Since ![]() $c\in {\mathcal{C}}$ was arbitrary we get that
$c\in {\mathcal{C}}$ was arbitrary we get that
is ![]() $0$ for
$0$ for ![]() $j\geqslant n+1$. Dually, we also have that
$j\geqslant n+1$. Dually, we also have that ![]() $R^{j}\unicode[STIX]{x1D708}^{-}=0$ for
$R^{j}\unicode[STIX]{x1D708}^{-}=0$ for ![]() $j\geqslant n+1$. The claim follows.
$j\geqslant n+1$. The claim follows.
A small ![]() $k$-linear category
$k$-linear category ![]() ${\mathcal{C}}^{\prime }$ is called left Gorenstein if
${\mathcal{C}}^{\prime }$ is called left Gorenstein if
Note that by [Reference Beligiannis5, Theorem 4.16] the category ![]() ${\mathcal{C}}^{\prime }$ is left Gorenstein if and only if
${\mathcal{C}}^{\prime }$ is left Gorenstein if and only if ![]() $\operatorname{gl.Gidim}{\mathcal{C}}^{\prime }\text{-}\!\operatorname{Mod}<\infty$, where
$\operatorname{gl.Gidim}{\mathcal{C}}^{\prime }\text{-}\!\operatorname{Mod}<\infty$, where ![]() $\operatorname{gl.Gidim}{\mathcal{C}}^{\prime }\text{-}\!\operatorname{Mod}$ is the global Gorenstein injective dimension of
$\operatorname{gl.Gidim}{\mathcal{C}}^{\prime }\text{-}\!\operatorname{Mod}$ is the global Gorenstein injective dimension of ![]() ${\mathcal{C}}^{\prime }\text{-}\!\operatorname{Mod}$. Furthermore, if
${\mathcal{C}}^{\prime }\text{-}\!\operatorname{Mod}$. Furthermore, if ![]() ${\mathcal{C}}^{\prime }$ is left Gorenstein then
${\mathcal{C}}^{\prime }$ is left Gorenstein then
and ![]() ${\mathcal{C}}^{\prime }$ is called left
${\mathcal{C}}^{\prime }$ is called left ![]() $m$-Gorenstein if this common number is
$m$-Gorenstein if this common number is ![]() $m$.
$m$.
Theorem 57. Let ![]() ${\mathcal{C}}^{\prime }$ be a small
${\mathcal{C}}^{\prime }$ be a small ![]() $k$-linear category, and assume
$k$-linear category, and assume ![]() ${\mathcal{C}}^{\prime }$ is left
${\mathcal{C}}^{\prime }$ is left ![]() $m$-Gorenstein. Furthermore, assume the functor
$m$-Gorenstein. Furthermore, assume the functor ![]() $P_{{\mathcal{C}}\text{-}\!\operatorname{Mod}}$ is
$P_{{\mathcal{C}}\text{-}\!\operatorname{Mod}}$ is ![]() $n$-Gorenstein. Then the category
$n$-Gorenstein. Then the category ![]() ${\mathcal{C}}^{\prime }\otimes {\mathcal{C}}$ is left
${\mathcal{C}}^{\prime }\otimes {\mathcal{C}}$ is left ![]() $p$-Gorenstein where
$p$-Gorenstein where ![]() $p\leqslant m+n$.
$p\leqslant m+n$.
Proof. This follows from Proposition 51, Theorem 53, and Lemma 56 applied to ![]() $({\mathcal{C}}^{\prime }\otimes _{k}{\mathcal{C}})\text{-}\!\operatorname{Mod}=(\operatorname{Mod}\!\text{-}{\mathcal{C}}^{\prime })^{{\mathcal{C}}}$.
$({\mathcal{C}}^{\prime }\otimes _{k}{\mathcal{C}})\text{-}\!\operatorname{Mod}=(\operatorname{Mod}\!\text{-}{\mathcal{C}}^{\prime })^{{\mathcal{C}}}$.
It would be interesting to know when the equality ![]() $p=m+n$ in Theorem 57 holds.
$p=m+n$ in Theorem 57 holds.
Remark 58. Following the conventions in [Reference Dell’Ambrogio, Stevenson and Stovicek12], we say that the category ![]() ${\mathcal{C}}$ has a Serre functor relative to
${\mathcal{C}}$ has a Serre functor relative to ![]() $k$ if there exists an equivalence
$k$ if there exists an equivalence ![]() $S:{\mathcal{C}}\rightarrow {\mathcal{C}}$ together with a natural isomorphism
$S:{\mathcal{C}}\rightarrow {\mathcal{C}}$ together with a natural isomorphism
for all ![]() $c_{1},c_{2}\in {\mathcal{C}}$. This implies in particular that
$c_{1},c_{2}\in {\mathcal{C}}$. This implies in particular that ![]() $P_{{\mathcal{C}}\text{-}\!\operatorname{Mod}}$ is
$P_{{\mathcal{C}}\text{-}\!\operatorname{Mod}}$ is ![]() $0$-Gorenstein. Theorem 57 therefore gives a partial generalization of [Reference Dell’Ambrogio, Stevenson and Stovicek12, Theorem 4.6].
$0$-Gorenstein. Theorem 57 therefore gives a partial generalization of [Reference Dell’Ambrogio, Stevenson and Stovicek12, Theorem 4.6].
4.3 Monic representations of a quiver
Let ![]() $Q=(Q_{0},Q_{1},s,t)$ be a quiver (not necessarily finite) such that for each vertex
$Q=(Q_{0},Q_{1},s,t)$ be a quiver (not necessarily finite) such that for each vertex ![]() $i\in Q_{0}$ there are only finitely many paths starting in
$i\in Q_{0}$ there are only finitely many paths starting in ![]() $i$ and only finitely many paths ending in
$i$ and only finitely many paths ending in ![]() $i$. Let
$i$. Let ![]() ${\mathcal{C}}=kQ$ be the
${\mathcal{C}}=kQ$ be the ![]() $k$-linearization of
$k$-linearization of ![]() $Q$. Obviously,
$Q$. Obviously, ![]() $kQ$ is a Hom-finite and locally bounded category. An object
$kQ$ is a Hom-finite and locally bounded category. An object ![]() $F\in {\mathcal{B}}^{kQ}$ is a representation of
$F\in {\mathcal{B}}^{kQ}$ is a representation of ![]() $Q$ over
$Q$ over ![]() ${\mathcal{B}}$, given by the datum
${\mathcal{B}}$, given by the datum ![]() $F=(F(i),f_{\unicode[STIX]{x1D6FC}},i\in Q_{0},\unicode[STIX]{x1D6FC}\in Q_{1})$, where
$F=(F(i),f_{\unicode[STIX]{x1D6FC}},i\in Q_{0},\unicode[STIX]{x1D6FC}\in Q_{1})$, where ![]() $F(i)\in {\mathcal{B}}$ and
$F(i)\in {\mathcal{B}}$ and ![]() $f_{\unicode[STIX]{x1D6FC}}:F(s(\unicode[STIX]{x1D6FC}))\rightarrow F(t(\unicode[STIX]{x1D6FC}))$ are morphisms in
$f_{\unicode[STIX]{x1D6FC}}:F(s(\unicode[STIX]{x1D6FC}))\rightarrow F(t(\unicode[STIX]{x1D6FC}))$ are morphisms in ![]() ${\mathcal{B}}$. A morphism
${\mathcal{B}}$. A morphism
is given by morphisms ![]() $\unicode[STIX]{x1D719}_{i}:F(i)\rightarrow F^{\prime }(i)$ for each
$\unicode[STIX]{x1D719}_{i}:F(i)\rightarrow F^{\prime }(i)$ for each ![]() $i\in Q_{0}$, such that the diagram
$i\in Q_{0}$, such that the diagram

commutes for each ![]() $\unicode[STIX]{x1D6FC}\in Q_{1}$. We let
$\unicode[STIX]{x1D6FC}\in Q_{1}$. We let ![]() $kQe_{i}$ and
$kQe_{i}$ and ![]() $e_{i}kQ$ denote the representable functors
$e_{i}kQ$ denote the representable functors ![]() $kQ(i,-)$ and
$kQ(i,-)$ and ![]() $kQ(-,i)$.
$kQ(-,i)$.
Definition 59. A representation ![]() $F=(F(i),f_{\unicode[STIX]{x1D6FC}},i\in Q_{0},\unicode[STIX]{x1D6FC}\in Q_{1})$ is monic if
$F=(F(i),f_{\unicode[STIX]{x1D6FC}},i\in Q_{0},\unicode[STIX]{x1D6FC}\in Q_{1})$ is monic if
is a monomorphism for all ![]() $i\in Q_{0}$.
$i\in Q_{0}$.
Let ![]() $\operatorname{Mon}(Q,{\mathcal{B}})$ denote the subcategory of
$\operatorname{Mon}(Q,{\mathcal{B}})$ denote the subcategory of ![]() ${\mathcal{B}}^{kQ}$ consisting of the monic representations. It was considered in [Reference Luo and Zhang29] for
${\mathcal{B}}^{kQ}$ consisting of the monic representations. It was considered in [Reference Luo and Zhang29] for ![]() $Q$ a finite acyclic quiver,
$Q$ a finite acyclic quiver, ![]() $k$ a field, and
$k$ a field, and ![]() ${\mathcal{B}}=\unicode[STIX]{x1D6EC}\text{-}\!\operatorname{mod}$ the category of finite-dimensional modules over a finite-dimensional algebra
${\mathcal{B}}=\unicode[STIX]{x1D6EC}\text{-}\!\operatorname{mod}$ the category of finite-dimensional modules over a finite-dimensional algebra ![]() $\unicode[STIX]{x1D6EC}$. It was also considered in [Reference Eshraghi, Hafezi and Salarian18] for
$\unicode[STIX]{x1D6EC}$. It was also considered in [Reference Eshraghi, Hafezi and Salarian18] for ![]() $Q$ a left rooted quiver and
$Q$ a left rooted quiver and ![]() ${\mathcal{B}}=\unicode[STIX]{x1D6EC}\text{-}\!\operatorname{Mod}$ for
${\mathcal{B}}=\unicode[STIX]{x1D6EC}\text{-}\!\operatorname{Mod}$ for ![]() $\unicode[STIX]{x1D6EC}$ an arbitrary ring. In both cases it is used to give a description of the Gorenstein projective objects in
$\unicode[STIX]{x1D6EC}$ an arbitrary ring. In both cases it is used to give a description of the Gorenstein projective objects in ![]() ${\mathcal{B}}^{kQ}$. We recover this description using the theory we have developed.
${\mathcal{B}}^{kQ}$. We recover this description using the theory we have developed.
Proposition 60. The following holds:
(i) The endofunctor
 $P_{kQ\text{-}\!\operatorname{Mod}}$ is
$P_{kQ\text{-}\!\operatorname{Mod}}$ is  $m$-Gorenstein where
$m$-Gorenstein where  $m\leqslant 1$;
$m\leqslant 1$;(ii) A representation
 $F\in {\mathcal{B}}^{kQ}$ is monic if and only if it is Gorenstein
$F\in {\mathcal{B}}^{kQ}$ is monic if and only if it is Gorenstein  $P_{{\mathcal{B}}^{kQ}}$-projective.
$P_{{\mathcal{B}}^{kQ}}$-projective.
Proof. Fix a vertex ![]() $i\in Q_{0}$, and let
$i\in Q_{0}$, and let ![]() $S_{i}\in \operatorname{Mod}\!\text{-}kQ$ be the representation
$S_{i}\in \operatorname{Mod}\!\text{-}kQ$ be the representation
We have a projective resolution of ![]() $S_{i}$ given by
$S_{i}$ given by
where the morphism ![]() $e_{s(\unicode[STIX]{x1D6FC})}kQ\rightarrow e_{i}kQ$ is induced from
$e_{s(\unicode[STIX]{x1D6FC})}kQ\rightarrow e_{i}kQ$ is induced from ![]() $\unicode[STIX]{x1D6FC}:s(\unicode[STIX]{x1D6FC})\rightarrow i$. This shows that
$\unicode[STIX]{x1D6FC}:s(\unicode[STIX]{x1D6FC})\rightarrow i$. This shows that ![]() $\operatorname{pdim}S_{i}\leqslant 1$ for all
$\operatorname{pdim}S_{i}\leqslant 1$ for all ![]() $i\in Q_{0}$. Also,
$i\in Q_{0}$. Also, ![]() $D(kQe_{i})$ has a filtration
$D(kQe_{i})$ has a filtration
in ![]() $\operatorname{mod}\!\text{-}kQ$ such that
$\operatorname{mod}\!\text{-}kQ$ such that ![]() $M_{i+1}/M_{i}\cong S_{j_{i}}$ for vertices
$M_{i+1}/M_{i}\cong S_{j_{i}}$ for vertices ![]() $j_{0},j_{1},\ldots ,j_{n-1}\in Q_{0}$. Therefore, we get that
$j_{0},j_{1},\ldots ,j_{n-1}\in Q_{0}$. Therefore, we get that ![]() $\operatorname{pdim}D(kQe_{i})\leqslant 1$ for all
$\operatorname{pdim}D(kQe_{i})\leqslant 1$ for all ![]() $i\in Q_{0}$. Dually, the same argument applied to
$i\in Q_{0}$. Dually, the same argument applied to ![]() $Q^{\text{op}}$ shows that
$Q^{\text{op}}$ shows that ![]() $\operatorname{pdim}D(e_{i}kQ)\leqslant 1$ for all
$\operatorname{pdim}D(e_{i}kQ)\leqslant 1$ for all ![]() $i\in Q_{0}$. This proves that the endofunctor
$i\in Q_{0}$. This proves that the endofunctor ![]() $P_{kQ\text{-}\!\operatorname{Mod}}$ is
$P_{kQ\text{-}\!\operatorname{Mod}}$ is ![]() $m$-Gorenstein where
$m$-Gorenstein where ![]() $m\leqslant 1$.
$m\leqslant 1$.
We now describe the objects which are Gorenstein ![]() $P_{{\mathcal{B}}^{kQ}}$-projective. By Lemma 56 we know that
$P_{{\mathcal{B}}^{kQ}}$-projective. By Lemma 56 we know that ![]() $P_{{\mathcal{B}}^{kQ}}$ is Iwanaga–Gorenstein of dimension
$P_{{\mathcal{B}}^{kQ}}$ is Iwanaga–Gorenstein of dimension ![]() $0$ or
$0$ or ![]() $1$. Hence, by Theorems 19 and 20 part (ii) the Gorenstein
$1$. Hence, by Theorems 19 and 20 part (ii) the Gorenstein ![]() $P_{{\mathcal{B}}^{kQ}}$-projective functors are precisely the functors
$P_{{\mathcal{B}}^{kQ}}$-projective functors are precisely the functors ![]() $F\in {\mathcal{B}}^{kQ}$ such that
$F\in {\mathcal{B}}^{kQ}$ such that
for all ![]() $i\in Q_{0}$. Now for all
$i\in Q_{0}$. Now for all ![]() $i\in Q_{0}$ we have an exact sequence
$i\in Q_{0}$ we have an exact sequence
obtained by applying ![]() $D(-)$ to the sequence (61) with
$D(-)$ to the sequence (61) with ![]() $Q$ replaced by
$Q$ replaced by ![]() $Q^{\text{op}}$. Hence, we get that
$Q^{\text{op}}$. Hence, we get that
by tensoring ![]() $F$ with the sequence in (63) and using Lemma 55. Conversely, from the filtration (62) we get that
$F$ with the sequence in (63) and using Lemma 55. Conversely, from the filtration (62) we get that
by repeated use of Lemma 55. Hence, ![]() $F$ is Gorenstein
$F$ is Gorenstein ![]() $P_{{\mathcal{B}}^{kQ}}$-projective if and only if
$P_{{\mathcal{B}}^{kQ}}$-projective if and only if ![]() $\operatorname{Tor}_{1}^{kQ}(S_{i},F)=0$ for all
$\operatorname{Tor}_{1}^{kQ}(S_{i},F)=0$ for all ![]() $i\in Q_{0}$. Tensoring the sequence (61) with
$i\in Q_{0}$. Tensoring the sequence (61) with ![]() $F$ gives the exact sequence
$F$ gives the exact sequence
Hence, ![]() $F$ is Gorenstein
$F$ is Gorenstein ![]() $P_{{\mathcal{B}}^{kQ}}$-projective if and only if it is monic.
$P_{{\mathcal{B}}^{kQ}}$-projective if and only if it is monic.
Proposition 65. Assume ![]() ${\mathcal{B}}$ has enough projectives. The following holds:
${\mathcal{B}}$ has enough projectives. The following holds:
(i) A functor
 $F=(F(i),f_{\unicode[STIX]{x1D6FC}},i\in Q_{0},\unicode[STIX]{x1D6FC}\in Q_{1})\in {\mathcal{B}}^{kQ}$ is Gorenstein projective if and only if it is monic and the cokernel of the map is Gorenstein projective in
$F=(F(i),f_{\unicode[STIX]{x1D6FC}},i\in Q_{0},\unicode[STIX]{x1D6FC}\in Q_{1})\in {\mathcal{B}}^{kQ}$ is Gorenstein projective if and only if it is monic and the cokernel of the map is Gorenstein projective in $$\begin{eqnarray}(f_{\unicode[STIX]{x1D6FC}})_{t(\unicode[STIX]{x1D6FC})=i}:\bigoplus _{t(\unicode[STIX]{x1D6FC})=i}F(s(\unicode[STIX]{x1D6FC}))\rightarrow F(i)\end{eqnarray}$$
$$\begin{eqnarray}(f_{\unicode[STIX]{x1D6FC}})_{t(\unicode[STIX]{x1D6FC})=i}:\bigoplus _{t(\unicode[STIX]{x1D6FC})=i}F(s(\unicode[STIX]{x1D6FC}))\rightarrow F(i)\end{eqnarray}$$ ${\mathcal{B}}$ for all
${\mathcal{B}}$ for all  $i\in Q_{0}$;
$i\in Q_{0}$;(ii) If
 $F$ is Gorenstein projective in
$F$ is Gorenstein projective in  ${\mathcal{B}}^{kQ}$, then
${\mathcal{B}}^{kQ}$, then  $F(i)$ is Gorenstein projective in
$F(i)$ is Gorenstein projective in  ${\mathcal{B}}$ for all
${\mathcal{B}}$ for all  $i\in Q_{0}$.
$i\in Q_{0}$.
Proof. We know by Corollary 43 and Proposition 60 that ![]() $F$ is Gorenstein projective if and only if it is monic and
$F$ is Gorenstein projective if and only if it is monic and ![]() $D(kQe_{i})\otimes _{kQ}F\in {\mathcal{G}}{\mathcal{P}}({\mathcal{B}})$ for all
$D(kQe_{i})\otimes _{kQ}F\in {\mathcal{G}}{\mathcal{P}}({\mathcal{B}})$ for all ![]() $i\in Q_{0}$. Assume
$i\in Q_{0}$. Assume ![]() $F$ is monic, and consider the exact sequence (63). Tensoring with
$F$ is monic, and consider the exact sequence (63). Tensoring with ![]() $F$ gives an exact sequence
$F$ gives an exact sequence
 $$\begin{eqnarray}0\rightarrow S_{i}\otimes _{kQ}F\rightarrow D(kQe_{i})\otimes _{kQ}F\rightarrow \left(\bigoplus _{t(\unicode[STIX]{x1D6FC})=i}D(kQe_{s(\unicode[STIX]{x1D6FC})})\right)\otimes _{kQ}F\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow S_{i}\otimes _{kQ}F\rightarrow D(kQe_{i})\otimes _{kQ}F\rightarrow \left(\bigoplus _{t(\unicode[STIX]{x1D6FC})=i}D(kQe_{s(\unicode[STIX]{x1D6FC})})\right)\otimes _{kQ}F\rightarrow 0\end{eqnarray}$$ since ![]() $\operatorname{Tor}_{kQ}^{1}(\bigoplus _{t(\unicode[STIX]{x1D6FC})=i}D(kQe_{s(\unicode[STIX]{x1D6FC})}),F)=0$. Hence, we get that
$\operatorname{Tor}_{kQ}^{1}(\bigoplus _{t(\unicode[STIX]{x1D6FC})=i}D(kQe_{s(\unicode[STIX]{x1D6FC})}),F)=0$. Hence, we get that
since ![]() ${\mathcal{G}}{\mathcal{P}}({\mathcal{B}})$ is closed under kernels of epimorphisms. Also, from the filtration in (62) we have an exact sequence
${\mathcal{G}}{\mathcal{P}}({\mathcal{B}})$ is closed under kernels of epimorphisms. Also, from the filtration in (62) we have an exact sequence
for each ![]() $0\leqslant i\leqslant n-1$. Tensoring this with
$0\leqslant i\leqslant n-1$. Tensoring this with ![]() $F$ gives an exact sequence
$F$ gives an exact sequence
since ![]() $\operatorname{Tor}_{kQ}^{1}(S_{j_{i}},F)=0$. Therefore,
$\operatorname{Tor}_{kQ}^{1}(S_{j_{i}},F)=0$. Therefore,
since ![]() ${\mathcal{G}}{\mathcal{P}}({\mathcal{B}})$ is closed under extensions. Hence, a functor
${\mathcal{G}}{\mathcal{P}}({\mathcal{B}})$ is closed under extensions. Hence, a functor ![]() $F\in {\mathcal{B}}^{kQ}$ is Gorenstein projective if and only if it is monic and
$F\in {\mathcal{B}}^{kQ}$ is Gorenstein projective if and only if it is monic and ![]() $S_{i}\otimes _{kQ}F\in {\mathcal{G}}{\mathcal{P}}({\mathcal{B}})$ for all
$S_{i}\otimes _{kQ}F\in {\mathcal{G}}{\mathcal{P}}({\mathcal{B}})$ for all ![]() $i\in Q_{0}$. By the exact sequence in (64) we see that
$i\in Q_{0}$. By the exact sequence in (64) we see that ![]() $S_{i}\otimes _{kQ}F$ is the cokernel of the map
$S_{i}\otimes _{kQ}F$ is the cokernel of the map
and the claim follows.
For statement (ii), note that ![]() $e_{i}kQ$ has a filtration
$e_{i}kQ$ has a filtration ![]() $0=M_{0}\subset M_{1}\subset \cdots \subset M_{n^{\prime }}=e_{i}kQ$ such that
$0=M_{0}\subset M_{1}\subset \cdots \subset M_{n^{\prime }}=e_{i}kQ$ such that ![]() $M_{i+1}/M_{i}\cong S_{j_{i}^{\prime }}$ for
$M_{i+1}/M_{i}\cong S_{j_{i}^{\prime }}$ for ![]() $j_{0}^{\prime },j_{1}^{\prime },\ldots ,j_{n^{\prime }-1}^{\prime }\in Q_{0}$. Hence, if
$j_{0}^{\prime },j_{1}^{\prime },\ldots ,j_{n^{\prime }-1}^{\prime }\in Q_{0}$. Hence, if ![]() $F$ is Gorenstein projective, then
$F$ is Gorenstein projective, then ![]() $e_{i}kQ\otimes _{kQ}F\cong F(i)$ is Gorenstein projective for all
$e_{i}kQ\otimes _{kQ}F\cong F(i)$ is Gorenstein projective for all ![]() $i\in Q_{0}$. This proves the claim.
$i\in Q_{0}$. This proves the claim.
4.4 More examples
In this subsection we calculate the Gorenstein projective objects in examples for the representation of quiver with relations over ![]() ${\mathcal{B}}$.
${\mathcal{B}}$.
Example 66. Let ![]() ${\mathcal{C}}$ be the
${\mathcal{C}}$ be the ![]() $k$-linear category generated by the quiver
$k$-linear category generated by the quiver
with vertex set ![]() $\{c_{i}\mid i\in \mathbb{Z}/n\mathbb{Z}\}$ and relations
$\{c_{i}\mid i\in \mathbb{Z}/n\mathbb{Z}\}$ and relations ![]() $d_{i}\circ d_{i+1}=0$. The category
$d_{i}\circ d_{i+1}=0$. The category ![]() ${\mathcal{B}}^{{\mathcal{C}}}$ can be identified with
${\mathcal{B}}^{{\mathcal{C}}}$ can be identified with ![]() $n$-periodic complexes over
$n$-periodic complexes over ![]() ${\mathcal{B}}$ (for
${\mathcal{B}}$ (for ![]() $n=0$ this is just unbounded complexes over
$n=0$ this is just unbounded complexes over ![]() ${\mathcal{B}}$). It was shown in [Reference Dell’Ambrogio, Stevenson and Stovicek12, Proposition 4.12] that
${\mathcal{B}}$). It was shown in [Reference Dell’Ambrogio, Stevenson and Stovicek12, Proposition 4.12] that ![]() ${\mathcal{C}}$ has a relative Serre functor
${\mathcal{C}}$ has a relative Serre functor ![]() $S$ given by
$S$ given by ![]() $S(c_{i})=c_{i-1}$ and
$S(c_{i})=c_{i-1}$ and ![]() $S(d_{i})=d_{i-1}$. Therefore, the endofunctor
$S(d_{i})=d_{i-1}$. Therefore, the endofunctor ![]() $P_{{\mathcal{C}}\text{-}\!\operatorname{Mod}}$ is
$P_{{\mathcal{C}}\text{-}\!\operatorname{Mod}}$ is ![]() $0$-Gorenstein. Hence, by Theorem 20 we get that
$0$-Gorenstein. Hence, by Theorem 20 we get that ![]() ${\mathcal{G}}{\mathcal{P}}_{P_{{\mathcal{B}}^{{\mathcal{C}}}}}({\mathcal{B}}^{{\mathcal{C}}})={\mathcal{B}}^{{\mathcal{C}}}$. If
${\mathcal{G}}{\mathcal{P}}_{P_{{\mathcal{B}}^{{\mathcal{C}}}}}({\mathcal{B}}^{{\mathcal{C}}})={\mathcal{B}}^{{\mathcal{C}}}$. If ![]() ${\mathcal{B}}$ has enough projectives, then the Gorenstein projective objects in
${\mathcal{B}}$ has enough projectives, then the Gorenstein projective objects in ![]() ${\mathcal{B}}^{{\mathcal{C}}}$ are precisely the functors
${\mathcal{B}}^{{\mathcal{C}}}$ are precisely the functors ![]() $F$ such that
$F$ such that
for all ![]() $c_{i}\in {\mathcal{C}}$. Note that for
$c_{i}\in {\mathcal{C}}$. Note that for ![]() $n=0$ this recovers the description obtained in [Reference Yang and Liu38, Theorem 2.2]. Also, if we put
$n=0$ this recovers the description obtained in [Reference Yang and Liu38, Theorem 2.2]. Also, if we put ![]() ${\mathcal{X}}={\mathcal{G}}{\mathcal{P}}_{P_{{\mathcal{B}}^{{\mathcal{C}}}}}({\mathcal{B}}^{{\mathcal{C}}})$ and
${\mathcal{X}}={\mathcal{G}}{\mathcal{P}}_{P_{{\mathcal{B}}^{{\mathcal{C}}}}}({\mathcal{B}}^{{\mathcal{C}}})$ and ![]() ${\mathcal{Y}}=\operatorname{Proj}({\mathcal{B}})$ in Theorem 36 we recover the result that the collection of
${\mathcal{Y}}=\operatorname{Proj}({\mathcal{B}})$ in Theorem 36 we recover the result that the collection of ![]() $n$-periodic complexes over
$n$-periodic complexes over ![]() ${\mathcal{B}}$ with projective components form a Frobenius exact category.
${\mathcal{B}}$ with projective components form a Frobenius exact category.
Example 67. Let ![]() ${\mathcal{C}}$ be the
${\mathcal{C}}$ be the ![]() $k$-linear category generated by the quiver
$k$-linear category generated by the quiver
with relations ![]() $d_{i}\circ d_{i+1}=0$ for
$d_{i}\circ d_{i+1}=0$ for ![]() $1\leqslant i\leqslant n-1$. Then
$1\leqslant i\leqslant n-1$. Then ![]() $D({\mathcal{C}}(c_{i},-))\cong {\mathcal{C}}(-,c_{i-1})$ in
$D({\mathcal{C}}(c_{i},-))\cong {\mathcal{C}}(-,c_{i-1})$ in ![]() $\operatorname{Mod}\!\text{-}{\mathcal{C}}$ for
$\operatorname{Mod}\!\text{-}{\mathcal{C}}$ for ![]() $1\leqslant i\leqslant n$ and
$1\leqslant i\leqslant n$ and ![]() $D({\mathcal{C}}(-,c_{i}))\cong {\mathcal{C}}(c_{i+1},-)$ in
$D({\mathcal{C}}(-,c_{i}))\cong {\mathcal{C}}(c_{i+1},-)$ in ![]() ${\mathcal{C}}\text{-}\!\operatorname{Mod}$ for
${\mathcal{C}}\text{-}\!\operatorname{Mod}$ for ![]() $0\leqslant i\leqslant n-1$. Furthermore, we have an exact sequence
$0\leqslant i\leqslant n-1$. Furthermore, we have an exact sequence
in ![]() $\operatorname{Mod}\!\text{-}{\mathcal{C}}$ and an exact sequence
$\operatorname{Mod}\!\text{-}{\mathcal{C}}$ and an exact sequence
in ![]() ${\mathcal{C}}\text{-}\!\operatorname{Mod}$. Hence, the endofunctor
${\mathcal{C}}\text{-}\!\operatorname{Mod}$. Hence, the endofunctor ![]() $P_{{\mathcal{C}}\text{-}\!\operatorname{Mod}}$ is
$P_{{\mathcal{C}}\text{-}\!\operatorname{Mod}}$ is ![]() $n$-Gorenstein. Let
$n$-Gorenstein. Let ![]() $F\in {\mathcal{B}}^{{\mathcal{C}}}$ be a functor. We can identify
$F\in {\mathcal{B}}^{{\mathcal{C}}}$ be a functor. We can identify ![]() $F$ with a complex
$F$ with a complex
with ![]() $n+1$ terms. Tensoring the sequence (68) with
$n+1$ terms. Tensoring the sequence (68) with ![]() $F$ gives a sequence
$F$ gives a sequence
By Theorem 20 part (ii) we get that ![]() $F$ is Gorenstein
$F$ is Gorenstein ![]() $P_{{\mathcal{B}}^{{\mathcal{C}}}}$-projective if and only if
$P_{{\mathcal{B}}^{{\mathcal{C}}}}$-projective if and only if ![]() $\operatorname{Tor}_{j}^{kQ}(D{\mathcal{C}}(c_{0},-),F)=0$ for all
$\operatorname{Tor}_{j}^{kQ}(D{\mathcal{C}}(c_{0},-),F)=0$ for all ![]() $1\leqslant j\leqslant n$. Since
$1\leqslant j\leqslant n$. Since
it follows that ![]() $F$ is Gorenstein
$F$ is Gorenstein ![]() $P_{{\mathcal{B}}^{{\mathcal{C}}}}$-projective if and only if the sequence
$P_{{\mathcal{B}}^{{\mathcal{C}}}}$-projective if and only if the sequence
is exact. Now assume ![]() ${\mathcal{B}}$ has enough projectives. Then
${\mathcal{B}}$ has enough projectives. Then ![]() ${\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P_{{\mathcal{B}}^{{\mathcal{C}}}}}({\mathcal{B}}^{{\mathcal{C}}}))={\mathcal{G}}{\mathcal{P}}({\mathcal{B}}^{{\mathcal{C}}})$ by Corollary 43. Therefore, the Gorenstein projective objects in
${\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P_{{\mathcal{B}}^{{\mathcal{C}}}}}({\mathcal{B}}^{{\mathcal{C}}}))={\mathcal{G}}{\mathcal{P}}({\mathcal{B}}^{{\mathcal{C}}})$ by Corollary 43. Therefore, the Gorenstein projective objects in ![]() ${\mathcal{B}}^{{\mathcal{C}}}$ are precisely the functors
${\mathcal{B}}^{{\mathcal{C}}}$ are precisely the functors ![]() $F$ such that sequence (69) is exact and
$F$ such that sequence (69) is exact and
Example 70. Let ![]() ${\mathcal{C}}$ be the
${\mathcal{C}}$ be the ![]() $k$-linear category generated by the quiver
$k$-linear category generated by the quiver

with relations ![]() $\unicode[STIX]{x1D6FD}\circ \unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FE}\circ \unicode[STIX]{x1D707}$. A functor
$\unicode[STIX]{x1D6FD}\circ \unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FE}\circ \unicode[STIX]{x1D707}$. A functor ![]() $F\in {\mathcal{B}}^{{\mathcal{C}}}$ is just a commutative diagram in
$F\in {\mathcal{B}}^{{\mathcal{C}}}$ is just a commutative diagram in ![]() ${\mathcal{B}}$. Note that
${\mathcal{B}}$. Note that ![]() ${\mathcal{C}}(-,c_{4})\cong D{\mathcal{C}}(c_{1},-)$. Also, there are exact sequences
${\mathcal{C}}(-,c_{4})\cong D{\mathcal{C}}(c_{1},-)$. Also, there are exact sequences
and
 $$\begin{eqnarray}\displaystyle 0\rightarrow {\mathcal{C}}(-,c_{1})\xrightarrow[{}]{\left[\begin{array}{@{}c@{}}-(\unicode[STIX]{x1D6FC}\circ -)\\ \unicode[STIX]{x1D707}\circ -\end{array}\right]}{\mathcal{C}}(-,c_{2})\oplus {\mathcal{C}}(-,c_{3})\xrightarrow[{}]{\left[\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FD}\circ - & \unicode[STIX]{x1D6FE}\circ -\end{array}\right]}{\mathcal{C}}(-,c_{4}) & & \displaystyle \nonumber\\ \displaystyle \rightarrow D{\mathcal{C}}(c_{4},-)\rightarrow 0 & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0\rightarrow {\mathcal{C}}(-,c_{1})\xrightarrow[{}]{\left[\begin{array}{@{}c@{}}-(\unicode[STIX]{x1D6FC}\circ -)\\ \unicode[STIX]{x1D707}\circ -\end{array}\right]}{\mathcal{C}}(-,c_{2})\oplus {\mathcal{C}}(-,c_{3})\xrightarrow[{}]{\left[\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FD}\circ - & \unicode[STIX]{x1D6FE}\circ -\end{array}\right]}{\mathcal{C}}(-,c_{4}) & & \displaystyle \nonumber\\ \displaystyle \rightarrow D{\mathcal{C}}(c_{4},-)\rightarrow 0 & & \displaystyle \nonumber\end{eqnarray}$$ in ![]() $\operatorname{Mod}\!\text{-}{\mathcal{C}}$. Since
$\operatorname{Mod}\!\text{-}{\mathcal{C}}$. Since ![]() ${\mathcal{C}}$ is isomorphic to
${\mathcal{C}}$ is isomorphic to ![]() ${\mathcal{C}}^{\text{op}}$ the same holds for
${\mathcal{C}}^{\text{op}}$ the same holds for ![]() ${\mathcal{C}}^{\text{op}}$. Hence, the endofunctor
${\mathcal{C}}^{\text{op}}$. Hence, the endofunctor ![]() $P_{{\mathcal{C}}\text{-}\!\operatorname{Mod}}$ is
$P_{{\mathcal{C}}\text{-}\!\operatorname{Mod}}$ is ![]() $2$-Gorenstein. By Theorem 20 part (ii) we get that
$2$-Gorenstein. By Theorem 20 part (ii) we get that ![]() $F\in {\mathcal{B}}^{{\mathcal{C}}}$ is Gorenstein
$F\in {\mathcal{B}}^{{\mathcal{C}}}$ is Gorenstein ![]() $P_{{\mathcal{B}}^{{\mathcal{C}}}}$-projective if and only if
$P_{{\mathcal{B}}^{{\mathcal{C}}}}$-projective if and only if ![]() $\operatorname{Tor}_{j}^{{\mathcal{C}}}(D({\mathcal{C}}(c_{i},-)),F)=0$ for
$\operatorname{Tor}_{j}^{{\mathcal{C}}}(D({\mathcal{C}}(c_{i},-)),F)=0$ for ![]() $1\leqslant j\leqslant 2$ and
$1\leqslant j\leqslant 2$ and ![]() $1\leqslant i\leqslant 4$. Tensoring
$1\leqslant i\leqslant 4$. Tensoring ![]() $F$ with the exact sequences above shows that
$F$ with the exact sequences above shows that ![]() $F\in {\mathcal{B}}^{{\mathcal{C}}}$ is Gorenstein
$F\in {\mathcal{B}}^{{\mathcal{C}}}$ is Gorenstein ![]() $P_{{\mathcal{B}}^{{\mathcal{C}}}}$-projective if and only if
$P_{{\mathcal{B}}^{{\mathcal{C}}}}$-projective if and only if
are monomorphisms and the diagram

is a pullback square. If ![]() ${\mathcal{B}}$ has enough projectives, then a functor
${\mathcal{B}}$ has enough projectives, then a functor ![]() $F\in {\mathcal{B}}^{{\mathcal{C}}}$ is Gorenstein projective if and only if it is Gorenstein
$F\in {\mathcal{B}}^{{\mathcal{C}}}$ is Gorenstein projective if and only if it is Gorenstein ![]() $P_{{\mathcal{B}}^{{\mathcal{C}}}}$-projective and
$P_{{\mathcal{B}}^{{\mathcal{C}}}}$-projective and
 $$\begin{eqnarray}\displaystyle & & \displaystyle D{\mathcal{C}}(c_{1},-)\otimes _{{\mathcal{C}}}F\cong F(c_{4})\in {\mathcal{G}}{\mathcal{P}}({\mathcal{B}})\nonumber\\ \displaystyle & & \displaystyle D{\mathcal{C}}(c_{2},-)\otimes _{{\mathcal{C}}}F\cong \operatorname{Coker}(F(c_{3})\xrightarrow[{}]{F(\unicode[STIX]{x1D6FE})}F(c_{4}))\in {\mathcal{G}}{\mathcal{P}}({\mathcal{B}})\nonumber\\ \displaystyle & & \displaystyle D{\mathcal{C}}(c_{3},-)\otimes _{{\mathcal{C}}}F\cong \operatorname{Coker}(F(c_{2})\xrightarrow[{}]{F(\unicode[STIX]{x1D6FD})}F(c_{4}))\in {\mathcal{G}}{\mathcal{P}}({\mathcal{B}})\nonumber\\ \displaystyle & & \displaystyle D{\mathcal{C}}(c_{4},-)\otimes _{{\mathcal{C}}}F\cong \operatorname{Coker}(F(c_{2})\oplus F(c_{3})\xrightarrow[{}]{\left[\begin{array}{@{}cc@{}}F(\unicode[STIX]{x1D6FD}) & F(\unicode[STIX]{x1D6FE})\end{array}\right]}F(c_{4}))\in {\mathcal{G}}{\mathcal{P}}({\mathcal{B}}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle D{\mathcal{C}}(c_{1},-)\otimes _{{\mathcal{C}}}F\cong F(c_{4})\in {\mathcal{G}}{\mathcal{P}}({\mathcal{B}})\nonumber\\ \displaystyle & & \displaystyle D{\mathcal{C}}(c_{2},-)\otimes _{{\mathcal{C}}}F\cong \operatorname{Coker}(F(c_{3})\xrightarrow[{}]{F(\unicode[STIX]{x1D6FE})}F(c_{4}))\in {\mathcal{G}}{\mathcal{P}}({\mathcal{B}})\nonumber\\ \displaystyle & & \displaystyle D{\mathcal{C}}(c_{3},-)\otimes _{{\mathcal{C}}}F\cong \operatorname{Coker}(F(c_{2})\xrightarrow[{}]{F(\unicode[STIX]{x1D6FD})}F(c_{4}))\in {\mathcal{G}}{\mathcal{P}}({\mathcal{B}})\nonumber\\ \displaystyle & & \displaystyle D{\mathcal{C}}(c_{4},-)\otimes _{{\mathcal{C}}}F\cong \operatorname{Coker}(F(c_{2})\oplus F(c_{3})\xrightarrow[{}]{\left[\begin{array}{@{}cc@{}}F(\unicode[STIX]{x1D6FD}) & F(\unicode[STIX]{x1D6FE})\end{array}\right]}F(c_{4}))\in {\mathcal{G}}{\mathcal{P}}({\mathcal{B}}).\nonumber\end{eqnarray}$$