Article contents
JET SCHEMES OF QUASI-ORDINARY SURFACE SINGULARITIES
Published online by Cambridge University Press: 20 September 2019
Abstract
We describe the irreducible components of the jet schemes with origin in the singular locus of a two-dimensional quasi-ordinary hypersurface singularity. A weighted graph is associated with these components and with their embedding dimensions and their codimensions in the jet schemes of the ambient space. We prove that the data of this weighted graph is equivalent to the data of the topological type of the singularity. We also determine a component of the jet schemes (equivalent to a divisorial valuation on 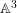 $\mathbb{A}^{3}$), that computes the log-canonical threshold of the singularity embedded in
$\mathbb{A}^{3}$), that computes the log-canonical threshold of the singularity embedded in 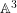 $\mathbb{A}^{3}$. This provides us with pairs
$\mathbb{A}^{3}$. This provides us with pairs 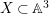 $X\subset \mathbb{A}^{3}$ whose log-canonical thresholds are not computed by monomial divisorial valuations. Note that for a pair
$X\subset \mathbb{A}^{3}$ whose log-canonical thresholds are not computed by monomial divisorial valuations. Note that for a pair 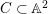 $C\subset \mathbb{A}^{2}$, where
$C\subset \mathbb{A}^{2}$, where 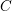 $C$ is a plane curve, the log-canonical threshold is always computed by a monomial divisorial valuation (in suitable coordinates of
$C$ is a plane curve, the log-canonical threshold is always computed by a monomial divisorial valuation (in suitable coordinates of 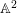 $\mathbb{A}^{2}$).
$\mathbb{A}^{2}$).
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © 2019 Foundation Nagoya Mathematical Journal
References
- 6
- Cited by


