Hostname: page-component-54dcc4c588-m259h Total loading time: 0 Render date: 2025-09-11T23:19:02.607Z Has data issue: false hasContentIssue false
  • English
  • Français

Local rigidity theorems of 2-type hypersurfaces in a hypersphere

Published online by Cambridge University Press:  22 January 2016

Bang-Yen Chen
Bang-Yen Chen*
Affiliation:
Department of Mathematics, Michigan State University, East Lansing, Michigan 48824-1027, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A submanifold M (connected but not necessary compact) of a Euclidean m-space Em is said to be of finite type if each component of its position vector X can be written as a finite sum of eigenfunctions of the Laplacian Δ of M, that is,

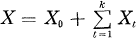
where X0 is a constant vector and ΔXt = λtXt, t = 1, 2, · · ·, k. If in particular all eigenvalues {λ1 , λ2, · · ·, λk are mutually different, then M is said to be of k-type (cf. [3] for details).

Information

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 122 , June 1991 , pp. 139 - 148
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1991

References

[1] Barros, M. and Garay, O. J., 2-type surfaces in S3 , Geometriae Dedicata, 24 nin (1987), 329–336.Google Scholar
[2] Chen, B. Y., Geometry of Submanifolds, M. Dekker, New York, 1973.Google Scholar
[3] Chen, B. Y., Total Mean Curvature and Submanifolds of Finite Type, World Scientific, Singapore-New Jersey-London-Hong Kong, 1984.Google Scholar
[4] Chen, B. Y., 2-type submanifolds and their applications, Chinese J. Math., 14 (1986), 1–14.Google Scholar
[5] Chen, B. Y., Barros, M. and Garay, O. J., Spherical finite type hypersurfaces, Algebras, Groups and Geometries, 4 (1987), 58–72.Google Scholar
[6] Hasanis, T. and Vlachos, T., A local classification of 2-type surfaces in S 3 , preprint.Google Scholar
[7] Otsuki, T., Minimal hypersurfaces in a Riemannian manifold of constant curvature, Amer. J. Math., 9, 2 (1970), 145–173.Google Scholar
[8] Otsuki, T., A certain property of geodesies of the family of Riemannian manifolds (I), Minimal Submanifolds and Geodesies, Kaigai Publ., Tokyo, Japan, 1978, 173–192.Google Scholar
[9] Ryan, P. J., Homogeneity and some curvature conditions for hypersurfaces, Tohoku Math. J., 21 (1969), 363–388.Google Scholar
[10] Takahashi, T., Minimal immersions of Riemannian manifolds, J. Math. Soc. Japan, 18 (1966), 380–385.Google Scholar