Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Dong, Jianfeng
and
Liu, Yu
2012.
The higher order Riesz transform and BMO type space associated to Schrödinger operators.
Mathematische Nachrichten,
Vol. 285,
Issue. 4,
p.
486.
Ma, Tao
Stinga, Pablo Raúl
Torrea, José L.
and
Zhang, Chao
2012.
Regularity properties of Schrödinger operators.
Journal of Mathematical Analysis and Applications,
Vol. 388,
Issue. 2,
p.
817.
Liu, Heping
Tang, Lin
and
Zhu, Hua
2012.
Weighted Hardy spaces and BMO spaces associated with Schrödinger operators.
Mathematische Nachrichten,
Vol. 285,
Issue. 17-18,
p.
2173.
Jiang, Yin-sheng
2012.
Some properties of Riesz potential associated with Schrödinger operator.
Applied Mathematics-A Journal of Chinese Universities,
Vol. 27,
Issue. 1,
p.
59.
Shi, Shaoguang
and
Fu, Zunwei
2013.
Estimates of Some Operators on One-Sided Weighted Morrey Spaces.
Abstract and Applied Analysis,
Vol. 2013,
Issue. ,
p.
1.
Li, Pengtao
Yang, Qixiang
and
Zhu, Yueping
2013.
Wavelets, Sobolev Multipliers, and Application to Schrödinger Type Operators with Nonsmooth Potentials.
Abstract and Applied Analysis,
Vol. 2013,
Issue. ,
p.
1.
Shi, Shaoguang
and
Lu, Shanzhen
2013.
Some characterizations of Campanato spaces via commutators on Morrey spaces.
Pacific Journal of Mathematics,
Vol. 264,
Issue. 1,
p.
221.
Liu, Yu
Huang, JiZheng
and
Dong, JianFeng
2013.
Commutators of Calderón-Zygmund operators related to admissible functions on spaces of homogeneous type and applications to Schrödinger operators.
Science China Mathematics,
Vol. 56,
Issue. 9,
p.
1895.
Liu, Yu
and
Dong, Jianfeng
2013.
The Higher Order Riesz Transform andBMOType Space Associated with Schrödinger Operators on Stratified Lie Groups.
Journal of Function Spaces and Applications,
Vol. 2013,
Issue. ,
p.
1.
Shi, Shaoguang
and
Lu, Shanzhen
2014.
A characterization of Campanato space via commutator of fractional integral.
Journal of Mathematical Analysis and Applications,
Vol. 419,
Issue. 1,
p.
123.
Chen, Dongxiang
and
Jin, Fangting
2014.
The Boundedness of Marcinkiewicz Integrals Associated with Schrödinger Operator on Morrey Spaces.
Journal of Function Spaces,
Vol. 2014,
Issue. ,
p.
1.
Stempak, Krzysztof
and
Tao, Xiangxing
2014.
Local Morrey and Campanato Spaces on Quasimetric Measure Spaces.
Journal of Function Spaces,
Vol. 2014,
Issue. ,
p.
1.
Bui, The Anh
2014.
Boundedness of variation operators and oscillation operators for certain semigroups.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 106,
Issue. ,
p.
124.
LIN, Haibo
and
YANG, Dachun
2014.
Pointwise multipliers for localized morrey-campanato spaces on RD-spaces.
Acta Mathematica Scientia,
Vol. 34,
Issue. 6,
p.
1677.
Ma, Tao
Stinga, Pablo Raúl
Torrea, José L.
and
Zhang, Chao
2014.
Regularity estimates in Hölder spaces for Schrödinger operators via a
$$T1$$
theorem.
Annali di Matematica Pura ed Applicata,
Vol. 193,
Issue. 2,
p.
561.
Shi, Shaoguang
and
Lu, Shanzhen
2015.
Characterization of the central Campanato space via the commutator operator of Hardy type.
Journal of Mathematical Analysis and Applications,
Vol. 429,
Issue. 2,
p.
713.
Alvarado, Ryan
and
Mitrea, Marius
2015.
Hardy Spaces on Ahlfors-Regular Quasi Metric Spaces.
Vol. 2142,
Issue. ,
p.
449.
Ky, Luong Dang
2015.
On the product of functions in BMO and H1 over spaces of homogeneous type.
Journal of Mathematical Analysis and Applications,
Vol. 425,
Issue. 2,
p.
807.
Trong, Nguyen Ngoc
and
Tung, Nguyen Thanh
2016.
Weighted BMO Type Spaces Associated to Admissible Functions and Applications.
Acta Mathematica Vietnamica,
Vol. 41,
Issue. 2,
p.
209.
Bongioanni, Bruno
Cabral, Adrián
and
Harboure, Eleonor
2016.
Schrödinger type singular integrals: weighted estimates for p=1.
Mathematische Nachrichten,
Vol. 289,
Issue. 11-12,
p.
1341.
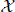 be a space of homogeneous type in the sense of Coifman and Weiss, and let
be a space of homogeneous type in the sense of Coifman and Weiss, and let 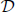 be a collection of balls in
be a collection of balls in 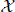 . The authors introduce the localized atomic Hardy space
. The authors introduce the localized atomic Hardy space 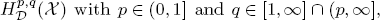 the localized Morrey-Campanato space
the localized Morrey-Campanato space 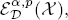 and the localized Morrey-Campanato-BLO (bounded lower oscillation) space
and the localized Morrey-Campanato-BLO (bounded lower oscillation) space 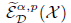 with α ∊ ℝ and p ∊ (0, ∞) , and they establish their basic properties, including
with α ∊ ℝ and p ∊ (0, ∞) , and they establish their basic properties, including 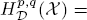
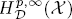 and several equivalent characterizations for
and several equivalent characterizations for 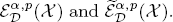 In particular, the authors prove that when α > 0 and p ∊ [1, ∞), then
In particular, the authors prove that when α > 0 and p ∊ [1, ∞), then 
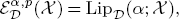 and when p ∈(0,1], then the dual space of
and when p ∈(0,1], then the dual space of 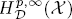 is
is 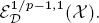 Let ρ be an admissible function modeled on the known auxiliary function determined by the Schrödinger operator. Denote the spaces
Let ρ be an admissible function modeled on the known auxiliary function determined by the Schrödinger operator. Denote the spaces 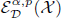 and
and 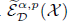 , respectively, by
, respectively, by 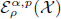 and
and 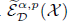 when
when 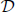 is determined by ρ. The authors then obtain the boundedness from
is determined by ρ. The authors then obtain the boundedness from 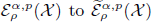 of the radial and the Poisson semigroup maximal functions and the Littlewood-Paley g-function, which are defined via kernels modeled on the semigroup generated by the Schrödinger operator. These results apply in a wide range of settings, for instance, the Schrödinger operator or the degenerate Schrödinger operator on ℝd , or the sub-Laplace Schrödinger operator on Heisenberg groups or connected and simply connected nilpotent Lie groups.
of the radial and the Poisson semigroup maximal functions and the Littlewood-Paley g-function, which are defined via kernels modeled on the semigroup generated by the Schrödinger operator. These results apply in a wide range of settings, for instance, the Schrödinger operator or the degenerate Schrödinger operator on ℝd , or the sub-Laplace Schrödinger operator on Heisenberg groups or connected and simply connected nilpotent Lie groups.
