Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hitsuda, Masuyuki
1974.
Mutual information in Gaussian channels.
Journal of Multivariate Analysis,
Vol. 4,
Issue. 1,
p.
66.
Pitt, Loren D.
1975.
Hida-Cramér Multiplicity Theory for Multiple Markov Processes and Goursat Representations.
Nagoya Mathematical Journal,
Vol. 57,
Issue. ,
p.
199.
Ihara, Shunsuke
1975.
Coding theory in Gaussian channel with feedback II: evaluation of the filtering error.
Nagoya Mathematical Journal,
Vol. 58,
Issue. ,
p.
127.
Siraya, T. N.
1978.
Canonical Representations of Second-Order Random Processes.
Theory of Probability & Its Applications,
Vol. 22,
Issue. 2,
p.
418.
Hitsuda, Masuyuki
1978.
Measure Theory Applications to Stochastic Analysis.
Vol. 695,
Issue. ,
p.
139.
Butov, A. A.
1982.
On the multiplicity of the observable process in the general kalman scheme.
Stochastics,
Vol. 6,
Issue. 3-4,
p.
175.
Gualtierotti, Antonio F.
2015.
Detection of Random Signals in Dependent Gaussian Noise.
p.
307.
Gualtierotti, Antonio F.
2015.
Detection of Random Signals in Dependent Gaussian Noise.
p.
3.
Gualtierotti, Antonio F.
2015.
Detection of Random Signals in Dependent Gaussian Noise.
p.
903.
Gualtierotti, Antonio F.
2015.
Detection of Random Signals in Dependent Gaussian Noise.
p.
927.
Gualtierotti, Antonio F.
2015.
Detection of Random Signals in Dependent Gaussian Noise.
p.
433.
Gualtierotti, Antonio F.
2015.
Detection of Random Signals in Dependent Gaussian Noise.
p.
529.
Gualtierotti, Antonio F.
2015.
Detection of Random Signals in Dependent Gaussian Noise.
p.
1087.
Gualtierotti, Antonio F.
2015.
Detection of Random Signals in Dependent Gaussian Noise.
p.
993.
Gualtierotti, Antonio F.
2015.
Detection of Random Signals in Dependent Gaussian Noise.
p.
505.
Gualtierotti, Antonio F.
2015.
Detection of Random Signals in Dependent Gaussian Noise.
p.
703.
Gualtierotti, Antonio F.
2015.
Detection of Random Signals in Dependent Gaussian Noise.
p.
217.
Gualtierotti, Antonio F.
2015.
Detection of Random Signals in Dependent Gaussian Noise.
p.
961.
Gualtierotti, Antonio F.
2015.
Detection of Random Signals in Dependent Gaussian Noise.
p.
795.
Gualtierotti, Antonio F.
2015.
Detection of Random Signals in Dependent Gaussian Noise.
p.
125.


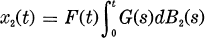 is a simpleMarkov process.
is a simpleMarkov process.