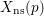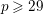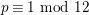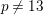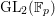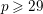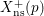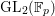Introduction
Modular curves can be constructed as compactifications of certain quotients of the upper half complex plane. When the genus exceeds 1, it is a classical question to ask if all of their automorphisms are induced by an automorphism of the upper half complex plane. Here we make some progress toward answering this question for nonsplit Cartan modular curves.
Let
![]() $N$
be a positive integer and let
$N$
be a positive integer and let
![]() $H$
be a subgroup of
$H$
be a subgroup of
![]() $\text{GL}_{2}(\mathbb{Z}/N\mathbb{Z})$
with the property that the determinant homomorphism from
$\text{GL}_{2}(\mathbb{Z}/N\mathbb{Z})$
with the property that the determinant homomorphism from
![]() $H$
to
$H$
to
![]() $\mathbb{Z}/N\mathbb{Z}^{\ast }$
is surjective. We write
$\mathbb{Z}/N\mathbb{Z}^{\ast }$
is surjective. We write
![]() $X_{H}$
for the modular curve over
$X_{H}$
for the modular curve over
![]() $\mathbb{Q}$
associated to the subgroup
$\mathbb{Q}$
associated to the subgroup
![]() $H$
. Let
$H$
. Let
![]() $\unicode[STIX]{x1D6E4}_{H}$
be the subgroup of
$\unicode[STIX]{x1D6E4}_{H}$
be the subgroup of
![]() $\text{SL}_{2}(\mathbb{Z})$
made up of the elements which reduce modulo
$\text{SL}_{2}(\mathbb{Z})$
made up of the elements which reduce modulo
![]() $N$
to an element in
$N$
to an element in
![]() $H$
. The complex points of
$H$
. The complex points of
![]() $X_{H}$
can be identified with the orbit space
$X_{H}$
can be identified with the orbit space
![]() ${\mathcal{H}}\cup \mathbb{Q}\cup \{\infty \}/\unicode[STIX]{x1D6E4}_{H}$
, where
${\mathcal{H}}\cup \mathbb{Q}\cup \{\infty \}/\unicode[STIX]{x1D6E4}_{H}$
, where
![]() ${\mathcal{H}}$
is the upper half complex plane on which any element of
${\mathcal{H}}$
is the upper half complex plane on which any element of
![]() $\text{SL}_{2}(\mathbb{R})$
acts as a Möbius transformation
$\text{SL}_{2}(\mathbb{R})$
acts as a Möbius transformation
![]() $\left(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!\right)\unicode[STIX]{x1D70F}=\frac{a\unicode[STIX]{x1D70F}+b}{c\unicode[STIX]{x1D70F}+d}$
, for every
$\left(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!\right)\unicode[STIX]{x1D70F}=\frac{a\unicode[STIX]{x1D70F}+b}{c\unicode[STIX]{x1D70F}+d}$
, for every
![]() $\unicode[STIX]{x1D70F}\in {\mathcal{H}}$
. Let
$\unicode[STIX]{x1D70F}\in {\mathcal{H}}$
. Let
![]() $\text{Norm}(\unicode[STIX]{x1D6E4}_{H})$
be the normalizer of
$\text{Norm}(\unicode[STIX]{x1D6E4}_{H})$
be the normalizer of
![]() $\unicode[STIX]{x1D6E4}_{H}$
in
$\unicode[STIX]{x1D6E4}_{H}$
in
![]() $\text{SL}_{2}(\mathbb{R})$
. An element of
$\text{SL}_{2}(\mathbb{R})$
. An element of
![]() $\text{Norm}(\unicode[STIX]{x1D6E4}_{H})$
induces naturally an automorphism of the curve
$\text{Norm}(\unicode[STIX]{x1D6E4}_{H})$
induces naturally an automorphism of the curve
![]() $X_{H}$
; hence the group
$X_{H}$
; hence the group
![]() $B(X_{H})\stackrel{\text{def}}{=}\text{Norm}(\unicode[STIX]{x1D6E4}_{H})/\unicode[STIX]{x1D6E4}_{H}$
can be considered as a subgroup of the automorphism group
$B(X_{H})\stackrel{\text{def}}{=}\text{Norm}(\unicode[STIX]{x1D6E4}_{H})/\unicode[STIX]{x1D6E4}_{H}$
can be considered as a subgroup of the automorphism group
![]() $\text{Aut}(X_{H})$
of
$\text{Aut}(X_{H})$
of
![]() $X_{H}$
. We call an element of
$X_{H}$
. We call an element of
![]() $B(X_{H})$
a modular automorphism of
$B(X_{H})$
a modular automorphism of
![]() $X_{H}$
. A nonmodular automorphism is also called exceptional.
$X_{H}$
. A nonmodular automorphism is also called exceptional.
If
![]() $H$
is a Borel subgroup of
$H$
is a Borel subgroup of
![]() $\text{GL}_{2}(\mathbb{Z}/N\mathbb{Z})$
, the curve
$\text{GL}_{2}(\mathbb{Z}/N\mathbb{Z})$
, the curve
![]() $X_{H}$
is the classical modular curve
$X_{H}$
is the classical modular curve
![]() $X_{0}(N)$
and
$X_{0}(N)$
and
![]() $\unicode[STIX]{x1D6E4}_{H}$
is the classical congruence subgroup
$\unicode[STIX]{x1D6E4}_{H}$
is the classical congruence subgroup
![]() $\unicode[STIX]{x1D6E4}_{0}(N)$
. For every positive integer
$\unicode[STIX]{x1D6E4}_{0}(N)$
. For every positive integer
![]() $N$
, the automorphism group of
$N$
, the automorphism group of
![]() $X_{0}(N)$
has been determined in [Reference OggOgg77, Reference Kenku and MomoseKM88, Reference ElkiesElk90, Reference HarrisonHar11], and if the genus of
$X_{0}(N)$
has been determined in [Reference OggOgg77, Reference Kenku and MomoseKM88, Reference ElkiesElk90, Reference HarrisonHar11], and if the genus of
![]() $X_{0}(N)$
is at least 2 and
$X_{0}(N)$
is at least 2 and
![]() $N\neq 37,63,108$
, we have
$N\neq 37,63,108$
, we have
![]() $\text{Aut}(X_{0}(N))=B(X_{0}(N))$
. If we take
$\text{Aut}(X_{0}(N))=B(X_{0}(N))$
. If we take
![]() $N=p$
a prime number, the group
$N=p$
a prime number, the group
![]() $B(X_{0}(p))$
is generated by the Atkin–Lehner involution
$B(X_{0}(p))$
is generated by the Atkin–Lehner involution
![]() $w_{p}$
. The automorphism group of
$w_{p}$
. The automorphism group of
![]() $X_{0}^{\ast }(p)\stackrel{\text{def}}{=}X_{0}(p)/\langle w_{p}\rangle$
has been determined in [Reference Baker and HasegawaBH03] and it is trivial when the genus exceeds
$X_{0}^{\ast }(p)\stackrel{\text{def}}{=}X_{0}(p)/\langle w_{p}\rangle$
has been determined in [Reference Baker and HasegawaBH03] and it is trivial when the genus exceeds
![]() $2$
. When
$2$
. When
![]() $X_{0}^{\ast }(p)$
has genus
$X_{0}^{\ast }(p)$
has genus
![]() $2$
, the curve
$2$
, the curve
![]() $X_{0}^{\ast }(p)$
is hyperelliptic, so it must admit an involution.
$X_{0}^{\ast }(p)$
is hyperelliptic, so it must admit an involution.
In this paper, we concentrate on the case of
![]() $H$
being a nonsplit Cartan subgroup of
$H$
being a nonsplit Cartan subgroup of
![]() $\text{GL}_{2}(\mathbb{F}_{p})$
, and we write
$\text{GL}_{2}(\mathbb{F}_{p})$
, and we write
![]() $X_{\text{ns}}(p)$
for the modular curve associated to
$X_{\text{ns}}(p)$
for the modular curve associated to
![]() $H$
. This curve always has a modular involution
$H$
. This curve always has a modular involution
![]() $w$
, because of the fact that a nonsplit Cartan subgroup of
$w$
, because of the fact that a nonsplit Cartan subgroup of
![]() $\text{GL}_{2}(\mathbb{F}_{p})$
has index 2 in its normalizer. We have
$\text{GL}_{2}(\mathbb{F}_{p})$
has index 2 in its normalizer. We have
![]() $B(X_{\text{ns}}(p))=\langle w\rangle$
(see Section 3). Let
$B(X_{\text{ns}}(p))=\langle w\rangle$
(see Section 3). Let
![]() $X_{\text{ns}}^{+}(p)\stackrel{\text{def}}{=}X_{\text{ns}}(p)/\langle w\rangle$
be the modular curve associated to the normalizer of a nonsplit Cartan subgroup of
$X_{\text{ns}}^{+}(p)\stackrel{\text{def}}{=}X_{\text{ns}}(p)/\langle w\rangle$
be the modular curve associated to the normalizer of a nonsplit Cartan subgroup of
![]() $\text{GL}_{2}(\mathbb{F}_{p})$
. The curve
$\text{GL}_{2}(\mathbb{F}_{p})$
. The curve
![]() $X_{\text{ns}}(p)$
has genus smaller than
$X_{\text{ns}}(p)$
has genus smaller than
![]() $2$
when
$2$
when
![]() $p\leqslant 7$
. The same happens for
$p\leqslant 7$
. The same happens for
![]() $X_{\text{ns}}^{+}(p)$
when
$X_{\text{ns}}^{+}(p)$
when
![]() $p\leqslant 11$
. It is not true that
$p\leqslant 11$
. It is not true that
![]() $\text{Aut}(X_{\text{ns}}(p))=\langle w\rangle$
whenever the genus is at least
$\text{Aut}(X_{\text{ns}}(p))=\langle w\rangle$
whenever the genus is at least
![]() $2$
. For example, the automorphism group of
$2$
. For example, the automorphism group of
![]() $X_{\text{ns}}(11)$
, determined in [Reference Dose, Fernández, González and SchoofDFGS14], is the Klein four group generated by
$X_{\text{ns}}(11)$
, determined in [Reference Dose, Fernández, González and SchoofDFGS14], is the Klein four group generated by
![]() $w$
and an exceptional involution.
$w$
and an exceptional involution.
Here, extending techniques of [Reference OggOgg74, Reference Kenku and MomoseKM88, Reference Baker and HasegawaBH03], we prove the following
Theorem 1.1 .
If
![]() $p\geqslant 11$
the modular curve
$p\geqslant 11$
the modular curve
![]() $X_{\text{ns}}(p)$
is not hyperelliptic. If
$X_{\text{ns}}(p)$
is not hyperelliptic. If
![]() $p\geqslant 13$
the modular curve
$p\geqslant 13$
the modular curve
![]() $X_{\text{ns}}^{+}(p)$
is not hyperelliptic.
$X_{\text{ns}}^{+}(p)$
is not hyperelliptic.
We remark that this result already follows directly from [Reference AbramovichAbr96, Theorem 0.1] for
![]() $X_{\text{ns}}(p)$
when
$X_{\text{ns}}(p)$
when
![]() $p\geqslant 23$
and for
$p\geqslant 23$
and for
![]() $X_{\text{ns}}^{+}(p)$
when
$X_{\text{ns}}^{+}(p)$
when
![]() $p\geqslant 29$
.
$p\geqslant 29$
.
Theorem 5.2 .
If
![]() $p\geqslant 29$
, all the automorphisms of
$p\geqslant 29$
, all the automorphisms of
![]() $X_{\text{ns}}(p)$
preserve the cusps. If
$X_{\text{ns}}(p)$
preserve the cusps. If
![]() $p\equiv 1~\text{mod}~12$
and
$p\equiv 1~\text{mod}~12$
and
![]() $p\neq 13$
, the automorphism group of
$p\neq 13$
, the automorphism group of
![]() $X_{\text{ns}}(p)$
is generated by the modular involution
$X_{\text{ns}}(p)$
is generated by the modular involution
![]() $w$
.
$w$
.
Some of the techniques used in this paper also apply to
![]() $X_{\text{ns}}^{+}(p)$
, but the main result does not seem to be reachable right away. In general, one can expect the automorphism group of
$X_{\text{ns}}^{+}(p)$
, but the main result does not seem to be reachable right away. In general, one can expect the automorphism group of
![]() $X_{\text{ns}}(p)$
to be generated by the modular involution
$X_{\text{ns}}(p)$
to be generated by the modular involution
![]() $w$
and the automorphism group of
$w$
and the automorphism group of
![]() $X_{\text{ns}}^{+}(p)$
to be trivial for
$X_{\text{ns}}^{+}(p)$
to be trivial for
![]() $p\geqslant 13$
.
$p\geqslant 13$
.
The interest in nonsplit Cartan modular curves comes mainly from Serre’s uniformity conjecture, which is an important statement regarding Galois representations attached to elliptic curves. It is equivalent to assert that for almost all
![]() $p$
and for every maximal subgroup
$p$
and for every maximal subgroup
![]() $H$
of
$H$
of
![]() $\text{GL}_{2}(\mathbb{F}_{p})$
, the modular curve
$\text{GL}_{2}(\mathbb{F}_{p})$
, the modular curve
![]() $X_{H}$
has no rational points except the cusps and the points associated to elliptic curves with complex multiplication, usually called CM points. The only case left to prove, concerns modular curves associated to the normalizer of a nonsplit Cartan subgroup of
$X_{H}$
has no rational points except the cusps and the points associated to elliptic curves with complex multiplication, usually called CM points. The only case left to prove, concerns modular curves associated to the normalizer of a nonsplit Cartan subgroup of
![]() $\text{GL}_{2}(\mathbb{F}_{p})$
.
$\text{GL}_{2}(\mathbb{F}_{p})$
.
We prove the following statement relating the existence of exceptional automorphisms of
![]() $X_{\text{ns}}(p)$
with the existence of non-CM rational points on
$X_{\text{ns}}(p)$
with the existence of non-CM rational points on
![]() $X_{\text{ns}}^{+}(p)$
.
$X_{\text{ns}}^{+}(p)$
.
Theorem 5.3 .
Let
![]() $p\geqslant 29$
. If there exists an exceptional automorphism of
$p\geqslant 29$
. If there exists an exceptional automorphism of
![]() $X_{\text{ns}}(p)$
defined over
$X_{\text{ns}}(p)$
defined over
![]() $\mathbb{Q}$
, then
$\mathbb{Q}$
, then
![]() $X_{\text{ns}}^{+}(p)$
has a non-CM rational point.
$X_{\text{ns}}^{+}(p)$
has a non-CM rational point.
Therefore, Serre’s uniformity conjecture implies the nonexistence of rational exceptional automorphisms of
![]() $X_{\text{ns}}(p)$
for almost all
$X_{\text{ns}}(p)$
for almost all
![]() $p$
.
$p$
.
1 Hyperelliptic modular curves of type
 $X_{\text{ns}}(p)$
and
$X_{\text{ns}}(p)$
and
 $X_{\text{ns}}^{+}(p)$
$X_{\text{ns}}^{+}(p)$
Let
![]() $p$
be a prime number. We recall that the modular curve
$p$
be a prime number. We recall that the modular curve
![]() $X_{\text{ns}}(p)$
has genus
$X_{\text{ns}}(p)$
has genus
![]() $0$
for
$0$
for
![]() $p\leqslant 5$
and is elliptic only for
$p\leqslant 5$
and is elliptic only for
![]() $p=7$
. The modular curve
$p=7$
. The modular curve
![]() $X_{\text{ns}}^{+}(p)$
has genus 0 for
$X_{\text{ns}}^{+}(p)$
has genus 0 for
![]() $p\leqslant 7$
and is elliptic only for
$p\leqslant 7$
and is elliptic only for
![]() $p=11$
[Reference BaranBar10].
$p=11$
[Reference BaranBar10].
Theorem 1.1. If
![]() $p\geqslant 11$
the modular curve
$p\geqslant 11$
the modular curve
![]() $X_{\text{ns}}(p)$
is not hyperelliptic. If
$X_{\text{ns}}(p)$
is not hyperelliptic. If
![]() $p\geqslant 13$
the modular curve
$p\geqslant 13$
the modular curve
![]() $X_{\text{ns}}^{+}(p)$
is not hyperelliptic.
$X_{\text{ns}}^{+}(p)$
is not hyperelliptic.
Proof. (Following [Reference OggOgg74, p. 455, Theorem 3]). Let
![]() $q\neq p$
be a prime number, let
$q\neq p$
be a prime number, let
![]() $\mathbb{F}_{q}$
be the finite field with
$\mathbb{F}_{q}$
be the finite field with
![]() $q$
elements and let
$q$
elements and let
![]() $\overline{\mathbb{F}_{q}}$
be an algebraic closure. The points of
$\overline{\mathbb{F}_{q}}$
be an algebraic closure. The points of
![]() $X_{\text{ns}}(p)(\overline{\mathbb{F}_{q}})$
parametrize pairs
$X_{\text{ns}}(p)(\overline{\mathbb{F}_{q}})$
parametrize pairs
![]() $(E,\unicode[STIX]{x1D711})$
, where
$(E,\unicode[STIX]{x1D711})$
, where
![]() $E$
is an elliptic curve over
$E$
is an elliptic curve over
![]() $\overline{\mathbb{F}_{q}}$
and
$\overline{\mathbb{F}_{q}}$
and
![]() $\unicode[STIX]{x1D711}$
is an isomorphism from the
$\unicode[STIX]{x1D711}$
is an isomorphism from the
![]() $p$
-torsion points of
$p$
-torsion points of
![]() $E$
to
$E$
to
![]() $\mathbb{Z}/p\mathbb{Z}\times \mathbb{Z}/p\mathbb{Z}$
. Moreover, two pairs
$\mathbb{Z}/p\mathbb{Z}\times \mathbb{Z}/p\mathbb{Z}$
. Moreover, two pairs
![]() $(E,\unicode[STIX]{x1D711})$
,
$(E,\unicode[STIX]{x1D711})$
,
![]() $(E^{\prime },\unicode[STIX]{x1D711}^{\prime })$
are parametrized by the same point of
$(E^{\prime },\unicode[STIX]{x1D711}^{\prime })$
are parametrized by the same point of
![]() $X_{\text{ns}}(p)(\overline{\mathbb{F}_{q}})$
if and only if there exist an isomorphism
$X_{\text{ns}}(p)(\overline{\mathbb{F}_{q}})$
if and only if there exist an isomorphism
![]() $f$
from
$f$
from
![]() $E$
to
$E$
to
![]() $E^{\prime }$
such that, on the
$E^{\prime }$
such that, on the
![]() $p$
-torsion of
$p$
-torsion of
![]() $E$
, we have
$E$
, we have
![]() $\unicode[STIX]{x1D711}^{\prime }\circ f=M\circ \unicode[STIX]{x1D711}$
, where
$\unicode[STIX]{x1D711}^{\prime }\circ f=M\circ \unicode[STIX]{x1D711}$
, where
![]() $M$
is a generator of a nonsplit Cartan subgroup
$M$
is a generator of a nonsplit Cartan subgroup
![]() $C$
of
$C$
of
![]() $\text{GL}_{2}(\mathbb{F}_{p})$
. The Frobenius automorphism
$\text{GL}_{2}(\mathbb{F}_{p})$
. The Frobenius automorphism
![]() $\unicode[STIX]{x1D70E}$
generating
$\unicode[STIX]{x1D70E}$
generating
![]() $\text{Gal}(\overline{\mathbb{F}_{q}}/\mathbb{F}_{q^{2}})$
acts on
$\text{Gal}(\overline{\mathbb{F}_{q}}/\mathbb{F}_{q^{2}})$
acts on
![]() $X_{\text{ns}}(p)(\overline{\mathbb{F}_{q}})$
as
$X_{\text{ns}}(p)(\overline{\mathbb{F}_{q}})$
as
![]() $\unicode[STIX]{x1D70E}(E,\unicode[STIX]{x1D711})=(E^{\unicode[STIX]{x1D70E}},\unicode[STIX]{x1D711}\circ \unicode[STIX]{x1D70E}^{-1}),$
so that every elliptic curve
$\unicode[STIX]{x1D70E}(E,\unicode[STIX]{x1D711})=(E^{\unicode[STIX]{x1D70E}},\unicode[STIX]{x1D711}\circ \unicode[STIX]{x1D70E}^{-1}),$
so that every elliptic curve
![]() $E$
over
$E$
over
![]() $\mathbb{F}_{q^{2}}$
gives a point
$\mathbb{F}_{q^{2}}$
gives a point
![]() $(E,\unicode[STIX]{x1D711})$
in
$(E,\unicode[STIX]{x1D711})$
in
![]() $X_{\text{ns}}(p)(\mathbb{F}_{q^{2}})$
if and only if
$X_{\text{ns}}(p)(\mathbb{F}_{q^{2}})$
if and only if
![]() $\unicode[STIX]{x1D711}\circ \unicode[STIX]{x1D70E}^{-1}\circ \unicode[STIX]{x1D711}^{-1}$
is contained in
$\unicode[STIX]{x1D711}\circ \unicode[STIX]{x1D70E}^{-1}\circ \unicode[STIX]{x1D711}^{-1}$
is contained in
![]() $C$
.
$C$
.
Take a supersingular elliptic curve
![]() $E$
over
$E$
over
![]() $\overline{\mathbb{F}_{q}}$
. This means that the
$\overline{\mathbb{F}_{q}}$
. This means that the
![]() $q$
-torsion of
$q$
-torsion of
![]() $E$
is trivial, that the endomorphism algebra
$E$
is trivial, that the endomorphism algebra
![]() $\text{End}(E)$
is an order in a quaternion algebra, and implies that
$\text{End}(E)$
is an order in a quaternion algebra, and implies that
![]() $E$
can be defined over
$E$
can be defined over
![]() $\mathbb{F}_{q^{2}}$
[Reference SilvermanSil09, p. 144, Theorem 3.1, (a)]. The fact that multiplication by
$\mathbb{F}_{q^{2}}$
[Reference SilvermanSil09, p. 144, Theorem 3.1, (a)]. The fact that multiplication by
![]() $q$
is purely inseparable implies that the
$q$
is purely inseparable implies that the
![]() $q^{2}$
th power Frobenius endomorphism
$q^{2}$
th power Frobenius endomorphism
![]() $\unicode[STIX]{x1D711}_{q^{2}}$
and multiplication by
$\unicode[STIX]{x1D711}_{q^{2}}$
and multiplication by
![]() $q$
differ by an automorphism of
$q$
differ by an automorphism of
![]() $E$
, which means that
$E$
, which means that
![]() $\unicode[STIX]{x1D711}_{q^{2}}=\unicode[STIX]{x1D701}q$
in
$\unicode[STIX]{x1D711}_{q^{2}}=\unicode[STIX]{x1D701}q$
in
![]() $\text{End}(E)$
and
$\text{End}(E)$
and
![]() $\unicode[STIX]{x1D701}$
is a root of unity. If
$\unicode[STIX]{x1D701}$
is a root of unity. If
![]() $j\neq 0,1728$
, we have
$j\neq 0,1728$
, we have
![]() $\unicode[STIX]{x1D711}_{q^{2}}=\pm q$
. If
$\unicode[STIX]{x1D711}_{q^{2}}=\pm q$
. If
![]() $j=0,1728$
, the elliptic curve
$j=0,1728$
, the elliptic curve
![]() $E$
is isomorphic over
$E$
is isomorphic over
![]() $\overline{\mathbb{F}_{q}}$
to a curve
$\overline{\mathbb{F}_{q}}$
to a curve
![]() $E^{\prime }$
defined over
$E^{\prime }$
defined over
![]() $\mathbb{F}_{q}$
with equation
$\mathbb{F}_{q}$
with equation
![]() $y^{2}+y=x^{3}$
or
$y^{2}+y=x^{3}$
or
![]() $y^{2}=x^{3}-x$
. We have
$y^{2}=x^{3}-x$
. We have
![]() $\#E^{\prime }(\mathbb{F}_{q})=q+1$
([Reference SilvermanSil09, p. 154, Exercise 5.10, (b)] when
$\#E^{\prime }(\mathbb{F}_{q})=q+1$
([Reference SilvermanSil09, p. 154, Exercise 5.10, (b)] when
![]() $q\geqslant 5$
, a direct count when
$q\geqslant 5$
, a direct count when
![]() $q=2,3$
). Hence the
$q=2,3$
). Hence the
![]() $q$
th power Frobenius endomorphism of
$q$
th power Frobenius endomorphism of
![]() $E^{\prime }$
has characteristic polynomial
$E^{\prime }$
has characteristic polynomial
![]() $x^{2}+q=0$
which implies that
$x^{2}+q=0$
which implies that
![]() $\unicode[STIX]{x1D711}_{q^{2}}=-q$
in
$\unicode[STIX]{x1D711}_{q^{2}}=-q$
in
![]() $\text{End}(E)$
.
$\text{End}(E)$
.
This shows that every supersingular elliptic curve over
![]() $\overline{\mathbb{F}_{q}}$
is isomorphic to a supersingular elliptic curve
$\overline{\mathbb{F}_{q}}$
is isomorphic to a supersingular elliptic curve
![]() $E$
defined over
$E$
defined over
![]() $\mathbb{F}_{q^{2}}$
, with the property that
$\mathbb{F}_{q^{2}}$
, with the property that
![]() $\unicode[STIX]{x1D711}_{q^{2}}$
acts on the
$\unicode[STIX]{x1D711}_{q^{2}}$
acts on the
![]() $p$
-torsion points as multiplication by
$p$
-torsion points as multiplication by
![]() $q$
or
$q$
or
![]() $-q$
. Which says that
$-q$
. Which says that
![]() $\unicode[STIX]{x1D711}_{q^{2}}$
acts on the
$\unicode[STIX]{x1D711}_{q^{2}}$
acts on the
![]() $p$
-torsion of
$p$
-torsion of
![]() $E$
as a scalar matrix of
$E$
as a scalar matrix of
![]() $\text{GL}_{2}(\mathbb{F}_{p})$
and therefore as an element contained in every conjugate of the nonsplit Cartan subgroup
$\text{GL}_{2}(\mathbb{F}_{p})$
and therefore as an element contained in every conjugate of the nonsplit Cartan subgroup
![]() $C$
in
$C$
in
![]() $\text{GL}_{2}(\mathbb{F}_{p})$
. Hence,
$\text{GL}_{2}(\mathbb{F}_{p})$
. Hence,
![]() $E$
gives a point in
$E$
gives a point in
![]() $X_{\text{ns}}(p)(\mathbb{F}_{q^{2}})$
for each conjugate of
$X_{\text{ns}}(p)(\mathbb{F}_{q^{2}})$
for each conjugate of
![]() $C$
in
$C$
in
![]() $\text{GL}_{2}(\mathbb{F}_{p})$
, up to automorphisms of
$\text{GL}_{2}(\mathbb{F}_{p})$
, up to automorphisms of
![]() $E$
, in the sense that a pair
$E$
, in the sense that a pair
![]() $(E,\unicode[STIX]{x1D711})$
gives the same point on
$(E,\unicode[STIX]{x1D711})$
gives the same point on
![]() $X_{\text{ns}}(p)$
as
$X_{\text{ns}}(p)$
as
![]() $(E,\unicode[STIX]{x1D711}\circ f)$
for any automorphism
$(E,\unicode[STIX]{x1D711}\circ f)$
for any automorphism
![]() $f$
of
$f$
of
![]() $E$
. Among the automorphisms of any supersingular elliptic curve, we have multiplication by
$E$
. Among the automorphisms of any supersingular elliptic curve, we have multiplication by
![]() $-1$
, which acts on torsion points as an element contained in
$-1$
, which acts on torsion points as an element contained in
![]() $C$
. Thus, since the index of a nonsplit Cartan subgroup in
$C$
. Thus, since the index of a nonsplit Cartan subgroup in
![]() $\text{GL}_{2}(\mathbb{F}_{p})$
is equal to
$\text{GL}_{2}(\mathbb{F}_{p})$
is equal to
![]() $p(p-1)$
, we have the following inequality
$p(p-1)$
, we have the following inequality
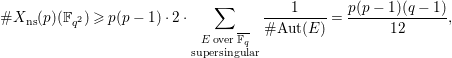 $$\begin{eqnarray}\#X_{\text{ns}}(p)(\mathbb{F}_{q^{2}})\geqslant p(p-1)\cdot 2\cdot \mathop{\sum }_{\substack{ E\;\text{over}\;\overline{\mathbb{F}_{q}} \\ \text{supersingular}}}\frac{1}{\#\text{Aut}(E)}=\frac{p(p-1)(q-1)}{12},\end{eqnarray}$$
$$\begin{eqnarray}\#X_{\text{ns}}(p)(\mathbb{F}_{q^{2}})\geqslant p(p-1)\cdot 2\cdot \mathop{\sum }_{\substack{ E\;\text{over}\;\overline{\mathbb{F}_{q}} \\ \text{supersingular}}}\frac{1}{\#\text{Aut}(E)}=\frac{p(p-1)(q-1)}{12},\end{eqnarray}$$
where in the last equality we used the Deuring–Eichler formula [Reference SilvermanSil09, p. 154, Exercise 5.9]
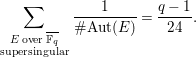 $$\begin{eqnarray}\mathop{\sum }_{\substack{ E\;\text{over}\;\overline{\mathbb{F}_{q}} \\ \text{supersingular}}}\frac{1}{\#\text{Aut}(E)}=\frac{q-1}{24}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ E\;\text{over}\;\overline{\mathbb{F}_{q}} \\ \text{supersingular}}}\frac{1}{\#\text{Aut}(E)}=\frac{q-1}{24}.\end{eqnarray}$$
Note that this lower bound on the number of supersingular points can also easily be deduced from [Reference Baker, González-Jiménez, González and PoonenBGJGP05, Lemmas 3.20 and 3.21].
Suppose now that
![]() $X_{\text{ns}}(p)$
is hyperelliptic. Then we have
$X_{\text{ns}}(p)$
is hyperelliptic. Then we have
where the second inequality holds because
![]() $X_{\text{ns}}(p)$
is hyperelliptic and because the projective line over
$X_{\text{ns}}(p)$
is hyperelliptic and because the projective line over
![]() $\mathbb{F}_{q^{2}}$
has exactly
$\mathbb{F}_{q^{2}}$
has exactly
![]() $q^{2}+1$
points. Now, putting
$q^{2}+1$
points. Now, putting
![]() $q=2$
we have
$q=2$
we have
and we obtain
![]() $p\leqslant 11$
which ends the proof for
$p\leqslant 11$
which ends the proof for
![]() $X_{\text{ns}}(p)$
in the case
$X_{\text{ns}}(p)$
in the case
![]() $p\geqslant 13$
. With an analogous reasoning, taking into account that the index of the normalizer of a nonsplit Cartan subgroup in
$p\geqslant 13$
. With an analogous reasoning, taking into account that the index of the normalizer of a nonsplit Cartan subgroup in
![]() $\text{GL}_{2}(\mathbb{F}_{p})$
is equal to
$\text{GL}_{2}(\mathbb{F}_{p})$
is equal to
![]() $\frac{p(p-1)}{2}$
, we obtain the statement for
$\frac{p(p-1)}{2}$
, we obtain the statement for
![]() $X_{\text{ns}}^{+}(p)$
in the case
$X_{\text{ns}}^{+}(p)$
in the case
![]() $p\geqslant 17$
.
$p\geqslant 17$
.
The case
![]() $p=11$
for
$p=11$
for
![]() $X_{\text{ns}}(p)$
and the case
$X_{\text{ns}}(p)$
and the case
![]() $p=13$
for
$p=13$
for
![]() $X_{\text{ns}}^{+}(p)$
can be worked out by explicitly counting the points over
$X_{\text{ns}}^{+}(p)$
can be worked out by explicitly counting the points over
![]() $\mathbb{F}_{4}$
of the respective curves. Recall that the Jacobian of
$\mathbb{F}_{4}$
of the respective curves. Recall that the Jacobian of
![]() $X_{\text{ns}}(p)$
is isogenous to the new part of the Jacobian of
$X_{\text{ns}}(p)$
is isogenous to the new part of the Jacobian of
![]() $X_{0}(p^{2})$
and the Jacobian of
$X_{0}(p^{2})$
and the Jacobian of
![]() $X_{\text{ns}}^{+}(p)$
is isogenous to the new part of the Jacobian of
$X_{\text{ns}}^{+}(p)$
is isogenous to the new part of the Jacobian of
![]() $X_{0}^{\ast }(p^{2})\stackrel{\text{def}}{=}X_{0}(p^{2})/\langle w_{p^{2}}\rangle$
, where
$X_{0}^{\ast }(p^{2})\stackrel{\text{def}}{=}X_{0}(p^{2})/\langle w_{p^{2}}\rangle$
, where
![]() $w_{p^{2}}$
is the Atkin–Lehner involution [Reference ChenChe98, Reference de Smit and EdixhovendSE00]. Then we can count the points over
$w_{p^{2}}$
is the Atkin–Lehner involution [Reference ChenChe98, Reference de Smit and EdixhovendSE00]. Then we can count the points over
![]() $\mathbb{F}_{4}$
by looking at the roots of the characteristic polynomial of a Frobenius at
$\mathbb{F}_{4}$
by looking at the roots of the characteristic polynomial of a Frobenius at
![]() $2$
on the Jacobian of
$2$
on the Jacobian of
![]() $X_{0}(p^{2})$
, and using the well- known formula
$X_{0}(p^{2})$
, and using the well- known formula
where
![]() $C$
is a nonsingular projective curve of genus
$C$
is a nonsingular projective curve of genus
![]() $g$
over the finite field
$g$
over the finite field
![]() $\mathbb{F}_{q}$
with
$\mathbb{F}_{q}$
with
![]() $q$
prime, and the
$q$
prime, and the
![]() $\unicode[STIX]{x1D6FC}_{i}$
’s are the roots of the characteristic polynomial of the Frobenius automorphism at
$\unicode[STIX]{x1D6FC}_{i}$
’s are the roots of the characteristic polynomial of the Frobenius automorphism at
![]() $q$
, acting on the Jacobian variety of
$q$
, acting on the Jacobian variety of
![]() $C$
.
$C$
.
Looking at the tables in [Reference SteinSte12] of weight-2 newforms for
![]() $\unicode[STIX]{x1D6E4}_{0}(121)$
, we see that the Jacobian of
$\unicode[STIX]{x1D6E4}_{0}(121)$
, we see that the Jacobian of
![]() $X_{\text{ns}}(11)$
is isogenous to the product of four elliptic curves for which the traces of a Frobenius automorphism at 2 are respectively
$X_{\text{ns}}(11)$
is isogenous to the product of four elliptic curves for which the traces of a Frobenius automorphism at 2 are respectively
![]() $-1$
,
$-1$
,
![]() $0$
,
$0$
,
![]() $1$
,
$1$
,
![]() $2$
, so that the roots of the characteristic polynomial of a Frobenius at 2 acting on the Jacobian of
$2$
, so that the roots of the characteristic polynomial of a Frobenius at 2 acting on the Jacobian of
![]() $X_{\text{ns}}(11)$
are
$X_{\text{ns}}(11)$
are
![]() $\frac{-1\pm \sqrt{-7}}{2}$
,
$\frac{-1\pm \sqrt{-7}}{2}$
,
![]() $\pm \sqrt{-2}$
,
$\pm \sqrt{-2}$
,
![]() $\frac{1\pm \sqrt{-7}}{2}$
,
$\frac{1\pm \sqrt{-7}}{2}$
,
![]() $1\pm i$
. Hence
$1\pm i$
. Hence
![]() $\#X_{\text{ns}}(11)(\mathbb{F}_{4})=15>10$
.
$\#X_{\text{ns}}(11)(\mathbb{F}_{4})=15>10$
.
Now, in the same tables, we look at the weight-2 newforms for
![]() $\unicode[STIX]{x1D6E4}_{0}(169)$
. We see that the Jacobian of
$\unicode[STIX]{x1D6E4}_{0}(169)$
. We see that the Jacobian of
![]() $X_{\text{ns}}^{+}(13)$
is isogenous to a simple abelian variety
$X_{\text{ns}}^{+}(13)$
is isogenous to a simple abelian variety
![]() $A$
over
$A$
over
![]() $\mathbb{Q}$
of dimension
$\mathbb{Q}$
of dimension
![]() $3$
. The eigenvalues of the Hecke operator
$3$
. The eigenvalues of the Hecke operator
![]() $T_{2}$
acting on
$T_{2}$
acting on
![]() $A$
are the roots
$A$
are the roots
![]() $a_{i}$
, with
$a_{i}$
, with
![]() $i=1,2,3$
, of the polynomial
$i=1,2,3$
, of the polynomial
![]() $x^{3}+2x^{2}-x-1$
. Then the characteristic polynomial of a Frobenius at 2 is the product
$x^{3}+2x^{2}-x-1$
. Then the characteristic polynomial of a Frobenius at 2 is the product
It allows us to compute
![]() $\#X_{\text{ns}}^{+}(13)(\mathbb{F}_{4})=11>10$
.◻
$\#X_{\text{ns}}^{+}(13)(\mathbb{F}_{4})=11>10$
.◻
2 Endomorphisms of the Jacobian variety of
 $X_{\text{ns}}(p)$
$X_{\text{ns}}(p)$
In this section, for any abelian variety
![]() $A$
over a field
$A$
over a field
![]() $K$
, an endomorphism of
$K$
, an endomorphism of
![]() $A$
is an endomorphism defined over an algebraic closure
$A$
is an endomorphism defined over an algebraic closure
![]() $\overline{K}$
of
$\overline{K}$
of
![]() $K$
, and we write
$K$
, and we write
![]() $\text{End}(A)$
for the ring of endomorphisms of
$\text{End}(A)$
for the ring of endomorphisms of
![]() $A$
defined over
$A$
defined over
![]() $\overline{K}$
. The endomorphism algebra
$\overline{K}$
. The endomorphism algebra
![]() $\text{End}(A)\otimes \mathbb{Q}$
is an invariant of the isogeny class of
$\text{End}(A)\otimes \mathbb{Q}$
is an invariant of the isogeny class of
![]() $A$
over
$A$
over
![]() $\overline{K}$
. The minimal field where every endomorphism of
$\overline{K}$
. The minimal field where every endomorphism of
![]() $A$
is defined is an invariant of the isogeny class over
$A$
is defined is an invariant of the isogeny class over
![]() $K$
of
$K$
of
![]() $A$
. We say that
$A$
. We say that
![]() $A$
is of CM-type if
$A$
is of CM-type if
![]() $\text{End}(A)\otimes \mathbb{Q}$
contains a commutative semisimple
$\text{End}(A)\otimes \mathbb{Q}$
contains a commutative semisimple
![]() $\mathbb{Q}$
-algebra of dimension equal to
$\mathbb{Q}$
-algebra of dimension equal to
![]() $2\cdot \dim A$
.
$2\cdot \dim A$
.
Proposition 2.1. Let
![]() $A$
be a semistable abelian variety over a field
$A$
be a semistable abelian variety over a field
![]() $K$
, complete with respect to a discrete valuation. Then every endomorphism of
$K$
, complete with respect to a discrete valuation. Then every endomorphism of
![]() $A$
is defined over an unramified extension of
$A$
is defined over an unramified extension of
![]() $K$
.
$K$
.
Proof. [Reference RibetRib75, p. 556, Theorem 1.1]. ◻
Proposition 2.2. Let
![]() $A$
be an abelian variety over a field
$A$
be an abelian variety over a field
![]() $K$
. Let
$K$
. Let
![]() $E$
be a subalgebra of
$E$
be a subalgebra of
![]() $\text{End}_{K}(A)\otimes \mathbb{Q}$
such that
$\text{End}_{K}(A)\otimes \mathbb{Q}$
such that
![]() $[E:\mathbb{Q}]=\dim A$
and suppose that
$[E:\mathbb{Q}]=\dim A$
and suppose that
![]() $E$
is a product
$E$
is a product
![]() $E_{1}\times \cdots \times E_{t}$
of totally real number fields. This gives rise to a decomposition
$E_{1}\times \cdots \times E_{t}$
of totally real number fields. This gives rise to a decomposition
![]() $A\sim A_{1}\times \cdots \times A_{t}$
of abelian varieties up to isogeny over
$A\sim A_{1}\times \cdots \times A_{t}$
of abelian varieties up to isogeny over
![]() $K$
. Suppose that no factor
$K$
. Suppose that no factor
![]() $A_{i}$
is of CM-type. Then
$A_{i}$
is of CM-type. Then
![]() $E$
is its own commutant in
$E$
is its own commutant in
![]() $\text{End}(A)\otimes \mathbb{Q}$
and every endomorphism of
$\text{End}(A)\otimes \mathbb{Q}$
and every endomorphism of
![]() $A$
is defined over a compositum of quadratic extensions of
$A$
is defined over a compositum of quadratic extensions of
![]() $K$
.
$K$
.
Proof. [Reference RibetRib75, p. 557, Theorem 2.3] ◻
Let
![]() $J_{0}(N)$
be the Jacobian variety of the modular curve
$J_{0}(N)$
be the Jacobian variety of the modular curve
![]() $X_{0}(N)$
. It is an abelian variety over
$X_{0}(N)$
. It is an abelian variety over
![]() $\mathbb{Q}$
.
$\mathbb{Q}$
.
Proposition 2.3. The abelian variety
![]() $J_{0}(N)$
is semistable at each prime
$J_{0}(N)$
is semistable at each prime
![]() $p$
such that
$p$
such that
![]() $p^{2}$
does not divide
$p^{2}$
does not divide
![]() $N$
.
$N$
.
Proof. [Reference Deligne and RapoportDR73, p. 286, Theorem 6.9]. ◻
For every integer
![]() $N>0$
, there exists a set of representatives
$N>0$
, there exists a set of representatives
![]() $f_{1},\ldots ,f_{t}$
of
$f_{1},\ldots ,f_{t}$
of
![]() $\text{Gal}(\overline{\mathbb{Q}}/\mathbb{Q})$
-conjugacy classes of normalized weight-2 cuspforms for
$\text{Gal}(\overline{\mathbb{Q}}/\mathbb{Q})$
-conjugacy classes of normalized weight-2 cuspforms for
![]() $\unicode[STIX]{x1D6E4}_{0}(N)$
, such that every
$\unicode[STIX]{x1D6E4}_{0}(N)$
, such that every
![]() $f_{i}$
is a newform at some level
$f_{i}$
is a newform at some level
![]() $M_{i}$
dividing
$M_{i}$
dividing
![]() $N$
, and
$N$
, and
![]() $\{f_{i}(n\unicode[STIX]{x1D70F}),n|N/M_{i},i=1\ldots t\}$
with their
$\{f_{i}(n\unicode[STIX]{x1D70F}),n|N/M_{i},i=1\ldots t\}$
with their
![]() $\text{Gal}(\overline{\mathbb{Q}}/\mathbb{Q})$
-conjugates form a basis of the complex vector space of weight-2 cuspforms for
$\text{Gal}(\overline{\mathbb{Q}}/\mathbb{Q})$
-conjugates form a basis of the complex vector space of weight-2 cuspforms for
![]() $\unicode[STIX]{x1D6E4}_{0}(N)$
. There is a decomposition of abelian varieties up to isogeny over
$\unicode[STIX]{x1D6E4}_{0}(N)$
. There is a decomposition of abelian varieties up to isogeny over
![]() $\mathbb{Q}$
$\mathbb{Q}$
where
![]() $A_{i}\stackrel{\text{def}}{=}A_{f_{i}}$
is the abelian variety up to isogeny over
$A_{i}\stackrel{\text{def}}{=}A_{f_{i}}$
is the abelian variety up to isogeny over
![]() $\mathbb{Q}$
associated to the
$\mathbb{Q}$
associated to the
![]() $\text{Gal}(\overline{\mathbb{Q}}/\mathbb{Q})$
-conjugacy class of
$\text{Gal}(\overline{\mathbb{Q}}/\mathbb{Q})$
-conjugacy class of
![]() $f_{i}$
, and
$f_{i}$
, and
![]() $m_{i}$
is the number of divisors of
$m_{i}$
is the number of divisors of
![]() $N/M_{i}$
(see [Reference Diamond and ShurmanDS05, §6.6]). Every
$N/M_{i}$
(see [Reference Diamond and ShurmanDS05, §6.6]). Every
![]() $A_{i}$
is a simple abelian variety over
$A_{i}$
is a simple abelian variety over
![]() $\mathbb{Q}$
.
$\mathbb{Q}$
.
Let
![]() $J_{0}^{C}(N)$
be the abelian variety up to isogeny over
$J_{0}^{C}(N)$
be the abelian variety up to isogeny over
![]() $\mathbb{Q}$
which is a product of the factors
$\mathbb{Q}$
which is a product of the factors
![]() $A_{i}^{m_{i}}$
such that
$A_{i}^{m_{i}}$
such that
![]() $A_{i}$
is of CM-type and let
$A_{i}$
is of CM-type and let
![]() $J_{0}^{H}(N)$
be the product of the remaining factors of the decomposition above. We recall here that if
$J_{0}^{H}(N)$
be the product of the remaining factors of the decomposition above. We recall here that if
![]() $A_{i}$
is of CM-type, then it is isogenous (over
$A_{i}$
is of CM-type, then it is isogenous (over
![]() $\overline{\mathbb{Q}}$
) to a product of copies of an elliptic curve with complex multiplication by an imaginary quadratic field
$\overline{\mathbb{Q}}$
) to a product of copies of an elliptic curve with complex multiplication by an imaginary quadratic field
![]() $K$
of discriminant
$K$
of discriminant
![]() $-D$
and
$-D$
and
![]() $f_{i}$
is a weight-2 cuspform for
$f_{i}$
is a weight-2 cuspform for
![]() $\unicode[STIX]{x1D6E4}_{0}(D\cdot \text{N}(\mathfrak{c}))$
, where
$\unicode[STIX]{x1D6E4}_{0}(D\cdot \text{N}(\mathfrak{c}))$
, where
![]() $\mathfrak{c}$
is the conductor of a primitive Hecke character of
$\mathfrak{c}$
is the conductor of a primitive Hecke character of
![]() $K$
(see [Reference ShimuraShi72, p. 138, Proposition 1.6], [Reference ShimuraShi71]). Any factor
$K$
(see [Reference ShimuraShi72, p. 138, Proposition 1.6], [Reference ShimuraShi71]). Any factor
![]() $A_{i}$
of
$A_{i}$
of
![]() $J_{0}^{H}(N)$
cannot be isogenous to any factor
$J_{0}^{H}(N)$
cannot be isogenous to any factor
![]() $A_{j}$
of
$A_{j}$
of
![]() $J_{0}^{C}(N)$
because
$J_{0}^{C}(N)$
because
![]() $A_{i}$
and
$A_{i}$
and
![]() $A_{j}$
have different endomorphism algebras. Hence, we have
$A_{j}$
have different endomorphism algebras. Hence, we have
![]() $J_{0}(N)\sim J_{0}^{H}(N)\times J_{0}^{C}(N)$
and
$J_{0}(N)\sim J_{0}^{H}(N)\times J_{0}^{C}(N)$
and
![]() $\text{End}(J_{0}(N))\otimes \mathbb{Q}\cong (\text{End}(J_{0}^{H}(N))\otimes \mathbb{Q})\times (\text{End}(J_{0}^{C}(N))\otimes \mathbb{Q})$
.
$\text{End}(J_{0}(N))\otimes \mathbb{Q}\cong (\text{End}(J_{0}^{H}(N))\otimes \mathbb{Q})\times (\text{End}(J_{0}^{C}(N))\otimes \mathbb{Q})$
.
Let
![]() $p$
be an odd prime number. We call
$p$
be an odd prime number. We call
![]() $K(p)=\mathbb{Q}(\sqrt{p})$
if
$K(p)=\mathbb{Q}(\sqrt{p})$
if
![]() $p\equiv 1~\text{mod}~4$
and
$p\equiv 1~\text{mod}~4$
and
![]() $K(p)=\mathbb{Q}(\sqrt{-p})$
if
$K(p)=\mathbb{Q}(\sqrt{-p})$
if
![]() $p\equiv 3~\text{mod}~4$
.
$p\equiv 3~\text{mod}~4$
.
Proposition 2.4. Every endomorphism of
![]() $J_{0}^{H}(p^{2})$
is defined over
$J_{0}^{H}(p^{2})$
is defined over
![]() $K(p)$
.
$K(p)$
.
Proof. Proposition 2.2 tells us that endomorphisms of
![]() $J_{0}^{H}(p^{2})$
can be defined over a field
$J_{0}^{H}(p^{2})$
can be defined over a field
![]() $K$
which is a compositum of quadratic extensions of
$K$
which is a compositum of quadratic extensions of
![]() $\mathbb{Q}$
. Furthermore, Propositions 2.1 and 2.3 imply that
$\mathbb{Q}$
. Furthermore, Propositions 2.1 and 2.3 imply that
![]() $K$
can be taken unramified outside
$K$
can be taken unramified outside
![]() $p$
. Thus, we can take
$p$
. Thus, we can take
![]() $K=\mathbb{Q}(\sqrt{p})$
if
$K=\mathbb{Q}(\sqrt{p})$
if
![]() $p\equiv 1~\text{mod}~4$
and
$p\equiv 1~\text{mod}~4$
and
![]() $K=\mathbb{Q}(\sqrt{-p})$
if
$K=\mathbb{Q}(\sqrt{-p})$
if
![]() $p\equiv 3~\text{mod}~4$
.◻
$p\equiv 3~\text{mod}~4$
.◻
Let
![]() $g_{0}(N)$
,
$g_{0}(N)$
,
![]() $g_{0}^{H}(N)$
,
$g_{0}^{H}(N)$
,
![]() $g_{0}^{C}(N)$
be respectively the dimensions of
$g_{0}^{C}(N)$
be respectively the dimensions of
![]() $J_{0}(N)$
,
$J_{0}(N)$
,
![]() $J_{0}^{H}(N)$
,
$J_{0}^{H}(N)$
,
![]() $J_{0}^{C}(N)$
.
$J_{0}^{C}(N)$
.
Let
![]() $J_{\text{ns}}(p)$
be the Jacobian of the modular curve
$J_{\text{ns}}(p)$
be the Jacobian of the modular curve
![]() $X_{\text{ns}}(p)$
. The abelian variety
$X_{\text{ns}}(p)$
. The abelian variety
![]() $J_{\text{ns}}(p)$
is isogenous over
$J_{\text{ns}}(p)$
is isogenous over
![]() $\mathbb{Q}$
to the new part of
$\mathbb{Q}$
to the new part of
![]() $J_{0}(p^{2})$
(see [Reference ChenChe98, Reference de Smit and EdixhovendSE00]). Let
$J_{0}(p^{2})$
(see [Reference ChenChe98, Reference de Smit and EdixhovendSE00]). Let
![]() $J_{0}^{\text{new}}(p^{2})$
and
$J_{0}^{\text{new}}(p^{2})$
and
![]() $J_{0}^{\text{old}}(p^{2})$
be respectively the new and the old part of
$J_{0}^{\text{old}}(p^{2})$
be respectively the new and the old part of
![]() $J_{0}(p^{2})$
and let us fix an isomorphism
$J_{0}(p^{2})$
and let us fix an isomorphism
![]() $\unicode[STIX]{x1D711}$
from
$\unicode[STIX]{x1D711}$
from
![]() $\text{End}(J_{\text{ns}}(p))\otimes \mathbb{Q}$
to
$\text{End}(J_{\text{ns}}(p))\otimes \mathbb{Q}$
to
![]() $\text{End}(J_{0}^{\text{new}}(p^{2}))\otimes \mathbb{Q}$
. We say, with abuse of notation, that an automorphism
$\text{End}(J_{0}^{\text{new}}(p^{2}))\otimes \mathbb{Q}$
. We say, with abuse of notation, that an automorphism
![]() $v$
of
$v$
of
![]() $X_{\text{ns}}(p)$
, induces the invertible element
$X_{\text{ns}}(p)$
, induces the invertible element
![]() $v\stackrel{\text{def}}{=}\unicode[STIX]{x1D711}(v)$
of
$v\stackrel{\text{def}}{=}\unicode[STIX]{x1D711}(v)$
of
where the first inclusion is given by sending
![]() $v$
to the invertible element that acts like
$v$
to the invertible element that acts like
![]() $v$
on the new part and as the identity on the old part.
$v$
on the new part and as the identity on the old part.
We can then define in an analogous way
![]() $J_{\text{ns}}^{H}(p)$
,
$J_{\text{ns}}^{H}(p)$
,
![]() $J_{\text{ns}}^{C}(p)$
, as factors of the new part of the decomposition (2.1). We also define the dimensions
$J_{\text{ns}}^{C}(p)$
, as factors of the new part of the decomposition (2.1). We also define the dimensions
![]() $g_{\text{ns}}(p)$
,
$g_{\text{ns}}(p)$
,
![]() $g_{\text{ns}}^{H}(p)$
,
$g_{\text{ns}}^{H}(p)$
,
![]() $g_{\text{ns}}^{C}(p)$
. We have
$g_{\text{ns}}^{C}(p)$
. We have
![]() $J_{\text{ns}}(p)\sim J_{\text{ns}}^{H}(p)\times J_{\text{ns}}^{C}(p)$
and
$J_{\text{ns}}(p)\sim J_{\text{ns}}^{H}(p)\times J_{\text{ns}}^{C}(p)$
and
![]() $\text{End}(J_{\text{ns}}(p))\otimes \mathbb{Q}\cong (\text{End}(J_{\text{ns}}^{H}(p))\otimes \mathbb{Q})\times (\text{End}(J_{\text{ns}}^{C}(p))\otimes \mathbb{Q})$
.
$\text{End}(J_{\text{ns}}(p))\otimes \mathbb{Q}\cong (\text{End}(J_{\text{ns}}^{H}(p))\otimes \mathbb{Q})\times (\text{End}(J_{\text{ns}}^{C}(p))\otimes \mathbb{Q})$
.
Theorem 2.5. If
![]() $g_{\text{ns}}(p)>p$
every automorphism of
$g_{\text{ns}}(p)>p$
every automorphism of
![]() $X_{\text{ns}}(p)$
is defined over
$X_{\text{ns}}(p)$
is defined over
![]() $K(p)$
.
$K(p)$
.
Proof. (Following [Reference Kenku and MomoseKM88, p. 55, Lemma 1.4]) Let
![]() $u$
be an automorphism of
$u$
be an automorphism of
![]() $X_{\text{ns}}(p)$
and
$X_{\text{ns}}(p)$
and
![]() $\unicode[STIX]{x1D70E}$
a element of
$\unicode[STIX]{x1D70E}$
a element of
![]() $\text{Gal}(\overline{\mathbb{Q}}/K(p))$
. We define
$\text{Gal}(\overline{\mathbb{Q}}/K(p))$
. We define
![]() $v=u^{\unicode[STIX]{x1D70E}}u^{-1}$
and let
$v=u^{\unicode[STIX]{x1D70E}}u^{-1}$
and let
![]() $d$
be the order of
$d$
be the order of
![]() $v$
in the automorphism group of
$v$
in the automorphism group of
![]() $X_{\text{ns}}(p)$
. We call
$X_{\text{ns}}(p)$
. We call
![]() $Y$
the quotient of
$Y$
the quotient of
![]() $X_{\text{ns}}(p)$
by the automorphism
$X_{\text{ns}}(p)$
by the automorphism
![]() $v$
. Let
$v$
. Let
![]() $g_{Y}$
be the genus of
$g_{Y}$
be the genus of
![]() $Y$
. We have that
$Y$
. We have that
![]() $v$
induces an automorphism of the Jacobian
$v$
induces an automorphism of the Jacobian
![]() $J_{\text{ns}}(p)\sim J_{\text{ns}}^{H}(p)\times J_{\text{ns}}^{C}(p)$
which acts trivially on
$J_{\text{ns}}(p)\sim J_{\text{ns}}^{H}(p)\times J_{\text{ns}}^{C}(p)$
which acts trivially on
![]() $J_{\text{ns}}^{H}(p)$
by Proposition 2.4, because
$J_{\text{ns}}^{H}(p)$
by Proposition 2.4, because
![]() $J_{\text{ns}}^{H}(p)$
is a factor of
$J_{\text{ns}}^{H}(p)$
is a factor of
![]() $J_{0}^{H}(p^{2})$
. Thus we have the following morphisms of abelian varieties with finite kernel
$J_{0}^{H}(p^{2})$
. Thus we have the following morphisms of abelian varieties with finite kernel
where the image of the composition is contained in
![]() $J_{\text{ns}}(p)^{v}\stackrel{\text{def}}{=}\{D\in J_{\text{ns}}(p):vD=D\}$
. Hence there are morphisms of group varieties
$J_{\text{ns}}(p)^{v}\stackrel{\text{def}}{=}\{D\in J_{\text{ns}}(p):vD=D\}$
. Hence there are morphisms of group varieties
where the second map is the push-forward of divisors, and the composition is a morphism of abelian varieties. Furthermore, both maps have finite kernel, hence
![]() $g_{Y}\geqslant g_{\text{ns}}^{H}(p)$
and we have by the Riemann–Hurwitz formula
$g_{Y}\geqslant g_{\text{ns}}^{H}(p)$
and we have by the Riemann–Hurwitz formula
where in the second inequality we supposed
![]() $d>1$
. Now using
$d>1$
. Now using
![]() $g_{\text{ns}}(p)=g_{\text{ns}}^{H}(p)+g_{\text{ns}}^{C}(p)$
we obtain
$g_{\text{ns}}(p)=g_{\text{ns}}^{H}(p)+g_{\text{ns}}^{C}(p)$
we obtain
![]() $g_{\text{ns}}(p)\leqslant 2g_{\text{ns}}^{C}(p)+1$
. Since
$g_{\text{ns}}(p)\leqslant 2g_{\text{ns}}^{C}(p)+1$
. Since
![]() $J_{\text{ns}}(p)$
is isogenous over
$J_{\text{ns}}(p)$
is isogenous over
![]() $\mathbb{Q}$
to the new part of
$\mathbb{Q}$
to the new part of
![]() $J_{0}(p^{2})$
we have
$J_{0}(p^{2})$
we have
![]() $g_{\text{ns}}^{C}(p)=g_{0}^{C}(p^{2})$
. Indeed, the old part of
$g_{\text{ns}}^{C}(p)=g_{0}^{C}(p^{2})$
. Indeed, the old part of
![]() $J_{0}(p^{2})$
is isogenous to the product of two copies of the Jacobian of
$J_{0}(p^{2})$
is isogenous to the product of two copies of the Jacobian of
![]() $J_{0}(p)$
and these cannot have abelian subvarieties of CM-type (see [Reference ShimuraShi72, p. 140, Remark 1.7]). Furthermore,
$J_{0}(p)$
and these cannot have abelian subvarieties of CM-type (see [Reference ShimuraShi72, p. 140, Remark 1.7]). Furthermore,
![]() $g_{0}^{C}(p^{2})=0$
if
$g_{0}^{C}(p^{2})=0$
if
![]() $p\equiv 1~\text{mod}~4$
and
$p\equiv 1~\text{mod}~4$
and
![]() $g_{0}^{C}(p^{2})=h(-p)$
if
$g_{0}^{C}(p^{2})=h(-p)$
if
![]() $p\equiv 3~\text{mod}~4$
, where
$p\equiv 3~\text{mod}~4$
, where
![]() $h(-p)$
is the class number of
$h(-p)$
is the class number of
![]() $\mathbb{Q}(\sqrt{-p})$
. Indeed, in the decomposition (2.1) with
$\mathbb{Q}(\sqrt{-p})$
. Indeed, in the decomposition (2.1) with
![]() $N=p^{2}$
, if a factor is of CM-type, then it is the product of copies of an elliptic curve with complex multiplication by an imaginary quadratic field
$N=p^{2}$
, if a factor is of CM-type, then it is the product of copies of an elliptic curve with complex multiplication by an imaginary quadratic field
![]() $K$
of discriminant
$K$
of discriminant
![]() $-p$
. This leaves no possibilities if
$-p$
. This leaves no possibilities if
![]() $p\equiv 1~\text{mod}~4$
and it implies
$p\equiv 1~\text{mod}~4$
and it implies
![]() $K=\mathbb{Q}(\sqrt{-p})$
when
$K=\mathbb{Q}(\sqrt{-p})$
when
![]() $p\equiv 3~\text{mod}~4$
. In the latter case the dimension is
$p\equiv 3~\text{mod}~4$
. In the latter case the dimension is
![]() $h(-p)$
because by the theory of complex multiplication, the elliptic curves with complex multiplication by
$h(-p)$
because by the theory of complex multiplication, the elliptic curves with complex multiplication by
![]() $\mathbb{Q}(\sqrt{-p})$
are all isogenous,
$\mathbb{Q}(\sqrt{-p})$
are all isogenous,
![]() $\text{Gal}(\overline{\mathbb{Q}}/\mathbb{Q})$
-conjugate and their cardinality is
$\text{Gal}(\overline{\mathbb{Q}}/\mathbb{Q})$
-conjugate and their cardinality is
![]() $h(-p)$
.
$h(-p)$
.
Then we can estimate
![]() $h(-p)$
using Dirichlet’s class number formula:
$h(-p)$
using Dirichlet’s class number formula:
where the first equality is [Reference DavenportDav80, p. 51, (19)] (we are assuming
![]() $p\equiv 3~\text{mod}~4$
and
$p\equiv 3~\text{mod}~4$
and
![]() $p\neq 3$
), and in the inequality we used that the Legendre symbol
$p\neq 3$
), and in the inequality we used that the Legendre symbol
![]() $\left(\frac{m}{p}\right)$
takes values in
$\left(\frac{m}{p}\right)$
takes values in
![]() $\{\pm 1\}$
. This implies
$\{\pm 1\}$
. This implies
![]() $g_{\text{ns}}(p)\leqslant p$
. Contradiction.◻
$g_{\text{ns}}(p)\leqslant p$
. Contradiction.◻
Corollary 2.6. If
![]() $p\geqslant 11$
every automorphism of
$p\geqslant 11$
every automorphism of
![]() $X_{\text{ns}}(p)$
is defined over
$X_{\text{ns}}(p)$
is defined over
![]() $K(p)$
.
$K(p)$
.
Proof. By [Reference BaranBar10, Theorem 7.2], we have that
![]() $g_{\text{ns}}(p)>p$
for
$g_{\text{ns}}(p)>p$
for
![]() $p\geqslant 19$
. Regarding
$p\geqslant 19$
. Regarding
![]() $p=13$
,
$p=13$
,
![]() $17$
, they are both congruent to
$17$
, they are both congruent to
![]() $1$
modulo
$1$
modulo
![]() $4$
, so in these cases
$4$
, so in these cases
![]() $g_{\text{ns}}^{C}(p)=g_{0}^{C}(p^{2})=0$
and we can use Proposition 2.4 together with the isogeny over
$g_{\text{ns}}^{C}(p)=g_{0}^{C}(p^{2})=0$
and we can use Proposition 2.4 together with the isogeny over
![]() $\mathbb{Q}$
between
$\mathbb{Q}$
between
![]() $J_{\text{ns}}(p)$
and the new part of
$J_{\text{ns}}(p)$
and the new part of
![]() $J_{0}(p^{2})$
. The automorphisms of
$J_{0}(p^{2})$
. The automorphisms of
![]() $X_{\text{ns}}(11)$
are explicitly computed in [Reference Dose, Fernández, González and SchoofDFGS14] and they are all defined over
$X_{\text{ns}}(11)$
are explicitly computed in [Reference Dose, Fernández, González and SchoofDFGS14] and they are all defined over
![]() $\mathbb{Q}$
.◻
$\mathbb{Q}$
.◻
The modular curve
![]() $X_{\text{ns}}(7)$
has genus
$X_{\text{ns}}(7)$
has genus
![]() $1$
, and it has the automorphisms defined as translation by points. Thus, in this case there are automorphisms defined over larger number fields.
$1$
, and it has the automorphisms defined as translation by points. Thus, in this case there are automorphisms defined over larger number fields.
Proposition 2.7. If an automorphism of
![]() $X_{\text{ns}}(p)$
is defined over
$X_{\text{ns}}(p)$
is defined over
![]() $\mathbb{Q}$
, then it induces an element of
$\mathbb{Q}$
, then it induces an element of
![]() $\text{End}(J_{0}^{H}(p^{2}))\otimes \mathbb{Q}$
contained in the Hecke algebra.
$\text{End}(J_{0}^{H}(p^{2}))\otimes \mathbb{Q}$
contained in the Hecke algebra.
Proof. Since
![]() $J_{\text{ns}}(p)$
is isogenous over
$J_{\text{ns}}(p)$
is isogenous over
![]() $\mathbb{Q}$
to the new part of
$\mathbb{Q}$
to the new part of
![]() $J_{0}(p^{2})$
, an automorphism
$J_{0}(p^{2})$
, an automorphism
![]() $u$
of
$u$
of
![]() $X_{\text{ns}}(p)$
defined over
$X_{\text{ns}}(p)$
defined over
![]() $\mathbb{Q}$
induces an element of
$\mathbb{Q}$
induces an element of
![]() $\text{End}_{\mathbb{Q}}(J_{0}(p^{2}))\otimes \mathbb{Q}\cong (\text{End}_{\mathbb{Q}}(J_{\text{ns}}^{H}(p))\otimes \mathbb{Q})\times (\text{End}_{\mathbb{Q}}(J_{\text{ns}}^{C}(p))\otimes \mathbb{Q})$
, as explained above. Since
$\text{End}_{\mathbb{Q}}(J_{0}(p^{2}))\otimes \mathbb{Q}\cong (\text{End}_{\mathbb{Q}}(J_{\text{ns}}^{H}(p))\otimes \mathbb{Q})\times (\text{End}_{\mathbb{Q}}(J_{\text{ns}}^{C}(p))\otimes \mathbb{Q})$
, as explained above. Since
![]() $J_{0}(p^{2})$
has good reduction outside
$J_{0}(p^{2})$
has good reduction outside
![]() $p$
, the reduction modulo
$p$
, the reduction modulo
![]() $l$
map is injective on the endomorphism ring of
$l$
map is injective on the endomorphism ring of
![]() $J_{0}(p^{2})$
for every prime number
$J_{0}(p^{2})$
for every prime number
![]() $l\neq p$
. Hence, by the Eichler–Shimura relations,
$l\neq p$
. Hence, by the Eichler–Shimura relations,
![]() $u$
commutes with every Hecke operator
$u$
commutes with every Hecke operator
![]() $T_{l}$
with
$T_{l}$
with
![]() $l\neq p$
, because
$l\neq p$
, because
![]() $u$
is defined over
$u$
is defined over
![]() $\mathbb{Q}$
. Moreover, the Hecke algebra acting on the new part is generated by the operators
$\mathbb{Q}$
. Moreover, the Hecke algebra acting on the new part is generated by the operators
![]() $T_{l}$
with
$T_{l}$
with
![]() $l\neq p$
, thus
$l\neq p$
, thus
![]() $u$
commutes with the whole Hecke algebra. Then, to prove the Proposition, we note that every factor of
$u$
commutes with the whole Hecke algebra. Then, to prove the Proposition, we note that every factor of
![]() $J_{0}^{H}(p^{2})$
is without complex multiplication and so the Hecke algebra is its own commutant in
$J_{0}^{H}(p^{2})$
is without complex multiplication and so the Hecke algebra is its own commutant in
![]() $\text{End}(J_{0}^{H}(p^{2}))\otimes \mathbb{Q}$
(Proposition 2.2).◻
$\text{End}(J_{0}^{H}(p^{2}))\otimes \mathbb{Q}$
(Proposition 2.2).◻
Lemma 2.8. If
![]() $g_{\text{ns}}(p)>p$
every automorphism of
$g_{\text{ns}}(p)>p$
every automorphism of
![]() $X_{\text{ns}}(p)$
defined over
$X_{\text{ns}}(p)$
defined over
![]() $\mathbb{Q}$
commutes with the modular involution
$\mathbb{Q}$
commutes with the modular involution
![]() $w$
.
$w$
.
Proof. Let
![]() $u$
be an automorphism of
$u$
be an automorphism of
![]() $X_{\text{ns}}(p)$
defined over
$X_{\text{ns}}(p)$
defined over
![]() $\mathbb{Q}$
. Then, by the previous Proposition,
$\mathbb{Q}$
. Then, by the previous Proposition,
![]() $u$
and
$u$
and
![]() $w$
induce elements in the Hecke algebra of
$w$
induce elements in the Hecke algebra of
![]() $J_{0}^{H}(p^{2})$
, which is a commutative algebra. Hence, if we define
$J_{0}^{H}(p^{2})$
, which is a commutative algebra. Hence, if we define
![]() $v=uwu^{-1}w^{-1}$
we have that
$v=uwu^{-1}w^{-1}$
we have that
![]() $v$
induces an invertible element of
$v$
induces an invertible element of
![]() $\text{End}(J_{0}(p^{2}))\otimes \mathbb{Q}$
which acts trivially on
$\text{End}(J_{0}(p^{2}))\otimes \mathbb{Q}$
which acts trivially on
![]() $J_{0}^{H}(p^{2})$
and
$J_{0}^{H}(p^{2})$
and
![]() $J_{\text{ns}}^{H}(p)$
. Then we can use the same proof as for Theorem 2.5 to see that
$J_{\text{ns}}^{H}(p)$
. Then we can use the same proof as for Theorem 2.5 to see that
![]() $v$
is trivial if
$v$
is trivial if
![]() $g_{\text{ns}}(p)>p$
.◻
$g_{\text{ns}}(p)>p$
.◻
Corollary 2.9. If
![]() $p\geqslant 11$
every automorphism of
$p\geqslant 11$
every automorphism of
![]() $X_{\text{ns}}(p)$
defined over
$X_{\text{ns}}(p)$
defined over
![]() $\mathbb{Q}$
commutes with the modular involution
$\mathbb{Q}$
commutes with the modular involution
![]() $w$
.
$w$
.
Proof. As for Corollary 2.6, we have that
![]() $g_{\text{ns}}(p)>p$
for
$g_{\text{ns}}(p)>p$
for
![]() $p\geqslant 19$
. Regarding
$p\geqslant 19$
. Regarding
![]() $p=13$
,
$p=13$
,
![]() $17$
, in these cases
$17$
, in these cases
![]() $g_{\text{ns}}^{C}(p)=g_{0}^{C}(p^{2})=0$
. Moreover,
$g_{\text{ns}}^{C}(p)=g_{0}^{C}(p^{2})=0$
. Moreover,
![]() $g_{\text{ns}}(p)\geqslant 2$
, so the natural map from the automorphism group of
$g_{\text{ns}}(p)\geqslant 2$
, so the natural map from the automorphism group of
![]() $X_{\text{ns}}(p)$
to the automorphism group of
$X_{\text{ns}}(p)$
to the automorphism group of
![]() $J_{\text{ns}}(p)$
is injective [Reference Baker and HasegawaBH03, Lemma 2.1], and we can use Proposition 2.7 together with the fact that the Hecke algebra is commutative. The automorphism group of
$J_{\text{ns}}(p)$
is injective [Reference Baker and HasegawaBH03, Lemma 2.1], and we can use Proposition 2.7 together with the fact that the Hecke algebra is commutative. The automorphism group of
![]() $X_{\text{ns}}(11)$
is the Klein four group (see [Reference Dose, Fernández, González and SchoofDFGS14]).◻
$X_{\text{ns}}(11)$
is the Klein four group (see [Reference Dose, Fernández, González and SchoofDFGS14]).◻
Corollary 2.10. If
![]() $p\geqslant 11$
every automorphism of
$p\geqslant 11$
every automorphism of
![]() $X_{\text{ns}}(p)$
defined over
$X_{\text{ns}}(p)$
defined over
![]() $\mathbb{Q}$
induces an automorphism of
$\mathbb{Q}$
induces an automorphism of
![]() $X_{\text{ns}}^{+}(p)$
defined over
$X_{\text{ns}}^{+}(p)$
defined over
![]() $\mathbb{Q}$
.
$\mathbb{Q}$
.
3 Automorphisms of
 $X_{\text{ns}}(p)$
preserving the cusps
$X_{\text{ns}}(p)$
preserving the cusps
Let
![]() $X_{H}$
be a modular curve. Then the orbit space
$X_{H}$
be a modular curve. Then the orbit space
![]() ${\mathcal{H}}\cup \mathbb{Q}\cup \{\infty \}/\unicode[STIX]{x1D6E4}_{H}$
can be identified with
${\mathcal{H}}\cup \mathbb{Q}\cup \{\infty \}/\unicode[STIX]{x1D6E4}_{H}$
can be identified with
![]() $X_{H}(\mathbb{C})$
. Let
$X_{H}(\mathbb{C})$
. Let
![]() $E\subset {\mathcal{H}}$
be the set of ramification points of the natural quotient map
$E\subset {\mathcal{H}}$
be the set of ramification points of the natural quotient map
![]() $\unicode[STIX]{x1D70B}:{\mathcal{H}}\rightarrow {\mathcal{H}}/\unicode[STIX]{x1D6E4}_{H}$
. This is a discrete set in
$\unicode[STIX]{x1D70B}:{\mathcal{H}}\rightarrow {\mathcal{H}}/\unicode[STIX]{x1D6E4}_{H}$
. This is a discrete set in
![]() ${\mathcal{H}}$
and it is the counter image of the set of elliptic points in
${\mathcal{H}}$
and it is the counter image of the set of elliptic points in
![]() $X_{H}(\mathbb{C})$
. For every
$X_{H}(\mathbb{C})$
. For every
![]() $z\in {\mathcal{H}}\smallsetminus E$
there exists a neighborhood
$z\in {\mathcal{H}}\smallsetminus E$
there exists a neighborhood
![]() $U\ni z$
such that
$U\ni z$
such that
![]() $\unicode[STIX]{x1D6FE}_{i}(U)\cap \unicode[STIX]{x1D6FE}_{j}(U)=\emptyset$
for every
$\unicode[STIX]{x1D6FE}_{i}(U)\cap \unicode[STIX]{x1D6FE}_{j}(U)=\emptyset$
for every
![]() $\unicode[STIX]{x1D6FE}_{i}\neq \pm \unicode[STIX]{x1D6FE}_{j}$
in
$\unicode[STIX]{x1D6FE}_{i}\neq \pm \unicode[STIX]{x1D6FE}_{j}$
in
![]() $\unicode[STIX]{x1D6E4}_{H}$
. This means that
$\unicode[STIX]{x1D6E4}_{H}$
. This means that
![]() ${\mathcal{H}}\smallsetminus E$
is a proper covering space of
${\mathcal{H}}\smallsetminus E$
is a proper covering space of
![]() $X_{H}(\mathbb{C})$
without the cusps and the elliptic points.
$X_{H}(\mathbb{C})$
without the cusps and the elliptic points.
Proposition 3.1. Let
![]() $u$
be an automorphism of
$u$
be an automorphism of
![]() $X_{H}$
. If
$X_{H}$
. If
![]() $u$
preserves the set of cusps and preserves the set of elliptic points of
$u$
preserves the set of cusps and preserves the set of elliptic points of
![]() $X_{H}$
, then
$X_{H}$
, then
![]() $u$
is induced by an automorphism of the Riemann surface
$u$
is induced by an automorphism of the Riemann surface
![]() ${\mathcal{H}}$
preserving
${\mathcal{H}}$
preserving
![]() $E$
.
$E$
.
Proof. Let
![]() $C$
be the set of cusps on
$C$
be the set of cusps on
![]() $X_{H}$
. Note that an automorphism
$X_{H}$
. Note that an automorphism
![]() $u$
of
$u$
of
![]() $X_{H}$
preserving the cusps and the elliptic points, defines naturally an automorphism of the open Riemann surface
$X_{H}$
preserving the cusps and the elliptic points, defines naturally an automorphism of the open Riemann surface
![]() $X_{H}(\mathbb{C})\smallsetminus (C\cup \unicode[STIX]{x1D70B}(E))$
. If
$X_{H}(\mathbb{C})\smallsetminus (C\cup \unicode[STIX]{x1D70B}(E))$
. If
![]() $X_{H}$
has no elliptic points (
$X_{H}$
has no elliptic points (
![]() $E=\emptyset$
), then the quotient
$E=\emptyset$
), then the quotient
![]() ${\mathcal{H}}\rightarrow {\mathcal{H}}/\unicode[STIX]{x1D6E4}_{H}\cong X_{H}(\mathbb{C})\smallsetminus C$
is the universal cover of
${\mathcal{H}}\rightarrow {\mathcal{H}}/\unicode[STIX]{x1D6E4}_{H}\cong X_{H}(\mathbb{C})\smallsetminus C$
is the universal cover of
![]() $X_{H}(\mathbb{C})\smallsetminus C$
. Then
$X_{H}(\mathbb{C})\smallsetminus C$
. Then
![]() $u$
automatically lifts to an automorphism of
$u$
automatically lifts to an automorphism of
![]() ${\mathcal{H}}$
. If instead
${\mathcal{H}}$
. If instead
![]() $E\neq \emptyset$
, to lift
$E\neq \emptyset$
, to lift
![]() $u$
to
$u$
to
![]() ${\mathcal{H}}\smallsetminus E$
, we need the push-forward by
${\mathcal{H}}\smallsetminus E$
, we need the push-forward by
![]() $u\circ \unicode[STIX]{x1D70B}$
of the fundamental group of
$u\circ \unicode[STIX]{x1D70B}$
of the fundamental group of
![]() ${\mathcal{H}}\smallsetminus E$
to be contained in its push-forward by
${\mathcal{H}}\smallsetminus E$
to be contained in its push-forward by
![]() $\unicode[STIX]{x1D70B}$
. But this is true because
$\unicode[STIX]{x1D70B}$
. But this is true because
![]() $u$
actually extends to an automorphism of
$u$
actually extends to an automorphism of
![]() $X_{H}(\mathbb{C})$
preserving
$X_{H}(\mathbb{C})$
preserving
![]() $C$
and
$C$
and
![]() $\unicode[STIX]{x1D70B}(E)$
. Hence
$\unicode[STIX]{x1D70B}(E)$
. Hence
![]() $u$
lifts to an automorphism of
$u$
lifts to an automorphism of
![]() ${\mathcal{H}}\smallsetminus E$
, which extends uniquely to
${\mathcal{H}}\smallsetminus E$
, which extends uniquely to
![]() ${\mathcal{H}}$
.◻
${\mathcal{H}}$
.◻
Let
![]() $p$
be a prime number.
$p$
be a prime number.
Proposition 3.2. Suppose that the genus of
![]() $X_{\text{ns}}(p)$
is at least 2. Let
$X_{\text{ns}}(p)$
is at least 2. Let
![]() $\unicode[STIX]{x1D6E4}_{\text{ns}}(p)$
be the subgroup of
$\unicode[STIX]{x1D6E4}_{\text{ns}}(p)$
be the subgroup of
![]() $\text{SL}_{2}(\mathbb{Z})$
made up of the elements which reduce modulo
$\text{SL}_{2}(\mathbb{Z})$
made up of the elements which reduce modulo
![]() $p$
to an element in a nonsplit Cartan subgroup of
$p$
to an element in a nonsplit Cartan subgroup of
![]() $\text{GL}_{2}(\mathbb{F}_{p})$
. Then the subgroup
$\text{GL}_{2}(\mathbb{F}_{p})$
. Then the subgroup
is generated by the modular involution
![]() $w$
.
$w$
.
Proof. Since the genus of
![]() $X_{\text{ns}}(p)$
is at least 2, the group
$X_{\text{ns}}(p)$
is at least 2, the group
![]() $B(X_{\text{ns}}(p))$
must be finite. This means that
$B(X_{\text{ns}}(p))$
must be finite. This means that
![]() $\text{Norm}(\unicode[STIX]{x1D6E4}_{\text{ns}}(p))$
is commensurable with
$\text{Norm}(\unicode[STIX]{x1D6E4}_{\text{ns}}(p))$
is commensurable with
![]() $\text{SL}_{2}(\mathbb{Z})$
in the sense that
$\text{SL}_{2}(\mathbb{Z})$
in the sense that
![]() $\text{Norm}(\unicode[STIX]{x1D6E4}_{\text{ns}}(p))\cap \text{SL}_{2}(\mathbb{Z})$
has finite index in both
$\text{Norm}(\unicode[STIX]{x1D6E4}_{\text{ns}}(p))\cap \text{SL}_{2}(\mathbb{Z})$
has finite index in both
![]() $\text{Norm}(\unicode[STIX]{x1D6E4}_{\text{ns}}(p))$
and
$\text{Norm}(\unicode[STIX]{x1D6E4}_{\text{ns}}(p))$
and
![]() $\text{SL}_{2}(\mathbb{Z})$
. Hence
$\text{SL}_{2}(\mathbb{Z})$
. Hence
![]() $\text{Norm}(\unicode[STIX]{x1D6E4}_{\text{ns}}(p))$
is a group acting on lattices of
$\text{Norm}(\unicode[STIX]{x1D6E4}_{\text{ns}}(p))$
is a group acting on lattices of
![]() $\mathbb{R}^{2}$
that are commensurable with
$\mathbb{R}^{2}$
that are commensurable with
![]() $\mathbb{Z}\times \mathbb{Z}$
, with the action given by right multiplication of row vectors in the lattice. Lattices commensurable with
$\mathbb{Z}\times \mathbb{Z}$
, with the action given by right multiplication of row vectors in the lattice. Lattices commensurable with
![]() $\mathbb{Z}\times \mathbb{Z}$
are the ones generated by two vectors
$\mathbb{Z}\times \mathbb{Z}$
are the ones generated by two vectors
![]() $(a,b)$
,
$(a,b)$
,
![]() $(c,d)$
with
$(c,d)$
with
![]() $a,b,c,d\in \mathbb{Q}$
, and if we consider them up to multiplication by a scalar (i.e., homothety), they all have a basis of the form
$a,b,c,d\in \mathbb{Q}$
, and if we consider them up to multiplication by a scalar (i.e., homothety), they all have a basis of the form
![]() $\{(M,\frac{g}{h}),(0,1)\}$
with
$\{(M,\frac{g}{h}),(0,1)\}$
with
![]() $M\in \mathbb{Q}^{+}$
,
$M\in \mathbb{Q}^{+}$
,
![]() $g,h\in \mathbb{Z}$
,
$g,h\in \mathbb{Z}$
,
![]() $\text{gcd}(g,h)=1$
and
$\text{gcd}(g,h)=1$
and
![]() $0\leqslant g<h$
(see [Reference ConwayCon96] for more details).
$0\leqslant g<h$
(see [Reference ConwayCon96] for more details).
Since
![]() $\unicode[STIX]{x1D6E4}_{\text{ns}}(p)\subset \unicode[STIX]{x1D6E4}(p)=\left\{\unicode[STIX]{x1D6FE}\in \text{SL}_{2}(\mathbb{Z})\text{ s. t. }\unicode[STIX]{x1D6FE}\equiv \text{Id mod }p\right\}$
, the lattices fixed by
$\unicode[STIX]{x1D6E4}_{\text{ns}}(p)\subset \unicode[STIX]{x1D6E4}(p)=\left\{\unicode[STIX]{x1D6FE}\in \text{SL}_{2}(\mathbb{Z})\text{ s. t. }\unicode[STIX]{x1D6FE}\equiv \text{Id mod }p\right\}$
, the lattices fixed by
![]() $\unicode[STIX]{x1D6E4}_{\text{ns}}(p)$
are a subset of the lattices fixed by
$\unicode[STIX]{x1D6E4}_{\text{ns}}(p)$
are a subset of the lattices fixed by
![]() $\unicode[STIX]{x1D6E4}(p)$
. The lattices fixed by
$\unicode[STIX]{x1D6E4}(p)$
. The lattices fixed by
![]() $\unicode[STIX]{x1D6E4}(p)$
are those who belong to one of the following type (see [Reference LangLan02, Lemma 4.1])
$\unicode[STIX]{x1D6E4}(p)$
are those who belong to one of the following type (see [Reference LangLan02, Lemma 4.1])
-
∙
 $M=\frac{1}{p}$
,
$M=\frac{1}{p}$
,
 $h=p$
,
$h=p$
,
 $g=0,\ldots ,p-1$
, which gives a lattice homothetic to
$g=0,\ldots ,p-1$
, which gives a lattice homothetic to
 $\langle (1,g),(0,p)\rangle$
;
$\langle (1,g),(0,p)\rangle$
; -
∙
 $M=\frac{1}{p}$
,
$M=\frac{1}{p}$
,
 $h=1$
,
$h=1$
,
 $g=0$
, which gives a lattice homothetic to
$g=0$
, which gives a lattice homothetic to
 $\langle (1,0),(0,p)\rangle$
;
$\langle (1,0),(0,p)\rangle$
; -
∙
 $M=p$
,
$M=p$
,
 $h=1$
,
$h=1$
,
 $g=0$
, which gives the lattice
$g=0$
, which gives the lattice
 $\langle (p,0),(0,1)\rangle$
;
$\langle (p,0),(0,1)\rangle$
; -
∙
 $M=1$
,
$M=1$
,
 $h=1$
,
$h=1$
,
 $g=0$
, which gives the lattice
$g=0$
, which gives the lattice
 $\langle (1,0),(0,1)\rangle =\mathbb{Z}\times \mathbb{Z}$
.
$\langle (1,0),(0,1)\rangle =\mathbb{Z}\times \mathbb{Z}$
.
Recall that
![]() $\unicode[STIX]{x1D6E4}_{\text{ns}}(p)$
is the subgroup of
$\unicode[STIX]{x1D6E4}_{\text{ns}}(p)$
is the subgroup of
![]() $\text{SL}_{2}(\mathbb{Z})$
made up of the elements
$\text{SL}_{2}(\mathbb{Z})$
made up of the elements
![]() $\unicode[STIX]{x1D6FE}$
such that
$\unicode[STIX]{x1D6FE}$
such that
for some
![]() $(x,y)\in \mathbb{F}_{p}^{2}$
and a nonsquare element
$(x,y)\in \mathbb{F}_{p}^{2}$
and a nonsquare element
![]() $\unicode[STIX]{x1D6FC}\in \mathbb{F}_{p}$
. Then, a straightforward computation modulo
$\unicode[STIX]{x1D6FC}\in \mathbb{F}_{p}$
. Then, a straightforward computation modulo
![]() $p$
shows that
$p$
shows that
![]() $\unicode[STIX]{x1D6FE}$
fixes lattices of the first three types, only if
$\unicode[STIX]{x1D6FE}$
fixes lattices of the first three types, only if
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}(p)$
, so that the only lattice up to homothety fixed by
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}(p)$
, so that the only lattice up to homothety fixed by
![]() $\unicode[STIX]{x1D6E4}_{\text{ns}}(p)$
is
$\unicode[STIX]{x1D6E4}_{\text{ns}}(p)$
is
![]() $\mathbb{Z}\times \mathbb{Z}$
.
$\mathbb{Z}\times \mathbb{Z}$
.
The normalizer in
![]() $\text{SL}_{2}(\mathbb{R})$
of
$\text{SL}_{2}(\mathbb{R})$
of
![]() $\unicode[STIX]{x1D6E4}_{\text{ns}}(p)$
must preserve, by definition, the set of lattices that are fixed by
$\unicode[STIX]{x1D6E4}_{\text{ns}}(p)$
must preserve, by definition, the set of lattices that are fixed by
![]() $\unicode[STIX]{x1D6E4}_{\text{ns}}(p)$
. Thus, also
$\unicode[STIX]{x1D6E4}_{\text{ns}}(p)$
. Thus, also
![]() $\text{Norm}(\unicode[STIX]{x1D6E4}_{\text{ns}}(p))$
fixes
$\text{Norm}(\unicode[STIX]{x1D6E4}_{\text{ns}}(p))$
fixes
![]() $\mathbb{Z}\times \mathbb{Z}$
. The stabilizer of
$\mathbb{Z}\times \mathbb{Z}$
. The stabilizer of
![]() $\mathbb{Z}\times \mathbb{Z}$
is
$\mathbb{Z}\times \mathbb{Z}$
is
![]() $\text{SL}_{2}(\mathbb{Z})$
, implying
$\text{SL}_{2}(\mathbb{Z})$
, implying
![]() $\text{Norm}(\unicode[STIX]{x1D6E4}_{\text{ns}}(p))\subset \text{SL}_{2}(\mathbb{Z})$
. Therefore,
$\text{Norm}(\unicode[STIX]{x1D6E4}_{\text{ns}}(p))\subset \text{SL}_{2}(\mathbb{Z})$
. Therefore,
![]() $\text{Norm}(\unicode[STIX]{x1D6E4}_{\text{ns}}(p))$
is made up of the elements of
$\text{Norm}(\unicode[STIX]{x1D6E4}_{\text{ns}}(p))$
is made up of the elements of
![]() $\text{SL}_{2}(\mathbb{Z})$
which reduce modulo
$\text{SL}_{2}(\mathbb{Z})$
which reduce modulo
![]() $p$
to an element in the normalizer of a nonsplit Cartan subgroup of
$p$
to an element in the normalizer of a nonsplit Cartan subgroup of
![]() $\text{GL}_{2}(\mathbb{F}_{p})$
, which proves the Proposition.◻
$\text{GL}_{2}(\mathbb{F}_{p})$
, which proves the Proposition.◻
Corollary 3.3. Suppose that the genus of
![]() $X_{\text{ns}}(p)$
is at least 2. If
$X_{\text{ns}}(p)$
is at least 2. If
![]() $p\equiv 1~\text{mod}~12$
, the only nontrivial automorphism of
$p\equiv 1~\text{mod}~12$
, the only nontrivial automorphism of
![]() $X_{\text{ns}}(p)$
preserving the cusps is the modular involution
$X_{\text{ns}}(p)$
preserving the cusps is the modular involution
![]() $w$
. If
$w$
. If
![]() $p\not \equiv 1~\text{mod}~12$
, the only nontrivial automorphism of
$p\not \equiv 1~\text{mod}~12$
, the only nontrivial automorphism of
![]() $X_{\text{ns}}(p)$
preserving the cusps and the elliptic points, is the modular involution
$X_{\text{ns}}(p)$
preserving the cusps and the elliptic points, is the modular involution
![]() $w$
. The only automorphism of
$w$
. The only automorphism of
![]() $X_{\text{ns}}^{+}(p)$
preserving the cusps and the elliptic points is the identity.
$X_{\text{ns}}^{+}(p)$
preserving the cusps and the elliptic points is the identity.
Proof. Let
![]() $\unicode[STIX]{x1D6E4}_{\text{ns}}(p)$
be the subgroup of
$\unicode[STIX]{x1D6E4}_{\text{ns}}(p)$
be the subgroup of
![]() $\text{SL}_{2}(\mathbb{Z})$
made up of the elements which reduce modulo
$\text{SL}_{2}(\mathbb{Z})$
made up of the elements which reduce modulo
![]() $p$
to an element in a nonsplit Cartan subgroup of
$p$
to an element in a nonsplit Cartan subgroup of
![]() $\text{GL}_{2}(\mathbb{F}_{p})$
, so that
$\text{GL}_{2}(\mathbb{F}_{p})$
, so that
![]() $X_{\text{ns}}(p)(\mathbb{C})\cong {\mathcal{H}}\cup \mathbb{Q}\cup \{\infty \}/\unicode[STIX]{x1D6E4}_{\text{ns}}(p)$
. Thus,
$X_{\text{ns}}(p)(\mathbb{C})\cong {\mathcal{H}}\cup \mathbb{Q}\cup \{\infty \}/\unicode[STIX]{x1D6E4}_{\text{ns}}(p)$
. Thus,
![]() $X_{\text{ns}}(p)$
has elliptic points if and only if
$X_{\text{ns}}(p)$
has elliptic points if and only if
![]() $\unicode[STIX]{x1D6E4}_{\text{ns}}(p)$
contains an element with characteristic polynomial equal to
$\unicode[STIX]{x1D6E4}_{\text{ns}}(p)$
contains an element with characteristic polynomial equal to
![]() $x^{2}+1$
or
$x^{2}+1$
or
![]() $x^{2}+x+1$
. Recall that the elements of a nonsplit Cartan subgroup of
$x^{2}+x+1$
. Recall that the elements of a nonsplit Cartan subgroup of
![]() $\text{GL}_{2}(\mathbb{F}_{p})$
(not belonging to the center) have irreducible characteristic polynomials. If
$\text{GL}_{2}(\mathbb{F}_{p})$
(not belonging to the center) have irreducible characteristic polynomials. If
![]() $p\equiv 1~\text{mod}~4$
and
$p\equiv 1~\text{mod}~4$
and
![]() $p\equiv 1~\text{mod}~3$
, the two polynomials above have both roots over
$p\equiv 1~\text{mod}~3$
, the two polynomials above have both roots over
![]() $\mathbb{F}_{p}$
. Hence, when
$\mathbb{F}_{p}$
. Hence, when
![]() $p\equiv 1~\text{mod}~12$
there are no elliptic points on
$p\equiv 1~\text{mod}~12$
there are no elliptic points on
![]() $X_{\text{ns}}(p)$
. The Corollary then follows from the two previous Propositions.◻
$X_{\text{ns}}(p)$
. The Corollary then follows from the two previous Propositions.◻
4 Automorphisms of
 $X_{\text{ns}}(p)$
not preserving the cusps
$X_{\text{ns}}(p)$
not preserving the cusps
Let
![]() $p$
be a prime number and
$p$
be a prime number and
![]() $l$
be another prime number different from
$l$
be another prime number different from
![]() $p$
. Let
$p$
. Let
![]() $T_{l}$
be the
$T_{l}$
be the
![]() $l$
th Hecke operator for the modular curve
$l$
th Hecke operator for the modular curve
![]() $X_{\text{ns}}(p)$
, defined as a modular correspondence (see [Reference ShimuraShi58, §2]). Let
$X_{\text{ns}}(p)$
, defined as a modular correspondence (see [Reference ShimuraShi58, §2]). Let
![]() $E$
be an elliptic curve over
$E$
be an elliptic curve over
![]() $\mathbb{C}$
and let
$\mathbb{C}$
and let
![]() $\unicode[STIX]{x1D711}$
be an isomorphism from the
$\unicode[STIX]{x1D711}$
be an isomorphism from the
![]() $p$
-torsion
$p$
-torsion
![]() $E[p]$
of
$E[p]$
of
![]() $E$
to
$E$
to
![]() $\mathbb{Z}/p\mathbb{Z}\times \mathbb{Z}/p\mathbb{Z}$
. Then the pair
$\mathbb{Z}/p\mathbb{Z}\times \mathbb{Z}/p\mathbb{Z}$
. Then the pair
![]() $(E,\unicode[STIX]{x1D711})$
gives a point on
$(E,\unicode[STIX]{x1D711})$
gives a point on
![]() $X_{\text{ns}}(p)$
. Let
$X_{\text{ns}}(p)$
. Let
![]() $A$
be a subgroup of
$A$
be a subgroup of
![]() $E$
of order
$E$
of order
![]() $l$
. Since
$l$
. Since
![]() $l\neq p$
, taking the quotient by
$l\neq p$
, taking the quotient by
![]() $A$
on
$A$
on
![]() $E$
induces an isomorphism from the
$E$
induces an isomorphism from the
![]() $p$
-torsion of
$p$
-torsion of
![]() $E$
to the
$E$
to the
![]() $p$
-torsion of
$p$
-torsion of
![]() $E/A$
so that
$E/A$
so that
![]() $\unicode[STIX]{x1D711}$
induces an isomorphism
$\unicode[STIX]{x1D711}$
induces an isomorphism
![]() $\unicode[STIX]{x1D711}_{A}$
from the
$\unicode[STIX]{x1D711}_{A}$
from the
![]() $p$
-torsion of
$p$
-torsion of
![]() $E/A$
to
$E/A$
to
![]() $\mathbb{Z}/p\mathbb{Z}\times \mathbb{Z}/p\mathbb{Z}$
. The operator
$\mathbb{Z}/p\mathbb{Z}\times \mathbb{Z}/p\mathbb{Z}$
. The operator
![]() $T_{l}$
acts on a noncuspidal point of
$T_{l}$
acts on a noncuspidal point of
![]() $X_{\text{ns}}(p)$
in the following way
$X_{\text{ns}}(p)$
in the following way
and it induces an element in the endomorphism algebra of
![]() $J_{\text{ns}}(p)$
.
$J_{\text{ns}}(p)$
.
For every pair
![]() $(E,\unicode[STIX]{x1D711})$
with
$(E,\unicode[STIX]{x1D711})$
with
![]() $E$
defined over
$E$
defined over
![]() $\overline{\mathbb{Q}}$
let
$\overline{\mathbb{Q}}$
let
![]() $\widetilde{E}$
be the reduction of
$\widetilde{E}$
be the reduction of
![]() $E$
modulo a prime ideal containing
$E$
modulo a prime ideal containing
![]() $l$
, and
$l$
, and
![]() $\widetilde{\unicode[STIX]{x1D711}}:\widetilde{E}[p]\rightarrow \mathbb{Z}/p\mathbb{Z}\times \mathbb{Z}/p\mathbb{Z}$
be the map naturally induced by
$\widetilde{\unicode[STIX]{x1D711}}:\widetilde{E}[p]\rightarrow \mathbb{Z}/p\mathbb{Z}\times \mathbb{Z}/p\mathbb{Z}$
be the map naturally induced by
![]() $\unicode[STIX]{x1D711}$
, since
$\unicode[STIX]{x1D711}$
, since
![]() $l\neq p$
. Then the pair
$l\neq p$
. Then the pair
![]() $(\widetilde{E},\widetilde{\unicode[STIX]{x1D711}})$
gives a point on
$(\widetilde{E},\widetilde{\unicode[STIX]{x1D711}})$
gives a point on
![]() $X_{\text{ns}}(p)$
over
$X_{\text{ns}}(p)$
over
![]() $\overline{\mathbb{F}_{l}}$
. Let
$\overline{\mathbb{F}_{l}}$
. Let
![]() $\text{Frob}_{l}$
be the generator of the Galois group
$\text{Frob}_{l}$
be the generator of the Galois group
![]() $\text{Gal}(\overline{\mathbb{F}_{l}}/\mathbb{F}_{l})$
and let
$\text{Gal}(\overline{\mathbb{F}_{l}}/\mathbb{F}_{l})$
and let
![]() $[l^{-1}]$
be the inverse of the multiplication by
$[l^{-1}]$
be the inverse of the multiplication by
![]() $l$
map on
$l$
map on
![]() $E[p]$
. We have
$E[p]$
. We have
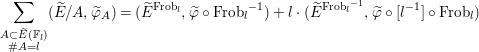 $$\begin{eqnarray}\mathop{\sum }_{\substack{ A\subset \widetilde{E}(\mathbb{\overline{}}\mathbb{F}_{l}) \\ \#A=l}}(\widetilde{E}/A,\widetilde{\unicode[STIX]{x1D711}}_{A})=(\widetilde{E}^{\text{Frob}_{l}},\widetilde{\unicode[STIX]{x1D711}}\circ {\text{Frob}_{l}}^{-1})+l\cdot (\widetilde{E}^{{\text{Frob}_{l}}^{-1}},\widetilde{\unicode[STIX]{x1D711}}\circ [l^{-1}]\circ \text{Frob}_{l})\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ A\subset \widetilde{E}(\mathbb{\overline{}}\mathbb{F}_{l}) \\ \#A=l}}(\widetilde{E}/A,\widetilde{\unicode[STIX]{x1D711}}_{A})=(\widetilde{E}^{\text{Frob}_{l}},\widetilde{\unicode[STIX]{x1D711}}\circ {\text{Frob}_{l}}^{-1})+l\cdot (\widetilde{E}^{{\text{Frob}_{l}}^{-1}},\widetilde{\unicode[STIX]{x1D711}}\circ [l^{-1}]\circ \text{Frob}_{l})\end{eqnarray}$$
as divisors of
![]() $X_{\text{ns}}(p)$
reduced modulo
$X_{\text{ns}}(p)$
reduced modulo
![]() $l$
(see, for example, the proofs in [Reference Diamond and ShurmanDS05, §8.7] regarding the modular curve
$l$
(see, for example, the proofs in [Reference Diamond and ShurmanDS05, §8.7] regarding the modular curve
![]() $X_{1}(N)$
). This implies the Eichler–Shimura relation:
$X_{1}(N)$
). This implies the Eichler–Shimura relation:
where both terms of the equation are homomorphisms on the divisor group of
![]() $X_{\text{ns}}(p)$
reduced modulo
$X_{\text{ns}}(p)$
reduced modulo
![]() $l$
. Note that the Eichler–Shimura relation acquires this form in this case because a nonsplit Cartan subgroup of
$l$
. Note that the Eichler–Shimura relation acquires this form in this case because a nonsplit Cartan subgroup of
![]() $\text{GL}_{2}(\mathbb{F}_{p})$
always contains the scalar matrix associated to
$\text{GL}_{2}(\mathbb{F}_{p})$
always contains the scalar matrix associated to
![]() $[l^{-1}]$
; hence, the pairs
$[l^{-1}]$
; hence, the pairs
![]() $(\widetilde{E}^{{\text{Frob}_{l}}^{-1}},\widetilde{\unicode[STIX]{x1D711}}\circ [l^{-1}]\circ \text{Frob}_{l})$
and
$(\widetilde{E}^{{\text{Frob}_{l}}^{-1}},\widetilde{\unicode[STIX]{x1D711}}\circ [l^{-1}]\circ \text{Frob}_{l})$
and
![]() $(\widetilde{E}^{{\text{Frob}_{l}}^{-1}},\widetilde{\unicode[STIX]{x1D711}}\circ \text{Frob}_{l})$
give the same point on
$(\widetilde{E}^{{\text{Frob}_{l}}^{-1}},\widetilde{\unicode[STIX]{x1D711}}\circ \text{Frob}_{l})$
give the same point on
![]() $X_{\text{ns}}(p)$
.
$X_{\text{ns}}(p)$
.
Since
![]() $T_{l}$
induces an endomorphism of
$T_{l}$
induces an endomorphism of
![]() $J_{\text{ns}}(p)$
, we will also write, with abuse of notation, the relation
$J_{\text{ns}}(p)$
, we will also write, with abuse of notation, the relation
![]() $T_{l}=\text{Frob}_{l}+l\cdot \text{Frob}_{l}^{-1}$
as endomorphisms of
$T_{l}=\text{Frob}_{l}+l\cdot \text{Frob}_{l}^{-1}$
as endomorphisms of
![]() $J_{\text{ns}}(p)$
reduced modulo
$J_{\text{ns}}(p)$
reduced modulo
![]() $l$
.
$l$
.
Lemma 4.1. Let
![]() $u$
be an automorphism of
$u$
be an automorphism of
![]() $X_{\text{ns}}(p)$
defined over the quadratic field
$X_{\text{ns}}(p)$
defined over the quadratic field
![]() $K(p)$
contained in the
$K(p)$
contained in the
![]() $p$
th cyclotomic field. Let
$p$
th cyclotomic field. Let
![]() $\unicode[STIX]{x1D70E}_{l}\in \text{Gal}(\overline{\mathbb{Q}}/\mathbb{Q})$
be a Frobenius element at
$\unicode[STIX]{x1D70E}_{l}\in \text{Gal}(\overline{\mathbb{Q}}/\mathbb{Q})$
be a Frobenius element at
![]() $l$
. Then if
$l$
. Then if
![]() $l\neq p$
we have
$l\neq p$
we have
as endomorphisms of
![]() $J_{\text{ns}}(p)$
, that is,
$J_{\text{ns}}(p)$
, that is,
where
![]() $\overline{u}$
is the
$\overline{u}$
is the
![]() $\text{Gal}(K(p)/\mathbb{Q})$
-conjugate of
$\text{Gal}(K(p)/\mathbb{Q})$
-conjugate of
![]() $u$
.
$u$
.
Proof. (Following [Reference Kenku and MomoseKM88, p. 64, Lemma 2.6]) Since
![]() $J_{\text{ns}}(p)$
has good reduction outside
$J_{\text{ns}}(p)$
has good reduction outside
![]() $p$
, the reduction modulo
$p$
, the reduction modulo
![]() $l$
map is injective on the endomorphism ring of
$l$
map is injective on the endomorphism ring of
![]() $J_{\text{ns}}(p)$
. Hence, the Lemma follows from the Eichler–Shimura relations and the fact that
$J_{\text{ns}}(p)$
. Hence, the Lemma follows from the Eichler–Shimura relations and the fact that
![]() $K(p)$
is a quadratic field.◻
$K(p)$
is a quadratic field.◻
Let
![]() $\unicode[STIX]{x1D701}_{p}$
be a primitive
$\unicode[STIX]{x1D701}_{p}$
be a primitive
![]() $p$
th root of unity. The modular curve
$p$
th root of unity. The modular curve
![]() $X_{\text{ns}}(p)$
has exactly
$X_{\text{ns}}(p)$
has exactly
![]() $p-1$
cusps, all defined over
$p-1$
cusps, all defined over
![]() $\mathbb{Q}(\unicode[STIX]{x1D701}_{p})$
and all conjugate under the action of
$\mathbb{Q}(\unicode[STIX]{x1D701}_{p})$
and all conjugate under the action of
![]() $\text{Gal}(\mathbb{Q}(\unicode[STIX]{x1D701}_{p})/\mathbb{Q})$
(see [Reference SerreSer89, p. 194–195]).
$\text{Gal}(\mathbb{Q}(\unicode[STIX]{x1D701}_{p})/\mathbb{Q})$
(see [Reference SerreSer89, p. 194–195]).
Proposition 4.2. Let
![]() $\unicode[STIX]{x1D70E}_{l}\in \text{Gal}(\overline{\mathbb{Q}}/\mathbb{Q})$
be a Frobenius element at
$\unicode[STIX]{x1D70E}_{l}\in \text{Gal}(\overline{\mathbb{Q}}/\mathbb{Q})$
be a Frobenius element at
![]() $l$
. Then we have
$l$
. Then we have
as divisors on
![]() $X_{\text{ns}}(p)$
, for every cusp
$X_{\text{ns}}(p)$
, for every cusp
![]() $C$
of
$C$
of
![]() $X_{\text{ns}}(p)$
.
$X_{\text{ns}}(p)$
.
Proof. The equality must hold modulo any prime ideal
![]() $\mathfrak{l}$
of
$\mathfrak{l}$
of
![]() $\mathbb{Q}(\unicode[STIX]{x1D701}_{p})$
over
$\mathbb{Q}(\unicode[STIX]{x1D701}_{p})$
over
![]() $l$
because of the Eichler–Shimura relations. Moreover, since
$l$
because of the Eichler–Shimura relations. Moreover, since
![]() $l\neq p$
, the modular curve
$l\neq p$
, the modular curve
![]() $X_{\text{ns}}(p)$
and its reduction modulo
$X_{\text{ns}}(p)$
and its reduction modulo
![]() $l$
have the same number of cusps. Therefore, reduction modulo
$l$
have the same number of cusps. Therefore, reduction modulo
![]() $\mathfrak{l}$
is injective on the set of cusps of
$\mathfrak{l}$
is injective on the set of cusps of
![]() $X_{\text{ns}}(p)$
, and the equality holds also over
$X_{\text{ns}}(p)$
, and the equality holds also over
![]() $\mathbb{Q}(\unicode[STIX]{x1D701}_{p})$
.◻
$\mathbb{Q}(\unicode[STIX]{x1D701}_{p})$
.◻
Lemma 4.3. Let
![]() $p\geqslant 11$
and let
$p\geqslant 11$
and let
![]() $u$
be an automorphism of
$u$
be an automorphism of
![]() $X_{\text{ns}}(p)$
defined over
$X_{\text{ns}}(p)$
defined over
![]() $K(p)$
. Let
$K(p)$
. Let
![]() $\unicode[STIX]{x1D70E}_{l}\in \text{Gal}(\overline{\mathbb{Q}}/\mathbb{Q})$
be a Frobenius element at
$\unicode[STIX]{x1D70E}_{l}\in \text{Gal}(\overline{\mathbb{Q}}/\mathbb{Q})$
be a Frobenius element at
![]() $l$
and let
$l$
and let
![]() $C$
be a cusp of
$C$
be a cusp of
![]() $X_{\text{ns}}(p)$
. If for every cusp
$X_{\text{ns}}(p)$
. If for every cusp
![]() $C^{\prime }$
of
$C^{\prime }$
of
![]() $X_{\text{ns}}(p)$
the divisor
$X_{\text{ns}}(p)$
the divisor
is the zero divisor, then
![]() $uC$
is a cusp, that is:
$uC$
is a cusp, that is:
If
![]() $u^{\unicode[STIX]{x1D70E}_{l}}T_{l}-T_{l}u$
is the zero operator on the group of divisors of
$u^{\unicode[STIX]{x1D70E}_{l}}T_{l}-T_{l}u$
is the zero operator on the group of divisors of
![]() $X_{\text{ns}}(p)$
of degree zero and supported in the cusps, then
$X_{\text{ns}}(p)$
of degree zero and supported in the cusps, then
![]() $u$
preserves the cusps.
$u$
preserves the cusps.
Proof. By the previous Proposition, for every cusp
![]() $C$
, we have
$C$
, we have
![]() $T_{l}C=C^{\unicode[STIX]{x1D70E}_{l}}+l\cdot C^{{\unicode[STIX]{x1D70E}_{l}}^{-1}}$
. Thus, we can choose a cusp
$T_{l}C=C^{\unicode[STIX]{x1D70E}_{l}}+l\cdot C^{{\unicode[STIX]{x1D70E}_{l}}^{-1}}$
. Thus, we can choose a cusp
![]() $C^{\prime }$
such that the supports of
$C^{\prime }$
such that the supports of
![]() $T_{l}C$
and
$T_{l}C$
and
![]() $T_{l}C^{\prime }$
are completely disjoint. For
$T_{l}C^{\prime }$
are completely disjoint. For
![]() $D_{l}$
to be the zero divisor, we must have
$D_{l}$
to be the zero divisor, we must have
Since we chose
![]() $C^{\prime }$
such that the supports of
$C^{\prime }$
such that the supports of
![]() $T_{l}C$
and
$T_{l}C$
and
![]() $T_{l}C^{\prime }$
are completely disjoint, we have
$T_{l}C^{\prime }$
are completely disjoint, we have
If
![]() $uC$
is not a cusp, it corresponds to an elliptic curve
$uC$
is not a cusp, it corresponds to an elliptic curve
![]() $E$
defined over
$E$
defined over
![]() $\mathbb{Q}(uC)\subset \mathbb{Q}(\unicode[STIX]{x1D701}_{p})$
.
$\mathbb{Q}(uC)\subset \mathbb{Q}(\unicode[STIX]{x1D701}_{p})$
.
Let
![]() $A$
and
$A$
and
![]() $B$
be two different cyclic groups of order
$B$
be two different cyclic groups of order
![]() $l$
in
$l$
in
![]() $E$
. Then the natural map
$E$
. Then the natural map
![]() $E/A\rightarrow E\rightarrow E/B$
has a cyclic kernel of order
$E/A\rightarrow E\rightarrow E/B$
has a cyclic kernel of order
![]() $l^{2}$
. Therefore, recalling the interpretation of the action of
$l^{2}$
. Therefore, recalling the interpretation of the action of
![]() $T_{l}$
on noncuspidal points, we have that equation (4.2) can hold only if
$T_{l}$
on noncuspidal points, we have that equation (4.2) can hold only if
![]() $E$
admits an endomorphism of degree
$E$
admits an endomorphism of degree
![]() $l^{2}$
with cyclic kernel. An elliptic curve without complex multiplication cannot have such an endomorphism, hence we obtain the Lemma as a consequence of the following Proposition.◻
$l^{2}$
with cyclic kernel. An elliptic curve without complex multiplication cannot have such an endomorphism, hence we obtain the Lemma as a consequence of the following Proposition.◻
Proposition 4.4. Let
![]() $p\geqslant 11$
and let
$p\geqslant 11$
and let
![]() $E$
be an elliptic curve over
$E$
be an elliptic curve over
![]() $\mathbb{C}$
with complex multiplication by an imaginary quadratic field
$\mathbb{C}$
with complex multiplication by an imaginary quadratic field
![]() $K$
. No point of
$K$
. No point of
![]() $X_{\text{ns}}(p)$
associated to
$X_{\text{ns}}(p)$
associated to
![]() $E$
is defined over
$E$
is defined over
![]() $\mathbb{Q}(\unicode[STIX]{x1D701}_{p})$
.
$\mathbb{Q}(\unicode[STIX]{x1D701}_{p})$
.
Proof. Let
![]() $P$
be a point of
$P$
be a point of
![]() $X_{\text{ns}}(p)$
associated to
$X_{\text{ns}}(p)$
associated to
![]() $E$
and defined over
$E$
and defined over
![]() $\mathbb{Q}(\unicode[STIX]{x1D701}_{p})$
. There are three cases:
$\mathbb{Q}(\unicode[STIX]{x1D701}_{p})$
. There are three cases:
![]() $p$
is inert,
$p$
is inert,
![]() $p$
splits or
$p$
splits or
![]() $p$
ramifies in
$p$
ramifies in
![]() $K$
.
$K$
.
If
![]() $p$
is inert in
$p$
is inert in
![]() $K$
, we consider the point
$K$
, we consider the point
![]() $Q$
of
$Q$
of
![]() $X_{\text{ns}}^{+}(p)$
given by
$X_{\text{ns}}^{+}(p)$
given by
![]() $\{P,wP\}$
. This point
$\{P,wP\}$
. This point
![]() $Q$
is defined over
$Q$
is defined over
![]() $L\subset \mathbb{Q}(\unicode[STIX]{x1D701}_{p})$
and lifts to points of
$L\subset \mathbb{Q}(\unicode[STIX]{x1D701}_{p})$
and lifts to points of
![]() $X_{\text{ns}}(p)$
defined over
$X_{\text{ns}}(p)$
defined over
![]() $LK$
(and no smaller fields) as explained in [Reference SerreSer89, p. 194–195]. But this is impossible since
$LK$
(and no smaller fields) as explained in [Reference SerreSer89, p. 194–195]. But this is impossible since
![]() $P,wP$
are defined over
$P,wP$
are defined over
![]() $\mathbb{Q}(\unicode[STIX]{x1D701}_{p})$
where
$\mathbb{Q}(\unicode[STIX]{x1D701}_{p})$
where
![]() $p$
ramifies completely.
$p$
ramifies completely.
If
![]() $p$
splits or ramifies in
$p$
splits or ramifies in
![]() $K$
, this means that the image of the
$K$
, this means that the image of the
![]() $\text{Gal}(\overline{\mathbb{Q}}/K(\unicode[STIX]{x1D701}_{p}))$
-representation modulo
$\text{Gal}(\overline{\mathbb{Q}}/K(\unicode[STIX]{x1D701}_{p}))$
-representation modulo
![]() $p$
attached to
$p$
attached to
![]() $E$
is contained in respectively a split Cartan or a Borel subgroup of
$E$
is contained in respectively a split Cartan or a Borel subgroup of
![]() $\text{GL}_{2}(\mathbb{F}_{p})$
(see loc. cit.). But since
$\text{GL}_{2}(\mathbb{F}_{p})$
(see loc. cit.). But since
![]() $P$
is defined over
$P$
is defined over
![]() $\mathbb{Q}(\unicode[STIX]{x1D701}_{p})$
, the image of such representation is also contained in a nonsplit Cartan subgroup. Therefore, in both cases, it is contained in the subgroup of scalar matrixes. Then, the properties of the Weil pairing imply that
$\mathbb{Q}(\unicode[STIX]{x1D701}_{p})$
, the image of such representation is also contained in a nonsplit Cartan subgroup. Therefore, in both cases, it is contained in the subgroup of scalar matrixes. Then, the properties of the Weil pairing imply that
![]() $\text{Gal}(\overline{\mathbb{Q}}/K(\unicode[STIX]{x1D701}_{p}))$
acts on the
$\text{Gal}(\overline{\mathbb{Q}}/K(\unicode[STIX]{x1D701}_{p}))$
acts on the
![]() $p$
-torsion of
$p$
-torsion of
![]() $E$
as a subgroup of
$E$
as a subgroup of
![]() $\{\pm 1\}$
. After choosing a suitable Weierstrass equation for
$\{\pm 1\}$
. After choosing a suitable Weierstrass equation for
![]() $E$
, this means that the
$E$
, this means that the
![]() $x$
-coordinates of the
$x$
-coordinates of the
![]() $p$
-torsion points of
$p$
-torsion points of
![]() $E$
are in
$E$
are in
![]() $K(\unicode[STIX]{x1D701}_{p})$
. The theory of complex multiplication tells us that the ray class field
$K(\unicode[STIX]{x1D701}_{p})$
. The theory of complex multiplication tells us that the ray class field
![]() $K_{(p)}$
modulo
$K_{(p)}$
modulo
![]() $(p)$
of
$(p)$
of
![]() $K$
is generated over
$K$
is generated over
![]() $K$
by the
$K$
by the
![]() $j$
-invariant of
$j$
-invariant of
![]() $E$
and by some rational function of the
$E$
and by some rational function of the
![]() $x$
-coordinates of the
$x$
-coordinates of the
![]() $p$
-torsion points of
$p$
-torsion points of
![]() $E$
[Reference SilvermanSil94, p. 135, Theorem 5.6]. Thus we obtain
$E$
[Reference SilvermanSil94, p. 135, Theorem 5.6]. Thus we obtain
![]() $K_{(p)}\subset K(\unicode[STIX]{x1D701}_{p})$
. It is always true that
$K_{(p)}\subset K(\unicode[STIX]{x1D701}_{p})$
. It is always true that
![]() $K(\unicode[STIX]{x1D701}_{p})\subset K_{(p)}$
, so the opposite inclusion holds if and only if
$K(\unicode[STIX]{x1D701}_{p})\subset K_{(p)}$
, so the opposite inclusion holds if and only if
![]() $[K_{(p)}:K]\leqslant [K(\unicode[STIX]{x1D701}_{p}):K]$
. We have
$[K_{(p)}:K]\leqslant [K(\unicode[STIX]{x1D701}_{p}):K]$
. We have
where
![]() $h_{K}$
is the class number of
$h_{K}$
is the class number of
![]() $K$
,
$K$
,
![]() $O_{K}$
is the ring of integers of
$O_{K}$
is the ring of integers of
![]() $K$
and
$K$
and
![]() $w_{K}$
is the number of roots of unity in
$w_{K}$
is the number of roots of unity in
![]() $K$
taken modulo
$K$
taken modulo
![]() $(p)$
. The group
$(p)$
. The group
![]() $(O_{K}/pO_{K})^{\ast }$
is isomorphic to
$(O_{K}/pO_{K})^{\ast }$
is isomorphic to
![]() $\mathbb{F}_{p^{2}}^{\ast }$
,
$\mathbb{F}_{p^{2}}^{\ast }$
,
![]() $\mathbb{F}_{p}^{\ast }\times \mathbb{F}_{p}^{\ast }$
or
$\mathbb{F}_{p}^{\ast }\times \mathbb{F}_{p}^{\ast }$
or
![]() $\mathbb{F}_{p}^{\ast }\times \langle a\rangle$
with
$\mathbb{F}_{p}^{\ast }\times \langle a\rangle$
with
![]() $a$
an element of order
$a$
an element of order
![]() $p$
. Thus to have the inequality
$p$
. Thus to have the inequality
![]() $[K_{(p)}:K]\leqslant [K(\unicode[STIX]{x1D701}_{p}):K]$
we must have
$[K_{(p)}:K]\leqslant [K(\unicode[STIX]{x1D701}_{p}):K]$
we must have
and hence
![]() $p\leqslant w_{K}+1$
. Since the roots of unity in an imaginary quadratic field are at most
$p\leqslant w_{K}+1$
. Since the roots of unity in an imaginary quadratic field are at most
![]() $6$
, we get
$6$
, we get
![]() $p\leqslant 7$
.◻
$p\leqslant 7$
.◻
Corollary 4.5. Let
![]() $p\geqslant 11$
and let
$p\geqslant 11$
and let
![]() $u$
be an automorphism of
$u$
be an automorphism of
![]() $X_{\text{ns}}(p)$
defined over
$X_{\text{ns}}(p)$
defined over
![]() $K(p)$
. If
$K(p)$
. If
![]() $u$
does not preserve the cusps, then there exists a nonconstant morphism
$u$
does not preserve the cusps, then there exists a nonconstant morphism
![]() $f$
from
$f$
from
![]() $X_{\text{ns}}(p)$
to
$X_{\text{ns}}(p)$
to
![]() $\mathbb{P}^{1}$
, defined over the field
$\mathbb{P}^{1}$
, defined over the field
![]() $\mathbb{Q}(\unicode[STIX]{x1D701}_{p})$
and with degree less or equal to
$\mathbb{Q}(\unicode[STIX]{x1D701}_{p})$
and with degree less or equal to
![]() $6$
, such that
$6$
, such that
![]() $f\circ w\neq f$
.
$f\circ w\neq f$
.
Proof. Since
![]() $u$
is defined over
$u$
is defined over
![]() $K(p)$
and does not preserve the cusps, we can apply Lemma 4.3 to obtain, for every prime
$K(p)$
and does not preserve the cusps, we can apply Lemma 4.3 to obtain, for every prime
![]() $l\neq p$
, a nonzero divisor
$l\neq p$
, a nonzero divisor
![]() $D_{l}$
on
$D_{l}$
on
![]() $X_{\text{ns}}(p)$
, of degree zero, defined over
$X_{\text{ns}}(p)$
, of degree zero, defined over
![]() $\mathbb{Q}(\unicode[STIX]{x1D701}_{p})$
, which is the difference of two effective divisors of degree at most
$\mathbb{Q}(\unicode[STIX]{x1D701}_{p})$
, which is the difference of two effective divisors of degree at most
![]() $2(l+1)$
. Moreover, we have
$2(l+1)$
. Moreover, we have
![]() $D_{l}=(u^{\unicode[STIX]{x1D70E}_{l}}T_{l}-T_{l}u)(C-C^{\prime })$
for two cusps
$D_{l}=(u^{\unicode[STIX]{x1D70E}_{l}}T_{l}-T_{l}u)(C-C^{\prime })$
for two cusps
![]() $C$
,
$C$
,
![]() $C^{\prime }$
of
$C^{\prime }$
of
![]() $X_{\text{ns}}(p)$
. Hence, by Lemma 4.1 we deduce that
$X_{\text{ns}}(p)$
. Hence, by Lemma 4.1 we deduce that
![]() $D_{l}$
must be zero in
$D_{l}$
must be zero in
![]() $J_{\text{ns}}(p)$
when
$J_{\text{ns}}(p)$
when
![]() $p\geqslant 11$
, which is to say that
$p\geqslant 11$
, which is to say that
![]() $D_{l}$
is a principal divisor. This gives us the existence of a nonconstant morphism
$D_{l}$
is a principal divisor. This gives us the existence of a nonconstant morphism
![]() $f$
from
$f$
from
![]() $X_{\text{ns}}(p)$
to
$X_{\text{ns}}(p)$
to
![]() $\mathbb{P}^{1}$
, defined over
$\mathbb{P}^{1}$
, defined over
![]() $\mathbb{Q}(\unicode[STIX]{x1D701}_{p})$
and with degree at most
$\mathbb{Q}(\unicode[STIX]{x1D701}_{p})$
and with degree at most
![]() $2(l+1)$
.
$2(l+1)$
.
Now we apply
![]() $w$
to
$w$
to
![]() $D_{l}$
. If
$D_{l}$
. If
![]() $D_{l}$
were invariant under the action of
$D_{l}$
were invariant under the action of
![]() $w$
, we would have
$w$
, we would have
where we used the computation in the proof of Lemma 4.3. In that proof, we also showed that the divisor
![]() $T_{l}uC$
is the sum of
$T_{l}uC$
is the sum of
![]() $l+1$
different points. Hence since
$l+1$
different points. Hence since
![]() $l\geqslant 2$
, to satisfy equation (4.3), the supports of
$l\geqslant 2$
, to satisfy equation (4.3), the supports of
![]() $T_{l}uC$
and
$T_{l}uC$
and
![]() $wT_{l}uC$
must have a nonempty intersection. This means that the support of
$wT_{l}uC$
must have a nonempty intersection. This means that the support of
![]() $T_{l}uC$
has either two different points exchanged by
$T_{l}uC$
has either two different points exchanged by
![]() $w$
or a point fixed by
$w$
or a point fixed by
![]() $w$
. The first case is impossible because the modular automorphism
$w$
. The first case is impossible because the modular automorphism
![]() $w$
preserves the isomorphism class over
$w$
preserves the isomorphism class over
![]() $\mathbb{C}$
of the elliptic curve associated to noncuspidal points, and we can apply the same argument at the end of the proof of Lemma 4.3. The second case is also impossible by the previous Proposition, because the points fixed by
$\mathbb{C}$
of the elliptic curve associated to noncuspidal points, and we can apply the same argument at the end of the proof of Lemma 4.3. The second case is also impossible by the previous Proposition, because the points fixed by
![]() $w$
are all associated with the elliptic curve with
$w$
are all associated with the elliptic curve with
![]() $j$
-invariant equal to
$j$
-invariant equal to
![]() $1728$
(see [Reference BaranBar10, Proposition 7.10]), which is an elliptic curve with complex multiplication.
$1728$
(see [Reference BaranBar10, Proposition 7.10]), which is an elliptic curve with complex multiplication.
Thus, for
![]() $l\geqslant 2$
, we have
$l\geqslant 2$
, we have
![]() $wD_{l}\neq D_{l}$
which implies
$wD_{l}\neq D_{l}$
which implies
![]() $f\circ w\neq f$
. The degree of
$f\circ w\neq f$
. The degree of
![]() $f$
is
$f$
is
![]() $2(l+1)$
, so by choosing
$2(l+1)$
, so by choosing
![]() $l=2$
we get the Corollary.◻
$l=2$
we get the Corollary.◻
5 Proof of main results
We first introduce a general Lemma.
Lemma 5.1. Let
![]() $X$
be a smooth projective curve over an algebraically closed field, and let
$X$
be a smooth projective curve over an algebraically closed field, and let
![]() $w$
be a nontrivial automorphism of
$w$
be a nontrivial automorphism of
![]() $X$
having
$X$
having
![]() $r$
fixed points. If there exists a morphism
$r$
fixed points. If there exists a morphism
![]() $f$
from
$f$
from
![]() $X$
to
$X$
to
![]() $\mathbb{P}^{1}$
of degree
$\mathbb{P}^{1}$
of degree
![]() $k$
such that
$k$
such that
![]() $f\circ w\neq f$
, then
$f\circ w\neq f$
, then
![]() $r\leqslant 2k$
.
$r\leqslant 2k$
.
Proof. [Reference Baker and HasegawaBH03, Lemma 3.5] Consider the rational function
![]() $g=f\circ w-f$
on
$g=f\circ w-f$
on
![]() $X$
. If
$X$
. If
![]() $g$
is constant, then the fixed points of
$g$
is constant, then the fixed points of
![]() $w$
must be poles of
$w$
must be poles of
![]() $f$
, implying
$f$
, implying
![]() $r\leqslant k$
. If
$r\leqslant k$
. If
![]() $g$
is not constant then the degree of
$g$
is not constant then the degree of
![]() $g$
is at most
$g$
is at most
![]() $2k-h$
, where
$2k-h$
, where
![]() $h$
is the number of poles that are also points fixed by
$h$
is the number of poles that are also points fixed by
![]() $w$
. On the other hand, the other
$w$
. On the other hand, the other
![]() $r-h$
points fixed by
$r-h$
points fixed by
![]() $w$
are zeros of
$w$
are zeros of
![]() $g$
, hence there are at most
$g$
, hence there are at most
![]() $\text{deg }g$
of them. So we have
$\text{deg }g$
of them. So we have
![]() $r-h\leqslant 2k-h$
which implies
$r-h\leqslant 2k-h$
which implies
![]() $r\leqslant 2k$
.◻
$r\leqslant 2k$
.◻
Let
![]() $p$
be an odd prime number.
$p$
be an odd prime number.
Theorem 5.2. If
![]() $p\geqslant 29$
, all the automorphisms of
$p\geqslant 29$
, all the automorphisms of
![]() $X_{\text{ns}}(p)$
preserve the cusps. If
$X_{\text{ns}}(p)$
preserve the cusps. If
![]() $p\equiv 1~\text{mod}~12$
and
$p\equiv 1~\text{mod}~12$
and
![]() $p\neq 13$
, the automorphism group of
$p\neq 13$
, the automorphism group of
![]() $X_{\text{ns}}(p)$
is generated by the modular involution
$X_{\text{ns}}(p)$
is generated by the modular involution
![]() $w$
.
$w$
.
Proof. Let
![]() $u$
be an automorphism of
$u$
be an automorphism of
![]() $X_{\text{ns}}(p)$
not preserving the cusps. By Corollary 2.6 we have that
$X_{\text{ns}}(p)$
not preserving the cusps. By Corollary 2.6 we have that
![]() $u$
is defined over
$u$
is defined over
![]() $K(p)$
. Then Corollary 4.5 tells us that there exists a nonconstant morphism from
$K(p)$
. Then Corollary 4.5 tells us that there exists a nonconstant morphism from
![]() $X_{\text{ns}}(p)$
to
$X_{\text{ns}}(p)$
to
![]() $\mathbb{P}^{1}$
, defined over
$\mathbb{P}^{1}$
, defined over
![]() $\mathbb{Q}(\unicode[STIX]{x1D701}_{p})$
, with degree less or equal to
$\mathbb{Q}(\unicode[STIX]{x1D701}_{p})$
, with degree less or equal to
![]() $6$
and such that
$6$
and such that
![]() $f\circ w\neq f$
. Then by the previous Lemma we have
$f\circ w\neq f$
. Then by the previous Lemma we have
Recall that the number of fixed points of
![]() $w$
is
$w$
is
![]() $\frac{p-1}{2}$
if
$\frac{p-1}{2}$
if
![]() $p\equiv 1~\text{mod}~4$
and it is
$p\equiv 1~\text{mod}~4$
and it is
![]() $\frac{p+1}{2}$
if
$\frac{p+1}{2}$
if
![]() $p\equiv 3~\text{mod}~4$
(see [Reference BaranBar10, Proposition 7.10]). This implies
$p\equiv 3~\text{mod}~4$
(see [Reference BaranBar10, Proposition 7.10]). This implies
![]() $p\leqslant 23$
and proves the first part of the Theorem. The second part is now a consequence of Corollary 3.3.◻
$p\leqslant 23$
and proves the first part of the Theorem. The second part is now a consequence of Corollary 3.3.◻
We remark that the first part of the Theorem above can also be achieved avoiding the discussion about the invariance of
![]() $f$
under the action of
$f$
under the action of
![]() $w$
, by using [Reference AbramovichAbr96, Theorem 0.1].
$w$
, by using [Reference AbramovichAbr96, Theorem 0.1].
Now we prove that Serre’s uniformity conjecture, implies the absence of rational exceptional automorphisms of
![]() $X_{\text{ns}}(p)$
for almost all
$X_{\text{ns}}(p)$
for almost all
![]() $p$
.
$p$
.
Theorem 5.3. Let
![]() $p\geqslant 29$
. If there exists an exceptional automorphism of
$p\geqslant 29$
. If there exists an exceptional automorphism of
![]() $X_{\text{ns}}(p)$
defined over
$X_{\text{ns}}(p)$
defined over
![]() $\mathbb{Q}$
, then
$\mathbb{Q}$
, then
![]() $X_{\text{ns}}^{+}(p)$
has a non-CM rational point.
$X_{\text{ns}}^{+}(p)$
has a non-CM rational point.
Proof. Let
![]() $u$
be an automorphism of
$u$
be an automorphism of
![]() $X_{\text{ns}}(p)$
defined over
$X_{\text{ns}}(p)$
defined over
![]() $\mathbb{Q}$
. By Corollary 2.9 we have that
$\mathbb{Q}$
. By Corollary 2.9 we have that
![]() $u$
commutes with
$u$
commutes with
![]() $w$
and it induces an automorphism of
$w$
and it induces an automorphism of
![]() $X_{\text{ns}}^{+}(p)$
defined over
$X_{\text{ns}}^{+}(p)$
defined over
![]() $\mathbb{Q}$
. Then it is enough to prove that
$\mathbb{Q}$
. Then it is enough to prove that
![]() $u$
preserves the rational CM points of
$u$
preserves the rational CM points of
![]() $X_{\text{ns}}^{+}(p)$
only if
$X_{\text{ns}}^{+}(p)$
only if
![]() $u$
is modular. Let
$u$
is modular. Let
![]() $\unicode[STIX]{x1D70B}:X_{\text{ns}}(p)\rightarrow X_{\text{ns}}^{+}(p)$
be the degree-2 modular morphism given by the inclusion of a nonsplit Cartan subgroup in its normalizer, and let
$\unicode[STIX]{x1D70B}:X_{\text{ns}}(p)\rightarrow X_{\text{ns}}^{+}(p)$
be the degree-2 modular morphism given by the inclusion of a nonsplit Cartan subgroup in its normalizer, and let
![]() $Q$
be a rational CM point of
$Q$
be a rational CM point of
![]() $X_{\text{ns}}^{+}(p)$
. Note that the two points in
$X_{\text{ns}}^{+}(p)$
. Note that the two points in
![]() $\unicode[STIX]{x1D70B}^{-1}(Q)$
are defined over the CM field of the elliptic curve associated to
$\unicode[STIX]{x1D70B}^{-1}(Q)$
are defined over the CM field of the elliptic curve associated to
![]() $Q$
(see [Reference SerreSer89, p. 194–195]). Hence
$Q$
(see [Reference SerreSer89, p. 194–195]). Hence
![]() $uQ$
cannot be a rational CM point different from
$uQ$
cannot be a rational CM point different from
![]() $Q$
because the two points in
$Q$
because the two points in
![]() $\unicode[STIX]{x1D70B}^{-1}(uQ)$
are defined over the same field as the points in
$\unicode[STIX]{x1D70B}^{-1}(uQ)$
are defined over the same field as the points in
![]() $\unicode[STIX]{x1D70B}^{-1}(Q)$
. Now we observe that the elliptic points of
$\unicode[STIX]{x1D70B}^{-1}(Q)$
. Now we observe that the elliptic points of
![]() $X_{\text{ns}}(p)$
are the inverse images by
$X_{\text{ns}}(p)$
are the inverse images by
![]() $\unicode[STIX]{x1D70B}$
of the rational CM points associated to the elliptic curves with
$\unicode[STIX]{x1D70B}$
of the rational CM points associated to the elliptic curves with
![]() $j$
-invariant equal to 0 or 1728 (see [Reference BaranBar10, Proposition 7.10]). Thus, if
$j$
-invariant equal to 0 or 1728 (see [Reference BaranBar10, Proposition 7.10]). Thus, if
![]() $u$
preserves the rational CM points of
$u$
preserves the rational CM points of
![]() $X_{\text{ns}}^{+}(p)$
, then it preserves the elliptic points of
$X_{\text{ns}}^{+}(p)$
, then it preserves the elliptic points of
![]() $X_{\text{ns}}(p)$
. Furthermore,
$X_{\text{ns}}(p)$
. Furthermore,
![]() $u$
also preserves the cusps by Theorem 5.2, hence it is modular by Corollary 3.3.◻
$u$
also preserves the cusps by Theorem 5.2, hence it is modular by Corollary 3.3.◻
Acknowledgments
The author would like to thank Prof. René Schoof and the Anonymous Referee for useful remarks on earlier versions of this paper.